Quando un gas viene compresso o si dilata, cioè quando viene modificata la sua pressione o il suo volume, sappiamo che anche l’energia cinetica delle particelle cambia; di conseguenza, cambia la loro velocità.
In un gas molto compresso le particelle si muoveranno più velocemente, mentre se il gas si espande la loro energia cinetica sarà minore.
Quando si parla vi velocità delle particelle, però, si può far riferimento a due tipi di velocità.
Possiamo considerare la velocità media delle particelle, espressa come la somma delle velocità delle singole particelle divisa per il numero di particelle:
$v_m = frac(v_1 + v_2 + … + v_n)(N) = 1/N * \sum_{i=1}^N v_i $
Oppure si può parlare di velocità quadratica media; questo tipo di velocità si ricava dalla definizione di energia cinetica media; come sappiamo, infatti, l’energia cinetica media si esprime come somma delle energie cinetiche delle singole particelle diviso il numero di particelle:
$K_m = frac(K_1 + K_2 + … + K_n)(N) = 1/N * \sum_{i=1}^N K_i $
Possiamo esprimere l’energia cinetica di ogni particelle come prodotto della sua massa per la sua velocità al quadrato diviso due (ipotizziamo che le particelle abbiano tutte la stesa massa):
$K_m = frac(K_1 + K_2 + … + K_n)(N) = $
$ = frac(1/2*m*(v_1)^2 + 1/2*m*(v_2)^2 + … + 1/2*m*(v_N)^2 )(N) $
Mettendo in evidenza i termini comuni, otteniamo l’espressione della media dei quadrati delle velocità delle particelle:
$1/2m * frac((v_1)^2 + (v_2)^2 + …. + (v_N)^2)(N) = 1/2 m * (v^2)_m $
La velocità quadratica media si ottiene come radice quadrata della media dei quadrati delle velocità:
$ 〈 v 〉 = sqrt(frac((v_1)^2 + (v_2)^2 + …. + (v_N)^2)(N)) = sqrt((v^2)_m) $
Generalmente, i due tipi di velocità sono diversi, ed in particolare, nel caso dei gas reali, si hanno valori maggiori della velocità quadratica media rispetto alla velocità media; nel caso ideale in cui tutte le velocità delle particelle sono uguali, si ottengono valori uguali delle due velocità.
La velocità quadratica media può essere espressa con una formula più sintetica, che permette di calcolare il suo valore senza conoscere i valori delle singole velocità delle particelle.
Possiamo ottenere questa espressione sostituendo il valore della velocità quadratica media nell’espressione dell’energia cinetica media:
$K_m = 1/2 m (〈 v 〉)^2 $
Come abbiamo già visto, l’energia cinetica media si esprime con il teorema di equipartizione dell’energia; consideriamo per questa scrittura tre gradi di libertà per le particelle, e quindi la seguente formula:
$K_m = 3/2 k_B * T $
Uguagliando le due espressioni possiamo ricavare la formula per la velocità quadratica media:
$ 1/2 m (〈 v 〉)^2 = 3/2 k_B * T to 〈 v 〉 = sqrt(frac(3k_B * T)(m)) $
La distribuzione di Maxwell
Nei gas reali le particelle che compongono il gas hanno tutte massa diversa e velocità diversa; in particolare, la loro velocità non è costante, e varia continuamente, anche in maniera non prevedibile.
E’ quindi impossibile stabilire, in un preciso momento, la velocità di una particella, così come non ha senso chiedersi quante particelle hanno in un determinato istante, una precisa velocità.
Tuttavia, può essere interessante determinare quante particelle di un gas hanno velocità compresa tra due valori distinti.
Nello studio della distribuzione statistica della velocità, Maxwell ebbe un ruolo fondamentale, in quanto egli fornì una formula che permette di relazionare il numero di particelle di un gas a temperatura T con una velocità, compresa tra v e v+∆v.
La formula che propose è la seguente:
$∆N = frac(4N)(sqrtπ) * (frac(m)(2k_B*T))^(3/2) * v^2 * e^(-frac(mv^2)(2k_B * T)) * ∆v $
In particolare, è possibile esprimere il rapporto ∆N/∆v in un piano cartesiano, ottenendo una particolare curva a campana, che prende il nome di curva di Maxwell, o distribuzione maxwelliana delle velocità.
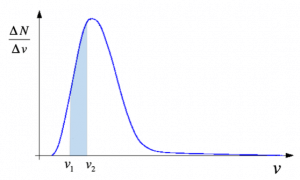
In particolare, l’area compresa tra la cura e l’asse delle ascisse, in un determinato intervallo, è pari al numero delle molecole che hanno velocità compresa tra i due valori di velocità che sono stati scelti come intervallo.
L’area dell’intera distribuzione, invece, fornisce il numero N di particelle totali che compongono il gas.
Dalla forma della curva si può notare che il numero di particelle con velocità particolarmente elevate, o particolarmente piccole, è esiguo, mentre la maggior parte di esse hanno valori di velocità che si avvicinano al valore medio.
Potrebbero interessarti
Appunti: L’energia interna
Appunti: La pressione dei gas perfetti dal punto di vista microscopico
