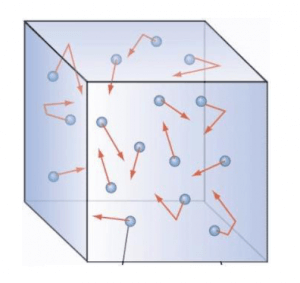
Come sappiamo, ogni gas contenuto in un recipiente esercita una pressione sulle pareti del recipiente che lo contiene. Interpretando la situazione da un punto di vista microscopico, come abbiamo già visto, notiamo che il gas è formato da un grandissimo numero di particelle che si muovono in maniera caotica e disordinata.
Queste particelle, nel loro moto, urtano inevitabilmente altre particelle e anche le pareti del recipiente. Tra i punti costituenti la teoria cinetico molecolare dei gas, abbiamo visto che tali urti sono urti elastici, e proprio essi sono responsabili della pressione che il gas esercita sul recipiente.
Infatti, ogni particella che urta la parete esercita una forza su di esso, e di conseguenza crea una pressione; sebbene la forza esercitata da ogni particella sia molto piccola, l’insieme delle numerosissime particelle, che si muovono molto rapidamente, crea una pressione totale notevole.
Anche in questo caso, come per l’energia cinetica, è stato possibile determinare la forza media che le particelle esercitano sulle pareti del recipiente, e di conseguenza anche la pressione media che ne deriva.
Poiché sono presenti degli urti, la quantità di moto si conserva; di conseguenza, la variazione della quantità di moto della parete è uguale alla variazione della quantità di moto della particella che la urta.
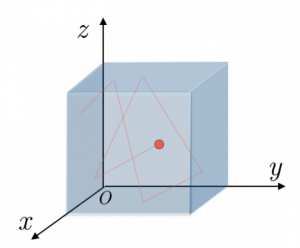
Il modo in cui le particelle urtano le pareti è molto variabile, e in particolare le particelle colpiscono le pareti in direzione obliqua; per questo, nella dimostrazione, per rendere i calcoli più semplici, si suppone che le particelle colpiscano tutte le pareti in modo perpendicolare, e con la stessa velocità. Inoltre, si suppone che il recipiente che contiene il gas sia un recipiente cubico, sul cui spigolo si trovi l’origine di un ipotetico sistema si riferimento in tre variabili:
Si utilizza, quindi, il teorema dell’impulso, considerando invece che la forza di una singola particella che agisce in un tempo molto breve, la forza media che viene esercitata in un intervallo di tempo ∆t.
Dal valore della forza media, conoscendo l’area di una singola parete del recipiente, e dividendo per questa il valore della forza, si ottiene un’espressione per la pressione media, che è riassunta nella seguente formula:
$ p = frac(2NK_m)(3V) $
dove N indica il numero di particelle, Km l’energia cinetica media e V il volume occupato dal gas.
Esercizio
Consideriamo un recipiente cubico all’interno del quale sono contenute $2,02 * 10^22$ molecole di un gas perfetto. Si sa che il gas esercita sulle pareti del recipiente una pressione di $5,50 * 10^4 Pa$, e che il volume che esso occupa è di $3,38 * 10^-3 m^3$. Calcoliamo la forza che il gas esercita sulle pareti del contenitore, e l’energia cinetica media delle particelle.
Dato che il recipiente all’interno del quale si trova il gas è di forma cubica, conoscendo il volume del gas possiamo determinare il valore del suo spigolo; infatti, il volume di un cubo si calcola come $l^3$, essendo l lo spigolo; abbiamo, quindi:
$V = l^3 to l = root(3)(V) $
Poiché ogni faccia del cubo è di forma quadrata, per determinare l’area di una faccia eleviamo al quadrato il suo lato:
$A = l^2 = (root(3)(V))^2 = V^(2/3) $
Sapendo che la pressione del gas è data dal rapporto della forza media delle molecole sulla superficie su cui è esercitata tale forza (in questo caso consideriamo una faccia), possiamo ricavare la formula inversa:
$ p = frac(F)(A) to F = p * A $
e quindi:
$ F = p * A = p * V^(2/3) $
Sostituendo i valori numerici otteniamo:
$F = 5,05 * 10^4 * (3,38 * 10^(-3))^(2/3) = 11,37 * 10^2 N = 1,14 * 10^3 N $
Determiniamo, ora, l’energia cinetica media delle particelle; per farlo, possiamo utilizzare la formula vista in precedenza, ricavando da essa la formula inversa per $K_m$:
$p = frac(2NK_m)(3V) to K_m = frac(3pV)(2N) $
Sostituiamo i valori numerici e determiniamo il valore di Km:
$ K_m = frac(3 * 5,05 * 10^4 * 3,38 * 10^(-3))(2 * 2,02 * 10^22) = 12,68 * 10^(-21) J = 1,27 * 10^(-20) J $
Potrebbero interessarti
Appunti: Il moto browniano
Appunti: La velocità quadratica media e la distribuzione di Maxwell
