La convezione
La convezione, come abbiamo già accennato, riguarda il trasferimento di calore attraverso sostanze liquide.
A differenza della conduzione, che prevede lo scambio di calore senza trasferimento di materia, la convezione è un trasferimento di energia che avviene proprio con trasporto di materia.
Lo spostamento di materia dipende dalla presenza delle correnti che vi sono all’interno dei fluidi.
Possiamo riscontrare questo comportamento dei fluidi in moltissime situazioni; ad esempio nel caso di una pentola d’ acqua sui fornelli, o del funzionamento dei termosifoni che permettono di riscaldare un ambiente.
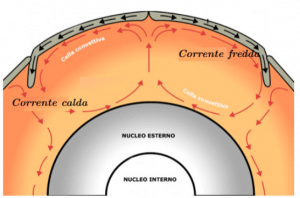
Anche all’interno della crosta terrestre, per esempio, sono presenti delle correnti convettive; queste permettono lo spostamento del magma, e sono responsabili della formazione dei rilievi montuosi.
Il magma più caldo, che si trova vicino al nucleo terrestre, tende a salire verso la superficie (corrente convettiva ascendente), e mano a mano che questo accade, il magma che sale diventa più freddo, e spinge sotto quello che si trova in superficie, formando così una corrente convettiva discendente.
L’irraggiamento
Un importante trasferimento di calore, indispensabile per la nostra sopravvivenza, è quello che riguarda il calore proveniente dal Sole. Come sappiamo, nello spazio vi è una regione di vuoto, cioè assenza di materia; ciò significa, quindi, che è possibile un trasferimento di calore anche in assenza di questa.
Questo particolare tipo di trasferimento è noto come irraggiamento.
L’irraggiamento è dovuto alla presenza di radiazioni elettromagnetiche che vengono emesse dai corpi. Qualunque corpo emette radiazioni, ma queste onde viaggiano su frequenze tali che gli esseri umano non sono in grado di percepire.
Tuttavia, quando le radiazioni provenienti da una sorgente colpiscono un corpo e possono essere assorbite da esso; di conseguenza, possono aumentare la sua temperatura, in quanto le radiazioni elettromagnetiche trasportano energia.
Come abbiamo detto in precedenza, qualunque corpo è in grado di emettere energia sotto forma di radiazioni elettromagnetiche, e l’intensità di queste radiazioni dipende da diversi fattori; tra questi la temperatura del corpo e la sua grandezza.
E’ possibile determinare la quantità di energia emessa da un corpo grazie ad una legge sperimentale nota come legge di Stefan-Boltzmann:
$frac(∆E)(∆t) = e * z * S * T^4 $
nella quale ∆E indica la quantità di energia che viene emessa dal corpo, e ∆t l’unità di tempo in cui è avvenuto tale trasferimento.
Inoltre, e rappresenta un numero compreso tra 0 e 1, e dipende dalle caratteristiche superficiali del corpo; S indica l’area della superficie interessata, e T è la temperatura del corpo espressa in K. z è una costante, definita costante di Stefan-Boltzmann, che vale:
$z = 5,67 * 10^(-8) * frac(J)(s * m^2 * K^4) $
Grazie a questa equazione è possibile determinare l’energia emessa da un corpo anche se non possiamo esaminarlo da vicino.
Infatti, grazie a questa legge, per esempio, possiamo conoscere l’intensità della radiazione emessa da una stella; per farlo dobbiamo conoscere la sua temperatura, da distanza dalla Terra, e il valore della sua superficie.
Esercizio
Consideriamo una sfera metallica di raggio 4,0 cm, che viene riscaldata fino alla temperatura di 260 k. Sappiamo che il valore di e, in questo caso, e di 0,30; quanta energia viene emessa dalla sfera in un minuto?
Per determinare l’energia emessa dalla sfera, possiamo ricavare tale valore dalla formula vista precedentemente; moltiplicando entrambi i membri dell’equazione per ∆t:
$frac(∆E)(∆t) = e * z * S * T^4 to ∆E = e * z * S * T^4 * ∆t$
Conosciamo i valori di e e di z, e sappiamo che il tempo da considerare è di 1 minuto, e quindi di 60 secondi; abbiamo il valore della temperatura e possiamo ricavare il valore della superficie del corpo interessata dall’irraggiamento.
Sapendo che il corpo in questione è una sfera, di cui conosciamo il raggio e ricordando che la superficie sferica si ottiene con la seguente espressione:
$S = 4πr^2 $
la formula precedente diventa:
$∆E = e * z * 4πr^2 * T^4 * ∆t$
Sostituiamo ora i valori numerici e determiniamo la quantità di energia che viene emessa:
$∆E = 0,3 * 5,67 * 10^(-8) * 4π (0,04)^2 * (260)^4 * 60 = 93,7 J $
Potrebbero interessarti
Appunti: Il trasferimento di calore mediante conduzione
