 |
Albergo da ampliare I gestori di un albergo prevedono di ampliare l’albergo stesso fino a raggiungere un numero di 200 stanze. Ogni stanza sarà dotata di un apparecchio telefonico. Al fine di spendere il meno possibile è stato deciso di utilizzare un centralino che serva i 200 apparecchi telefonici e abbia n linee in uscita. L’obiettivo dei gestori è di installare il minor numero possibile di linee in uscita, garantendo però ai propri clienti di trovare una linea libera almeno al 99% dei tentativi di chiamata. |
| soluzione |
soluzione Servono almeno 7 linee
Il simulatore del sistema di Pablo (Paolo Furlani)
I risultati delle simulazioni con 6 linee [125 kB] e 7 linee [131 kB] .
La soluzione di Luca Barletta:
Cerchiamo di inquadrare correttamente il problema: c'è una popolazione finita (i clienti dell'albergo) che si contende un mezzo condiviso (le linee in uscita); lo scopo è quello di mascherare al 99% la presenza del mezzo condiviso agli utenti.
Ogni utente genera un tasso di chiamate al giorno (3 ch/giorno -> 2,083*10^(-3) ch/min) e il centralino è in grado di smaltire un altro tasso di chiamate al minuto (5 min/ch -> 0,2 ch/min). Possiamo asserire che in media ogni utente offre un traffico:
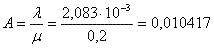
Questo sistema lo possiamo riassumere in una rappresentazione a stati: ogni stato del sistema è caratterizzato dal numero di utenti che stanno usufruendo del servizio; si può solo passare da uno stato i al successivo i +1, evento in cui un utente inizia una chiamata (per ipotesi non arrivano più chiamate contemporaneamente), e si può passare dallo stato i al precedente i -1, evento in cui un utente termina una chiamata.
Logicamente avremo N +1 stati (da 0 a N , con N incognita del problema).
Bisonga determinare con quale tasso si passa da uno stato al successivo e da uno stato al precedente:
- Quando passiamo da uno stato al successivo, significa che un utente ha appena iniziato una chiamata; indicando con S la popolazione totale e con i lo stato corrente, la probabilità di passare dallo stato i a quello i +1 è:
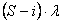
- Quando passiamo da uno stato al precedente, significa che un utente ha appena terminato una chiamata; indicando con i lo stato corrente, la probabilità che il centralino liberi una linea è:
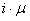
Ecco uno schema esplicativo del diagramma a stati del sistema:
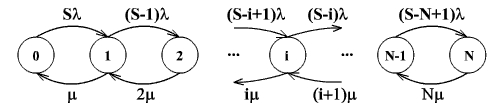
Dobbiamo trovare la probabilità di trovarci in un dato stato del sistema, ovvero la probabilità che ci siano i utenti in linea.
Cominciamo col scrivere l'equazione d'equilibrio per gli stati 0 ed 1; indicando con pi_greco(i ) la probabilità di trovarsi nello stato i -esimo si ricava la seguente:
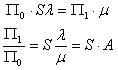
scriviamo la stessa equazione per gli stati 1 e 2:
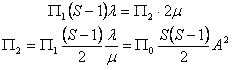
iteriamo il procedimento fino allo stato i -esimo:
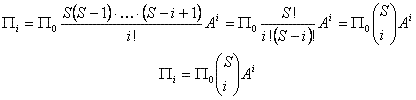
La somma di tutte le probabilità deve essere unitaria:
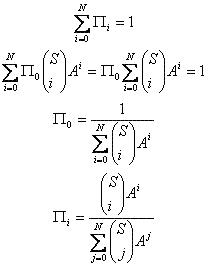
Ora è possibile calcolare la probabilità di perdita.
Non bisogna commettere l'errore di confondere la probabilità di perdita di una chiamata con la probabilità di blocco del sistema. Infatti il sistema si dice in blocco una volta raggiunto lo stato i -esimo, mentre si ha la perdita di una chiamata quando, raggiunto lo stato di blocco del sistema, un nuovo utente tenta di chiamare.
Pertanto si può impostare la seguente relazione:
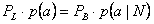
dove al primo membro troviamo il prodotto tra la probabilità di perdita e la probabilità istantanea che un utente chiami, al secondo membro troviamo il prodotto tra la probabilità di blocco e la probabilità istantanea che un utente chiami sapendo che ci sono già N utenti in linea (lo stato è in blocco).
Le probabilità istantanee di chiamata sono:
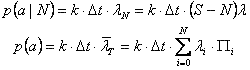
A noi interessa la probabilità di perdita:
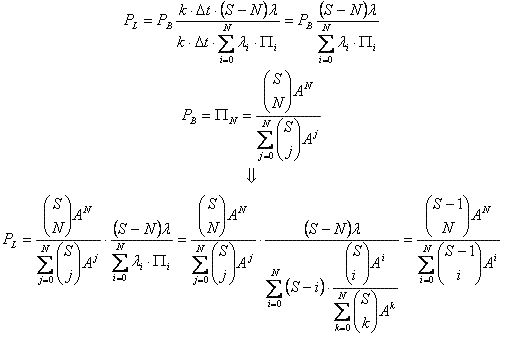
Pertanto dovremo risolvere la seguente disequazione in N , con N numero intero positivo:
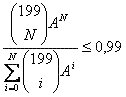
Per la risoluzione utilizzo un foglio di calcolo [101 kB] Excel, trovando N =7.
