Da un foglio di cartone quadrato di 100 cm di lato, ricavare la scatola di volume massimo. La scatola deve essere ottenuta ritagliando dal foglio di cartone le sei facce e incollandole con il nastro adesivo.
Un esempio di questo tipo viene spesso utilizzato nei libri di analisi per applicare la teoria dei massimi e minimi vincolati per le funzioni di due variabili. In realtà, almeno in questo caso i vincoli sono difficili da determinare. Si richiedeva un’ulteriore analisi del problema.
Dallo studio della funzione V=xyz con 2xy+2xz+2yz =A si ottiene la soluzione x=y=z=SQR(A/6), dove A è la superficie del cartone. La scatola di volume massimo sembrerebbe un cubo di lato 40,82 cm e volume 68041,38cm^3. A questo punto si pone il problema di verificare se è possibile ritagliare i sei quadrati di lato 40,82. Infatti la condizione 2xy+2xz+2yz=A riguarda soltanto la superficie del cartone di partenza e non la sua forma.
La difficoltà del quesito doveva essere questa. Sono stato però superficiale nella scelta delle misure del cartone di partenza. Chi ha fatto tutti conti è caduto nella trappola che gli avevo ‘amichevolmente(?)’ teso, chi ha avuto un approccio più intuitivo è stato fortunato nell’imbattersi nella soluzione.
La soluzione ottimale si ottiene cercando di utilizzare tutta la superficie disponibile e allo stesso tempo di ottenere quante più facce quadrate possibili. Una dimostrazione rigorosa non ce l’ho e nessuno l’ha inviata.
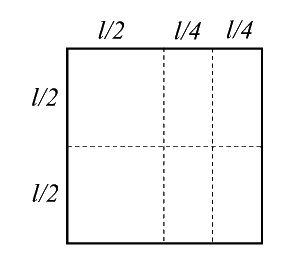
Tra le soluzioni più complete quella di Vinciprova Francesco (.pdf) .

penso quadrati di 33 cm di lato