Torre di Hanoi

Figura 1. La torre di Hanoi

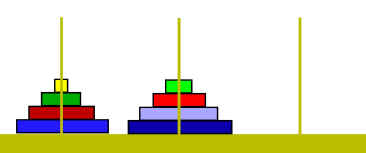
Figura 2. Partenza

Figura 3. Arrivo

La torre di Hanoi

La Torre di Hanoi è un notissimo gioco inventato dal matematico francese Lucas verso la fine dell'800. Si tratta di spostare una torre di 8 dischi di dimensioni variabili da un piolo ad un altro, avendone a disposizione un terzo. Le regole sono poche e semplici: si può spostare un disco per volta e mai un disco più largo deve poggiare su uno più piccolo.
Il bello di questo gioco, tutt'altro che banale, è che può essere risolto brillantemente in modo iterativo; in particolare, l'aritmetica binaria dà un senso generale a tutte le mosse. Per chi non abbia mai provato il gioco, con un po' di buona volontà non gli sarà difficile dimostrare che il numero minimo di mosse con cui può essere risolto è 255. In generale per N dischi il numero di mosse richiesto è 2^N – 1. 
Una leggenda narra di un tempio a Benares, in India, dove un prete muove un disco ogni secondo della sua torre di 64 dischi dorati… pare che sia ancora lì.

Ma veniamo al nostro gioco, che è una variante del classico. Con le regole della Torre di Hanoi, vi chiedo: qual è il numero minimo di mosse con cui si può passare dalla posizione iniziale, che potremmo definire "scalata", mostrata in figura 2, a quella finale (figura 3) con tutta la torre costruita sul piolo centrale?"