Enunciato del teorema
Nell’enunciato del teorema di Carnot si fa riferimento ad un particolare tipo di macchina termica, che viene definito reversibile.
Una macchina termica reversibile è uno strumento che permette di compiere una trasformazione ciclica reversibile.
E’ importante sottolineare che non esistono macchine termiche capaci di produrre lavoro utile sfruttando una sola sorgente di calore. Come sappiamo, infatti, una parte energia che viene prodotta non si trasforma in lavoro, ma viene convogliata ad una seconda sorgente (più fredda) per permettere al ciclo di ricominciare.
Una macchina termica reversibile quindi, deve funzionare con due sorgenti di calore, che si trovano a temperature differenti: chiamiamo con T1 la sorgente che si trova a temperatura minore (definita fredda) e con T2 quella a temperatura maggiore (calda).
Il teorema di Carnot afferma che se si considerano due macchine termiche, di cui una reversibile e l’altra no, il rendimento della macchina termica è sempre maggiore o uguale del rendimento dell’altra; i due rendimenti possono essere uguali solo nel caso in cui entrambe le macchine siano reversibili.
$η_R ≥ η $
In particolare, dal teorema di Carnot segue un importante corollario che afferma che tutte le macchine reversibili che lavorano tra le stesse temperature e utilizzano le stesse sorgenti di calore hanno lo stesso rendimento, indipendentemente dalle loro caratteristiche di funzionamento. Inoltre, il rendimento della macchina di Carnot dipende esclusivamente dalle temperature tra le quali esse lavora, e non dal particolare fluido o gas che essa impiega.
Per questo, è particolarmente utile studiare il funzionamento delle macchine termiche il cui funzionamento si basa sull’utilizzo di un gas perfetto.
In questo caso, infatti, è possibile dimostrare che sussiste la seguente relazione:
$frac(|Q_2|)(|Q_1|) = frac(T_2)(T_1)$
dove si indicano con $T_1$ e $T_2$ le temperature delle sorgenti di calore, e con $Q_1$ e $Q_2$ i calori che vengono scambiati dal sistema con le due sorgenti di calore.
Il rendimento di una macchina di Carnot, quindi, può essere espresso nel seguente modo:
$η_c = 1 – frac(|Q_2|)(|Q_1|) = 1 – frac(T_2)(T_1)$
Questa relazione, individuata per un gas perfetto, ha validità per macchine termiche reversibili che lavorano con qualsiasi tipo di fluido, in quanto, come abbiamo detto in precedenza, il rendimento di tali macchine dipende solo dalle temperature tra le quali esse lavorano.
Il ciclo di Carnot
Una macchina di Carnot esegue una particolare trasformazione ciclica, che viene definita, appunto, ciclo di Carnot.
Questa trasformazione è costituita da quattro fasi che si susseguono, che sono: un’espansione temperatura costante, un’espansione adiabatica, una compressione a temperatura costante e infine un’altra compressione adiabatica.
Consideriamo il caso di un gas contenuto all’interno di un cilindro dotato di pistone mobile.
- Nella seconda trasformazione, il gas continua ad espandersi, ma questa volta il recipiente viene isolato; in questo modo non vi sono scambi di calore con l’esterno.
- Durante la prima espansione, che può avvenire grazie ad una diminuzione della pressione esterna sul pistone, il gas si espande; la sorgente di calore mantiene costante la sua temperatura. In questo caso, il gas compie un lavoro positivo; per mantenere la sua temperatura costante esso assorbe calore dalla sorgente calda (Q2).
- Nella terza trasformazione il gas viene compresso grazie ad un aumento della pressione esterna sul pistone; la sua temperatura viene mantenuta costante dalla sorgente. In questo caso, quindi, il gas compie un lavoro negativo; per mantenere costante la sua temperatura, quindi, cede calore alla sorgente fredda (Q1).
- L’ultima trasformazione è una compressione adiabatica; il gas continua ad essere compresso, ma questa volta il sistema è isolato termicamente, e non può scambiare calore con l’esterno; la sua temperatura subirà, quindi, un aumento, fino a tornare a quella che si aveva all’inizio delle trasformazioni.
E’ possibile rappresentare in un piano pressione-volume la curva che descrive un cilc di Carnot:
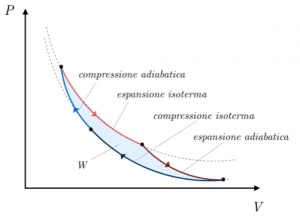
Alla fine del ciclo la macchina di Carnot compie un lavoro pari a:
$W = Q_2 – |Q_1| $
che si ottiene calcolando l’area della parte di piano racchiusa dal grafico della trasformazione ciclica.
Potrebbero interessarti
Appunti: Trasformazioni termodinamiche
Appunti: Trasformazioni dei gas e Leggi di Gay-Lussac
Appunti: La legge di Boyle e i gas perfetti
