Le equazioni di terzo grado nel mondo arabo e un loro possibile utilizzo didattico

Quello delle equazioni di terzo grado, è un tema quasi sempre omesso nelle scuole superiori, perché i professori, stretti con i tempi, preferiscono trattare argomenti più classici, come da programma ministeriale.

Tuttavia ritengo che sia utile spendere tre o quattro lezioni alla trattazione di questo tema, per i motivi che avanzerò nel seguito di questa relazione. Poiché per le equazioni di terzo grado esiste una formula risolutiva (nota come “formula cardanica”¹), in tutto e per tutto analoga alla formula risolutiva delle equazioni di secondo grado che si studia al secondo anno di scuola superiore, le equazioni cubiche richiedono gli stessi prerequisiti richiesti dalle equazioni quadratiche (ossia una certa abilità con il calcolo algebrico). Tuttavia, trattare le equazioni di terzo grado in questo modo, cioè mostrando la formula cardanica e applicarla meccanicamente, è, sebbene culturalmente interessante, didatticamente poco prolifero, in quanto si tratta solamente di un esercizio di calcolo algebrico. Tuttavia, come vedremo, c’è un profondo legame tra le soluzioni (reali) delle equazioni di terzo grado e i punti di intersezione tra due coniche; legame che era stato mostrato in qualche caso particolare da alcuni matematici antichi (Menecmo, Archimede, Pappo ed altri) e che venne trattato sistematicamente dal matematico arabo Al-Khayyam. Per cui, qualora si vogliano trattare le equazioni cubiche, credo che sia opportuno farlo in una classe terza di scuola superiore, solamente dopo aver trattato le sezioni coniche, con le modalità che vedremo in questa relazione. Una tale trattazione porta, secondo me, beneficio ad entrambi gli argomenti: da una parte si consolida l’apprendimento delle sezioni coniche, in quanto se ne vede una applicazione esterna all’ambiente nel quale vengono immerse didatticamente (cioè la geometria analitica) che sottolinea fortemente il legame tra algebra e geometria. Dall’altra parte, si mostra come le soluzioni di equazioni possono essere “visualizzate” geometricamente, cioè come la forma delle curve possa dare informazioni sulla natura puramente algebrica delle equazioni, cioè si introduce l’idea di “risolvere graficamente” un’equazione. Infine, alla luce di questo, un altro prerequisito fondamentale che si richiede è quello di saper utilizzare software di disegno geometrico, per tracciare le suddette curve e visualizzarne i punti di intersezione.

Lezione 1: notizie storiche e introduzione all’argomento²

Soffiava una brezza tiepida quel giorno di primavera. Il mare era calmo, solcato dall’immensa flotta di navi dalle vele rosse, disposte tutte intorno alle mura della città, che finalmente, dopo due lunghi anni di assedio, fu espugnata. Alla calma del mare si contrapponeva la paura dei cittadini, intenti a scappare disordinatamente a destra e a manca per evitare la furia dei soldati, di quell’esercito dai rossi vessilli che mai nessuno era riuscito a fermare. L’esercito avanzava come una grande e lenta tartaruga, i soldati avevano le corazze dorate come il sole e gli scudi rossi come il sangue e non avevano pietà, uccidendo chiunque gli fosse dinanzi: compresi anziani, donne e bambini. I superstiti fuggirono verso la spiaggia, fuori dalle mura della città, ma i soldati li inseguirono, li raggiunsero e gli ordinarono la resa. Nella confusione generale, un soldato, impugnata la spada, impartì un colpo mortale ad un vecchietto, il quale era serenamente intento a disegnare figure sulla sabbia, quasi non curante di tutto quello che stava accadendo. Il vecchietto, prima di esalare l’ultimo respiro, pregò il soldato di non rovinare il suo disegno. Il nome del soldato rimarrà per sempre ignoto. Il nome del vecchietto rimarrà per sempre nella storia: Archimede.³ Ho riportato questo racconto (riferito da Plutarco⁴), per due motivi: anzitutto perché è un bellissimo racconto, coinvolgente, e quindi attiva nel nostro cervello aree che coinvolgono le emozioni⁵ (tecnicamente questo meccanismo viene detto “storytelling”⁶) e ci fa vincere la timidezza e la noia che potremmo avere riguardo gli argomenti che si tratteranno in seguito. Il secondo motivo è perché ho pensato di iniziare la trattazione delle equazioni di terzo grado partendo da tre problemi aperti della matematica ellenistica: il lemma di Archimede, la duplicazione del cubo e la trisezione dell’angolo.

Vedremo in seguito di cosa trattano e come possono essere affrontati questi problemi. Voglio solo ricordare che per i matematici ellenistici risolvere un problema significava trovare una serie di passaggi effettuabili con riga e compasso che permettessero di disegnare l’oggetto cercato. Allora i tre problemi citati sopra erano considerati aperti in quanto nessuno aveva trovato il modo di costruire la soluzione con riga e compasso. Come spesso avviene nella matematica, uno stesso problema è impossibile da risolvere con degli strumenti, ma cambiando strumenti si riesce a risolvere. Ora, i tre problemi citati sono impossibili da risolvere con riga e compasso, tuttavia si possono cercare nuovi strumenti con i quali è possibile risolverli. I matematici arabi successivi ad Al-Khwarizmi (780 circa – 850 circa) avevano a disposizione un nuovo strumento matematico: il calcolo algebrico. Fin da subito, si cominciò ad affrontare i problemi geometrici con le nuove tecniche algebriche, cioè ponendo l’oggetto incognito uguale a “$x$” (diremmo noi oggi) e poi tradurre la figura geometrica in un’equazione per “$x$”, risolvere l’equazione ed interpretare geometricamente la soluzione. Sfortunatamente, nel caso dei tre problemi citati sopra, questo procedimento porta ad equazioni di terzo grado, che Al-Khwarizmi non aveva trattato nel suo libro; la loro trattazione sarà dovuta ad Al-Khayyam (1048 – 1131).⁷ Ma prima di vedere i risultati di Al-Khayyam, vediamo in cosa consistono i tre problemi citati, come sono stati affrontati geometricamente dai matematici antichi e, algebricamente, a quali equazioni conducono.

Lezione 2: i problemi aperti

Vediamo ora, più in dettaglio, in cosa consistono i tre problemi citati sopra e quali sono state le soluzioni proposte dai matematici antichi. Vedremo che in tutti e tre i casi la soluzione è stata trovata intersecando due coniche e inoltre tutti e tre i casi, trascritti algebricamente, conducono ad equazioni di terzo grado. Per cui lo scopo di questa lezione è far vedere come si possono utilizzare due coniche per trovare la soluzioni di particolari equazioni di terzo grado (nella prossima lezione si generalizzerà il concetto ad una generica equazione di terzo grado.)

1) Il lemma di Archimede⁸

Il primo problema che affrontiamo è il lemma di Archimede: data una sfera di diametro $AB$, trovare un punto $X$ sul diametro $AB$ tale che il piano passante per $X$  e perpendicolare ad $AB$ divida la sfera in due calotte i cui volumi siano in un dato rapporto $k$. Per risolvere il problema, Archimede prolunga il diametro $AB$ di un segmento $BZ$ uguale al raggio della sfera: $BZ = BO = 1/2 AB$ . Dopodiché fissa su $BZ$ un punto $T$ tale che il rapporto dato $k$ sia uguale al rapporto $TZ:TB$ . In queste condizioni Archimede dimostra che il punto $X$ cercato soddisfa la proporzione : $AX^2:AB^2=TZ:XZ$ e afferma, infine, che il punto $X$ si può trovare⁹.

Purtroppo il testo di Archimede non ci è giunto interamente, in particolare manca la costruzione del punto $X$.

Algebricamente questo problema fu affrontato dal matematico arabo Al-Mahani (attivo intorno all’850, quindi di poco successivo ad Al-Khwarizmi) il quale, introducendo una unità di misura per la lunghezza dei segmenti, può associare ad ogni segmento un numero (che ne indica la lunghezza) e, ponendo un’incognita uguale a “$x$”, può trovare un’equazione. Poniamo: \[AB=2r \] \[BZ = r \] \[TZ = s \,\, \mbox{(dipende dal rapporto dato } k)\]  \[ AX = x \mbox{(il segmento incognito)}\] Da cui: \( XZ = BZ + XB = r + 2r -x = 3r -x \) . In questo modo la proporzione \( AX^2:AB^2 = TZ:XZ\) diventa: \( x^2:(2r)^2 = s : (3r-x)\); che conduce alla seguente equazione di terzo grado: \( x^3+4r^2s=3rx^2 \), che Al-Mahani non sa risolvere algebricamente. Tuttavia il matematico bizantino Eutocio di Ascalona (attivo intorno all’anno 500 d.C.), nei suoi commenti all’opera di Archimede, afferma di aver ritrovato in un vecchio libro la costruzione del punto $X$, probabilmente scritta da Archimede stesso. In questo testo il punto $X$ è individuato mediante l’intersezione di due coniche: una parabola ed un’iperbole equilatera. Vediamo più in dettaglio i passaggi. Innanzitutto si costruisce la parabola con vertice in $A$, asse perpendicolare ad $AZ$e lato retto pari ai $2/3$ di AB (in rosso nella figura).¹⁰ Dopodiché, fissato il punto $T$ su $BZ$, si traccia l’iperbole equilatera passante per $S$, tale che  $AS = TZ = ZL $ e con asintoti le rette perpendicolari supporto dei segmenti $ZA$ e $ZL$ (in blu nella figura). Questa iperbole dipende dal punto $T$, e quindi dal dato rapporto $k$. Detto $P$ il punto di intersezione delle due coniche, $AX$ risolve il problema, dove $X$  è la proiezione di $P$ su $AB$. Infatti, poiché $P$ appartiene alla parabola, si ha che: \(AX^2=\frac{2}{3}AB \cdot PX \rightarrow \frac{AX^2}{AB^2} = \frac{2/3PX}{AB}=\frac{2PX}{3AB}\). Inoltre, dato che $P$ appartiene all’iperbole: \(  PX \cdot XZ = AZ \cdot TZ \rightarrow \frac{TZ}{XZ} = \frac{PX}{3/2AB} = \frac{2PX}{3AB}\).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Per cui, uguagliando le due espressioni: \( \frac{AX^2}{AB^2} = \frac{TZ}{XZ}\); che era ciò che volevamo costruire.¹¹

2) Trisezione dell’angolo

Un altro famoso problema aperto della matematica ellenistica è la trisezione dell’angolo. Questo problema consiste nel tracciare la trisettrice dell’angolo, cioè quella semiretta che ha origine nel vertice dell’angolo e lo divide in due parti di cui una è il doppio dell’altra (cosicché la parte minore è proprio la terza parte dell’angolo dato). 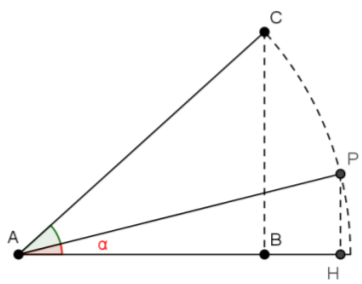Procedendo per via algebrica, otteniamo di nuovo un’equazione di terzo grado: sia $BAC = 3 alpha$ l’angolo dato e sia $AC=1$ , inoltre sia $HAP = alpha$ l’angolo da trovare. Poniamo $AH = x = cos alpha$. $AB = cos 3alpha = c $ noto (perché $3 alpha$ è noto). $c = cos 3 alpha = cos (2alpha + alpha) = … = 4 (cos alpha)^3 – 3 cos \alpha$.
Quindi trisecare l’angolo, dal punto di vista algebrico si riduce a risolvere l’equazione di terzo grado: $4x^3 – 3x = c $.
Il problema è impossibile utilizzando riga e compasso, tuttavia, già nel II secolo a.C. si riuscì a risolverlo utilizzando oggetti diversi da rette e circonferenze. Per esempio, Nicomede (contemporaneo di Archimede) introdusse una curva ideata ad hoc per risolvere questo problema: la concoide.¹² Successivamente anche Pappo risolse il problema intersecando una circonferenza e un’iperbole, ossia mediante sezioni coniche.¹³

3) Duplicazione del cubo:¹⁴

Il problema della duplicazione del cubo consiste nel determinare lo spigolo di un cubo il cui volume sia doppio di quello di un cubo di spigolo dato. Algebricamente la questione è molto semplice: noto , che è la lunghezza dello spigolo di un cubo, trovare $x$, che è la lunghezza dello spigolo del cubo il cui volume sia doppio di quello del cubo di spigolo $a$ . Basta risolvere l’equazione $x^3 = 2a^3$.

Anche per questo problema sono state proposte varie soluzioni che non facciano uso solamente di rette e circonferenze.

La soluzione proposta da Menecmo (380 a.C. circa – 320 a.C. circa) consiste nell’intersecare due parabole, i cui assi siano perpendicolari tra loro, che hanno il vertice in comune e i cui lati retti siano uno il doppio dell’altro. Sia $VA = a$  (noto), è il lato retto della prima parabola (in blu) e $BV = 2a$ il lato retto della seconda (in rosso), allora le equazioni delle due coniche, in termini moderni, sono: $x^2 = ay$ e $y^2=2ax$. L’ascissa del punto P d’intersezione delle due curve soddisfa l’equazione: $x^3=2a^3$. ¹⁵

Lezione 3: La trattazione sistematica di Al-Khayyam

Sulla scia di Al-Khwarizmi, anche Al-Khayyam classifica tutti i modi possibili di combinare tra loro numeri, lati ($x$), quadrati ($x^2$) e cubi ($x^3$) al fine di ottenere equazioni di primo, secondo e terzo grado con coefficienti positivi. Trascurando quelle di primo grado, quelle di secondo già trattare da Al-Khwarizmi e quelle che si riducono ad equazioni di secondo grado, ne rimangono quattordici del tutto nuove (ovviamente tutte di terzo grado).¹⁶ Tutti e quattordici i casi vengono analizzati e risolti con lo stesso procedimento: attraverso l’intersezione di due coniche. Come abbiamo visto nella lezione precedente, quella di Al-Khayyam non è un’idea nuova, tuttavia ad egli va il merito di aver analizzato sistematicamente il problema, trattando, di conseguenza, anche equazioni di terzo grado “potenziali” ossia che attualmente non si riferiscono ad un problema geometrico in particolare (come invece lo sono, ad esempio, le equazioni di terzo grado viste la lezione precedente, cioè quelle relative al lemma di Archimede, alla trisezione dell’angolo o alla duplicazione del cubo), bensì equazioni generiche che si potrebbero incontrare in futuro studiando qualche problema particolare¹⁷.

Non potendo in questa relazione (per ovvi motivi di spazio e tempo) illustrare la risoluzione di Al- Khayyam per tutti e quattordici i tipi di equazioni¹⁸, tratteremo solo i casi che si riferiscono alle tre equazioni di terzo grado viste nella lezione precedente (quelle relative ai tre problemi aperti), con lo scopo di mostrare il procedimento utilizzato da Al-Khayyam notando che è lo stesso in tutti e tre i casi.¹⁹

1. Equazione del tipo: $x^3=c$ (duplicazione del cubo)

Innanzitutto si rende omogenea l’equazione, ponendo $c=p^2q$.

L’equazione diventa: \(x^3=p^2q \rightarrow \frac{p^2}{x^2} = \frac{x}{q} \).

Che equivale alla proporzione: $p:x=x:y=y:q$. La quale da luogo alle due uguaglianze: \[  \begin{cases} \frac{p}{x} = \frac{x}{y} \rightarrow y = \frac{x^2}{p} \\\frac{x}{y} = \frac{y}{q} \rightarrow x = \frac{y^2}{q} \end{cases}\] Che, in un sistema di riferimento cartesiano, rappresentano le equazioni di due parabole con vertice nell’origine e con asse, l’asse delle y e l’asse delle x rispettivamente. L’ascissa del loro punto di intersezione è il valore di $x$ che risolve l’equazione.

2. Equazione del tipo: $x^3=bx+c$ (trisezione dell’angolo)

Innanzitutto si rende omogenea l’equazione, ponendo $c=p^2q$ e $b=p^2$. L’equazione diventa: \(x^3=p^2x+p^2q\rightarrow \frac{p^2}{x^2} = \frac{x}{(x+q)}\)

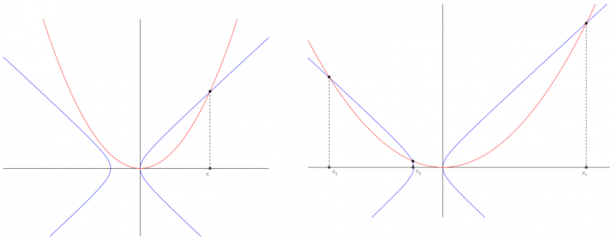
Che equivale alla proporzione: \( p:x = x:y = y:(x+q)\). La quale da luogo alle due uguaglianze: \[ \begin{cases} \frac{p}{x} = \frac{x}{y} \rightarrow y = \frac{x^2}{p} \\ \frac{x}{y} = \frac{y}{x+q} \rightarrow x^2-y^2+xq=0 \end{cases} \] Che, in un sistema di riferimento cartesiano, rappresentano le equazioni di una parabola con vertice nell’origine e con asse, l’asse delle y e di un’iperbole rispettivamente. L’ascissa del loro punto di intersezione è il valore di $x$ che risolve l’equazione. È da notare che questa equazione può presentare una sola radice positiva, oppure una radice positiva e due negative, a seconda dei valori dei coefficienti, come mostrano i seguenti grafici:

 

 

 

 

 

 

 

 

 

3. Equazione del tipo: $x^3+c = ax^2$ (lemma di Archimede)

Innanzitutto si rende omogenea l’equazione, ponendo $c=p^3$.

L’equazione diventa: \(x^3+p^3=ax^2\rightarrow \frac{p^2}{x^2}=\frac{a-x}{p}\). Che equivale alla proporzione: \( p:x = y:p = (a-x):y \). La quale da luogo alle due uguaglianze: \[ \begin{cases} \frac{p}{x} = \frac{y}{p} \rightarrow xy=p^2 \\ \frac{y}{p} = \frac{a-x}{y} \rightarrow x = -\frac{y^2}{p} + a \end{cases} \] Che, in un sistema di riferimento cartesiano, rappresentano le equazioni di un’iperbole equilatera e di una parabola con vertice nel punto (a,0) e con asse, l’asse delle x rispettivamente.

L’ascissa del loro punto di intersezione è il valore di $x$ che risolve l’equazione. È da notare che questa equazione può presentare una sola radice negativa, oppure una radice negativa e due positive, a seconda dei valori dei coefficienti, come mostrano i seguenti grafici:

 

 

 

 

 

 

 

 

 

 

Didatticamente questi grafici sono molto utili per mostrare come la forma delle curve, da una parte dipenda dal valore dei coefficienti dell’equazione e dall’altra dia informazioni riguardo la natura delle soluzioni (quante ce ne sono, se sono positive o negative, quale è la maggiore, quale la minore). Per crearli si possono utilizzare software di disegno geometrico. I grafici presenti in questa relazione sono stati realizzati con il software di geometria dinamica GeoGebra, scaricabile gratuitamente da internet. Questo software è molto utile in quanto, anzitutto permette di tracciare figure perfette (che hanno una bellezza e una armonia indiscutibili e generano un senso di appagamento sensoriale per chi le guarda, coinvolgendo aree celebrali legate alle emozioni) e in secondo luogo permette di modificare la figura, in questo modo “giocando” con il software (per esempio modificando la posizione del fuoco della parabola) lo studente può visualizzare infinite figure diverse tra loro ma dotate di una stessa struttura e può capire meglio quali sono le proprietà fondamentali che caratterizzano una curva e quali, invece, sono ausiliarie, cioè possono variare senza modificare la sostanza dalla figura. A questo punto sorgono spontanee alcune osservazioni, che è utile fare agli studenti a scuola e lasciarli pensare autonomamente per qualche minuto: le due sezioni coniche utilizzate per risolvere l’equazione possono, in qualche caso, non incontrarsi? Se si, in quali casi? Cosa si può dire, allora, a riguardo dell’equazione? Ovviamente ciò può succedere, e già Al-Khayyam aveva individuato i cinque tipi di equazione in cui ciò avviene (una delle quali è proprio quella relativa al lemma di Archimede²⁰ : $x^3+c=ax^2$).

Quando questo avviene l’equazione è impossibile!²¹ È ovvio che una stessa equazione può in certi casi avere soluzioni (e dunque le coniche in questione si intersecano) ed in certi casi non averle (le coniche non si intersecano), dipendentemente dal valore dei coefficienti che appaiono nell’equazione, e ciò era noto ad Al- Khayyam. Tuttavia egli non fu in grado di trovare le condizioni che devono soddisfare i coefficienti dell’equazione per garantirne la risolubilità, e questo suo insuccesso lo amareggiò fortemente.²² Il suo successore, il matematico persiano Al-Tusi (1201-1274), risolse questo problema sviluppando una tecnica completamente innovativa, basata sull’idea fondamentale di studiare localmente la “funzione” vicino al suo valore massimo²³ .

Lezione 4: Facoltativa

A questo punto, esaurita la trattazione delle equazioni, fatta alla maniera di Al-Khayyam, tempo permettendo, si può pensare di fare una ulteriore lezione, soprattutto se ci troviamo in un liceo scientifico e/o gli studenti sono fortemente interessati all’argomento. In realtà ci sarebbero ancora almeno un paio di argomenti da poter affrontare:

1. Il primo consiste nel vedere le idee e le conclusioni di Al-Tusi. In questo modo si espone agli studenti l’idea di poter analizzare una funzione nelle vicinanze di un suo punto (di un punto di massimo o di minimo). Inoltre si fa vedere quale proprietà caratterizza il massimo relativo di una funzione, e cercare, alla luce di questa proprietà, un modo per calcolarlo.²⁴
2. Un altro argomento che si può affrontare in questa ipotetica quarta lezione sulle equazioni cubiche è la formula cardanica. Si può, per esempio, raccontare la storia e le tortuose vicende che hanno portato alla scoperta (da parte di Dal Ferro prima e, indipendentemente, Tartaglia poi) e alla pubblicazione (da parte di Cardano) della tanto rinomata formula segreta. Si può mostrare quale è l’idea fondamentale che ha portato alla sua scoperta (ossia quella di guadagnare un grado di libertà scrivendo l’incognita come somma di due parametri, sviluppare il cubo di binomio e poi riassorbire il grado di libertà guadagnato, uguagliando termine a termine l’espressione dell’equazione con quella ottenuta dallo sviluppo del cubo di binomio) e infine si possono fare diversi esercizi di applicazione.

Esercizi

Vorrei concludere questa relazione presentando alcuni esercizi che è possibile assegnare al termine di questo ciclo di lezioni (o anche durante).²⁵

4. Proposta di lavoro di gruppo

Si dividono gli studenti in gruppi da due o da tre (a seconda della numerosità della classe) e a ciascun gruppo si assegna uno dei quattordici tipi di equazioni di terzo grado trattati da Al-Khayyam. Il gruppo deve ripetere tutti i passaggi indicati da Al-Khayyam (visti nella lezione 3) ed individuare che tipo di coniche intervengono nella risoluzione della propria equazione. Dopodiché si da a caso un valore numerico a ciascun coefficiente (a, b, c), ottenendo un’equazione tutta numerica e si disegnano con il software adatto (attualmente si consiglia GeoGebra) le coniche relative. Individuando infine, il loro punto di intersezione, si chiede al gruppo di calcolare approssimativamente il valore della/delle soluzioni. Questo può essere fatto in due modi: si può stampare su un foglio di carta l’immagine disegnata con il software e, stando attenti all’unità di misura riportate in scala, misurare con un righello l’ascissa del punto di intersezione delle coniche; oppure, se gli studenti sono in grado (magari perché frequentano una scuola superiore ad indirizzo informatico²⁶), si può calcolare la soluzione mediante l’algoritmo numerico della bisezione.²⁷

5. Tradurre ognuna delle seguenti affermazioni in un’equazione, individuare di che tipo si tratta (uno tra i quattordici tipi studiati da Al-Khayyam), disegnare con un software la soluzione, e calcolarla approssimativamente

1. Dividere dieci in due parti in modo tale che la somma dei loro quadrati, aggiunta al loro quoziente, faccia settantadue.
2. Si trovi un certo numero cubo che, insieme a due suoi quadrati e a dieci radici è uguale a venti (problemi proposti da Giovanni da Palermo a Fibonacci).²⁸
3. Trovare un numero che, sommato alla sua radice cubica, dia come risultato sei.
4. Un ebreo presta un capitale a condizione che alla fine dell’anno gli venga pagata come interesse la radice cubica del capitale. Alla fine dell’anno, l’ebreo riceve otto ducati, tra capitale ed interessi. Qual era il capitale? (problemi proposti da Antonio Maria Del Fiore a Tartaglia)²⁹

6. Per ognuna delle seguenti equazioni di terzo grado, disegnare con un software la soluzione intersecando due coniche, e calcolarla approssimativamente:

1. $x^3-2x-4=0$
2. $x^3-6x+4=0$
3. $x^3+x^2-2x-1 = 0$
4. $x^3=3x+1$
5. $x^3=6x+40$
6. $x^3=15x+4$

 

Riferimenti (bibliografia e sitografia)

1. Dijksterhuis E. J., Archimede, Firenze, Ponte alle grazie, 1989
2. Enciclopedia Treccani, online: http://www.treccani.it
3. Catastini L., Ghione F., Rashed R., Algebra. Origini e sviluppi tra mondo arabo e mondo latino, Roma, Carrocci Editore, 2016.
4. Wikipedia, enciclopedia libera online: https://it.wikipedia.org
5. Bernardo A., La formula risolutiva per l’equazione di terzo grado, in “Matematicamente”, 2007

Note

1. Tale formula venne pubblicata per la prima volta da Gerolamo Cardano nella sua opera “Ars Magna” nel 1545. ↑
2. Ritengo che sia utile introdurre un argomento dal punto di vista storico in quanto si può studiare l’origine e quindi le motivazioni per cui l’argomento è stato introdotto e le tecniche con cui è stato affrontato, nonché l’ambiente economico, sociale e culturale in cui si è sviluppato il concetto. Inoltre questo permette un facile collegamento interdisciplinare (con la storia, la geografia, l’arte, la filosofia); per esempio, nel nostro caso, si può pensare di fare una lezione insieme al docente di storia sulla civiltà araba durante il medioevo, focalizzando l’attenzione sullo sviluppo sociale, economico, tecnologico e culturale, che solitamente viene solo accennato a scuola, in quanto si preferisce studiare il medioevo latino piuttosto che quello arabo. ↑
3. Esistono varie versioni riguardo la morte di Archimede, come raccontano gli storici Tito Livio, Valerio Massimo, Plutarco e, più realisticamente Polibio. [1] ↑
4. Plutarco, “Vita di Marcello”. [1] ↑
5. Ossia l’emisfero destro; che è sede anche dell’intuito, della memoria visiva, della percezione sensoriale e della capacità di sintesi. Al contrario, l’emisfero sinistro è sede del linguaggio, della percezione razionale e del ragionamento logico-deduttivo. Ovviamente un problema di matematica stimola la parte sinistra dell’encefalo; tuttavia sarebbe preferibile porre problemi che stimolino entrambi gli emisferi celebrali, di modo che si attivino maggiori sinapsi e quindi si comprende e si risolve più facilmente il problema. Un modo per stimolare anche l’emisfero destro è quello di inserire il problema all’interno di uno sfondo narrativo oppure porre un problema che non si risolva solamente con carta e penna, ma anche manualmente, empiricamente (e per fare questo può aiutare il legame tra matematica e fisica). [2] ↑
6. Letteralmente lo storytelling è l’arte di scrivere o raccontare storie catturando l’attenzione e l’interesse del pubblico, è usata soprattutto in politica e in ambito aziendale. Tuttavia credo che possa essere usata anche in ambito didattico per creare uno sfondo nel quale inserire gli argomenti trattati, in modo che l’ascoltatore (lo studente) possa collocare i concetti in uno scenario reale, o comunque verosimile, di modo da renderne la loro comprensione e memorizzazione più salda. [2] ↑
7. Come riferiscono Catastini, Ghione, Rashed. [3] ↑
8. Quanto esposto in questo paragrafo è preso interamente dal libro di Catastini, Ghione, Rashed. [3] ↑
9. Archimede, “Trattato sulla sfera e sul cilindro”. [1] ↑
10. Era in uso nell’antichità definire la parabola come il luogo dei punti la cui ordinata è media proporzionale tra l’ascissa e il lato retto. Per ascissa di un punto $P$si intende la distanza tra il vertice $V$ della parabola e la proiezione $Q$ del punto sull’asse della parabola, ossia la lunghezza del segmento $VQ$. L’ordinata è la lunghezza del segmento $PQ$. [3] ↑
11. Chi mi assicura che le due coniche si intersecano? Archimede dimostra che il punto $P$ di intersezione esiste sempre mostrando che l’iperbole ha un punto interno alla parabola e uno esterno, allora per motivi di continuità e convessità, le due curve si incontreranno. Archimede non giustifica questa conclusione, supponendo implicitamente il fatto che le due curve siano continue e abbiano la giusta concavità. Tale supposizione implicita (presente anche in Euclide) è forse dettata dal fatto che queste curve si possono tracciare con continuità (con un filo teso, per esempio). ↑
12. Ometto il procedimento di Nicomede (che tra l’altro si potrebbe presentare a scuola per mostrare agli studenti curve diverse da quelle usuali) poiché in questa trattazione vorrei mostrare il legame tra equazioni di terzo grado e sezioni coniche, al fine di poter pensare di trattare nelle scuole questi due argomenti parallelamente in modo che ciascuno arricchisca e migliori la comprensione dell’altro. ↑
13. Una brevissima spiegazione del procedimento di Pappo si trova su wikipedia. [4] ↑
14. Quanto esposto in questo paragrafo è tratto da wikipedia. [4]Anche per questo problema sono state proposte varie soluzioni che non facciano uso solamente di rette e circonferenze. ↑
15. Ripetendo questo ragionamento con due parabole di lato retto $a$ ed $na$, si può trovare la radice cubica del numero $n$ (positivo) misurando la lunghezza del segmento $VX$ (ascissa del punto di P intersezione). ↑
16. I quattordici nuovi tipi di equazioni studiate da Al-Khayyam sono, come riferiscono Catastini, Ghione e Rashed: \( x^3=c, x^3+bx=c, x^3 + c = bx, x^3=bx+c, x^3+ax^2=c, x^3+c=ax^2, x^3=ax^2+c, x^3+ax^2+bx=c, x^3+ax^2+c=bx, x^3+bx+c=ax^2, x^3=ax^2+bx+c, x^3+ax^2 = bx+c, x^3+bx=ax^2+c\) e \(x^3+c=ax^2+bx, \mbox{ con } a, b, c \mbox{ positivi}\). [3] ↑
17. Come riferiscono Catastini, Ghione e Rashed, una cosa analoga fu fatta nell’ VIII secolo dal linguista arabo Al-Khalil, il quale ebbe il compito di costruire un vocabolario della lingua araba. Tale vocabolario, oltre a contenere parole in uso a quei tempi, conteneva parole “potenziali”, che rispettavano tutte le regole linguistiche fonetiche, ma a cui, tuttavia, ancora non era stato attribuito alcun significato. [3] ↑
18. Si rimanda a tal proposito all’appendice del libro di Catastini, Ghione, Rashed. [3] ↑
19. Quanto segue, è tratto dall’appendice del libro di Catastini, Ghione, Rashed. [3] ↑
20. Come riferiscono Catastini, Ghione e Rashed, gli altri tipi di equazioni in cui ciò avviene sono: \(x^3+c=bx, x^3+ax^2+c=bx, x^3+bx+c=ax^2\) e \(x^3+c=ax^2+bx\). [3] ↑
21. Più precisamente l’equazione non ha soluzioni reali. Se agli studenti sono già stati presentati i numeri immaginari, si può affermare che l’equazione non ha soluzioni reali, ma complesse; in caso contrario, è preferibile asserire che il problema è impossibile piuttosto che dire “l’equazione non ha soluzione”. In effetti il problema in questione è trovare il punto di intersezione tra due curve; ed è naturale pensare che se le curve non si intersecano, questo problema è di fatto impossibile. ↑
22. Credo che sia importante a scuola mostrare, oltre ai successi della matematica, anche gli insuccessi, come questo di Al-Khayyam, con un duplice scopo: innanzitutto si fa capire agli studenti che nessuno è un genio (in effetti è di tendenza attribuire i risultati matematici e fisici a pochi grandi protagonisti idealizzati come dei geni, non mostrando la travagliata storia che c’è dietro ogni scoperta, fatta di sconfitte, ripensamenti, vittorie parziali, idee brillanti, cambiamenti di prospettiva, errori clamorosi, sistematizzazioni, applicazioni, modellizzazioni); in secondo luogo è bene mostrare agli studenti come, spesso, per risolvere questioni matematiche attualmente impossibili, sia necessario un radicale cambiamento di prospettiva ed affrontare il problema con altre tecniche, altri strumenti ed altre idee. ↑
23. Troviamo in Al-Tusi la prima formulazione del concetto di derivata, come testimoniano Catastini, Ghione e Rashed. [3] ↑
24. Ovviamente una trattazione rigorosa di questo argomento richiede prerequisiti che studenti di un terzo anno non hanno, ossia la familiarità con il concetto di funzione e un minimo di topologia della retta reale (per lo meno avere chiaro il concetto di punto di accumulazione e di intorno di un punto). ↑
25. In effetti è bene corredare ogni argomento trattato con esercizi adeguati, in quanto, la mancanza di esercizi da svolgere autonomamente (o in gruppo), trasforma la lezione in una conferenza e lo studente, non vedendo l’applicazione e l’utilità, potrebbe disinteressarsi all’argomento. ↑
26. Effettivamente negli ultimi anni sono aumentati gli istituti di istruzione superiore ad indirizzo informatico (per esempio recentemente è stato introdotto il liceo scientifico informatico, in cui l’insegnamento della lingua latina è stato sostituito con l’insegnamento dell’informatica per tutti e cinque gli anni di studio). ↑
27. Si possono formare i gruppi in maniera tale che in ognuno ci sia uno studente più portato per la matematica, in modo da rendere il livello di ogni gruppo omogeneo (in questo modo però si rischia che nel gruppo lavori solo lo studente “bravo”); oppure si possono formare gruppi raggruppando studenti “dello stesso livello”, in tal caso è preferibile assegnare ai gruppi “meno portati” le equazioni più facili, mentre al “più portato” si può assegnare una delle cinque equazioni le cui soluzioni dipendono dai coefficienti, richiedendo di cercare quale sia la condizione che devono verificare i coefficienti per garantire la risolubilità dell’equazione (questo si può fare soprattutto se è stata svolta la quarta lezione sul metodo di Al-Tusi). ↑
28. Come riferiscono Catastini, Ghione e Rashed. [3] ↑
29. Come riferisce Bernardo. [5] ↑

Commenti

commenti