La legge di gravitazione universale garantisce che qualsiasi corpo dotato di massa esercita una forza su un altro corpo, anch’esso dotato di massa.
Ciò che è difficile spiegare, però, è come sia possibile che questo avvenga anche nel vuoto.
Infatti, tra i pianeti del sistema solare non è presente materia, ma vi è una regione di vuoto cosmico; attraverso il quale non è possibile trasmettere questo tipo di interazioni.
Le masse modificano lo spazio circostante
Per spiegare, quindi, l’esistenza di queste forze a distanza, si suppose che una qualsiasi massa che si trova in uno spazio è in grado di modificare lo spazio circostante semplicemente con la sua presenza.
Si intuisce che, se nello spazio è presente solo tale massa, non si possono notare gli effetti di tale deformazione; tuttavia, se sono presenti anche alti corpi, possiamo notare la deformazione dello spazio grazie agli effetti che questi subiscono.
Questa situazione viene descritta dicendo che la presenza di un corpo crea un campo gravitazionale nello spazio in cui si trova.
Per capire il concetto del campo gravitazionale, osserviamo un esempio.
Consideriamo una sfera che si trova al centro di un tappeto elastico; notiamo che la forza-peso che agisce sulla sfera fa si che il telo si avvalli a causa della sua presenza. La sfera, quindi, ha modificato lo spazio che vi era precedentemente.
Poniamo una sferetta più piccola (massa spia, o esploratrice, o di prova) sul bordo del telo; ci accorgiamo che essa non rimane ferma, ma tende a seguire la curvatura del telo, scivolando verso il centro, dove si trova la sfera più grande.

La massa di prova è una massa molto piccola rispetto a quella che crea il campo gravitazionale; per questo la sua presenza non modifica il campo circostante.
Quindi, questa sferetta si muove non tanto perché è attratta dalla sfera più grande, ma perché risente della deformazione dello spazio che questa ha creato.
Per i pianeti desistemmo solare accade una cosa analoga; essi, quindi, non si muovono perché attratti da una forza gravitazionale verso gli altri pianeti, ma poiché si trovano in un campo gravitazionale creato dal Sole, che è la massa più grande.
Il vettore campo gravitazionale
Il vettore campo gravitazionale è una nuova grandezza che permette di studiare gli effetti del campo gravitazionale su una massa di prova; tale vettore è dato dal rapporto del vettore forza con la massa di prova m:
$ vec g = frac(vec F)(m) $
tale vettore non dipende dal valore della massa di prova, ma solamente dalle masse che creano il campo gravitazionale.
Consideriamo un campo gravitazionale generato da una massa M, all’interno del quale si trova una massa di prova m. Il vettore forza e il vettore campo gravitazionale hanno stessa direzione (retta che congiunge le due masse) e stesso verso (diretto da m a M):
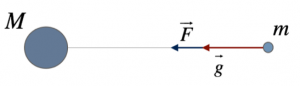
il modulo della forza gravitazionale che agisce sulle due masse è dato dalla legge di gravitazione universale:
$ F = G * frac(m*M)(r^2) $
Il modulo del vettore campo gravitazionale si ottiene dividendo il modulo della forza F per la massa di prova m:
$ g = frac(F)(m) = G * frac(M)(r^2) $
Il modulo di questo vettore è indipendente dalla massa di prova; esso dipende solo dalla massa M che genera il campo.
Inoltre, il modulo del vettore è inversamente proporzionale al quadrato della distanza; se consideriamo, quindi, una massa di prova molto distante da quella che genera il campo, essa risentirà poco della deformazione di esso.
I vettori campo gravitazionale diventano sempre più piccoli a mano a mano che ci si allontana dalla massa generatrice.
Da notare che, a causa dell’effetto del campo gravitazionale, quando una massa di prova si allontana dalla massa che genera il campo, la forza a distanza che agisce sulla massa non diminuisce in maniera istantanea; la diminuzione avviene con un ritardo che è proporzionale alla distanza che separa le due masse.
Questo fatto è spiegabile dalla presenza del campo gravitazionale; infatti, quando la massa m si allontana da M, vi è una variazione del campo gravitazionale, e la velocità con cui esso si propaga coincide con la velocità della luce. Il ritardo con cui diminuisce la forza è dato dal rapporto tra la distanza fra le masse e la velocità della luce:
$ ∆t = frac(r)(c) $
Potrebbero interessarti
Video lezioni: Le leggi di Keplero
Appunti: Le leggi di Keplero
Appunti: La gravitazione
Appunti: Il moto dei satelliti
Appunti: Dimostrazione delle leggi di Keplero
Appunti: Energia potenziale gravitazionale
