Le leggi di Keplero - Matematicamente

Fin dai tempi di Aristotele il modello cosmologico ritenuto esatto era quello che prevedeva la Terra al centro del Sistema Solare, e tutti i pianeti, compreso il Sole, che ruotavano attorno ad essa (modello geocentrico).

Nel corso del 1600, però, Niccolò Copernico propose un modello cosmologico che si basava sul fatto che il Sole si trovasse al centro del Sistema Solare, e i pianeti ruotassero attorno ad esso (modello eliocentrico).

Keplero, astronomo tedesco, perfezionò il modello eliocentrico proposto da Copernico, che presentava alcune lacune; Copernico supponeva, infatti, che le orbite percorse dai pianeti fossero orbite circolari, il che non permette di spiegare completamente il moto dei pianeti attorno al Sole.

Le deduzioni di Keplero furono esposte in tre leggi, note appunto come leggi di Keplero.

Prima legge di Keplero

Keplero ipotizzò che le orbite dei pianeti attorno al Sole non fossero orbite circolari, ma orbite ellittiche; in particolare, il Sole si trova esattamente nella posizione di uno dei due fuochi di tale ellisse.

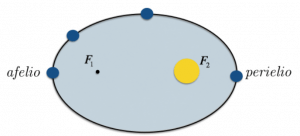
Ricordiamo che i fuochi sono punti interni all’ellisse tali che la somma delle distanze dei punti dell’ellisse da essi rimane costante.

Durante il suo moto, un pianeta può trovarsi in diverse posizioni rispetto al Sole: la posizione di maggior distanza dal Sole prende il nome di afelio, mentre quella di minor distanza viene detta perielio.

Seconda legge di Keplero

La seconda legge di Keplero afferma che il raggio vettore che determina la posizione di un pianeta (che parte, quindi, dal Sole e ha come estremo la posizione occupata dal pianeta) spazza aree uguali in tempi uguali.

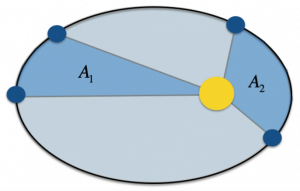
Questa legge ci suggerisce, quindi, che un pianeta si muoverà con velocità maggiore quando si trova nei pressi del perielio, ed è quindi più vicino al Sole, rispetto a quando esso si trova nell’afelio.

In riferimento al moto terrestre, possiamo notare che la primavera e l’estate, che si hanno quando la Terra si trova più lontana dal Sole, sono stagioni più lunghe dell’inverno e l’autunno, in quanto in quest’ultime la Terra è più vicina al Sole, e percorrerà la sua orbita con velocità maggiore.

La terza legge di Keplero

Chiamiamo T il periodo di rivoluzione del pianeta attorno al sole, e con a il semiasse maggiore dell’ellisse.

La terza legge di Keplero afferma che il rapporto tra il quadrato del periodo di rivoluzione e il cubo del semiasse maggiore è costante:

$ frac(T^2)(a^3) = cost$

Quindi, sappiamo che il quadrato del periodo di rivoluzione è direttamente proporzionale al cubo del semiasse maggiore; quindi, all’aumentare della distanza di un pianeta dal Sole, aumenta il tempo che esso impiega a percorrere la sua orbita.

Il valore di tale costante dipende dal corpo celeste che stiamo considerando; ad esempio, i pianeti che orbitano attorno al cole possono avere costanti diverse dei satelliti che orbitano attorno ad un pianeta.

Poiché le orbite dei pianeti sono quasi circolari, spesso per comodità si approssimano le loro orbite alle circonferenze; nella terza delle, ad esempio, si sostituisce al semiasse maggiore il raggio della circonferenza.

Esercizio

Il periodo orbitale della Terra è di 365,26 d, e la distanza media Terra-Sole è di $1,50 * 10^11 m$. Sapendo che il periodo dell’orbita di Marte è di 686,98 d, calcolare la distanza media di Marte dal Sole.

Come abbiamo detto in precedenza, la terza legge di Keplero funziona anche se approssimiamo le orbite dei pianeti con delle circonferenze; per questo, è possibile considerare delle orbite circolari che hanno raggio uguale alla distanza media Pianeta-Sole.

Per prima cosa, trasformiamo i dati nelle giuste unità di misura, in quanto il periodo dei pianeti va espresso in secondi, e non in giorni:

$ 365,26 d = 365,26*24*06*60 s = 3,16 * 10^7 s$

$ 686,98 d = 686,98*24*06*60 s = 5,94 * 10^7 s$

Applicando la terza legge di Keplero ai dati relativi al moto terrestre, possiamo determinare il valore della costante:

$ frac(T_T ^2)(R_(T-S) ^3) = frac((3,16 * 10^7 s)^2)((1,50 * 10^11 m)^3) = $

$= frac(9,98 * 10^14 s^2)(3,38 * 10^33 m^3)= 2,95 * 10^-19 s^2/m^3 $

Applichiamo, ora, la terza legge di Keplero con i dati relativi a Marte, e ricaviamo la formula inversa per trovare il raggio dell’orbita (supposte circolare) attorno alla quale ruota il pianeta:

$ frac(T_M^2)(R_(M-S) ^3) = cost to R_(M-S) = root(3)(frac(T_M^2)(cost))$

Sostituiamo i dati trovati precedentemente:

$R_(M-S) = root(3)(frac(T_M^2)(cost)) = root(3)(frac(35,28 * 10^14 s^2)(2,95 * 10^-19 s^2/m^3)) =$

$ = root(3) (11,96 * 10^33 m^3) = 2,29 * 10^11 m$