Keplero formulò le sue leggi, che spiegavano il movimento dei pianeti e dei satelliti, come leggi sperimentali, e non fornì, quindi, una dimostrazione concreta della loro veridicità.
Queste leggi possono essere spiegate ora per mezzo dei principi della dinamica e della legge di gravitazione universale.
Dimostrazione della prima legge di Keplero
Ricordiamo che la prima legge di Keplero afferma che i pianeti compiono attorno al Sole orbite ellittiche. Su un pianeta che orbita attorno al Sole agisce la forza di attrazione gravitazionale dovuta alle due masse.
Considerando la relazione $F = m*a$, è possibile dimostrare, attraverso procedimenti matematici che sfruttano le proprietà della legge di gravitazione universale, che le traiettorie possibili che un pianeta può compiere durante il suo moto sono solamente tre: l’ellisse, la parabola e l’iperbole.
Di conseguenza, poiché il pianeta compie un percorso chiuso attorno al Sole, esso si muoverà per forza compiendo una traiettoria ellittica o, come caso particolare, con traiettoria circolare.
Dimostrazione della seconda legge di Keplero
La seconda legge di Keplero, che afferma che il raggio vettore che collega il Sole con la posizione occupata dal pianeta spazza aree uguali in tempi uguali, può essere spiegata come conseguenza della conservazione del momento angolare.
Consideriamo la Terra quando occupa le posizioni di afelio e perielio rispetto al Sole, cioè quando si trova nelle posizioni di massima distanza e minima distanza da esso.
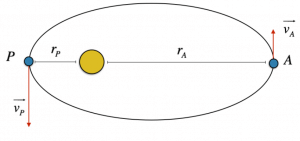
Chiamiamo con $r_A$ la distanza Terra-Sole quando la Terra si trova nell’afelio, e $r_P$ tale distanza quando la Terra si trova nel perielio; chiamiamo inoltre con $v_A$ e $v_P$ le velocità della Terra in afelio e in perielio.
I momenti angolari della Terra nei due punti, come sappiamo, possono essere calcolati come prodotto vettoriale tra il raggio vettore Sole-Terra e la quantità di moto della Terra stessa; sapendo che in P e in A il vettore velocità è perpendicolare al raggio vettore, abbiamo che il modulo del momento angolare è semplicemente $L = M*v * r$, quindi nei due casi si ha:
$ L_P = M_T * v_P * r_P$
$ L_A = M_T * v_A * r_A$
Essendo noti la massa terrestre, la distanza Terra-Sole nell’afelio e nel perielio, e le rispettive velocità, è stato possibile calcolare il memento angolare nei due punti che, effettivamente, è risultato essere lo stesso.
Si può concludere, quindi, che nel perielio, dove il raggio è più piccolo, affinché L rimanga costante, deve necessariamente aumentare la velocità $v_P$; analogamente, nell’afelio, dove invece la distanza è maggiore, la velocità deve essere minore.
Dimostrazione della terza legge di Keplero
La terza legge di Keplero ci fornisce la relazione
$ frac(T^2)(a^3) = cost $
dove T è il periodo di rivoluzione e a è la lunghezza del semiasse maggiore. Per dimostrare questa formula, ricordiamo che nel caso di un moto circolare uniforme (a cui può essere approssimato quello dei pianeti), la velocità è data dal rapporto $(2πR)/T$.
Abbiamo visto che, nel caso dei satelliti, o comunque dei pianeti in orbita, la velocità di percorrenza della traiettoria può essere calcolata come:
$ v = sqrt(frac(G*M)(R))$
Uguagliando le due espressioni noteremmo che il rapporto tra il quadrato del periodo e il cubo del raggio è effettivamente una quantità costante, che dipende dalla massa M, e che varia quindi da pianeta a pianeta.
$ sqrt(frac(G*M)(R)) = frac(2πR)(T) to frac(G*M)(R) = frac(4π^2R^2)(T^2) to frac(T^2)(R^3) = frac(4π^2)(G*M)$
Esercizio
Consideriamo il moto del pianeta Marte attorno al Sole; è noto che le distanze del pianeta dal Sole nel punto di afelio e nel punto di perielio sono, rispettivamente, $r_A = 2,46 * 10^11 m$ e $r_P = 2,05 * 10^11 m$. Calcolare il rapporto tra la velocità di Marte nel punto di afelio e quella nel punto di perielio.
Come abbiamo visto in precedenza, possiamo determinare la velocità di un pianeta in orbita attorno al Sole con la formula:
$ v = sqrt(frac(G*M)(R))$
Le velocità del pianeta nei punti di afelio e perielio, quindi, sono date da:
$ v_A = sqrt(frac(G*M)(r_A))$ , $ v_P = sqrt(frac(G*M)(r_P))$
Calcoliamo ora il rapporto tra $v_A$ e $v_P$:
$ frac(v_A)(v_P) = frac(sqrt(frac(G*M)(r_a)))(sqrt(frac(G*M)(r_P))) = sqrt(frac(G*M)(r_A) * frac(r_P)(G*M)) = sqrt(frac(r_P)(r_A))$
Notiamo, quindi, che il rapporto tra le velocità è indipendente dalla massa del pianeta, ma dipende solo dalla sua distanza dal Sole nei due punti. Sostituiamo i valori numerici:
$ frac(v_A)(v_P) = sqrt(frac(r_P)(r_A)) = sqrt(frac(2,05 * 10^11 m)(2,46 * 10^11 m)) = 0,91$
Potrebbero interessarti
Video lezioni: Le leggi di Keplero
Video lezioni: La gravitazione universale
Appunti: Le leggi di Keplero
Appunti: La gravitazione
Appunti: Il moto dei satelliti
Appunti: Il campo gravitazionale
Appunti: Energia potenziale gravitazionale
