Nel caso degli specchi curvi, è possibile determinare la posizione dell’oggetto riflesso, e quella dell’immagine che si forma in due modi: il primo consiste nel disegnare le rette che rappresentano i raggi di luce, determinare le loro intersezioni, e trovare quindi il punto in cui si forma l’immagine.
Ad esempio, consideriamo uno specchio in cui l’oggetto che dobbiamo riflettere si trova molto lontano dallo specchio, oltre il centro.
Consideriamo due raggi principali che partono dall’oggetto: uno di essi ha direzione parallela all’asse ottico, quindi il raggio riflesso passerà per il fuoco; l’altro viene proiettato sullo specchio torna indietro; la loro intersezione ci darà la posizione dell’immagine reale che si forma:
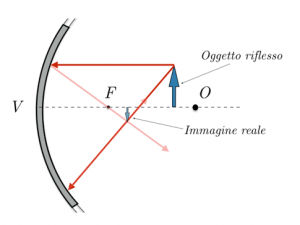
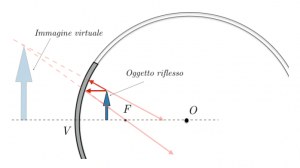
Nel caso in cui l’oggetto che viene riflesso si trovi tra il fuoco e lo specchio, allora l’immagine che si viene a creare è individuata dal prolungamento dei raggi riflessi, ed è quindi un’immagine virtuale;
infatti, come possiamo vedere, in questo caso non vi è intersezione tra i raggi riflessi, ma l’intersezione si può formare dietro lo specchio con i loro prolungamenti:
Il secondo metodo, invece, utilizza una determinata formula, che prende il nome di legge dei punti coniugati:
$1/p + 1/q = 1/f$
Dove p india la distanza dell’oggetto dallo specchio, q la distanza dell’immagine dallo specchio, e f è la distanza focale. In questo modo, conoscendo due delle distanze citate, è possibile ricavare la terza senza procedimenti pratici.
In particolare, nel caso di uno specchio convesso, sapendo che la distanza focale equivale alla metà del raggio, possiamo modificare la formula precedente inserendo questa informazione:
$1/p + 1/q = -2/r$
Si usa il segno meno perché in uno specchio convesso il fuoco si trova dalla parte opposta rispetto all’oggetto da riflettere, quindi il fuoco stesso è virtuale. Dall’uguaglianza possiamo notare che, poiché la distanza oggetto-specchio è positiva, in quanto l’oggetto si trova davanti allo specchio convesso, anche la distanza q risulta negativa.
Si conclude, quindi, che in questo caso l’immagine che si forma si troverà dietro lo specchio, e sarà quindi un’immagine virtuale.
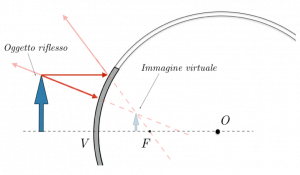
Possiamo esaminare questo aspetto anche dal punto di vista grafico; l’oggetto in questione si trova davanti allo specchio. Prendiamo due raggi principali, uno dei quali con direzione parallela all’asse ottico, l’altro di direzione diversa.
Anche in questo caso, i raggi riflessi non si incontrano, ma si possono incontrare i loro prolungamenti; il punto di incontro ci fornisce la posizione dell’immagine virtuale che si forma:
Ingrandimento lineare
Come abbiamo visto negli esempi precedenti, sia che l’immagine sia reale, sia che essa sia virtuale, è possibile che l’immagine riflessa risulti ingrandita o rimpicciolita rispetto a come è l’oggetto di partenza.
Definiamo, quindi, l’ingrandimento lineare come il rapporto tra la lunghezza dell’immagine riflessa e la lunghezza dell’oggetto.
E’ possibile dimostrare che tale rapporto equivale al rapporto tra la distanze dell’immagine dallo specchio e la distanza dell’oggetto dallo specchio:
$G = frac(q)(p)$
Esercizio
Consideriamo la riflessione su uno specchio concavo di un oggetto che si trova a 70 cm dalla superficie dello specchio, che è stato ricavato da una sfera di diametro 1,30 m.
Calcoliamo la distanza dallo specchio dell’immagine che si forma, e il relativo ingrandimento.
Dai dati del problema sappiamo che il diametro della sfera è di 1,30 m, quindi il suo raggio misura 0,65 m. Dato che lo specchio in questione è uno specchio concavo, sappiamo che la distanza focale, cioè la distanza del fuoco dallo specchio, è esattamente uguale al raggio.
Inoltre, il problema fornisce la distanza dell’oggetto dallo specchio (p); possiamo, quindi, applicare la legge dei punti coniugati per ricavare la distanza dell’immagine dallo specchio:
$1/p + 1/q = 1/f to 1/q = 1/f – 1/p = frac(p-f)(fp) to q = frac(fp)(p-f)$
Ricordando che la distanza focale è uguale alla metà del raggio, si ottiene:
$ q = frac(fp)(p-f) = frac(r/2 * p)(p – r/2)$
Possiamo ora sostituire i valori numerici:
$ q = frac(0,325 * 0,7)(0,7 – 0,325) = 0,61 m$
L’ingrandimento dell’immagine si calcola come rapporto tra la distanza dell’immagine dallo specchio e la distanza dell’oggetto dallo specchio; quindi si ha:
$ G = q/p = frac(0,61)(0,7) = 0,87 $
Potrebbero interessarti
Video lezioni: La luce
Appunti: La riflessione della luce
Appunti: La riflessione totale
Appunti: La formula delle lenti sottili e le aberrazioni delle lenti
Appunti: La rifrazione della luce
Appunti: Le lenti sferiche
