Abbiamo visto, nel caso di uno specchio, che i raggi riflessi ci permettono di determinare la posizione dell’immagine riflessa di un oggetto.
E’ possibile ottenere un’immagine riflessa non solo con degli specchi, ma anche per esempio con una superficie d’acqua.
In questo caso, però, non si parla più di riflessione, ma di rifrazione. Il fenomeno riguarda il passaggio dei raggi di luce da un messo ad un altro.
Ad esempio raggi provenienti ad esempio dal sole, e che si propagano quindi nell’aria, vengono a contatto con la superficie dell’acqua, e si inabissano in essa.
Il passaggio da un mezzo all’altro fa si che i raggi non si trasmettano in linea retta, ma subiscono una variazione di angolo. In particolare, se i raggi provengono dall’aria, essi creeranno dei raggi rifratti, che si formano sotto la superficie dell’acqua, che tendono ad avvicinarsi alla perpendicolare alla superficie:
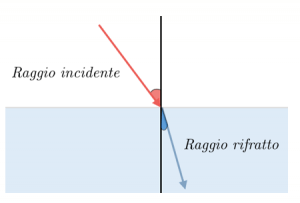
Nel caso in cui, invece, i raggi provengano proprio dall’acqua, il passaggio di mezzo è l’opposto, in quanto esso passerà dall’acqua all’aria; in questo caso, il raggio rifratto presenterà un angolo tale da farlo allontanare dalla verticale:
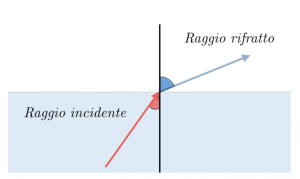
Come abbiamo già visto, la velocità di propagazione di un’onda dipende dal mezzo in cui essa si trova; la velocità della luce, in particolare, è minore nei mezzi trasparenti, rispetto alla velocità che avrebbe nel vuoto.
E’ utile individuare il rapporto tra la velocità della luce nel vuoto e la sua velocità in un determinato mezzo; questa grandezza viene definita indice di rifrazione assoluto:
$ n = frac(c)(v) $
Questo valore è sempre maggiore di 1, tranne nel caso in cui il mezzo di propagazione dell’onda sia proprio il vuoto; in questo caso, infatti, l’indice di rifrazione è massimo e vale 1.
Possiamo individuare, sperimentalmente, le caratteristiche della rifrazione dei raggi luminosi quando essi passano da un mezzo all’altro, che presentano indici di rifrazione differenti, mediante le seguenti due leggi:
- il raggio incidente, il raggio rifratto che si forma, e la perpendicolare alla superficie nel punto di incidenza possono essere rappresentati con delle rette che appartengono allo stesso piano;
- il rapporto tra i seni degli angoli che si formano con la retta perpendicolare, cioè l’angolo di incidenza e quello di rifrazione, è costante; tale rapporto, inoltre, è uguale al rapporto tra gli indici di rifrazione dei due mezzi che vengono attraversati.
Quest’ultima legge è rappresentata dalla formula che prende il nome di formula di Snell, ed è la seguente:
$frac(sin \hat{i})(sin \hat{j}) = frac(n_2)(n_1)$
dove i e j rappresentano, rispettivamente, l’angolo di incidenza e l’angolo di rifrazione; n2 e n1 sono, rispettivamente, gli indici di rifrazione del secondo e del primo mezzo.
In particolare, il rapporto tra gli indici di rifrazione dei mezzi viene definito indice di rifrazione relativo.
L’indice di riflessione relativo di un determinato mezzo rispetto ad un altro è uguale al reciproco di quello del secondo mezzo rispetto al primo.
In base a tale indice possiamo definire delle caratteristiche reciproche dei due mezzi: se l’indice di rifrazione è maggiore di 1, si dice che il secondo mezzo è più rifrangente del primo, o che esso è più otticamente denso.
Esercizio
Consideriamo un raggio di luce indicente che forma con la superficie di separazione tra aria e acqua un angolo di incidenza di 46°. Sapendo che l’indice di rifrazione dell’acqua vale 1,33, determinare l’angolo di rifrazione quando il raggio passa dall’aria all’acqua.
I questo caso, il raggio incidente proviene dall’aria, che presenta indice di rifrazione uguale a 1; l’aria, quindi, rappresenta il primo mezzo, mentre il secondo è l’acqua. Per determinare l’angolo di rifrazione che si forma, possiamo applicare la legge di Snell, e ricavare con la formula inversa il valore del seno del secondo angolo:
$frac(sin θ_2)(sin θ_1) = frac(n_1)(n_2) to sin θ_2 = frac(n_1)(n_2) * sin θ_1$
Determiniamo il seno dell’angolo cercato sostituendo i valori numerici:
$sin θ_2 = frac(n_1)(n_2) * sin θ_1 = frac(1)(1,33) * sin 46° = 0,54$
Calcolando la funzione inversa del seno, possiamo trovare il valore dell’angolo di rifrazione:
$θ_2 = arcsin (0,54) = 33° $
Potrebbero interessarti
Video lezioni: La luce
Appunti: La riflessione della luce
Appunti: La riflessione totale
Appunti: La legge dei punti coniugati
Appunti: La formula delle lenti sottili e le aberrazioni delle lenti
Appunti: Le lenti sferiche
