Due automobili partono contemporaneamente dallo stesso punto ma in direzioni opposte. La prima viaggia alla velocità media di $116$ Km/h e la seconda alla velocità media di $126$ Km/h. Calcolare a che distanza si ritroveranno le due auto dopo tre ore e mezza.

Soluzione

Le due auto si ritroveranno a:

$(116xx3+116:2)+(126xx3+126:2)=(348+58)+(378+63)=406+441=847 km$

oppure

$116*3,5+126*3,5=406+441=847km$

Testo del problema

Marco ha acquistato uno stereo versando alla consegna euro 70, dopo una settimana, euro 30 e pagando il rimanente in 12 rate. Qual è l’importo di ogni rata se il prezzo dello stereo è di 1000 euro?

Soluzione

L’importo di ogni rata è $(1000-30-70):12=900:12=75$

Un Signore si reca alla Posta per pagare 6 bollette tutte della stessa cifra. Se paga con un biglietto da 100 euro e riceve il resto di 22 euro, quale somma avrà pagato per ogni bolletta se si devono aggiungere euro 0,50 di commissione per ogni bolletta?

Soluzione

Il signore avra pagato $(100-22-0,50xx6):6=(78-3):6=75:6=12,50$ euro

Una studentessa  universitaria guadagna 18 euro all’ora dando lezioni private. Quanto guadagna in una settimana se è impegnata 2 ore il l’unedì ed il martedì, 3 ore il mercoledì e il venerdì e 4 ore il giovedì?

Soluzione

Guadagna $18xx(2+2+3+3+4)=18xx14=252$ euro.

Due imbianchini per 10 giorni di lavoro ricevono una paga di Euro 1730. Sapendo che la paga giornaliera di uno dei due è di Euro 82, calcola la paga giornaliera dell’altro.

Soluzione

La paga giornaliera del secondo imbianchino è: $(1730-82xx10):10=(1730-820):10=910:10=91$ euro.

Un impiegato rivece uno stipendio mensile di 1650 Euro. Alla fine dell’anno ottiene un premio di 800 euro. Se le sue spese annuali per vitto e alloggio e tutto il resto ammontano a 18700 Euro, quanto sara il suo risparmio annuale?

Soluzione

Cominciamo a calcolare quanto guadagna in un anno l’impiegato

Ha uno stipendio mensile di $1650$ Euro, quindi in una anno guadagna: $ 1650 xx 12 = 19800 $ Euro.

A questi va aggiunto il premio di fine anno di $800$ euro.

L’impiegato guadagna così in un anno: $ 19800 + 800 = 20600 $ Euro.

Per conoscere il suo risparmio annuale, dobbiamo togliere al suo guadagno annuale le spese annuali:
$ 20600 – 18700 = 1900 $ Euro.

L’abbonamento annuale a un settimanale, il cui prezzo di copertina è di 3 euro, costa 104 euro e l’abbonamento a un mensile, il cui prezzo di copertina è 4 euro, costa 36 euro. Quanto si risparmia in totale con gli abbonamenti? (Considera l’anno formato da 52 settimane)

Soluzione

Con l’abbonamento al settimanale si risparmiano $3xx52-104=156-104=52$ euro.

Con l’abbonamento mensile si risparmiano $4xx12-36=48-36=12$ euro.

Con i due abbonamenti, in un anno ri risparmiano $52+12=64$ euro. 

Per la distribuzione dell’energia elettrica in un nuovo quartiere , L’ENEL deve sistemare tre nuove linee di fili tra due cabine che distano 750 metri tra loro. Vengono usate bobine di cavi lunghi 50 metri l’uno. Quante bobine occorrono e a quanto ammonta la spesa se ogni bobina costa 350 euro?

Vengono usate $750:50xx3=15xx3=45$ bobine.

La spesa ammonta a $45xx350=15750$ euro. 

Una vasca riceve acqua da due condutture che versano rispettivamente 70 e 50 litri al minuto.In quante ore si riempirà la vasca sapendo che la sua capacità è di 216 ettolitri?

$216$ ettolitri $=21600$ litri.

Soluzione

Le due condutture versano nella vasca in un minuto $ 70 + 50 = 120$ litri.

La capacità della vasca è di $216$ ettolitri = $216 xx 100$ litri = $21600$ litri.

Dividiamo quindi la capacità in litri della vasca per il numero di litri versati dalle condutture in un minuto, per ottenere il numero di minuti necessari a riempire la vasca: $21600 : 120 = 180$ minuti.

Per conoscere il numero di ore, basta allora dividere $180$ minuti per il numero di minuti in un’ora: $180 : 60 = 3$ ore.

In un frutteto ci sono 32 file di 24 meli ciascuna. Sapendo che in media ogni pianta produce 80 kg di mele, calcola quanto si ricava vendendole a 1 euro al kg.

Soluzione

Dalla vendita delle mele si ricaverà $32xx24xx80=61440$ euro 

Una ditta per la produzione di plastica ha 25 operai e 6 impiegati a cui corrisponde un salario rispettivamente di 830 euro e di euro 905 in media al mese. Una ditta per la produzione di bottoni ha 22 operai e 8 impiegati a cui corrisponde un salario rispettivamente un salario di euro 810 e euro 910 in media al mese. Quale ditta spende di più in un mese?

Soluzione

La ditta per la produzione della plastica spende al mese: $25xx830+6xx950=20750+5430=26180$

La ditta per la produzione di bottoni spemde al mese: $22xx810+8xx910=17820+7280=25100$

La ditta per la produzione di plastica spende in più $26180-25100=1080$

Due falegnami per costruire una libreria percepiscono una paga oraria rispettivamente di 18 Euro e di 21 Euro. Sapendo che mediamente hanno lavorato per 9 ore al giorno e che alla consegna della libreria il secondo falegname riceve 297 euro più del primo, calcola quanti giorni hanno lavorato.

Soluzione

Si può ragionare in questo modo:

Calcoliamo innanzitutto quanto guadagnano al giorno i due falegnami:

Il primo guadagna: $ 18 xx 9 = 162 $ Euro.

Il secondo guadagna: $ 21 xx 9 = 189 $ Euro.

Troviamo ora quanto guadagna il secondo falegname in più del primo in un giorno: $ 189 – 162 = 27 $ Euro.

Quindi è facile ora trovare il numero di giorni lavorati dai due, dividendo quanto ha ricevuto in più il secondo lavoratore alla fine del lavoro per quanto ricevuto in un giorno: $ 297 : 27 = 11 $.

Una massaia acquista 10 bottiglie di vino e 8 bottiglie di Coca-cola spendendo in tutto 28 euro. Quanto costa una bottiglia di vino e quanto una lattina di Coca-cola se una bottiglia di vino costa quanto due lattine di Coca-cola?

Soluzione

Siccome 2 lattine di Coca-cola costano come una bottiglia di vino, avremmo pagato la stessa cifra di $28$ euro, se per ognuna delle bottiglie di vino avessimo preso invece 2 lattine di Coca. Quindi per $28$ euro ci avrebbero dato $ 10 xx 2 + 8 = 28 $ lattine.

Una singola lattina costa allora: $ 28 : 28 = 1 $ euro.

E per una singola bottiglia di vino, costando il doppio, si spende: $ 1 xx 2 = 2 $ euro.

In un azienda agricola si devono insaccare 5565 kg di farina in due tipi di sacchi della capacità rispettivamente di 85 kg e 45 kg. Compiuta l’operazione si contano 48 sacchi da 85 kg. Il resto è stato insaccato in sacchi di 45 kg. Quanti sacchi vengono riempiti in tutto?

Soluzione

In tutto vengono riempiti:

$5565-48xx85:45+48=5565-4080:45+48=1485:45+48=33+48=81$ sacchi di farina.

Tre amici devono dividersi una vincita al lotto di 60000 euro in modo tale che al secondo e al terzo vadano rispettivamente il doppio e il triplo della somma spettante al primo; quanto deve ricevere ogni amico?

Soluzione

Il primo amico riceverà $60000:(3+2+1)=60000:6=10000$ euro;

Il secondo amico riceverà $10000xx2=20000$ euro;

Il terzo amico riceverà $10000xx3=30000$ euro. 

Un allevatore vende 670 polli a 3 euro l’uno e 510 galline ad una cifra pari alla metà del costo di un pollo più 1 euro. Quanto ricava in tutto dalla vendita?

Soluzione

Ricava dalla vendita $670xx3+[510xx(3:2+1)]= 2010+[510xx(1,5+1)]=2010+510xx2,5=2010+1275=3285$ euro.

Una ditta per preparare una confezione da 20 foulard di seta utilizza 10 metri di stoffa del costo di 80 euro il metro. Il lavoro per ogni foulard è costato 12 euro. Quanto costa un solo foulard? Quanto costa ogni confezione?

Ogni foulard costa $12+10xx80:20=12+800:20=12+40=52$ euro.

Ogni confezione costa $10xx80+(12xx20)=800+240=1040$ euro 

Un falegname lavora 6 ore al giorno per riparare un mobile e presenta un conto di 344 euro. Se per il materiale necessario alla riparazione ha speso 74 euro, qual è la sua retribuzione per ogni ora di lavoro?

Soluzione

Al conto presentato va tolta la spesa per il materiale, il risultato va poi diviso per il numero di ore lavorate. Quindi abbiamo che la sua retribuzione per ogni ora di lavoro è di $(344-74):6=270:6=45$ euro.

Per partecipare ad una gita scolastica ogni alunno versa una quota di 18 Euro. I partecipanti, che sono 36, devono inoltre dividere fra di loro una spesa extra di 144 Euro. Quanto spende in totale ciascun alunno?

Soluzione

La spesa extra deve essere equamente divisa tra i 36 alunni. Quindi ogni partecipante alla gita spende in più $144:36=4$ Euro.

A questi $4$ Euro si deve aggiungere la quota normale per la gita di $18$ Euro: $4 + 18 = 22$ Euro.

Ogni alunno deve spendere quindi in tutto $22$ euro per partecipare alla gita.

Un autocarro trasporta 35 sacchi di fruento che pesano ognuno 65 kg. Durante il viaggio verso il mulino 8 sacchi cadono dall’ autocarro. Quanti sacchi di frumento arrivano al mulino? Quanti kg si sono persi?

Soluzione

Al mulino arrivano $35-8=27$ sacchi e se ne sono persi $65xx8=520$ kg

Un segmento $AB$ è lungo 30cm. Calcola quanto misurano i $\frac{2}{3}$, i $\frac{3}{5}$ e i $\frac{5}{15}$ del segmento.

$\frac{2}{3}AB=30:3xx2=10xx2=20cm$

$\frac{3}{5}AB=30:5xx3=6xx3=18cm$

$\frac{5}{15}AB=30:15xx5=2xx5=10cm$

Un segmento $AB$ è lungo 50cm. Calcola quanto misurano i $\frac{2}{5}$, i $\frac{3}{5}$ e i $\frac{5}{10}$

Soluzione

$\frac{2}{5}AB=50:5xx2=10xx2=20$

$\frac{3}{5}AB=50:5xx3=10xx3=30$

$\frac{5}{15}AB=50:10xx5=5xx5=25$

Calcola i $\frac{3}{4}$ delle seguenti misure di lunghezza: $80cm,16cm,32cm,160cm$

Soluzione

$80:4xx3=20xx3=60$

$16:4xx3=4xx3=12$

$32:4xx3=8xx3=24$

$1604xx3=40xx3=120$

Soluzione

Prendere i $2/3$ di qualcosa significa dividerla per $3$ e poi prenderne $2$ parti.

Dobbiamo allora calcolare le seguenti espressioni.

$60:3xx2=20xx2=40$

$90:3xx2=30xx2=60$

$18:3xx2=6xx2=12$

$36:3xx2=12xx2=24$

Due triangoli isosceli sono isoperimetrici. Calcola il lato obliquo del secondo triangolo sapendo che la base e il lato obliquo del primo misurano rispettivamente 20 cm e 25 cm e che la base del secondo triangolo è la metà della base del primo triangolo.

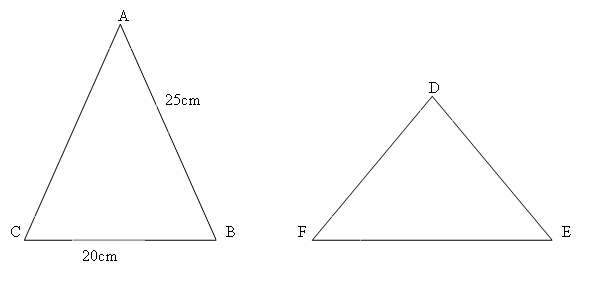
$AB=25cm$

$BC=20cm$

$2p_(ABC)=2p_(DEF)=20+25xx2=20+50=70$

$FE=CB:2=20:2=10$

$DE=(2p_(DEF)-10):2=(70-10):2=60:2=30)$

Un commerciante ha due botti che contengono complessivamente 145 l di vino. Vende 40 l da una botte e 31 l dalla seconda botte. Così nelle due botti  rimane una stessa quantita di vino. Quale è la capacità di ciascuna botte?

Soluzione

Dai 145 litri si tolgono 40 l e 31 l, quello che rimane va diviso per 2, in modo da ottenere il vino rimasto in ciascuna botte.

$[145-(40+31)]:2=(145-71):2=74:2=37$

La prima botte contiene $37+40=77\ litri$

La seconda botte contiene $37+31=68\ litri$