Corrente e portata di un fluido

La portata di un fluido

Quando si studia il moto di un fluido è importante conoscere il tipo di corrente che lo caratterizza, cioè il suo modo di procedere, il movimento ordinato che esso compie.

Ad esempio, nel caso di un fiume la corrente è rappresentata dal suo modo di percorrere il letto scendendo verso valle.

Notiamo che quando si parla di corrente si fa sempre riferimento ad un moto ordinato; nel caso, ad esempio, di un sasso lanciato in acqua, gli schizzi che vengono prodotti non rappresentano una corrente.

Per descrivere l’intensità della corrente di un fluido si considera il rapporto tra il volume di fluido che, nell’intervallo di tempo considerato, attraversa una determinata sezione trasversale della conduttura in cui si trova. (La conduttura può essere un tubo all’interno del quale scorre il liquido, o nel caso di un fiume il suo letto.)

Tale rapporto prende il nome di portata del liquido (o del gas):

$ q = frac(∆V)(∆t)$

La portata di un liquido può essere costante nel tempo, qualunque sia la sezione della conduttura considerata; in questo caso la corrente si dice stazionaria.

Quando si lascia un rubinetto aperto, e non si agisce su di esse per modificare il flusso, il getto d’acqua che fuoriesce fornisce lo stesso volume di liquido in ogni secondo; perciò, in questo caso si ha una corrente stazionaria.

Nel momento in cui il rubinetto viene chiuso, la quantità di acqua che ne fuoriesce diminuisce in ogni secondo fino ad esaurirsi completamente; in questo caso, quindi, non si ha una corrente stazionaria.

L’equazione di continuità

La portata di un fluido è direttamente proporzionale sia all’area della sezione della conduttura, via alla velocità del fluido, secondo la seguente legge:

$q = S * v$

Ciò significa che possiamo avere la stessa portata di un fluido in due diverse situazioni: in un tratto di conduttura piuttosto piccolo in cui il fluido si muove velocemente; oppure in un tratto di conduttura più ampio, in cui però la velocità del fluido è minore.

Una corrente, quindi, può essere stazionaria anche se la sua conduttura non è omogenea, ma presenta tratti più stretti e tratti più larghi; la condizione è che la sua portata sia costante nel tempo nei diversi tratti.

Una delle caratteristiche dei liquidi è il fatto che essi, nella maggior parte dei casi, sono incomprimibili; il loro volume, cioè, non viene modificato anche nel caso in cui si applica una pressione su di essi.

Quando un liquido fluisce in una conduttura, il volume di liquido che si trova in una determinata sezione, fluendo attraverso essa, ne sposta una uguale quantità che si trova in un’altra sezione; il volume di liquido spostato, quindi, è lo stesso.

Sappiamo che l’area della conduttura attraverso la quale fluisce il liquido è inversamente proporzionale alla velocità con cui esso vi scorre. In particolare, considerando la portata del liquido costante in tratti diversi, possiamo stabilire la seguente relazione:

$S_A * v_A = S_B * v_B$

Dove con A e B indichiamo i tratti che stiamo considerando; $S_A$ e $S_B$ sono, quindi, le aree che il fluido attraversa; $v_A$ e $v_B$ le relative velocità del fluido quando passa attraverso quelle sezioni.

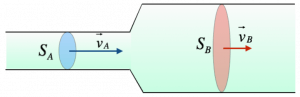
portata-fluidi — La portata di un fluido è differente a seconda della sezione del tratto di tubo che sta attraversando.

La relazione precedente prende il nome di equazione di continuità; essa ha validità solo nel caso in cui la conduttura esaminata non presenta sorgenti né pozzi, cioè se non sono presenti diramazioni o altre tubature che si immettono in essa.

Esercizio

Consideriamo un tubo di plastica all’interno del quale, nel tratto iniziale, in cui la sezione ha una raggio di 5,0 cm, l’acqua fluisce con una velocità di 1,5 m/s. Nel tratto finale il tubo si restringe, e il raggio della sezione misura 2,5 cm. Determinare la velocità dell’acqua nel tratto finale.

Il problema può essere risolto con l’equazione di continuità; possiamo, quindi, determinare le aree delle sezioni del tratto iniziale e in quello finale:

$S_i = 2πr_i = 2π*0,05 m = 0,31 m^2$

$S_f = 2πr_f = 2π*0,025 m = 0,16 m^2$

Applicando l’equazione, possiamo ricavare la velocità finale:

$S_i * v_i = S_f * v_f to v_f = frac(S_i * v_i)(S_f) = frac(0,31*1,5)(0,16) = 2,9 m/s$