 L’obiettivo didattico di questo progetto è lo studio dell’ellisse da un punto di vista analitico. Il Progetto è strutturato in 4 Lezioni, suddivise in paragrafi, nei quali verranno trattati specifici argomenti. Una Introduzione illustrerà, sinteticamente, la linea di sviluppo del Progetto e alcuni esempi rappresentativi del mondo reale. Un Test finale, a risposta multipla, offrirà la possibilità di verificare le conoscenze apprese. Il tempo medio di fruizione dell’intero modulo è di 4 ore.
L’obiettivo didattico di questo progetto è lo studio dell’ellisse da un punto di vista analitico. Il Progetto è strutturato in 4 Lezioni, suddivise in paragrafi, nei quali verranno trattati specifici argomenti. Una Introduzione illustrerà, sinteticamente, la linea di sviluppo del Progetto e alcuni esempi rappresentativi del mondo reale. Un Test finale, a risposta multipla, offrirà la possibilità di verificare le conoscenze apprese. Il tempo medio di fruizione dell’intero modulo è di 4 ore.
Autore: Antonio Bernardo
Sul calcolo della radice ennesima e sul reciproco della radice quadrata di un numero
Calcolo di Pi greco nella storia della matematica
 Per molti $pi$ è un tasto della calcolatrice che contiene un suo valore numerico, nella storia della matematica nessun’altra quantità ha colpito l’attenzione di tante persone quanto il calcolo di questo numero. Tuttavia, non c’è proprio niente di misterioso nel numero $pi$. Si sa da secoli (dagli antichi studiosi greci) che è collegato alla circonferenza ed all’area del cerchio nel seguente rapporto:
Per molti $pi$ è un tasto della calcolatrice che contiene un suo valore numerico, nella storia della matematica nessun’altra quantità ha colpito l’attenzione di tante persone quanto il calcolo di questo numero. Tuttavia, non c’è proprio niente di misterioso nel numero $pi$. Si sa da secoli (dagli antichi studiosi greci) che è collegato alla circonferenza ed all’area del cerchio nel seguente rapporto:
Programma per risolvere equazioni algebriche di grado elevato
 Il presente eseguibile è dedicato alla risoluzione di equazioni algebriche di grado anche superiore al 4°, e aventi coefficienti costituiti da numeri interi o decimali, sia negativi che positivi. Si possono pertanto calcolare e trovare tutte le radici sia reali che complesse coniugate di una equazione algebrica di qualsiasi grado a partire dal 2° sino ad arrivare a gradi elevati ( 10°, 20°, 30°, 40°, ….. ).
Il presente eseguibile è dedicato alla risoluzione di equazioni algebriche di grado anche superiore al 4°, e aventi coefficienti costituiti da numeri interi o decimali, sia negativi che positivi. Si possono pertanto calcolare e trovare tutte le radici sia reali che complesse coniugate di una equazione algebrica di qualsiasi grado a partire dal 2° sino ad arrivare a gradi elevati ( 10°, 20°, 30°, 40°, ….. ).
Si tenga presente che la precisione dei valori ottenibili per le radici dipende sia dal grado sia dai valori numerici dei coefficienti dell’equazione: più è elevato il grado dell’equazione e grande il numero di cifre che compongono i valori numerici dei coefficienti, minore sarà la precisione ottenibile per le radici dato che si opera con un aritmetica limitata alla doppia precisione. Per le equazioni di 3° e 4° grado i valori trovati per le radici possono essere confrontati con quelli calcolati tramite le formule classiche relative alla soluzione per radicali. Per l’illustrazione e la spiegazione dell’algoritmo utilizzato e la conseguente realizzazione del relativo programma si rimanda alla consultazione del seguente articolo:
La risoluzione di equazioni algebriche di grado elevato, pubblicato nella sezione Approfondimenti.
Scarica da qui il file eseguibile
Esercizi svolti sulle equazioni
Sudoku da scaricare e stampare
Bibliografia
ABBAGNANO,FORNERO De Agostini, Espresso 2006 Storia della Filosofia 7: dall’ Ermeneutica alla Filosofia analitica
ABRAVANEL,R. Garzanti 2008 Meritocrazia: 4 proposte per il talento e rendere il nostro paese più ricco e giusto.
ADAIR,J. F.Angeli 2008 Decision Making & Problem Solving Strategies
ALBERTI,GANDOLFI,LARGHI F.Angeli 2008 La pratica del problem solving: come analizzare e risolvere i problemi di management
AMATO,CHIAPPI F.Angeli 2009 Tecniche di Project Management (nuova edizione aggiornata con 6 appendici)
AMBROSINO, SCIOMACHEN Comp. & Op. Res. 2009 A heuristic for a regional fleet assignment location-routing problem. (Feb.)
ANZELLOTTI, DEL PRETE Sironi 2008 Matematici al lavoro: cinquanta e più storie di laureati in matematica
APRILE,BRIZOLI Impiantistica Italiana 2006 Il Project Management in sanità (Lug/Ago)
ARENA, CIMIOTTI Ingegneria economica 2007 Metodi di analisi dei ritardi nelle grandi opere (N°83,84)
ATIYAH,M.F. Di Renzo 2007 Siamo tutti matematici
AZZARITI,MAZZON Rcs, Etas 2006 Il valore della conoscenza: teoria e pratica del knowledge management.
BAITAGI,B.H. Springer 2008 Econometrics (Useful Introduction and solid training)
BARBUTO,M. Edises 2007 Teoria dei gochi: modelli e strategie per vincere e minimizzare i rischi
BARRON,N. Wiley 2008 Game Theory: an introduction BARTOCCI,C. Einaudi 2007 Racconti matematici
BASAK, VERSTER, JAIN Ingegneria economica 2006 ICEC & IPMA Congress On Cost Engineering (N°80, 3°trim)
BEUTELSPACHER,A. A.Salani 2008 Le meraviglie della matematica BIANCO, CARAMIA Hoepli 2006 Metodi quantitativi per il Project Management
BINDO, COSTABILE Magazine N°2 – Apr 2007 Per una nuova didattica della matematca (www.matematicamente.it)
BONACINA,G. Impiantistica Italiana 2009 Intervista a H.J. O’Donnell – A.D. attività operative
SAIPEM (Mar-Apr) BONALUMI,G. Impiantistica Italiana 2009 La flotta Saipem nel mar Caspio (Mar-Apr)
BONCINELLI,E. Laterza 2008 Come nascono le idee (I libri del festival della mente di Sarzana)
BRIZENDINE,L. Rizzoli 2007 Il cervello delle donne
BAROZZI, BERGAMINI Zanichelli 2009 La matematica per il cittadino: idee per insegnare
BRUZZANTI, BRUZZO Vallardi 2009 Finalmente ho capito a cosa serve la matematica
BUTERA,F. a cura di Mondadori 2008 Knowledge Working: Lavoro, lavoratori, società della conoscenza
CALABRESE,A. Impiantistica Italiana 2009 Italian Project Management Academy (programmi, best practice) Lug/Ago
CANTAMESSA,COBOS Isedi 2008 Il Project Management: un approccio sistemico alla gestione dei progetti
CAPPELLINI, CIMIOTTI Ingegneria economica 2007 Il Time related Cost Index: impatto dei variation order (caso Impregilo) (N°83,84)
CARON,FUMAGALLI Impiantistica Italiana 2006 Valutazioni del rischio per progetti di E & C (Nov/Dic)
CAVEDINI,P. San paolo 2006 Decidere con efficacia: neurobiologia delle decisioni
CERUTTI,A. Ingegneria economica 2008 Risk management nel processo edilizio (N°85,86)
CHIAPPI,R. Springer 2006 Problm Solving nelle organizzazioni: idee, metodi e strumenti da Mosè a Mintzberg.
CHIAPPI,R. Springer-Animp 2006 Mod.e met. per la pian. ed il contr. dei progetti: la cassetta degli attrezzi del P.M.
CHIAPPI,R. Ingegneria economica 2006 Linked Plan: Pianificare e controllare i progetti con l’aiuto del foglio elettronico (N° 78)
CHIAPPI,R. Impiantistica Italiana 2006 Filosofia e Matematica per il Project Management ed il Problem Solving (Gen/Feb)
CHIAPPI,R. Impiantistica Italiana 2006 Modelli e metodi per la pianificazione ed il controllo dei progetti (Mar/Apr)
CHIAPPI,R. Impiantistica Italiana 2006 Matematica e neuroeconomia nel "problem solving" (parte prima – Nov/Dic)
CHIAPPI,R. Impiantistica Italiana 2007 Matematica e neuroeconomia nel "problem solving" (parte seconda – Mar/Apr)
CHIAPPI,R. Impiantistica Italiana 2008 Strumenti di Problem Solving: programmazione lineare (Set/Ott)
CHIAPPI,R. F.Angeli 2008 Il foglio elettronico per il problem solving: metodi e modelli per le organizzazioni
CHIAPPI,R. Matematicamente.it 2009 Filosofia e Matematica per il P.Management e il P.Solving
CHIAPPI,R. Impiantistica Italiana 2009 Strumenti di Problem Solving: programmazione non lineare e discreta (Mag-Giu)
CHIAPPI,R. Impiantistica Italiana 2009 Strumenti di Problem Solving: tecniche per le decisioni (Set/Ott)
CIARDELLO,A Impiantistica Italiana 2006 Nuova tecnica di Risk Management (per progetto Qatif in Arabia Saudita) (Gen/Feb)
CILIBERTO,SALERI Springer 2008 I Numeri nel cuore
CLOUGH,SEARS J.Wiley 2008 Construction Project Management
COGNO, GATTI Impiantistica Italiana 2007 Analisi del rischio per la gestione del procurement (Mag/Giu)
COLICCHIA,C. Impiantistica Italiana 2008 Corso avanzato in project management (Mag/Giu)
CONCARI, MONTEFIORE Impiantistica Italiana 2006 Rapporto tra EPC contractor e fornitori nei "mega project" (Gen/Feb)
COOPER, LOWE, SORBI Springer 2008 New Computational Paradigms: changing conception of what is computable
CORBELLINI, RIVINO Sestante 2007 GIE: Competizione e successo nella storia dell’industria elettromeccanica italiana
CORBELLINI,F. Impiantistica Italiana 2008 Il nucleare italiano si farà all’estero (Mar/Apr)
CORBELLINI,G. Longanesi 2009 Perché gli scienziati non sono pericolosi
CORNOLDI,C. Il Mulino 2007 L’intelligenza
COSTANTINO, TRONCI Impiantistica Italiana 2009 Approccio fuzzy all’analisi dei rischi della manutenzione (Lug/Ago)
COSTIN,A. Elsevier 2008 Managing Difficult Projects
CRAINER, DEARLOVE Rcs, Etas 2006 Il grande libro dei Guru: i pensatori che hanno fatto il management
DADDA,L. Polipress 2006 La nascita dell’informatica in Italia
DE BIASE, L. Feltrinelli 2008 Economia della felicità: dalla blog-sfera al valore del dono e oltre
DE FINETTI Cortina 2006 L’invenzione della verità: il testamento filosofico di un grandissimo matematico.
DE MARCO, Rafele Ingegneria economica 2006 Using System Dynamics To Understand Project Performance (N°79, 2° trim)
DE MARCO,A. Impiantistica Italiana 2007 Comprendere la performance dei progetti-simulazione dinamica (Sett/Ott)
DI CASTRI,G. Flaccovio 2009 Project Management per l’ edilizia
Di GIULIO,ARLATI Impiantistica Italiana 2008 Efficienza versus efficacia nel Procurement: gli asset differenziali (Gen/Feb)
DI MAIO,RAMANELLI Impiantistica Italiana 2007 Life Cycle Management & Project Control: Esperienze Ansaldo Trasporti (Gen/Feb)
DILWORTH,C Springer 2008 Scientific Progress (Reletion Between Successive Scientific Theories)
DONAL O’SHEA Rizzoli 2007 La congettura di Poincaré EISNER,H. Wiley 2008 Essentials of Project and Systems Engineering Management
EMMER,M. Springer 2006 Matematica e cultura 2006.
FERRARI,C. Impiantistica Italiana 2007 A modest proposal: vendere le cariche pubbliche ? (Gen/Feb)
FERRARI,C. Impiantistica Italiana 2007 PIL-lole di economia spicciola (importanza del PIL e sua determinazione) (Mag/Giu)
FIUME, DI GIULIO Impiantistica Italiana 2008 Project risk management nel settore EPC (Nov-Dic)
FLOREANI,A. Rcs, Etas 2006 Introduzione al Risk Management: approccio integrato alla gest. dei rischi aziendali.
FORZAN,A Impiantistica Italiana 2008 "Leadership in Safety", strumento Saipem per la sicurezza sul lavoro (Lug/Ago)
FURLANETTO,L: F.Angeli 2008 Ingegneria della manutenzione
GIANNINI,R. Impiantistica Italiana 2008 Gestione delle risorse umane in attività di frontiera (Mar/Apr)
GLAVINCH,T.E. Wiley 2008 Contractors Guide to Green Building Construction
GRASSELLI, MENINI Hoepli 2008 Sistemi dinamici: Introduzione all’analisi e primi strumenti di controllo
GUADAGNO,G Impiantistica Italiana 2009 Project Management Excellence applicata a un progetto complesso (Gen-Feb)
GUALA,MOTTERLINI Università Bocconi 2008 L’economia cognitiva e sperimentale HELDMAN, KIM Wiley 2009 PMP: Project Management Professional Exam, Certification Kit.
HUGHES,J.W. UPNE 2007 Enviromental Problem Solving: A How-To Guide
IPERTI,L. Impiantistica Italiana 2007 La storia del GIE, un protagonista dell’impiantistica italiana (Nov/Dic)
ISABELLA,A. Impiantistica Italiana 2006 Creare valore attraverso l’eccellenza nelle attività di approvvigionamento (Mar/Apr)
JESTON, NELIS Elsevier 2008 Management by Process: A pratical road-map to sustainable B.P.M.
JMMERSON,C. Productivity Press 2007 A3 Problem Solving for Healthcare: A Pratical Method for Eliminating Waste
KLEIN,L.R. Il Mulino 2007 Macroeconomia, econometria e politica economica
KOOMEY,J.G. Analytics Press 2008 Turning Numbers Into Knowledge: Mastering the art of Problem Solving
La ROSA,E., IACONO,G. Impiantistica Italiana 2008 Focus sul Project Management: prima girnata nazionale del P.M. (Gen/Feb)
LEGRENZI,P. Il Sole 24 Ore 2007 Psicologia e investimenti finanziari:finanza comportamentale e scelte d’investimento
LUCCHETTI,R. Springer 2007 Passione per Trilli. Alcune idee della matematica
MANTEL,MEREDITH;SHAFER Wiley 2007 Project Management in Practice (MS-Project, Crystal Ball, PMI)
MATTEO,M. Impiantistica Italiana 2007 Project management nel settore del fashion (creatività) (Sett/Ott)
MEESTER,R. Springer 2008 A Natural Introduction to Probability Theory
MEGHINI, BERETTA Impiantistica Italiana 2007 PM alla Siemens: nuova metodologia, tecnologia WiMax (Sett/Ott)
MENKES,J. Rcs, Etas 2006 La nuova intelligenza manageriale: oltre l’intelligenza emotiva. Il QI dei leader.
MEREDITH,MANTEL John Wiley 2008 Project Management : a managerial approach
MESSI,C. Impiantistica Italiana 2008 Sicurezza: il cantiere Techint per l’impianto di metanolo in Egitto (Lug/Ago)
MICHELI, DI GIULIO, TRINGALI Impiantistica Italiana 2008 Selezione dei fornitori rischio-efficienti (Mar/Apr)
MILLAN GASCA,A. Springer 2006 Fabbriche, Sistemi, organizzazioni: storia dell’ingegneria industriale.
MORI,R. Impiantistica Italiana 2006 Il Project Management questo noto sconosciuto (Mag/Giu)
MORRIS, PINTO Wiley 2007 The Wiley Guide to Project, Program and Portfolio Management
MORRIS, PINTO Wiley 2007 The Wiley Guide to Project Control
MORRIS, PINTO Wiley 2007 The Wiley Guide to Project Organization and Project Management Competencies
MORRIS, PINTO Wiley 2007 The Wiley Guide to Project Technology, Supply Chain, and Procurement Management
MOTTERLINI,M. Rizzoli 2006 Economia Emotiva: che cosa si nasconde dietro i nostri conti quotidiani
MOTTERLINI,M. Rizzoli 2008 Trappole mentali: come difendersi dalle proprie illusioni e dagli inganni altrui
MUIR, N.C. Wiley 2009 Computers for seniors for Dummies
NANCI, MARTELLUCCI Ingegneria economica 2007 Isotherm Plant (esempio di network impiantistico) (N°83,84)
NEPI,A. F.Angeli 2006 Analisi e Gestione dei Rischi di Progetto
NOTARBARTOLO,M. Impiantistica Italiana 2008 Progetti per l’utilizzo delle sabbie bituminose in Canada (Mag/Giu)
ODIFREDDI,P. Mondadori 2009 Il Club dei matematici solitari OKASHA,S. Einaudi 2006 Il primo libro di filosofia della scienza
O’REGAN,G. Springer 2008 A Brief History of Computng (dal 3000 A.C. a Microsoft)
OSBORNE,R. Editori riuniti 2007 La filosofia a fumetti
OZZOLA,V. Ingegneria economica 2006 Ricordi e Riflessioni di un ricercatore operativo in ambito petrolifero (N°78, 1° trim))
OZZOLA,V. Alinea editrice 2007 Divertimento su temi di Ricerca operativa: immersione del reale nella matematica
PALLADINO, D&C Carocci 2007 Logiche non classiche. Un introduzione
PARNELL, DRISCOLL Wiley 2008 Decision Making in Systems Engineering and Management.
PATRONE, PETRILLI Ingegneria economica 2006 Valore della durata delle concessioni: teoria e problemi applicativi (N°81, 4°trim)
PELLEGRINI U. Impiantistica Italiana 2006 Gestione di un contratto EPC in Cina (Nov/Dic)
PELLEGRINI U. Impiantistica Italiana 2007 Gestione di un contratto EPC in Cina (Sett/Ott)
PERRIN,R. Wiley 2008 Real World project Management
PIATTOLI,TRIPODO Impiantistica Italiana 2007 Andamento del mercato impiantistico (Lug/Ago)
PINTO,G. Impiantistica Italiana 2007 Qualità, ambiente, sicurezza, etica: futuro o nuova moda (Sett/Ott)
PINTO,R. Impiantistica Italiana 2007 Introduzione alla gestione del rischio nella supply chain (Nov/Dic)
PIOVANO,SICA Impiantistica Italiana 2006 Il Project Management per i XX Giochi Olimpici di Torino 2006 (Lug/Ago)
PORCELLACCHIA,C. Impiantistica Italiana 2007 Sistema di controllo di progetto e di processo (Sett/Ott)
POWELL,BAKER Wiley 2007 Management Science: The art of modeling with Spreafsheet
RAGO,E. Ingegneria economica 2006 The Multidimensional ity of the Project Management Prodess (N°79, 2°trim)
RANIERI,L. Impiantistica Italiana 2007 Risk management nello sviluppo per progetti (20° IPMA Congess) (Gen/Feb)
RANIERI,L. Impiantistica Italiana 2007 Gestione dell’incertezza sui tempi di un progetto d’ingegneria (Sett/Ott)
RICOLFI,L. Guerini 2008 Ostaggi dello stato: le origini politiche del declino e della insicurezza
RORY,VJ. Wiley 2008 The Executive Guide to Boosting Cash Flow and Shareholder Value
ROSSI,G. Impiantistica Italiana 2006 Sistema di controllo dei general contractor (Nov/Dic)
RUBINSTEIN, KROESE Wiley 2007 Simulation and Monte Carlo method
SANVITO,P. Impiantistica Italiana 2007 Identificazione dei rischi e delle opportunità contrattuali (Sett/Ott)
SCHIAVINA,L. F.Angeli 2006 Metodi e strumenti per la modellizzazione aziendale. Come gestire il Problem Solving
SHEN,A, Springer 2008 Algoritms and Programming: problems and solutions
STACKPOLE,C. Wiley 2009 PMP certification All-In One Desk Reference For Dummies TALEB N.N: il Saggiatore 2008 Il Cigno nero: come l’improbabile governa la nostra vita
TARTARI,R. F.Angeli 2006 Il Sei Sigma con Excel
TERNA, BOERO, MORINI, … Il Mulino 2006 Modelli per la complessità: la simulazione ad agenti in economia.
TITOLO,M. Impiantistica Italiana 2007 Diagnosi aziendale: auditing delle carenze e criticità (Mag/Giu)
TONCHIA, NONINO Il Sole 24 Ore 2008 Il Project Management: gestire l’innovazione nei prodotti e nei servizi
TORRE,M Luiss University Press 2006 Project Management: teoria ed esercizi
TOSI,F. Impiantistica Italiana 2006 Tecniche di controllo nel Project management (Nov/Dic)
TUCCI,CARLI Impiantistica Italiana 2006 Sistemi informativi nei processi di Engineering & Contracting (Mag/Giu)
TURRA,E. Impiantistica Italiana 2007 Project management per l’innovazione nella pubblica amministrazione (Sett/Ott)
VERCELLIS,C. CLUP 2006 Business Intelligence e teoria delle decisioni
VERCELLIS,C. Wiley 2008 Business Intelligence: Data mining and Optimization for Decision Making
VERZHU,E. Wiley 2008 The Fast Forword MBA in Project Management: PMP Certification
VILLA,A. Impiantistica Italiana 2007 Elementi per la preparazione di un claim contrattuale, 1° parte (Mar/Apr)
VILLA,A. Impiantistica Italiana 2007 Elementi per la preparazione di un claim contrattuale, 2° parte (Mag/Giu)
VRAKAS,VLAHAVAS Idea Group Inc 2008 Artificial Intelligence for Advanced Problem Solving Techniques
Rombo – matematica elementare
Pagina Web creata con Crossword Compiler.
Scarica il gioco in formato RTF.
6 Sudoku da stampare livello Medio
6 Sudoku da stampare livello Facile
Scarica e stampa 6 Sudoku di livello "facile" tutti in una pagina.
Scarica da qui il file DOC
6 Sudoku da stampare livello Molto facile
Scarica e stampa 6 Sudoku di livello "molto facile". Sei schemi per pagina.
Scarica da qui il file DOC
6 Sudoku da stampare livello Difficile
Scarica e stampa sei Sudoku di livello difficile in un solo foglio.
Scarica da qui il file DOC
Crucinumero: semplici espressioni numeriche
Il simobolo “^” è il segno di elevato alla potezna. Per esempio 3^2 = 9.
Pagina Web creata con Crossword Compiler.
CruciPuzzle – Informatica
Pagina Web creata con Crossword Compiler.
CruciPuzzle – Matematica elementare
Pagina Web creata con Crossword Compiler.
CONCORSO “Ridere di Matematica”: De Angelis vince il primo premio
 "L’alba del numero" di De Angelis è la vignetta vincitrice del concorso Ridere di Matematica.
"L’alba del numero" di De Angelis è la vignetta vincitrice del concorso Ridere di Matematica.
2° "Cominciò tutto così" di Cominelli
3° "Sulla punta delle dita" di Dinnocenzi
4° "Compiti" di Dako
5° "Le espressioni" di Veci
Vedi tutte le vignette
Vedi le 100 più votate
Ridere di matematica
15 dicembre 2007 – 31 marzo 2008
Si conclude il concorso dedicato a vignettisti e aspiranti tali sul tema dell’umorismo nella matematica, che ha il fine di promuove una immagine della matematica più amichevole, divertente e vicina alla vita di tutti i giorni.
Sulla base delle votazione degli utenti iscritti alla community Matematicamente.it, la giuria ha dato le seguenti valutazioni
1) L’ALBA DEL NUMERO di De Angelis, voti della giuria 8+10+10+9 totale 37
2) COMINCIO’ TUTTO COSI’ di Cominelli, voti della giuria 9+5+6 totale 20
3) SULLA PUNTA DELLE DITA di Dinnocenzi, voti della giuria 9+5+1 totale 15
4) COMPITI di Dako, voti della giuria 8+4 totale 12
5) LE ESPRESSIONI di Veci, voti della giuria 3+8 totale 11
Hanno ottenuto voti da parte della giuria
FIBONACCI Vs. MORFEO di Bruno voti 10
LA MATEMATICA VISTA DAI GIOVANI di Rododentro voti 10
1 + 1 = 2 di Farina voti 7+2
E’ IL PENSIERO CHE CONTA di Luttazi voti 9
LA RADICE QUADRATA di Gigante voti 1+7
NOBBITA FUMA LA PIPA di Piro voti 8
LA SIGNORA CARLOTTA di Rododentro voti 7
NOBBITA di Piro voti 7
I VERI PROBLEMI DELLA MATEMATICA di Piazza voti 6
SORSEGGIANDO LA MATEMATICA di Luttazi voti 6
PROBLEMI DI COMUNICAZIONE di Mau voti 4+1
ADDIZIONE di Samilruvido voti 2+3
POPOLARITA’ DELLA MATEMATICA di Piazza voti 5
NOI RAGAZZI SCHIZZINOSI di Rododentro voti 5
URLO di Cannistra voti 04
LA RIVOLTA DEI NUMERI di Gallino voti 04
CIVICA SOMMA di Bruno voti 3
LEZIONE DI MATEMATICA di Cannistra voti 2
DEFORMAZIONE PROFESSIONALE di Pace voti 1
La giuria ha ritenuto anche di segnalare le seguenti vignette non arrivate tra le prime 50
GIORNO DI PIOGGIA di Amcw
TEOREMA di Graz
SINFONIA di Zepponi
LA FATICA di Pieroni
MATEMATICA A MONTECITORIO di Morandi
LE PROPRIETA’ DELLO ZERO di Spina
PIU’ O MENO BELLO di Ravazzoni
NUOTO NEI NUMERI di Elisa
I vincitori dei 5 premi sono pregati di contattare la redazione all’indirizzo [email protected] per indicare il recapito dove consegnare il premio.
– – – – – – – – – – – – – – – – – –
La matematica viene spesso ‘evitata’ dalla comunicazione di massa per il senso di paura e frustrazione che la accompagna. L’immagine comune che si dà di questa scienza e di chi la pratica è quella di una disciplina grigia, che non fa ridere, adatta a robot, calcolatrici, computer o per umani che aspirano a diventare tali e poco adatta a persone ricche di emozioni, inclini all’umorismo e al divertimento. Gli organizzatori si propongono di promuovere un’immagine della matematica più familiare, più vicina al mondo dei ragazzi e alla vita sociale di tutti.
|
|
|
GIURIA
Roberto Mangosi
Vignettista satirico, collabora con diversi periodici tra i quali La Settimana Enigmistica, Linus, Playboy, PM, Domenica Quiz, Gente Enigmistica e con il TG1 per la rubrica "Filo Diretto"
http://enteroclisma.blogspot.com/
Pasquale Todisco a.k.a. Squaz
Fumettista e illustratore, collabora con Frigidaire, Urban, Inguine, Ma(h)gazine, Rolling Stone, XL, Slowfood, Internazionale.
http://it.dada.net/freeweb/vtodisco/biografia.htm
Ennio Peres
Enigmista e ‘giocologo’ matematico collabora con La Stampa, Paese Sera, L’Unità, Linus ha scritto diversi libri di giochi matematici. http://it.wikipedia.org/wiki/Ennio_Peres
Fioravante Patrone
Docente ordinario di Teoria dei giochi presso l’Università di Genova
http://www.diptem.unige.it/patrone/
REGOLAMENTO
Al concorso posso partecipare persone di ogni età e nazionalità.
E’ ammessa l’associazione tra partecipanti per un elaborato a più mani.
Le vignette possono essere realizzate con qualsiasi tecnica grafica, computer compreso, a colori o in bianco e nero.
Ogni autore può presentare al più tre vignette.
Le vignette dovranno avere carattere ironico ma non irriverente e offensivo nei confronti di persone singole, categorie o gruppi.
Le vignette e i dati del concorrente dovranno essere presentati in forma esclusivamente elettronica all’indirizzo e-mail: [email protected] nelle modalità indicate in fondo al regolamento.
Di ogni vignetta, il concorrente dovrà inviare un file TIF ad alta risoluzione entro il 29 febbraio 2008.
La partecipazione al concorso è gratuita.
Le vignette inviate saranno pubblicate sul sito www.matematicamente.it con link alla pagina personale dell’autore o degli autori.
I promotori dell’iniziativa si riservano il diritto di non pubblicare le vignette che non riterranno idonee.
Gli autori, inviando i loro lavori acconsentono automaticamente a concedere gratuitamente la pubblicazione delle immagini sul sito www.matematicamente.it.
Gli autori manterranno i diritti verso eventuali terzi che ne dovessero richiedere il riutilizzo.
L’invio degli elaborati e la compilazione dei dati personali richiesti comporta automaticamente l’accettazione del presente regolamento.
MODALITA’ DI VOTAZIONE
Gli utenti registrati a Matematicamente.it potranno esprimere per ogni vignetta un voto.
La giuria sceglierà le vignette vincitrici tra le 20 50 (aumentato a causa dell’elevato numero di partecipanti) vignette più votate.
I premi non possono essere cumulati dalla stessa persona.
|
calendario |
|
| 15 dicembre 2007 | inizio invio dei lavori |
| 29 febbraio 2008 | fine invio dei lavori |
| 1 marzo 2008 | inizio votazione degli utenti |
| 25 marzo 2008 | fine votazione degli utenti |
| 31 marzo 2008 | proclamazione dei vincitori da parte della giuria |
Con la collaborazione di Gabriella Zammillo
|
Inviare le vignette a [email protected] Oggetto della e-mail: Partecipazione al concorso Nel messaggio indicare: 1. Nome d’arte o firma da pubblicare (sarà indicato come l’autore della vignetta). 2. Cognome e nome (indica prima il cognome e poi il nome – se vuoto significa che l’autore preferisce far conoscere solo il nome d’arte). 3. Indirizzo da mail (sarà indicato tra i dati dell’autore – se vuoto significa che l’autore preferisce non pubblicare il proprio indirizzo e-mail). 4. Sito web dell’autore (se vuoto significa che l’autore non ha un proprio sito web o non intende renderlo noto). 5. Breve biografia (non superare i 1000 caratteri, altrimenti la redazione sarà costretta a sintetizzare). 6. Per ogni vignetta allegata indicare un titolo. |
————————-
concorso segnalato da
Geometria elementare
Pagina Web creata con Crossword Compiler.
Scarica il gioco in formato RTF.
CruciPuzzle – parole di fisica
 Un giochino che piace sempre, il crucipuzzle non è molto impegnativo ma può essere utile per familiarizzare con termini tecnici. Individua nello schema tutte le parole dell’elenco e scoprirai la frase nascosta.
Un giochino che piace sempre, il crucipuzzle non è molto impegnativo ma può essere utile per familiarizzare con termini tecnici. Individua nello schema tutte le parole dell’elenco e scoprirai la frase nascosta.
Pagina Web creata con Crossword Compiler.
Sperimentazione di didattica della matematica con Cabri
Dov’è Moriarty? Cerchiamo la via più breve con Mathcad
 Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, “Qual è la via più breve tra tre punti ? o tra quattro punti?” Per esempio, fate conto di essere Sherlock Holmes che si sta avvicinando al suo mortale nemico, Moriarty. Dalle informazioni che avete in mano, sapete che Moriarty…
Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, “Qual è la via più breve tra tre punti ? o tra quattro punti?” Per esempio, fate conto di essere Sherlock Holmes che si sta avvicinando al suo mortale nemico, Moriarty. Dalle informazioni che avete in mano, sapete che Moriarty…
Fantasio Festival
Sta per tornare il FantasioFestival di Moony Witcher: musica, pittura, gioco, creatività e tanti concorsi dedicati alle scuole.
La grande festa della creatività dei ragazzi è già pronta. Torna a Perugia dal 16 al 20 aprile 2008 il Fantasio Festival, manifestazione nazionale dedicata alla creatività dei ragazzi per la direzione artistica della scrittrice fantasy Moony Witcher che lo scorso anno ha visto aggirarsi nel centro storico di Perugia ben 50 mila creativi, più o meno “in erba”, in soli 4 giorni.
La novità di quest’anno si chiama Fantasio Giovani, uno spazio dedicati agli adolescenti in cui saranno protagonisti gli studenti degli istituti d’arte e dei conservatori musicali. Ma sono tantissime anche le riconferme e le iniziative rivolte a giovani e giovanissimi.
Il Fantasio Festival 2008 tornerà dunque nella sua veste tradizionale, dedicata ai tanti linguaggi della creatività con laboratori di pittura, filosofia, giocoleria, enigmistica etc.., gli spettacoli teatrali, musica e gli incontri con i più amati scrittori per bambini.
Il Fantasio Giovani, invece, si aprirà il 18 aprile: i ragazzi potranno essere davvero protagonisti e, accanto ai giovani aspiranti scrittori, i Gas, che hanno già partecipato lo scorso anno, quest’anno arriveranno anche gli aspiranti musicisti e gli aspiranti pittori, cioè i ragazzi che frequentano gli istituti d’arte, i licei artistici e i conservatori musicali. Non mancheranno laboratori di giornalismo, incontri con artisti e filosofi, spettacoli teatrali, mostre. Il Fantasio Festival ha già portato fortuna ai giovani artisti: gli scrittori in erba che hanno partecipato lo scorso anno hanno visto i loro racconti pubblicati in un libro a cura dell’organizzazione e alcuni di loro hanno proseguito camminando sulle loro gambe e pubblicando poi con case editrici.
Le scuole continuano ad essere le protagoniste. Agli istituti di ogni ordine e grado sono indirizzati i vari concorsi proposti dal Fantasio festival. Eccoli, in sintesi.
Le avventure di Gatto Fantasio – Scuole Primarie. Quattro incipit, scritti da Moony Witcher apriranno la porta ad altrettanti mondi fantastici. I bambini dovranno scrivere il finale di un delle storie attraverso le modalità creative che sentiranno più consone. (Pittura, scrittura etc). Per informazioni: [email protected]
Noi e Geno. ( A cura di Giunti Editore) – Scuole Primarie. A tutto teatro con la rappresentazione vivente di brani tratti dai libri di Moony Witcher. Per informazioni: [email protected]
Gas al minimo 1 e 2. Scuole secondarie e superiori. Si tratta di concorsi di scrittura dedicati ai ragazzi delle scuole secondarie e delle superiori. Vi possono partecipare come scuola o singolarmente. I 20 più bei racconti di ogni categoria verranno selezionati dalle scrittrici Moony Witcher, Giusy Quarenghi e Patrizia Finucci Gallo e pubblicati in un libro che verrà presentato durante le giornate del FantasioFestival. Per informazioni [email protected] per i ragazzi dagli 11 ai 13 anni; [email protected] per i ragazzi delle scuole superiori.
Sperimentare l’arte. Dipingere la Libertà – Licei artistici e scuole d’arte. I ragazzi si esibiranno in una performance artistica sul tema della libertà durante le giornate del festival, secondo le modalità previste dall’organizzazione. Per informazioni: [email protected]
Sperimentare la musica. Suonare la libertà. – Conservatori o Istituti di musica. Gli studenti dovranno spedire entro il 20 gennaio 2008 la scheda d’iscrizione e un dvd contenente un’esibizione singola o di gruppo di un brano inedito da loro composto che abbia come tema la libertà, della durata massima di 3 minuti, che eseguiranno durante le performance musicali previste al Fantasio Giovani. Per informazioni [email protected].
Per ogni informazione e aggiornamento visitate il sito www.fantasiofestival.it.
Il teorema del resto cinese
 Nel primo secolo d. C. lo scrittore cinese Sun-Tse pose la domanda: quale numero diviso per 3, per 5 e per 7, dà come resti 2, 3 e 2 rispettivamente?
Nel primo secolo d. C. lo scrittore cinese Sun-Tse pose la domanda: quale numero diviso per 3, per 5 e per 7, dà come resti 2, 3 e 2 rispettivamente?
MateSalento
 Percorsi matematici a Lecce e dintorni
Percorsi matematici a Lecce e dintorni
Si svolgerà dal 26 novembre al 19 dicembre 2007 a Lecce, presso l’edificio Studium 2000 dell’Università del Salento, la mostra MateSalento in cui il visitatore è invitato ad avvicinarsi in modo piacevole alla più astratta delle discipline e guardare con occhi nuovi il Salento e il suo territorio.
 La mostra MATESALENTO, la cui realizzazione è stata resa possibile grazie al contributo della Regione Puglia, nasce dalla collaborazione intrapresa tra il Seminario Permanente “Matematica: Scienza senza Frontiere” dell’Università del Salento e l’unità locale di Trento del Centro Interuniversitario di Ricerca “Matematita” per la Comunicazione e l’Apprendimento Informale della Matematica allo scopo, non solo, di suscitare curiosità e interesse nel campo matematico, ma di contribuire alla valorizzazione del patrimonio culturale di un luogo ricco di arte, architettura e più generale creatività umana quale appunto il Salento. Il visitatore è pertanto invitato a “fare esperienza” di matematica, divertendosi a scoprire le geometrie nascoste nelle opere d’arte, nelle composizioni architettoniche e nella vegetazione di cui i comuni salentini sono straordinariamente ricchi. Topologia, visualizzazione e simmetria le aree tematiche affrontate; poster, multimedia, video e teatro virtuale 3D con ricostruzioni tridimensionali e rappresentazioni virtuali gli strumenti messi a disposizione. Prezioso a tal proposito il supporto scientifico del Coordinamento SIBA, del Laboratorio DIDA e del Museo dell’Ambiente dell’Università del Salento, coinvolti nella realizzazione dell’evento. Una mostra dunque, come strumento per avvicinare il pubblico in maniera stimolante a problemi sotto certi aspetti anche complessi, che consente di toccare la matematica con mano, ma al tempo stesso di apprezzare e valorizzare il meraviglioso patrimonio artistico e culturale custodito dal territorio salentino.
La mostra MATESALENTO, la cui realizzazione è stata resa possibile grazie al contributo della Regione Puglia, nasce dalla collaborazione intrapresa tra il Seminario Permanente “Matematica: Scienza senza Frontiere” dell’Università del Salento e l’unità locale di Trento del Centro Interuniversitario di Ricerca “Matematita” per la Comunicazione e l’Apprendimento Informale della Matematica allo scopo, non solo, di suscitare curiosità e interesse nel campo matematico, ma di contribuire alla valorizzazione del patrimonio culturale di un luogo ricco di arte, architettura e più generale creatività umana quale appunto il Salento. Il visitatore è pertanto invitato a “fare esperienza” di matematica, divertendosi a scoprire le geometrie nascoste nelle opere d’arte, nelle composizioni architettoniche e nella vegetazione di cui i comuni salentini sono straordinariamente ricchi. Topologia, visualizzazione e simmetria le aree tematiche affrontate; poster, multimedia, video e teatro virtuale 3D con ricostruzioni tridimensionali e rappresentazioni virtuali gli strumenti messi a disposizione. Prezioso a tal proposito il supporto scientifico del Coordinamento SIBA, del Laboratorio DIDA e del Museo dell’Ambiente dell’Università del Salento, coinvolti nella realizzazione dell’evento. Una mostra dunque, come strumento per avvicinare il pubblico in maniera stimolante a problemi sotto certi aspetti anche complessi, che consente di toccare la matematica con mano, ma al tempo stesso di apprezzare e valorizzare il meraviglioso patrimonio artistico e culturale custodito dal territorio salentino.
L’ingresso è gratuito.
E’ obbligatoria la prenotazione per le scuole.
E’ gradita la partecipazione.
Orari di apertura: dal 26 novembre al 19 dicembre 2007 dal lunedì al venerdì ore 09.00 – 13.00
Geometria differenziale delle curve con Mathematica
Scarica il file in formato nb (Notebook Mathematica 10 MB)
Laboratorio di Informatica per Economia
Scarica il file in formato XLS
Le nuove figure professionali
Modulazioni dell’e-business
Analisi tecnica dei mercati finanziari: analisi algoritmica
Internet
L’informazione digitale
L’informazione: codifica ed elaborazione
Appunti di Antonio Bernardo per il Corso di Informatica di base
Scarica la dispensa completa della lezione di informatica (.pdf 424 KB)
. . . . . . . . . .
I temi della dispensa sono in sintesi i seguenti
Cos’è l’informatica
Studio sistematico degli algoritmi che descrivono e trasformano l’informazione: la loro teoria, analisi, progetto, efficienza, realizzazione e applicazione
ACM (Association for Computing Machinery)
Scienza della rappresentazione e dell’elaborazione dell’informazione Supporti e codifica I livelli dell’informazione
I livelli dell’informazione
Livello sintattico
Livello semantico
Livello pragmatico
L’informazione sintattica
1928 R. Hartley – 1948 C. Shannon
Adeguatezza del supporto
Accuratezza della trasmissione La codifica binaria
L’alfabeto più semplice che si può adottare è costituito da due soli simboli solitamente indicati con 0 1
Dispositivi bistabili – bit (binary digit)
Bit – unità elementare di informazione Informazione analogica / digitale
Nella forma analogica una grandezza è rappresentata in modo continuo. Nella forma digitale una grandezza è rappresentata in modo discreto.
Standard IEC per i prefissi binari
Con k bit si possono rappresentare 2k informazioni
8 bit formano 1 byte
I multipli del byte sono:
Chilo byte KB corrisponde a 210=1024 byte, approssimativamente 1KB = 1000 byte
Mega byte, approssimativamente 1MB=1.000.000 byte
Giga byte, approssimativamente 1GB=1.000.000.000 byte
Tera byte, approssimativamente 1TB=1.000.000.000.000 byte
Codifica binaria di dati numerici
Standard per la codifica binaria del testo
Quanta memoria occupa il testo di un libro?
I formati di testo
.TXT caratteri ASCII nella forma estesa ISO-Latin-8859
.DOC formato di Microsoft Word
.RTF Rich Text Format
.HTML documenti per il browser
.PDF Portable Document Format
.SXW Open office
.ZIP formato compresso lossless LZW
La codifica delle immagini
Mappa di pixel – formato bitmap: l’immagine viene memorizzata come insieme di pixel, ognuno con le sue caratteristiche (colore, luminosità, trasparenza) raggruppate in una matrice di pixel
Descrizione geometrica – formato vettoriale: l’immagine viene archiviata in forma di descrizione geometrica e una serie di caratteristiche di apparenza (dimensione della penna, colore, tipo di linea, …)
Immagine bitmap con PAINT
Immagine vettoriale con PowerPoint
Sistema additivo e sottrattivo dei colori
RGB (Red Green Blu) per visualizzare immagini su schermo
CMYK (Ciano-azzurro Magenta-rosso Giallo –Black) per stampare le immagini in quadricromia Codice colori in html
Formati di immagini
Come per i caratteri si è cercato di stabilire alcuni standard per la codifica delle immagini
GIF è un formato proprietario permette di archiviare in formato compresso immagini con colori a 8 bit per pixel, ossia 256 colori, permette la codifica di immagini animate, usa un algoritmo di compressione lossless (vedi nota) ossia senza perdita di informazioni
BMP formato per sistemi operativi Microsoft e OS/2 utilizzato ormai in tutti i sistemi operativi permette di archiviare con diversa profondità di colore: 1, 4, 8, 24 bit
PNG dovrebbe sostituire il formato GIF ma non ammette l’animazione
TIFF nato per semplificare lo scambio di immagini tra scanner e programmi applicativi è applicato in diversi ambiti professionali è senza perdita di informazioni (lossy)
JPG formato di archiviazione con perdita di informazione, può comprimere con un rapporto elevatissimo, viene visualizzata in RGB a 24 bit per pixel
File audio
Il suono è un segnale continuo, per essere memorizzato deve essere campionato ottenendo così un segnale digitale. I parametri che caratterizzano il campionamento sono
1. Il numero di canali: la modalità mono ha uno solo canale mentre quella Stereo ne ha due separati, sinistro e destro. Ovviamente un segnale stereo occupa il doppio di uno mono. Nelle applicazioni più recenti il numero di canali è notevolmente aumentato (surround).
2. La risoluzione: Rappresenta il numero di bit utilizzati per rappresentare i campioni. Solitamente si utilizzano 8 o 16 bit per campione, nel primo caso si hanno 256 valori possibili, relativamente pochi perché offrono una qualità del suono inferiore a quella di un nastro, nel secondo si hanno circa 65.000 valori.
3. La frequenza di campionamento: È il numero di campioni al secondo, può variare da 11 khz adatta alla registrazione della voce, a 22 khz adatta alla registrazione di un nastro fino a 44 khz per una registrazione a qualità cd. Questo parametro deve esser scelto in modo da poter ricostruire il segnale originario da quello campionato.
File audio e compressione
Analogica (dischi in vinile) Digitale (CD anni ’80)
• WAVE (formato non compresso)
• MP3 (formato compresso)
• MIDI (formato vettoriale)
• Streaming audio
Per approfondire test ECDL
Architettura di un calcolatore
Appunti di teoria dei grafi per Sociologia
|
1. Problemi classici che coinvolgono i grafi
I quattro esempi "storici" proposti mettono in evidenza come problemi molto diversi tra loro possono essere modellati mediante la stessa struttura matematica: il grafo. Tra le altre applicazioni:
Nella tabella seguente alcuni esempi di situazioni problematiche concrete che possono ricnodnotte ai problemi classici:
2. Grafi : definizioni e proprietà fondamentali GRAFO NON ORIENTATO
Notiamo subito che : ADIACENZA E INCIDENZA GRADO DI UN VERTICE TEOREMA Indicando con vi un vertice di un grafo, con nv il numero di vertici e con ns il numero di spigoli, si ha MULTIGRAFO PASSEGGIATA – PERCORSO – SENTIERO – CICLO LEMMA
|
In un grafo, ogni ciclo deve avere lunghezza maggiore o uguale a 3
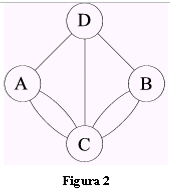
GRAFO CONNESSO
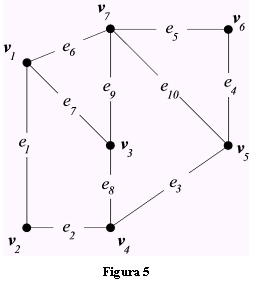
Un grafo si dice connesso (Fig.6) se esiste un sentiero tra due qualsiasi suoi vertici. In fig.7 è riportato un esempio di grafo non connesso (p.e., non esiste un sentiero da v4 a v7 ).
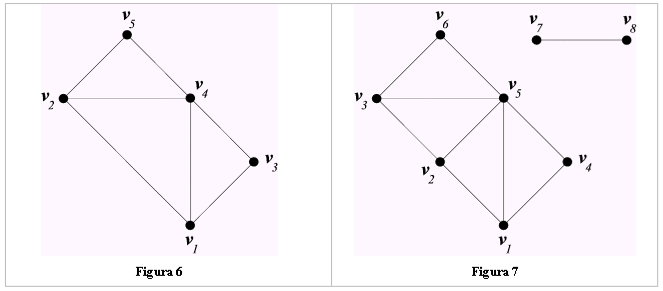
GRAFO TRAVERSABILE
Un grafo (o un multigrafo) si dice traversabile se può essere disegnato senza mai alzare la penna dal foglio e senza mai passare due volte per lo stesso spigolo.
In un grafo traversabile, quindi, esiste un passeggiata nella quale sono inclusi tutti i vertici e dove vengono usati tutti gli spigoli una sola volta (mentre si può passare per un vertice quante volte si vuole). Tale passeggiata si chiama percorso traversabile. Un esempio di grafo traversabile è dato in Fig. 6: (v1 , v2 , v4 , v1 , v3 , v4 , v5 ) è un percorso traversabile.
|
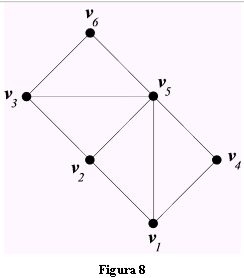
A titolo di esempio determiniamo le caratteristiche del grafo connesso di Fig.8. Consideriamo la passeggiata da v4 a v6 : (v4, v1, v2, v5, v1, v2, v3, v6). Questa passeggiata non è un percorso, perché lo spigolo (v1, v2) viene usato due volte. La successione (v4, v1, v5, v2, v6) non è una passeggiata, perché manca lo spigolo (v2, v6). La successione (v4, v1, v5, v2, v3, v5, v6) |
|
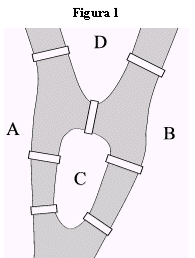
3. Analisi del grafo dei ponti di Koenigsberg
Siamo ora in grado di studiare il problema dei ponti di Koenigsberg.
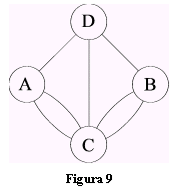
Il problema ammette soluzioni se si riesce a dimostrare che il multigrafo associato al problema (fig.9) è traversabile.
| Vediamo come ha ragionato Eulero. Consideriamo un multigrafo traversabile, e supponiamo che un percorso traversabile P non inizi (e quindi non finisca) in V. Il vertice V è sicuramente di grado pari perché ogni volta che P entra in V da uno spigolo, deve sempre uscirne da uno spigolo non usato in precedenza; in altre parole nel vertice V il numero di ingressi è uguale al numero di uscite, e quindi il grado di V è pari. Questo significa che se un vertice U ha grado dispari, allora il percorso P deve iniziare e finire in U. Di conseguenza, se un multigrafo ha più di due vertici dispari, allora non è traversabile. Il grafo fig. 9 ha quattro vertici dispari, e quindi non è traversabile: il problema dei ponti di Koenigsberg non ha soluzione. |
|
Eulero, in effetti, dimostrò la proposizione inversa a quella esposta in precedenza. In particolare dimostrò il seguente teorema.
TEOREMA DI EULERO
Un grafo connesso finito è un GRAFO traversabile se e solo se ha due vertici di valenza dispari, oppure nessuno.
4. Grafi hamiltoniani
I grafi traversabili si chiamano grafi euleriani. In questi grafi, esiste una passeggiata chiusa che comprende tutti gli spigoli del grafo una sola volta.
Il matematico William Rowland Hamilton si pose il problema duale: quali sono le condizioni affinché esista una passeggiata chiusa che includa tutti i vertici una sola volta? Tale passeggiata è evidentemente un ciclo, e prende il nome di ciclo di Hamilton. Non è ancora stato trovato un metodo generale per determinare il ciclo hamiltoniano di un grafo qualunque, e molti matematici sono attualmente impegnati nella ricerca di questo metodo.
Un interessante problema "hamiltoniano" è il problema del commesso viaggiatore, già accennato all’inizio: un commesso viaggiatore deve visitare dei clienti in alcune città. Come deve scegliere il percorso stradale che collega tutte le città da visitare con la città di partenza, in modo da minimizzare i chilometri da percorrere?
Il problema può essere modellato da un grafo, in cui i vertici sono le città (e qualche incrocio stradale…), mentre gli spigoli sono tutte le strade percorribili che collegato le città tra di loro (compresa la città di partenza)
Il lettore provi a risolvere il problema seguente, costruendo il grafo appropriato.
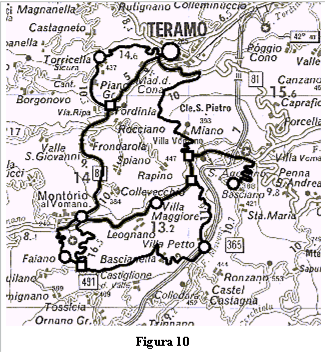
| Problema
Un tecnico di manutenzione di impianti termici, residente a Teramo, deve visitare dei clienti nelle seguenti località: · Torricella Sicura · Montorio · Faiano · Villa Petto · Villa Maggiore · Castel Castagna · Basciano
Il tecnico vuole percorrere meno strada possibile. Qual è il percorso minimo? O, in altri termini, qual è il ciclo hamiltoniano del grafo associato al problema? I dati sulle lunghezze delle strade sono inseriti nella cartina. |
|
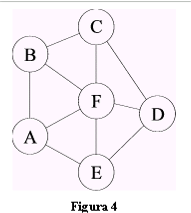
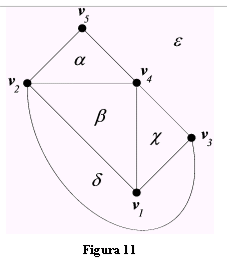
5. Grafi planari
Un grafo si dice planare se può essere tracciato in un piano e se i suo spigoli non si intersecano. Chiameremo mappa un grafo planare. Una mappa divide in facce il piano che la contiene.
| Per esempio la mappa in fig. 11 è suddivisa in cinque facce TEOREMA |
|
Importante (anche nella geometria solida) è il seguente:
TEOREMA DI EULERO
Indicando con nv il numero di vertici di una mappa connessa M, con ns il numero di spigoli e con il numero delle facce, si ha: nv – ns + nF =2
6. Mappe colorate
Consideriamo una mappa M. Due facce di M si dicono adiacenti se hanno uno spigolo in comune. Una colorazione di M consiste nell’assegnare ad ogni faccia di M un colore in modo che facce adiacenti abbiano colori diversi.
Una mappa M è n-colorabile se bastano n colori. Possiamo ora esaminare il seguente teorema :
TEOREMA DEI QUATTRO COLORI
Ogni mappa è 4-colorabile
La formulazione del teorema è di una semplicità disarmante. Nonostante questo, la sua dimostrazione ha impegnato per quasi 130 anni i migliori matematici. La sua prima formulazione risale al 1852, quando l’inglese Francis Guthrie in una lettera lo propose al fratello Frederick, allievo del famoso matematico Augustus De Morgan. Del problema venne a conoscenza Hamilton, al quale De Morgan il 23 ottobre del 1852 scriveva :
"… un mio studente mi ha chiesto oggi il perché di un fatto. Egli dice che se si divide una figura, in modo qualsiasi, in regioni e si vogliono colorare queste regioni in modo diverso, cioè in modo che regioni confinanti risultino colorate in modo diverso, possono essere necessari quattro colori ma non di più: ossia ogni carta geografica può essere colorata con un massimo di 4 colori".
Il problema non interessò immediatamente né Hamilton né i matematici dell’epoca. Tuttavia, il fatto che non si riusciva a trovare una dimostrazione coinvolse via via sempre più matematici. Per 124 anni il teorema rimase una congettura fino a che, nel 1976, due matematici dell’Università dell’Illinois (USA), Kenneth Appel e Wolfgang Haken, con l’ausilio determinante dei più potenti calcolatori dell’epoca, riuscirono a dimostrare il teorema. Occorsero più di 1200 ore di tempo-macchina su tre diversi elaboratori elettronici. Era la prima volta che un teorema veniva dimostrato con l’ausilio di un elaboratore elettronico, cosa che suscitò all’epoca non poche discussioni tra i matematici.
7. Il salto del cavallo
Il matematico Dudeney inventò 80 anni fa il seguente problema, assai facile da risolvere con un grafo, ma che presenta notevoli difficoltà se risolto per tentativi.
Consideriamo la scacchiera ridotta di fig. 12, in cui ci sono 2 cavalli neri e due cavalli bianchi. Il gioco consiste nello scambiare di posto i due cavalli bianchi con i due neri.
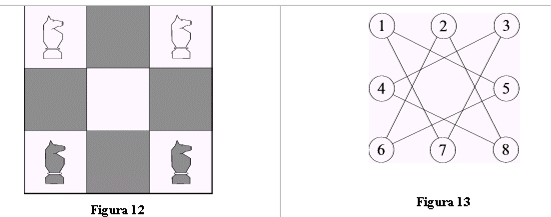
Costruito il grafo del problema (fig.13), notiamo innanzitutto che il grafo non è planare. Ma questo non è un problema: si può fare in modo di disegnare un grafo equivalente a quello di fig.13, ma senza lati che si intersecano.
Un’interessante articolo su un problema analogo a questo (con una scacchiera più grande di quella di fig.12) può essere letto alla pagina
http://space.tin.it/scuola/vdepetr/t18/Text18.htm
Giovanni Valentini
Matematica delle elezioni
Appunti di teoria dei giochi
Appunti di probabilità per Sociologia
La tua età al cioccolato
Calcoli psicologici
 Ti verranno proposti alcuni esercizi di calcolo che molte volte portano a dei risultati strani… La cosa importante è svolgere i calcoli il più velocemente possibile senza ragionarci troppo…
Ti verranno proposti alcuni esercizi di calcolo che molte volte portano a dei risultati strani… La cosa importante è svolgere i calcoli il più velocemente possibile senza ragionarci troppo…

P/17 Holmes: una pazza cometa
 In questi giorni di fine ottobre la cometa P/17 Holmes ha deciso di sorprenderci, come solo una cometa sa fare. In poche ore la sua luminosità è cresciuta di un milione di volte facendole fare un balzo in avanti di circa 14 magnitudini e rendendola facilmente visibile come una stella sfuocata di seconda grandezza, nella costellazione del Perseo.
In questi giorni di fine ottobre la cometa P/17 Holmes ha deciso di sorprenderci, come solo una cometa sa fare. In poche ore la sua luminosità è cresciuta di un milione di volte facendole fare un balzo in avanti di circa 14 magnitudini e rendendola facilmente visibile come una stella sfuocata di seconda grandezza, nella costellazione del Perseo.
 In questi giorni di fine ottobre la cometa P/17 Holmes ha deciso di sorprenderci, come solo una cometa sa fare. In poche ore la sua luminosità è cresciuta di un milione di volte facendole fare un balzo in avanti di circa 14 magnitudini e rendendola facilmente visibile come una stella sfuocata di seconda grandezza, nella costellazione del Perseo. Essendo molto lontana dal Sole una tale attività è probabilmente dovuta ad un collasso di strutture superficiali che hanno messo a nudo per la prima volta ingenti quantità di ghiaccio. La peculiarità di questa cometa è che anche in un telescopio di 30 cm si presenta quasi perfettamente sferica senza alcun accenno di coda (al 29 Ottobre quantomeno). E’ la prima volta che mi capita di vedere un oggetto simile. Tra l’altro anche le dimensioni apparenti sono notevoli. L’immagine a lato è stata acquisita con lo stesso setup strumentale e mostra che la Holmes è estesa quanto il Mare Serenitatis. La chioma continua ad espandersi e al momento non è chiaro cosa succederà nei prossimi giorni. Purtroppo da queste parti il meteo difficilmente consentirà ulteriori riprese. Consiglio pertanto un giro sulle pagine della gallery di spaceweather.com dove sono raccolte immagini provenienti da ogni parte del mondo.
In questi giorni di fine ottobre la cometa P/17 Holmes ha deciso di sorprenderci, come solo una cometa sa fare. In poche ore la sua luminosità è cresciuta di un milione di volte facendole fare un balzo in avanti di circa 14 magnitudini e rendendola facilmente visibile come una stella sfuocata di seconda grandezza, nella costellazione del Perseo. Essendo molto lontana dal Sole una tale attività è probabilmente dovuta ad un collasso di strutture superficiali che hanno messo a nudo per la prima volta ingenti quantità di ghiaccio. La peculiarità di questa cometa è che anche in un telescopio di 30 cm si presenta quasi perfettamente sferica senza alcun accenno di coda (al 29 Ottobre quantomeno). E’ la prima volta che mi capita di vedere un oggetto simile. Tra l’altro anche le dimensioni apparenti sono notevoli. L’immagine a lato è stata acquisita con lo stesso setup strumentale e mostra che la Holmes è estesa quanto il Mare Serenitatis. La chioma continua ad espandersi e al momento non è chiaro cosa succederà nei prossimi giorni. Purtroppo da queste parti il meteo difficilmente consentirà ulteriori riprese. Consiglio pertanto un giro sulle pagine della gallery di spaceweather.com dove sono raccolte immagini provenienti da ogni parte del mondo.
 30 ottobre 2007. Dopo aver aspettato un varco tra le nuvole per ore, qualche volta invano, sono alla fine riuscito a riprendere nuovamente questa interessantissima cometa. La chioma si espande molto rapidamente come evidenzia il confronto tra le immagini del 29 e del 30 Ottobre, ma a causa della diversa efficacia della pressione di radiazione solare la shell di polvere tende a perdere la simmetria sferica originaria. L’alone verdognolo costituito probabilmente da gas sembra ricalcare la struttura della shell di polvere, il che significherebbe una qualche connessione tra le due componenti.
30 ottobre 2007. Dopo aver aspettato un varco tra le nuvole per ore, qualche volta invano, sono alla fine riuscito a riprendere nuovamente questa interessantissima cometa. La chioma si espande molto rapidamente come evidenzia il confronto tra le immagini del 29 e del 30 Ottobre, ma a causa della diversa efficacia della pressione di radiazione solare la shell di polvere tende a perdere la simmetria sferica originaria. L’alone verdognolo costituito probabilmente da gas sembra ricalcare la struttura della shell di polvere, il che significherebbe una qualche connessione tra le due componenti.
1 novembre 2007. Questa cometa continua imperterrita a dare spettacolo. In un buco tra le nuvole di una ventina di minuti ho ripreso alcune immagini che dimostrano l’ulteriore espansione della chioma. Ormai le dimensioni sono quasi al limite del campo utile della mia CCD e si attestano attorno ai 10′. L’offset tra le regioni centrali e quelle più esterne continua ad aumentare; inoltre, la zona in direzione antisolare è più sfumata di quella frontale. Non si intravede alcuna coda nonostante l’integrazione abbastanza lunga a causa della persistente velatura del cielo. Infatti, chi ha avuto la possibilità di effettuare riprese a lunghissima posa sotto cieli migliori, ha evidenziato una tenue coda di gas strutturata in vari filamenti che inizia a far capolino. Uno spettacolare esempio lo trovate sul sito del validissimo Lorenzo Comolli. L’elaborazione, in particolare mediante l’algoritmo di Larson-Sekanina, evidenzia alcuni getti piuttosto attivi alcuni dei quali si dipartono dal nucleo. Secondo Francois Colas dall’Osservatorio del Pic du Midi se si segue "…the evolution of dust stream in the inner coma. Here you can see details moving, so there are real. It is clear that all the trails are coming from pieces of the comet ejected at the begining the the bigger event on October 24th." Cosa abbia innescato questo processo esplosivo è tuttora un mistero. Oltretutto è la seconda volta che accade dopo l’outburst del 1892, per cui sembrerebbe un fenomeno connesso alla struttura stessa della cometa piuttosto che a fattori esterni.
 5 novembre 2007. Finalmente qualche ora di sereno dopo tante nuvole. La cometa è davvero notevole. Vista al telescopio assomiglia ad una medusa, una sorta di Pelagia noctiluca cosmica. La chioma, la cui struttura interna è molto articolata, continua ad espandersi mantenendo comunque una luminosità elevata. L’immagine a sinistra è stata ottenuta con un semi-apo da 80mm dato che le strutture periferiche non entrano più nel campo di vista della ccd con il 300mm. La chioma interna è estesa più di 12′ mentre quella di gas esterna ha superato i 40′. Nelle riprese profonde si nota finalmente un accenno di coda. Purtroppo la cometa è quasi lungo la linea di vista della Terra per cui la osserviamo quasi frontalmente. Anche se probabilmente la coda è molto estesa nello spazio non riusciremo a vederla. L’aspetto positivo è che con questa configurazione geometrica la cometa è visibile quasi per tutta la notte.
5 novembre 2007. Finalmente qualche ora di sereno dopo tante nuvole. La cometa è davvero notevole. Vista al telescopio assomiglia ad una medusa, una sorta di Pelagia noctiluca cosmica. La chioma, la cui struttura interna è molto articolata, continua ad espandersi mantenendo comunque una luminosità elevata. L’immagine a sinistra è stata ottenuta con un semi-apo da 80mm dato che le strutture periferiche non entrano più nel campo di vista della ccd con il 300mm. La chioma interna è estesa più di 12′ mentre quella di gas esterna ha superato i 40′. Nelle riprese profonde si nota finalmente un accenno di coda. Purtroppo la cometa è quasi lungo la linea di vista della Terra per cui la osserviamo quasi frontalmente. Anche se probabilmente la coda è molto estesa nello spazio non riusciremo a vederla. L’aspetto positivo è che con questa configurazione geometrica la cometa è visibile quasi per tutta la notte.
http://www.dlcosmos.eu/pagine/kosmos/dlcosmos_photo_of_the_week.htm
Area e volume di un solido con Excel
 Un semplice foglio Excel per studenti della secondaria di primo grado dove si mostrano le formule da inserire per il calcolo dell’area della superficie e il volume dei solidi.
Un semplice foglio Excel per studenti della secondaria di primo grado dove si mostrano le formule da inserire per il calcolo dell’area della superficie e il volume dei solidi.
La natura del numero
 Continua il ciclo degli “Incontri 2007 tra scienza e filosofia” del Centro Studi Enriques di Livorno, dedicato alla riflessione sui temi e gli orientamenti della cultura scientifica. Mercoledì 14 novembre alle 16 alla Biblioteca Labronica di Livorno si terrà una Tavola rotonda che avrà per tema “La natura del numero”, con interventi di Paolo Bussotti, Giuseppe Puglisi e Franco Turini.
Continua il ciclo degli “Incontri 2007 tra scienza e filosofia” del Centro Studi Enriques di Livorno, dedicato alla riflessione sui temi e gli orientamenti della cultura scientifica. Mercoledì 14 novembre alle 16 alla Biblioteca Labronica di Livorno si terrà una Tavola rotonda che avrà per tema “La natura del numero”, con interventi di Paolo Bussotti, Giuseppe Puglisi e Franco Turini.
Kit di sopravvivenza alle matrici di Hadamard
 Il mio primo incontro con le matrici H avvenne a pagina 167 del secondo libro di calcolo di Tom Apostol: appena mezza pagina in caratteri piccoli, con la definizione ed alcune nozioni elementari. La cosa sarebbe potuta finire lì se undici pagine dopo il buon Apostol non avesse proposto tra gli esercizi due strane matrici quadrate, una di ordine 4 e una di ordine 6 composte soltanto da 1 e da -1, delle quali invitava a calcolare i determinanti.
Il mio primo incontro con le matrici H avvenne a pagina 167 del secondo libro di calcolo di Tom Apostol: appena mezza pagina in caratteri piccoli, con la definizione ed alcune nozioni elementari. La cosa sarebbe potuta finire lì se undici pagine dopo il buon Apostol non avesse proposto tra gli esercizi due strane matrici quadrate, una di ordine 4 e una di ordine 6 composte soltanto da 1 e da -1, delle quali invitava a calcolare i determinanti.
Script per il metodo di bisezione
function[c,fc,it,err]= bisezioni(a,b,fun,toll)
%%%METODO DELLE BISEZIONI
%%%
%%%Dati di input
%%% a,b = estremi dell’intervallo
%%% fun = funzione f
%%% toll = tolleranza sull’errore per accettare la soluzione
%%%
%%%Dati di output
%%% c = soluzione approssimata
%%% fc = valore di f in c
%%% it = iterate necessarie per approssimare c
%%% err = errore commesso nell’approssimazione
subplot(1,2,1),
fplot(fun,[a b]), hold on,
it=0;
%i valori della funzione negli estremi sono
fa = feval(fun,a);
fb = feval(fun,b);
subplot(1,2,1)
plot(a,fa,’r*’,b,fb,’r*’),hold on,
%verifico se sono soddisfatte le ipotesi del teorema di esistenza degli zeri
if(fa*fb)>=0
disp(‘Il metodo non è applicabile o lo zero è un estremo dell”intervallo’);
else
err = abs(a-b);
subplot(1,2,2),
semilogy(it,err,’r*’), hold on,
%blocco iterativo della funzione
while(it<101 & err>toll)
it = it+1;
c = (a+b)/2;
fc = feval(fun,c);
if(fa*fc)<0
b=c;
else a=c;
end
err = abs(a-b);
subplot(1,2,2),
semilogy(it,err,’g*’), hold on,
end
fa = feval(fun,a);
fb = feval(fun,b);
subplot(1,2,1),
plot(a,fa,’bo’,b,fb,’bo’),
subplot(1,2,2)
semilogy(it,err,’g*’), hold on
end
subplot(1,2,1), hold off
subplot(1,2,2), hold off
Matematica e computer: 2° convegno nazionale
 Giornata di lavoro con gli studenti protagonisti.
Giornata di lavoro con gli studenti protagonisti.
Rende 23 novembre 2007
Aula Magna Università della Calabria
Scarica la locandina del convegno
Aiuta Matematicamente.it votalo per il premio WWW del Sole24ore
 Vota 5 stelline per il nostro sito nella categoria Istruzione e Lavoro.
Vota 5 stelline per il nostro sito nella categoria Istruzione e Lavoro.
Puoi vincere un’auto o un computer
http://premiowww.ilsole24ore.com/vota.php?category_id=9
Rilasciata la versione 8 di ORIGIN software per l’Analisi dei dati
Da un comunicato pervenuto alla Redazione
Comunicato Stampa – 6 Novembre 2007
Rilasciata la nuova versione 8 di Origin®, il software leader di mercato per l’Analisi dati e la Grafica Scientifica
I ricercatori e i professionisti in diverse aree del mondo della Ricerca, dell’Industria e Universitario, necessitano di strumenti di analisi e di grafica molto potenti e intuitivi che possano interagire con i loro dati e creare report personalizzati.
Origin 8 include una serie di caratteristiche che soddisfano al meglio le necessità sia di scienziati che di ingegneri; i File di lavoro a fogli multipli, la pubblicazione di grafici di grande qualità e gli strumenti di analisi standardizzati forniscono un solido e integrato ambiente software per importare, esplorare e analizzare dati, creare e modificare grafici e pubblicare il proprio lavoro.
Per essere certi che Origin risponda a tutte le necessità di analisi dati sono stati integrati nella versione 8 strumenti per statistica avanzata, regressione, analisi non lineare delle curve, processamento di segnali, processamento di immagini e analisi dei picchi. Siccome ogni operazione di analisi può essere definita per essere automaticamente riaggiornata, è possibile utilizzare i propri progetti come template per lavori futuri, in modo da semplificare la routine quotidiana.
Caratteristiche principali di Origin 8
File di lavoro a fogli multipli
Il nuovo ambiente di lavoro a fogli multipli di Origin 8 con la formattazione rich-text permette di consolidare e gestire i dati importati, le immagini, le query su database, i risultati e i grafici delle relative analisi.
Grafici, immagini e note possono essere inclusi nelle celle del foglio di lavoro facilitando una miglior organizzazione del progetto e creazione di documentazione e report.
Importazione di dati all’interno di Origin
Rendere disponibili i dati all’interno di Origin 8 è estremamente semplice; è possibile accedere ai dati da una grande varietà di risorse sia importando i file utilizzando query SQL, sia aprendo direttamente file Excel.
I formati di file importabili includono:
ASCII, Etas Inca, imc Mess-Systeme GmbH – Famos, Molecular Devices® pCLamp, Mathematica®, Matlab®, Minitab®, National Instruments® LabView e DIAdem, Princeton Instruments e Thermo®, SPC data files o qualsiasi formato programmato dall’utente.
L’Import Wizard di Origin importa e analizza i dati attraverso un’anteprima dei dati contenuti nei file ASCII con informazioni nella testata o nei file binari con strutture conosciute.
Pubblicazione di grafici di grande qualità
All’interno di Origin è possibile creare con un semplice click un enorme varietà di grafici 2D, 3D, statistici e a curve. E’ possibile aggiungere istantaneamente una nuova elaborazione grafica in un grafico esistente utilizzando il drag-and-drog da un foglio Origin o Excel.
Tutti gli elementi di un grafico possono essere personalizzati a proprio piacimento utilizzando l’interfaccia point-and-click. La formattazione di un grafico può essere copiata e incollata in un altro o salvata come tema e applicata in seguito, attraverso il Theme Organizer.
Nella nuova versione 8 sono stati aggiunti i seguenti tipi di grafico:
Contour plot directly from XYZ data using triangulation; Contour plot boundary support; Polar Contour plot; Scatter Matrix plot; Stacked Lines by Y Offset plot.
Potente analisi di dati
Origin 8 offre una grande scelta di analisi, incluse Descriptive Statistics, Hypothesis Testing, One-Way and Two-Way ANOVA, Baseline and Peak Analysis, FFT, Filtering, Smoothing, Linear Regression e Nonlinear Curve Fitting.
E’ possibile controllare tutti gli aspetti delle analisi utilizzando le specifiche interfacce standardizzate; i settaggi preferiti possono essere salvati come temi per utilizzi futuri.
Origin 8 può aggiornare automaticamente qualsiasi operazione di analisi quando la fonte dati o i parametri delle analisi vengono variati.
Questa potente caratteristica può essere utilizzata per creare template preconfigurati per sviluppare analisi o aggiornare i risultati. Un template di analisi può essere costituito sia da un singolo file di lavoro Origin che da un intero progetto.
Programmazione
Origin offre uno stabile e robusto ambiente di programmazione e, introduce nella versione 8, una nuova tecnologia chiamata X-Functions.
X-Functions, programmi scritti nel linguaggio proprio di Origin Origin C, forniscono una intelaiatura per creare programmi personalizzati che funzionano all’interno di Origin, permettendo di sviluppare e condividere le proprie specifiche operazioni di analisi e graficazione.
Origin 8 è compatibile con Windows Vista o precedenti.
Risoluzione di un sistema lineare
Scarica il file in formato XLS
Risoluzione di un’equazione non elementare
Scarica il file in formato XLS
Ricerca operativa
Scarica il file in formato XLS
Ricerca obiettivo esercizio 1
Scarica il file in formato XLS
Grafico di una funzione
Scarica il file in formato XLS
Calcolo matriciale
Scarica il file in formato XLS

 livello
livello 





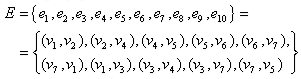
 Calcoli matematici per scoprire la tua personalità e …
Calcoli matematici per scoprire la tua personalità e … 