Autore: Alfredo Bochicchio

Calcola l’altezza relativa all’ipotenusa di un triangolo rettangolo conoscendo la misura dei lati

Calcola l’altezza relativa all’ipotenusa di un triangolo rettangolo sapendo che la misura dei lati è $15cm$, $20cm$ e $25cm$

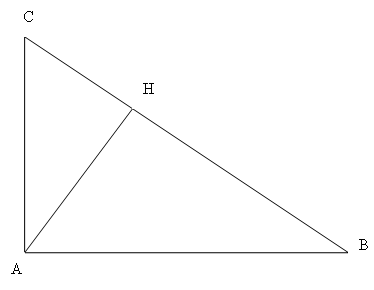
Figura triangolo con altezza

$AB=20cm$
$AC=15cm$
$BC=25cm$
$AH=……..$

Soluzione

Per calcolare l’altezza dell’ipotenusa dobbiamo calcolare prima l’area e poi possiamo ottenerla con le formule.

$A=(ABxxAC)/2=(15xx20)/2=15xx10=150$

Ora possiamo calcolare la misura di $AH$

$A = (CB xx AH) / 2 => A xx 2 = CB xx AH => $

$ => AH = (A xx 2) / (CB) = (150 xx 2) / 25 = 12$

$AH=12cm$

 

Puoi trovare altri esercizi completamente risolti di geometria, in forma di videolezione, per la seconda media sul sito delle videolezioni di Matematicamente.it.

 

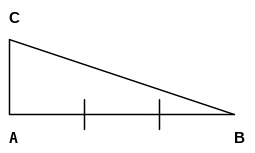
In un triangolo rettangolo i cateti sono uno il triplo dell’altro e la loro differenza è $24cm$.

In un triangolo rettangolo i cateti sono uno il triplo dell’altro e la loro differenza è $24cm$. Calcola l’area del triangolo.

Soluzione

Triangolo rettangolo

$AB=3AC$

$AB-CA=24cm$

$A=…$

In questo caso conosciamo la differenza e conosciamo che un cateto è il triplo dell’altro.

Dobbiamo vedere da quante parti è fatta la differenza. Siccome $AB=3AC$ il numero della parti che compongono la differenza è $2$.

Se la differenza è composta da $2$ parti e misura $24cm$, allora
$AC=24:2=12$, perchè $AC$ è composto da una sola parte.

$AB=3/2xx24=12xx3=36$ perchè $AB$ è composto da tre parti.

È facile allora a questo punto calcolare l’area del triangolo:
$A=(ABxxAC)/2=(12xx36)/2=12xx18=216cm^2$

$A=216cm^2$.

In un parallelogrammo il perimetro è di $86cm$ e la misura di ciascun lato minore è inferiore di 7cm

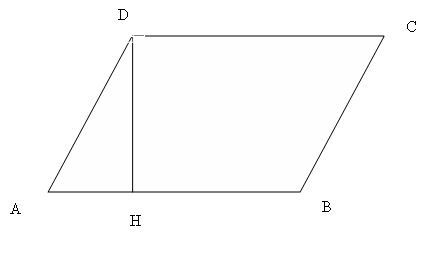
In un parallelogrammo il perimetro è di $86cm$ e la misura di ciascun lato minore è inferiore di $7cm$ di quella di ciascun lato maggiore. Calcola la misura dell’altezza relativa al lato maggiore, sapendo che l’altezza relativa al lato minore è lunga $20cm$Figura parallelogramma

$P=86cm$

$AD=BC=AB-7$

$DK=20cm$

$DH=……$

 

 

 

 

Bisogna calcolare la misura della base e del lato obliquo. Sappiamo anche che $AB-AD=7cm$, perciò sottraiamo al semiperimetro la differenza fra i lati e dividiamo per due, in modo da ottenere il lato obliquo.

$AD=(86:2-7):2=(43-7):2=36:2=18$

$AB=AD+7=18+7=25$

Ora ci possiamo calcolare l’area.

$A=BCxxDK=20xx18=360$

Ora che conosciamo l’area e la misura del lato maggiore,del lato minore, e dell’altezza relativa al lato minore, possiamo calcolare la misura di DH dividendo l’area per l’altro lato.

$DH=360:25=14,4$

$DH=14,4cm$

 

In un parallelogrammo la differenza delle misure della base e dell’altezza ad essa relativa è $8m$

In un parallelogrammo la differenza delle misure della base e dell’altezza ad essa relativa è $8m$. Calcola l’area del parallelogrammo sapendo che la base è $3/2$ dell’altezza.Figura del parallelogramma di altezza H

 

$AB-DH=8m$

$AB=(3)/(2)DH$

$A=……$

 

 

 

 

Sapendo quanto vale la differenza tra base e altezza e da quanti pezzi è composta la base e l’altezza possiamo calcolarne la misura.

$AB=8xx3=24$

$DH=8xx2=16$

Oppure:

$DH=(2)/(3)AB=2/3xx24=16$

Ora ci possiamo calcolare l’area.

$A=ABxxDH=24xx16=384$

 

 

$A=384m^2$

Nel parallelogramma ABCD della figura, il lato AB misura 10m e l’altezza DH ad esso relativa è lunga

Nel parallelogramma ABCD della figura, il lato AB misura 10m e l’altezza DH ad esso relativa è lunga 4m. Calcola la misura dell’altezza relativa al lato BC sapendo che esso è lungo 8Parallelogramma di altezza Hm.

 

$AB=10m$

$DH=4m$

$BC=8m$

$DK=……$

 

 

 

Per calcolare la misura di $DB$ si deve prima calcolare l’area del parallelogrammo. Per calcolarla possiamo prendere o come base $AB$ e la relativa altezza o $BC$ e la relativa altezza. Dovendo calcolare l’altezza relativa a $BC$ prendiamo in considerazione $AB$ come base.

$A=ABxxDH=10xx4=40$

A questo punto possiamo calcolre la misura di $DB$:

$DK=A:BC=40:8=5$

Si può riunire tutto in un unica formula:

$DB=ABxxDH:CB=10xx4:8=40:8=5$

 

$DB=5m$

In un Parallelogrammo la somma delle misure della base e dell’ altezza ad essa relativa è di $50cm$

In un parallelogrammo la somma delle misure della base e dell’ altezza a essa relativa è di $50cm$ Calcola l’area sapendo che l’altezza è $2/3$ della base.

Parallelogramma con altezza

 

 

$AB+DH=50cm$

$DH=(2)/(3)AB$

$A=……$

 

 

 

 

Soluzione

Dobbiamo trovare l’area conoscendo la somma di altezza e base e che frazione è l’altezza della base. Possiamo ricavarci base e altezza vedendo da quante parti è fatto l’intero.

$2+3=5$

$AB=50:5xx3=10xx3=30$

$DH=50:5xx2=10xx2=20$

Possiamo calcolarci $DH$ anche facendo:

$DH=(2)/(3)AB=2/3xx30=20$

Ora possiamo calcolare l’area:

$ABxxDH=30xx20=600$

$A=600cm^2$

In un rettangolo l’area è di $2464dm^2$ e l’altezza misura $44dm$.

In un rettangolo l’area è di $2464dm^2$ e l’altezza misura $44 dm$. rettangolo.pngCalcola il suo perimetro.

 $A=2464dm^2$

$AD=44dm$

$AB=$……

$P=$……

 

 

 

 

Sappiamo che l’area del rettangolo si calcola con base per altezza. Da questo ci possiamo ricavare le formule inverse: $b=a:h$ $h=a:b$.

Per calcolare il perimetro dobbiamo sapere quanto misura la base:

$AB=A:AD=2464:44=56dm$

Ora possiamo calcolarci il perimetro:

$(AB+AD)xx2=(56+44)xx2=100xx2=200dm$

Si può svolgere tutto in un unico passaggio:

$(AD+A:AD)xx2=(44+2464:44)xx2=(44+56)xx2=100xx2=200$

 

$AB=56dm$

$P=200dm$

${(2/5+2/15+1/45)xx [(11/8+1/5+7/40)xx(12/5-2/15+7/30)xx4/5+5/2]xx9/10}+1/3$

${(2/5+2/15+1/45)xx [(11/8+1/5+7/40)xx(12/5-2/15+7/30)xx4/5+5/2]xx9/10}+1/3$

${(18+6+1)/45xx[(55+8+7)/40xx(72-4+7)/30xx4/5+5/2]xx9/10}+1/3$

${25/45xx[70/40xx75/30xx4/5+5/2]xx9/10}+1/3$

${5/9xx[7/4xx5/2xx4/5+5/2]xx9/10}+1/3$

${5/9xx[(7xx5xx4)/(4xx2xx5)+5/2]xx9/10}+1/3$

${5/9xx[140/40+5/2]xx9/10}+1/3$

${5/9xx[7/2+5/2]xx9/10}+1/3$

${5/9xx12/2xx9/10}+1/3$

$(5xx13xx9)/(9xx2xx10)+1/3$

$12/4+1/3$

$3+1/3$

$(9+1)/3$

$10/3$