Sai ched’è la statistica? È na’ cosa
che serve pe fà un conto in generale
de la gente che nasce, che sta male,
che more, che va in carcere e che spósa.
Ma pè me la statistica curiosa
è dove c’entra la percentuale,
pè via che, lì, la media è sempre eguale
puro co’ la persona bisognosa.
Me spiego: da li conti che se fanno
seconno le statistiche d’adesso
risurta che te tocca un pollo all’anno:
e, se nun entra nelle spese tue,
t’entra ne la statistica lo stesso
perch’è c’è un antro che ne magna due.

Trilussa spiega bene, nella sua poesia provocatoria perché la media da sola non basta a caratterizzare una situazione. E’ anche necessario tener conto del caso peggiore. E’ vero che il computo del caso peggiori è già incluso nel valor medio, ma non è sufficiente. Per valutare correttamente il benestare di una popolazione è necessario, oltre a considerare il reddito medio, pesare quello della classe più povera.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Le riflessioni che seguono sono indotte dal bell’articolo di Maurizio Rosina (Rif. 1) recentemente comparso su www.matematicamente.it ,che tra l’altro invoca la semplicità nel proporre indici per le decisioni in quanto i decisori, (top manager o politici che siano) e non del tutto a torto, malvolentieri accettano risultati basati su indicatori complessi di cui non comprendono bene la natura.

 

 

 

 

 

 

 

 

 

 

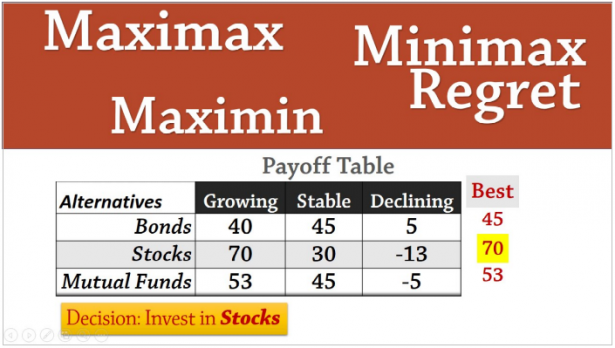
Nella analisi delle decisioni in condizioni di rischio o di incertezza (Rif. 9) esistono criteri consolidati da tempo tra cui il criterio del “Massimo valor medio” e quello di Wald o del “Massimo valore Peggiore”. Il criterio del valor medio è stato criticato perché non tiene abbastanza conto dei rischi derivanti dal fatto che le cose possano anche andar male ( In figura scenario Declining). Si è pensato di rimediare introducendo, in negativo, anche lo scarto quadratico medio come misura di dispersione rispetto alla media, ma non si capisce bene perché anche una dispersione verso risultati migliori della media debbano essere considerati penalizzanti.

Il criterio di Wald, che considera tutti gli scenari peggiori, e poi seleziona l’alternativa con lo scenario meno peggiore (In figura Bonds), è stato criticato perché considera, pessimisticamente, solo gli scenari peggiori. Hurwicz ha allora introdotto un nuovo metodo che considera la media ponderata (con un parametro alfa compreso tra zero e uno) tra lo scenario migliore e lo scenario peggiore. Anche questo criterio è stato però criticato perché ignora tutti gli scenari intermedi. Mi è allora venuto in mente (Rif. 9) di proporre un semplice indicatore (Indice di Rob) che ponderasse valore medio e valore peggiore.

Indice di Rob: alfa*Med.Pond + (1-alfa)*MaxPeggiore

In questa maniera si da un peso ponderato a tutti gli scenari possibili ed inoltre, se le cose andranno male, si predilige il meno peggiore.

 

 

 

 

 

 

 

 

 

 

 

Lo stesso indicatore si può utilizzare nel caso delle decisioni a criteri multipli (Rif.5), in questo caso però è necessario normalizzare i valori poiché i vari criteri hanno in genere unità di misura differenti (Denaro, percentuali, anni, numeri indice, ecc.). Per normalizzare i valori (Rif. 8) si è scelto di dividere il valore di un criterio per il valore migliore che esso ha in una alternativa, dunque questa alternativa avrà valore 1 e tutte le altre un valore compreso tra zero ed uno. Se il criterio migliore è quello a valore più basso, come ad esempio accade per il Pay Back di un investimento, che si misura di solito in anni, allora si fa il rapporto inverso: Caso migliore / Caso corrente. A parole la questione appare intricata, vediamo dunque un esempio numerico concreto ripreso dall’articolo di Rosina che, a sua volta lo riprende da un altro articolo (Rif. 10).

Criteri di valutazione
g1 g2 g3 g4
Alternativa/decisione (DCF miliardi) (CFROI) (Value ROI) (Payback anni)
a1 6 14% 20% 1
a2 8 16% 21% 2
a3 15 18% 23% 5
a4 3 17% 15% 3
a5 10 20% 25% 4
Pesi 0.3 0.2 0.2 0.3

Si tratta di scegliere tra 5 alternative di investimento (a1,…,a5) misurate su quattro criteri (g1,…,g4). Non si entra nella spiegazione della natura dei vari criteri (chi fosse interessato può vedere il citato riferimento 10). Qui interessa osservare che il primo criterio è misurato in miliardi, il secondo ed il terzo in percentuale ed il quarto in anni. In blu sono segnati per ciascun criterio i valori migliori: 15 miliardi, 20%, 25%, 1 anno. Dunque secondo g1 l’alternativa migliore è a3, secondo g2 e g3 l’alternativa migliore è a5 e secondo g4 l’alternativa migliore è a1. Come mettere insieme questi risultati? L’accurata analisi (Rif. 1) di Rosina (spero da me ripresa correttamente) considera otto metodi di valutazione a criteri multipli, riportati nella tabella sottostante sulle righe, mentre sulle colonne sono riportate le cinque alternative:

Punteggi/posizioni attributi dai vari Metodi
Metodi/Alternative a1 a2 a3 a4 a5
Pareto 3° 4° 1° 5° 2°
Electre 4° 3° 1° 5° 2°
Sow 0.17 0.39 0.89 0.25 0.80
Topsis 0.22 0.38 0.86 0.31 0.73
Ahp 0.13 0.18 0.29 0.15 0.25
MaxMin 0.00 0.25 0.67 0.00 0.58
MaxMax 0.50 0.60 1.00 0.50 1.00
Lessicografico 2° 3° 1° 4° 5°

Si vede dunque chiaramente che tutti i metodi concordano sulla scelta della alternativa a3 e solo in seconda battuta sulla alternativa a5.
Vediamo ora i conteggi secondo il metodo (Rob) da me proposto. Innanzi tutto è necessario normalizzare la tabella alternative/criteri riportata all’inizio da Rosina, ecco il risultato:

Criteri di Valutazione normalizzati assumendo pari a 1 il valore migliore di ciascun criterio
g1 g2 g3 g4
a1 0.40 0.70 0.80 1.00
a2 0.53 0.80 0.84 0.50
a3 1.00 0.90 0.92 0.20
a4 0.20 0.85 0.60 0.33
a5 0.67 1.00 1.00 0.25 Totale
Pesi 30.0% 20.0% 20.0% 30.0% 100.0%

Come si vede in corrispondenza dei valori migliori si ha il valore 1, tutti gli altri valori sono più bassi rispetto ad esso. Applichiamo ora alla tabella normalizzata il Metodo di Rob evidenziando separatamente, per maggior chiarezza la media ponderata e il valore peggiore, ponendo alfa = 0.7 (si da più peso alla media rispetto al valore peggiore perché questo è già comunque compreso nel valore medio):

Indice di Rob: 0.7*Med.Pond + 0.3*MaxPeggiore

Media Ponderata Max-Min alpha= Rob
a1 0.720 0.400 0.7 0.624
a2 0.64 0.500 0.597
a3 0.724 0.200 0.567
a4 0.45 0.200 0.375
a5 0.68 0.250 0.548

Sotto il calcolo è riportato in forma tabellare: Alternative sulle colonne, Metodi sulle righe in modo da poterli confrontare più facilmente con i metodi esaminati da Rosina.

Alternative/Metodo a1 a2 a3 a4 a5
Media 0.720 0.638 0.724 0.450 0.675
Peggiore 0.400 0.500 0.200 0.200 0.250
Rob. 0.624 0.597 0.567 0.375 0.548

Si può per prima cosa osservare che l’alternativa a3, che è scelta dal valor Medio ponderato dei valori normalizzati, è in perfetta concordanza con i criteri calcolati nell’articolo di Rosina. L’alternativa a3 ha però un forte handicap in quanto il tempo di recupero dell’investimento è di ben 5 anni contro 1 anno dell’alternativa a1 scelta dal criterio di Rob. Questo è un handicap non da poco in quanto il pay back è anche una misura della liquidità del progetto, cioè della capacità di generare rapidi rientri e quindi di diminuire l’indebitamento con le banche oppure, se il capitale per l’investimento è proprio, di consentire rapidamente il lancio di nuovi progetti. Inoltre se siamo in scenari di rischio o di incertezza avere rientri del capitale rapidi è molto più sicuro. Si deve poi osservare che a fronte di questi vantaggi l’alternativa a1 ha anche rispetto a3 un minor valore quantizzabile in termini di valor medio ponderato sugli indici normalizzati di solo: 0.720 – 0.724 = -0.004.

Infine si deve osservare che la scelta di a1 è molto stabile rispetto ai valori del parametro alfa (peso del valor medio) che nei calcoli precedenti è stato posto pari 0.7, infatti pur portando il peso alfa del valor medio ponderato ad un valore molto alto (0.97) la preferenza del criterio di Rob è sempre per l’alternativa a1 (0.710 > 0.708).

Indice di Rob: 0.97*Med.Pond + 0.03*MaxPeggiore

Alternative/Metodo a1 a2 a3 a4 a5
Media 0.720 0.638 0.724 0.450 0.675
Peggiore 0.400 0.500 0.200 0.200 0.250
Rob 0.710 0.634 0.708 0.443 0.662

Abbandoniamo il tema della microeconomia aziendale per vedere come l’indice di Rob, qui proposto, possa essere utile anche in macroeconomia.

Negli anni recenti si è sempre più prestata attenzione nei vari paesi, piuttosto che ai redditi e ai patrimoni, alle differenze di reddito e di patrimonio all’interno delle nazioni considerando auspicabile che queste differenze siano non troppo alte (tra gli altri economisti si citano Stiglitz negli Stati Uniti ed il francese Piketty autore del famoso best-seller “Il Capitale del XXI secolo). L’indice di Gini (0 nessuna diseguaglianza 1 disuguaglianza massima) ci dice che ordinando i continenti/paesi per diseguaglianze crescenti si trova: Australia, Europa, Canada, Russia, India, Cina, Paesi Mussulmani, Stai Uniti, Sud America, Africa. Va detto per completezza che per molti paesi africani e mussulmani il calcolo dell’indice di Gini non è disponibile. Ora è evidente che la considerazione delle diseguaglianze, di per se non è sufficiente per fare delle scelte ponderate: pochi preferirebbero vivere in Siberia piuttosto che in California. Del resto è palese che un paese dove tutti muoiono di fame ha diseguaglianze nulle, ma è ben poco attraente. La cultura popolare ha coniato diverse pillole di saggezza, ne citiamo due: “Fare la torta grande e buona prima di pensare a come dividerla”, “Combattere la povertà, non la ricchezza”. Il secondo presidente della repubblica italiana, economista liberale, Luigi Einaudi, in Prediche Inutili scriveva: “…Gli uomini dal temperamento socialistico oltrepassano il punto critico della progressività nelle imposte anche perché, contrariamente ai liberali, si sono ficcati in testa una divulgatissima opinione; che oggi il vero problema sociale sia quello della distribuzione della ricchezza e non più come in passato, della sua produzione. Opinione, oltreché strana, manifestamente sbagliata…”.

Tra gli economisti (e i sociologi/filosofi) si è a lungo discusso sulla opportunità di considerare solo il PIL (Prodotto Interno Lordo) come indicatore della prosperità/benessere di una nazione: si va dagli estremi di alcuni neo liberisti che lo ritengono sempre e comunque corretto ad alcuni progressisti ideologizzati, che ritengono il denaro, non frutto del lavoro e del merito, ma: “sterco del diavolo”.
Consideriamo dunque indici multi criteri tipo BIL (Benessere Interno Lordo) o FIL (Felicità Interna Lorda) che accanto al PIL (g4) considerano altri criteri. Il PIL comunque ha sempre un peso notevole poiché, senza valori soddisfacenti di esso, difficilmente si possono migliorare gli altri aspetti della società. Di seguito i criteri presi in esame (tra parentesi i pesi).

  • g1) Salute, Welfare, Ambiente (30%);
  • g2) Istruzione, Educazione, Cultura (20%);
  • g3) Democrazie e Libertà (20%);
  • g4) PIL: Prodotto Interno Lordo (30%).

Supponiamo che le nazioni da confrontare, sui quattro criteri, siano cinque (Paese1,…,Paese5) e che i dati siano identici a quelli ripresi dall’articolo di Rosina e poi normalizzati. I pesi (30%) mostrano che i criteri valutati più importanti sono: g1 (Salute, Welfare, Ambiente) e g4 (Prodotto interno Lordo). Secondariamente (20%) ci sono i criteri g2 (Istruzione, Educazione, Cultura) e g3 (Democrazie e Libertà.).

Il paese preferito, secondo l’indice di Rob, risulta essere il Paese1 che presenta un elevato PIL (g4) e buoni livelli di Istruzione, Educazione e Cultura (g2) e Democrazia e Libertà (g3), anche se dal punto di vista di Salute, Welfare e Ambiente (g1) il valore è, sebbene non all’ultimo posto, piuttosto basso.

Indice di Rob: 0.7*Med.Pond + 0.3*MaxPeggiore

g1 g2 g3 g4
Paese1 0.40 0.70 0.80 1.00
Paese2 0.53 0.80 0.84 0.50
Paese3 1.00 0.90 0.92 0.20
Paese4 0.20 0.85 0.60 0.33
Paese5 0.67 1.00 1.00 0.25 Totale
Pesi 30.0% 20.0% 20.0% 30.0% 100.0%

 

Alternative/Metodo Paese1 Paese2 Paese3 Paese4 Paese5
Media 0.720 0.638 0.724 0.450 0.675
Peggiore 0.400 0.500 0.200 0.200 0.250
Rob. 0.624 0.597 0.567 0.375 0.548

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Concentriamoci infine, restando sempre in campo macroeconomico, su un caso e valori numerici diversi che confrontano le nazioni sulla base dei redditi misurati con: Valor Medio (Medio), Povertà (Peggiore) e Disuguaglianza (Gini). I Paesi presi in considerazione sono tre:

Diseguaglianze Reddito alfa
0.7 Soglie di
(Gini) (Medio) (Peggiore) (Rob.) alfa
Paese1 0.60 0.90 0.20 0.690 0.84
Paese2 0.36 0.86 0.40 0.722 <<Max
Paese3 0.25 0.50 0.45 0.485 0.12

L’indice di Rob. (per ampi valori di alfa compresi tra 0.84 e 0.12) privilegia la situazione del Paese2 che presenta un buon reddito medio e un grado di povertà non troppo elevato. L’indice di Gini invece, se utilizzato da solo, può portare (0.25) a privilegiare una maggior uguaglianza dove tutti hanno un reddito medio piuttosto basso..
Si osservi che il parametro alfa, in questa nuova ottica può essere considerato come una manopola che, se girata completamente a sinistra (alfa = 0), privilegia un approccio più socialista di totale attenzione alla riduzione delle condizioni di estremo disagio, se girata completamente a destra (alfa = 1) privilegia un approccio più liberale di totale attenzione al merito e al benessere medio dei cittadini. A parere di chi scrive questo approccio, basato sul tentativo di misurare il livello medio e di ridurre le condizioni di estremo disagio, appare più interessante e costruttivo di quello che si concentra unicamente sulle diseguaglianze (Indice di Gini), oppure quello che si concentra unicamente sul reddito medio.

Riferimenti

 

Commenti

commenti