Vi sono alcuni dispositivi che permettono di trasformare l’energia elettrica in energia meccanica, e altri che, invece, trasformane l’energia meccanica in energia elettrica.
Nel primo caso si parla di motori elettrici, mentre nel secondo caso gli strumenti sono le dinamo, o gli alternatori.
Il motore elettrico
Esaminiamo il funzionamento di un motore elettrico; generalmente, un motore elettrico è costituito da un involucro (armatura) che contiene delle calamite, una parte rotante (rotore), attorno la quale sono avvolte delle bobine di filo conduttore, e delle spazzole che sfiorano il rotore.
Le spazzole sono collegate ad una pila, che genera una differenza di potenziale; la corrente elettrica che viene fatta circolare, quindi, passa attraverso le spazzole, e da esse nel rotore, fino a raggiungere le bobine.
Passando attraverso i fili conduttori, la corrente elettrica genera un campo magnetico, cosicché l’intera bobina si trasformerà in un magnete.
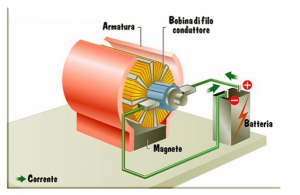
Il dispositivo è costruito in modo che la bobina e le calamite poste nell’involucro esterno rivolgano l’un l’altra i poli opposti, e si respingano; essendo respinta, la bobina genera un movimento, e mette in rotazione il rotore.
Il processo, poi, continua in maniera automatica, in quanto ogni volta che il rotore compie una parziale rotazione, le spazzole lo sfiorano in parti diverse, e ciò implica che la corrente elettrica scorra nella bobina in verso opposto. Il rotore, quindi, riprende a ruotare nel senso opposto a quello precedente.
Il momento magnetico
Nel caso del motore elettrico, abbiamo visto che il passaggio di corrente e la formazione di un campo magnetico provocano la rotazione di un rotore. Tale rotazione è indotta da una serie di forze che entrano in gioco; per questo, ha senso parlare di momento torcente delle forze che agiscono sul rotore.
Consideriamo un rotore di forma rettangolare, schematizzabile con una spira rettangolare, immerso in un campo magnetico.
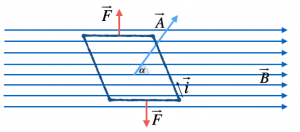
Sulla spira agisce una coppia di forze che permette la sua rotazione. Ogni volta che la corrente si inverte anche le forze cambiano verso, cosicché la spira possa continuare a ruotare.
Si può dimostrare che sulla spira la coppia di forze genera un momento torcente che viene definito dal seguente prodotto vettoriale:
$ M = vec μ_m × vec B$
dove μ rappresenta una grandezza vettoriale detta momento magnetico della spira; questo vettore è definito come prodotto dell’intensità di corrente che circola nella spira e del vettore A che descrive la superficie racchiusa dalla spira stessa:
$ vecμ_m = i * vec A$
Come sappiamo, nel caso di prodotti vettoriali, il modulo del vettore risultante è dato dal prodotto dei moduli dei vettori di partenza per l’angolo che si forma tra essi; in questo caso, quindi, il modulo del momento torcente delle forze che agiscono sulla spira è dato da:
$ M = μ_m * B * sin α = i * A * B * sin α$
Dato che il seno di un angolo si annulla nel caso in cui l’angolo sia un multiplo di 0 e 2π, notiamo che il momento torcente si annulla quando l’angolo tra il vettore superficie A e il vettore campo magnetico è di 0°, cioè quando i due vettori sono paralleli.
Esercizio
Consideriamo una spira rettangolare immersa in un campo magnetico di intensità $7,1 * 10^-3 T$. E’ noto che le dimensioni della spira sono 2,5 cm per 7,8 cm, e che all’interno di essa circola una corrente di intensità 3,5 A. Sapendo che il momento torcente delle forze che agiscono sulla spira è di $5,5 * 10^-6 N * m$, calcolare l’angolo che si forma tra il vettore superficie e il vettore campo magnetico.
Possiamo risolvere il problema considerando la definizione di momento torcente vista per il motore elettrico; sappiamo, infatti, che il modulo del momento torcente è dato dal seguente prodotto:
$ M = i * A * B * sin α$
Possiamo quindi ricavare la formula inversa e determinare il seno dell’angolo richiesto:
$ M = i * A * B * sin α to sin α = frac(M)(i * A * B)$
Il modulo del vettore superficie è dato dall’area della superficie racchiusa dalla spira, di forma rettangolare.
Dopo aver espresso le grandezze nelle giuste unità di misura, possiamo sostituirle nella formula precedente:
$sin α = frac(M)(i * A * B) = (5,5 * 10^-6 N * m)(3,5 A * 1,95 * 10^(-3) m^2 * 7,1 * 10^-3 T) = 0,114 $
La formula inversa del seno ci fornisce il valore dell’angolo cercato:
$α = sin^(-1) (0,114) = 6,55 °$
Potrebbero interessarti
Video Lezioni: Elettromagnetismo
Vide Lezioni: Onde e Luce
Appunti: La forza di Coulomb
Appunti: La forza di Lorentz
Appunti: La forza magnetica
Appunti: Il campo magnetico
Appunti: Moto di una carica in un campo magnetico
Appunti: L’effetto Hall
Appunti: La legge di Lenz
Appunti: La legge di Faraday – Neumann
Appunti: Le equazioni di Maxwell
