Dal flusso di emoglobina alla Gittata Cardiaca! Stabilito che la retta del secondo quadrante in realtà non è una retta, ma una regressione attendibile, le applicazioni in biologia, sociologia e antropologia diventano innumerevoli. Resta da mettere in evidenza come la mente umana pur diventando più ricca di mezzi e conoscenze non cambi sostanzialmente il suo approccio ai problemi, imparando dalla esperienza e dalla sua analisi.
Ne volete una dimostrazione? Una terapia già in uso da anni in caso di malattie estremamente gravi del midollo osseo o di tumori solidi del peritoneo con metastasi diffuse, prevede di somministrare una dose di farmaci e radiazioni ben oltre la dose “mortale”, teoricamente in grado però di distruggere le cellule midollari ossee geneticamente malate o del tumore (ereditario o acquisito). Il trapianto di midollo osseo, messo in atto qualche giorno dopo questa terapia, assodato in alcuni campi, ma sperimentale e di estrema ratio in altri, fa si che il paziente a volte, guarisca, esattamente come Benvenuto Cellini. Il sopravvissuto ora ha due patrimoni genetici; uno suo proprio e uno del donatore di midollo.
I Greci che davanti un bicchiere di sidro filosofeggiavano, avevano immaginato un simile mitico animale come qualcosa con la testa di un aquila, il corpo di leone e la coda di serpente e l’avevano chiamata Chimera. Ne esistono di bellissimi esemplari scultorei Etruschi. Ora dopo venti secoli, ogni volta che si procede ad un trapianto non c’è più bisogno di alcool (“Al cool “ovvero “il Demonio” per gli arabi) per vedere le Chimere, dimostrando una volta per tutte, che è vero che se non hai fantasia non puoi fare lo Scienziato!
Stabilito nel quadrante due il flusso di Emoglobina kg/min in 750 ml determiniamo la concentrazione nell’atleta in esame (di solito è attorno a 15gr/100ml nell’uomo, un po’ meno nella donna, in questo campo non si è ancora raggiunta la parità!)
I 15 gr di emoglobina di un uomo normale trasportano circa 20 ml di ossigeno ( 1g Hb = 1,34 ml O2o Q.
Come tutti i fenomeni naturali (scientifici e ripetibili) il tutto è compresso in un’elegante formula conosciuta come formula di Fick, che contiene tutti gli elementi esaminati nel diagramma di Margaria.
Questa è l’equazione nella sua forma piu semplice $Q=(VO_2)/(C(a-v) O_2)$ dove $C(a-v)O_2$ sta per contenuto arterioso meno il venoso di ossigeno.
Il Contenuto arterioso di Ossigeno si calcola come CaO2= Hb x 1,34 x Saturazione O2+PaO2x0,003.
Dando per scontato una pressione parziale di O2 da noi calcolata ai polmoni di 100mhg e concentrazione di 15gr di Emoglobina, il Ca di O2di seguire fino in fondo.
ossigeno con il quoziente respiratorio, nel calcolo si può usare la CO2O2 ma non ci complichiamo la vita!
Per usare questa formula in maniera cruenta che serve anche per la determinazione della gettata di un singolo organo basta prendere il sangue refluo dall’organismo, che arriva alle sezione destre del cuore, meglio ancora in arteria polmonare. Abbiamo affermato che oltre al metodo del gas esiste la possibilità di misurare la gittata con l’iniezione di un colorante o di una soluzione un pò piu fredda dei 37 C° perché tra i due metodi di misura c’è una buona correlazione.
Per la precisione del linguaggio scientifico occorrerà capire meglio il significato di questo termine. Poniamo il caso di raccogliere le gittate di diversi pazienti con i due sistemi che chiameremo V (consumo di Ossigeno) e D (diluizione). Riportiamo i dati su un grafico cartesiano e leggiamo che l’atleta Uno ha sulle asse delle X (met Fick) una gittata di 2,2 litri e 3,2 sulle Y (termodiluizione o colorante). Il numero Due 3,9 litri e 4 litri; cosi via fino ad ottenere un grafico di questo tipo:
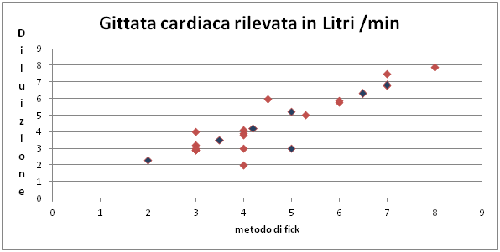
Gia a prima vista questa disposizione di dati, fa vedere che la correlazione tra essi è alta e quindi i due metodi di misura sono probabilmente sovrapponibili. L’indice di correlazione statistica varia da -1 (correlazione inversa, passa per 0, quando non c’è nessuna correlazione) e va a +1 quando la correlazione è altissima.
In questo caso (con dati fittizi) i punti tendono a formare una retta e la correlazione calcolata è di 0,9 (molto alta) e indica che i due metodi sono sovrapponibili. L’indice ritenuto “buona correlazione” con le scienze sociali è di 0,6. Per le discipline più meccaniche ed ingegneristice, come questa è di 0,8. Se non vi fosse nessuna correlazione i dati tenderebbero a trasformarsi in un cerchio o una figura informe, senza nessun orientamento o quasi. Addirittura al crescere della grandezza Y il valore delle X potrebbe anche scendere, la disposizione dei dati avrebbe allora i valori asin del grafico più in alto di quelli della sezione destra (correlazione inversa).
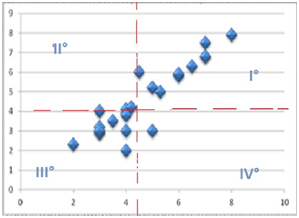
Per approfondire la precisione, tracciamo ora una linea retta che divida orizzontalmente i dati (sotto la linea rossa tratteggiata). Dei 18 punti, ne lasciamo nove sopra e nove sotto; questa retta si chiama mediana orizzontale.
Tracciamo ora la mediana verticale, con gli stessi criteri e segniamo i quattro quadranti cosi ottenuti numerandoli da destra in alto, in senso antiorario I – II – III – IV.
Individuiamo ora i due quadranti opposti che raccolgono piu punti, in questo caso il primo e il terzo e tracciamo le due mediane, dei quadranti esattamente come prima.
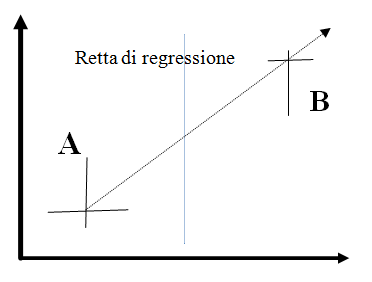
Segniamo i punti d’intersezione A e B e uniamoli con una retta: questa retta si chiama retta di regressione ed è utile quando vogliamo prevedere l’andamento di un fenomeno correlato a un’altra grandezza.
Vi ricorda niente? Si tratta di una retta di regressione solo che stavolta l’abbiamo costruita manualmente.
Altius Citius Fortior
Non ci crederete,; ma possiamo fare di più. Ammettiamo che i dati del vostro atleta siano raccolti non da voi stessi ma che più allenatori partecipino al buon andamento dell’allenamento o che diversi medici di turno provvedano alla misurazione della gittata cardiaca. Colorando in maniera personalizzata i dati di ciascun sperimentatore, avrete una analisi di “stratificazione“; vedrete cioè i dati stratificati, evidenziando chi li ha raccolti e verificando ancora una volta “de visu”, la buona aderenza o meno degli operatori al metodo di misura.
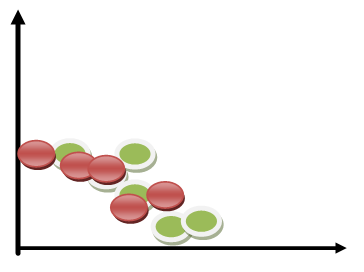
In figura sono rappresentati dati raccolti da due diversi operatori: il grafico dimostra che al crescere della X il valore di Y diminuisce (correlazione inversa) ma anche che la correlazione tra i dati dei due rilevatori è buona!
Ovviamente ottenuta la gittata cardiaca dividendo per la frequenza (quante volte al minuto il cuore batte) avrete la gittata pulsatoria o stroke volume; trovate così che i circa 3750 litri che abbiamo calcolato mandano in circolo 75 ml di sangue ad ogni battito e 50 ml di ossigeno.
Abbiamo concluso con questo il III e IV quadrante e ora potremmo trattare i dati sul quaderno in giardino, senza laptop! Dopo tutto fu così che, nei primi del Novecento, Gosset, meglio conosciuto con lo pseudonimo di Student scoprì che occorreva dare al terreno il concime azotato nei mesi primaverili altrimenti le piogge lo avrebbe dilavato troppo presto per il periodo della semina!





