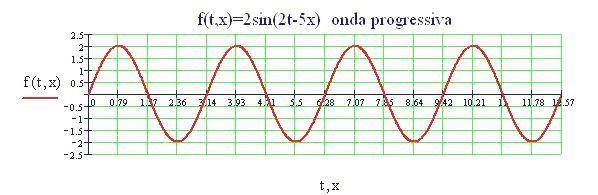
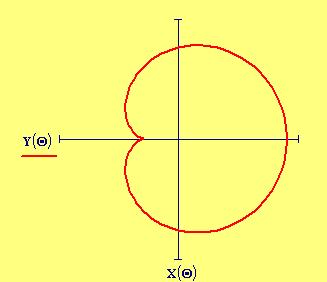
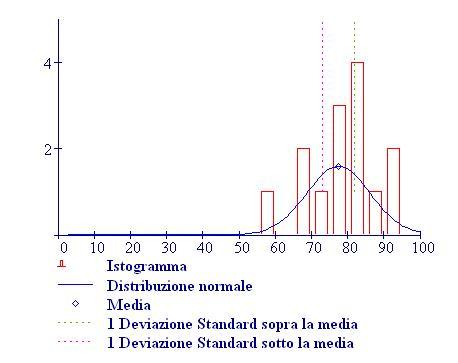
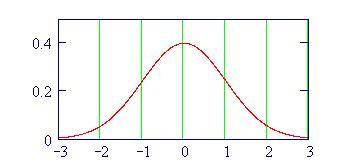
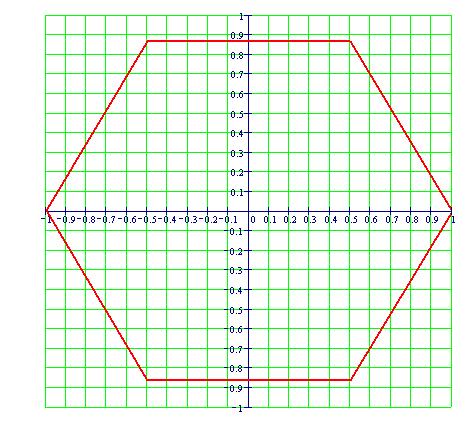
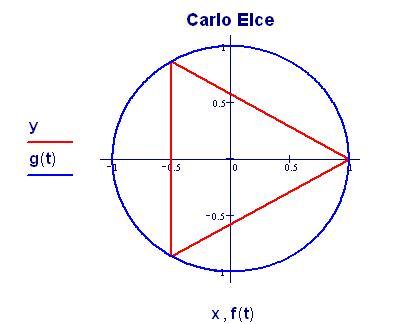
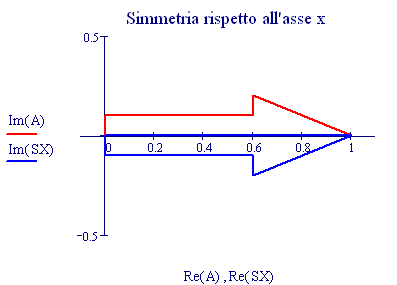
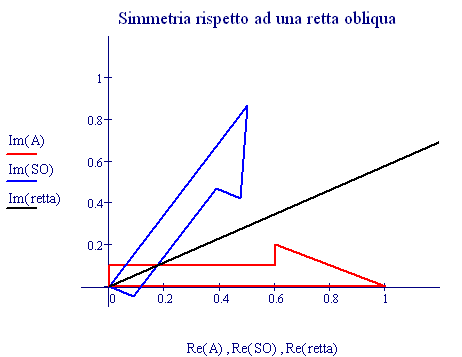
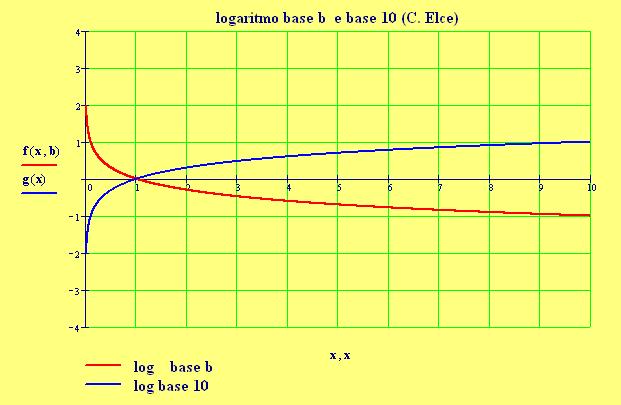
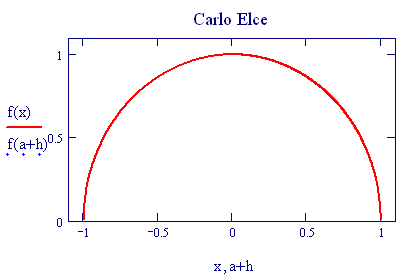
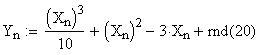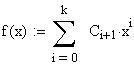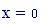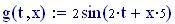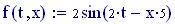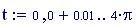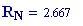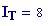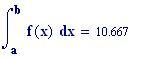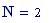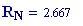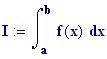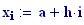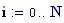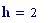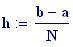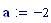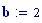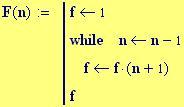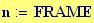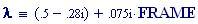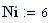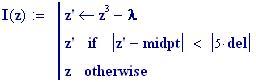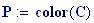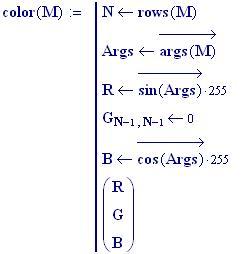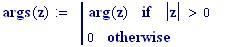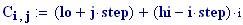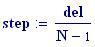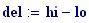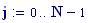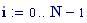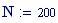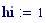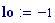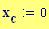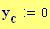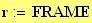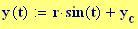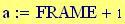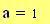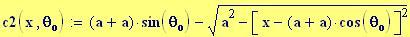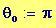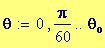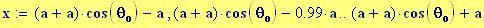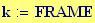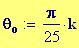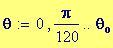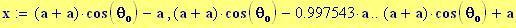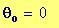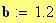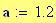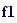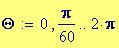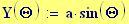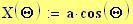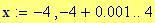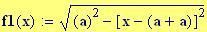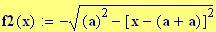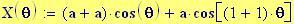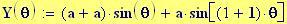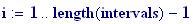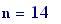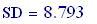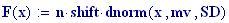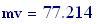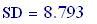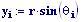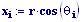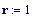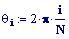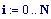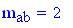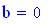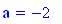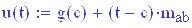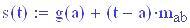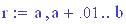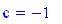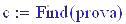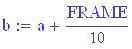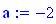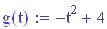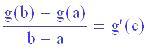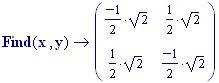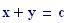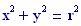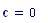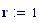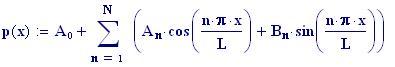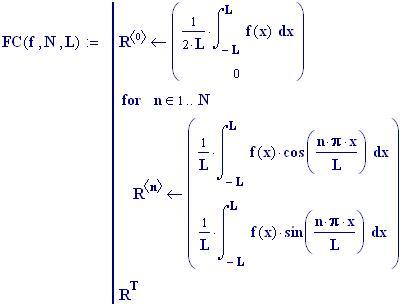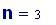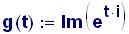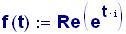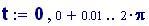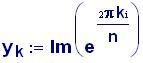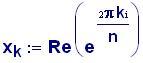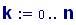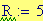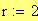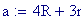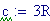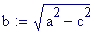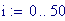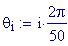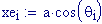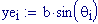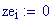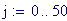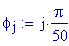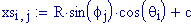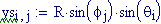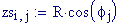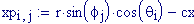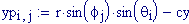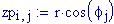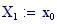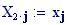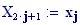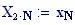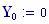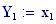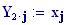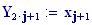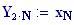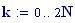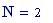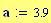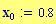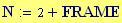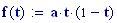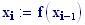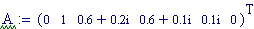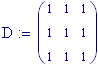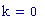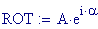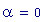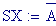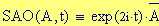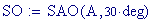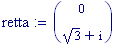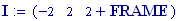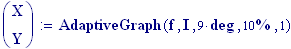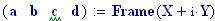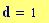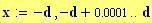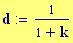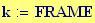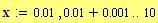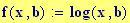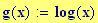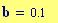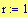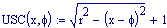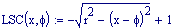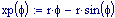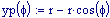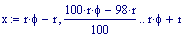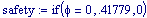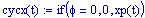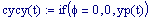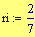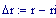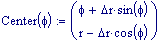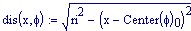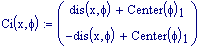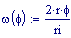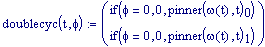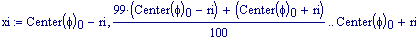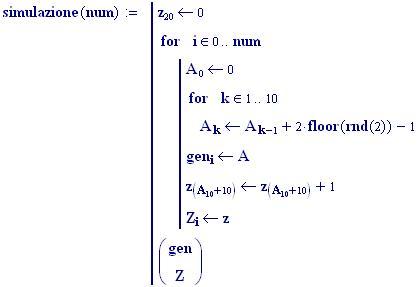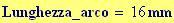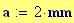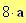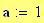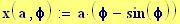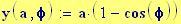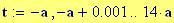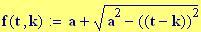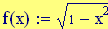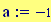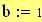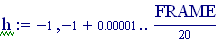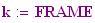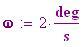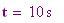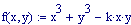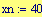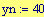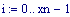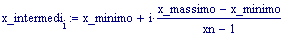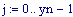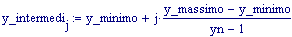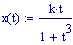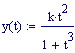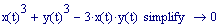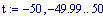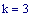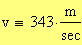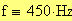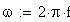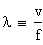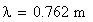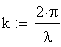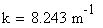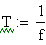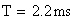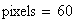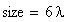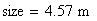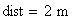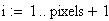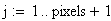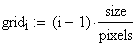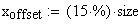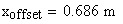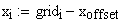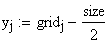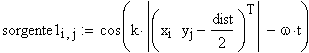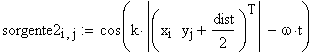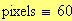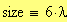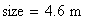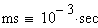I fenomeni, che si verificano quando due onde vengono a sovrapporsi in una regione dello spazio, sono chiamati fenomeni di interferenza.
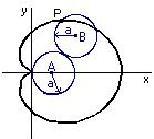
Due sorgenti sonore, che oscillano in fase, emettono un’onda sonora sinusoidale con la stessa frequenza delle sorgenti. Queste frange di interferenza si costruiscono semplicemente sommando due onde sonore coerenti emesse da due sorgenti poste ad una certa distanza tra loro. I punti dello spazio, la cui differenza delle distanze dalle due sorgenti è uguale ad un multiplo pari di mezza lunghezza d’onda, oscillano con una un’ampiezza di oscillazione che è somma delle due ampiezze di partenza (interferenza costruttiva). In questi punti l’oscillazione ha un massimo o un minimo. Nei punti invece, la cui differenza delle distanze dalle due sorgenti è un multiplo dispari di mezza lunghezza d’onda, i vettori oscillazione si sottraggono e si elidono a vicenda (interferenza distruttiva). In questi punti l’ampiezza di oscillazione è nulla.
Per visualizzare questo processo, possiamo usare il menu Tools/Animation/Record di Mathcad e, dopo aver selezionata l’area in cui localizzato il grafico del fenomeno espresso mediante funzioni parametriche, clicchiamo sul pulsante Record Animation/Animate.
A tale scopo, per prima cosa, definiamo i parametri caratteristici dell’onda sonora.
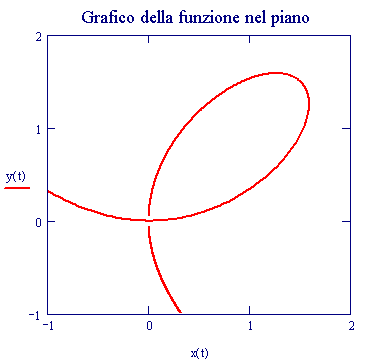
Velocit del suono:
Frequenza del suono:
A partire dal valore di questi due parametri, troviamo le altre caratteristiche dell’onda usando le formule seguenti:
Pulsazione:
Lunghezza d’onda :
Frequenza spaziale:
Periodo:
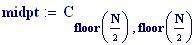
Risoluzione del grafico in pixels :
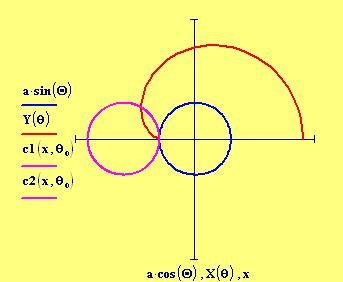
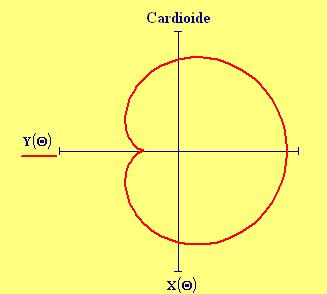
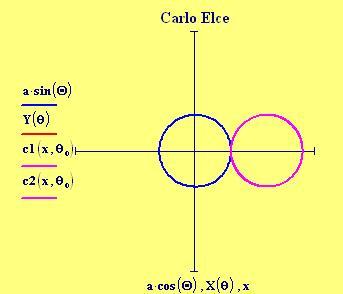
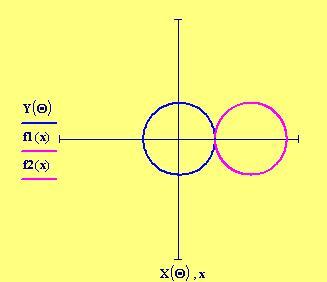
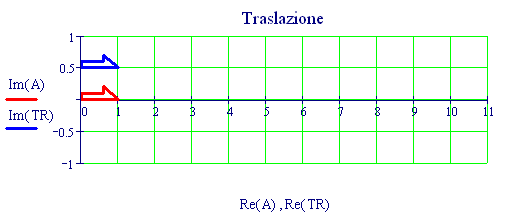
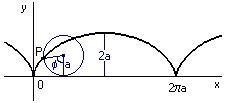
La dimensione della finestra grafica viene posta uguale a 6 lunghezze d’onda. Una lunghezza d’onda corrisponde alla distanza tra due cerchi concentrici nei grafici seguenti:
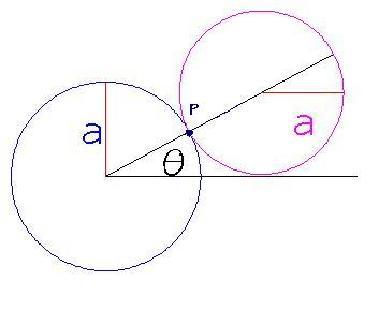
Distanza tra le due sorgenti:
Il nostro prossimo passo sar quello di definire la griglia per il grafico della nostra superficie.
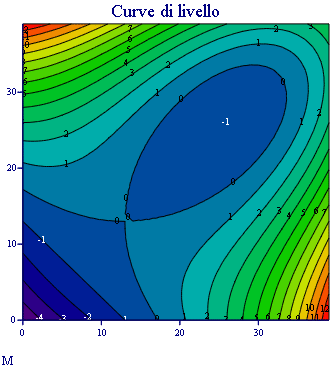
Immettiamo le equazioni delle nostre onde al lavoro:
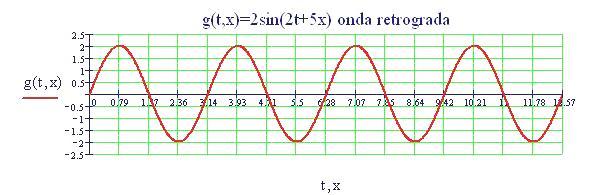
Queste due funzioni in due variabili, periodiche nel tempo e nello spazio, sono le equazioni delle onde in due dimensioni (rispetto alle coordinate x e y ).
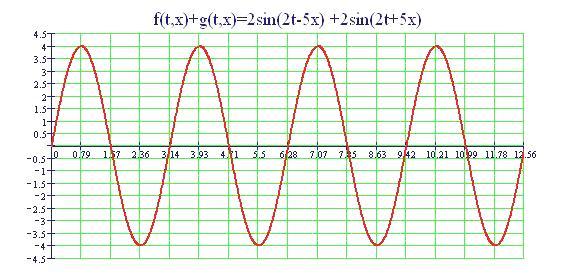
Per ottenere le frange di interferenza dobbiamo comporre le due onde sommando le funzioni sorgente1 e sorgente2 :
I grafici seguenti sono controllati dalle seguenti variabili globali che restano tali in tutta l’animazione Si potrebbero modificare tali valori e vedere come appaiono i grafici..
Alla risoluzione in pixels viene assegnato il valore:
Alla dimensione della finestra grafica viene assegnato il valore:
Distanza tra le due sorgenti :
Per avere una computazione agevole dell’animazione stata usata la variabile incorporata FRAME, come parametro variabile, in relazione alla variabile tempo, considerata come variabile globale.