Equivalenza massa-energia - Matematicamente

La fisica classica prevede che l’energia possa essere espressa in varie forme (cinetica, potenziale, …), ma che in generale essa si conserva; anche la massa di un sistema si conserva in seguito ad un certo fenomeno fisico per la legge di Lavoisier; tale legge prevede, infatti, che in una qualsiasi reazione chimica la massa dei reagenti deve essere uguale a quella dei prodotti.

Nella teoria della relatività, però, anche queste affermazioni perdono validità; Albert Einstein, infatti, affermò che la massa e l’energia sono quantità fisiche collegate tra loro, e in particolare il rapporto che c’è tra esse dipende dal quadrato della velocità della luce nel vuoto.

Questa relazione si traduce nella famosa formula:

$ E = m * c^2 $

dove E indica l’energia complessiva del corpo in questione (espressa in J), cioè la somma di tutte le energie che esso possiede; m indica la massa del corpo a riposo (espressa in kg); c è la velocità della luce nel vuoto (espressa in m/s).

Da questa relazione si può dedurre che la massa di un corpo non si conserva come prevedeva la fisica classica, ma varia in base alle variazioni di energia cui il corpo è sottoposto.

Di conseguenza, se il corpo assorbe energia si avrà un aumento della sua massa; se esso cede energia, invece, anche la massa subisce una diminuzione.

La massa di un corpo, quindi, è in ogni caso una forma di energia; qualsiasi corpo, quindi, che ha massa possiede una quantità di energia pari a $mc^2$.

Energia di un corpo a riposo

Si definisce l’energia di un corpo a riposo come il prodotto del quadrato della velocità per la massa a riposo del corpo:

$ E_0 = m_0 * c^2 $

In generale un corpo in movimento, possiede energia cinetica; quindi, l’energia totale del corpo sarà data dalla somma di tutte le energie che esso possiede:

$ E = m_0 * c^2 + 1/2 m_0 * v^2 = m_0 * c^2 (1 + 1/2 frac(v^2)(c^2))$

L’espressione tra parentesi può essere approssimata, ( nel caso in cui la velocità v è molto piccola rispetto a c), come coefficiente di dilatazione γ; l’equazione generale dell’energia, quindi, assume la seguente forma:

$ E = frac(m_0 c^2)(sqrt(1 – frac(v^2)(c^2))) = m_0 * c^2 γ $

Rappresentando il grafico dell’energia E in funzione della velocità v, notiamo che la curva presenta un asintoto verticale v = c;

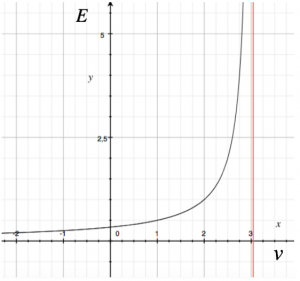
grafico-energia-velocità

possiamo dedurre, quindi, che se la velocità del corpo si avvicina a quella della luce, la sua energia aumenta, fino a raggiungere un valore infinito.

Ciò significa che un corpo si può muovere alla velocità della luce solo se esso possiede una quantità infinita di energia; dato che ciò non è possibile nella realtà, otteniamo un’ulteriore conferma del fatto che velocità della luce non può essere raggiunta da nessun corpo che possiede massa, e rappresenta quindi una velocità limite.

L’energia cinetica relativistica

Conoscendo l’espressione generale dell’energia totale di un corpo, possiamo definire l’energia cinetica relativistica; essa corrisponde alla differenza tra l’energia totale e l’energia che il corpo possiede quando è fermo, cioè l’energia a riposo del corpo.

L’energia cinetica, quindi, assume la seguente espressione:

$ k = m_0 * c^2 γ – m_0 * c^2 = m_0 * c^2 ( γ – 1) $

A partire dall’energia totale, inoltre, possiamo anche definire la massa relativistica di un corpo; essa è data dal prodotto della massa a riposo del corpo per il coefficiente γ:

$ m = m_0 * γ $

Vediamo, quindi, che con il variare della velocità del corpo, non solo si modificano tempi e lunghezze, ma anche la massa subisce variazioni. Mano a mano che la velocità diminuisce, la massa del corpo diventa sempre più piccola; per v=0 si raggiunge il valore minimo, corrispondente a quello della massa a riposo.

Come sappiamo, per un corpo che ha massa e si muove a velocità v, possiamo definire la quantità di moto del corpo come prodotto della massa per la velocità. Avendo introdotto il concetto di massa relativistica, è naturale parlare anche di quantità di moto relativistica, che si esprime come:

$ p = mv = m_0 * γ * v = frac(m_0 * v)(sqrt(1 – frac(v^2)(c^2)))$