Come abbiamo già visto, l’ipotesi della natura ondulatoria della luce fu giustificata con diversi esperimenti a metà dell’ottocento; tuttavia, solo con le equazioni di Maxwell fu possibile affermare che le onde luminose sono onde elettromagnetiche.
Fino ad allora, quindi, non era ben chiaro di che tipo di onde fossero quelle luminose, e si ipotizzò che esse si propagassero in un mezzo materiale particolare, definito etere luminifero, presente in tutto l’universo. Il moto della Terra e dei pianeti causava lo spostamento di questo etere, dando luogo al cosiddetto “vento d’etere”.
Si ipotizzò, quindi, che le equazioni dell’elettromagnetismo fossero applicabili alle onde luminose solo nel caso in cui il sistema di riferimento considerato fosse quello in cui l’etere fosse in quiete.
Per studiare, quindi, il moto delle onde luminose e calcolare così la velocità della luce, era necessario tener conto anche del vento d’etere causato dal moto della Terra attraverso questo mezzo.
I primi esperimenti a riguardo furono condotti dai fisici Michelson e Morley.
Il primo esperimento
Il primo che essi condussero prevedeva lo studio dell’interferenza della luce, generata da un fascio di luce monocromatica diretta su uno specchio semiriflettente, cioè tale da riflettere una parte dei raggi che lo colpiscono, e farsi attraversare da altri.
Ai lati di tale specchio (H) sono disposti altri tre specchi (A, B e C), sui quali vengono riflessi i raggi giungenti dal primo.
In particolare, i raggi di luce che partono dalla sorgente colpiscono H e vengono riflessi e proiettati in A e in B; da qui tornano indietro allo specchio H e vengono proiettati in C.
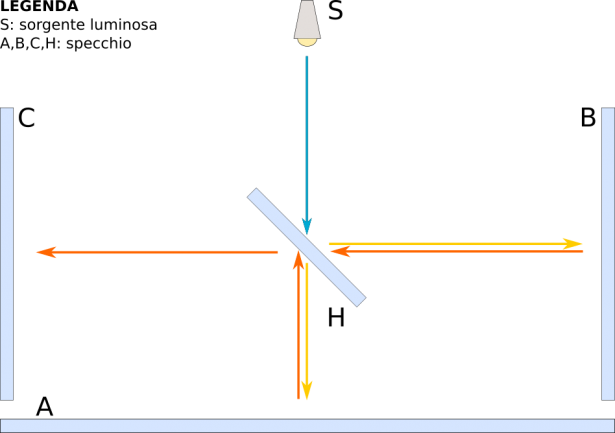
Analizzando il moto della luce nei tratti AH e BH (che sono uguali come distanze), e considerando anche la presenza del vento d’etere e idem moto della Terra, è stato possibile risalire alla velocità della luce.
Vediamo in dettaglio i tratti considerati.
Il tratto A-H
Nell’esperimento si utilizza come sistema di riferimento quello solare, e si suppone che la velocità della Terra (v) sia diretta nel senso negativo dell’asse y.
In questo modo, quando la luce percorre il tratto HA, la sua velocità, per le leggi della meccanica, ha modulo pari a (c – v), perché ha verso opposto a quello della velocità della Terra; nel tratto AH, invece, la velocità della luce e quella della Terra hanno stessa direzione e stesso verso, quindi la velocità della luce ha modulo (c + v):
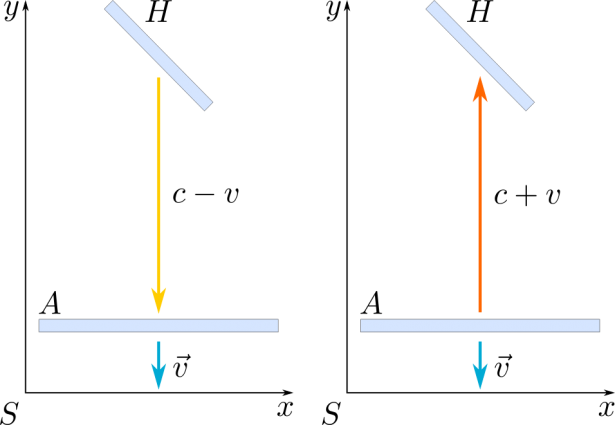
Se osservassimo la situazione dal sistema di riferimento terrestre, potremmo dire che la Terra è ferma, mentre è presente un vento d’etere che, nel primo caso ha velocità (di modulo v) opposta a quella della luce, mentre nel secondo caso ha velocità parallela a quella della luce.
Se indichiamo con l la distanza AH, è possibile determinare il tempo impiegato dalla luce nel percorrere il tratto AH e tornare indietro:
$ ∆t_1 = frac(l)(c – v) + frac(l)(c + v) = frac(2lc)(c^2 – v^2)$
Il tratto H – B
Nel tratto HB, il moto della luce è perpendicolare allo spostamento della Terra, e quindi anche alla direzione della velocità del vento d’etere; in questo caso, quindi, il vettore velocità della luce deve essere espresso come composizione di due vettori: la velocità risultante (diretta da H a B all’andata, e da B a H al ritorno), e la velocità del vento d’etere, opposta in verso a quella terrestre.
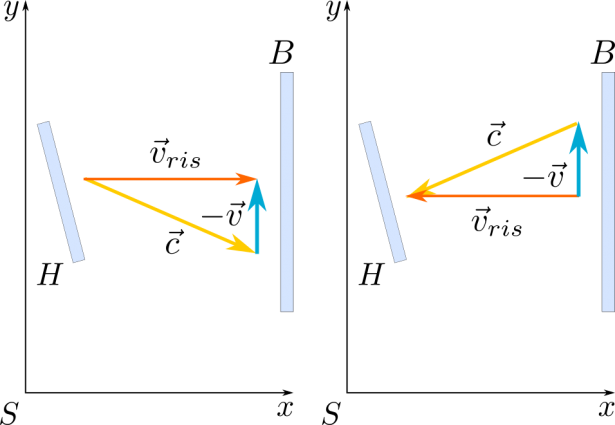
Figura 3
La velocità risultante può essere ottenuta come se fosse il cateto di un triangolo rettangolo, in cui l’ipotenusa è data dal vettore velocità della luce, e l’altro cateto dal vettore velocità del vento d’etere.
Per cui si ha:
$ v_(ris) = sqrt(c^2 – v^2)$
Anche in questo caso, considerando lo spazio percorso da H a B e da B a H, pari a 2l, possiamo ricavare il tempo impiegato:
$ ∆t_2 = frac(2l)(v_(ris)) = frac(2lc)(sqrt(c^2 – v^2)) $
Conclusioni
Come possiamo notare, nonostante i tratti AH e BH siano uguali, i tempi di percorrenza della luce sono differenti. Questa differenza temporale da luogo a dei fenomeni di interferenza, che si generano quando i due fasci di luce vengono in contatto, e dipende da tale differenza e dai valori delle velocità.
I due tempi sarebbero uguali solo nel caso in cui la Terra fosse ferma, e quindi fosse assente anche il vento d’etere.
L’esperimento fu riproposto ipotizzando che l’apparato sperimentale si trovasse immerso nel mercurio, in modo che nel tratto BH la velocità della luce fosse parallela al vento d’etere, e nel tratto AH vi fosse perpendicolare.
In questo caso, si ricavò che nel tratto HB-BH il tempo di percorrenza era pari a $∆t1$, e nel tratto HA-AH pari a $∆t_2$.
Poiché è presente una differenza temporale, è naturale aspettarsi che, quando i fasci di luce si combinano, danno luogo ad una figura di interferenza diversa da quella dell’esperimento precedente (in questo caso, infatti, la differenza temporale è -( $∆t_1$ – $∆t_2$)) ; tuttavia, in questo caso non si registrò alcuna variazione nella figura di interferenza rispetto all’esperimento precedente.
Si concluse, quindi, che la teoria del vento d’etere non poteva essere valida per spiegare il moto della luce.
Potrebbero Interessarti
Video Lezioni: Relatività
Appunti: La velocità della luce
Appunti: La relatività ristretta
Appunti: La dilatazione del tempo
Appunti: La contrazione delle lunghezze
Appunti: Le trasformazioni di Lorentz
Appunti: L’intervallo invariante
Appunti: Lo spazio-tempo di Minkowski
Appunti: Equivalenza massa-energia
Appunti: L’effetto doppler relativistico
Appunti: La relatività generale
Appunti: La curvatura dello spazio-tempo
Appunti: La deflessione gravitazionale della luce
