Le trasformazioni di Lorentz

Come abbiamo visto nel caso della meccanica classica, esistono delle formule che permettono di descrivere il moto di un punto materiale relativamente a due sistemi di riferimento inerziali differenti; in particolare, i due sistemi di riferimento inerziali possono essere l’uno in moto rispetto all’altro.

Detto S il sistema di riferimento inerziale fermo, con origine in O e assi x e y, e S’ il sistema di riferimento inerziale, con origine in O’ e assi x’ e y’, in moto rispetto al primo con velocità v, le equazioni che descrivono il moto di un punto P nei due sistemi di riferimento sono dette trasformazioni di Galileo, e sono le seguenti:

${(vec s = vec s’ + vec v * t), (t = t’):} , {(vec s’ = vec s – vec v * t), (t’ = t):} $

Queste leggi, però, non possono essere utilizzate nell’ambito della relatività, in quanto come abbiamo visto, nel caso di velocità molto elevate e prossime a quelle della luce, si ha una dilatazione dei tempi e una contrazione delle lunghezze in base al sistema di riferimento considerato.

Per questo, le equazione di trasformazione che si utilizzano sono differenti, e sono state formulate dal fisico olandese Lorentz; egli suppose che tali trasformazioni fossero quelle per cui le equazioni dell’elettromagnetismo rimangano invariate nel passaggio da un sistema di riferimento ad un altro, in moto relativo rispetto al primo.

Le leggi a cui facciamo riferimento, quindi, vengono definite trasformazioni di Lorentz, e hanno la seguente forma:

${(x’ = frac(x – vt)(sqrt(1 – frac(v^2)(c^2))) = γ * (x – vt)), (t’ = frac(t – frac(vx)(c^2))(sqrt(1 – frac(v^2)(c^2))) = γ *(t – frac(vx)(c^2))):}$

In questo caso, x’ indica lo spostamento nel sistema di riferimento S’, cioè quello in moto rispetto ad S, e t’ indica il tempo misurato in tale sistema di riferimento.

Applicazioni delle trasformazioni di Lorentz

Vediamo ora alcune applicazioni della formula di trasformazione di Lorentz che mettano in evidenza il fenomeno della dilatazione dei tempi e della contrazione delle lunghezze.

Supponiamo che un determinato fenomeno A avvenga nel sistema di riferimento S all’istante di tempo $t = 0$ e alla posizione $x = 0$, mentre un altro fenomeno B avvenga in S in un tempo successivo, che chiamiamo $t_0$, sempre nell’origine.

Indichiamo l’intervallo di tempo che separa due fenomeni con $∆t=t_0$ .

Consideriamo ora il sistema di riferimento S’, in moto rispetto ad S; il primo fenomeno A avviene sempre nell’origine del sistema, cioè in $x’ = 0$ al tempo $t’ = 0$; la posizione in cui avviene il fenomeno B può essere calcolata con le formule di trasformazione di Lorentz:

$ x’ = γ * (x – vt) = γ * (0 – vt) = – γvt $

Allo stesso modo calcoliamo ora l’istante di tempo in cui avviene il fenomeno:

$ t’ = γ * (t_0 – frac(vx)(c^2)) = γ * (t_0 – 0) = γ * t_0$

Nel sistema di riferimento S’, quindi, l’intervallo di tempo ∆t’ che intercorre tra i due eventi è dato da:

$∆t’ = t’ = γ * t_0 = γ * ∆t$

Vediamo quindi che nel sistema di riferimento S’ l’intervallo di tempo che separa i due eventi è maggiore dell’intervallo che si ha nel sistema S, in accordo con la dilatazione del tempo previsto dalla teoria della relatività.

Vediamo ora il caso di una sbarretta di lunghezza ∆x nel sistema di riferimento S, ferma rispetto ad esso. Vogliamo conoscere la lunghezza della sbarretta nel sistema S’, che si muove a velocità v, verso destre, rispetto ad S.

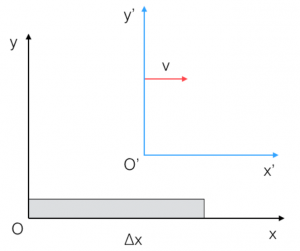
Supponiamo che all’istante di tempo $t = 0$ e $t’ = 0$ le origini dei due sistemi di riferimento coincidano. Per determinare la lunghezza ∆x’ della sbarra nel sistema S’ dobbiamo determinare le posizioni che vengono assunte dall’estremo nell’istante iniziale e nell’istante finale, quando tale estremo si viene a trovare in O’ (infatti, nel sistema S’ si vede la sbarra muoversi con velocità v verso sinistra).

Utilizzando le trasformazioni di Lorentz, possiamo determinare la coordinata x’ dell’estremo destro e il tempo t’ corrispondente a tale posizione:

${(x’ = γ * (x – vt) = γ * (∆x – vt)), (t’ = γ * (t – frac(vx)(c^2)) = γ * (t – frac(v)(c^2) * ∆x)):}$

Possiamo determinare la lunghezza della sbarra considerano il momento in cui l’estremo destro di essa passa per l’origine O’; in questo caso si ha x’ = 0. Sostituendo questa espressione della prima equazione troviamo:

$ 0 = γ * (∆x – vt) to t = frac(∆x)(v)$

Sostituendo questa espressione nella seconda equazione otteniamo:

$ t’ = frac(∆x)(vγ)$

Nel sistema di riferimento S’, la sbarretta si sta spostando verso sinistra con velocità v; di conseguenza, il tempo t’ che l’estremo destro impiega per passare dalla posizione x’ alla posizione $x’ = 0$ è dato dal rapporto $∆x’/v$.

Confrontando questa espressione con l’espressione precedente per t’, troviamo una relazione tra le lunghezze della sbarretta misurate nel due sistemi di riferimento:

${(t’ = frac(∆x)(vγ)), (t’ = frac(∆x’)(v)):} to ∆x’ = frac(∆x)(γ) $

In accordo con la relatività ristretta, vediamo che la misura della lunghezza in S’ risulta minore di quella misurata in S.