La curvatura dello spazio-tempo

Con la teoria della relatività generale furono impiegati dei nuovi modelli geometrici, scoperti a partire dai primi anni dell’ottocento, definiti geometrie non euclidee. In base a queste nuove geometrie fu possibile introdurre il concetto di spazio curvo, e in particolare di geometrie sferiche, ellittiche, iperboliche, ecc.

Sulla base di questi concetti matematici, fu possibile per Einstein formulare altri due concetti di grande importanza.

La presenza di masse incurva lo spazio-tempo

Il primo concetto consiste nell’affermare che la presenza di masse incurva lo spazio-tempo, ed è responsabile, in determinate situazioni, del moto dei corpi. Ad esempio, questa formulazione rappresenta un nuovo modo di considerare l’attrazione tra due corpi che era stata spiegata con la forma di attrazione gravitazionale.

Come sappiamo dalla fisica classica, due corpi che possiedono una massa sono attratti tra loro da una forza direttamente proporzionale alle masse e inversamente proporzionale al quadrato della distanza. Secondo la relatività generale, invece, tale forza non esiste.

Einstein affermò che la presenza di una massa incurva lo spazio in cui essa si trova, e tale deformazione è responsabile dell’avvicinamento delle due masse. Lo spazio-tempo presenta deformazioni più accentuate nelle zone più vicine alle masse, rispetto a quelle più lontane.

Esempio del telo elastico

Questo concetto può essere facilmente rappresentato per mezzo di un esempio classico; consideriamo una massa che viene posta al centro di un telo elastico; notiamo che la massa, a causa del suo peso, crea una deformazione del telo.

Supponiamo, ora, di posizionare una massa molto più piccola sul bordo del telo; anche la seconda massa è responsabile di una piccola deformazione del telo nella zona circostante, ma questa risulta trascurabile rispetto a quella della massa più grande.

Inoltre, la massa piccola tende a scivolare verso quella più grande, come se fosse attratta da essa.

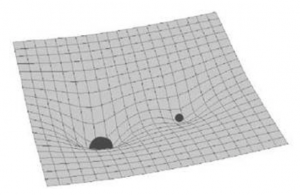
curvatura-spazio-tempo

Possiamo immaginare una situazione analoga per i pianeti che su muovono attorno al sole, e per la luna che orbita attorno alla Terra.

I corpi soggetti alla forza di gravità si muovono nello spazio curvo come particelle libere

Il secondo concetto che fu introdotto da Einstein è che i corpi soggetti alla forza di gravità si muovono nello spazio curvo come particelle libere, seguendo linee di minima lunghezza che congiungono due punti distinti; tali linee vengono definite geodetiche.

In uno spazio piano, le curve geodetiche sono costituite da segmenti di retta, perché come sappiamo, il cammino più breve che congiunge due punti in un piano è il segmento che li unisce.

In uno spazio curvo, però, tali curve assumono un significato differente. Per prima cosa, dobbiamo definire il concetto di retta in uno spazio curvo: si definisce una retta passante per due punti una linea rappresentata dalla circonferenza massima , cioè l’intersezione della sfera con un piano passante per il centro di essa.

In questo modo, un segmento di tale curva rappresenta il cammino minimo che congiunge i due punti.

Quando due masse si attraggono per effetto della curvatura dello spazio, esse si muovono l’una verso l’altra come se seguissero tali segmenti di retta, cioè percorrendo le geodetiche.

Esempio della superficie sferica

Consideriamo, ad esempio, due masse di uguali dimensione, che generano nello spazio-tempo la stessa deformazione; supponiamo che nello stesso spazio sia presente anche una terza massa, molto più grande delle precedenti, che genera quindi una deformazione dello spazio-tempo molto più rilevante. Le due masse piccole, quindi, sono attratte in modo uguale verso la massa più grande, per effetto della deformazione creata da quest’ultima.

Rappresentiamo la stessa situazione in un contesto diverso, in cui può essere messo bene in evidenza il percorso seguito dalle masse.

Ipotizziamo che la massa più grande si trovi sulla sommità di una sfera, e le due masse più piccole sulla sua superficie;

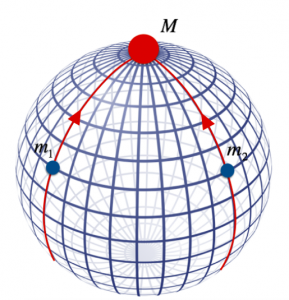
curvatura-spazio-tempo

La deformazione dello spazio fa si che le masse minori si avvicinino a quella più grande seguendo due archi di circonferenza massima; questi si ottengono a partire da due circonferenze massime passanti per la posizione iniziale delle singole masse piccole, e per la sommità della sfera.