Dal dilatazione del tempo è un fenomeno che può essere visto come conseguenza dei principi della Relatività.
Vediamo di cosa si tratta con un pratico esempio; consideriamo lo spazio che viene precorso da un raggio di luce emesso da una sorgente A e diretto in un punto B nel caso in cui la situazione è osservata in due sistemi di riferimento diversi, che sono in moto l’uno rispetto all’altro con velocità relativa v*; noteremo che il tempo impiegato dal raggio di luce nei due casi risulta diverso.
Sistema di riferimento con sorgente e ricevitore fermi
Inizialmente consideriamo un sistema di riferimento S’, in cui la sorgente A e il ricevitore B siano fermi, e posti ad una distanza L’ l’uno dall’altro, in posizione verticale.
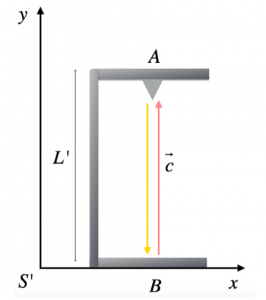
Se misuriamo il tempo impiegato dal raggio di luce a nel percorrere il tratto da A a B, tornare indietro (da B ad A), il tempo che misuriamo sarà pari a:
$ ∆t_1 = frac(2L’)(c)$
In questo caso, poiché l’apparato è fermo sen sistema S’, l’emissione del raggio di luce dalla sorgente, e la ricezione finale del raggio, dopo che esso ha percorso la distanza 2L’, avvengono nello stesso punto A.
In questo caso, il tempo che impiega la luce a percorre tale tratto viene definito tempo proprio, e può essere misurato utilizzando un solo orologio posto nel punto A.
Sistema di riferimento in moto
Vediamo ora il secondo caso, in cui, nel sistema di riferimento S’, l’apparato visto precedentemente si sta muovendo a velocità v*. Di conseguenza, rispetto a S’ tutti i punti si muovono a velocità v*, compresi la sorgente A e il primo rivelatore B.
Sebbene il raggio di luce emesso da A si muove in linea retta da A a B, per un osservatore posto in S il percorso del raggio di luce apparirà differente; in particolare, il punto in cui il raggio di luce viene emesso è differente dal punto in cui viene visto tornare dopo aver percorso il suo tragitto.
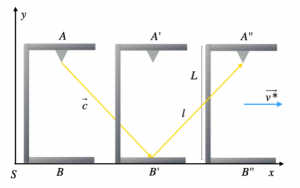
Per un osservatore in S, quindi, è come se il raggio di luce descrivesse un tragitto che può essere visto come l’ipotenusa di un triangolo rettangolo i cui cateti sono la distanza A-B e la distanza B-B’; chiamiamo tale ipotenusa con l.
In questo caso, quindi, il tempo che si misura dalla partenza del raggi di luce in A, all’arrivo del raggio di luce in A’’ è sicuramente diverso da quello misurato nel primo caso, in quanto la luce percorre uno spazio maggiore.
Il coefficiente di dilatazione
Si può dimostrare che tra i due intervalli di tempo sussiste la seguente relazione:
$ ∆t_2 = γ * ∆t_1 = frac(1)(sqrt(1 – (frac(v*)(c))^2 )) * ∆t_1 $
Il fattore γ si definisce coefficiente di dilatazione, e mostra di quanto il tempo rilevato dall’osservatore in S varia rispetto a quello dell’osservatore in S’.
Questa relazione è un’ulteriore prova che la velocità della luce non può essere raggiunta ne superata da nessun corpo; infatti, se la velocità v* diventasse molto grande, fino a raggiungere il valore di c, avremmo al denominatore della frazione il valore 0, e ciò è impossibile.
Inoltre, se v* fosse maggiore di c, il rapporto v*/c sarebbe maggiore di 1, e ciò implicherebbe un valore negativo all’interno della radice quadrata, cosa che non può verificarsi per un valore temporale.
La dilatazione dei tempi, quindi, mostra che la durata di un fenomeno è minima se essa viene misurata nel sistema di riferimento solidale con il sistema dei corpi che stiamo considerando, e nel quale ha inizio il fenomeno.
Orologi in posizioni diverse
Ipotizziamo ora di voler misurare la durata del tempo da orologi posti in posizioni diverse.
Il primo orologio ( $O_1$ ) è posto sull’apparecchiatura che si muove a velocità v*, ed è quello che misura il tempo $∆t_1$ . Altri due orologi sono fermi nelle posizioni che verranno occupate dall’apparecchio durante il suo moto, e che abbiamo denotato con A’ (in cui si trova $O_2$ ) e A’’ (in cui si trova $O_3$ ).
Confrontando le rilevazioni effettuate dagli orologi fermi e dall’orologio in moto; possiamo affermare che quest’ultimo ritarda rispetto agli orologi fermi e sincronizzati in S.
Si può dire, quindi, che per un osservatore posto in S il tempo che si misura in S’ sembra scorrere più lentamente che in S’.
Potrebbero Interessarti
Video Lezioni: Relatività
Appunti: La velocità della luce
Appunti: L’esperimento di Michelson-Morley
Appunti: La relatività ristretta
Appunti: La contrazione delle lunghezze
Appunti: Le trasformazioni di Lorentz
Appunti: L’intervallo invariante
Appunti: Lo spazio-tempo di Minkowski
Appunti: Equivalenza massa-energia
Appunti: L’effetto doppler relativistico
Appunti: La relatività generale
Appunti: La curvatura dello spazio-tempo
Appunti: La deflessione gravitazionale della luce
