Lo spazio-tempo di Minkowski

I sistemi di riferimento a quattro dimensioni

Il concetto di spazio-tempo è strettamente legato a quello di intervallo invariante; come abbiamo già visto, mentre in fisica classica gli spazi utilizzati per descrivere i fenomeni hanno due o tre dimensioni, e servono generalmente per individuare la posizione di un determinato corpo, nel caso della relatività è necessario tenere in considerazione anche il fattore tempo.

Per questo, si utilizzano dei sistemi di riferimento che presentano sia delle coordinate spaziali, sia delle coordinate temporali, per individuare la posizione di un corpo in un certo istante di tempo.

I sistemi di riferimento di questo tipo descrivono uno spazio a quattro dimensioni, che viene definito spazio-tempo, o anche spazio di Minkowski.

Uno spazio a quattro dimensioni è un concetto puramente matematico, e non ha proprietà fisiche; ogni punto che appartiene a tale spazio rappresenta un evento, e viene definito quindi punto-evento.

Anche in questo caso, è valido il concetto di intervallo invariante; se consideriamo due eventi, sappiamo che la differenza di coordinate che li descrivono varia in base al sistema di riferimento scelto, ma l’intervallo invariante è lo stesso in tutti i sistemi di riferimento inerziali. Ricordiamo che l’espressione di intervallo invariante è la seguente:

$ (∆σ)^2 = (c * ∆t)^2 – (∆x)^2 – (∆y)^2 – (∆z)^2$

L’intervallo invariante può essere considerato, nello spazio-tempo, al pari di un vettore spostamento di un normale sistema di riferimento.

L’intervallo invariante nello spazio-tempo

L’intervallo invariante può essere positivo, negativo o nullo, e in base a questo si parla di intervallo di tipo tempo, di tipo spazio, o di tipo luce.

Nel primo caso, considerando due eventi A e B, esiste un sistema di riferimento in cui gli eventi avvengono nello stesso luogo con un certo intervallo di tempo che li separa; nel secondo caso, invece, esiste un sistema di riferimento in cui gli eventi A e B avvengono nello stesso istante, ma in luoghi diversi.

Infine, nel terzo caso gli eventi sono separati da un intervallo di tipo luce, cioè esiste un raggio di luce che collega l’evento A con l’evento B.

Le componenti del vettore sono quattro, una per ogni dimensione dello spazio-tempo. Avremo quindi tre componenti spaziali (quelle relative agli assi x, y e z) e una componente temporale (quella lungo t).

I vettori di questo tipo sono definiti quadrivettori, o tetravettori, in quanto sono costituiti da una quaterna ordinata. Tuttavia, poiché spazio e tempo non sono grandezze omogenee, e quindi non possono essere sommate tra loro, le coordinate di un punto appartenente allo spazio di Minkowski vengono rappresentate in questo modo: (x, y, z, ct), dove c è la velocità della luce.

Il modulo del vettore in questo caso, cioè il quadrato della sua lunghezza, è dato dal quadrato della componente temporale a cui vengono sottratti i quadrati delle componenti spaziali.

La linea d’universo

Per semplicità, consideriamo uno spazio-tempo bidimensionale, in cui compare la coordinate temporale e la coordinata spaziale x; costruiamo in grafico ponendo la coordinate x come ascissa, mentre la coordinata ct come ordinata.

In un grafico di questo tipo, il moto di una qualsiasi particella è una curva, che viene definita linea d’universo; l’asse spaziale, quindi, rappresenta la linea d’universo di un oggetto fermo, mentre l’asse temporale rappresenta l’insieme di tutti gli eventi che avvengono simultaneamente ad un evento dato, preso come riferimento.

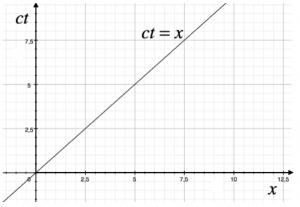
Il cono di luce

Una retta inclinata di 45° rispetto l’asse delle ascisse, cioè una retta di equazione $ct = x$ , rappresenta la linea d’universo di una particella che si muove alla velocità della luce.

A partire da questa retta, e considerando uno spazio tridimensionale, possiamo costruire il cosiddetto cono di luce:

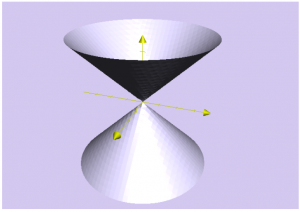
Cono-di-luce-costruito — Cono di luce costruito a partire da una linea d’universo.

Il moto di particelle dotate di massa è rappresentato da curve, ovvero linee d’universo, che sono contenute interamente all’interno del cono di luce, e non ne fuoriescono mai. Le linee d’universo, invece, che giacciono sulla superficie del cono sono quelle che rappresentano i raggi di luce.