Manuale di Fisica con licenza Creative Commons CC-BY-ND per la scuola secondaria di secondo grado. Il testo nasce dall’esperienza delle lezioni per gli studenti dei licei sulla fisica delle particelle, da me tenute nell’ambito dei programmi per l’orientamento e del Piano Lauree Scientifiche. Molti insegnanti, al termine delle mie lezioni, mi hanno chiesto materiale da utilizzare per riproporre in classe alcuni degli argomenti trattati, lamentando l’indisponibilità di testi adeguati. Per questo ho pensato di cominciare a scrivere queste note, con l’intento di ampliarle il piú possibile nel corso del tempo, includendovi anche materiale piú tradizionale.
Il titolo
Il titolo di questo volume non è stato scelto a caso. L’Italiano è una lingua che si presta a diverse, interessanti, e talvolta divertenti, interpretazioni del significato delle parole. In particolare l’aggettivo sperimentale utilizzato nel titolo ha in questo testo significati diversi, tutti contemporaneamente validi.
È sperimentale, come abbiamo detto sopra, il modo in cui il testo è realizzato e distribuito. Si tratta, cioè, della sperimentazione, della ricerca di un nuovo modello economico.
L’aggettivo sperimentale si riferisce anche al taglio dato all’introduzione dei concetti della fisica. Molti testi di fisica appaiono piú come libri di matematica, nei quali si danno certe definizioni allo studente e se ne traggono le conseguenze. Le definizioni, in molti casi, piovono dall’alto, senza una spiegazione plausibile sul perché sia il caso di introdurle o su quale sia la loro ragion d’essere. In questo testo la fisica viene introdotta attraverso l’esperimento. Ogni argomento viene analizzato a partire dalle osservazioni sperimentali, che determinano le grandezze fisiche d’interesse, portando naturalmente alla formulazione delle leggi fisiche.
Infine, è sperimentale il mezzo scelto per la realizzazione del testo. Il supporto elettronico consente di fruire di contenuti multimediali e delle potenzialità dell’ipertesto. Si potrebbe fare molto di piú, in effetti. La tecnologia è matura. Ma, spesso a causa di scelte determinate dal modello economico di cui parliamo sopra, molti produttori di software non consentono di usare in maniera semplice le innovazioni disponibili. Naturalmente il problema si potrebbe superare realizzando ad hoc anche i lettori per il supporto, ma questo avrebbe un costo eccessivo per noi (almeno in questa fase) e in ogni caso limiterebbe la platea di potenziali fruitori dell’opera. Possiamo solo sperare che il sistema avrà successo e ci consentirà, in futuro, di aumentare sempre di piú l’offerta.
Formare, non informare
Il semplice trasferimento di conoscenza non ha molto senso. Conoscere le leggi della fisica è utile, ma non indispensabile nella vita di una persona, tanto meno se questa conoscenza si limita alla mera capacità di scrivere le formule corrispondenti senza capirle.
Capire le leggi della fisica e il processo che ha condotto alla loro formulazione, al contrario, è di fondamentale importanza per la formazione complessiva degli studenti. Ecco perché questo testo pone l’accento piú sul come si arrivi a formulare le leggi fisiche piuttosto che su queste ultime. In particolare, le leggi fisiche davvero fondamentali sono poche ed è su queste che si concentra tutta la struttura del volume. Le leggi derivate da quelle fondamentali sono trattate come esercizi e non come parte integrante del testo. Questo non vuol dire che si possano ignorare, ma che non si devono necessariamente ricordare. Laddove esistano relazioni particolari che vale la pena siano ricordate a memoria per la frequenza con la quale si usano o per l’importanza che rivestono nel loro ambito, queste sono evidenziate in rosso, anche negli esercizi.
La matematica presente in ogni parte del volume (a parte gli esercizi) è ridotta al minimo indispensabile e non si assume la conoscenza di concetti avanzati, in modo tale che il testo possa essere usato da scuole diverse (Licei scientifici, classici, scuole professionali).
Per l’insegnante
Il testo contiene molto piú materiale rispetto a quello che si può normalmente pensare d’insegnare alla maggior parte degli studenti. La lunghezza del testo non deve spaventare: abbiamo scelto di spendere molte parole perché crediamo che della fisica si debba insegnare sopra tutto il metodo e non tanto i contenuti, pure indispensabili. È importante capire il significato delle equazioni e il modo in cui si ricavano. Non è quindi il numero di pagine che suggerisce di limitare gli argomenti, ma il fatto che oggettivamente alcuni sono molto (troppo) difficili per molti studenti. Lasciarli però consente agli insegnanti di preparare gli argomenti da trattare in maniera piú consapevole e completa, e agli studenti piú bravi di approfondire da soli argomenti che altrimenti sarebbero rimasti troppo vaghi.
INDICE
Indice
Prefazione 1
Alla scoperta dell’Universo 7
1 Scoprire la Fisica 11
1.1 Il problema della misura . . . . . . . 11
1.2 La luce . . . . . . . . . . . . . . . . . 11
1.3 Le onde . . . . . . . . . . . . . . . . 11
1.4 Il moto, il lavoro e l’energia . . . . . 12
1.5 La termodinamica . . . . . . . . . . . 12
1.6 Campi di forze . . . . . . . . . . . . 13
1.7 Correnti elettriche . . . . . . . . . . . 13
1.8 Campi magnetici . . . . . . . . . . . 13
1.9 Corpi rigidi . . . . . . . . . . . . . . 13
1.10 Onde elettromagnetiche . . . . . . . 13
1.11 Ancora sulla natura della luce . . . . 13
1.12 L’entropia e il secondo principio . . . 14
1.13 Le particelle elementari . . . . . . . . 14
2 Il ruolo della misura in Fisica 15
2.1 Misure e teorie . . . . . . . . . . . . 16
2.2 Le misure di base . . . . . . . . . . . 18
2.3 Gli strumenti . . . . . . . . . . . . . 21
2.4 Notazione scientifica . . . . . . . . . 23
2.5 Un esperimento istruttivo . . . . . . 24
2.6 Proprietà statistiche delle variabili casuali 25
2.7 L’interpretazione delle misure . . . . 28
2.8 Analisi statistica delle misure . . . . 30
2.9 Errori sistematici . . . . . . . . . . . 32
2.10 Propagazione degli errori . . . . . . . 34
2.10.1 La media pesata . . . . . . . 37
3 Definire le grandezze fisiche 39
3.1 Massa e Peso . . . . . . . . . . . . . 39
3.2 La radioattività . . . . . . . . . . . . 41
3.2.1 La regressione lineare . . . . . 42
3.2.2 La costruzione di un modello 44
3.3 La Temperatura . . . . . . . . . . . . 46
4 Calore e temperatura 51
4.1 La teoria del calorico . . . . . . . . . 51
4.2 Trasporto del calore . . . . . . . . . . 53
4.3 Falsificare una teoria . . . . . . . . . 56
5 Ottica geometrica 59
5.1 Riflessione della luce . . . . . . . . . 59
5.2 Una prima interpretazione . . . . . . 64
5.3 La rifrazione . . . . . . . . . . . . . . 65
5.4 Conferma della teoria corpuscolare . 68
5.5 Applicazioni . . . . . . . . . . . . . . 69
6 Le onde e i fenomeni ondulatori 73
6.1 Caratterizzazione delle onde . . . . . 74
6.2 Riflessione e rifrazione delle onde . . 77
7 Interferenza 79
7.1 Casi particolari . . . . . . . . . . . . 80
7.2 Onde stazionarie . . . . . . . . . . . 83
8 Effetti del moto sulle onde 85
8.1 L’effetto Doppler . . . . . . . . . . . 85
8.2 Effetto Doppler Relativistico . . . . . 87
8.3 L’effetto Cerenkov . . . . . . . . . . 88
8.4 Il red shift delle galassie . . . . . . . 90
9 La diffrazione 93
9.1 Sperimentiamo la diffrazione . . . . . 94
9.2 Definiamo la natura della luce . . . . 95
9.3 La matematica della diffrazione . . . 97
9.3.1 Diffrazione da fenditura sottile 97
9.3.2 Diffrazione da una doppia fenditura 98
9.3.3 I fasori . . . . . . . . . . . . . 104
9.3.4 Diffrazione da reticolo . . . . 106
9.3.5 Diffrazione da una fenditura larga 109
9.3.6 Potere risolutivo . . . . . . . 111
9.3.7 Diffrazione di raggi X . . . . . 112
10 Eppur si muove 113
10.1 Voi siete qui . . . . . . . . . . . . . . 113
10.1.1 Premessa metodologica . . . . 115
10.2 I vettori . . . . . . . . . . . . . . . . 116
10.3 Descrivere il moto . . . . . . . . . . . 123
10.4 Il moto rettilineo uniforme . . . . . . 128
10.5 Esperimenti con il moto dei corpi . . 131
10.6 Il moto uniformemente accelerato . . 134
10.7 Il moto lungo un piano inclinato . . . 135
10.8 Moti non rettilinei . . . . . . . . . . 137
10.9 Considerazioni finali . . . . . . . . . 147
11 Punti di vista 149
11.1 La relatività . . . . . . . . . . . . . . 150
12 Le Leggi di Newton 153
12.1 Il primo principio della dinamica . . 153
12.2 La misura delle forze . . . . . . . . . 156
12.3 Il secondo principio della dinamica . 160
13 La forza sia con te 165
13.1 La forza peso . . . . . . . . . . . . . 166
13.1.1 Conseguenze della forza peso . 167
13.2 Le funi . . . . . . . . . . . . . . . . . 169
13.2.1 L’esperimento del carrello . . 171
13.3 La forza elastica . . . . . . . . . . . . 172
13.4 Il pendolo semplice . . . . . . . . . . 178
13.5 Le forze di attrito . . . . . . . . . . . 181
13.5.1 Attrito statico . . . . . . . . . 182
13.5.2 Attrito dinamico . . . . . . . 185
13.5.3 Attrito volvente . . . . . . . . 186
13.5.4 Attrito viscoso . . . . . . . . 187
13.6 Altre forze . . . . . . . . . . . . . . . 189
14 Forze apparenti 191
14.1 Sistemi accelerati . . . . . . . . . . . 191
14.2 La forza centrifuga . . . . . . . . . . 193
14.3 La Forza di Coriolis . . . . . . . . . . 195
15 Lavorare stanca 201
15.1 Il lavoro . . . . . . . . . . . . . . . . 201
15.2 Il lavoro del facchino . . . . . . . . . 204
15.3 Il lavoro della forza peso . . . . . . . 205
15.4 Il lavoro delle forze elastiche . . . . . 206
16 Una misura del movimento 209
16.1 La natura dell’energia cinetica . . . . 210
17 Lavori speciali 213
17.1 L’energia potenziale . . . . . . . . . . 215
17.2 La conservazione dell’energia . . . . . 215
17.3 Forze conservative . . . . . . . . . . . 216
17.4 L’energia potenziale elastica . . . . . 217
17.5 Forze conservative . . . . . . . . . . . 218
18 Il terzo principio 221
18.1 Molle e biglie . . . . . . . . . . . . . 221
18.2 Oltre le biglie . . . . . . . . . . . . . 222
18.3 Muoversi col terzo principio . . . . . 223
19 La quantità di moto 225
19.1 Analisi dell’esperimento . . . . . . . 225
19.2 La conservazione della quantità di
moto . . . . . . . . . . . . . . . . . . 226
20 Urti 229
20.1 Urti unidimensionali . . . . . . . . . 229
20.2 Moderatori di neutroni . . . . . . . . 231
20.3 Urti anelastici . . . . . . . . . . . . . 231
21 Simmetria e conservazione 233
21.1 La conservazione dell’energia . . . . . 233
21.2 L’omogeneità dello spazio . . . . . . 235
22 Le leggi dei gas 237
22.1 Lo stato dei gas . . . . . . . . . . . . 238
22.1.1 La pressione . . . . . . . . . . 238
22.2 L’equazione di stato dei gas . . . . . 240
22.3 La trasformazione di un gas . . . . . 243
22.4 Il lavoro fatto da un gas . . . . . . . 244
INDICE vii
22.5 Il calore scambiato col gas . . . . . . 245
22.6 Trasformazioni speciali . . . . . . . . 247
22.6.1 Trasformazioni isobare . . . . 247
22.6.2 Trasformazioni isocore . . . . 248
22.6.3 Trasformazioni isoterme . . . 249
22.6.4 Trasformazioni adiabatiche . . 250
22.7 Il lavoro termodinamico . . . . . . . 251
23 La teoria cinetica dei gas 255
23.1 Un gas ideale . . . . . . . . . . . . . 256
23.2 Lo scioglimento del ghiaccio . . . . . 258
24 Il primo principio della termodinamica261
24.1 L’energia interna . . . . . . . . . . . 262
24.2 L’espansione libera di un gas perfetto 264
24.3 I calori specifici dei gas . . . . . . . . 264
24.4 L’equazione dell’adiabatica . . . . . . 267
25 L’entropia 269
25.1 Macchine termiche . . . . . . . . . . 269
25.2 La Macchina di Carnot . . . . . . . . 271
25.3 Entropia . . . . . . . . . . . . . . . . 274
25.4 Il secondo principio della termodinamica
. . . . . . . . . . . . . . . . . . 274
25.4.1 Passaggi di calore a volume
costante . . . . . . . . . . . . 276
25.5 L’espansione irreversibile di un gas . 277
25.6 Interpretazione microscopica dell’entropia
. . . . . . . . . . . . . . . . . 280
25.7 La media e la varianza di una
distribuzione . . . . . . . . . . . . . . 284
26 Forze elettriche 289
26.1 Esperimenti elettrizzanti . . . . . . . 289
26.2 La misura della forza elettrica . . . . 290
26.3 Conduttori e isolanti . . . . . . . . . 291
26.4 L’induzione . . . . . . . . . . . . . . 293
26.5 Polarizzazione . . . . . . . . . . . . . 294
26.6 Il processo di elettrizzazione . . . . . 295
26.7 Schermo elettrostatico . . . . . . . . 296
26.8 Altri fenomeni rilevanti . . . . . . . . 296
27 Il magnetismo 299
27.1 Un po’ di esperimenti . . . . . . . . . 299
27.2 I magneti da frigo . . . . . . . . . . . 300
28 Campi di forze 303
28.1 Il concetto di campo . . . . . . . . . 303
28.2 La rappresentazione del campo . . . 304
29 Un importante Teorema 311
29.1 Il teorema di Gauss . . . . . . . . . . 313
29.2 Il flusso di un campo generico . . . . 315
30 Il flusso dei campi 319
30.1 Il flusso di una carica elettrica
puntiforme . . . . . . . . . . . . . . . 320
30.2 Il flusso di una distribuzione di cariche321
30.3 Il flusso di una distribuzione sferica . 321
30.4 Il flusso di un campo uniforme . . . . 322
30.5 Il campo nei conduttori . . . . . . . . 324
30.6 Intrappolare il campo . . . . . . . . . 325
30.7 Il campo della forza peso . . . . . . . 326
30.8 La materia oscura . . . . . . . . . . . 331
30.9 Il flusso del campo magnetico . . . . 333
31 Energia e potenziale 335
31.1 Il lavoro di una forza centrale . . . . 335
31.1.1 L’energia potenziale gravitazionale
. . . . . . . . . . . . . 338
32 Il potenziale dei campi 343
32.1 Rappresentazioni del campo: le superfici
equipotenziali . . . . . . . . . 344
32.2 La misura dei potenziali . . . . . . . 347
33 La corrente elettrica 349
33.1 Un contenitore d’energia elettrica . . 349
33.2 Svuotiamo il condensatore . . . . . . 352
33.3 Vedere l’energia . . . . . . . . . . . . 355
33.4 Condensatori combinati . . . . . . . 355
33.5 Le pile . . . . . . . . . . . . . . . . . 357
33.6 La Legge di Ohm . . . . . . . . . . . 359
34 Circuiti in Corrente Continua 363
34.1 Combinazioni di resistori . . . . . . . 364
34.2 Generatori reali . . . . . . . . . . . . 365
34.3 Le Leggi di Kirchhoff . . . . . . . . . 367
34.4 Il circuito RC . . . . . . . . . . . . . 370
35 Elettromagnetismo 375
35.1 Correnti e forze magnetiche . . . . . 375
35.2 Il campo magnetico di una spira . . . 378
35.3 Il campo magnetico di molte spire . . 379
35.4 Il giogo di un magnete . . . . . . . . 381
36 Applicazioni dell’elettromagnetismo 383
36.1 I motori . . . . . . . . . . . . . . . . 383
36.2 La misura delle correnti . . . . . . . 386
37 La Forza di Lorentz 389
37.1 L’effetto Hall . . . . . . . . . . . . . 390
38 Il teorema di Ampère 393
38.1 Il campo magnetico di un solenoide . 396
38.2 La corrente di spostamento . . . . . . 397
39 Produrre elettricità 401
39.1 Produrre elettricità . . . . . . . . . . 402
39.2 L’energia magnetica . . . . . . . . . . 407
39.3 Energia elettromagnetica . . . . . . . 413
40 Equazioni di Maxwell 415
40.1 Onde elettromagnetiche . . . . . . . 416
40.2 Antenne . . . . . . . . . . . . . . . . 421
40.3 La natura della luce . . . . . . . . . . 422
41 Gira che ti rigira… 427
41.1 Un esercizio . . . . . . . . . . . . . . 427
41.2 Il prodotto vettoriale . . . . . . . . . 429
41.3 La seconda Legge della dinamica . . 431
41.4 La fisica dei momenti . . . . . . . . . 431
41.5 Pianeti e stelle . . . . . . . . . . . . 433
42 La teoria della Relatività Ristretta 437
42.1 Le trasformazioni di Lorentz . . . . . 437
42.2 La dilatazione del tempo . . . . . . . 439
42.3 Contrazione della lunghezza . . . . . 441
42.4 Composizione delle velocità . . . . . 442
42.5 I quadrivettori . . . . . . . . . . . . . 443
42.6 Il quadrivettore energia–impulso . . . 444
43 Muoversi tra sistemi 451
43.1 Una tecnica alternativa . . . . . . . . 452
43.2 Acceleratori e collider . . . . . . . . . 455
44 La Relatività Generale 457
44.1 La misura nei vari sistemi di riferimento
. . . . . . . . . . . . . . . . . 457
44.2 Il principio di equivalenza . . . . . . 458
44.3 la geometria dell’Universo . . . . . . 460
44.4 Effetti gravitazionali sul tempo . . . 462
45 Onde Gravitazionali 465
45.1 La generazione di onde gravitazionali 465
45.2 La misura di un’onda gravitazionale . 469
46 La Meccanica Quantistica 471
46.1 Il corpo nero . . . . . . . . . . . . . . 471
46.2 L’effetto fotoelettrico . . . . . . . . . 473
46.3 L’effetto Compton . . . . . . . . . . 475
46.4 La misura e il Principio d’indeterminazione
. . . . . . . . . . . . . . . . . 476
46.5 Onde di materia . . . . . . . . . . . . 478
46.6 Gli atomi . . . . . . . . . . . . . . . 478
46.6.1 Gli spettri atomici . . . . . . 479
46.7 Quantizzazione del momento angolare 480
46.8 Lo spin degli elettroni . . . . . . . . 481
46.9 Il Principio di Pauli . . . . . . . . . . 483
46.9.1 La chimica . . . . . . . . . . . 484
46.9.2 Semiconduttori . . . . . . . . 487
46.9.3 Il diodo . . . . . . . . . . . . 488
46.9.4 Il transistor . . . . . . . . . . 489
46.10 L’equazione di Schrödinger . . . . . . 490
47 Una storia esemplare 495
47.1 La scarica degli elettroscopi . . . . . 495
47.2 La scoperta dei raggi cosmici . . . . . 497
47.3 Caratteristiche dei raggi cosmici . . . 497
48 Chi l’ha ordinato? 501
48.1 Particelle penetranti . . . . . . . . . 501
48.2 L’ipotesi del neutrino . . . . . . . . . 502
48.3 L’antimateria . . . . . . . . . . . . . 504
48.4 La scoperta del muone . . . . . . . . 505
48.5 La scoperta del pione . . . . . . . . . 505
48.6 La lambda e i mesoni K . . . . . . . 506
49 I nuovi numeri quantici 509
49.1 I leptoni . . . . . . . . . . . . . . . . 509
49.2 I barioni . . . . . . . . . . . . . . . . 509
49.3 I mesoni . . . . . . . . . . . . . . . . 510
49.4 Gli adroni . . . . . . . . . . . . . . . 510
49.5 Classificazione in base allo spin . . . 511
50 Imitare la Natura 513
50.1 Gli acceleratori di particelle . . . . . 513
51 Studiare le particelle 515
51.1 Sezione d’urto . . . . . . . . . . . . . 515
51.2 Vita media . . . . . . . . . . . . . . . 516
52 Le risonanze 521
52.1 Urti tra particelle . . . . . . . . . . . 521
52.2 La massa invariante . . . . . . . . . . 523
53 Le particelle strane 527
53.1 I decadimenti della � . . . . . . . . . 527
53.2 Produzione associata . . . . . . . . . 528
54 Il Modello a Quark 531
54.1 Tre nuove Tavole Periodiche . . . . . 531
54.2 L’ipotesi dei quark . . . . . . . . . . 533
54.3 L’ottetto di mesoni . . . . . . . . . . 534
54.4 L’ottetto di barioni . . . . . . . . . . 534
54.5 Quark colorati . . . . . . . . . . . . . 535
55 Il Modello Standard 539
55.1 I costituenti della materia . . . . . . 539
56 Campi e Particelle 541
56.1 Le forze fondamentali . . . . . . . . . 541
56.2 Una rivisitazione del concetto di
energia . . . . . . . . . . . . . . . . . 542
56.3 L’energia delle interazioni tra particelle
. . . . . . . . . . . . . . . . . . 544
56.4 Altri processi . . . . . . . . . . . . . 548
56.5 L’antimateria . . . . . . . . . . . . . 549
56.6 La produzione delle particelle strane 549
56.7 L’interazione debole . . . . . . . . . . 549
57 Il bosone di Higgs 551
57.1 Richiami sul concetto di energia . . . 551
57.2 Campi autointeragenti . . . . . . . . 553
57.3 Sul significato dell’energia . . . . . . 553
57.4 L’introduzione della relatività . . . . 554
57.5 Il Meccanismo di Higgs . . . . . . . . 554
57.6 Sulla forma del potenziale di Higgs . 555
57.7 Campi massivi . . . . . . . . . . . . . 557
57.8 La massa dei bosoni vettori . . . . . 558
Appendice 561
Approssimazione di funzioni . . . . . 561
Equazioni differenziali a variabili
separabili . . . . . . . . . . . . . . . 563
Unità naturali . . . . . . . . . . . . . 567
Soluzione degli esercizi 569
L’AUTORE
Prof. Giovanni Organtini
“Sapienza”, Università di Roma
Dip.to di Fisica
P.le Aldo Moro, 2
00185 ROMA (Italy)
Tel: +39 06 4991 4329 Fax: +39 06 4453 829
e–mail: [email protected]
 FISICA SPERIMENTALE (111 MB) 23 dicembre 2016
FISICA SPERIMENTALE (111 MB) 23 dicembre 2016


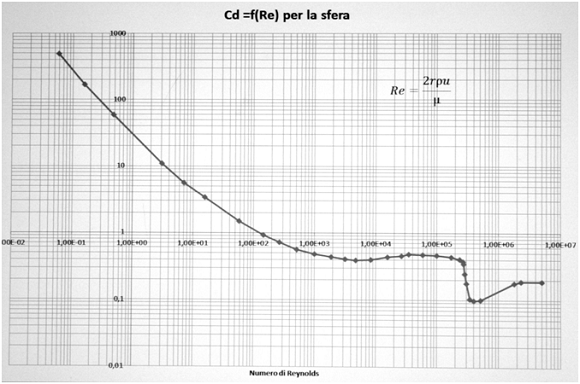
 figura 1
figura 1 figura 2
figura 2