L’asta è un sistema di allocazione delle risorse caratterizzato da un insieme di regole che presiedono allo scambio tra agenti economici, specificando la procedura utilizzata per determinare il rapporto di scambio, ovvero il prezzo, che deve essere pagato per il godimento di un bene, un servizio o un diritto. La Teoria delle Aste si occupa del comportamento degli individui nei mercati ad asta stabilendone le strategie ottimali che conducono ad equilibri stabili. La teoria delle aste è egualmente usata come uno strumento per informare la progettazione delle aste reali e costituisce una branca della Teoria dei Giochi, più precisamente dei cosiddetti “giochi ad informazione incompleta”; tra i più rilevanti esempi di asta, dal punto di vista dei valori realizzati, vi sono quelli della privatizzazione delle aziende del settore pubblico o della vendita delle autorizzazioni governative.
Scarica il file https://www.matematicamente.it/staticfiles/teoria/economia_unile/Angele-Teoria_aste.pdf
Sunto
Principali tipologie d’astaIn letteratura vengono individuate essenzialmente quattro tipologie d’asta, le cui proprietà variano essenzialmente in relazione al meccanismo istituzionale che caratterizza la regola di selezione del vincitore e la determinazione del prezzo da pagare:a) Asta inglese aperta (English Auction). Il meccanismo di determinazione del vincitore e del prezzo per questo tipo di asta è il seguente: si parte da un prezzo iniziale (base d’asta), che viene aumentato in modo discreto, fino al momento in cui non resta che un solo partecipante, il quale si aggiudica il bene pagando l’ultimo prezzo annunciato (corrispondente alla dichiarazione dell’offerente che per ultimo abbandona la competizione).b) Asta olandese aperta (Dutch Auction). Il meccanismo di funzionamento di quest’asta è opposto a quello dell’asta inglese aperta. Si parte da un prezzo elevato che viene via via ridotto, in modo discreto, fino al punto in cui un partecipante dichiari la propria volontà di acquistare a quel prezzo.c) Asta in busta chiusa e pagamento del prezzo più alto (First Price Sealed Bid Auction). In questo caso si aggiudica l’oggetto colui che, in busta chiusa, effettua l’offerta più elevata. d) Asta in busta chiusa e pagamento del secondo prezzo più alto (Second Price Sealed Bid Auction). In questo tipo di asta l’oggetto viene aggiudicato a colui che effettua l’offerta più elevata, ma il prezzo che egli deve pagare è pari alla seconda offerta più elevata. Esiste dunque separazione tra dichiarazione e prezzo da pagare.Aste e Teoria dei GiochiNella Teoria dei Giochi le aste vengono considerate come giochi statici con azioni simultanee ad informazione incompleta, in quanto non si conosce la caratteristica privata di ciascuno degli avversari, ovvero la valutazione del bene.In tali situazioni esiste, inoltre, incertezza strategica, in quanto ciascun agente deve formare la propria strategia senza conoscere il comportamento tenuto dagli avversari.Tali giochi ad informazione incompleta possono essere trasformati in giochi ad informazione imperfetta tramite la soluzione di Harsanyi (1967/68). Il gioco viene trasformato assumendo che la Natura, facendo la prima mossa, abbia assegnato casualmente a ciascun agente la propria valutazione. Tale valutazione viene recepita da ogni agente come realizzazione indipendente di una variabile causale di distribuzione nota a tutti ed indicata con F(v), si assume che tale distribuzione è identica per ogni individuo ed è conosciuta da tutti. In base all’assunzione di imperfetta informazione diviene possibile applicare il concetto di equilibrio di Nash-Bayes.
Vediamo ora qualche concetto teorico circa la Teoria delle Aste.
[…]Aste nel settore della telecomunicazioniL’asta nel Regno Unito per le licenze UMTS La prima asta per la vendita delle licenze UMTS avvenne in Inghilterra nei mesi di marzo e aprile del 2000. Quest’asta è sicuramente quella maggiormente riuscita in Europa relativamente all’UMTS, non solo è anche forse l’asta che storicamente ha dato al venditore (in questo caso il governo britannico) il maggior risultato economico, con un record storico di ben 39 miliardi di Euro. Il disegno del modello d’asta applicato fu studiato e preparato nel giro di tre anni, il problema principale è che originariamente erano presenti quattro licenze e sul mercato erano presenti già quattro grandi colossi della telefonia di seconda generazione: • Cellnet (partecipata al 60% da British Telecom) • One-2-one • Orange • Vodafone L’intento era quello di evitare che nuove aziende non entrassero all’interno dell’asta per paura dei gruppi già presenti, dato che questi ultimi oltre ad una maggiore conoscenza del mercato delle telecomunicazioni possedevano già un parco clienti e tecnologie già esistenti che potevano essere aggiornate verso quelle nuove. Si decise quindi di utilizzare il meccanismo d’asta Anglo-Olandese in modo che la parte d’asta ascendente durasse fino ad avere cinque sopravvissuti e poi continuare con la parte d’asta in busta chiusa per distribuire le quattro licenze. Questo meccanismo venne poi abbandonato, in quanto il governo optò per cinque licenze, e queste cinque potevano essere vendute solo ad altrettanti cinque offerenti. In tal maniera almeno una licenza sarebbe finita nelle mani di un’azienda entrante e si sarebbero ridotti i casi di collusione in maniera drastica. Si decise per un’asta ascendente multipla che coinvolse oltre alle quattro imprese già presenti ben nove nuove aziende entranti, stabilendo appunto un guadagno totale di 39 miliardi di Euro. L’asta nei Paesi Bassi per le licenze UMTSLo sfondo su cui si svolse la vendita di licenze nei Paesi Bassi è simile a quella nel Regno Unito e il governo si ispirò appunto ad essa per il disegno d’asta. Infatti anche qui erano presenti cinque possibili candidati per cinque licenze disponibili. Non vi fu purtroppo lo stesso successo, i nuovi entranti riconoscendo la loro posizione di inferiorità fecero dei contratti con i colossi, permettendo la partecipazione ad aziende quali Deutsche Telekom, DoCoMo e Hutchinson, in questa maniera il disegno d’asta si rivelo non funzionale. L’unico nuovo entrante partecipante all’asta fu Versatel che dovette però fermarsi nelle offerte dopo aver ricevuto delle minacce legali dal colosso Telfort. Versatel nonostante ripetuti appelli al governo, non venne ascoltata perché quest’ultimo voleva evitare perdite di contanti e quindi si decise di non sospendere l’asta. Il risultato fu insoddisfacente ed il governo olandese ottenne un guadagno di soltanto 3 miliardi di Euro, rispetto ai 10 pronosticati dopo aver osservato l’asta britannica. Probabilmente l’utilizzo di un’asta anglo-olandese avrebbe permesso ad altri entranti, oltre a Versatel, di partecipare all’asta e di evitare patti ed alleanze prima dell’inizio della stessa. Sei mesi dopo il parlamento olandese inizio un indagine per investigare sull’intero processo d’asta. L’asta in Italia per l’assegnazione delle licenze UMTSLe società interessate alla gara per l’assegnazione delle licenze della telefonia mobile di terza generazione hanno avuto tempo fino al 10 agosto 2000 per presentare le domande di partecipazione. Già da prima dell’uscita del bando sulla Gazzetta Ufficiale, in via ufficiosa, si sono conosciute le scadenze principali riguardanti, ad esempio, l’ammissione o meno entro il 2 settembre alla presentazione dei rispettivi piani tecnico-commerciali (l’11 settembre 2000, entro le ore 12:00). L’asta vera e propria sarebbe dovuta partire, ed è partita, da un importo minimo per l’aggiudicazione di ogni licenza pari a 4.000 miliardi di lire. Condizione preliminare è stata altresì il rilancio minimo, fissato nel 5% dell’importo base (ossia in 200 miliardi di lire) che comunque poteva scendere al 2%, in seguito alla decima tornata di rilanci, se i partecipanti fossero stati meno di otto.Dal punto di vista dei rilanci, l’offerta non poteva superare della metà la più bassa delle cinque offerte più alte nella tornata precedente, mentre il deposito minimo necessario per prendere parte alla gara era di 5 miliardi di lire. Inoltre, le società prendenti parte alla competizione dovevano godere di un capitale sociale di almeno 800 miliardi e di garanzie bancarie per minimo 4.000 miliardi, il tutto espresso in lire. In principio ciascuna licenza concessa doveva durare 15 anni, ma poi, a fine novembre 2001, il ministro delle Comunicazioni Maurizio Gasparri ha annunciato, assieme al presidente dell’Authority Enzo Cheli e in seguito alle richieste di Tim, Vodafone Omnitel, Wind, Ipse 2000 e H3G, il prolungamento fino a 20 anni, a partire dal 1° gennaio 2002. La licenza non può essere ceduta a terzi per almeno 48 mesi dalla data del rilascio e comunque mai senza l’autorizzazione dell’Authority. Per quanto riguarda i requisiti minimi per la costruzione delle reti e il lancio dei servizi, gli assegnatari delle licenze hanno tempo fino al prossimo giugno venturo per adempiere all’obbligo di copertura dei capoluoghi di regione e di altri 30 mesi per i capoluoghi di provincia. I piani tecnici da presentare coattivamente dovevano contenere tutte le indicazioni circa i tempi di realizzazione delle opere, circa il fabbisogno di personale, le previsioni di mercato, i piani d’investimento; queste informazioni sono servite alle autorità di competenza in primo luogo a chiarire l’idoneità o meno di una società a partecipare al grande evento dell’asta.Un articolo del bando di gara imponeva che due delle nuove società entranti e ottenenti le licenze pagassero le porzioni di spettro mediante un ulteriore versamento di 1.600 miliardi di lire; tuttavia questa e le altre tasse d’ingresso hanno creato non poche, pericolose spaccature politiche, alimentando una “aperta crisi di governo”, così definita dal Sottosegretario alle Comunicazioni Michele Lauria. Certo è che i costi complessivi delle licenze nell’asta italiana sono risultati di gran lunga maggiori rispetto a quegli esborsati dai Paesi Bassi e dalla Spagna, mentre di molto inferiori rispetto a quelli affrontati dall’Inghilterra e dalla Germania. Per riassumere, il metodo utilizzato in Italia per l’assegnazione delle licenze UMTS è una combinazione unica tra i Paesi OCSE di elementi di beauty contest e di asta. In seguito ad una decisione presa dall’AGCOM (Autorità per le Garanzie nelle Comunicazioni) e pubblicata sulla Gazzetta Ufficiale il 14 gennaio 2000, il rilascio di licenze nazionali per il sistema mobile di terza generazione doveva seguire un iter suddivisibile in due fasi: 1) una di pre-selezione, basata sull’esame del business plan tecnico-commerciale e sull’accertamento di altri requisiti documentabili; 2) una di selezione, identificata successivamente con la procedura di asta. Accettate e seguite queste regole, alla prima fase della procedura si sono iscritti otto canditati: i quattro operatori già esistenti nel settore della telefonia mobile e quattro nuovi entranti. Nonostante ciò, solo sei candidati sono riusciti a passare alla fase selettiva. L’asta ha così avuto inizio il 19 ottobre 2000 e si è conclusa dopo 11 tornate il 23 ottobre, rimpinguando le casse dello Stato di ben 26.750 miliardi di lire. Le aste in Germania e Austria per le licenze UMTSIn Germania si optò per un modello diverso da quelli precedenti, in cui il numero delle licenze non era pre-determinato ma decisa dagli offerenti. Si misero in asta venti blocchi di spettro dai quali gli offerenti dovevano creare licenze di due o tre blocchi. Ad esempio quattro aziende potevano vincere licenze da tre blocchi, oppure sei aziende potevano vincere licenze da due blocchi. Questi venti blocchi vennero venduti in un’asta simultanea ascendente simile a quella vista nei casi precedenti. L’obiettivo di questo modello era far vincere gli offerenti che avevano a disposizione maggiore informazione sulla nuova tecnologia, questo per colmare l’asimmetria d’informazione del governo. Quello che però non convinse è che si poteva decidere precedentemente come dividere le licenze, osservano i risultati delle tre aste già svolte, evitando di dare troppo potere decisionale ai partecipanti. Tale meccanismo permetteva inoltre collusioni e associazioni tra alcune aziende entranti che però analogamente alla questione olandese non furono punite per evitare di perdere ulteriormente guadagni. Nonostante questi difetti e diversi comportamenti di segnalazione sospetta da parte delle parti, il guadagno fu piuttosto alto circa il 94% del risultato inglese, probabilmente a causa del meccanismo più complesso che confuse le strategie dei partecipanti. L’Austria decise di accodarsi al modello tedesco, ma il risultato mostrò tutta l’inadeguatezza di un adattamento così grossolano, in quanto ci furono solo sei partecipanti per i venti blocchi di spettro. Il risultato fu appena un sesto del guadagno tedesco a causa dello stesso errore svizzero di fissare un prezzo di riserva ridicolmente basso. Le aste in Svizzera, Belgio, Grecia e DanimarcaIn Svizzera nel periodo di novembre e dicembre emulando nuovamente l’asta britannica ottenne il peggiore risultato di tutti. Gli errori svizzeri furono diversi oltre al cattivo disegno d’asta, infatti si permise all’ultimo minuto di fare delle offerte congiunte, cosa che permise in pratica di legalizzare le collusioni. I nove offerenti si ridussero immediatamente a quattro offerenti per le quattro licenze disponibili. L’ultimo errore fu quello di non aver fissato un prezzo di riserva abbastanza alto, e nonostante si cercò di rimandare l’asta di un mese per cambiare le regole, ci furono ricorsi da parte delle aziende che obbligarono a svolgere il tutto in maniera immutata. In Belgio e Grecia le cose si svolsero in maniera più semplice a causa dello scarso interesse che le aziende prestavano per esse. In Belgio la presenza di Belgacom’s Proximus, un solo grosso colosso possedente ben due terzi dell’intero mercato mobile esistente, intimidì l’entrata di nuove aziende. In Grecia, regione meno ricca, non si ebbe interesse a fissare un adeguato prezzo di riserva in quanto le aziende stavano ancora consolidando il mercato telefonico di seconda generazione e non erano interessante alle nuove proposte dell’UMTS. Il caso veramente interessante del 2001 fu la Danimarca che oltre a trovarsi in una situazione in cui le valutazioni erano tenute basse, fu l’unica ad imparare dagli errori delle aste precedenti. Ci furono sempre quattro licenze vendute ma si optò per l’utilizzo di un’asta a busta chiusa per permettere alle aziende entranti più deboli di fare le loro offerte. Il risultato fu ottimo attraendo delle offerte serie dalle nuove aziende entranti ed ottenendo un guadagno di 95 euro pro capite, ben il doppio di quello che ci si aspettava. La vendita Alitalia La teoria delle aste suggerisce che il modo migliore per vendere un’azienda come Alitalia è quello di fornire dall’inizio il massimo di informazione sulle condizioni di vendita e di usare un formato ascendente, tipo asta con banditore. Più o meno il contrario di quanto si è fatto fino a ora.L’analisi delle aste di oggetti multipli con possibili sinergie tra i diversi oggetti, come sarebbe il caso se Alitalia venisse smembrata e i suoi assets venissero venduti separatamente, è invece più recente.Il bando della gara Alitalia iniziale era a metà tra l’asta e il beauty contest. Con l’asta si aggiudica l’oggetto a chi è disposto a pagarlo di più. Con il beauty contest il venditore assegna l’oggetto ‘a chi è più bello’, o se vogliamo a chi più se lo merita (secondo i criteri del venditore). In questo caso, il merito era dato dalla presentazione di un piano industriale che risultasse gradito al governo. Si era comunque fatto presente che il governo avrebbe preferito, tra i partecipanti con piani industriali soddisfacenti, chi offrisse un prezzo più alto.Le condizioni richieste dal governo nel bando includevano: garanzie sui livelli occupazionali, mantenimento della identità nazionale, adeguata offerta dei servizi e copertura del territorio. Un’analisi superficiale può far pensare che non ci sono grossi problemi se queste ambiguità vengono risolte con il tempo, possibilmente dopo la vendita.La teoria delle aste suggerisce che il comportamento degli offerenti è parecchio differente a seconda che l’oggetto in vendita sia a valori privati o a valori comuni.L’asta è a valori privati quando il valore dell’oggetto per un potenziale acquirente è indipendente dal valore che a tale oggetto assegnano gli altri partecipanti. Per esempio, se sono disposto a spendere fino a 100 euro per comprare un mobile che mi piace e che intendo mettere in casa mia, risulta irrilevante il fatto che altri offerenti non siano disposti a spendere più di 50 euro. Il mobile deve piacere secondo preferenze soggettive, e quanto sono disposto a spendere dipende unicamente da quanto piace il mobile. Questo è il classico caso di valori privati.L’asta è invece a valori comuni quando il valore che un offerente assegna all’oggetto è il frutto di una stima del reddito che l’oggetto può generare in futuro, e tale stima del reddito è simile per tutti gli offerenti. Questo è il tipico caso dei beni d’investimento, e in particolare delle aziende. In una simile situazione conoscere la valutazione degli altri è importante, perché ci dice quali stime sono state fatte da altri offerenti sulla potenzialità futura di reddito. Se, per esempio, si è stimato che un’azienda vale 10 milioni di euro, e si scopre che tutti gli altri la valutano solo 2 milioni di euro allora è probabile che le stime effettuate siano troppo ottimiste. Nella teoria delle aste si parla di maledizione del vincitore per indicare il fatto che se un acquirente è disposto a pagare fino al valore da lui stimato finisce per vincere quando le sue stime sono eccessivamente ottimistiche (e quindi più alte delle stime degli altri acquirenti), finendo quindi per pagare troppo. Per evitare tale fenomeno, la strategia ottima degli acquirenti determina un prezzo massimo che si è disposti a pagare inferiore alla stima fatta del valore dell’oggetto.L’asta Alitalia è intermedia ai due casi, con una prevalenza del modello a valori comuni. Il valore comune in tal caso viene dall’aumento di redditività che può derivare da una gestione meno dissennata dell’azienda. Tali guadagni sono probabilmente simili tra i diversi potenziali acquirenti. Una componente di valore privato esiste, poiché alcuni offerenti hanno vantaggi specifici di cui non godono gli altri; l’ovvio esempio è la possibile monopolizzazione della tratta Milano-Roma per AirOne. Ai fini della determinazione della procedura ottima di vendita bisogna considerare la componente di valore comune che risulta più importante.Una caratteristica importante delle aste a valori comuni è che il venditore può aumentare il prezzo atteso di vendita massimizzando la quantità di informazione relativa all’oggetto disponibile agli acquirenti. L’intuizione è come segue. Si pensi che il venditore, il proprietario dell’azienda, sappia che il flusso di reddito che l’azienda può generare vale esattamente 100 milioni di euro. Se tale informazione viene comunicata in modo credibile agli acquirenti allora la concorrenza tra loro genererà un prezzo di 100 milioni di euro. Infatti, in tal caso non esiste incertezza sul vero valore dell’oggetto e l’acquirente non deve preoccuparsi di aver sovrastimato il valore dell’oggetto. Nel caso in cui il venditore non riesca a trasmettere tale informazione, gli acquirenti cercheranno di raccogliere informazioni per proprio conto e arriveranno a una stima imprecisa del valore dell’azienda. Essendo temuta la maledizione del vincitore, le offerte saranno inferiori alle stime. Se le stime sono adeguatamente previste risulteranno intorno al reale valore, quindi in media il prezzo sarà inferiore al valore reale dell’oggetto.In altre parole, il ritardo nella comunicazione di informazione fa perdere soldi al venditore. Risulta quindi un po’ curiosa la riluttanza del governo nel fornire informazioni su Alitalia, infatti il materiale informativo è stato inviato solo in uno stadio avanzato della procedura, in quanto aumentare al massimo la trasparenza può generare una maggiore partecipazione all’asta, alzando quindi il prezzo atteso di vendita.In un’asta a valori comuni l’aumento dell’incertezza ha il risultato di rendere più cauti gli acquirenti, che finiscono per offrire meno. In sostanza, l’incapacità di definire dall’inizio e con chiarezza gli obiettivi genera un inferiore prezzo atteso. Si noti che questa è una perdita per le casse pubbliche in aggiunta a quella che deriva dal fatto che i vincoli posti dal governo sulla gestione di Alitalia comunque ne riducono il valore. Per esempio, richiedere il mantenimento dell’identità nazionale è una pessima idea che probabilmente ha allontanato potenziali clienti e quindi ridotto il prezzo atteso di vendita. Invece, l’incertezza degli obiettivi governativi genera addizionali perdite dovute al fatto che i partecipanti all’asta, per proteggersi dalla maledizione del vincitore, riducono le proprie offerte.Un’asta a prezzi crescenti è migliore delle offerte in busta chiusa. Un importante risultato della teoria delle aste afferma che, in presenza di valori comuni, l’asta ascendente all’inglese genera un prezzo di vendita atteso più alto di un’asta in cui i partecipanti fanno offerte in busta chiusa. La logica è la stessa discussa al punto precedente. In un’asta a valori comuni, fare un’offerta senza sapere cosa offrono gli altri costringe ad essere prudente per evitare la maledizione del vincitore. Se la stima soggettiva di un’azienda è 100 non si è disposti a offrire più di 90. La riduzione di 10 serve a evitare situazioni in cui la stima degli altri concorrenti è più bassa e si finisce per vincere sovrastimando l’azienda. Mentre considerando l’asta all’inglese, se il prezzo arriva a 90 e gli altri partecipanti sono disposti a comprare a quel prezzo allora si può star tranquilli che la propria stima non è l’unica ad essere alta, per questo la propensione ad offrire un prezzo maggiore sarà più alta.Il bando del governo era ambiguo anche su questo punto, non era chiaro fino a che punto le offerte formulate erano rinegoziabili anche alla luce delle offerte dei concorrenti. Un problema grave è che l’uso di criteri ambigui di beauty contest rende poco chiaro come si debba svolgere la concorrenza tra diversi offerenti. Se il governo preferisce l’offerta di A all’offerta di B, non è chiaro cosa deve fare B per cercare di vincere, se aumentare il prezzo o migliorare le garanzia all’occupazione.La soluzione migliore per la vendita Alitalia in modo indiviso sarebbe quella di venderla senza vincoli al miglior offerente mediante un’asta all’inglese e fornendo da subito il massimo di informazione possibile, in modo da eliminare al massimo l’incertezza nelle stime del valore dell’azienda. Servizi d’asta on-lineAsta al rialzo: eBayFondato nel settembre del 1995, eBay è il servizio d’asta on-line più conosciuto al mondo e a oggi conta più di duecentoventi milioni di utenti registrati.E’ una piattaforma che consente agli acquirenti di trovare un’infinita gamma di prodotti a prezzi convenienti e ai venditori di incontrare un grandissimo numero di compratori. Le aste possono avere come oggetto o un prodotto usato o un prodotto nuovo, messo in asta ad esempio da un negozio on-line. E’ inoltre richiesta la registrazione per partecipare alle aste sia come compratore che come venditore.Il meccanismo si basa sulla classica asta ascendente ma al secondo prezzo aumentato di 0,50 cent, con la possibilità di fissare un prezzo di riserva. La caratteristica che lo contraddistingue è la durata limitata del tempo di una contrattazione.In questa forma ad asta la strategia migliore al fine di evitare di far lievitare troppo il prezzo finale dell’oggetto è quella di fare la propria offerta pochi istanti prima della scadenza. Infatti in base alle caratteristiche d’asta eBay, ossia durata limitata ad un certo periodo di tempo e offerta che supera di 0,50 cent di euro l’offerta fatta dal secondo miglior offerente, la strategia migliore per ogni utente è quella di offrire la somma massima che si è disposti a pagare nei minuti finali prima della conclusione della vendita.Al fine di delineare al meglio l’asta in eBay ipotizziamo una simulazione semplificata dello svolgimento d’asta.Ipotizziamo che un venditore metta all’asta un bene indivisibile con un prezzo di partenza pari a 1€. Dall’altro lato abbiamo due potenziali acquirenti A e B, che valutano il bene rispettivamente10€ e 9€. Ogni giocatore si propone di spendere meno rispetto alla sua valutazione di quel bene. Ipotizziamo che ogni offerta fatta deve essere di minimo un euro.
Figura 1: Durata dell’astaPer semplicità ipotizziamo la durata dell’asta pari a dieci minuti e per effettuare un’offerta occorre un minuto, in questo modo l’intera asta può essere divisa in 10 istanti temporali (Figura 1). Una volta iniziata l’asta le possibili dinamiche che la caratterizzano sono diverse, vi possono essere una serie di rilanci e contro rilanci o può esservi uno scambio di offerte negli ultimi minuti dell’asta. Bisogna ricordare che il prezzo pubblico visibile è sempre quello del secondo miglior offerente aumentato di 0,50 cent di euro.Se il prezzo sale gradualmente di minuto in minuto, si arriverà sicuramente a superare la massima disponibilità ad offrire di B e A sarà il vincitore dell’asta, con un prezzo di 9,50€.Un’altra situazione è quella per la quale le offerte vengono fatte negli istanti finali se si esclude la situazione nella quale A vada ad offrire direttamente la propria offerta massima, l’esito finale potrebbe vedere come vincitore il giocatore B. Infatti, dato che il tempo occorrente per l’offerta è di un minuto potrebbe accadere che se al settimo minuto A offre 5, B potrebbe rilanciare offrendo direttamente 9 (offerta massima di B), dato che il prezzo visibile sarà di 5,5€, A potrà rilanciare nell’ultimo minuto di 2. Ciò comporterà che B si aggiudicherà l’oggetto al prezzo di 7,5€.Un altro esempio che possa evidenziare la strategia ottimale, ossia quella di vincere l’asta evitando che il prezzo salga eccessivamente, è il seguente. Ipotizziamo:• Due giocatori.• Prezzo di partenza pari a 0€ per un bene indivisibile.• Rilancio minimo di 5€.• Due istanti temporali in cui avvengono le mosse dei giocatori: T+1 e T+2.Consideriamo tutte le possibili combinazioni di mosse che avvengono nei due istanti di tempo del gioco:NN: entrambi i giocatori non offrono, (situazione coerente nel primo istante di tempo del gioco, incoerente nel secondo istante temporale in quanto non vi sarebbe interesse allo svolgimento dell’asta).ON: un giocatore offre e l’altro non offre.OO: entrambi i giocatori offrono.
Figura2: Schema delle possibili combinazioni di mosse associate ai payoffDalla figura 2 si evince che la strategia per la quale nessun giocatore effettua offerte non verrà presa in considerazione in quanto poco significativa ai fini del gioco. In base ai payoff considerati la strategia che risulta ottimale per non alzare troppo il prezzo finale dell’asta è NN (Tacit Collusion) , ossia quella di non effettuare offerte nel primo istante temporale del gioco e offrire nel secondo istante temporale in modo da accaparrarsi l’asta.Nel secondo istante temporale la strategia che si verificherà potrà essere: ON se uno dei due giocatori reputerà il prezzo offerto dall’altro troppo alto; altrimenti, OO nel caso in cui entrambi facciano l’offerta.Bisogna inoltre sottolineare che in eBay il prezzo di rilancio visibile al pubblico è quello del secondo miglior offerente aumentato di 0,50 cent, tale regola fa in modo che il prezzo di chiusura rimanga minore dell’offerta massima fatta dal vincitore dell’asta. Asta al ribasso: AsteClickAsteclick è un altro servizio d’asta on-line ma al ribasso. Ogni utente ha l’opportunità di acquistare prodotti ad un prezzo inferiore a quello di mercato e tale opportunità è organizzata sullo stile di un’asta al buio al ribasso. Il vincitore sarà colui che avrà effettuato la sua offerta di acquisto risultante la più bassa ed unica, quindi si aggiudicherà il prodotto e lo acquisterà al prezzo offerto. Qualora alla fine dell’asta non risulti una singola offerta più bassa, vincerà il prezzo offerto meno volte e tra gli offerenti di quel prezzo, risulterà vincitore colui che per primo ha effettuato l’offerta. Ogni utente deve avere dei crediti spendibili per poter fare una singola offerta nell’asta, quindi più offerte implicano l’uso di più crediti. Ad ogni asta il numero dei crediti varia a seconda dell’oggetto messo in vendita.Il costo per ogni 100 crediti è di un 1€ e solitamente il numero di crediti per effettuare un’offerta varia da 100 a 200 a seconda dell’oggetto messo in asta.In questo tipo di asta risulta difficile trovare una strategia ottimale, sicuramente aumentando il numero delle offerte si aumentano le possibilità di vincita. Se prendiamo come esempio l’asta di un Macbook Air dal valore commerciale di 1700 euro, per ogni offerta occorrono 200 crediti. In media le aste passate hanno visto un prezzo finale inferiore a 20€. Se si decidesse di coprire tutte le possibili somme inferiori a 20€ si dovrebbero effettuare 2000 offerte, ciò comporterebbe un costo di 4000€ senza avere la certezza di vincere l’asta. A nostro giudizio questo semplice esempio è potrebbe essere sufficiente a dimostrare come in questo tipo d’asta vi sia una maggiore incertezza di vincita rispetto ad altri tipi d’asta.
 Euclide, nato ad Alessandria attorno al 350 a.C., sistematizzò tutte le conoscenze di geometria sviluppate dai greci nell’era classica. Basandosi sulla logica di Aristotele scrisse gli Elementi. Il modo di procedere, esemplare e stringente per risolvere i problemi geometrici, si basa da un lato su assiomi e postulati immediatamente evidenti e dall’altro su teoremi, corollari e lemmi che vengono dimostrati a partire da premesse certe.
Euclide, nato ad Alessandria attorno al 350 a.C., sistematizzò tutte le conoscenze di geometria sviluppate dai greci nell’era classica. Basandosi sulla logica di Aristotele scrisse gli Elementi. Il modo di procedere, esemplare e stringente per risolvere i problemi geometrici, si basa da un lato su assiomi e postulati immediatamente evidenti e dall’altro su teoremi, corollari e lemmi che vengono dimostrati a partire da premesse certe. 
 Se in una serata, durante le feste di Natale, avete invitato un po’ di amici e mentre la pizza stenta a cuocere volete intrattenerli un po’, potete proporre questo gioco. E’ un gioco originale, nessuno vi dirà “ah, sì, lo conosco, il solito gioco, …”. Dopo il gioco, durante la cena, avete anche modo di discutere di come funziona, ognuno potrà spiegare quale ragionamento ha fatto e confrontarsi con i vicini.
Se in una serata, durante le feste di Natale, avete invitato un po’ di amici e mentre la pizza stenta a cuocere volete intrattenerli un po’, potete proporre questo gioco. E’ un gioco originale, nessuno vi dirà “ah, sì, lo conosco, il solito gioco, …”. Dopo il gioco, durante la cena, avete anche modo di discutere di come funziona, ognuno potrà spiegare quale ragionamento ha fatto e confrontarsi con i vicini.  Scarica i Sudoku, stampali e risolvili comodamente in vacanza, in treno, nel pulman. 16 Sodoku di diversi livelli di difficoltà dai più facili ai più difficili.
Scarica i Sudoku, stampali e risolvili comodamente in vacanza, in treno, nel pulman. 16 Sodoku di diversi livelli di difficoltà dai più facili ai più difficili. 

 Se hai idee simpatiche e divertenti partecipa alla realizzazione del prossimo diario scolastico Piccolatomopaco e potrai vincere un Apple Ipod da 8 Gb e le copie del nuovo diario! Tre le sezioni in cui si può partecipare.
Se hai idee simpatiche e divertenti partecipa alla realizzazione del prossimo diario scolastico Piccolatomopaco e potrai vincere un Apple Ipod da 8 Gb e le copie del nuovo diario! Tre le sezioni in cui si può partecipare.  Nell’estate 2007 hanno suscitato interesse i dati su insuccessi in Matematica e il Ministro della Pubblica Istruzione ha costituito un “Comitato Scientifico per il miglioramento della qualità dell’insegnamento della matematica”. Nel decreto ministeriale sulle Indicazioni nazionali è previsto che le istituzioni scolastiche verifichino «la congruità dei contenuti proposti e la loro articolazione per campi di esperienza, aree, discipline e competenze, anche al fine di eventuali modificazioni e integrazioni». Tra gli obiettivi di questo libro c’è quello di mettere a disposizione, di singoli e di istituzioni, spunti di riflessione sull’apprendimento e sull’insegnamento della Matematica ai vari livelli scolastici, anche con e per proposte di miglioramento.
Nell’estate 2007 hanno suscitato interesse i dati su insuccessi in Matematica e il Ministro della Pubblica Istruzione ha costituito un “Comitato Scientifico per il miglioramento della qualità dell’insegnamento della matematica”. Nel decreto ministeriale sulle Indicazioni nazionali è previsto che le istituzioni scolastiche verifichino «la congruità dei contenuti proposti e la loro articolazione per campi di esperienza, aree, discipline e competenze, anche al fine di eventuali modificazioni e integrazioni». Tra gli obiettivi di questo libro c’è quello di mettere a disposizione, di singoli e di istituzioni, spunti di riflessione sull’apprendimento e sull’insegnamento della Matematica ai vari livelli scolastici, anche con e per proposte di miglioramento.  Un semplice test sulle tabelline in PowerPoint, per studenti della scuola primaria e secondaria di primo grado. Un gioco divertente per ripassare le tabelline.
Un semplice test sulle tabelline in PowerPoint, per studenti della scuola primaria e secondaria di primo grado. Un gioco divertente per ripassare le tabelline. 
 Distruggi le palline in modo che la somma sia sempre dieci. Attento a non far cadere a terra le palline. Man mano che passa il tempo le palline diventano sempre più veloci. Occhio alle palle speciali: la bomba fa scoppiare tutte le palline vicine, la bomba atomica fa scoppiare tutte le palline, l’orologio rallenta la caduta delle palline. Buon divertimento.
Distruggi le palline in modo che la somma sia sempre dieci. Attento a non far cadere a terra le palline. Man mano che passa il tempo le palline diventano sempre più veloci. Occhio alle palle speciali: la bomba fa scoppiare tutte le palline vicine, la bomba atomica fa scoppiare tutte le palline, l’orologio rallenta la caduta delle palline. Buon divertimento. 
 "Pianificate quello che è difficile quando è ancora facile, fate quello che è grande quando è ancora piccolo. Le imprese più difficili debbono essere iniziate quando sono ancora facili, le imprese più grandi devono essere fatte quando sono ancora piccole. Per questo motivo i saggi non fanno mai imprese troppo grandi, e questo è il motivo per cui raggiungono la loro grandezza". Sun Tzu, L’arte della guerra, circa 500-300 a.C.
"Pianificate quello che è difficile quando è ancora facile, fate quello che è grande quando è ancora piccolo. Le imprese più difficili debbono essere iniziate quando sono ancora facili, le imprese più grandi devono essere fatte quando sono ancora piccole. Per questo motivo i saggi non fanno mai imprese troppo grandi, e questo è il motivo per cui raggiungono la loro grandezza". Sun Tzu, L’arte della guerra, circa 500-300 a.C.  Anna Cerasoli, Sono il numero 1, come mi sono divertito a diventare bravo in matematica, Feltrinelli, 2008, euro 13,00, pagg. 130
Anna Cerasoli, Sono il numero 1, come mi sono divertito a diventare bravo in matematica, Feltrinelli, 2008, euro 13,00, pagg. 130  La Bella Addormentata si sottopone a un esperimento nel quale viene addormenta ipnoticamente. I ricercatori lanciano una moneta: se il risultato del lancio della moneta è testa la Bella Addormentata viene svegliata e poi interrogata; se il risultato della moneta è croce viene svegliata, interrogata, riaddormentata imponendole di non ricordare niente del precedente risveglio, viene svegliata di nuovo e reinterrogata.
La Bella Addormentata si sottopone a un esperimento nel quale viene addormenta ipnoticamente. I ricercatori lanciano una moneta: se il risultato del lancio della moneta è testa la Bella Addormentata viene svegliata e poi interrogata; se il risultato della moneta è croce viene svegliata, interrogata, riaddormentata imponendole di non ricordare niente del precedente risveglio, viene svegliata di nuovo e reinterrogata.  Questo lavoro riguarda l’analisi dei prezzi di chiusura di alcuni indici scaricati dal Yahoo Finanza, in particolare si è fatto riferimento alle quotazioni di Enel. L’esecutore del programma potrà di volta in volta scegliere quale titolo analizzare. I prezzi di chiusura possono essere visti come una serie di dati, denominata serie storica. I dati, ordinate temporalmente, vengono racchiusi in un vettore, su questo vettore si concentrerà l’analisi. Dopo aver sinteticamente descritto le funzionalità di Matlab nel primo e nel secondo capitolo, di valutare la statistica descrittiva nel terzo, il quarto capitolo si occup dell’analisi del trend. Il quinto capitolo riguarda la valutazione del trading system per mezzo di Matlab, il codice creato verrà dettagliatamente spiegato.
Questo lavoro riguarda l’analisi dei prezzi di chiusura di alcuni indici scaricati dal Yahoo Finanza, in particolare si è fatto riferimento alle quotazioni di Enel. L’esecutore del programma potrà di volta in volta scegliere quale titolo analizzare. I prezzi di chiusura possono essere visti come una serie di dati, denominata serie storica. I dati, ordinate temporalmente, vengono racchiusi in un vettore, su questo vettore si concentrerà l’analisi. Dopo aver sinteticamente descritto le funzionalità di Matlab nel primo e nel secondo capitolo, di valutare la statistica descrittiva nel terzo, il quarto capitolo si occup dell’analisi del trend. Il quinto capitolo riguarda la valutazione del trading system per mezzo di Matlab, il codice creato verrà dettagliatamente spiegato.  Nelle pagine che seguono affronteremo la costruzione rigorosa dei numeri reali effettuata verso la fine del secolo scorso (1872) da Georg Cantor. La costruzione di Cantor fu la prima costruzione rigorosa dell’insieme dei numeri reali e fu contemporanea ad un’altra costruzione, altrettanto rigorosa, effettuata da R. Dedekind. La coincidenza temporale delle due costruzioni non é casuale: nacque infatti da una precisa esigenza di sistemazione rigorosa di tutta la matematica, cominciata già verso la seconda metà del secolo scorso.
Nelle pagine che seguono affronteremo la costruzione rigorosa dei numeri reali effettuata verso la fine del secolo scorso (1872) da Georg Cantor. La costruzione di Cantor fu la prima costruzione rigorosa dell’insieme dei numeri reali e fu contemporanea ad un’altra costruzione, altrettanto rigorosa, effettuata da R. Dedekind. La coincidenza temporale delle due costruzioni non é casuale: nacque infatti da una precisa esigenza di sistemazione rigorosa di tutta la matematica, cominciata già verso la seconda metà del secolo scorso.  Comincia per tempo il dibattito sulla prova di matematica per l’esame di stato nei licei scientifici. Ogni anno le discussioni sono tantissime. Lo scorso hanno si è costituito un comitato di insegnanti di matematica che a gran voce ha cercato di sollevare il problema e di far pervenire le proprie opinioni al ministero. Quest’anno se ne comincia già a parlare. Di seguito alcuni interventi.
Comincia per tempo il dibattito sulla prova di matematica per l’esame di stato nei licei scientifici. Ogni anno le discussioni sono tantissime. Lo scorso hanno si è costituito un comitato di insegnanti di matematica che a gran voce ha cercato di sollevare il problema e di far pervenire le proprie opinioni al ministero. Quest’anno se ne comincia già a parlare. Di seguito alcuni interventi.  Venerdì 19 dicembre 2008 ore 20.45 – ISIS O. Romero – Aula Magna – viale A. Moro 51, ALBINO. Relatore Dott. Sergio Bertolucci, Direttore della ricerca del CERN di Ginevra.
Venerdì 19 dicembre 2008 ore 20.45 – ISIS O. Romero – Aula Magna – viale A. Moro 51, ALBINO. Relatore Dott. Sergio Bertolucci, Direttore della ricerca del CERN di Ginevra.  Socrate sa di non sapere ….. ma attraverso la maieutica e l’ironia cerca di concretizzare -o realizzare?- le potenzialità delle persone e quindi anche le capacità di gestire i problemi.
Socrate sa di non sapere ….. ma attraverso la maieutica e l’ironia cerca di concretizzare -o realizzare?- le potenzialità delle persone e quindi anche le capacità di gestire i problemi.  Ecco i risultati del nostro sondaggio su cosa ne pensano i nostri utenti sulle idee e sull’operato del Ministro Mariastella Gelmini
Ecco i risultati del nostro sondaggio su cosa ne pensano i nostri utenti sulle idee e sull’operato del Ministro Mariastella Gelmini 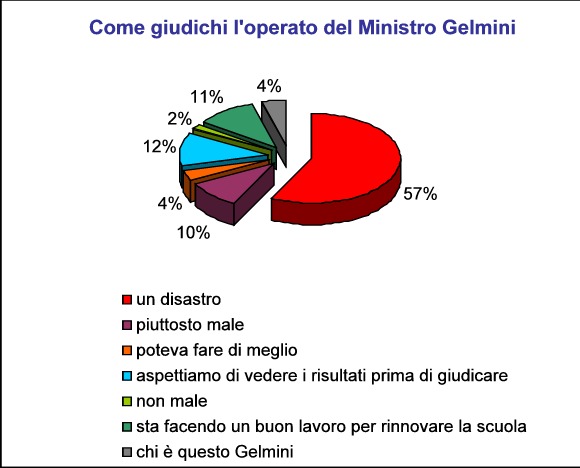

 Scaricabile on line il Quaderno del gruppo di ricerca USR e IRRE Emilia-Romagna. Il volume ‘Matematica’ è il risultato di un lavoro coordinato tra Ufficio Scolastico Regionale per l’Emilia-Romagna e IRRE Emilia-Romagna, nell’ambito del progetto “Gruppi di ricerca”. Il volume si rivolge agli insegnanti di matematica e propone contributi di carattere didattico e metodologico sul curricolo di matematica nei diversi ordini di scuola. Offre spunti per una riflessione sui cambiamenti in atto prendendo in considerazione i programmi passati, le Indicazioni Nazionali, le proposte di curricoli sviluppate dall’UMI, senza tralasciare le prassi didattiche ormai consolidate.
Scaricabile on line il Quaderno del gruppo di ricerca USR e IRRE Emilia-Romagna. Il volume ‘Matematica’ è il risultato di un lavoro coordinato tra Ufficio Scolastico Regionale per l’Emilia-Romagna e IRRE Emilia-Romagna, nell’ambito del progetto “Gruppi di ricerca”. Il volume si rivolge agli insegnanti di matematica e propone contributi di carattere didattico e metodologico sul curricolo di matematica nei diversi ordini di scuola. Offre spunti per una riflessione sui cambiamenti in atto prendendo in considerazione i programmi passati, le Indicazioni Nazionali, le proposte di curricoli sviluppate dall’UMI, senza tralasciare le prassi didattiche ormai consolidate. 
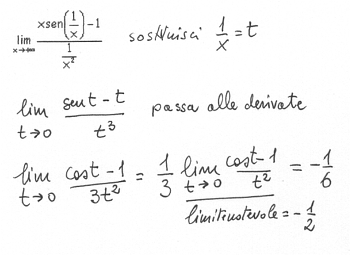
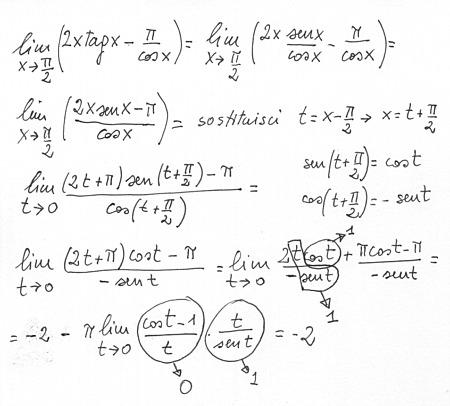





 … nello stesso fiume son sempre acque diverse quelle in cui ci bagnamo: non è possibile bagnarsi due volte nel medesimo fiume.
… nello stesso fiume son sempre acque diverse quelle in cui ci bagnamo: non è possibile bagnarsi due volte nel medesimo fiume.  "E’ la stessa cosa il vivo ed il morto, il desto e il dormiente, il giovane ed il vecchio: giacchè ognuno di questi opposti mutandosi è l’altro e a sua volta l’altro mutandosi è l’uno" (fr.88).
"E’ la stessa cosa il vivo ed il morto, il desto e il dormiente, il giovane ed il vecchio: giacchè ognuno di questi opposti mutandosi è l’altro e a sua volta l’altro mutandosi è l’uno" (fr.88).  Sandro Teti Editore presenta la III edizione di una biografia di successo sul grande scienziato siracusano. Il libro uscirà il 20 Novembre 2008 e verrà presentato alla Fiera della piccola e media editoria di Roma (Palazzo dei Congressi EUR dal 5 all’8 Dicembre). Questa III edizione è arricchita dalla presentazione di Luciano Canfora, editorialista del Corriere della Sera.
Sandro Teti Editore presenta la III edizione di una biografia di successo sul grande scienziato siracusano. Il libro uscirà il 20 Novembre 2008 e verrà presentato alla Fiera della piccola e media editoria di Roma (Palazzo dei Congressi EUR dal 5 all’8 Dicembre). Questa III edizione è arricchita dalla presentazione di Luciano Canfora, editorialista del Corriere della Sera.