 Il concorso a premio ha come obiettivo la ricerca e l’elaborazione di proposte per la sistemazione di una vasta area immediatamente a ridosso della Tangenziale est di Milano. Per studenti universitari di Ingegneria, Architettura e Scienze.
Il concorso a premio ha come obiettivo la ricerca e l’elaborazione di proposte per la sistemazione di una vasta area immediatamente a ridosso della Tangenziale est di Milano. Per studenti universitari di Ingegneria, Architettura e Scienze.
BANDO
Comitato amici del Metrobosco – Parco della Lambretta
Premessa
Le motivazioni che ci hanno spinto a indire il concorso di idee, su un area denominata dai cittadini di zona 3 di Milano Parco della Lambretta, parte dell’area Metrobosco voluto dalla Provincia di Milano, sono diverse e le vogliamo condividere con voi.
La coerenza: rispettare i nostri principi costitutivi e passare dalla fase del DIRE alla fase del FARE.
La sfida: il nostro mondo, la Terra, ogni anno consuma aree verdi per la responsabilità di noi uomini. Desideriamo dare il nostro contributo per iniziare ad invertire la tendenza e riqualificare a verde una vecchia zona industriale dove era ubicata una delle vecchie e gloriose fabbriche di Milano, la Innocenti, dove fu inventata, ideata e costruita la Lambretta.
L’opportunità: dare la possibilità a giovani laureandi in diverse discipline di affacciarsi al difficile mondo del lavoro avendo avuto la possibilità di confrontarsi con un tema difficile: la difesa degli equilibri ecologici il rispetto del protocollo di Kyoto, il riutilizzo positivo delle aree industriali dimesse e il mantenimento di un impianto industriale ancora funzionante, cercando di mettere insieme molte idee nella creazione di un parco del tutto particolare che vogliamo chiamare “Il Parco della Lambretta“.
L’opportunità ai vincitori: ricevere una nomination conferita da una giuria di alto profilo, nomination data dalla classifica dei migliori lavori.
L’immaginazione: l’immaginazione al potere, i vincoli costruttivi sono molto limitati e si riferiscono unicamente alla superficie e alla presenza nel parco della Lambretta di un vecchio insediamento industriale la Demag INNSE, insediamento ancora operante e produttivo.
Il sogno: Gli uomini sognano, tutte le grandi idee sono iniziate con grandi sogni. Sogniamo il Parco della Lambretta nel Metrobosco, perché no, perché sì, perché lo vogliamo.
1. Obiettivi e contenuti
Il Comitato AMICI del METROBOSCO Parco della Lambretta e il sito www.parcolambretta.it promuovono il concorso di idee oggi facciamo un albero, domani facciamo un bosco. Il concorso ha per scopo l’elaborazione di proposte per il futuro Parco della Lambretta nell’ambito del progetto Metrobosco promosso dalla Provincia di Milano.
I promotori – allo scopo di allargare il confronto e promuovere un’iniziativa a scala internazionale – intendono coinvolgere la creatività e la curiosità degli Allievi delle Facoltà di Architettura, di Ingegneria Edile, di Ingegneria Edile-Architettura, Ingegneria ambientale e alle Facoltà di Scienze (in particolare i Corsi di Laurea in Scienze Naturali, Scienze della Terra e Scienze Ambientali, Scienze Geologiche) italiane e straniere che saranno futuri architetti, in genieri, progettisti, inventori di forme, per elaborare proposte e contributi finalizzati alla realizzazione del parco pubblico previsto in fregio a via Rubattino a Milano su parte dell’area dove fino a qualche anno fa erano localizzati gli stabilimenti Innocenti.
L’area su cui dovrà sorgere il parco della Lambretta è prevista come standard nel Piano Attuativo in corso di discussione, tuttavia le lungaggini burocratiche e le oggettive difficoltà dell’attuale stagione urbanistica hanno per diversi anni protratto la realizzazione delle aspettative di questa parte di città densamente edificata che guarda al parco come dovuto e possibile polmone verde e – al contempo – quale risarcimento nei confronti di quella memoria dei luoghi e della fatica del lavoro che rischia di andar dispersa con l’allontanamento dello stabilimento dell’Innocenti (dove – tra l’altro – si produceva la Lambretta).
Il Concorso ha come obiettivo la ricerca e l’elaborazione di proposte per la sistemazione di una vasta area immediatamente a ridosso della Tangenziale est di Milano e in contiguità con il quartiere di recente costruzione nell’ambito del P.R.U. Rubattino.
Ai partecipanti è lasciata la massima libertà nell’espressione delle proprie idee per l’area, tenendo tuttavia conto che le proposte dovranno comunque tendere alla realizzazione di un parco urbano a risarcimento di questo quadrante della città di Milano. I progetti dovranno favorire l’utilizzo del parco e dei suoi spazi da parte di tutti i cittadini nel loro tempo libero, tenendo conto della particolarità del luogo ove dovrà comunque permanere un edificio industriale ancora in uso (destinazioni compatibili). Sarà da prevedersi nell’ambito dell’istituendo parco uno spazio per feste e socialità di rilevanza zonale. Relativamente ai tipi di piante ed alle essenze compatibili con i requisiti ambientali del sito si assumono come riferimento le normative della Provincia di Milano, con particolare riguardo al Parco Sud, al Parco della Media Valle del Lambro ed al futuro Metrobosco.
I progetti dovranno contenere proposte per la riqualificazione paesaggistica e ambientale tenendo conto della particolare natura del luogo (presenza industriale e prossimità opere infrastruttura di elevato impatto) e del più generale progetto Metrobosco ideato e promosso dalla Provincia di Milano, volto alla creazione di un vasto parco di cintura della città di Milano innervato sulle dorsali delle autostrade e delle tangenziali che circondano la metropoli.
2. Destinatari
Il Concorso è indirizzato alla formazione di giovani progettisti ed è aperto alle Facoltà italiane e straniere di Architettura, di Ingegneria Edile, di Ingegneria Edile-Architettura, Ingegneria ambientale e alle Facoltà di Scienze (in particolare i Corsi di Laurea in Scienze Naturali, Scienze della Terra e Scienze Ambientali, Scienze Umane dell’Ambiente del Territorio del Paesaggio). I concorrenti dovranno produrre alla consegna – unitamente agli elaborati – anche un certificato di iscrizione quali studenti alle rispettive Facoltà in italiano inglese, tedesco, francese o spagnolo.
Al Concorso potranno partecipare anche gli Allievi laureandi della sessione estiva dell’A.A. 2007/2008. Si può partecipare al concorso individualmente o con un gruppo di progettazione inter/multi-disciplinare.
3. Modalità e criteri di elaborazione
Il materiale grafico sviluppato dovrà essere riprodotto su tavole formato A1 orizzontali in un numero non superiore a due tavole montate su supporto rigido spessore max 5mm. Ogni tavola dovrà riportare un frontespizio costituito da una banda di sei centimetri posta a partire dal bordo superiore della tavola entro il formato prescritto. Il frontespizio, oltre alle indicazioni atte a esplicare il contenuto della tavola medesima, recherà il MOTTO scelto da ciascun gruppo di progettazione e garantirà l’anonimato rispetto al lavoro effettuato da ciascun partecipante. Su nessuno degli elaborati – che dovranno essere rigorosamente anonimi – dovranno comparire diciture, segni, simboli o rimandi che consentano di ricondurre a riconoscibilità il lavoro del partecipante.
I progetti dovranno essere presentati così da rendere di immediata comprensione l’idea elaborata per mezzo di viste generali (pianta, prospetti, sezioni, dettagli costruttivi) e quanto altro utile alla spiegazione della proposta progettuale (come l’uso di fotomontaggi, prospettive o assonometrie, immagini di modelli). Alle tavole dovrà essere allegata una relazione equivalente a massimo sei cartelle dattiloscritte in italiano, francese, inglese, formato A3 orizzontale (incluso frontespizio) comprendente la descrizione del progetto presentato e le due tavole grafiche ridotte. Gli elaborati (tavole e relazione) dovranno essere consegnati anche su supporto digitale con files di estensione WORD per la relazione e PSD o COREL (livelli aperti), JPG, PDF e TIFF 300 dpi per le tavole.
Di ciascuna delle due tavole grafiche dovrà altresì essere consegnata copia digitale in formato .pdf a 72 dpi per eventuale messa in rete/presentazione, sia nel corso dei lavori della giuria, sia nella successiva fase di pubblicizzazione del Concorso. Con la consegna a cura dei partecipanti degli elaborati previsti, l’Associazione banditrice del concorso si intende fin d’ora autorizzata a pubblicare, presentare, riprodurre, diffondere sia in versione digitale sia in altre qualsivoglia pubblicazioni gli elaborati del Concorso stesso.
4. Valutazione
Le proposte presentate verranno valutate in ragione dell’originalità dell’idea, della loro coerenza progettuale e tecnica, della qualità paesaggistica, della fruibilità da parte dei cittadini di ogni età durante il loro tempo libero, della realizzabilità e dei relativi costi comunque considerando che le opere dovranno essere eseguite in condizioni di scarsità di risorse, dei contenuti di sostenibilità ambientale con particolare attenzione all’impiego di materiali di riuso/riciclo, in ogni caso con caratteristiche innovative e compatibili con l’ambiente e la prossimità dell’edificato, della coerenza con la legislazione paesaggistica e la normativa esistente.
Al fine di individuare e selezionare le idee progettuali presentate, verrà istituita un’apposita Commissione Giudicatrice composta dai seguenti membri:
- Arch. Mario Allodi, architetto paesaggista AIAPP
- Dott.ssa Alessandra Bassan direttore generale dell’Istituto IARD
- Prof. Giovanni Bianchi, Presidente Circoli Dossetti già Presidente Nazionale delle ACLI
- Prof. Arch. Francesco Collotti, docente Facoltà di Architettura – Università degli Studi di Firenze
- Prof. Arch. Sergio Graziosi, docente Facoltà di Architettura – Politecnico di Milano
- Sig. Giuseppe La rovere, rappresentante del Comitato Pru Rubattino
- Dott. Gianni Mura, giornalista La Repubblica
- Dott. Paolo Pardini, giornalista di Rai 3
- Sig.ra Sara Rossin, rappresentante del Comitato Amici del Metrobosco, il Parco della Lambretta
- Sig. Paolo Schiavocampo, artista e progettista del parco di Hattingen, Ruhr, Germania
- Arch. Rita Sicchi, architetto paesaggista
- Prof. Ignazio Tabacco, docente DST Geofisica – Università degli Studi di Firenze
- Prof.sa Maria Cristina Treu docente del Politecnico di Milano dove svolge attività didattica di ricerca scientifica;
- Prof. Arch. Dustin Tusnovics, docente Fachhochschule Salzburg
- Dott. Piergiorgio Valentini, responsabile progetto per la Provincia di Milano per il Metrobosco
Le decisioni della Commissione Giudicatrice sono inappellabili.
5. Iscrizione e termini di consegna
Il Bando del concorso sarà pubblicato sul sito www.parcolambretta.it
Saranno iscritti coloro che – essendosi registrati al sito precedentemente alla consegna – trasmetteranno al Comitato banditore gli elaborati di concorso come di seguito definito.
Gli elaborati di progetto dovranno pervenire per mezzo posta o corriere o recapitati a mano entro e non oltre le ore 17,00 del 30 marzo 2008 30 aprile 2008 (farà fede il timbro di spedizione) in un plico chiuso realizzato in materiale idoneo e adatto a impedire il deterioramento del contenuto durante il trasporto e la consegna alla sede del concorso seguente indirizzo:
Comitato AMICI del METROBOSCO
Il Parco della LAMBRETTA
C/o Circolo ACLI Lambrate, via Conte Rosso 5
20134 – MILANO (Italia)
Non saranno ammessi alla partecipazione al Premio:
- I componenti della Commissione Giudicatrice, i loro coniugi e i loro parenti fino al terzo grado di parentela compreso;
- Coloro che abbiano qualsiasi rapporto di lavoro o di collaborazione continuativa con i membri della Commissione;
- Coloro che partecipano alla stesura del Bando e dei documenti allegati.
Non avranno validità alcuna le partecipazioni al Premio se:
- Non sottoscritte ove richiesto (informativa sulla privacy compresa);
- Non corredate dalla documentazione obbligatoriamente richiesta.
Dovrà, inoltre, pervenire a corredo della documentazione presentata e all’interno del plico una ulteriore busta sigillata (totalmente bianca non trasparente, senza alcuna sigla o altre indicazioni) contenente i seguenti documenti:
- Fotocopia del documento di identità o passaporto di ogni componente del gruppo di progettazione;
- Copia del certificato di iscrizione alla Facoltà o al Corso di Laurea per l’Anno Accademico corrente o autocertificazione resa ai sensi di legge da parte di ogni singolo componente del gruppo, debitamente sottoscritta;
- Eventuale autocertificazione con dichiarazione per i soli Allievi che discuteranno la Tesi di Laurea nella sessione estiva dell’A.A. 2007/2008;
- Dichiarazione di autorizzazione al trattamento dei dati personali a sensi di quanto previsto dalla Legge 31/12/1996 n. 675 sulla tutela della privacy, da parte di ogni singolo componente del gruppo, debitamente sottoscritta.
6. Vincitori e premi
Il Premio si concluderà con una graduatoria di merito.
Ai primi tre vincitori sarà data facoltà di partecipare a uno stage di due mesi presso gli Uffici della Provincia di Milano che stanno sostenendo l’iniziativa del Metrobosco.
La giuria avrà a disposizione complessivamente € 4.500,00 di rimborso spese da assegnare ai vincitori singoli o a gruppi e classificati nella graduatoria di merito ai primi tre posti.
Nel caso di partecipazione di gruppo, sarà il gruppo a individuare il partecipante o la partecipante allo stage.
A ogni partecipante verrà consegnato un attestato di partecipazione sottoscritto da tutti i membri della Commissione Giudicatrice.
I risultati del Premio saranno resi noti attraverso i siti web menzionati entro e non oltre il 15 luglio 2008.
Il Comitato e il sito pubblicizzeranno attraverso il sito www.parcolambretta.it l’iniziativa concorsuale, pubblicando i progetti vincitori secondo la graduatoria di merito redatta fino al ventesimo progetto.
E’ prevista la realizzazione di una pubblicazione che conterrà una selezione dei progetti presentati.
Sarà organizzata una mostra degli elaborati presentati su supporto rigido. Tutti gli elaborati potranno essere restituiti agli Autori (con pagamento in contrassegno per le spese di spedizione) dopo avere provveduto alla verifica del contenuto dei supporti digitali presentati, facendone richiesta direttamente alla sede del concorso dopo il 1 gennaio 2009.
7. Segreteria Organizzativa
Richieste di chiarimenti relativi al Bando dovranno pervenire esclusivamente via e-mail alla Segreteria Organizzativa entro il 1 dicembre 2007 1 marzo 2008 che provvederà alle risposte. Ai concorrenti è vietato interpellare i componenti della Commissione Giudicatrice.
8. Lingue ufficiali
Le lingue ufficiali del concorso sono italiano, francese e inglese.
Calendario del Premio:
- Visita alla località sabato 20 ottobre 2007 ore 10 a.m. e sabato 24 novembre ore 10 a.m. con ritrovo presso Bar Il Lambrettino Piazza Vigili del Fuoco, Lambrate, Milano;
Richiesta chiarimenti entro il 1 dicembre 2007; - Consegna degli elaborati entro il
30 marzo 2008 30 aprile 2008;
- Conclusione dei lavori della Commissione Giudicatrice e graduatoria di merito entro il 15 luglio 2008.
- Visita alla località sabato 15 dicembre 2007, sabato 26 gennaio 2008, sabato 16 febbraio 2008, alle ore 10,00 a.m. con ritrovo presso il Bar Il Lambrettino Piazza Vigili del Fuoco – Lambrate – Milano;
- Richiesta chiarimenti entro il
1 febbraio 2008 1 marzo 2008;
http://parcolambretta.it
Da una comunicazione pervenuta in redazione

 Pare che la dea Afrodite fosse strabica. In certi casi sembra che lo sia anche la Borsa italiana. Un esempio da manuale è offerto dall’Alitalia, di cui sono quotati due titoli: le azioni ordinarie e le obbligazioni convertibili 7,5% 22-7-2010. Per le azioni alcuni trovano esagerati i recenti prezzi molto sopra ai 10-12 centesimi, corrispondenti al valore di un’azione Air France ogni 160 azioni Alitalia, quale sarebbe il rapporto dell’annunciata Offerta pubblica di acquisto e scambio (Opas). Alcuni giudicano stracciati i prezzi delle obbligazioni sotto i 70 euro.
Pare che la dea Afrodite fosse strabica. In certi casi sembra che lo sia anche la Borsa italiana. Un esempio da manuale è offerto dall’Alitalia, di cui sono quotati due titoli: le azioni ordinarie e le obbligazioni convertibili 7,5% 22-7-2010. Per le azioni alcuni trovano esagerati i recenti prezzi molto sopra ai 10-12 centesimi, corrispondenti al valore di un’azione Air France ogni 160 azioni Alitalia, quale sarebbe il rapporto dell’annunciata Offerta pubblica di acquisto e scambio (Opas). Alcuni giudicano stracciati i prezzi delle obbligazioni sotto i 70 euro. 
 Le equazioni e disequazioni matematiche sono sempre state un problema per tanti. Lo stesso vale per la comprensione del concetto di numero. Perché 5 è più grande di 4? Perché 4+1 è uguale a 5? Questo gioco matematico permette di familiarizzare con questi concetti.
Le equazioni e disequazioni matematiche sono sempre state un problema per tanti. Lo stesso vale per la comprensione del concetto di numero. Perché 5 è più grande di 4? Perché 4+1 è uguale a 5? Questo gioco matematico permette di familiarizzare con questi concetti. 



 Applicando il
Applicando il  Il Comune di Milazzo Assessorato Politiche Scolastiche e P.I. in rete con le scuole, organizza il Meeting Mylaematica sul tema Giochi, Modelli e Tecnologie per la Nuova Didattica della Matematica 26-27-28-29 marzo 2008 Duomo Antico, Milazzo (ME)
Il Comune di Milazzo Assessorato Politiche Scolastiche e P.I. in rete con le scuole, organizza il Meeting Mylaematica sul tema Giochi, Modelli e Tecnologie per la Nuova Didattica della Matematica 26-27-28-29 marzo 2008 Duomo Antico, Milazzo (ME)  Un’attività di laboratorio per comprendere i numeri irrazionali e accettarne l’esistenza. L’attività richiede l’uso di carta millimetrata. Obiettivi: distinguere tra aspetto fisico della misurazione, aspetto algoritmico del calcolo algebrico e aspetto razionale dell’osservazione geometrica; comprendere la differenza tra l’operazione di contare e quella di misurare; osservare che gli algoritmi finiti di calcolo e, conseguentemente, l’uso della calcolatrice danno luogo a risultati approssimati.
Un’attività di laboratorio per comprendere i numeri irrazionali e accettarne l’esistenza. L’attività richiede l’uso di carta millimetrata. Obiettivi: distinguere tra aspetto fisico della misurazione, aspetto algoritmico del calcolo algebrico e aspetto razionale dell’osservazione geometrica; comprendere la differenza tra l’operazione di contare e quella di misurare; osservare che gli algoritmi finiti di calcolo e, conseguentemente, l’uso della calcolatrice danno luogo a risultati approssimati.  Il 20 aprile 2008, a Bologna, si terrà la prima Assemblea Nazionale per costituire l’Associazione Nazionale degli Insegnanti di Matematica (ANIMat). L’invito a partecipare all’assemblea è rivolto a tutti coloro che insegnano o hanno insegnato matematica nelle diverse classi di concorso e nei diversi ordini e gradi di scuola (dalla scuola primaria all’università), indipendentemente dal tipo di diploma o laurea conseguita.
Il 20 aprile 2008, a Bologna, si terrà la prima Assemblea Nazionale per costituire l’Associazione Nazionale degli Insegnanti di Matematica (ANIMat). L’invito a partecipare all’assemblea è rivolto a tutti coloro che insegnano o hanno insegnato matematica nelle diverse classi di concorso e nei diversi ordini e gradi di scuola (dalla scuola primaria all’università), indipendentemente dal tipo di diploma o laurea conseguita.  Una serie di conferenza divulgative presso il dipartimento di Matematica del Politecnico di Torino: Spazi vettoriali: giocando con l’algebra lineare; Numeri complessi: trigonometria con e senza la "H"; Le equazioni di Euclide e Diofanto: clessidre e noci di cocco; Matrici e gruppi di simmetria: l’Alhambra di Granada; Cayley-Hamilton: i predatori della matrice perduta; Curve: traiettorie e orbite; Superfici nello spazio: mescolando le coniche M. Ferrarotti.
Una serie di conferenza divulgative presso il dipartimento di Matematica del Politecnico di Torino: Spazi vettoriali: giocando con l’algebra lineare; Numeri complessi: trigonometria con e senza la "H"; Le equazioni di Euclide e Diofanto: clessidre e noci di cocco; Matrici e gruppi di simmetria: l’Alhambra di Granada; Cayley-Hamilton: i predatori della matrice perduta; Curve: traiettorie e orbite; Superfici nello spazio: mescolando le coniche M. Ferrarotti.  In un articolo recentemente apparso su
In un articolo recentemente apparso su  Tutti gli studenti di terza media quest’anno affronteranno, il 17 giugno, una terza prova scritta di italiano e matematica comune a tutte le scuole italiane. La prova sarà di tipo strutturata (a risposta multipla) o semistrutturata (con qualche domanda aperta) e sarà assegnata dal Ministero della Pubblica Istruzione. Su questo sito puoi esercitarti con
Tutti gli studenti di terza media quest’anno affronteranno, il 17 giugno, una terza prova scritta di italiano e matematica comune a tutte le scuole italiane. La prova sarà di tipo strutturata (a risposta multipla) o semistrutturata (con qualche domanda aperta) e sarà assegnata dal Ministero della Pubblica Istruzione. Su questo sito puoi esercitarti con 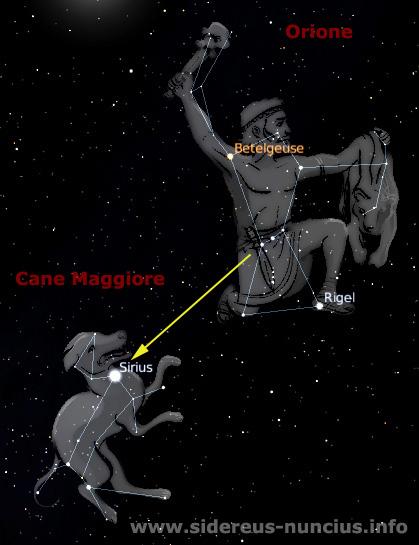 In alcuni casi Sirio è chiamata anche la “Stella del Cane”, fa parte infatti della costellazione del Cane Maggiore, il cane del cacciatore Orione, che lo si vede ergersi sulle zampe posteriori, vicino al suo padrone.
In alcuni casi Sirio è chiamata anche la “Stella del Cane”, fa parte infatti della costellazione del Cane Maggiore, il cane del cacciatore Orione, che lo si vede ergersi sulle zampe posteriori, vicino al suo padrone.  Matematicamente primo sito italiano per la categoria Istruzione e lavoro. La motivazione della giuria:
Matematicamente primo sito italiano per la categoria Istruzione e lavoro. La motivazione della giuria:  Una grande crescita per la nostra community, in grado ormai di stare alla pari (o quasi) con i big del web, da Google a Wikipedia, da eBay a Beppe Grillo… e poi Ferrariworld, Turisti per caso, Reporter, Quattroruote…
Una grande crescita per la nostra community, in grado ormai di stare alla pari (o quasi) con i big del web, da Google a Wikipedia, da eBay a Beppe Grillo… e poi Ferrariworld, Turisti per caso, Reporter, Quattroruote… 
 Con grande sorpresa e piacere tra i premiati abbiamo incontrato i nostri amici di
Con grande sorpresa e piacere tra i premiati abbiamo incontrato i nostri amici di 

 Tesina multidisciplinare di matematica, filosofia e fisica, per l’esame di maturità scientifica. Ho scelto questo tema prendendo spunto da una curiosità personale: la matematica è una scoperta o un’invenzione? Attraverso la stesura di questa tesina mi sono fatta un’idea più chiara, anche se non credo di essere arrivata ad una certezza, visto che illustri matematici di tutto il mondo ancora ne discutono.
Tesina multidisciplinare di matematica, filosofia e fisica, per l’esame di maturità scientifica. Ho scelto questo tema prendendo spunto da una curiosità personale: la matematica è una scoperta o un’invenzione? Attraverso la stesura di questa tesina mi sono fatta un’idea più chiara, anche se non credo di essere arrivata ad una certezza, visto che illustri matematici di tutto il mondo ancora ne discutono. 


 Due mercanti medievali, legati da grande amicizia, avevano studiato la struttura dei numeri, le proprietà dei numeri perfetti, i misteri della cabala, e avevano deciso in omaggio a complicate concezioni astrologiche, di operare sempre con numeri che fossero esatti divisori delle loro proprietà.
Due mercanti medievali, legati da grande amicizia, avevano studiato la struttura dei numeri, le proprietà dei numeri perfetti, i misteri della cabala, e avevano deciso in omaggio a complicate concezioni astrologiche, di operare sempre con numeri che fossero esatti divisori delle loro proprietà. 
 Gara organizzata dall’Associazione Patavina Mathesis, riservata a studenti iscritti alle due ultime classi delle Scuole medie superiori del Veneto, si svolgerà sabato 15 Marzo 2008 alle ore 16.
Gara organizzata dall’Associazione Patavina Mathesis, riservata a studenti iscritti alle due ultime classi delle Scuole medie superiori del Veneto, si svolgerà sabato 15 Marzo 2008 alle ore 16. 
 Il concorso a premio ha come obiettivo la ricerca e l’elaborazione di proposte per la sistemazione di una vasta area immediatamente a ridosso della Tangenziale est di Milano. Per studenti universitari di Ingegneria, Architettura e Scienze.
Il concorso a premio ha come obiettivo la ricerca e l’elaborazione di proposte per la sistemazione di una vasta area immediatamente a ridosso della Tangenziale est di Milano. Per studenti universitari di Ingegneria, Architettura e Scienze.