Ripassa il calcolo numerico con numeri interi, numeri decimali, frazioni e numeri relativi, il computer di sfida ai calci di rigore. Un gioco per grandi e piccini!
Autore: Antonio Bernardo
Terza prova liceo classico tipologia B
Numerose prove di matematica per l’esame di stato, terza prova liceo classico. Argometni: analisi, trigonometria, geometria nello spazio.
Scarica il file pdf delle prove di matematica
Le prove sono un libero adattamento di prove realmente date e tratte dall’archivio ATP.
Come diventare ricchi
Come ci si può arricchire? In tanti modi. Sposando un’ereditiera, meglio ancora se carina. Facendosi venire una brillante idea e riuscendo a sfruttarla abilmente. Certo, un po’ di fortuna ci vuole. Le componenti di questo metodo sono tre …
Come ci si può arricchire? In tanti modi. Sposando un’ereditiera, meglio ancora se carina. Facendosi venire una brillante idea e riuscendo a sfruttarla abilmente. Certo, un po’ di fortuna ci vuole: ho scoperto recentemente che una splendida attrice hollywoodiana, Hedwig Eva Maria Kiesler (meglio nota col nome d’arte di Hedy Lamarr), aveva nientepopodimenoche brevettato (assieme a un pianista, sic!) un metodo straordinariamente innovativo per la codifica di trasmissioni radio. Peccato che quel brevetto (vedi: http://www.pat2pdf.org/patents/pat2292387.pdf ) sia arrivato “troppo presto”. Per quanto ne so, gli inventori non sono stati in grado di sfruttare commercialmente il frutto del loro ingegno, che pure è un precursore dei metodi attualmente usati nelle trasmissioni UMTS.
Tornando al tema dell’arricchirsi, ce la si può fare grazie a un investimento particolarmente oculato (e fortunato). I metodi fin qui descritti sono tendenzialmente considerati leciti nelle società capitalistiche. Altri metodi sono meno accetti. Per esempio la rapina a mano armata (è pur vero che, se chi la compie è uno Stato potente che manda il suo esercito ad attaccarne un altro perché gli fanno gola le sue riserve petrolifere, si usano altri nomi…). Altri metodi che sono tendenzialmente considerati illegali sono lo sfruttamento della prostituzione, il traffico di droga, lo strozzinaggio, etc.
Come sempre, c’è una zona grigia di frontiera, Lo abbiamo già visto per le rapine. Un altro esempio è offerto proprio dallo strozzinaggio: dire quando un prestito è ad usura non è per nulla facile. Tanto è vero che, quando fu introdotta una legge (Legge 7 marzo 1996, n. 108 – Disposizioni in materia di usura) che fissava una regola per determinare quando un tasso di interesse fosse da considerarsi da usura, vi furono economisti che espressero delle perplessità: ricordo di aver ascoltato commenti caustici dalla viva voce del sempre acuto Giacomo Costa. Permettere prestiti a tasso di interesse molto elevato, da strozzinaggio, dovrebbe consentire (al complesso delle banche e dei potenziali prestatari) di poter siglare un maggior numero di contratti, ottenendo quindi un risultato globalmente migliore. Non è, d’altronde, così ovvio che impedire alle banche di prestare soldi a tassi molto elevati a soggetti a forte rischio di insolvenza sia una buona idea. Da un punto di vista sociale, ci si potrebbe chiedere: a chi si rivolgeranno coloro ai quali è precluso l’accesso a fonti di credito legali?
Un classico esempio che pone problemi “di frontiera” è la truffa. Ricordo, dal Codice Penale (Titolo XII: Dei reati contro il patrimonio; Capo II: Dei delitti contro il patrimonio mediante frode):
Art. 640
Chiunque, con artifizi o raggiri, inducendo taluno in errore, procura a sé o ad altri un ingiusto profitto con altrui danno, è punito con la reclusione da sei mesi a tre anni e con la multa da 51 € a 1032 €. La pena è della reclusione da uno a cinque anni e della multa da 309,87 € a 1549,37 €: 1) se il fatto è commesso a danno dello Stato o di un altro ente pubblico o col pretesto di far esonerare taluno dal servizio militare; 2) se il fatto è commesso ingenerando nella persona offesa il timore di un pericolo immaginario o l’erroneo convincimento di dovere eseguire un ordine dell’Autorità. Il delitto è punibile a querela della persona offesa, salvo che ricorra taluna delle circostanze previste dal capoverso precedente o un’altra circostanza aggravante (1). (1) Comma aggiunto dalla L. 24 novembre 1981, n. 689.
Naturalmente, i confini sono labili e si può provare a sfruttarli a proprio vantaggio. Aiutandosi, magari, con un pizzico di calcolo delle probabilità. Si tratta di prestare attenzione a quanto diceva il poeta:
Things fall apart, the centre cannot hold
Insomma, si tratta di sfruttare abilmente le “code” di una distribuzione di probabilità. A questo proposito, in rete c’è già una mia divagazione (sui lemons, ovvero i “bidoni”, di Akerlof), in cui escogito un sistema per cercare di sfruttare a mio favore l’incertezza che ha un acquirente su un oggetto che ho messo in vendita. Semplicemente, offro al potenziale acquirente un po’ di informazione aggiuntiva (per giunta a gratis! Dovrei farmela pagare…) sulle caratteristiche dell’oggetto. E, sia chiaro, il tutto alla luce del sole, verificabile. I
n queste poche righe propongo un metodo comodo per arricchirsi, senza che sia suscettibile di dare adito ad azioni legali (presumo! Avverto che non sono un esperto legale). Le componenti di questo metodo sono tre:
– proporre di effettuare una azione che può permettere di ottenere un guadagno considerevole. S’intende, con bassa probabilità (per i miracoli rivolgersi altrove)
– suggerire a chi effettua tale azione che vi possa essere una influenza da parte nostra sul risultato
– menzionare a chi compie l’azione che, visto quanto detto al punto precedente, in caso di lauto guadagno potrebbe mostrarsi generoso con noi
Un esempio banale è fornito da un suggerimento simile ad uno già proposto sul forum di matematicamente.it. Dire che nostra nonna in sogno ci ha dato un prezioso suggerimento: andare al casinò e puntare alla roulette 100 euro sul 17 e poi ripuntare tutto quello guadagnato ancora sul 17. Aggiungere che noi seguiremo quel suggerimento, e che ci è sembrato carino metterlo a disposizione di tutti, senza volere nulla in cambio. Al più, confidiamo sulla generosità di chi dovesse vincere grazie al nostro altruismo.
Questa è la struttura di base della proposta, che poi sarà opportunamente incipriata ed imbellettata per renderla adeguatamente accattivante.
Mi sembra fin troppo evidente dove stia il trucco. Dopotutto eventi anche improbabili non sono impossibili (che esca il 17 due volte di fila ha una probabilità di 1 su 1369) e, se il messaggio viene mandato e colto da un buon numero di persone, che qualcuno vinca usando il nostro metodo diventa assai probabile. Quanti siano i vincenti che si “ricordano” di noi, è una stima un po’ più difficile da fare.
E’ un “artifizio”? Un “raggiro”? Induciamo qualcuno in errore? Forse sfruttiamo il fatto che il livello di conoscenza del calcolo delle probabilità è un po’ basso. Ma è colpa nostra?
Ricaviamo “un ingiusto profitto con altrui danno”? Ma scherziamo? Non gli abbiamo chiesto niente… Sarà difficile chiamare “ingiusto profitto” un dono spontaneo che dovessimo ricevere. E, poi, se lo riceviamo, chi ce lo manda ha vinto un sacco di soldi “grazie” a noi. Dov’è il danno? Lo vedete voi uno, che si è arricchito grazie a voi, che vi querela (non vedo aggravanti in circolazione)?.
Notare che la frase è “un ingiusto profitto con altrui danno”. Cioè devono verificarsi entrambe le circostanze. Sarebbe stato ben diverso se fosse stato scritto: “un ingiusto profitto o altrui danno”. In tal caso, avrebbero potuto perseguirci (forse) quelli che avessero giocato e perso. Ma c’è “con”, col significato di congiunzione.
Insomma, approfittatene. Prima che venga cambiata la legge a seguito della falla mostrata da questo articolo :)
Un paio di link.
Per l’esempio sul tema dei “lemons”: http://www.diptem.unige.it/patrone/decisori_razionali_interagenti/decisori_razionali_interagenti_web.htm
Per intervenire sul forum, dove già sono presenti interessanti contributi alla discussione: https://www.matematicamente.it//forum/tdg-teoria-dei-giochi-vf27.html
Fioravante Patrone
Il Numero 6 (Maggio 2008) completo di Matematicamente.it Magazine
In questo numero si parla di: uno scritto di Ennio De Giorgi sui giovani e la matematica, il paradiso di Cantor e il purgatorio di Russell, delusioni d’amore e pasticcini, le avventure del dottor G nei labirinti della mente, logica fuzzy per la ricerca sociale, Montessory e Piaget, geometria descrittiva in natura e in architettura, due rilevanti esperienze di didattica: Ragiocando e La bottega del matematico, lo scaffale dei libri con le novità in libreria. Questo numero della rivista ospita il Numero 0 del Bolletino Mathesis.
* * * * * * * * * *
Scarica da qui il Numero 6 completo di Matematicamente.it Magazine (PDF 1,9 MB)
Il giusto peso: per bambini di scuola primaria
Willy, Geggio, Eddy e Plinio devono attraversare un fiume con l’aiuto di una zattera. Trasporta quanti più bambini puoi ma fai attenzione a non fare affondare la zattera. Ricorda che la zattera non può viaggiare da sola, deve sempre esserci almeno un bambino che la guida.
Un metodo di rappresentazione geometrica dei coefficienti di correlazione e di determinazione
Il coefficiente di correlazione è un importante strumento statistico che consente di stabilire il grado di relazione lineare tra due serie di dati. Fu lo scienziato Francis Galton cugino di Charles Darwin, ad utilizzare per la prima volta il coefficiente di correlazione, proposto dal collega Karl Pearson, per quantificare il “grado di associazione” tra due variabili. Tale coefficiente, noto come coefficiente di Pearson, viene definito come …
Shapes
Gioco per bambini e adulti da 5 a 105 anni. Una figura geometrica viene tagliata in due e più parti e un colpo di vento improvviso sposta i vari pezzi. Memoria, attenzione e intuito geometrico ti serviranno per ricostruire la figura. Si comincia facile ma le difficoltà crescono in fretta.
Un esempio di test per la terza prova
Un esempio di terza prova di matematica per l’esame di maturità. 28 domande con valutazione immediata sui principali temi dell’analisi matematica. Il test è utile anche per ripassare un po’ di matematica in vista dell’esame scritto.
| Terza prova esame di maturità |
Scarica il test in formato RTF
MatematiCup 2008: la premiazione
Presso l’Aula Rizzo del Dip. di Ingegneria, Università del Salento, si è svolta la manifestazione di premiazione delle gare on line MatematiCup ed EcologicaCup. Hanno partecipato numerosi ragazzi delle squadre vincitrici provenienti da diverse città. MatematiCup è la prima gara di matematica completamente on-line e in modalità collaborativa a squadre riservata a studenti delle scuole medie. La competizione, giunta alla seconda edizione è stata organizzata in collaborazione tra il DIDA-lab dell’Università del Salento, il Gruppo Editoriale L’Espresso, il sito Matematicamente.it e con il patrocinio della Mathesis l’associazione nazionale degli insegnanti di matematica e del Ministero dell’Istruzione. 
Un esercito di 8500 studenti della scuola media di primo grado, di 210 scuole secondarie di primo grado, organizzati in più di 360 squadre da altrettanti docenti-allenatori, si sono trovati il 13 maggio alle ore 9 simultaneamente davanti ai monitor per sfidarsi a colpi di operazioni matematiche e ragionamenti logici. Dopo tre ore di click e tasti pigiati, di disegni e calcoli sul quaderno, di discussioni animate, sana collaborazione e soprattutto tanta adrenalina, la squadra che si è classificata al primo posto è risultata “L’esercito di Franca”, allenata dalla professoressa Franca Panelli, della scuola “Beato Arnaldo da Limena” di Limena, provincia di Padova. La professoressa Panelli tiene orami da alcuni anni, presso la sua scuola, un laboratorio permanente di giochi matematici, dove i ragazzi si esercitano settimanalmente a risolvere quesiti di matematica assegnati nelle varie gare nazionali. 
Una delegazione costituita da due ragazzi e un docente è venuta a Lecce a ritirare l’ambito trofeo durante la cerimonia di premiazione che si è tenuta il 22 maggio a Lecce presso l’Aula Rizzo della Facoltà di Ingegneria dell’Università del Salento. Alla domanda: – qual è stato il problema più difficile? I ragazzi hanno risposto: – quello in cui c’era l’acquario che si inclinava di un certo angolo per far uscire l’acqua e poi bisognava riempirlo con altrettanta acqua pulita. La seconda squadra classificata è stata il “Team Tanzi” allenata dalla prof.ssa Meliota Giovanna, della Scuola Secondaria di primo grado “Tanzi” di Mola di Bari. La squadra composta da una rappresentanza di ragazzi di ogni classe dell’istituto ha partecipato per tutto l’anno scolastico a una specifica attività di formazione sui problemi matematici, attività finanziata dal Fondo Sociale Europeo. 
«Il gruppo degli studenti di classe prima – ha raccontato la professoressa Meliota che è venuta a ritirare il trofeo – ha vissuto con molta ansia la prova, molto di più rispetto alle normali verifiche di matematica. Quando la squadra ha cominciato ad allenarsi – ha continuato la professoressa – i ragazzi pensavano di non farcela e di non essere all’altezza delle altre squadre che stavano molto più avanti negli allenamenti. Si è trattato di allenarsi e applicarsi con costanza, entrando gradualmente nella tipologia di quesiti che erano diversi rispetto alle altre gare, perché fortemente correlati con problemi e situazioni reali, e mostravano le applicazioni della matematica al mondo reale. Alla fine siamo arrivati secondi – ha concluso soddisfatta – perché l’applicazione continua e il metodo di lavoro sono importanti e fanno raggiungere i risultati.» La terza squadra classificata è stata “I Disastri 2 (la vendetta)”, allenata dalla professoressa De Palma Sara, dell’Istituto “Gianelli” di Rapallo (GE). L’Istituto Gianelli si è piazzato ottimamente in più classifiche ed è stata la scuola che ha raggiunto globalmente il punteggio più elevato. Anche la squadra tutta al femminile “Matematiche!” che si è classificata prima squadra femminile è dell’Istituto Gianelli. La seconda scuola classificata è stata l’Istituto “Sacro Cuore” di Firenze. 
Terza scuola in classifica l’Istituto “Madre Teresa Quaranta” di Grottaglie (TA); una delegazione di studenti e insegnati ha ritirato la targa. La professoressa Eligia Crescente e suor Agnese, che accompagnavano un gruppo di ragazzi in rappresentanza della scuola ha sottolineato l’’importanza di un’attività didattica di questo tipo, perché stimola l’interesse e la curiosità verso una disciplina vista spesso con noia e indifferenza. 
La giuria ha premiato come squadra migliore negli allenamenti la squadra “Istituto comprensivo Muro Leccese” di Muro (LE), allenata dalla prof.ssa Carlà Teresa per la costanza e regolarità negli allenamenti e per aver raggiunto il miglior punteggio. Gli allenamenti per la gara sono infatti durati da gennaio a maggio e quindi per una lunga fase dell’anno scolastico. Le professoresse Teresa Carlà e Michela Occhioni, dell’Istituto di Muro hanno utilizzato gli strumenti didattici messi a disposizione da MatematiCup per svolgere parte delle attività di specifici progetti PON dedicati al recupero e all’eccellenza in matematica. Dalla scuola di Muro leccese, vicina alla sede della premiazione, è venuta una folta rappresentanza di studenti entusiasti anche di conoscere una delle sedi dell’Università del Salento, possibile traguardo finale del loro percorso di studi. L’Aula Rizzo dove si è svolta la manifestazione è una delle aule maggiormente attrezzate dal punto di vista tecnologico, dotata di maxi-schermo, e di varie telecamere per le riprese ed ha consentito di realizzare un DVD con il video della manifestazione. Altre squadre si sono segnalate nella gara per aver raggiunto posizioni di primo piano nelle rispettive classifiche a tema: migliore gruppo di classe prima la squadra “Lampi di genio”, allenata da Angelo Remitti, della Scuola Media di Maranello (MO); migliore gruppo di classe seconda: “I giovani Newton”, allenata da Silvana Serra, della S. S. Primo Grado “Elisa Sala” di Monza; migliore gruppo di classe terza: “I + della Rodari”, allenata da Rossella Bonora, dell’Istituto “G. Rodari” di Santa Giustina (Belluno); migliore squadra in geometria “Mathematic Wizard” allenata da Anna Lisa De Donato della S. M. S. “Via Martiri D’Ungheria” Scafati (Salerno); migliore squadra in logica e insiemistica: “Eta Beta” allenata da Liviana Lucchetti dell’Istituto Comprensivo “Ancona Centro” di Ancona; migliore squadra in statistica, probabilità e combinatorica: “Tendenti all’infinito” allenata da Giulia Garello dell’Istituto “P. Gobetti” di Rivoli (TO). 
La prof.ssa Anna Maria Maronna dell’Istituto “Quinto Ennio” di Lecce con tutta la squadra “Math’s girls” è venuta per ritirare il trofeo come migliore squadra in aritmetica e logica. «Le ragazze hanno ragionato in modo autonomo, senza nessun aiuto – ha voluto precisare la professoressa – e hanno capito che la matematica è importante per risolvere tanti problemi, anche quotidiani». La squadra Math’s girls” si è anche classificata seconda nella classifica delle squadre femminili. La gara aveva per obiettivo quello di recuperare l’interesse dei giovani per la matematica e rafforzare le competenze per applicare la matematica nel vissuto quotidiano. I contesti dei quiz hanno infatti riguardato l’ambito personale, quello familiare e quello scolastico, il mondo della scuola e quello del lavoro, l’economia, le scelte pubbliche e sociali, la scienza e la tecnologia. Per quanto riguarda i contenuti più prettamente matematici i quesiti hanno riguardato: numeri e relazioni (aritmetica e algebra), forme e misure (geometria), dati e previsioni (statistica, probabilità e calcolo combinatorio) logica e insiemistica. Il vero aspetto innovativo della gara è la sua modalità di realizzazione che avviene attraverso Internet in modalità sincrona e collaborativa. Sincrona perché i quesiti vengono erogati contemporaneamente su tutti i computer dei partecipanti alla gara. Collaborativi perché ogni squadra è formata da tre gruppi, uno di classe I, uno di classe II e uno di classe III, che concorrono a risolvere i quesiti assegnati alla gara e sommando i punteggi raggiunti. Analogamente il punteggio raggiunto da una scuola è dato dalla somma dei punteggi ottenuti da tutte le squadre che vi partecipano. Insomma, un vero e proprio esercito di menti matematiche per un gioco che gioco non è e che ha richiesto, oltre ad una buona preparazione, tanto sangue freddo per cliccare al momento giusto e nel punto giusto, spirito di squadra e soprattutto una lunga fase di allenamento che è cominciata a gennaio. Non a caso le squadre che si sono piazzate hai primi posti hanno seguito per tutto l’anno scolastico specifici laboratori di giochi matematici.
Cicloide animata
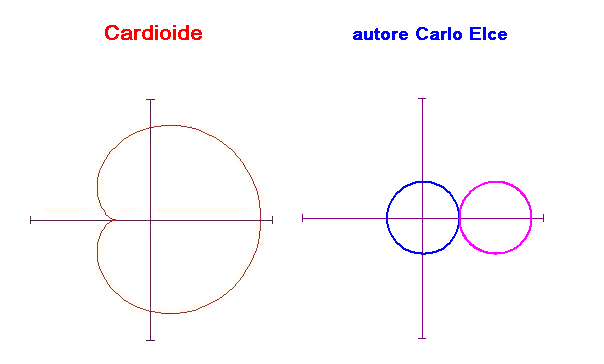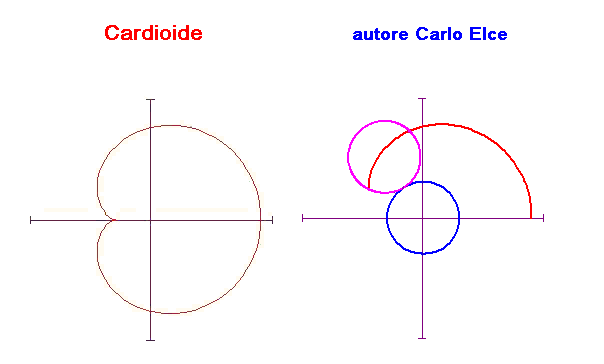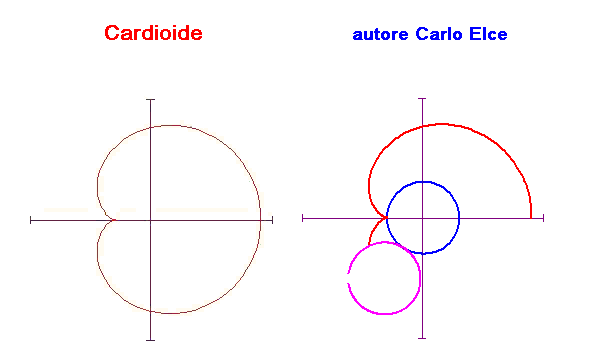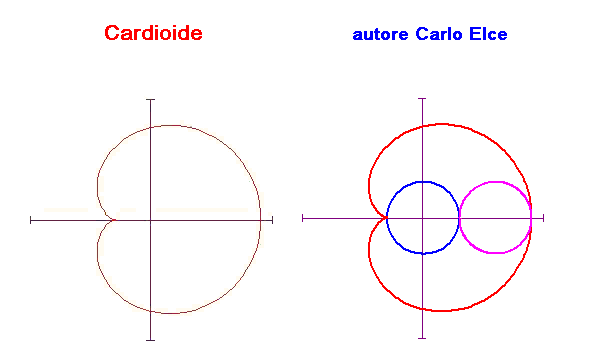
L’immagine animata mostra come si genera la cardiode. Questa curva si ottiene facendo rotolare una circonferenza attorno a un’altra con lo stesso raggio e tenendo la traccia di un punto fisso della circonferenza che rotola.
Scuola estiva di astronomia per insegnanti
Scuola estiva di astronomia organizzata dalla Società Astronomica Italiana (SAIt) a Saltara (Pesaro-Urbino) nel periodo 15-18 luglio: Astronomia e Astrofisica nella progettazione di percorsi formativi. Il tema per l’edizione 2008 è: In preparazione del 2009 – anno galileiano. Infatti, nel quattrocentesimo anniversario delle prime osservazioni telescopiche di Galileo, è stato proclamato il 2009 “International year of astronomy”. Alla scuola possono partecipare 25 docenti di scuola secondaria di ogni disciplina. Iscrizioni entro il 30 maggio, quota 50,00 euro.
Scuola Estiva SAIt 2008 di Saltara 15-18 luglio 2008 Museo del Balì, Saltara (Pesaro-Urbino)
Nell’ambito del Protocollo d’intesa rinnovato nel 2004 tra MPI e SAIt-SIF-AIF, la Società Astronomica Italiana (SAIt), in collaborazione con l’Istituto Nazionale di Astrofisica e la Fondazione “Museo del Balì” e d’intesa con il Ministero della Pubblica Istruzione – Direzione Generale Ordinamenti Scolastici, organizza la III Scuola Estiva di Astronomia:
Astronomia e Astrofisica nella progettazione di percorsi formativi
Il tema per l’edizione 2008 della scuola è:
In preparazione del 2009 – anno galileiano
Nel quattrocentesimo anniversario delle prime osservazioni telescopiche di Galileo, l’International Astronomical Union, l’Unesco e l’ONU hanno deciso di proclamare il 2009 “International year of astronomy”.
La SAIt ha pertanto ritenuto importante dedicare le sue Scuole estive di astronomia, in preparazione delle attività scolastiche 2008-2009, a tematiche legate a questo anniversario. L
a SAIt ha tra i suoi compiti statutari quello di incentivare e migliorare l’insegnamento dell’astronomia in Italia, evidenziandone l’elevato carattere interdisciplinare e la forte valenza culturale e formativa. L’argomento scelto per la terza edizione della scuola di Saltara – la celebrazione dell’anno galileiano – si caratterizza per la sua natura interdisciplinare, andando dal campo scientifico a quello filosofico ed etico. S
i ritiene che la scuola possa costituire un incentivo all’insegnamento dell’astronomia, non come fatto puramente tecnico ma «come una ricerca, con immancabili dubbi e mancate risposte, come azione congiunta tra esperimento, osservazione e teoria, metodo scientifico e interazione tra scienza, tecnologia e società».
Ci si occuperà di come le osservazioni galileiane abbiano portato una fondamentale rivoluzione nella visione della natura e del cielo e nella percezione del posto dell’uomo nel cosmo e di come questo non solo abbia favorito l’evoluzione dell’astronomia fino alle moderne concezioni dell’universo, ma abbia avuto profonde implicazioni nello sviluppo delle scienze, della tecnologia, della filosofia e della cultura in generale.
Si intende, così, sia sollecitare l’interesse per lo sviluppo delle conoscenze scientifiche – evidenziandone le caratteristiche di fattore unificante della cultura e di stimolo al rinnovamento didattico – sia trasmettere il convincimento che l’astronomia possa costituire una parte integrante e unificante di una preparazione che voglia andare oltre la “scala umana” per allargarsi in un quadro ben bilanciato delle conoscenze.
Direttore della scuola estiva è la prof.ssa Angela Misiano del Consiglio Direttivo della SAIt.
Alla scuola possono partecipare 25 docenti di scuola secondaria di secondo grado delle materie scientifiche, storico-filosofiche, letterarie, artistiche e linguistiche.
La quota di iscrizione fissata in 50,00 Euro. Le spese di soggiorno (vitto e alloggio) per i 15 docenti non locali sono a carico degli organizzatori, restano a carico dei partecipanti le spese di viaggio. Le spese del solo vitto per i 10 docenti locali sono a carico degli organizzatori.
La selezione dei partecipanti sarà eseguita dalla SAIt in collaborazione con la Fondazione Villa del Balì. In funzione delle disponibilità logistiche, la commissione che seleziona gli iscritti si riserva di ammettere, in qualità di ‘uditori’, un numero limitato di quei docenti che non rientrano nelle priorità determinate. La quota di iscrizione per gli ‘uditori’ è ridotta a 25.00 Euro e le spese di vitto e alloggio sono a loro carico.
Ai partecipanti verrà dato un attestato di partecipazione alla scuola. Le iscrizioni devono pervenire entro il 30 maggio p.v., scrivendo a entrambi i seguenti indirizzi di posta elettronica:
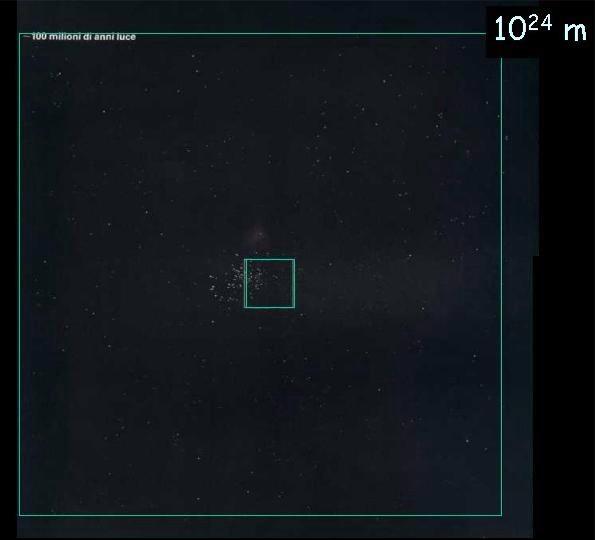
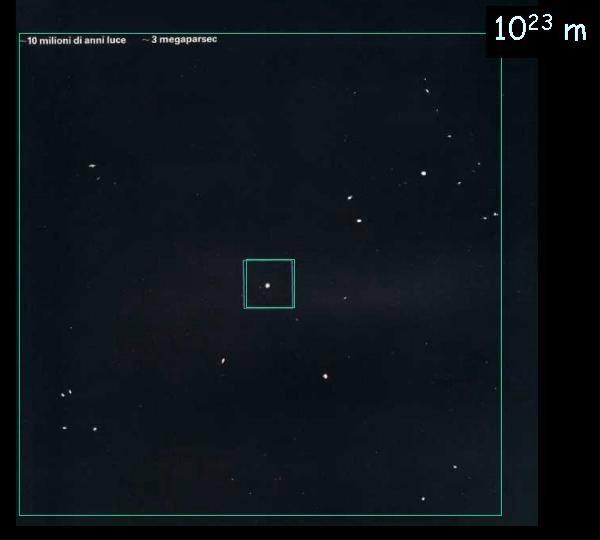
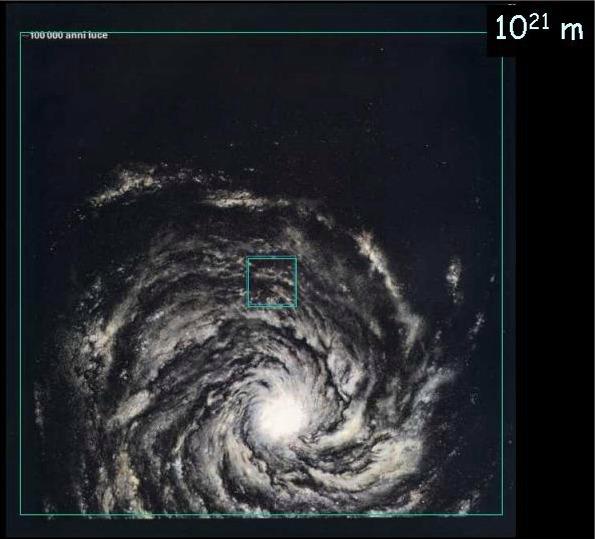
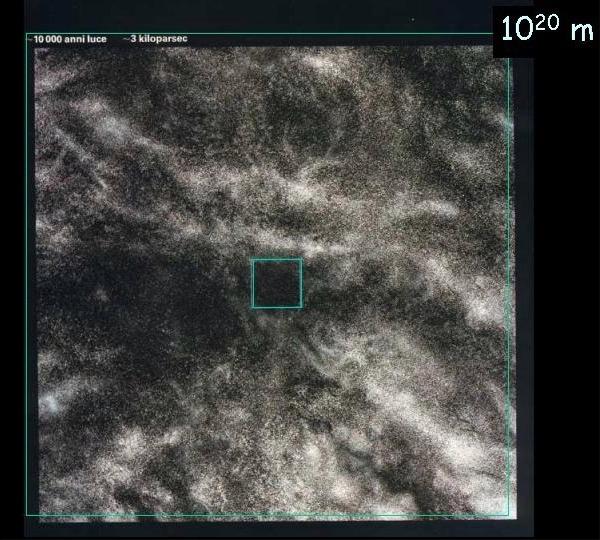
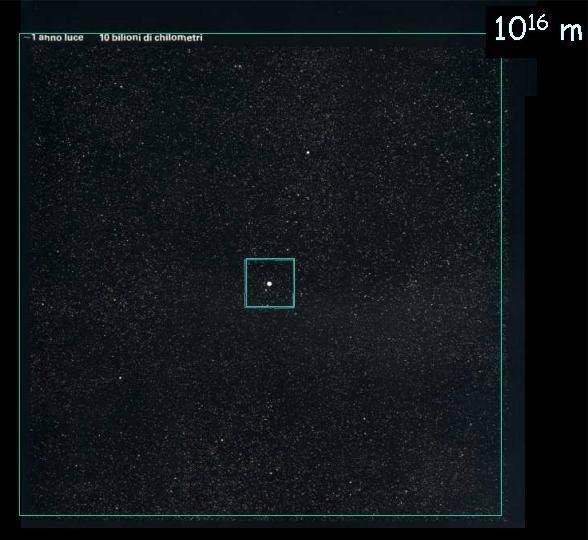
Potenze del 10
Una sequenza di immagini accattivanti che danno l’idea dell’ordine di grandezza delle potenze di dieci. Le immagini sono estratte da una presentazione PowerPoint di R. G. M. Caciuffo inviatami da Giuseppe Rivoli. Le pubblico per il loro elevato valore didattico; i legittimi proprietari possono rivendicarne la proprietà. 
C. Pellegrino e L. Zuccheri, Tre in uno
Consolato Pellegrino e Luciana Zuccheri, Tre in uno. Piccola enciclopedia della matematica intrigante, Ediz. ATHENA, 2008. Tre in uno è il risultato di una lunga esperienza degli autori nel campo della di didattica della matematica. In poco più di 130 pagine hanno condensato un approccio didattico strutturato su più livelli.
Nella Parte Prima fa da sfondo un dialogo tra Andrea, giovane amante del gioco e della matematica, e Sofia, nonna di Andrea. Il dialogo è strutturato in forma ‘teatrale’, può essere utilizzato per una rappresentazione a scuola, può essere trasposto in un fumetto o in un film.
I personaggi sono tipici delle situazioni di apprendimento: un nipote che vuole imparare insegnando e una nonnina che fa finta di non sapere e qualche volta effettivamente non sa. Si sa i bambini trovano più facile parlare con i nonni che con i genitori, perché sono più pazienti e accettano le lezioni dei nipoti ‘io so tutto’; di tanto in tanto, al momento giusto, sanno anche come raddrizzare un percorso che rischia di perdersi nel vuoto.
Nonna Sofia parte da quello che sta facendo Andrea: sta giocando al Tangram, un antico gioco orientale che si fa disponendo opportunamente sette pezzi di legno dalle forme geometriche ben definite. Come un po’ tutti i giochi non è un semplice passatempo, Sofia probabilmente lo sa ma provocatoriamente dice: “E’ roba da ragazzini!” Da qui la reazione di Andrea che spiega il gioco per far vedere che è tutt’altro che roba da ragazzini. Quanto più nonna Sofia cerca di dire che il Tangram è un inutile perditempo tanto più Andrea cerca di dimostrare il contrario.
Il gioco del Tangram ha molte analogie con la ricerca matematica e i problemi studiati dai matematici. Il racconto ha poi un altro livello di lettura, specifico per gli insegnanti, che quasi a ogni frase del dialogo possono trovare, nelle ricche e numerose note al testo, spunti per riflessioni e approfondimenti, riferimenti bibliografici e a siti Internet. Dalle numerose note ci si rende conto le parole del dialogo non sono lasciate a caso, ogni affermazione è frutto di un riferimento a studi sistematici sul tema.
La Parte Seconda presenta un percorso più o meno libero sulla matematica e la sua storia. Si parte anche qui dal gioco, si passa per la divulgazione e i premi ai matematici famosi, per approdare alla storia della matematica. Anche nel percorso storico gli autori partono dall’indovinello più vecchio del mondo per passare ai tre famosi problemi dell’antichità e arrivare ai moderni problemi dell’infinito matematico.
Altri itinerari lungo la storia della matematica sono il rapporto tra la matematica dilettevole e la ricerca matematica dall’altra. Gli autori danno alcuni esempi di situazioni ludiche dalle quali sono nati significativi problemi e teorie matematiche, dal calcolo delle probabilità nato dal gioco dei dadi alla topologia nata da un popolare rompicapo sui ponti di Koenigsberg.
Una ulteriore passeggiata nella storia della matematica è quella fatta attraverso le competizioni e le gare, dai rompicapo dell’età classica, come il ‘problema dei buoi’ proposto da Archimede, alle disfide di Fibonacci che hanno consentito di affermare la notazione arabo-indiana per i numeri, alle disfide di Tartaglia fino alle attuali olimpiadi e gare matematiche per ragazzi.
La Parte Terza del libro è una nutrita e puntuale raccolta di riferimenti bibliografici a libri e articoli in italiano che si conclude con una selezione di riferimenti Web raggruppati per categorie.
Un libro pensato e dedicato agli insegnanti che vogliono interessare e motivare gli alunni allo studio della matematica, dal quale possono trarre spunto per attività laboratoriali e di storia della matematica che non siano un semplice riferimento biografico. Chi è interessato può vedere un video degli stessi autori sul tangram e suoi rapporti con la matematica.
De Angelis e Cominelli ringraziano con una vignetta matematica
Marco De Angelis e Ugo Cominelli, vincitori del concorso sulle vignette di matematica, hanno ricevuto l’ambito premio, l’Ipod touch, e ringraziano con due vignette divertenti. Che ci fanno due Ipod tra gli uomini della pietra? Per la verità De Angelis e Cominelli più che uomini della pietra sono uomini dell’era della matita, che evidentemente non è ancora stata sconfitta dal mouse.
 |
 |
Grazie a entrambi e a tutti quelli che hanno partecipato all’iniziativa, un sorriso in più fa sempre bene!
Metodo di Gauss-Chio per la risoluzione di sistemi lineari
Un procedimento analogo a quello seguito per ricavare il metodo di Chiò per il calcolo di un determinante permette di ottenere un algoritmo semplice per la risoluzione dei sistemi lineari, utilizzando solo determinanti del 2° ordine. In questo articolo si dà una dimostrazione del metodo e si presenta un foglio excel per risolvere i sistemi.
Scarica il foglio Excel per la risoluzione dei sistemi lineari con il metodo di Gauss-Chio.
Dare il resto
Tom è il cassiere di un supermercato, purtroppo non è veloce a dare il resto ai clienti. Dagli una mano! Il tuo scopo è di dare il resto giusto ai clienti. Esercitati con le cifre decimali: gioco adatto per la scuola primaria ma anche per quella secondaria.
Il gioco richiede l’installazione di Adobe Flash Player.
Asimmetrie – Anno 3 Numero 6
E’ uscito il Numero 6 (anno III) di "asimmetrie" la rivista dell’Istituto Nazionale di Fisica Nucleare (INFN). La rivista è gratuita e può essere richiesta nel formato cartaceo o scaricata liberamente nel formato pdf. In questo numero si parla degli acceleratori di particelle: acceleratori per la ricerca sulla materia, acceleratori per la medicina, acceleratori per l’industria … e anche per la letteratura.
"Caspita! – esclamò Rutherford compiaciuto – Se avessi una batteria di cannoni più potenti!"
Ernest Rutherford stava bombardando un sottilissimo foglio d’oro con raggi $alpha$ emessi da sorgenti radioattive e fu sorpreso dai risultati ottenuti. Fu l’esperimento che diede origine alla ricerca nella fisica nucleare. Da allora i fisici hanno cercato di bombardare la materia con particelle sempre più veloci per rompere le particelle elementari di cui si compone la materia e studiare cosa accade durante questi scontri a velocità pazzesche, ormai prossime a quelle della luce.
Nel 1929 R. van de Graaff costruì una macchina per accelerare le particelle, poco dopo E. Lawrence inventò il ciclotrone. Divenne da subito chiaro che queste macchine per accelerare le particelle avevano un grande potenziale nella medicina e nelle applicazioni industriali.
Oggi, dopo ottanta anni di ricerca, gli acceleratori in tutto il mondo sono più di 15.000, il 97% di essi viene impiegato nella medicina e nella tecnologia
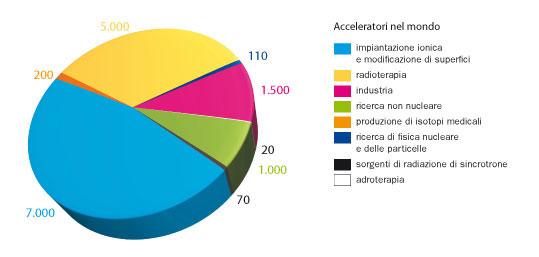
Questo numero di "Asimmetrie" è interamente dedicato allo stato di questa ricerca, a partire dalla storia di queste macchine e della fisica che c’è sotto.
Particolare attenzione è dedicata alle applicazioni alla salute dell’uomo:
– comprendere i danni provocati dalle radiazioni sulle cellule umane per sviluppare precauzioni e terapie;
– curare i tumori bombardando in maniera mirata gli organi danneggiati, anche con acceleratori ‘tascabili’;
– visualizzare immagini bidimensionali e tridimensionali di organi umani per diagnosticare patologie.
Molta attenzione anche alle applicazioni alla tecnologia, quella di uso quotidiano ma anche quella sulla trasmutazione delle scorie radioattive.
Conclude questo numero un articolo dello scrittore Bruno Arpia che presenta il suo progetto di un romanzo sulla fisica di oggi.
Insomma, un numero da non perdere:
L’immagine "Acceleratori nel mondo" è presa dall’articolo di Crisostomo Sciacca "Acceleratori, non solo ricerca".
MatematiCup 2008: i vincitori
"L’esercito di Franca", "Team Tanzi" e "I Disastri 2 (la vendetta)" sono le tre squadre vincitrici della MatematiCup 2008. La prima scuola classificata è l’Istituto Gianelli di Rapallo (GE). Vincono gli allenamenti "Istituto comprensivo Muro". Prima squadra femminile le "Matemitiche!
La gara di matematica per ragazzi della scuola secondaria di primo grado si è svolta la mattina del 7 maggio. Hanno partecipato 8500 alunni, divisi in 360 squadre, di 210 scuole distinte. Dopo tre ore di calcoli, disegni e clic ecco le classifiche e i premi.
1a squadra classificata: "L’esercito di Franca", allenata da Franca Panellli, dell’Istituto Beato Arnaldo da Limena (Padova); vince Coppa, medaglie, libri e un abbonamento di 6 mesi al filtro Internet a protezione dei minori fornito da KBIT srl
2a squadra classificata: "Team Tanzi", allenata da Meliota Giovanna, della Scuola Secondaria di primo grado Tanzi di Mola di Bari; vince Coppa, medaglie, libri e 6 mesi di filtro Internet KBIT
3a squadra classificata: "I Disastri 2 (la vendetta)", allenata da De Palma Sara, dell’Istituto Gianelli di Rapallo (GE); vince Coppa, medaglie, libri e 6 mesi di filtro Internet KBIT
1a squadra femminile: "Matemitiche!", allenata da Solinghi Lucia, dell’Istituto Gianelli di Rapallo (GE); vince Coppa, medaglie, libri e 6 mesi di filtro Internet KBIT
1a scuola classificata: "Istituto Gianelli" di Rapallo Genova, dirigente Graziella Mazza; vince Targa, libri e 6 mesi di filtro Internet KBIT
2a scuola classificata: "Istituto Sacro Cuore" di Firenze, dirigente Giancarla Lupoi; vince Targa, e 6 mesi di filtro Internet KBIT (premio aggiunto)
3a scuola classificata: "Istituto Madre Teresa Quaranta" di Grottaglie (TA), dirigente Bianca maria Cartella; vince Targa, e 6 mesi di filtro Internet KBIT (premio aggiunto); mezione al merito alla squadra "Pi Greco"
Migliore squadra negli allenamenti: "Istituto comprensivo Muro Leccese" di Muro (LE), allenata da Carlà Teresa; vince Coppa e 6 mesi di filtro Internet KBIT (vince il premio per la regolarità negli allenamenti)
Altri premi, non comulabili con i precedenti (come da regolamento) sono stati assegnati a
Migliore gruppo di classe prima: "Lampi di genio", allenata da Angelo Remitti, della Scuola Media di Maranello (MO); vince Coppa e 6 mesi di filtro Internet KBIT (vince il premio perché le squadre che nella relativa classifica si sono piazzate prima hanno vinto premi in altre categorie)
Migliore gruppo di classe seconda: "I giovani Newton", allenata da Silvana Serra, della S.S. Primo Grado Elisa Sala di Monza; vince Coppa e 6 mesi di filtro Internet KBIT (vince il premio perché le squadre che nella relativa classifica si sono piazzate prima hanno vinto premi in altre categorie)
Migliore gruppo di classe terza: "I + della Rodari", allenata da Rossella Bonora, dell’Istituto "G. Rodari" di Santa Giustina (Belluno); vince Coppa e 6 mesi di filtro Internet KBIT (vince il premio perché le squadre che nella relativa classifica si sono piazzate prima hanno vinto premi in altre categorie)
Migliore squadra in aritmetica e algebra: "Math’s girls" allenata da Anna Maria Maronna dell’Ist. Quinto Ennio di Lecce; vince Coppa e 6 mesi di filtro Internet KBIT (vince il premio perché le squadre che nella relativa classifica si sono piazzate prima hanno vinto premi in altre categorie)
Migliore squadra in geometria: "Mathematic Wizard" allenata da Anna Lisa De Donato della S. M. S. Via Martiri D’Ungheria Scafati (Salerno); vince Coppa e 6 mesi di filtro Internet KBIT (vince il premio perché le squadre che nella relativa classifica si sono piazzate prima hanno vinto premi in altre categorie)
Migliore squadra in logica e insiemistica: "Eta Beta" allenata da Liviana Lucchetti dell’Ist. C. Ancona Centro di Ancona; vince Coppa e 6 mesi di filtro Internet KBIT
Migliore squadra in statistica, probabilità e combinatorica: "Tendenti all’infinito" allenata da Giulia Garello dell’I. P. Gobetti di Rivoli (TO); vince Coppa e 6 mesi di filtro Internet KBIT (vince il premio perché le squadre che nella relativa classifica si sono piazzate prima hanno vinto premi in altre categorie)
* * * * * * * * * *
Il comitato organizzatore ha ritenuto, come da regolamento, di non cumulare i premi perché le squadre che sono risultate prime nella classifica squadre risultano quasi automaticamente prime nelle sottoclassifiche per classi e per temi.
Si ringraziano tutti i partecipanti per l’entusiasmo con cui si sono allenati e hanno gareggiato, in particolare i docenti che si sono fatti carico di organizzare le squadre … e i computer!
Istogramma delle scuole partecipanti per regione (I e II edizione)
I professori che vogliono avere l’attestato per i propri allievi devono richiederlo a [email protected]
Gruppo promotore: Antonio Bernardo (Matematicamente.it), Mario Bochicchio (DIDA-Lab Uni. Salento), Massimo Mazzitelli (Kataweb), Domenico Lenzi (Mathesis)
Comitato tecnico scientifico: Antonio Bernardo, Mario Bochicchio, Domenico Lenzi, Laura Todisco.
Redattori e revisori dei quesiti: Antonio Bernardo, Laura Todisco, Domenico Lenzi, Luca Barletta, Flavio Cimolin, Luca Lussardi, Luciano Sarra, Paolo Giovanni Zanin
Direzione sviluppo software: Federico Zanchetta (Kataweb)
Si ringrazia Michela Occhioni per le verifiche e il controllo sull’uso degli esercizi di allenamento nelle proprie classi.
Roberto Chiappi, Problem solving nelle organizzazioni
Roberto Chiappi, Problem solving nelle organizzazioni: idee, metodi e strumenti da Mosè a Mintzberg, Springer, 2006, pp. 208
Roberto Chiappi ha operato per tantissimi anni nel gruppo E.N.I. nei settori dell’analisi degli investimenti, nella pianificazione strategica e soprattutto nella formazione, in questo libro raccoglie oltre cento schede di strumenti e metodi utilizzati da matematici e filosofi per risolvere i molteplici problemi delle organizzazioni.
Il libro si presenta come una lunga carrellata di casi studio che vuole essere una “mappatura della genealogia filosofica e matematica dei metodi di risoluzione dei problemi organizzativi”.
L’autore mette in rilievo l’apporto che filosofia e matematica possono dare, anche in termini pratici, al problem solving e al decision making.
L’Introduzione del libro costituisce una sintetica e ben strutturata presentazione del cosiddetto problem solving.
Per parlare di risoluzione di problemi, occorre prima di tutto intendersi su cos’è un problema. L’autore lo descrive come una discrepanza tra la situazione presente e una situazione ideale desiderata. Il problem solving è allora il processo attraverso il quale si copre questa distanza, passando dalla situazione attuale a un’altra il più vicino possibile a quella ideale.
La prima riflessione è sui soggetti che devono risolvere un problema, in relazione al loro grado di competenza: gli esperti solitamente impiegano una lunga e articolata fase iniziale per inquadrare il problema all’interno di schemi a loro noti, i naif tendono a saltare questa fase iniziale salvo a perdere poi tempo procedendo per tentativi ed errori.
La seconda riflessione è sui processi che gli individui possono mettere in atto. Esperti e gruppi di lavoro specializzati affrontano i problemi attraverso i seguenti passi fondamentali: problem finding, in cui ci si rende conto di qual è il problema; problem setting in cui si definisce e si delimita il problema; problem analysis in cui lo si analizza con strumenti specifici; problem solving in cui si cerca di risolverlo; decision making in cui si scelgono le linee di azione più adeguate. L’esperto, quindi, dedica particolare attenzione al problem setting e cioè all’identificazione del problema vero e proprio, cercando di darne anche una rappresentazione e modellazione.
La terza riflessione riguarda il problema di per sé: un problema ben strutturato (sono tipici quelli della matematica) può essere affrontato con adeguati algoritmi, viceversa per un problema mal strutturato l’algoritmo risolutivo può non portare alla soluzione oppure pervenire a una soluzione del tutto errata.
Circa le attività cognitive messe in atto dai singoli individui per risolvere i problemi, Chiappi ne dà una classificazione in tredici distinte categorie. Ne riportiamo qualcuna: le attività semiotiche in cui si sostituisce un oggetto o una situazione con un simbolo (un gesto, un segnale) che lo rappresenta; le attività di classificazione, di ordinamento e quantificazione; il procedimento per tentativi ed errori con il quale l’individuo tenta una prima soluzione del problema, individua gli errori che quella soluzione produce e affina la soluzione cercando di eliminare gli errori precedenti, quindi ripete il ciclo con la nuova soluzione. Altri metodi di risoluzione appartengono al gruppo delle inferenze: inferenze per analogia, per deduzione e per induzione. L’elenco si chiude con la verifica e la falsificazione.
Una parte rilevante della capacità di risolvere problemi è legata ai metodi dell’apprendimento, di cui Chiappi riporta alcune regole ormai generalmente condivise. Anche di queste regole riportiamo un assaggio: l’apprendimento risulta più efficace quando il soggetto è motivato ad apprendere, quando ha compiti comprensibili, quando ha una conferma della positività del comportamento adottato in un’esperienza precedente, quando gli allievi partecipano attivamente al processo di apprendimento, quando è di tipo sistemico invece che sequenziale, quando non è affidato esclusivamente sul discorso verbale o scritto.
Tra le tesi presentate in questo libro citiamo la circolarità bidirezionale tra Project Management, Problem solving. Cioè significa, secondo l’autore, che si può partire con un problema e sviluppare dei progetti per risolverlo oppure si può partire con un progetto di cambiamento e avere, per realizzarlo, molteplici problemi da risolvere.
Giovani ricercatori a Cipro: età 12-18 anni
A Cipro si organizza la "European Student Conference in Mathematics EUROMATH2009". La conferenza si terrà dal 5 all’8 febbraio 2009 a Cipro. Chi è interessato a partecipare, con o senza una propria presentazione, può inviare un messaggio con i propri dati al comitato organizzatore.
La deadline per la presentazione degli abstracts è il 17 October 2008.
La Conferenza consiste in diversi workshops/symposiums/sessions che riguardano diversi temi. La lingua ufficiale della conferenza è l’inglese. I temi sono:
Applications of Mathematics
Mathematics and Sciences
Mathematics and Life
Mathematics and Technology
Mathematics and Social Sciences
Mathematics and Space
Fractals and Geometry
Mathematics and Economy
Mathematics and Literature
Mathematics and Music
Mathematics and Law
Mathematics and Statistics
History of Mathematics
Mathematics and Society
Mathematics and Europe
Mathematics and Philosophy
Mathematics and Computer Science
Famous Numbers
Per manifestare la dimostrzione di interesse inviare una e-mail o fax:
Fax: +357-22379122
E-mail: [email protected]
Per informazioni: www.euromath.org , www.cms.org.cy
Comitato organizzativo: [email protected]
In Italia contattare: [email protected]
150 esercizi svolti sui limiti, per l’università e la scuola secondaria
Tantissimi esercizi sui limiti svolti passo passo esercizi svolti sui limiti , una delle più ricche collezione di esercizi svolti di matematica scaricabili gratuitamente Esercizi svolti di matematica. Per commentare gli esercizi, confrontarsi e chiedere consigli consulta il forum di matematica.
Come difendere i propri risparmi: proposte da evitare, scelte da preferire
Corso gratuito di 2 giorni – Assessorato al commercio SCUOLA DEL CONSUMO CONSAPEVOLE Corsi e seminari 2008 Area finanziaria. Coordinatore: Beppe Scienza, Dipartimento di Matematica dell’Università di Torino MERCOLEDí 4 E VENERDí 6 GIUGNO 2008 Scuola di Amministrazione Aziendale Via Ventimiglia 115 – Torino
|
Assessorato al commercio
SCUOLA DEL CONSUMO CONSAPEVOLE Corsi e seminari 2008 Area finanziaria. Corso di due giornate Come difendere i propri risparmi: proposte da evitare, scelte da preferire Coordinatore: Beppe Scienza, MERCOLEDí 4 E VENERDí 6 GIUGNO 2008 MERCOLEDí 4 GIUGNO 2008 Ore 11.00 – 13.00 13.00: pranzo presso la Scuola di Amministrazione Aziendale Ore 14.00 – 16.00 Ore 16.00 – 17.30 VENERDí 6 GIUGNO 2008 Ore 11.00 – 13.00 13.00: pranzo presso la Scuola di Amministrazione Aziendale Ore 14.00 – 15:30 Ore 15.30 –16.30 Ore 16.30 – 17.30
|
|
|
Informazioni e iscrizioni: Vanna Tessore La partecipazione al corso è gratuita. |
|
Rotazione di un dodecaedro
Dodecaedro stellato
Solidi: Dirhombicosidodecahedron
La Programmazione Lineare e l’Algoritmo del Simplesso
Scarica il documento in formato PDF.
Il cubo di Rubik, come si risolve: VIDEO7 (ultima lezione)
La settima e ultima video lezione per imparare a risolvere il cubo di Rubik. Un gioco che appassiona tantissimi ma che per molti resta un rompicapo difficile. Davide Lettieri vi spiega uno dei metodi possibili.
Gioca con il cubo di Rubik on line.
L’ape buca palloni: calcolo mentale rapido con le 4 operazioni
Gioco per bambini per velocizzare il calcolo mentale: semplici calcoli con le quattro operazioni. In un prato un bambino gonfia i palloncini ma un’ape li fa scoppiare, quelli giusti però!
gioco matematico per bambini
Il cubo di Rubik, come si risolve: VIDEO 5
La quinta video lezione per imparare a risolvere il cubo di Rubik. Un gioco che appassiona tantissimi ma che per molti resta un rompicapo difficile. Davide Lettieri vi spiega uno dei metodi possibili.
Macchine matematiche (virtuali)
Animazioni che ricostruiscono in modo virtuale il comportamento di alcune macchine matematiche: il compasso perfetto, la guida rettilinea, il meccanismo di Watt, l’inversione circolare, l’ingranditore o pantografo e le macchine per costruire ellisse, iperbole e parabola. Una raccolta di applet java di grande valore didattico. L’argomento è stato pubblicato sulla rivista “Nuova secondaria” n. 5 del 15 gennaio 2003, Editrice LA SCUOLA, qui si presenta la versione dinamica e interattiva.
IL COMPASSO E LA RIGA
Nel porre l’attenzione ai primi strumenti matematici (la riga e il compasso), ci imbattiamo in alcune “curiosità” che vogliamo mettere a fuoco.
Come vediamo, nella figura 1 sono rappresentati 4 oggetti: una riga, un oggetto rotondo, un rettangolo con un grosso foro nel centro e un compasso. Viene spontaneo associare tra loro il compasso, l’oggetto rotondo e il rettangolo forato, lasciando da sola la riga, l’unica che non permette di disegnare circonferenze. Se invece riflettiamo un po’ ci accorgiamo che l’unico strumento che deve stare isolato è il compasso dato che è l’unico che ” non contiene in sé ” l’oggetto da rappresentare.
(Fig. 1)
In altre parole: con la riga si può disegnare una retta perché ” è già immagine di una retta “; con l’oggetto rotondo e col rettangolo forato possiamo disegnare una circonferenza perché ” sono già immagini di circonferenze “.
Siamo di fronte quindi ad una sorta di circolo vizioso logico: per tracciare una retta bisogna già averne una (la riga) a disposizione! Per tracciare una circonferenza bisogna già averne una a disposizione (l’oggetto rotondo o il rettangolo forato)!
Il compasso, lo ribadiamo, ” non contiene in sé ” l’oggetto da rappresentare (la circonferenza).
La riga e il compasso sono quindi le prime macchine matematiche che prendiamo in considerazione.
DAL COMPASSO AL COMPASSO PERFETTO
Normalmente si pensa di usare un compasso con l’asta fissa verticale (perpendicolare cioè al piano del disegno). Vediamo invece come stanno le cose con una simulazione realizzata con CABRI.
Le animazioni ci permettono di ricostruire un compasso virtuale e di farlo funzionare come se fosse reale.
Come vediamo (animazione di sinistra), l’asta fissa non è verticale ma forma insieme a quella scrivente un triangolo isoscele. Il perno che viene retto durante la costruzione della circonferenza non ruota su se stesso ma compie anch’esso una circonferenza. E’ questa disposizione che ci permette di disegnare (entro certi limiti) circonferenze di raggio “qualsiasi”. Se invece l’asta fissa fosse perfettamente perpendicolare al piano del disegno, potremmo disegnare solo una determinata circonferenza. Per variare il raggio occorrerebbe che la punta scrivente si potesse allungare o accorciare, come vediamo nella simulazione di destra.
$(7x+2)/(2x-3)+(5x+4)/x=(34x^2+43x-2)/(4x^2-9)+(10-x)/(2x^2-3x)$
$2^(3x-2)*4^(1-x)=sqrt(8)$
$x^3-x^2+x-1=0$
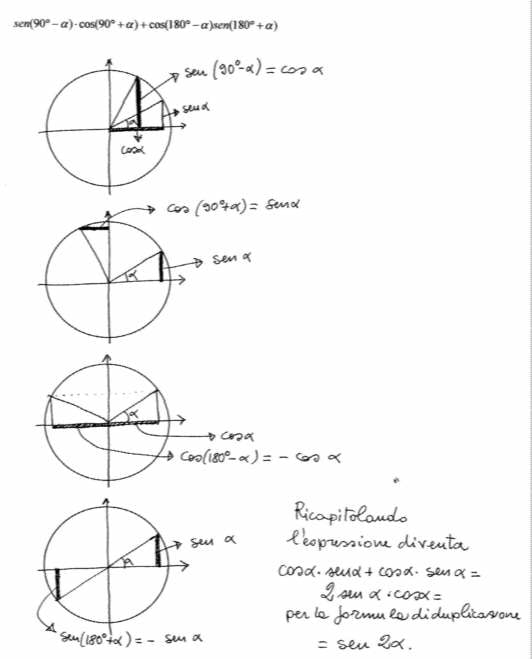
$sen(90circ-alpha)*cos(90circ+alpha)+cos(180circ-alpha)sen(180circ+alpha)$
Esercizio svolto di trigonometria sugli archi associati
$x/(b-2)-(x-2)/(b^2+2b+4)=((b^2+4)x+6b+b^2)/(b^3-8)$
Equazione letterale risolta
$2^(2x+1)+4^(x-1)+8^(2x/3)=13$
Equazione esponenziale
1° TROFEO di scacchi Matematicamente.it
Parte il Primo Trofeo di scacchi di Matematicamente.it. Registrati al sito, accedi alla sezione schacchi e sfida chiunque. Alla fine di ogni mese il primo classificato sarà lo scacchista del mese e vincerà la maglietta di Matematicamente. Alla fine dell’anno il primo in classifica sarà riconosciuto come vincitore del trofeo 2008 e riceverà un adeguato trofeo. L’iscrizione al torneo è gratuita. Dal 1° maggio partirà la nuova classifica con premiazione. La classifica attuale sarà azzerata e si ricomincerà da capo. Le partite iniziate prima dell’1 maggio potranno essere continuate ma non daranno diritto a punteggio nella classifica.
Alla fine di ogni mese il primo classificato sarà lo Scacchista del mese e vincerà la maglietta di Matematicamente. I premi mensili non sono cumulabili.
Alla fine dell’anno il primo in classifica sarà riconosciuto come vincitore del trofeo 2008, riceverà un adeguato trofeo. Questo premio è cumulabile con i premi mensili.
Per il primo mese la regola è semplice, il vincitore del mese è il giocatore che alle 24.00 del 31 maggio risulterà il primo in classifica. Le partite non concluse entro il 31 maggio potranno essere continuate nel mese seguente.
A partire da giugno sarà introdotta un’altra regola: in ogni sfida il vincitore riceverà un punteggio aggiuntivo proporzionale al punteggio dell’avversario.
Per quali valori di K l’equazione $x^2-2(k-6)x+5=0$ ha …
$|2x-1|=|x+1|+|x-2|$
$2/(1-3^x)+6/(9^x-1)+2/(3^x+1)=1/(1+3^(-x))$
$3^x+6/3^x=29/3$
$6/((logx)^2-1)+3/(logx+1)=(logx+1)/(logx-1)$
$(log(x-1))/log(x^3-8x+5)=1/3$
$2*logx-log(2x+1)+log3=log(x-2)$
$(a^2/(4a^2+4ab+b^2)-(a-b)/(6a+3b)):(a^3-b^3)/(12a+6b)$
$[10/7*5-(1/2+3/14):1/5]:(2+1/2)-2/3-1/7$
$(1-5/7)*2/7:[(3/5*10/9+1/4):7/12-3/2+6/7]$
$(b+2)/(b-2)-(b+1)/(b-1)-2/(b^2-3b+2)$
$(7/3+1/14)(9/2-3/5):(1/6-5/4)+[(3/10-2/5+1/2)]*2/3+(1/4+1/3)
$[2a^4-(a^2+b+1)(a^2-b-1)][a^4-(b+1)^2]+(b+1)^4$
