.
.
.
.
.Per esercitarti segui questo link –>
.
I punteggi acquisiti durante questa sessione di ESERCITAZIONE non danno diritto a punteggi per l’ ALLENAMENTO della gara vera e propria.
.
.
.
.
.
.
.Per esercitarti segui questo link –>
.
I punteggi acquisiti durante questa sessione di ESERCITAZIONE non danno diritto a punteggi per l’ ALLENAMENTO della gara vera e propria.
.
.
 La seconda video lezione per imparare a risolvere il cubo di Rubik. Un gioco che appassiona tantissimi ma che per molti resta un rompicapo difficilissimo. Davide Lettieri vi mostra alcuni metodi per risolvere il gioco.
La seconda video lezione per imparare a risolvere il cubo di Rubik. Un gioco che appassiona tantissimi ma che per molti resta un rompicapo difficilissimo. Davide Lettieri vi mostra alcuni metodi per risolvere il gioco.
 La prima video lezione per imparare a risolvere il cubo di Rubik, il gioco più venduto della storia, con circa 300.000.000 di pezzi in tutto il mondo. 9 quadrati su ogni faccia, per un totale di 54 quadrati, che differiscono per il colore. Quando il gioco matematico è risolto, ogni faccia si presenta con un unico colore.
La prima video lezione per imparare a risolvere il cubo di Rubik, il gioco più venduto della storia, con circa 300.000.000 di pezzi in tutto il mondo. 9 quadrati su ogni faccia, per un totale di 54 quadrati, che differiscono per il colore. Quando il gioco matematico è risolto, ogni faccia si presenta con un unico colore.Ecco uno dei metodi per risolvere il cubo di Rubik:
 La rivista culturale Controluce con la collaborazione del Comune di Monte Compatri e della Comunità Montana Castelli Romani e Prenestini presenta la conferenza Incontri tra Arte e Scienza: "Caos e immaginazione nell’arte e nella scienza" 10 Maggio 2008 ore 15:00 Monte Compatri Tinello Borghese
La rivista culturale Controluce con la collaborazione del Comune di Monte Compatri e della Comunità Montana Castelli Romani e Prenestini presenta la conferenza Incontri tra Arte e Scienza: "Caos e immaginazione nell’arte e nella scienza" 10 Maggio 2008 ore 15:00 Monte Compatri Tinello Borghese Programma:
15:00 Domenico Rotella (direttore responsabile di Controluce) – Introduzione
15:10 Maria Grazia Dardanelli (preside Istituto d’Arte ISA Roma2) – Presentazione della Mostra
15:20 Luca Nicotra (ingegnere e giornalista scientifico) – L’immaginazione creativa nell ‘arte e nella scienza
I meccanismi alla base della creatività dell’immaginazione. Punti di contatto e di separazione fra creazione artistica e scientifica, immaginazione, follia e ragione. L’immaginazione in aiuto alla tecnica e la tecnica in aiuto all’immaginazione. L’immaginazione vista da tre ottiche eccellenti: un matematico (Bruno de Finetti), un letterato (Luigi Pirandello), un filosofo (Antonio Aliotta).
15:50 Giordano Bruno (matematico – Università La Sapienza di Roma) – Segni del caos, da Lucrezio a Pollok … e ritorno!
Il caos e la complessità sono i nuovi paradigmi lungo i quali si muove l’attuale ricerca scientifica. Si cerca di tracciare un percorso che parte da lontano e cheli sembra ricondurci, lasciando "segni" che si possono rinvenire nella letteratura, nell’arte e nella musica, ovvero in quelle che sono tra le più alte manifestazioni dello spirito umano.
16:20 Franco Voltaggio (storico della scienza – Università La Sapienza di Roma) – Serendipity in matematica
16:50 Intervallo – Buffet
17:20 Gian Italo Bischi (matematico – Università di Urbino) – Caos deterministico, un ossimoro della matematica moderna
17:50 Silvia Coletti (filosofo e giornalista scientifico) – La funzione cognitiva dell’immaginazione: un nesso fra arte e conoscenza
18:20 Giorgio Aterno (giudice della Corte dei Conti) – Caos e ordine giuridico
18:50 Fauzia Colletti presenta alcuni libri del filosofo Lucio Colletti
19:00 Discussionme aperta al pubblico
Presidenti onorari: Fulvia de Finetti e Fierluigi Firandello
Ingresso libero Info: 3392437079
 Calitri, Latina, Minturno, Napoli1 e Napoli2. Qual è il ruolo culturale ed interdisciplinare delle scienze fisiche e matematiche? Ipotesi e prospettive. Lunedì 19 maggio 2008 ore 9.00-18.30, Liceo Linguistico e socio-Psico-Pedagogico Statale "N. Jommelli" Aversa (CE).
Calitri, Latina, Minturno, Napoli1 e Napoli2. Qual è il ruolo culturale ed interdisciplinare delle scienze fisiche e matematiche? Ipotesi e prospettive. Lunedì 19 maggio 2008 ore 9.00-18.30, Liceo Linguistico e socio-Psico-Pedagogico Statale "N. Jommelli" Aversa (CE). Riferimenti
Liceo Linguistico e socio-Psico-Pedagogico Statale "N. Jommelli"
Via Ovidio, 15 81031 Aversa (Ce)- Tel. 081 5020840
Per info logistiche dell’evento:
Prof. Gabriella Clemente
Cell. 339 3627000

$(a-b)/(a+b)-…/(a^2+2ab+b^2)=(a-3b)/(a+b)$
* * * * * * * * * *

In un triangolo rettangolo la somma delle lunghezze dei due cateti misura 11.2 cm e la loro differenza 1.6 cm. Calcola la misura delle proiezioni dei cateti sull’ipotenusa.
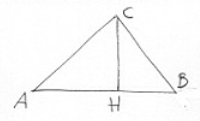 Si ha:
Si ha:
$bar(AC)+bar(BC)=11.2\ cm$
$bar(AC)-bar(BC)=1.6\ cm$
Sommando membro a membro le due equazioni, otteniamo:
$2bar(AC) = 12.8\ cm => bar(AC)=(12 \cdot 8)/2\ cm = 6.4\ cm$
$bar(BC) = 11.2\ cm – 6.4\ cm = 4.8\ cm$
Per il teorema di Pitagora si ha:
$bar(AB) = sqrt((6.4\ cm)^2 + (4.8\ cm)^2) = 8\ cm$
Per il 1° teorema di Euclide abbiamo poi:
$bar(AC)^2 = bar(AH)\cdot bar(AB) => bar(AH) = bar(AC)^2 / bar(AB) = (6.4\ cm)^2 / 8\ cm = 5.12\ cm$
$bar(BC)^2 = bar(BH) \cdot bar(AB) => bar(BH) = bar(BC)^2 / bar(HB) = (4.8\ cm)^2/8\ cm = 2.88\ cm$
In un triangolo ABC l’angolo a è 105° e quello B è 30. Sapendo che l’altezza AH è di 20cm, trova il perimetro e l’area.
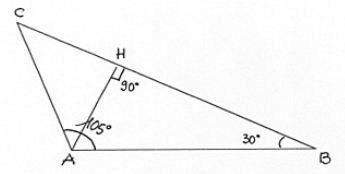 La somma degli angoli interni di un triangolo è sempre $180°$.
La somma degli angoli interni di un triangolo è sempre $180°$.
Nel triangolo $AHB$, l’angolo in $hat(A) = 60°$
Poiché tutto l’angolo in $hat(A)$, cioè $hat(CAB)$, vale $105°$, si ha $hat(CAH) = 45°$.
Consideriamo ora il triangolo $CHA$. Poiché $hat(H) = 90°$, $hat(A) = 45°$. allora anche $hat(C) = 45°$.
In definitiva, $CAH$ è metà di un quadrato, $AHB$ è metà di un triangolo equilatero.
$bar(AH) = 20 cm = bar(CH)$.
Applichiamo ora il teorema di Pitagora per ricavare $CA$:
$bar(CA) = sqrt(400+400) cm = sqrt(800) cm = 28.28 cm text(circa)$
Passiamo ora al triangolo $AHB$
Si ha:
$bar(AB) = 2cdot bar(AH) = 40 cm$.
Applichiamo di nuovo il teorema di Pitagora:
$bar(HB) = sqrt(40^2-20^2) = sqrt(1200) = 34.64 cm text(circa)$
Il perimetro del triangolo $ABC$ si ottine da
$40 cm + 28.28 cm + 20 cm + 34.64 cm$
L’area si ottiene da $((20+34.64)cdot 20)/2 cm^2$
L’ipotenusa BC di un triangolo rettangolo ABC è di 30 cm e il cateto AB di 18 cm. Dal punto P del cateto AC tale che PC sia il doppio di AP, si conduce la parallela all’ipotenusa, che incontra in M il cateto AB, e la parallela …

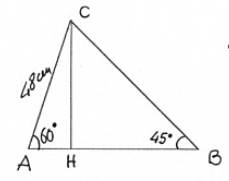 Nel triangolo scaleno ABC i due angoli alla base misurano rispettivamente 45° e 60°. Sapendo che il lato AC misra 48 cm, calcola perimetro e area del triangolo.
Nel triangolo scaleno ABC i due angoli alla base misurano rispettivamente 45° e 60°. Sapendo che il lato AC misra 48 cm, calcola perimetro e area del triangolo.
Osserva che il triangolo
Esamina prima il triangolo ACH: \(\overline{AC} = 48 \text{cm}\), \(\overline{AH} = \frac{1}{2}\overline{AC} = 24\text{cm}\)
Applica il teorema di Pitagora per ricavare \(\overline{CH}\)
\(\overline{CH} = \sqrt{{48}^2-{24}^2} \text{cm} = \sqrt{1728}\text{cm,}\), cioè circa \(41.57\text{cm}\).
Passa poi al triangolo \(\text{CHB}\):
\(CH = 41.57\text{cm} = HB\)
Applica il teorema di Pitagora per ricavare \(\overline{CB}\)
\(\overline{CB} = \sqrt{\overline{CH}^2 + \overline{HB}^2} = \sqrt{3465}\text{cm}\), circa \(58.79\text{cm}\)
Perimentro:\((48 + 24 + 41.57 + 58.79)\text{cm} = 172.36\text{cm}\)
Area:\(\frac{\overline{AB}+\overline{CH}}{2} = \frac{(24+41.57)\cdot 41.57}{2}\text{cm}^2\), circa \(1362,87\text{cm}^2\)
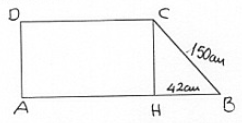 In un trapezio rettangolo la differenza delle basi e il lato obliquo, misurano rispettivamente 42 cm e 150 cm e l’altezza è otto terzi della base minore. Calcola l’area del trapezio.
In un trapezio rettangolo la differenza delle basi e il lato obliquo, misurano rispettivamente 42 cm e 150 cm e l’altezza è otto terzi della base minore. Calcola l’area del trapezio.
Differenza delle basi: \(\overline{AB}-\overline{DC}=\overline{HB}=42 \text{cm}\)
Lato obliquo: \(CB = 150 \text{cm}\)
Applica il teorema di Pitagora al triangolo \(\text{CHB}\), ottieni:
\(\overline{CH} = \sqrt{150^2-42^2} = 144 \text{cm}\)
Si sa che l’altezza è \(\frac{8}{3}\) della base minore, cioè \(\overline{CH} = \frac{8}{3}\text{DC}\), da ciò
\(\overline{DC} = \frac{3}{8}\overline{CH}\), quindi \(\overline{DC} = \frac{3}{8} \cdot 144 \text{cm} = 54 \text{cm}\).
La base maggiore è \(AB = (54+42) \text{cm} = 96 \text{cm}\)
\(A = \frac{(96+54)\cdot 144)}{2} \text{cm}^2 = 10800 \text{cm}^2\)
 A Bologna, domenica 20 aprile 2008, nasce ANIMAT, Associazione Nazionale degli Insegnanti di Matematica. Una proposta per tutti coloro che insegnano matematica, in ogni ordine e grado Bologna, domenica 20 Aprile 2008 Assemblea costitutiva nazionale dalle 9,00 alle 18,00, Sala polivalente, Via Berti 2/9, Bologna
A Bologna, domenica 20 aprile 2008, nasce ANIMAT, Associazione Nazionale degli Insegnanti di Matematica. Una proposta per tutti coloro che insegnano matematica, in ogni ordine e grado Bologna, domenica 20 Aprile 2008 Assemblea costitutiva nazionale dalle 9,00 alle 18,00, Sala polivalente, Via Berti 2/9, Bologna Animat intende rappresentare tutti coloro che insegnano matematica per superare l’isolamento del lavoro docente, favorire la comunicazione, il coordinamento, la discussione, lo scambio di studi ed esperienze di lavoro, contribuendo a costruire punti di vista condivisi anche in relazione con l’opinione pubblica e con le istituzioni.
Animat intende perseguire un insegnamento della matematica che:
• per quanto riguarda le finalità, contribuisca, nel quadro di una scuola di qualità, alla formazione di cittadini consapevoli e dotati di efficaci strumenti di indagine razionale;
• per quanto riguarda i contenuti, non si riduca al mero addestramento al calcolo, ma punti ad affrontare gli aspetti problematici e i nodi concettuali della materia, le sue dinamiche storiche e culturali, mirando dunque a superare l’abituale separatezza tra cultura umanistica e cultura scientifica;
• per quanto riguarda i metodi, sviluppi il più possibile pratiche attive, costruttive e collaborative, anche attraverso l’uso dei mezzi informatici.
– – – – – – – – – – – –
All’assemblea possono partecipare e intervenire tutti coloro che già sono iscritti alle sezioni locali, tutti coloro che intendono iscriversi e, comunque, tutti coloro che sono interessati.
La piattaforma costituiva di ANIMAT, lo Statuto e i nominativi dei promotori sono scaricabili dal sito www.animatinrete.it
E’ possibile partecipare alla lista di discussione sulla fondazione di ANIMAT inviando un messaggio vuoto e seguendo poi le istruzioni a: [email protected]
Programma dei lavori
9.00-9.30 Laura Catastini, Presidente pro-tempore di ANIMAT
Presentazione della Associazione, motivazioni, scopi e organizzazione
9.30–10.00 Franca Ferri, insegnante di scuola elementare, Modena
Insegnare matematica in una società ascientifica e mediatica nella scuola primaria
10.00–10.30 Rossella Garuti, Dirigente scolastico, Modena
La prova di matematica all’esame di terza media: un ponte fra primo e secondo ciclo
10.30–11.00 Walter Maraschini, insegnante di Matematica e Fisica in una scuola secondaria, Roma
Insegnare matematica in una società ascientifica e mediatica nella scuola secondaria.
11.00–11.30 Intervallo
11.30–13.00 Dibattito
13.00–14.30 Pranzo (buffet sul posto a 15 euro)
14.30 – 15,00 Sylviane Beltrame, insegnante di Matematica in una scuola secondaria, Udine
Presentazione e scelta del logo dell’Associazione
15,00 – 17,00 Elezioni, cariche e incarichi, votazioni e formazione di eventuali gruppi di lavoro
17,00 – 18,00 Incontro tra i docenti interessati a partecipare a gruppi di studio per l’avvio di un confronto e organizzazione dei lavori a distanza.
Saluti e chiusura dei lavori
– – – – – –
Come arrivare alla Sala polivalente di via Berti 2/9
Per chi viene in auto: uscire dall’autostrada e prendere la tangenziale fino all’uscita LAME (5). Seguire la direzione centro, andando sempre dritto per un paio di Km, fino ad arrivare di fronte a Porta Lame, sui viali esterni al centro. Percorrere pochi metri a destra, per poi piegare a destra in via Pier De Crescenzi. Dopo un centinaio di metri si incrocia via Berti. Andare a sinistra per parcheggiare e siete di fronte al cancello di ingresso. Per chi viene in treno: uscendo dalla stazione si può andare a piedi, girando alla destra del piazzale e seguendo sempre il viale esterno al centro. Appena superata Porta Lame vedete verso destra l’imbocco di via Pier De Crescenzi, che seguirete per un centinaio di metri, per poi piegare a sinistra in via Berti (in tutto 15-20 minuti). Potete prendere anche l’autobus dalla stazione n.33 e scendere dopo circa 5 minuti a Porta Lame e cercare l’ingresso di via Pier De Crescenzi.
Pernottamento
L’eventuale pernottamento a Bologna va gestito individualmente. Via internet, saranno comunque date alcune indicazioni dai colleghi di Bologna.
Iscrizione e prenotazioni
Non è prevista alcuna quota di iscrizione, salvo quella all’Associazione (€20,00).
E’ invece importante comunicare la presenza all’Assemblea (propria o cumulativa) da effettuare via e-mail a [email protected]
Scarica la locandina dell’assemblea
INTRODUZIONE
I matematici cercarono di usare il calcolo infinitesimale per risolvere nuovi problemi fisici e si trovarono presto costretti a trattare una nuova classe di problemi. Essi fecero più di quanto si erano prefissi di fare. I problemi più semplici conducevano a quadrature che potevano essere valutate mediante le funzioni elementari. Una di queste è costituita dai problemi che rientrano nell’area oggi generalmente nota come teoria dell’elasticità.
Quelli un poco più difficili conducevano a quadrature che non potevano essere espresse in questo modo, come nel caso degli integrali ellittici. Entrambi questi tipi di problemi cadevano nel raggio d’azione del calcolo infinitesimale. Tuttavia, la soluzione di problemi ancora più complicati richiedeva l’uso di tecniche specialistiche; fu così che nacque la teoria delle equazioni differenziali. Numerose classi di problemi fisici fornirono le motivazioni alle ricerche sulle equazioni differenziali. Un corpo è elastico se si deforma sotto l’azione di una forza e riacquista la sua forma originale quando la forza viene rimossa.
Un triangolo isoscele ha l’area e l’altezza rispettivamente di 108 cm2 e 12 cm. Calcola l’area del triangolo equilatero che ha lo stesso perimetro del triangoli isoscele. 
Ho un triangolo rettangolo di cui conosco l’ipotenusa e l’altezza relativa all’ipotenusa. Devo calcolare i due cateti 
Dato un triangolo equilatero ABC di lato a, determina un punto M sul lato AB tale che … 
Dimostra che in un triangolo qualunque ABC, con l’angolo B>C , la bisettrice dell’angolo A forma con il lato BC due angoli la cui differenza è uguale a B-C. 
Il papà recinta il giardino con una siepe. Pianta 120 arbusti alla distanza di 50 cm l’uno dall’altro. Quanti metri è lungo il bordo del giardino?
Per semplificare suddividiamo il recinto con 12 arbusti come nel disegno seguente 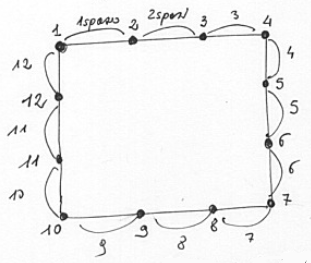
Tra i 12 arbusti ci sono 12 spazi da 50 cm. Quindi tra 120 arbusti ci saranno 120 spazi da 50 cm.
$120 xx 50 cm = 6000 cm = 60 m$.
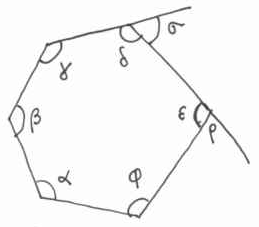 Di un esagono si hanno i seguenti dati:
Di un esagono si hanno i seguenti dati:
Calcola la misura dell’ampiezza degli angoli interni dell’esagono
$alpha = beta = 118° 50’$
$gamma = alpha – 20° 40′ = 118° 50′ – 20° 40′ = 98° 10’$
$delta = 180° – sigma = 180° – 45° 10’\ 20”$
$epsilon = 180° – rho = 180° – 50° 40’\ 50”$
La somma degli angoli interni di un poligono è data da $180° xx (text(numero lati) – 2) = 180° xx 4 = 720°$
$phi = 720° – (alpha – beta – gamma – delta – epsilon)$
$alpha + beta + gamma + delta + epsilon) = 599° 58’\ 50”$
$phi = 720° 0’\ 0” – 599° 58’\ 50” = 120° 1’\ 10”$
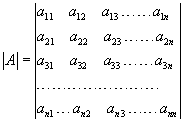
 Per calcolare il determinante di una matrice c’è un metodo poco noto detto metodo di Chiò, dal nome del matematico Felice Chiò. Si riporta brevemente questo metodo, la sua giustificazione e un foglio Excel con le relative formule.
Per calcolare il determinante di una matrice c’è un metodo poco noto detto metodo di Chiò, dal nome del matematico Felice Chiò. Si riporta brevemente questo metodo, la sua giustificazione e un foglio Excel con le relative formule.
Il determinante di una matrice
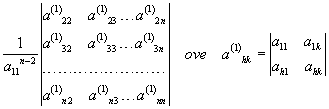
sono tutti i minori orlati del 2° ordine di a11 ( a11 ≠0 e h, k≥2).
Dimostrazione
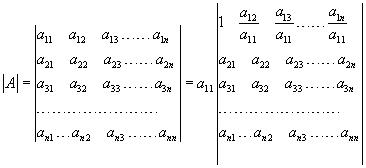
si è divisa la 1° riga per a11
si sostituisce alla 2° riga la seguente combinazione lineare: somma della 2° riga con la 1° moltiplicata per -a21;
si sostituisce alla 3° riga la seguente combinazione lineare: somma della 3° riga con la 1° moltiplicata per –a31;
……………………………………………………………………………………………………………………………………………….
si sostituisce alla n° riga la seguente combinazione lineare: somma della n° riga con la 1° moltiplicata per –an1.
Si ottiene:
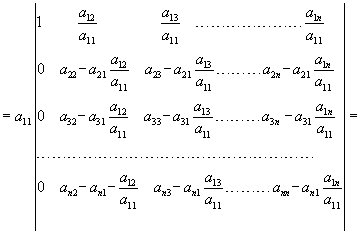
Si moltiplicano tutte le righe, tranne la 1°, per a11 e si ottiene:
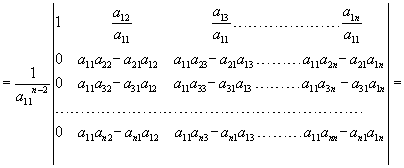
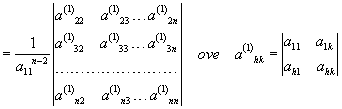
sono tutti i minori orlati del 2° ordine di a11 (ovviamente a11 deve essere ≠0 e h, k≥2.
Esempi di risoluzione
|
1 |
2 |
4 |
8 |
16 |
|
1 |
1 |
1 |
1 |
|
|
|
2 |
1 |
1 |
1 |
1 |
1 |
|
1 |
3 |
9 |
27 |
81 |
|
1 |
2 |
3 |
4 |
|
|
|
1 |
2 |
1 |
1 |
1 |
1 |
|
1 |
4 |
16 |
64 |
256 |
|
1 |
3 |
6 |
10 |
|
|
|
1 |
1 |
2 |
1 |
1 |
1 |
|
1 |
5 |
25 |
125 |
625 |
|
1 |
4 |
10 |
20 |
|
|
|
1 |
1 |
1 |
2 |
1 |
1 |
|
1 |
6 |
36 |
216 |
1296 |
|
|
1 |
2 |
3 |
|
|
|
1 |
1 |
1 |
1 |
2 |
1 |
|
|
1 |
5 |
19 |
65 |
|
|
2 |
5 |
9 |
|
|
|
1 |
1 |
1 |
1 |
1 |
2 |
|
|
2 |
12 |
56 |
240 |
|
|
3 |
9 |
19 |
|
|
|
|
3 |
1 |
1 |
1 |
1 |
|
|
3 |
21 |
117 |
609 |
|
|
|
1 |
3 |
|
|
|
|
1 |
3 |
1 |
1 |
1 |
|
|
4 |
32 |
208 |
1280 |
|
|
|
3 |
10 |
|
|
|
|
1 |
1 |
3 |
1 |
1 |
|
|
|
2 |
18 |
110 |
|
|
|
|
1 |
|
|
|
|
1 |
1 |
1 |
3 |
1 |
|
|
|
6 |
60 |
414 |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
3 |
|
|
|
12 |
132 |
1020 |
|
determinante= |
1 |
|
|
|
|
|
8 |
2 |
2 |
2 |
||
|
|
|
|
12 |
168 |
|
|
|
|
|
|
|
|
|
|
2 |
8 |
2 |
2 |
|
|
|
|
48 |
720 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
8 |
2 |
|
|
|
|
|
576 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
12 |
12 |
|
|
determinante= |
288 |
|
|
|
|
|
|
|
|
|
|
|
12 |
60 |
12 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
12 |
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3456 |
576 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
576 |
3456 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11612160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
determinante= |
7 |
||
Con excel è possibile programmare in modo semplice il calcolo del determinante con questo metodo (vedi il file determinante con Chiò )
|
|
 Quale sarà la maglietta per Matematicamente.it Winner? Dopo il voto spontaneo degli iscritti, il voto dei moderatori del forum e il sondaggio condotto tra 50 partecipanti del forum, rimane una selezione di 25 magliette. Vedi le 25 magliette selezionate.
Quale sarà la maglietta per Matematicamente.it Winner? Dopo il voto spontaneo degli iscritti, il voto dei moderatori del forum e il sondaggio condotto tra 50 partecipanti del forum, rimane una selezione di 25 magliette. Vedi le 25 magliette selezionate.
Un ulteriore sondaggio tra i frequentatori del forum permetterà di decidere quale sarà la maglietta vincitrice. Gli iscritti selezionati per il sondaggio saranno scelti a caso. Non scrivete nessuna mail spontaneamente. Contatteremo noi chi dovrà rispondere al sondaggio.
Tante belle magliette non sono state selezionate, ci dispiace per gli autori, li ringraziamo per la gentile partecipazione.
Scadenza e sottomissione
Presentare il bozzetto entro il 31 maggio 2008.
E’ possibile presentare il bozzetto sulla sagoma di maglietta o semplicemente come disegno a sè.
E’ possibile utilizzare il davanti, il dietro e le maniche della maglietta.
Nel disegno ci sarà una scritta o una immagine che caratterizzerà la maglietta come appertenente alal categoria winner (vincitore).
Va specificato il colore della maglietta.
Il bozzetto può essere inviato in un formato idoneo per il web: gif, jpg, png o altro.
A scelta del concorrente potrà essere usato il logo attuale del sito, scaricabile dal lik sotto.
Ogni concorrente potrà inviare fino a 3 varianti nel colore o nel disegno.
Il file con tutti gli allegati deve essere inviato al seguente indirizzo mail: [email protected]
Nell’oggetto della mail riportare "Concorso maglietta".
Partecipando al concorso si afferma automaticamente che il lavoro presentato è di proprietà e creazione esclusiva del concorrente, ossia che non è stato copiato né è mai stato utilizzato o pubblicato.
L’autore può aggiungere una fima al disegno.
Votazioni e giuria
La maglietta vincitrice sarà scelta con un doppio sistema di votazione. In prima votazione potranno votare tutti gli iscritti a Matematicamente.it, in una seconda fase voterà la giuria che sarà costituita dai moderatori del forum di Matematicamente.it.
Si potrà votare dall’1 al 25 giugno, La giuria deciderà entro il 30 giugno.
Premi e realizzazione della maglietta
Il vincitore del concorso avrà l’incarico di disegnare in base al bozzetto presentato il disegno vero e proprio che sarà consegnato alla stamperia.
Il disegno sarà consegnato in alta risoluzione, nel formato e nelle dimensioni che saranno indicate.
Per questo lavoro sarà corrisposto un compenso di 200 euro.
Il commissionante (Matematicamente.it) può richiedere piccole modifiche o ritocchi al disegno.
La maglietta sarà realizzata in tiratura limitata e non sarà in vendita.
La proprietà intellettuale del disegno resterà dell’autore, tuttavia la maglietta potrà essere stampata esclusivamente da Matematicamente.it di Antonio Bernardo.
Strumenti utili
Non è obbligatorio usare il logo o il template di seguito allegati. La maglietta deve essere a maniche corte.
logo 1 , logo 2, template maglietta
Segnalato da
 Henri Poincaré (1854/1912), francese, matematico, fisico, astronomo e filosofo della scienza, grande divulgatore, è l’ultimo grande sapiente dell’Ottocento e il primo scienziato del Novecento. Precursore della teoria della relatività e dodici volte candidato al premio Nobel – che non vince mai – racconta la propria esperienza e il proprio pensiero sulla creatività e sui processi mentali che generano intuizioni creative nel 1906, all’interno del libro Scienza e metodo, una raccolta di saggi su questioni di metodologia scientifica scritto con straordinaria chiarezza. Da Nuovoeutile.it
Henri Poincaré (1854/1912), francese, matematico, fisico, astronomo e filosofo della scienza, grande divulgatore, è l’ultimo grande sapiente dell’Ottocento e il primo scienziato del Novecento. Precursore della teoria della relatività e dodici volte candidato al premio Nobel – che non vince mai – racconta la propria esperienza e il proprio pensiero sulla creatività e sui processi mentali che generano intuizioni creative nel 1906, all’interno del libro Scienza e metodo, una raccolta di saggi su questioni di metodologia scientifica scritto con straordinaria chiarezza. Da Nuovoeutile.it
Sono cenni brevi che però riescono a dare un’idea precisa del tema, fino a configurare la definizione di creatività forse più soddisfacente fra le moltissime formulate fino a oggi:
«Un risultato nuovo ha valore, se ne ha, nel caso in cui stabilendo un legame tra elementi noti da tempo, ma fino ad allora sparsi e in apparenza estranei gli uni agli altri, mette ordine, immediatamente, là dove sembrava regnare il disordine […] Inventare consiste proprio nel non costruire le combinazioni inutili e nel costruire unicamente quelle utili, che sono un’esigua minoranza. Inventare è discernere, è scegliere […] fra tutte le combinazioni che si potranno scegliere, le più feconde saranno quelle formate da elementi tratti da settori molto distanti. Non intendo dire che per inventare sia sufficiente mettere insieme oggetti quanto più possibile disparati: la maggior parte delle combinazioni che si formerebbero in tal modo sarebbero del tutto sterili. Ma alcune di queste, assai rare, sono le più feconde di tutte.
[…] Quel che più lascia colpiti è il fenomeno di queste improvvise illuminazioni, segno manifesto di un lungo lavoro inconscio precedente […] a proposito delle condizioni in cui avviene il lavoro inconscio, vi è un’altra osservazione da fare: esso è impossibile, e in ogni caso rimane sterile, se non è preceduto e seguito da un periodo di lavoro cosciente.
Le ispirazioni improvvise […] non avvengono mai se non dopo alcuni giorni di sforzi volontari, che sono sembrati completamente infruttuosi […] come vanno le cose, allora? Tra le numerosissime combinazioni che l’io subliminale ha formato alla cieca, quasi tutte sono prive di interese e senza utilità; ma proprio per questo motivo non esercitano alcuna influenza sulla sensibilità estetica: la coscienza non arriverà mai a conoscerle. Soltanto alcune di esse sono armoniose – utili e belle insieme». (Jules Henri Poincaré – Scienza e metodo – Einaudi, 1997 – a cura di Claudio Bartocci)
In sintesi, Poincaré parla di creatività come della capacità di unire elementi preesistenti in combinazioni nuove, che siano utili, e dice che il criterio intuitivo per riconoscere l’utilità della combinazione nuova è "che sia bella". Ovviamente non sta parlando di bellezza in senso strettamente estetico, ma di qualcosa che ha a che fare con l’eleganza così come la intendono i matematici: armonia, economia dei segni, rispondenza funzionale allo scopo.
La definizione di Poincaré è valida per le scienze, le arti, la tecnologia. Individua il fenomeno-creatività, dice in che cosa consiste (una "produzione di nuove combinazioni utili") e come lo si ottiene (attraverso un processo che prevede l’"unione di elementi preesistenti"). Indica anche presupposti, condizioni e risultati del processo.
• Presupposti: niente si crea dal niente (si parte da "elementi preesistenti": qualcosa che c’è già)
• Condizioni: è necessaria una specifica capacità (unire elementi) che può essere applicata a qualsiasi argomento, e deve unirsi a un’altra capacità, quella di selezionare, tra tutti i disponibili, gli elementi giusti da combinare. L’abilità nel selezionare presenta, a sua volta, quattro aspetti:
1. competenza: per individuare gli elementi che vanno uniti bisogna conoscerli. (Pasteur: le hasard favorise l’esprit preparé).
2. intuizione (e forse anche istinto): permette di fare una scelta funzionale tra molte opzioni disponibili, anche quando non è possibile valutare in modo esauriente la complessità di tutte le variabili in gioco.
3. esperienza: sviluppa l’intuizione e affina l’istinto.
4. tenacia: si procede per prove ed errori. È faticoso, può essere frustrante (Thomas Edison: genius is one per cent inspiration and ninety-nine per cent perspiration. Accordingly, a "genius" is often merely a talented person who has done all of his or her homework)
• Risultati: c’è una prima caratteristica necessaria (le combinazioni prodotte devono essere nuove), e c’è un criterio per stabilire se la novità prodotta ha valore creativo (che le combinazioni trovate siano, oltre che nuove, anche utili è la condizione necessaria e sufficiente).
Le categorie di nuovo e utile spiegano l’essenza dell’atto creativo: superare le regole (il nuovo) per istituire una migliore regola condivisa (l’utile).
Insomma, Poincaré istituisce una norma semplice e generale – è qualcosa che i matematici sanno fare molto bene – che riconduce la multiformità dei gesti creativi possibili alla formula
C = n u
In sostanza la creatività è il prodotto di una quantità di "nuovo" e di una quantità di "utile". Le quantità possono variare da "moltissimo" a "poco". Questo, fra l’altro, dà conto del motivo per cui alcune forme o espressioni di creatività ci appaiono intuitivamente più rilevanti di altre: la loro novità o la loro utilità, o entrambe le caratteristiche, sono davvero alte.
In ogni caso novità e utilità devono essere compresenti, e non possono essere uguali a zero: in totale assenza di novità, o di utilità, non possiamo definire "creativa" un’idea.
Consulta l’articolo originale
Gioco da IPRASE Trentino
Lupo e lepre
Dinamica: In questo gioco siamo nei panni di un povero leprotto che deve scappare dal lupo cattivo. Per essere salvi dobbiamo raggiungere la riva opposta del mare saltando su dei barili. Per ogni salto dobbiamo risolvere mentalmente delle operazioni aritmetiche. La difficoltà dell’operazione e la velocità del lupo possono essere impostate dall’utente in base al proprio livello di partenza. Questo gioco, impostato ai massimi livelli di difficoltà può rappresentare una sfida anche per una mente allenata e veloce.
Abilità: Risolvere le operazioni correttamente e velocemente.
Contenuto: Calcolo mentale rapido
Età: Da 7 anni in poi
Ti interessano i giochi di matematica? Da’ un’occhiata a questi libri:
 Il mistermind si può giocare anche con i numeri, utilizzando carta e penna. E’ un gioco di logica più che di aritmetica. Occorre osservare e dedurre le giuste conclusioni in base alle informazioni che si hanno. Di seguito si illustra come si gioca con carta e penna a questo semplice gioco logico e matematico.
Il mistermind si può giocare anche con i numeri, utilizzando carta e penna. E’ un gioco di logica più che di aritmetica. Occorre osservare e dedurre le giuste conclusioni in base alle informazioni che si hanno. Di seguito si illustra come si gioca con carta e penna a questo semplice gioco logico e matematico.
Il Master Mind numerico si gioca in due giocatori.
Ogni giocatore avrà un foglietto e una penna.
Ciascun giocatore sceglie segretamente un numero di 4 cifre che non abbia cifre ripetute e non cominci con la cifra 0.
Numeri che si possono scegliere: 1234 – 2537 – 9067
Numeri che non si possono scegliere: 0123 – 1122 – 23454
Ciascun giocatore divide in due colonne il foglio e scrive nella colonna di sinistra il proprio numero segreto, nella colonna di destra scrive i tentativi che farà per indovinare il numero dell’avversario.
A turno i giocatori comunicano all’avversario un numero di quattro cifre che rispetti le condizioni del gioco. L’altro giocatore segna nella colonna di sinistra, sotto il proprio numero segreto, il numero detto dall’avversario e lo confronta con il proprio numero. Per ogni cifra indovinata che occupa esattamente la posizione il giocatore comunica un “quadrato”; per ogni cifra indovinata che non è nella posizione giusta comunica un “cerchio”.
Per esempio, se il numero chiamato dall’avversario è 1243 ed il numero segreto è 5013 il punteggio è un “1 quadrato e 1 cerchio” perché è stato indovinato il numero 3 nella posizione corretta ed è stato indovinato il numero 1 ma non nella posizione corretta.
Ragionando sui punteggi ottenuti un giocatore può chiamare dei numeri opportuni e dopo alcuni tentativi riesce a indovinare il numero.
Vince chi indovina il numero con meno chiamate. Se i due giocatori indovinano il numero dell’avversario nello stesso numero di chiamate, il gioco finisce pari.
Vediamo, come esempio, l’inizio di una partita.
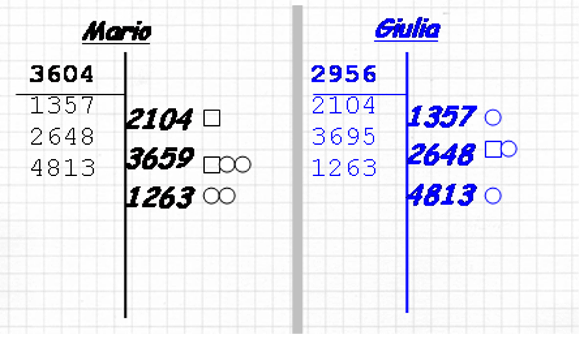
• Mario ha scelto come numero segreto 3604.
• Giulia ha scelto come numero segreto 2956.
• Mario chiama il numero 2104; Giulia risponde “1 quadrato”, infatti Mario ha indovinato il numero 2 nella posizione giusta.
Ciascun giocatore si segna la chiamata che ha fatto e il punteggio ottenuto: Mario che ha chiamato segna il numero nella colonna di destra; Giulia che ha ricevuto la chiamata lo segna sotto il proprio numero segreto, in modo da confrontarlo facilemente e dare le risposte senza sbagliare.
• Giulia chiama il numero 1357; Mario risponde "1 cerchio", infatti Giulia ha indovinato il numero 3 ma non nella posizione giusta.
E così via
Un rombo ha un angolo ampio 60° e la diagonale maggiore lunga 51.96 cm. Calcolare il perimetro e l’area del rombo.
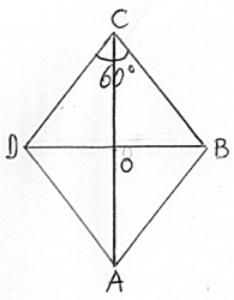 Il triangolo $OBC$ è un triangolo rettangolo particolare: è metà di un triangolo equilatero.
Il triangolo $OBC$ è un triangolo rettangolo particolare: è metà di un triangolo equilatero.
Le sue misure sono nella seguente relazione:
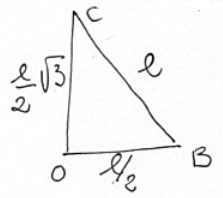 $bar(CO) = 25.9$, $bar(OB) = 25.98/sqrt(3)$, $bar(CB) = 51.96/sqrt(3)$.
$bar(CO) = 25.9$, $bar(OB) = 25.98/sqrt(3)$, $bar(CB) = 51.96/sqrt(3)$.
Di conseguenza il perimetro misura $4 cdot bar(CB) = 4 cdot (51.96 / sqrt(3))$
L’area sarà infine:
$bar(DB)cdot bar(CA) / 2 = 51.96 / sqrt(3) cdot 51.96 cdot (1/2)$
Nel triangolo ABC rettangolo in C, la retta della bisettrice BP relativa all’angolo B interseca in Q la perpendicolare in A ad AB. Dimostrare che APQ è un triangolo isoscele.

Una piramide retta ha per base un triangolo isoscele avente la misura della base di $8,4\ dm$ e l’altezza di $5,6\ dm$; sapendo che l’altezza della piramide misura $2,8\ dm$, calcola l’area della superficie totale della piramide.
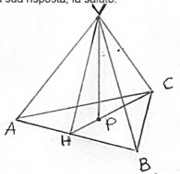 $ bar(AB) = 8.4\ dm$, $ bar(CH) = 5.6\ dm$, $ bar(VP) = 2.8\ dm$.
$ bar(AB) = 8.4\ dm$, $ bar(CH) = 5.6\ dm$, $ bar(VP) = 2.8\ dm$.
Superficie di base:
$ (8.4 xx 5,6) / 2 = 23.52 $
Per calcolare l’apotema, considera il triangolo $ABC$ del secondo disegno. 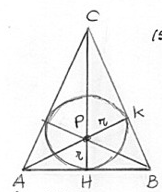
I triangoli $ CHB $ e $ CKP $ sono simili quindi
$ CP text(:) PK = CB text(:) HB $ e si ha:
$ CP = 5,6 – r $
$ PK = 2 $
$ HB = 4.2 $
$ CB = sqrt(CH^2+HB^2) = sqrt(31.36 + 17.64) = 7 $
e quindi abbiamo:
$ (5.6 – r) : r = 7 : 4.2 $
$ (5.6 -r + r) : r = (7 + 4.2) : 4.2 $
$ 5.6 : r = 11.2 : 4.2 $
$ r = (5.6 xx 4.2) / 11.2 = 2.1 $
Ora ritorna alla piramide e considera il triangolo rettangolo $ VHP $.
L’apotema $ bar(VH) = sqrt(bar(VP)^2+bar(HP)^2) = sqrt(7.84+4.41) = 3.5 $
Si ha allora:
$ text(Superficie laterale) = (text(perimetro di base) xx text(apotema)) / 2 = (8.4+7+7) xx 3.5/2=39.2 $
$ text(Superficie totale) = 23.52 + 39.2 = 62.72 $
Su un tavolo ci sono quattro sfere. Ognuna di esse tocca il piano del tavolo e le altre tre sfere. Tre di esse hanno il raggio di 10cm. Determina il raggio della quarta sfera.

Il rettangolo $ABCD$ ha il perimetro ed il lato $AB$ lunghi rispettivamente $268 cm$ e $6 dm$. Sul lato $DC$ si è preso il punto $P$ tale che la misura del segmento $DP$ superi quella di $PC$ di $52 cm$, e si è congiunto $P$ con $A$ e $B$.
Calcola l’area e la misura del perimetro di ciascuno dei tre triangoli in cui il rettangolo è diviso.
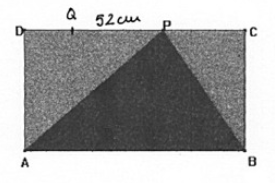 Il segmento $DP$ si compone di due parti: $DQ = PC$ e $QP = 52 cm$.
Il segmento $DP$ si compone di due parti: $DQ = PC$ e $QP = 52 cm$.
Poiché $bar(AB) = bar(DC) = 60 cm$, sottraendo $52 cm$ otteniamo $8 cm$, che è la misura di $bar(DQ)$ e $bar(PC)$ insieme. Quindi $bar(PC) = 4 cm$, $bar(DP)=56 cm$.
Per calcolare $bar(DA)$ dividiamo per due il perimetro e sottriamo $bar(AB)$:
$bar(DA) = 134 cm – 60 cm = 74 cm$.
Per calcolare $bar(AP)$ applichiamo il teorema di Pitagora al triangolo $ADP$.
Per calcolare $bar(PB)$ applichiamo il teorema di Pitagora al triangolo $PCB$.
Con queste informazioni possiamo calcolare i perimetri dei tre triangoli.
Abbiamo infine:
$text(Area(ADP)) = (bar(AD)cdot bar(DP))/2$
$text(Area(PCB))= (bar(PC)cdot bar(CB))/2$
$text(Area(APB))= text(Area rettangolo) – text(Area(ADP)) – text(Area(PCB))$

Bisogna dividere un bastone lungo 184 cm in tre parti in modo che la seconda parte superi la prima di 8 cm e la terza superi la seconda di $24$ cm. Quanto è lunga ciascuna parte?
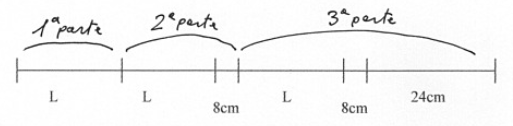 Per calcolare il valore di $L$ ci affidiamo alla figura. Abbiamo:
Per calcolare il valore di $L$ ci affidiamo alla figura. Abbiamo:
$184 cm – 8 cm – 8 cm – 24 cm = 144 cm$
$L = 144/3 cm = 48 cm$
Un trapezio isoscele di perimetro 40 cm è circoscritto ad una circonferenza di raggio radical21. Determinare le misure dei suoi lati

Dimostrare che, se le proiezioni dei lati di un trapezio sopra una retta parallela alle basi sono congruenti, il trapezio è isoscele 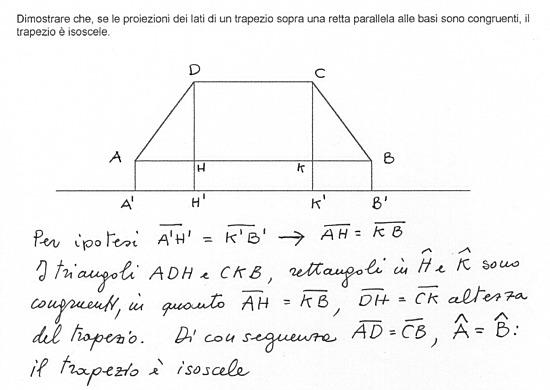
 Sono state pubblicate le prime lezioni del corso di scacchi di Veriano Veracini. Un corso semplice per chi vuole imparare i fondamenti per giocare a scacchi.
Sono state pubblicate le prime lezioni del corso di scacchi di Veriano Veracini. Un corso semplice per chi vuole imparare i fondamenti per giocare a scacchi.
Per giocare a scacchi con altri amici di Matematicamente

Emma Castelnuovo, L’Officina matematica, ragionare con i materiali, La Meridiana, 2008, pp. 166
L’Officina matematica raccoglie nove lezioni di Emma Castelnuovo e documenta sei anni di esperienza delle attività laboratoriali presso la Casa-laboratorio di Cenci nel comune di Amelia (TR).
"Guardo, osservo e poi passo dal concreto all’astratto, cioè matematizzo il fenomeno osservato", con queste parole Castelnuovo spiega il significato e il ruolo della matematica nel processo di osservazione e di comprensione del mondo. Nelle lezioni presentate in questo libro ci sono diverse attività-problemi che partono dall’osservazione concreta di semplici fatti ottenuti utilizzando i cosiddetti materiali poveri (pezzi di spago, blocchetti di argilla, sbarrette, elastici, ecc.). Rettangoli formati con lo stesso pezzo di spago hanno lo stesso perimetro, la misura della loro area genera una curva, la parabola, che è la stessa curva che descrive una palla da gioco; triangoli formati con lo stesso pezzo di spago formano invece un’ellisse che è la stessa figura che calpestiamo quando camminando per strada mettiamo il piede sull’ombra di un segnale stradale circolare.
Il ruolo del ‘materiale’ nella scoperta matematica è uno dei temi cari alla ricerca di Castelnuovo: mettere le mani in pasta, sui materiali per andare verso l’astrazione. L’autrice dà un percorso storico a questo modo di procedere (dalla duplicazione del cubo di Menecmo al metodo meccanico di Archimede, a Galileo) per giustificarne l’efficacia come metodo didattico; un metodo che qualche decennio fa appariva non solo povero didatticamente ma anche fuorviante rispetto all’astrattezza dei fondamenti logici e puri della matematica. L’anziana ricercatrice testimonia, con la sua lunghissima attività, che partendo da materiale semplicissimo si possono costruire tutti i capitoli della matematica. Tra i problemi semplici, quelli di massimo e minimo permettono di attraversare tanti livelli di astrattezza della matematica. In una delle lezioni pubblicate in questo libro, ne presenta due che si possono affrontare con ragazzi della secondaria di primo grado: con un filo di ferro si costruiscono dei poligoni, quale di essi ha l’area massima? Con una certa quantità di argilla si possono formare dei solidi (cubo, cilindro, piramide) tutti dello stesso volume, quale di questi ha la superficie minima?
Per quanto attiene più da vicino l’aritmetica, Castelnuovo si sofferma sui problemi di proporzionalità, che nascono nella notte dei tempi, dal famoso Papiro di Rhind, passando per Talete, Archimede, Brahmagupta, e che fino a oggi sono sempre stati incontrati dall’uomo, soprattutto nelle situazioni di lavoro e in generale nell’economia. Sulla proporzionalità inversa, presenta un’esperienza fisica legata alla capillarità, nella quale si utilizzano due vetri uniti da un lato con delle mollette e dall’altro separati da stuzzicadenti; i vetri vengono messi a contatto con dell’acqua colorata posta in una bacinella; l’acqua risale lungo i vetri per capillarità formando un’iperbole. Questa semplice esperienza fa vedere il profondo legame non solo tra l’aritmetica (proporzionalità inversa) e la geometria (iperbole) ma anche tra la matematica, la fisica, la botanica e le scienze in generale.
La geometria, osserva Castelnuovo, ha subìto negli ultimi anni una caduta di interesse da parte sia degli studenti, sia degli insegnanti, i quali senza particolari direttive da parte di nessuno si sono tacitamente uniti in questo rifiuto, molto spesso per pigrizia di entrambi: difficoltà nell’apprendere e difficoltà nell’insegnare. Occorre evidentemente recuperare questo interesse, perché la geometria ha un ruolo formativo indispensabile. Lo studio attraverso i materiali e l’osservazione del movimento potrebbero, a suo avviso, portare l’apprendimento di questa disciplina su un piano più pratico e osservativo, facilitandone il ritorno nella scuola.
Nella seconda parte del libro sono pubblicate quattro attività laboratoriali dell’Officina matematica: 1. Spago ed elastico; 2. Dal problema dell’ubriaco alla teoria dell’evoluzione di Darwin; 3. Una matematica …a tutto tondo; 4. Angoli e ombre. Conclude il libro una conversazione tra Franco Lorenzoni ed Emma Castelnuovo.
Il sito dell’editore www.lameridiana.it
Il sito della Casa-laboratorio di Cenci
Il capitolo 4 del libro scaricabile liberamente
Una parte dell’intervista a Castelnuovo
 In questo breve documento si discute la scoperta dei buchi neri, la loro possibile formazione nell’universo, gli scienziati e gli astronomi che hanno contribuito alla loro scoperta, infine una rapida rassegna su alcune scoperte recenti su buchi neri, mini buchi neri, buchi bianchi, buchi verme.
In questo breve documento si discute la scoperta dei buchi neri, la loro possibile formazione nell’universo, gli scienziati e gli astronomi che hanno contribuito alla loro scoperta, infine una rapida rassegna su alcune scoperte recenti su buchi neri, mini buchi neri, buchi bianchi, buchi verme. Si dice buco nero una concentrazione di materia associata a un campo gravitazionale cosi intenso da far richiudere lo spazio tempo su se stesso; da un tale campo gravitazionale nulla potrà sfuggire neppure la luce. I buchi neri si hanno in concentrazioni di materia a densità molto elevate; cioè una quantità piccola di materia compressa a densità elevatissime; oppure il contrario, si ha questo fenomeno, nel caso in cui, la quantità di materia sia grandissima a una densità relativamente piccola.
Il primo a suggerire la possibile esistenza dei buchi neri fu John Michell (1724-1793) Geologo, Astronomo e sacerdote inglese; presento le sue idee relative all’esistenza di possibili “stelle oscure”; era il mese di Novembre dell’anno 1783. Michell fondava i propri calcoli sulla teoria della gravitazione universale di Newton e sulla teoria corpuscolare della luce; infatti egli supponeva che le particelle della luce erano anch’esse, come ogni altro oggetto della vita comune, gli oggetti evidenti e macroscopici, soggette alla gravità. Ole Rømer (astronomo danese, 1644-1710), aveva misurato la velocità della luce. Michell riusci a determinare quanto doveva essere grande un oggetto con la stessa densità del Sole per avere una velocità di fuga maggiore alla velocità della luce (il discorso è riferito alla velocità di fuga che deve avere un corpo celeste per sottrarsi all’azione gravitazionale di un buco nero): un oggetto del diametro 500 volte quello del Sole avrebbe una velocità di fuga > c. Se tali oggetti esistessero, la luce non potrebbe uscirne, ed essi sarebbero bui.
Il matematico e astronomo francese Pierre Simon de Laplace (1749-1827) arrivo nel 1796 alla stessa conclusione di Michell il quale affermo “se qualche corpo luminifero dovesse orbitare attorno a essi noi potremo, forse, dal moto di questi corpi orbitanti, inferire l’esistenza dei corpi centrali”. In altre parole, suggerì l’idea che i buchi neri possono essere scoperti molto facilmente qualora facessero parte di sistemi binari.
Nell’Ottocento la nozione dei buchi neri non fu presa molto in considerazione. Nel secolo scorso, quando gli astronomi compresero la teoria della relatività generale di Albert Einstein (1879-1955), capirono che esisteva un altro modo di produzione di buchi neri. Uno dei primi astronomi ad analizzare le implicazioni della teoria di Einstein fu Karl Schwarzchild.
La teoria della relatività generale spiega la forza di gravità come causa, come perché, si ha un incurvatura dello spazio-tempo. Schwarzchild calcolo matematicamente la geometria dello spazio-tempo attorno a una massa sferica, questi calcoli esprimono il fatto che ogni massa ha un raggio critico chiamato raggio di Schwarzchild; corrispondente a una distorsione dello spazio-tempo. Il raggio di Schwarzchild per un corpo celeste è dato dalla formula:
$R_s=(2GM)/c^2$
$G$ è la costante di gravitazione universale
$M$ è la massa del corpo celeste
$c$ è la velocità della luce nel vuoto
I calcoli di Schwarzchild dimostrarono che se un oggetto può essere compresso fino a occupare uno spazio sferico $R_s$, tali corpi sarebbero isolati dall’universo esterno diventando buchi neri. Le scoperte astronomiche degli anni 20 e 30 hanno permesso di conoscere nuovi corpi, quali le nane bianche e l’evoluzione stellare, in particolare quando una stella si spegne essa è destinata a contrarsi ancora, una tale contrazione può dare origine alla formazione di una stella di neutroni; agli inizi queste teorie non furono accettate, nel 1967 fu pero dimostrata l’esistenza delle stelle di neutroni grazie alla scoperta delle prime pulsar; tali scoperte riaccesero l’interesse per i buchi neri, poiché la stelle di neutroni sono destinate a trasformarsi in buchi neri.
Recenti studi teorici dimostrano che i buchi neri sono definiti da tre sole proprietà: la massa, la carica elettrica e il momento angolare. È probabile che i buchi neri siano dotati di un moto di rotazione e non abbiano carica. Si pensa oggi giorno che i buchi neri siano prodotti dall’esplosione di grandi stelle come supernovae; e qualsiasi residuo compatto di supernova di massa inferiore a tre masse solari poteva formare una stella di neutroni; se questo valore fosse maggiore di tre masse solari si avrebbe un buco nero. Se un buco nero ruotasse in orbita attorno a una stella, le strapperebbe materia formando un disco di materiale caldissimo; la temperatura nel disco diventerebbe talmente elevata da poter emettere raggi X, l’emissione dei raggi X è dovuta all’ assorbimento di materia stellare nel buco nero; ciò può rendere visibile il buco nero. Nel 1994 un sistema noto come V404 Cygni è diventato il migliore candidato a buco nero finora noto; esso è formato da una stella di circa 0,7 masse solari intorno a una sorgente di raggi X di circa 12 masse solari. Un buco nero isolato è nero e non rilevabile attraverso l’effetto di lente gravitazionale. Molte stelle dunque, come abbiamo detto in precedenza, dovrebbero terminare la loro vita come stelle di neutroni o buchi neri. Possono esistere buchi neri situati al centro di una galassie attive e i quasar costituenti, i buchi neri, la loro fonte di energia principale, tali corpi sono chiamati buchi neri di massa ultrastellare. Nel 1994 il telescopio Hubble scopri un corpo a forma di disco di materiale caldissimo orbitante nella galassia M87 (la galassia M87 è distante circa 15 milioni di parsec dalla nostra). Sono state studiate le velocità orbitali del disco ed esse costituiscono la prova decisiva che esso è soggetto al controllo gravitazionale di un buco nero di massa enorme. Sempre nell’ anno 1994 alcuni astronomi dell’università di Oxford hanno identificato un buco nero di massa stellare nel sistema V404Cygni; qui l’uomo a potuto “pensare” il buco nero con maggior precisione, provando che esso ha una massa di 12 masse solari ed è accompagnato da una stella di 0,7 masse solari. Questo prova l’esistenza dei buchi neri. Esistono oltre ai buchi neri veri e propri; dei mini buchi neri chiamati anche buchi neri primordiali, essi sono minuscoli buchi neri che posso essersi formati durante il Big Bang; non si ha la certezza che tali corpi microscopici (paragonabili al nucleo di un atomo), di grande massa (dell’ordine $10^11 Kg$) possano esistere realmente, ma sarebbe molto difficile dimostrare che non esistono (anche se la maggior parte dei teorici dubita l’esistenza dei mini buchi neri).
Questa ipotesi fu resa popolare negli anni settanta da Stephen Hawking il quale disse che tali oggetti devono evaporare fino ad esplodere dando origine alla radiazione di Hawking; si stima l’esplosione di questi corpi nei nostri giorni, cioè 15 miliardi di anni circa dopo l’esplosione cosmica; il fondo di raggi gamma è pero troppo debole da indurre a pensare che tali corpi possano esplodere oggi e in passato.
Altri buchi neri esistenti sono i buchi neri di Schwarzchild; cioè buchi neri non ruotanti e privi di carica elettrica, essi rappresentano il tipo più semplice di buco nero; inoltre un altro tipo di buco nero derivante da corpi privi di carica elettrica ma ruotanti a differenza dei buchi neri di Schwarzchild, sono i buchi neri di kerr; essi sono buchi neri nati dal collasso di una stella in rotazione, tali buchi neri sono forse i più corrispondenti a quelli reali, sono quelli diciamo più familiari; aventi una forma ad anello e con due orizzonti degli eventi distinti, (l’orizzonte degli eventi è quella superficie immaginaria attorno a un buco nero, la velocità di fuga dall’orizzonte degli eventi è pari alla velocità della luce); la rotazione del buco nero di kerr si forma nell’Ergosfera cioè una regione di trascinamento il cui confine tende a combaciare ai poli con l’orizzonte degli eventi, mentre e più lontano all’equatore, cioè la distanza tra ergosfera e orizzonte degli eventi è massima all’equatore e minima ai poli.
Altri tipi importanti, ma meno noti, di buchi sono i wormhole (i buchi verme), e i buchi bianchi. I wormhole sono dei veri e propri tunnel cosmici, essi rappresentano a livello intuitivo una “scorciatoia” da un punto dell’universo a un altro. Non si ha la certezza dell’esistenza di un wormhole, se esistessero tali tunnel cosmici creerebbero una serie di problemi, tra i quali anche il viaggio nel tempo. Molti fisici teorici dubitano dell’esistenza di tali tunnel, pensando che ci sia qualcosa nelle leggi fisiche che proibisca l’esistenza di tali buchi verme.
Un altro corpo celeste misterioso di cui vale la pena parlare è il buco bianco. I buchi bianchi sono un ipotetica controparte dei buchi neri, essi sono una regione dalla quale emergono materia ed energia entrando nell’universo. Anche sui buchi bianchi non si ha la certezza che essi possano esistere realmente, perché non sono mai stati identificati in modo certo; nonostante ciò diversi fisici e astronomi contemporanei ritengono che l’universo si sia formato da un buco bianco. Poco tempo dopo la scoperta dei quasar, si suggerì l’ipotesi che la violenta espulsione di energia associata a questi oggetti astronomici simili a stelle, potrebbe essere un esempio di attività dei buchi bianchi, anche se gli astronomi hanno rifiutato sempre questa idea. La materia che fuoriesce da un buco bianco ha un energia molto elevata tale da acquistare uno spostamento verso l’azzurro, trasformandosi in antimateria. Una congettura sostiene che i buchi bianchi siano l’altro estremo dei buchi neri, connessi da cunicoli spazio-temporale, un cunicolo spazio-temporale può essere considerato una sorta di metropolitana cosmica che collega due buchi neri o un buco nero e un buco bianco; tuttavia questa congettura è molto vaga. Riassumendo i buchi bianchi sono la perfetta controparte dei buchi neri, come abbiamo trattato da tali corpi niente può entrare ma da essi esce materia.
BIBLIOGRAFIA E SITOGRAFIA.
• John Griblin Enciclopedia di Astronomia e Cosmologia Garzanti.
• http://www.arrigoamadori.com/lezioni/ricerca.php
Un quadrato ha il perimetro di cm 48 ed è equivalente ai 12/35 di un trapezio isoscele avente la base maggiore e la base minore rispettivamente uguali al triplo e alla metà del perimentro del quadrato.
Calcolare
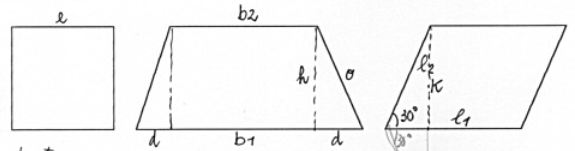
Quadrato Perimetro = $48\ cm$, da cui $l = 48/4\ cm = 12\ cm$. La diagonale del quadrato è allora: diagonale = $l \cdot sqrt(2) = 12 \cdot sqrt(2)\ cm$, cioè circa $16,97\ cm$.
Si ha poi che l’area del quadrato vale: $A_q = l^2 = 144\ cm^2$.
Trapezio isoscele
Base maggiore: $b_1 = 3 \cdot 48 (text(perimetro quadrato) = 144$;
Base minore: $b_2 = 48 / 2 = 24\ cm$;
Area trapezio: $A_t = 35/12 \cdot Aq = 35/12\cdot 144\ cm^2 = 420\ cm^2$.
Nota che $35/12$ è il reciproco della frazione data.
Per il segmento abbiamo: $d = (b_1 – b_2) / 2 = 120 / 2 = 60\ cm$.
Per calcolare il lato obliquo del trapezio applichiamo il teorema di Pitagora: $theta = sqrt(h^2+d^2) = sqrt(25+360) ~= 19.62\ cm$.
Il perimetro del trapezio è dato da $b_1 + b_2 + 2theta$.
Parallelogramma
$l_1 = 12\ cm$; $l_2 = 2/3 \cdot 12 = 8\ cm$.
Per calcolare l’altezza $k$ del parallelogramma osserviamo che il triangolo a sinistra è metà di un triangolo equilatero.
$k = 1/2 l_2 = 4\ cm$.
Area parallelogramma = base per altezza = $12 \cdot 4\ cm = 48\ cm$.
In questo video si mostra come un cilindro interseca un piano perpendicolare all’asse
{avi}animazioni/cilindro_piano3{/avi}
In questa animazioni si mostra come un cilidro si interseca con un piano parallelo all’asse del cilindro.
{avi}animazioni/cilindro_piano2{/avi}
In questa animazione si mostrano le intersezioni di un cilindro con un piano inclinato
{avi}animazioni/cilindro_piano{/avi}
I meridiani si ottengono dall’intersezione tra la sfera e un piano
{avi}animazioni/meridiani{/avi}
Le sezioni si una sfera con un piano
{avi}animazioni/sfera_piano{/avi}
 Cerchio, ellisse, parabola e iperbole si possono ottenere sezionando un doppio cono (tipo clessidra) con un piano. In queste animazioni tridensionali si evidenzia questa caratteristica.
Cerchio, ellisse, parabola e iperbole si possono ottenere sezionando un doppio cono (tipo clessidra) con un piano. In queste animazioni tridensionali si evidenzia questa caratteristica.
Il cerchio come intersezione di un cono con un piano
{avi}animazioni/cerchio{/avi}
L’ellisse come intersezione di un cono con un piano
{avi}animazioni/cerchio{/avi}
La parabola come intersezione di un cono con un piano
{avi}animazioni/cerchio{/avi}
L’iperbole come intersezione di un cono con un piano
{avi}animazioni/cerchio{/avi}
Visita la sezione delle animazioni di matematica
{avi}animazioni/parabola{/avi}
In questo video si mostra come la parabola può essere ottenuta intersecando un piano opportunamente inclinato con un cono.
{avi}animazioni/iperbole{/avi}
In questa animazione si mostra come un’iperbole può essere ottenuta dall’intersezione di un piano opportunamente inclinato con un cono.
{avi}animazioni/ellissi{/avi}
Un ellissi è una sezione conica, ossia si ottiene dall’intersezione di un cono con un piano.
Il cerchio si ottiene dalla sezione di un cono con un piano perpendicolare al suo asse.
 E’ appena uscito presso l’Editore Bulgarini Firenze, l’edizione 2008 del libro Temi svolti di matematica, Eserciziario per l’Esame di Stato del Liceo Scientifico di Ordinamento e PNI, gli autori sono A. Bernardo, M. Pedone, N. De Rosa. Il libro presenta delle schede teoriche di riferimento per lo studente che deve affrontare la maturità e i temi svolti per l’esame di matematica dal 2007 al 2001. Il costo è di 13,50 euro e si può acquistare nelle librerie scolastiche.
E’ appena uscito presso l’Editore Bulgarini Firenze, l’edizione 2008 del libro Temi svolti di matematica, Eserciziario per l’Esame di Stato del Liceo Scientifico di Ordinamento e PNI, gli autori sono A. Bernardo, M. Pedone, N. De Rosa. Il libro presenta delle schede teoriche di riferimento per lo studente che deve affrontare la maturità e i temi svolti per l’esame di matematica dal 2007 al 2001. Il costo è di 13,50 euro e si può acquistare nelle librerie scolastiche. Modulo per il calcolo della riduzione delle coordinate equatoriali (AR, δ) dall’epoca J2000.0 alla data in esame
(effetto della precessione degli equinozi – nuovo sistema standard FK5/J2000.0)