 In prossimità degli esami di stato impara a riconoscere i grafici delle funzioni elementari. Le funzioni elementari sono le basi per lo studio dell’analisi matematica.
In prossimità degli esami di stato impara a riconoscere i grafici delle funzioni elementari. Le funzioni elementari sono le basi per lo studio dell’analisi matematica.
| Grafici di funzioni elementari |
 In prossimità degli esami di stato impara a riconoscere i grafici delle funzioni elementari. Le funzioni elementari sono le basi per lo studio dell’analisi matematica.
In prossimità degli esami di stato impara a riconoscere i grafici delle funzioni elementari. Le funzioni elementari sono le basi per lo studio dell’analisi matematica.
| Grafici di funzioni elementari |
 Imagine Cup è il più importante concorso di information tecnlogy dedicato a studenti, a livello mondiale, organizzato da Microsoft. Il tema di quest’anno è "Immagina un mondo dove la tecnologia permette uno sviluppo sostenibile".
Imagine Cup è il più importante concorso di information tecnlogy dedicato a studenti, a livello mondiale, organizzato da Microsoft. Il tema di quest’anno è "Immagina un mondo dove la tecnologia permette uno sviluppo sostenibile".
.
Salve ragazzi,
vi presento brevemente Imagine Cup, il più importante concorso di information tecnlogy dedicato a studenti, a livello mondiale.
Imagine Cup è un’iniziativa mondiale nata per incoraggiare gli studenti a utilizzare la loro immaginazione, passione e creatività per cambiare il mondo. La sfida lanciata da Microsoft è semplice: cercare soluzioni a problemi concreti attraverso le nuove tecnologie. Nel corso degli anni la competizione ha riscosso sempre più successo, raccogliendo idee, progetti e adesioni entusiastiche.
Il tema che impegnerà le menti più brillanti per quest’anno è "Immagina un mondo dove la tecnologia permette uno sviluppo sostenibile".
Il concorso è diviso per categorie ed è possibile iscriversi ad una o più categorie tra quelle aperte.
Allo stato attuale le uniche ad essere ancora aperte sono Photogry e Software Design. Le categorie spaziano su ogni skill: ci sono quelle più tecniche, più tecnologiche e quelle artistiche… La più importante è senza dubbio Software Design ed è l’unica che prevede la finale italiana, dove chi vince vola a Parigi per la finale mondiale. Per tutte le altre categorie, invece, i primi 10 mondiali vanno a Parigi.
Le categorie in breve:
Software Design. Nella competizione software design, gli studenti creano applicazioni reali e dinamiche utilizzando tecnologia Microsoft. I partecipanti devono dimostrare innovazione con il Microsoft .NET Framework e la piattaforma Microsoft Windows quando sviluppano, testano e creano applicazioni. Questa competizione è la sola che prevede delle finali italiane che permetteranno al miglior progetto di accedere alle finali mondiali. La data ultima per la partecipazione al progetto è quella del 20 Aprile.
Embedded Development. Le soluzioni tecnologiche stanno diventando piccole, più portatili e stanno generando un grande impatto nelle nostre vite quotidiane. La Windows Embedded Student Challenge cerca di spingere gli studenti al di là del desktop, sviluppando la loro creatività per costruire soluzioni hardware e software usando Windows CE e l’hardware fornito. Team di tre-quattro partecipanti e un mentore costruiranno un prototipo che deve migliorare a risolvere problemi reali.
Game Development. Quest’anno "Xbox 360 Games for Change Challenge" rappresenterà per la prima volta una categoria di sviluppo giochi di Imagine Cup. Utilizzando il nuovo XNA Game Studio Express gli studenti avranno la possibilità di mostrare i loro giochi a tutto il mondo. Non vinceranno solo soldi, ma avranno l’opportunità di mostrare al team manageriale di Microsoft i loro giochi e la possibilità di vedere il loro progetto pubblicato Xsu box LIVE Arcade service o sul sito MSN Games. Il primo posto vincerà anche l’opportunità di diventare apprendista presso il Microsoft’s Interactive Entertainment Business.
Project Hoshimi. I programmatori hanno la possibilità di competere direttamente online con studenti di tutto il mondo per vedere chi crea un programma più velocemente. Il gioco richiede capacità di coding e algoritmiche per creare strategie per un gioco a più partecipanti. Il risultato sarà un gioco in tempo reale a tre dimensioni visibile a tutti.
IT Challenge. Gli studenti devono sviluppare e mantenere sistemi IT che siano efficienti, funzionali, robusti e sicuri. Inoltre, gli studenti devono dimostrare professionalità con networks, databases e servers, le aree di analisi e decision making in ambienti IT.
Algorithm. Attraverso una serie di enigmi, codici e puzzles algoritmci, gli studenti scoprono e sviluppano algoritmi. Lo scopo è quello di mostrare abilità nella risoluzione di problemi reali utilizzando algoritmi.
Photography. Usando la fotografia, gli studenti devono cercare di comunicare una storia restando in tema con lo sviluppo sostenibile e usando la foto come mezzo di comunicazione.
Short Film. Questa categoria evidenzia l’arte di raccontare storie. Gli studenti sono invitati a sviluppare una prospettiva su Imagine Cup attraverso media digitali. Dal concetto e storyboard all’editoria, i partecipanti devono creare un film che catturi l’audience e che abbia un forte significato.
Interface Design. Creatività e usabilità sono gli ingredienti necessari per creare una buona user-interface, che contribuisca a una applicazione Web. Questa categoria permette a disegnatori di tutto il mondo di creare interfacce che guardano al futuro. I partecipanti devono creare una applicazione collegata al tema di Imagine Cup mostrando le loro qualità.
Come detto però le uniche due categoria ad essere aperte sono: Software Design e Photography.
 Molto spesso, in gruppi di una ventina o più di persone (come una classe, ad esempio) si nota con sorpresa che due persone compiono gli anni lo stesso giorno dell’anno. E’ veramente così sorprendente?
Molto spesso, in gruppi di una ventina o più di persone (come una classe, ad esempio) si nota con sorpresa che due persone compiono gli anni lo stesso giorno dell’anno. E’ veramente così sorprendente?
Una risposta ce la fornisce la teoria della probabilità, secondo la quale, già in un gruppo formato da 23 persone si ha più del 50% delle probabilità che due persone siano nate lo stesso giorno dell’anno.
Il risultato, a prima vista, può sembrare incredibile, dato che i giorni dell’anno sono ben 365, davvero molti di più di quelle “misere” 23 persone!
Eppure vedremo che un semplice calcolo matematico mostra che ciò che accade è proprio questo.
In teoria delle probabilità si usa spesso il trucchetto di “girare al contrario” il problema, calcolando, anziché la probabilità dell’evento a cui si è interessati, quella dell’evento opposto. Questo è uno dei casi in cui la cosa funziona, dato che il calcolo diventa immediatamente molto più semplice.
Calcoliamo quindi la probabilità che 23 persone compiano gli anni in giorni differenti. Consideriamo le persone una per volta:
1. La prima persona può compiere gli anni in qualsiasi giorno;
2. La seconda ha probabilità 364/365 di compiere gli anni in un giorno diverso dalla prima;
3. La terza ha probabilità 363/365 di compiere gli anni in un giorno diverso dalle prime due, e così via…
In totale avremo quindi una probabilità complessiva di 364/365 * 363/365 * … * 343/365 = 0.492702.
A questo punto diventa immediato calcolare la probabilità che due persone nel gruppo abbiano lo stesso giorno di nascita dalla semplice sottrazione 1 – 0.492702 = 0.507298, corrispondente appunto a poco più del 50%.
La prossima volta che ad una festa con una trentina o più di partecipanti scopriremo che due persone sono nate lo stesso giorno non avremo quindi più da meravigliarci, ma solo… da festeggiare!
 La matematica è sinonimo di razionalità, la magia invece è legata indissolubilmente all’irrazionalità e al mistero. Eppure questi due estremi qualche volta si incontrano. Un piccolo trucco per sbalordire (o per meravigliare) i tuoi amici e farli scervellare un po’.
La matematica è sinonimo di razionalità, la magia invece è legata indissolubilmente all’irrazionalità e al mistero. Eppure questi due estremi qualche volta si incontrano. Un piccolo trucco per sbalordire (o per meravigliare) i tuoi amici e farli scervellare un po’.
.
.
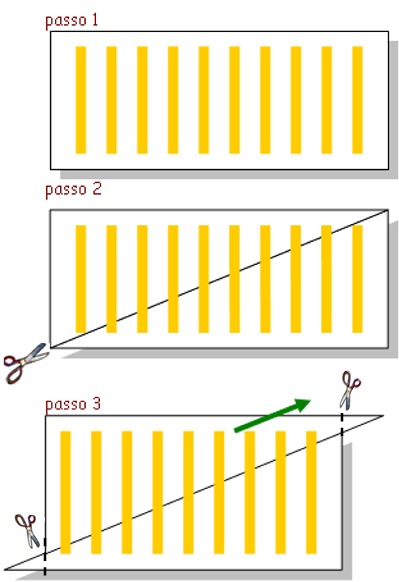 Passo 1
Passo 1
Su un cartoncino disegna 10 bastoncini verticali come nella figura; usa un pennarello spesso in modo che i bastoncini siano ben visibili, dirai che sono 10 lingotti d’oro.
Fai contare i lingotti d’oro ai tuoi amici.
Dopo che li hanno contati puoi dire la parola magica supersegreta, che non ti posso dire perché è veramente segreta.
Passo 2
La magia: senza farti vedere, ritaglia il cartoncino lungo la diagonale.
Passo 3
Fai scivolare la parte triangolare superiore del cartoncino come mostrato nella figura, finché il primo lingotto si sovrapporrà al pezzo inferiore del secondo lingotto. Ritaglia i triangolini ai bordi in modo che il cartoncino torni a essere un rettangolo.
Fai contare ora i lingotti d’oro: sono diventati 9.
Che si è fregato il lingotto?
Se questo giochino ti è piaciuto ti consiglio di leggere il libro di Sarcone e Waeber, Matemagica, giochi d’ingegno con la matematica, Edizioni La Meridiana, Molfetta (BA), 2005.
# Sgabello.
# Script addattato da:
# http://ayapin.film.s.dendai.ac.jp/~matuda/Gnuplot/pm3d.html
#
f1(x,y)=x**6+3*y**2*x**4+(3*y**4-4*y**2)*x**2+y**6
C=1
set pm3d hidden 100
set style line 100 lt 6
set ticslevel 0
set nokey
set xrange[-C:C]
set yrange[-C:C]
set isosamples 30,30
set hidden3d
set size square
set contour
set cntrparam levels discrete 0.05,0,-0.05,-0.5
set terminal jpeg medium size 480,480
set output "sgabello.jpeg"
splot -f1(x,y) w pm3d, -f1(x,y)
set output
# Conchiglia.
# Script addattato da:
# http://ayapin.film.s.dendai.ac.jp/~matuda/Gnuplot/pm3d.html
#
cot(x)=1/tan(x)
x(u,v)=D*(A*sin(b)*cos(u)+R*cos(v+phi)*cos(u+W)-R*sin(m)*sin(v+phi)*sin(u+W))*exp(u*cot(a))
y(u,v)=(-A*sin(b)*sin(u)-R*cos(v+phi)*sin(u+W)-R*sin(m)*sin(v+phi)*cos(u+W))*exp(u*cot(a))
z(u,v)=(-A*cos(b)+R*sin(v+phi)*cos(m))*exp(u*cot(a))
D=1;a=4*pi/9;b=2*pi/9;phi=11*pi/36;m=pi/18;W=pi/6;A=25;R=16
L=300
set xrange[-L+50:L+50]
set yrange[-L:L]
set zrange[-1.5*L:0.5*L]
set pm3d explicit
set palette rgb 8,7,27
unset colorbox
set parametric
set hidden3d
set ticslevel 0
set size square
set view 65,30,2.4,1
set vrange[0:2*pi]
unset key
unset border
unset xtics
unset ytics
unset ztics
set isosamples 96,24
set urange[-2*pi:4*pi]
set terminal jpeg medium size 480,480
set output "conchiglia.jpeg"
set multiplot
splot x(u,v),y(u,v),z(u,v) w pm3d
splot x(u,v),y(u,v),z(u,v) lt 5
unset multiplot
set output
# Bottiglia di Klein a forma di 8.
# Script addattato da:
# http://ayapin.film.s.dendai.ac.jp/~matuda/Gnuplot/pm3d.html
#
x(u,v)= cos(u)*(cos(u/2)*cos(v)+sin(u/2)*sin(2*v)+3.0)
y(u,v)= -sin(u)*(cos(u/2)*cos(v)+sin(u/2)*sin(2*v)+3.0)
z(u,v)= -sin(u/2)*cos(v)+cos(u/2)*sin(2*v)
set pm3d explicit
set palette rgb 3,7,9
unset colorbox
set parametric
set hidden3d
set ticslevel 0
unset key
set isosamples 40,40
set view 65,70,1,1
set urange[-0.5*pi:1.5*pi]
set vrange[-pi:pi]
set zrange[-2:2]
set terminal jpeg medium size 480,480
set output "klein.jpeg"
set multiplot
splot x(u,v),y(u,v),z(u,v) w pm3d
splot x(u,v),y(u,v),z(u,v) lt 6
unset multiplot
set output
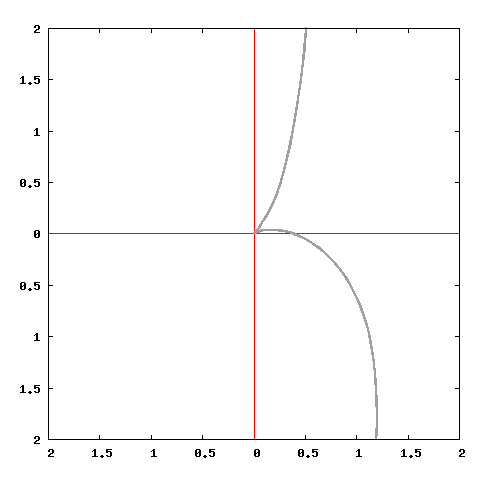
set terminal png medium size 480,480
set output "cissoide.png"
set polar
set size ratio 1
set zeroaxis ls 1
set xrange [-2:2]
set yrange [-2:2]
a = 1.2
plot a*(sin(t-a/2)**2/cos(t)) notitle with line lc "black" lw 2
set output
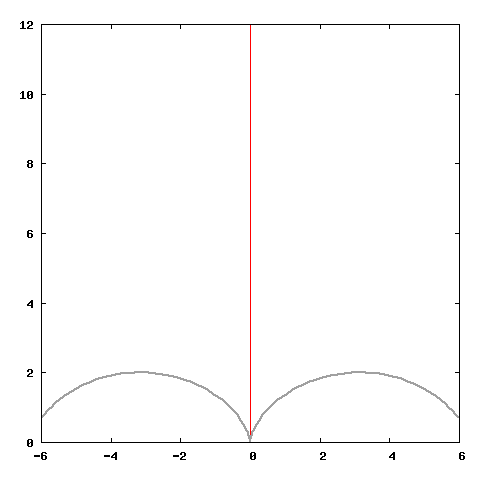
set terminal png medium size 480,480
set output "cicloide.png"
set parametric
set size ratio 1
set zeroaxis ls 1
set xrange [-6:6]
set yrange [0:12]
plot t-sin(t), 1-cos(t) notitle with line lc "black" lw 2
set output

set terminal png medium size 480,480
set output "catenaria.png"
set size ratio 1
set zeroaxis ls 1
set xrange [-2:2]
set yrange [0:4]
e = exp(1)
plot (e**x+e**(-x))/2 notitle with line lc "black" lw 2
set output
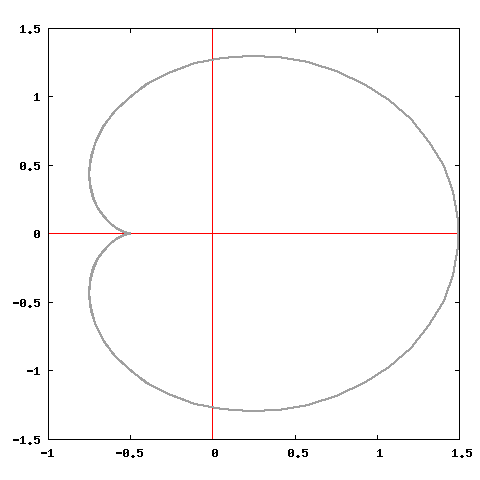
set terminal png medium size 480,480
set output "cardioide.png"
set parametric
set size ratio 1
set zeroaxis ls 1
plot cos(t)+0.5*cos(2*t),sin(t)+0.5*sin(2*t) notitle with line lc "black" lw 2
set output
Tesina ipertestuale sulla storia delle particelle elementari
I primi studi sull’atomo
Quante persone osservando i piccolissimi granelli di una manciata di sabbia possono aver pensato ai più piccoli e rigidi granelli che costituiscono tutte le forme di materia? L’affermazione esplicita che la materia sia composta da particelle indivisibili chiamata atomi la rintracciamo nell’antica città d’Abdera, sulle coste della Tracia. Là, verso la fine del V secolo a.C., i filosofi greci Leucippo e Democrito insegnavano che tutta la materia è fatta di atomi e di spazio vuoto. […]
Modelli atomici
Le particelle elementari
L’origine delle particelle: il Big Bang
Alcune applicazioni
Scarica la tesina completa (.zip 1,3 MB)
Premessa
Fin dall’antichità la luna è una presenza costante nella vita e nell’immaginario degli uomini, è il simbolo più classico e suggestivo del paesaggio naturale. Lo dimostrano anche i tanti modi di dire, entrati nell’uso comune, che fanno riferimento alla luna: avere la luna di traverso, lunatico, faccia da luna piena, promettere la luna e così via.
Il primo calendario, costruito in Mesopotamia osservando la regolarità delle fasi lunari, risale al III millennio a.C.
Numerose e antiche credenze attribuiscono alla luna un influsso sui comportamenti umani, sulla crescita delle piante, sul periodo delle nascite e addirittura sulla riuscita o meno dell’imbottigliamento del vino.
Poiché la luna cresce, cala e scompare per poi rinascere è anche l’immagine dell’eterno ritorno e ha sempre rappresentato nei miti e in diverse religioni il ciclo morte/rinascita. E’ stata quindi associata alla fecondità, ma anche, al contrario, al mondo dell’aldilà.
La variabilità del suo aspetto e la faccia nascosta ne fanno anche un simbolo di ambiguità, avvolgendola di mistero, basti pensare ai rituali magici durante il plenilunio, alle leggende sui licantropi o agli uomini-tigre. Simbolo dell’Impero turco, la mezza luna figura oggi sulle bandiere nazionali di numerosi paesi di religione islamica. Infine, quella della luna è stata la prima superficie non terrestre calpestata dagli uomini (20 luglio 1969).
Io sono sempre stato affascinato dall’astronomia, una materia troppo vasta, però, per una tesina. Ho quindi circoscritto l’argomento al nostro satellite, che mi consente di approfondire diversi temi nelle singole materie d’esame.
Dopo l’esame del Canto notturno di un pastore errante dell’Asia (italiano), ho affrontato il tema del rapporto uomo-natura in Lucrezio (latino), poi ho messo a confronto il pessimismo leopardiano con quello di Schopenhauer (filosofia). Per il filosofo tedesco si può superare il dolore del mondo attraverso il nirvana, liberandosi dalla volontà di vivere.
Ben diversa è la posizione del movimento futurista: la volontà di vivere è sinonimo di “azione, slancio, passione, audacia gioconda e festosità”. Ho preso allora in considerazione il manifesto di Marinetti, Uccidiamo il chiaro di luna e il quadro di Balla, Lampada ad arco (storia dell’arte). Per i futuristi la guerra era il momento culminante dell’esuberanza sociale, un dispendio giocoso di energie e furono fra i più accesi interventisti prima dell’entrata in guerra dell’Italia.
Ho quindi analizzato il primo conflitto mondiale (storia), con una breve appendice sulla conquista della luna e la competizione USA-URSS negli anni della guerra fredda. I romantici inglesi e, in particolare To the Moon di Percy Bysshe Shelley sono l’argomento che ho approfondito per inglese, mentre ho scelto la descrizione del sistema solare per scienze.
Tesina completa da scaricare (.pdf 770KB)
 "Quando a ottobre presentai ai miei professori l’argomento della mia tesina rimasero attoniti, bisogna ammettere che non è un argomento abituale, di solito si cercano temi più “ordinari” per presentarsi al colloquio d’esame. Io non amo le cose “normali” per cui era necessario per me trovare un soggetto trattabile, ma allo stesso tempo un po’ stravagante; un argomento che potesse, insomma, rispecchiare il mio carattere e il mio modo di essere." Tesina multidisciplinare sulle bolle di sapone.
"Quando a ottobre presentai ai miei professori l’argomento della mia tesina rimasero attoniti, bisogna ammettere che non è un argomento abituale, di solito si cercano temi più “ordinari” per presentarsi al colloquio d’esame. Io non amo le cose “normali” per cui era necessario per me trovare un soggetto trattabile, ma allo stesso tempo un po’ stravagante; un argomento che potesse, insomma, rispecchiare il mio carattere e il mio modo di essere." Tesina multidisciplinare sulle bolle di sapone.
INDICE
Premessa
Minimi e massimi nello studio di funzione
J. A. F. Plateau e le superfici minime
Reti minime
La proprietà isoperimetrica
La curvatura
La tensione superficiale
Cellule, virus e bolle medicinali
Bolle nella letteratura: Aldo Palazzeschi la leggerezza; Italo Calvino la leggerezza è una virtù della letteratura che deve essere mantenuta nei secoli;
Francese: Alphonse Lamartine
Inglese: Flatland: a romance of many dimensions, by Edwin Abbot
Le bolle nell’arte: Jean Baptiste Siméon Chardin (1699-1779) Les bulles de Savon; la Souffleuse de Savon di Boucher, Manet Gamin faisant bulles de savon.
Architettura: la fondazione di Cartagine, Frei Otto e le tensile structures, la visione utopica.
Bibliografia
PREMESSA
L’IDEA
Quando a ottobre presentai ai miei professori l’argomento della mia tesina rimasero attoniti, bisogna ammettere che non è un argomento abituale, di solito si cercano temi più “ordinari” per presentarsi al colloquio d’esame. Io non amo le cose “normali” per cui era necessario per me trovare un soggetto trattabile, ma allo stesso tempo un po’ stravagante; un argomento che potesse, insomma, rispecchiare il mio carattere e il mio modo di essere.
La traduzione da teorico a pratico della mia idea non è stata semplice, chi mi ha supportato (o sopportato?!) in questi mesi lo sa bene: oltre a trovare i “collegamenti interdisciplinari” era per me doveroso riuscire a creare qualcosa di semplice da seguire e che riuscisse a coinvolgere anche chi non ama la matematica e le materie scientifiche, perni di questa tesina.
L’ARGOMENTO
Le bolle di sapone sono uno degli argomenti più interessanti in molti settori della ricerca scientifica: dalla matematica alla chimica, dalla fisica alla biologia, ma non solo, anche nell’architettura e nell’arte, nel design e perfino nella pubblicità.
Un fisico britannico di fine ‘800, Charles Vernon Boys, in un suo affascinante libro sulle bolle di sapone scrisse: «ci sono più cose in una comune bolla di sapone di quante non ne sappia immaginare chi si limiti a vederla come un gioco». Effettivamente per i matematici le bolle di sapone sono modelli di una geometria delle forme molto stabili, e per gli artisti sono il simbolo della vanità, della fragilità delle ambizioni umane, della vita stessa.
Le bolle, non solo di sapone, le troviamo ovunque: nell’industria alimentare, nella schiuma da barba, nei serbatoi delle navette spaziali, nelle plastiche, nel nostro corpo,…
L’ESECUZIONE
Questa tesina è nata con la volontà di trattare come argomento principale un tema relativo alla matematica, materia spesso odiata dagli studenti forse perché, per così dire, è impantanata in un linguaggio di simboli estranei alla maggior parte di noi; almeno l’arte la si può vedere, anche la filosofia e la letteratura, per quanto a volte oscure, hanno se non altro il vantaggio di poter essere espresse in una lingua!
Nella stesura delle parti relative a materie come fisica, biologia, arte e architettura non ho approfondito troppo la questione, ho dato solo nozioni fondamentali, spesso usando anche termini impropri che però “rendevano meglio l’idea”, per poter almeno far intuire la complessità delle bolle (non solo di sapone) e dei principi su cui si basano, tralasciando tanti altri campi quali l’ottica, le superfici metalliche, la scienza dei materiali, la gastronomia (ebbene sì, tante prelibatezze e tante bevande hanno il loro aspetto caratteristico grazie alla schiuma!),…
La letteratura merita invece una spiegazione a sé, poiché nei miei propositi iniziali c’era l’idea di trovare autori che avessero utilizzato di frequente la metafora della bolla di sapone, poi, visto che veramente pochi scrittori hanno scelto come simbolo le bolle, mi sono chiesta quali immagini potessero suggerire le bolle di sapone, la risposta che mi sono data (con l’aiuto delle mie professoresse) è stata “leggerezza e precarietà”, per questo gli autori italiani e francesi scelti, sono autori che hanno dedicato parte delle loro opere ad una di queste due sensazioni. Per la letteratura inglese, invece, sono tornata a parlare della sfera in termini più matematici e, forse, più surreali e fantasiosi.
BIBLIOGRAFIA
GENERICO
S. Perkowitz, La teoria del cappuccino, traduzione di S. Coyaud dall’originale Universal Foam, Garzanti, 2001
A. Beutelspacher, Matematica da tasca, traduzione di A. Peroni dall’originale Mathematik für die Westentesche, Ponte alle Grazie, 2003
ARTE & ARCHITETTURA
C. Bassi, www.artdreamguide.com
FISICA
M. Ageno, Elementi di fisica, Boringhieri, 1972
FRANCESE
K.A. Blüher, Oeuvres & Critiques, Paul Valéry Perspectives de la réception, Ed. Jean-Michel Place, 1984
J. Robinson, L’analyse de l’esprit dans les cahiers de Valéry, Librairie José Corti, 1963
J. Charpier, Essai sur Paul Valéry, Ed. Pierre Seghers, 1958
AA. VV., Centenaire de Paul Valéry, Europe – revue littéraire mensuelle, juillet 1971
M. Parent e J. Levaillant, Paul Valéry contemporain, Ed. klincksieck, 1974
INGLESE
E. Abbott, Flatlandia – Racconto fantastico a più dimensioni, traduzione di M. d’Amico dall’originale Flatland – A romance of many dimensions, Adelphi, 2002
ITALIANO
I. Calvino, Lezioni americane – Sei proposte per il prossimo millennio, Mondatori, 2002
A. Palazzeschi, Il Codice di Perelà, SE, 1991
Piero Pieri, Il Codice di Perelà di Palazzeschi. L’altro del fumo, l’oltre dell’uomo, Fascicolo edito dalla casa editrice Gedit e frutto di una collaborazione con il Dipartimento di Italianistica dell’Università di Bologna, 2003
MATEMATICA
M. Cazzanelli, K. Soraruf, I. Tamanini, Matematica e bolle di sapone, un viaggio alla scoperta di strutture geometriche e principi variazionali, Fascicolo del Laboratorio di Ricerca sui Materiali e i Metodi per la Didattica e la Divulgazione della Matematica del Dipartimento di Matematica dell’Università degli studi di Trento, 2001
R. Courant e H. Robbins, Che cos’è la matematica?, traduzione di L. Ragusa Gilli dall’originale What is mathematics? An elementary approach to ideas and methods, Universale Bollati Boringhieri, 2002
M. Emmer, Matematica e cultura 2002, Springer, 2003 AA. VV., Matemilano – percorsi matematici in città, Springer, 2003
I. Petersen, Il turista matematico, Biblioteca Scientifica Sansoni, 2003
Scarica la tesina Bolle di sapone.
 Applicazione delle trasformazioni di Schwarz-Christoffel per la progettazione assistita dal calcolatore di dispositivi elettromeccanici. Tesi di laurea Ingegneria, Dipartimento di Ingegneria Elettrica.
Applicazione delle trasformazioni di Schwarz-Christoffel per la progettazione assistita dal calcolatore di dispositivi elettromeccanici. Tesi di laurea Ingegneria, Dipartimento di Ingegneria Elettrica.
Introduzione
La trasformazione di Schwarz-Christoffel (basata sull’omonima formula ricavata in modo indipendente dai due matematici tedeschi attorno al 1860), e, in generale, il metodo della trasformazione conforme, sono stati per un lungo periodo un capitolo molto importante dell’analisi complessa, con svariate applicazione nei campi della fisica e della matematica.
Uno dei maggiori pregi è senza dubbio la possibilità di fornire, quando possibile, la soluzione analitica ad un problema di campo elettrico o magnetico in domini per lo più aperti, insieme alla possibilità di studiare come cambi questa soluzione al variare dei parametri che figurano nel problema.
Sfogliando però i testi disponibili in letteratura ci si rende subito conto di come una soluzione analitica sia estremamente difficile da ottenere in casi significativi per le applicazioni, anche se semplici: ci si imbatte immediatamente in pagine piene di calcoli lunghi e complicati, in cui compaiono integrali ellittici ed iperellittici, e loro espressioni in termini di funzioni ellittiche di Jacobi, riduzioni ad integrali di Legendre o sviluppi in serie degli integrandi.
Queste difficoltà, assieme all’impossibilità di gestire un’ampia casistica di condizioni al contorno per i problemi, hanno portato al progressivo abbandono del metodo nel corso degli anni ’70, soppiantato dall’introduzione del calcolatore e dagli emergenti metodi delle differenze finite (FDM) e degli elementi finiti (FEM), che hanno spostato (con successo) su un piano puramente numerico il modo di affrontare certi problemi: in particolare, il potente e versatile FEM è stato accuratamente ottimizzato per l’esecuzione su calcolatore, e viene oggi utilizzato, in tutte le sue varianti, per le simulazioni in quasi tutti i campi dell’ingegneria, dall’analisi elettromagnetica a quella meccanica, fino alla conduzione del calore.
La disponibilità di una grande potenza di calcolo, oltre ad essere impiegata per metodi già noti (si pensi ad esempio al tensore degli sforzi di Maxwell), ha determinato la comparsa di altri sofisticati strumenti di analisi fino a pochi anni fa impensabili in pratica per la mole di operazioni che richiedono, fra cui le reti neurali (NNM), le reti di riluttanze (RNM) e gli algoritmi genetici (GA): queste tecniche, utilizzate singolarmente o associate, consentono un’accurata ottimizzazione dei parametri caratterizzanti un sistema, migliorandone notevolmente le prestazioni.
Queste metodologie presentano tuttavia dei costi di implementazione in termini di tempo, talvolta indubbiamente onerosi: anche utilizzando un hardware di ultima generazione, la verifica di un’idea di progettazione e la relativa ottimizzazione può richiedere giorni interi di calcolo. Si presenta quindi la necessità di disporre di tecniche che, senza pretendere di ottenere risultati estremamente accurati, consentano di verificare rapidamente la validità di un progetto, magari avvicinandosi ad un punto di ottimo, per poi condurre un’analisi più ”fine” con altri strumenti.
Nel corso degli anni la trasformazione di Schwarz-Christoffel non è stata del tutto abbandonata: si è però preferito indirizzare gli sforzi ad un approccio numerico, in modo da affrontare problemi analiticamente intrattabili, e ciò ha determinato la comparsa di un certo numero di pacchetti software destinati a questo scopo. Sulla scia del successo di questi ultimi, e nel tentativo di venire a capo di difficoltà di natura numerica incontrate in questa prima fase, la ricerca si è reindirizzata sulle proprietà algebriche e geometriche della trasformazione, giungendo a produrre algoritmi (ancora oggi in fase di studio ed approfondimento) che permettono di trattare problemi fino a poco tempo fa ritenuti inadatti o addirittura impossibili per un tipo di metodo che – precisiamolo – è di natura squisitamente geometrica.
Questo lavoro di Tesi sfrutta lo stato di conoscenza attuale sulle trasformazioni di Schwarz- Christoffel per cercare di capire se possano in qualche modo essere uno strumento di progettazione utile, e quindi venire incontro alle esigenze sopra discusse. Fermi restando certi limiti intrinseci nel metodo (come ad esempio la difficoltà di gestire le condizioni al contorno nei casi più generali), ci si chiede se si possa oggi impostare per mezzo di esso un’analisi che abbia insieme le caratteristiche dell’affidabilità e della velocità, rimandando ad altri strumenti la ricerca dell’accuratezza.
A tal fine nel corso dei capitoli vengono affrontati due problemi:
il primo, molto semplice, riguarda la forma che dovrebbero avere le armature di un condensatore piano per mantenere il campo elettrico il più uniforme possibile fra esse; un algoritmo di ottimazione sfrutta la trasformazione di Schwarz-Christoffel per minimizzare l’errore commesso.
Il secondo problema, a cui sono dedicati gli ultimi due capitoli, per affrontare il quale vengono utilizzati i più moderni algoritmi di calcolo della trasformazione, si presenta in tutte le macchine rotanti a magneti permanenti: la coppia parassita d’impuntamento.
Scarica la tesi completa (3MB)
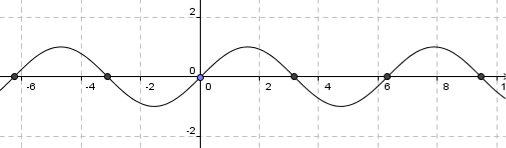
 $f(x)=x^2$ è una funzione pari, $f(-x)=f(x)$
$f(x)=x^2$ è una funzione pari, $f(-x)=f(x)$ 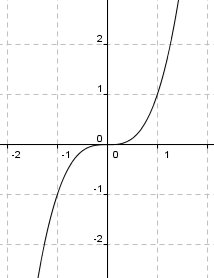 $f(x)=x^3$ è una funzione dispari, $f(-x)=-f(x)$
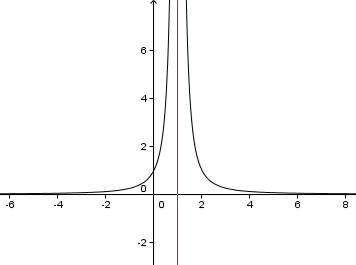
$f(x)=x^3$ è una funzione dispari, $f(-x)=-f(x)$ 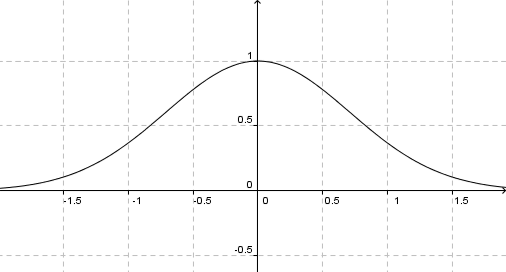 $f(x) = e^{-x^2}$ è pari
$f(x) = e^{-x^2}$ è pari 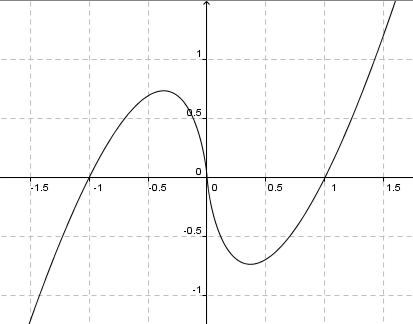 $f(x) = x*ln(x^2)$ è dispari,
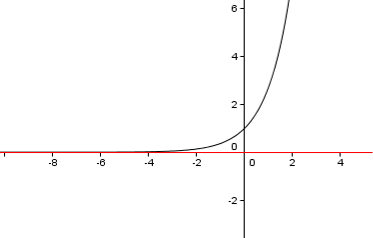
$f(x) = x*ln(x^2)$ è dispari, 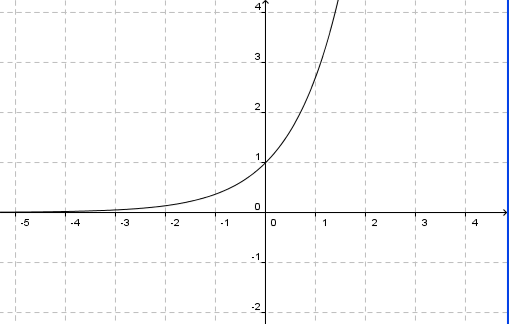 $f(x) = e^x$ non è né pari né dispari.
$f(x) = e^x$ non è né pari né dispari. 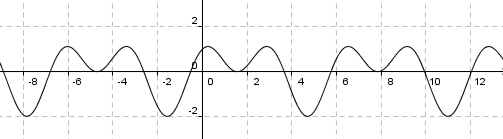
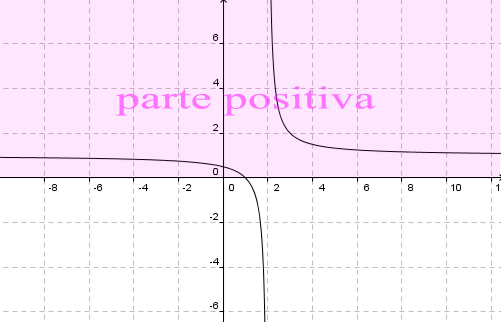
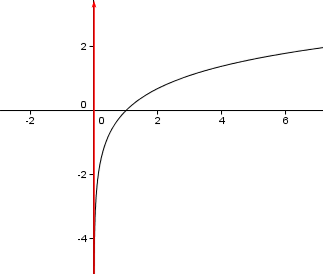
se $lim_{x o x_0^-} f(x) = +infty$ (o $-infty)$, allora la retta $x = x_0$ è un asintoto verticale sinistro;
se $lim_{x o x_0^+} f(x) = +infty$ (o $-infty)$, allora la retta $x = x_0$ è un asintoto verticale destro;
se $lim_{x o x_0} f(x) = +infty$ (o $-infty)$, allora la retta $x = x_0$ è un asintoto verticale (sia destro che sinistro).

 Misura con i ditloidi la tua flessibilità mentale e la tua creatività. 29=G di F in 1AB -> 29 sono i giorni di febbraio in un anno bisestile. Una specie di indovinelli matematici? Qualcosa di più e qualcosa di meno. Un linguaggio sintetico moderno, per anticipare i tempi. Vai alla sezione dei giochi matematici.
Misura con i ditloidi la tua flessibilità mentale e la tua creatività. 29=G di F in 1AB -> 29 sono i giorni di febbraio in un anno bisestile. Una specie di indovinelli matematici? Qualcosa di più e qualcosa di meno. Un linguaggio sintetico moderno, per anticipare i tempi. Vai alla sezione dei giochi matematici.
Vai alla sezione dei ditloidi.
Tesina multimediale per gli esami di maturità scientifica sull’Intelligenza artificiale.
Ipertesto multimediale di Mario Di Bacco elaborato per il concorso Arte e Scienza espressione di creatività umana come dialogo tra culture.
Contenuti e metodologie
Il lavoro "Il Pensiero sulla Macchina – prospettive sull’IA" è un ipertesto multimediale che indaga gli aspetti più moderni del progresso nell’ambito della realizzazione di tecnologie intelligenti. Tali tecnologie, che vengono raggruppate sotto la disciplina nota come Intelligenza Artificiale (I.A.), comprendono in realtà numerosi studi su più versanti del sapere umano.
Dall’analisi di tali aspetti giungono numerosissimi spunti che vertono sul progresso e sul suo significato, sulle difficoltà nella costruzione di enti pensanti, sull’etica della creazione di macchine intelligenti, sui motivi che spingono l’uomo (consciamente o inconsciamente) a competere con un sogno che porta avanti da secoli. All’Intelligenza Artificiale sono connessi anche aspetti molto interessanti, come le visioni del rapporto uomo-macchina da parte di autori di letteratura italiani e stranieri e da artisti del nostro secolo.
Il lavoro è completato con le opinioni e gli spunti di riflessione dati da creazioni cinematografiche attuali e soprattutto da studiosi contemporanei della materia, che dagli aspetti concreti del loro lavoro e dalle proprie aspirazioni personali, giungono a proporre delle vere e proprie filosofie moderne ed estremamente interessanti.
I contenuti del lavoro sono originali, basati sull’esame e la rielaborazione di fonti autorevoli e sulla produzione personale. Istituto Liceo Scientifico "E. Fermi" Sulmona (AQ).
L’ipertesto è stato realizzato interamente e personalmente da Mario Di Bacco.
L’ipertesto è costruito con la struttura di un sito web, che consente ormai una eccellente facilità d’uso grazie alla diffusa tecnologia che utilizza. Per realizzarlo sono state utilizzate varie forme espressive, quali testi, immagini, animazioni, musiche e video. Queste sono state elaborate con programmi professionali e semiprofessionali come editor html (Macromedia Dreamweaver MX), editor di animazioni vettoriali (Macromedia Flash MX), editor audio (Sound Forge, Acid Music…), editor di immagini (Corel Draw…). Mezzo fondamentale per la realizzazione del lavoro, negli aspetti della progettazione e del reperimento dei materiali, è stato la rete Internet.
Scarica la tesina multimediale
 La notte fra mercoledì 20 e giovedì 21 febbraio la Luna sparirà, oscurata dal cono d’ombra del nostro pianeta. L’INAF, Istituto Nazionale di Astrofisica, rivolge a tutti gli appassionati del cielo l’invito a inviare disegni e foto dell’eclissi: tutti i contributi saranno pubblicati e visibili in rete nella galleria multimediale dell’INAF.
La notte fra mercoledì 20 e giovedì 21 febbraio la Luna sparirà, oscurata dal cono d’ombra del nostro pianeta. L’INAF, Istituto Nazionale di Astrofisica, rivolge a tutti gli appassionati del cielo l’invito a inviare disegni e foto dell’eclissi: tutti i contributi saranno pubblicati e visibili in rete nella galleria multimediale dell’INAF.
Se una notte d’inverno un’eclissi di Luna… Reporter celesti per una notte
Ecco l’invito che l’INAF, l’Istituto Nazionale di Astrofisica, rivolge a tutte e tutti gli appassionati del cielo: inviare disegni e foto della prossima eclissi di Luna che avverrà nella notte fra mercoledì 20 e giovedì 21 febbraio prossimi.
Tutti i contributi saranno pubblicati e visibili in rete nella galleria multimediale dell’INAF www.guardacheluna.com
La notte fra mercoledì 20 e giovedì 21 febbraio la Luna sparirà, oscurata dal cono d’ombra del nostro pianeta. Un fenomeno molto suggestivo, quello dell’eclissi di Luna, che chiunque puògodersi in tutta tranquillità: a differenza di quanto avviene con le eclissi di Sole, infatti, osservare un’eclissi di Luna non comporta rischi per gli occhi, e non è necessaria alcuna strumentazione particolare.
Tempo permettendo, la si può seguire in ogni sua fase anche a occhio nudo, o con un semplice binocolo. Magari con l’ausilio di una tazza di caffé caldo, vistoche il fenomeno raggiungerà l’apice attorno alle quattro di notte! E se le condizioniatmosferiche lo permettono, durante la totalità il nostro satellite potrà assumere una bellissima colorazione rossa, tipica solo dei momenti di eclissi.
Proprio perché si tratta di un evento al quale tutti possono prendere attivamente parte, e anche sulla scia del successo dell’iniziativa del 2007 (quasi un milione di contatti e oltre 800 fotografie inviate), l’INAF propone a chiunque abbia voglia di condividere le proprie immagini e le proprie emozioni relative all’eclissi — dagli studenti agli appassionati — di diventare «reporter celesti per una notte», inviando fotografie e disegni da raccogliere nella galleria multimediale INAF.
Per partecipare, caricare le proprie immagini e anche per avereinformazioni dettagliate su come prepararsi al meglio all’evento, è sufficiente andare sul sitowww.guardacheluna.com. L’eclissi avrà inizio verso le 01.35, quando la Luna toccherà la penombra (cioè il bordo esternodell’ombra terrestre). Più tardi il disco lunare comincerà a transitare attraverso l’ombra della Terra, e il bordo dell’ombra sarà ben visibile sulla faccia della Luna, che sparirà poco a poco.Alle 04.00 circa inizierà la fase di totalità, che durerà 51 minuti, poi piano piano la Luna sisposterà ancora nella penombra e
finalmente ne uscirà, alle 07.17: questo però avverrà quando la Luna sarà già sotto l’orizzonte. Il tramonto della Luna, infatti, avverrà poco dopo le 6:40. Il fenomeno dell’eclissi in tutto durerà quasi sei ore.
Per informazioni:
Ufficio comunicazione INAF, [email protected] , tel. 06.3553.3390
Altre risorse: I contributi inviati nel 2007 per l’evento «Quando la Luna sparì… io ero lì» sono ancora visibili in rete all’indirizzo http://www.media.inaf.it/galleries/mooneclipse/
Domenico Licchelli
Tesina di maturità ipertestuale e multidisciplinare sul tema del progresso
In senso generico, atto del progredire, avanzamento di qualsiasi genere, evoluzione, con l’andar del tempo. Per lo più include l’idea di un avvicinamento alla meta stabilita o anche di uno sviluppo, di un accrescimento graduale e continuo (talvolta in senso negativo).
Più comunemente, accostamento progressivo verso migliori condizioni, perfezionamento graduale, sviluppo verso forme più complete e soddisfacenti: progresso intellettuale, sociale, industriale, progresso della ricerca scientifica, della tecnica.
Con valore assoluto: evoluzione della società verso condizioni di vita e di civiltà sempre più avanzate ed adatte a soddisfare i bisogni fondamentali dell’uomo, attraverso la diffusione della cultura,l’applicazione pratica della scienza,il miglioramento delle condizioni morali e sociali.
In senso storico, il progresso, concetto secondo cui l’umanità si sviluppa e si muove sempre verso stadi più alti, in un procedere ascendente da gradi inferiori a gradi più elevati.
Scarica la tesina completa (.zip 3,4MB)
Tesina di maturità ipertestuale e multidisciplinare presentata all’esame per ITIS.
L’Ottocento è stato indubbiamente un secolo di grande innovazione nell’ambito scientifico e tecnico. Nella mia tesina ho trattato solo alcune delle numerose scoperte che hanno permesso all’uomo di compiere notevoli passi avanti e migliorare sensibilmente le proprie condizioni di vita. Con le equazioni di Maxwell ad esempio si compì il passaggio dalla fisica classica a quella moderna mentre nell’ambito della chimica vennero realizzati dispositivi (le pile e le batterie) in grado di generare una corrente continua la cui intensità rimane costante nel tempo. La pila di Daniell venne utilizzata per alimentare il telegrafo, primo mezzo di comunicazione che eliminava le distanze. Nell’ambito della biologia l’introduzione della teoria evoluzionistica di Darwin mise in crisi definitivamente quella della creazione divina.
Tali innovazioni tecnico-scientifiche ebbero origine soprattutto in Inghilterra dove, dalla fine del Settecento, si assisteva alla Rivoluzione Industriale: questo fenomeno non aveva solo trasformato radicalmente il modo di produzione ma aveva avuto delle importanti conseguenze sociali che inizialmente potevano far pensare ad un incessante progresso dell’umanità. Le classi sociali più elevate ne avevano infatti tratto notevoli benefici economici, anche se i lavoratori precipitavano pericolosamente nella miseria più profonda. Le condizioni di vita degli operai peggiorarono a seguito dell’inurbamento di masse di contadini in cerca di impiego, fenomeno che abbassava il costo della manodopera e riduceva i salari. Intere famiglie di operai vivevano in case dormitorio prive di servizi igienici e in condizioni di precarietà economica; ampiamente sfruttato era anche il lavoro minorile, per cui molti adolescenti non usufruivano del diritto all’istruzione e crescevano deboli e malati. Di fronte alla situazione sociale descritta si può parlare di effettivo progresso?
Lentamente gli operai presero coscienza di essere l’anello fondamentale della produzione e, di conseguenza, cercarono di partecipare più attivamente alla vita politica: proprio in questo momento iniziarono le lotte con cui gli operai volevano ottenere un maggior peso politico e volevano migliorare le condizioni di vita dei lavoratori.
A tal proposito i primi provvedimenti presi in diversi paesi europei (Italia compresa) contro il lavoro minorile risalgono proprio alla metà dell’Ottocento ma condussero a risultati solamente parziali: fino al 1902 in Italia potevano lavorare bambini dell’età di nove anni. L’analisi del contesto storico ottocentesco sottolinea dunque l’esistenza di numerose contraddizioni che mettono in crisi l’idea di progresso; la lettura di alcune opere letterarie mi ha portato a considerazioni analoghe nell’ambito della cultura europea e della letteratura italiana.
Scarica la tesina completa (.zip 7MB)
 Uno degli argomenti fissi dell’esame di matematica è il calcolo integrale. Spesso in classe non si svolgono molti esercizi su questo argomento e non se ne vedono i collegamenti con altre parti del programma. In questo lavoro si dà una breve premessa teorica sulla funzione integrale e si discutono alcuni quesiti dell’esame di stato.
Uno degli argomenti fissi dell’esame di matematica è il calcolo integrale. Spesso in classe non si svolgono molti esercizi su questo argomento e non se ne vedono i collegamenti con altre parti del programma. In questo lavoro si dà una breve premessa teorica sulla funzione integrale e si discutono alcuni quesiti dell’esame di stato.
tags: esame di stato, esame di matematica, esame di maturità, calcolo integrale, funzione integrale, quesiti maturità scientifica, temi svolti di matematica
 La figura della Terra
La figura della Terra
di Michele T. Mazzucato
Libreria Clup, Milano, 2003
Il libro di Michele Mazzucato propone un viaggio storico nell’esplorazione del nostro pianeta: una storia che comincia nella notte dei tempi, lì dove è possibile arrivare con i pochi documenti in nostro possesso, e si conclude con i satelliti artificiali.
In questi millenni si sono avvicendate teorie, si sono scontrati scienziati, sono state intraprese avventurose esplorazioni e soprattutto è stata creata tanta matematica per fornire gli strumenti teorici e pratici di questa esplorazione.
Attualmente, per ‘vedere’ la Terra dall’esterno, cioè dallo spazio, è sufficiente collegarsi ai siti Internet specialistici (p.e. http://www.fourmilab.ch/cgi-bin/uncgi/Earth ) ma il percorso che l’uomo ha fatto per giungere a questo semplice clic non è stato facile. Ripercorrerlo è un’esperienza emozionante e particolarmente istruttiva.
E’ pressoché impossibile dire, all’inizio della storia di questa esplorazione, quando la rappresentazione poetica e artistica diviene un vero e proprio modello matematico, secondo la concezione scientifica moderna. L’autore riporta diverse visioni cosmografiche antiche che probabilmente sono delle immaginazioni artistiche tipo l’universo di Dante.
Le misure di Eratostene di Cirene, sono invece la testimonianza di una cultura scientifica molto avanzata. Intorno al 240 a.C. circa, Eratostene, direttore del più importante centro di cultura del mondo ellenistico, la biblioteca d’Alessandria d’Egitto, misurando la differenza delle altezze del Sole tra Alessandria e Siene e tenendo conto della distanza stimata tra le due città, ricava una buona stima della misura della circonferenza della Terra.
Prima di vedere altri contributi scientifici significativi, bisogna attendere 19 secoli. Nel XVII secolo viene applicato il metodo della triangolazione per ottenere misure più precise del meridiano terrestre e per rilevare le anomalie nella forma della Terra. La triangolazione è un metodo di rilevamento che consiste nel collegare dei punti della superficie terrestre scelti in modo da formare un insieme di triangoli aventi a due a due un lato in comune.
Una serie di spedizioni in tutto il globo terrestre permisero tra i secoli XVII e XIX di conoscere in dettaglio le deformazione del globo terrestre: forma ellissoidale, schiacciamento, raggio polare, raggio equatoriale e tanti altri parametri. Il libro è semplice e appassionante da leggere, le conoscenze di matematica richieste non sono elevate, e può servire da stimolo per studiare formule e metodi matematici visti nella loro applicazione pratica. Nelle appendici sono riportate le formule più complesse e notizie storiche più dettagliate.
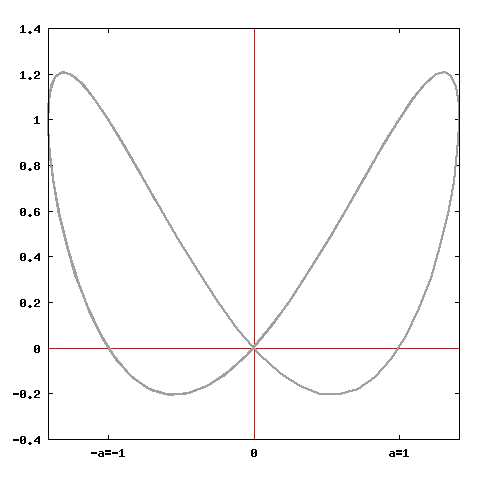
# Bisaccia.
# Equazione parametrica:
# x = a cos(t) – b sin(t)
# y = -x sin(t)
#
set terminal png medium size 480,480
set output "bisaccia.png"
set parametric
set size ratio 1
set zeroaxis ls 1
set xtics ("-a=-1" -1, "0" 0, "a=1" 1)
a = 1
b = 1
plot a*cos(t)-b*sin(t), -sin(t)*(a*cos(t)-b*sin(t))
notitle with line lc "black" lw 2
set output
 Il lungo cammino dell’uomo verso la scoperta e la conquista dell’infinito coincide con l’acquisizione della complementarietà tra due concezioni di esso: l’infinito potenziale, “negativo”, senza una fine, irrimediabilmente aperto e l’infinito Attuale, “positivo”, perfetto e chiuso, perché atto legittimo concepito dalla mente umana. Una tesina multidisciplinare per l’esame di maturità.
Il lungo cammino dell’uomo verso la scoperta e la conquista dell’infinito coincide con l’acquisizione della complementarietà tra due concezioni di esso: l’infinito potenziale, “negativo”, senza una fine, irrimediabilmente aperto e l’infinito Attuale, “positivo”, perfetto e chiuso, perché atto legittimo concepito dalla mente umana. Una tesina multidisciplinare per l’esame di maturità.
Indice
Filosofia
1 Da Pitagora a Euclide
2 L’infinito nel meccanicismo di Galilei
2.1 Il Paradosso dei quadrati
2.2 Il Paradosso della Ruota
3 Il criticismo kantiano
3.1 L’infinito sul piano teoretico: la ricerca del vero
4 Kant e Galilei
4.1 L’infinito sul piano etico: la ricerca del Sommo Bene
4.2 L’infinito sul piano del sentimento: il Sublime
5 Il Romanticismo
6 L’idealismo hegeliano
6.1 L’apriorità
6.2 La legge dialettica
6.3 ” La fenomenologia dello spirito”
6.4 Il momento soggettivo: la Fenomenologia
6.5 L’ infelicità esistenziale
6.6 La ragione
6.7 La filosofia della storia
6.8 Lo Stato etico
6.9 I limiti del pensiero filosofico dal meccanicismo all’idealismo
Letteratura Italiana
7 Il paradiso nell’infinito leopardiano
8 L’Infinito del “fanciullino” nel Simbolismo pascoliano
9 L’Infinito nell’Umorismo pirandelliano
9.1 Il coraggio della coscienza ne “Il fu Mattia Pascal”
Letteratura Inglese
10 Samuel Beckett
11 The Theory of Absurdity
11.1 Beckett’s absurd characters: “Waiting for Godot”
11.2 The real main theme
11.3 The new sight of the audience
12 The Theatre of Absurd
12.1 The Theatre of Absurd and the Sophists
12.2 The role of Beckett’s absurd man
Matematica
13 I livelli di Infinito
13.1 Ipotesi generalizzata del Continuo
13.2 L’Assioma della Scelta
13.4 I “Principia Matematica”
Geografia Astronomica
14 La teoria del Big Bang
15 Le due Teorie dell’universo inflazionario
15.1 La Teoria Standard
15.2 La Teoria dell’Universo a Bolle
16 L’età dell’Universo
16.1 La formazione delle stelle
16.2 La radiazione cosmica di fondo
16.3 Ammassi globulari e sorgenti radio quasi stellari (QUASAR)
16.4 I buchi neri
17 Teorie sull’evoluzione e sul destino dell’Universo
18 La materia oscura
Fisica
19 La Relatività Ristretta
19.1 Conseguenze
20 La Relatività Generale
20.1 L’intuizione di Einstein
20.2 Caratteristiche
20.3 Conseguenze
21 L’ipotesi risolutiva: l’Universo parallelo
Storia
22 La guerra di Einstein
22.1 La bomba atomica
22.2 La “guerra fredda”
22.3 Il “Manifesto Russel-Einstein”
Scarica la tesina In viaggio verso l’infinito.
La scelta di questa tematica per la tesina di maturità non e’ assolutamente casuale ma vuole essere testimonianza della fantasia che sopravvive anche dopo la “maturità’”e che, a mio parere, trova spazio nell’individuo adulto proprio attraverso le visioni oniriche e la fantascienza. Ma da dove nasce il sogno? E da quando l’uomo si e’ spinto all’investigazione delle visioni oniriche? E la fantascienza?
Il sogno ed i problemi ad esso connessi fanno la loro prima apparizione nel mondo greco; varie sono le discussioni relative alle visioni oniriche, che lasciano tracce importanti anche nel mondo latino: si ricordino Cicerone,Ovidio ed Apuleio. Le considerazioni relative alle visioni oniriche ed alle loro origini mutano nei secoli, investendo letterati del calibro di Dante, Tasso, Shakespeare e Pedro Calderon de la Barca. Nel Novecento il sogno comunque lascia la letteratura per entrare nel campo scientifico e filosofico….
 La quarta edizione del convegno "Scuola, Scienza e Società" si terrà a La Maddalena nei giorni 6-7-8 marzo 2008. L’evento è organizzato dal Liceo “G. Garibaldi”, dall’I. T. Nautico “D. Millelire” di La Maddalena e dall’I. T. Commerciale e Geometri “G. Falcone e P. Borsellino” di Palau. Il Convegno si propone di suscitare riflessioni sulla stretta connessione tra prosperità, livello della ricerca scientifica e sistema scolastico.
La quarta edizione del convegno "Scuola, Scienza e Società" si terrà a La Maddalena nei giorni 6-7-8 marzo 2008. L’evento è organizzato dal Liceo “G. Garibaldi”, dall’I. T. Nautico “D. Millelire” di La Maddalena e dall’I. T. Commerciale e Geometri “G. Falcone e P. Borsellino” di Palau. Il Convegno si propone di suscitare riflessioni sulla stretta connessione tra prosperità, livello della ricerca scientifica e sistema scolastico.
L’evento è organizzato dal Liceo “G. Garibaldi”, dall’Istituto Tecnico Nautico “D. Millelire” di La Maddalena e dall’Istituto Tecnico Commerciale e Geometri “G. Falcone e P. Borsellino” di Palau, in collaborazione con Prof. Sebastiano Seatzu, professore ordinario di Analisi Numerica dell’Università degli Studi di Cagliari.
Esso rappresenta la quarta edizione di convegni, con lo stesso titolo, svoltisi, sempre a La Maddalena, dal 2005.
Il Convegno si propone di suscitare riflessioni sulla stretta ed ineludibile connessione tra prosperità, livello della ricerca scientifica e sistema scolastico di un Paese.
Gli obiettivi principali sono quelli di fornire agli studenti informazioni rilevanti sul mondo della ricerca scientifica, sulla stretta dipendenza tra sviluppo scientifico e tecnologico e sulle opportunità che gli studi scientifici offrono per una realizzazione professionale dei giovani e di contribuire ad eliminare i pregiudizi, del tutto infondati, sia sulla scarsa gratificazione dello studio delle materie scientifiche in generale e della matematica in particolare, sia sulle doti che debbono essere possedute per indirizzarsi verso studi universitari di tipo scientifico o tecnologico.
L’iniziativa è destinata principalmente agli studenti delle Scuole organizzatrici e a quelli delle ultime classi dei Licei e degli Istituti Tecnici della provincia di Olbia-Tempio, ma al convegno parteciparanno anche altre scuole della Sardegna e una rappresentanza di un Liceo Scientifico di Lodi.
Info più dettagliate sul sito www.scuolascienzaesocieta.it
 Il progetto di cui si presenta il prodotto conclusivo ha per obiettivo quello di aiutare i ragazzi a guardare meno distrattamente la realtà che li circonda, aumentare la sensibilità al miglioramento dell’ambiente. Si tratta di una raccolta di notizie botaniche, curiosità, miti e leggende su fiori e alberi del giardino della scuola. I ragazzi dopo aver imparato a riconoscere e descrivere le varietà delle specie presenti, affascinati dalla storia di ogni albero e fiore, si sono cimentati in varie produzioni di scrittura creativa. La realizzazione di questo testo è il risultato del lavoro di diverse classi e diverse insegnanti della scuola secondaria di primo grado "Ardigò" di Monza.
Il progetto di cui si presenta il prodotto conclusivo ha per obiettivo quello di aiutare i ragazzi a guardare meno distrattamente la realtà che li circonda, aumentare la sensibilità al miglioramento dell’ambiente. Si tratta di una raccolta di notizie botaniche, curiosità, miti e leggende su fiori e alberi del giardino della scuola. I ragazzi dopo aver imparato a riconoscere e descrivere le varietà delle specie presenti, affascinati dalla storia di ogni albero e fiore, si sono cimentati in varie produzioni di scrittura creativa. La realizzazione di questo testo è il risultato del lavoro di diverse classi e diverse insegnanti della scuola secondaria di primo grado "Ardigò" di Monza.
Permette di realizzare e visualizzare elenchi, quanti se ne vogliono, di numeri interi consecutivi a partire da un numero dato scomposti ciascuno in fattori primi, ovvero primo. Ogni elenco può iniziare da un qualsiasi numero >1 e può essere formato da un insieme anche di 1000 numeri. Si fa presente che per avere risultati esatti ogni numero dell’elenco non deve avere più di 15 cifre. Anche per un elenco ad esempio di 35 numeri consecutivi ciascuno di 15 cifre, il tempo di calcolo necessario per la loro scomposizione in fattori primi e la loro relativa visualizzazione risulta al più di qualche decina di secondi.
Il seguente programma è un eseguibile, garantito da Matematicamente.it Non è un virus e non contiene codice dannoso.
https://www.matematicamente.it//staticfiles/approfondimenti/approfondimenti/ELPRIFAT.EXE
L’obiettivo di questo breve lavoro è quello di illustrare, partendo da una configurazione geometrica relativamente semplice, il comportamento di una particolare funzione goniometrica soprattutto nei suoi punti di massimo relativo.
scarica il file di Cabri
Curva a bifoglio
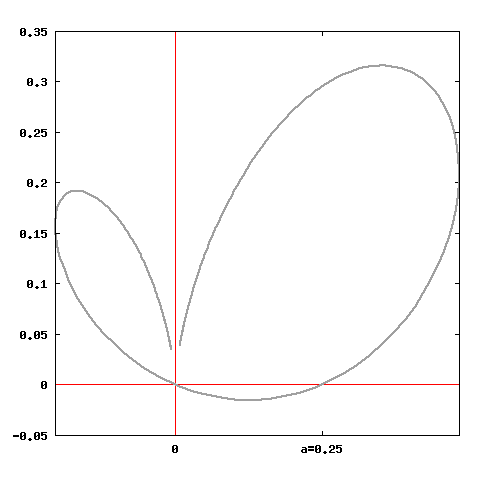
# Bifoglio.
# Equazione parametrica:
# x = (a+bt) / (1+t^2)^2
# y = tx
#
set terminal png medium size 480,480
set output "bifoglio.png"
set parametric
set size ratio 1
set zeroaxis ls 1
set xtics ("0" 0, "a=0.25" 0.25)
a = 0.25
set samples 400
plot (a+t)/(1+t**2)**2, t*((a+t)/(1+t**2)**2)
notitle with line lc "black" lw 2
set output
 E’ possibile determinare la potenza di un fucile a molla quando sono note la costante elastica K della molla, la misura d della compressione e la massa m del proiettile sparato? La risposta è affermativa. Vedremo che è possibile e servono proprio i tre parametri K, d, m indicati. Visita il sito del prof. Lecci, ricchissimo di materiali per la didattica della matematica.
E’ possibile determinare la potenza di un fucile a molla quando sono note la costante elastica K della molla, la misura d della compressione e la massa m del proiettile sparato? La risposta è affermativa. Vedremo che è possibile e servono proprio i tre parametri K, d, m indicati. Visita il sito del prof. Lecci, ricchissimo di materiali per la didattica della matematica.
Tags: approfondimenti, ingegneria, fisica, matematica, molla, fucile a molla, costante elastica, applicazioni della matematica
 Questo foglio Excel permette di calcolare facilmente le conversioni termometriche da gradi Celsius a gradi Reaumur, kelvin, Rankine, Fahrenheit
Questo foglio Excel permette di calcolare facilmente le conversioni termometriche da gradi Celsius a gradi Reaumur, kelvin, Rankine, Fahrenheit
Scarica il file Excel (22KB)
 Anche la calcolatrice tascabile può essere un passatempo, con un po’ di fantasia e di curiosità si possono scoprire cose curiose e divertenti.
Anche la calcolatrice tascabile può essere un passatempo, con un po’ di fantasia e di curiosità si possono scoprire cose curiose e divertenti.
La calcolatrice è di solito un noioso strumento di lavoro, o di studio per fare i calcoli noiosi.
Qualche volta però può capitare che per battere la noia ci si mette a pigiare sui tasti per vedere cosa appare sul display. Ci sono diverse cose curiose che si possono fare, per esempio tanti conti dai risultati curiosi.
Se non hai niente da fare, prendi la calcolatrice e provali.
5 + 6 = 11
55 + 56 = 111
555 + 556 = 1111
5555 + 5556 =…
…
27 + 28 = 55
277 + 278 = 555
2777 + 2778 = 5555
27777 + 27778 = …
…
12 + 21 = 33
123 + 321 = 444
1234 + 4321 = …
12345 + 54321 = …
…
1 x 1 = 1
11 x 11 = 121
111 x 111 = …
1111 x 1111 = …
11111 x 11111 = …
…
9 x 1 + 2 = 11
9 x 12 + 3 = …
9 x 123 +4 = …
9 x 1234 + 5 = …
9 x 12345 + 6 = …
…
8 x 1 +1 = 9
8 x 12 + 2 = 98
8 x 123 + 3 = …
8 x 1234 + 4 = …
8 x 12345 + 5 = …
…
9 x 9 + 7 = 88
9 x 98 + 6 = …
9 x 987 +5 = …
9 x 9876 + 4 = …
9 x 98765 + 3 = …
…
Un altro modo per divertirti con amici/amiche è quello di far leggere, a chi vi sta di fronte, alcuni numeri sul display. Chi sta di fronte li leggerà a testa in giù … e non leggerà numeri.
Provate a digitare questi numeri, girate la calcolatrice e leggete:
0.7738 (non dimenticare di scriver il punto dopo lo 0)
3718193771
0.5535
0.50709
0.907018
0.5380
0.5537
709
Ed ecco il vocabolario completo
8 3 6 9 4 1 7 0 5 2
B E G g h I L O S Z
Tags: giochi matematici, matematica divertente, calcolatrice, passatempi matematici, indovinelli di matematica, giochi di numeri, giochi di matematica per bambini
Risorse analoghe
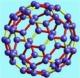 Le buckyballs (già conosciute come molecole di carbonio-60) sono molecole cave composte da 60 atomi di carbonio strutturate come un pallone da calcio e unite da legami chimici semplici e doppi. In questo documento si esplorano alcune proprietà interessanti delle buckyballs.
Le buckyballs (già conosciute come molecole di carbonio-60) sono molecole cave composte da 60 atomi di carbonio strutturate come un pallone da calcio e unite da legami chimici semplici e doppi. In questo documento si esplorano alcune proprietà interessanti delle buckyballs.
A causa della sua struttura tutta di carbonio e alla sua straordinaria stabilità chimica, il carbonio-60 è stato spesso considerato come la terza forma più importante di carbonio puro, dopo il diamante e la grafite.
L e Buckyballs prendono il loro nome dall’americano R. Buckminster Fuller architetto, inventore, predicatore, che progettò una cupola geodesica di forma simile. Infatti il nome ufficiale delle buckyballs è buckminsterfullerenes.
Prima della scoperta delle buckyballs, le uniche forme conosciute di carbonio puro erano la grafite ed il diamante, ambedue materiali cristallini. Di contro, i materiali formati dalle buckyballs sono solidi molecolari, e ciò significa che consistono di molecole fullerene singole e autocontenute, che non sono legate chimicamente l’una all’altra. 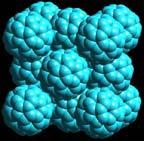
Questa figura illustra come le buckyballs siano ammassate a traliccio. Noterete che le palle sono disposte in una struttura tipo FCC, disposizione presente nell’aggregazione di atomi singoli in un cristallo.
Le Buckyballs sono normalmente ottenute provocando una scarica elettrica tra due elettrodi di grafite con un apparecchio simile ad un saldatore ad arco, che avrete probabilmente visto molte volte nei cantieri edili. Il calore generato nei punti di contatto tra gli elettrodi fa evaporare il carbonio e forma della cenere, buckyballs, e altri composti del carbonio. Le buckyballs vengono poi estratte dalla cenere attraverso tecniche di separazione chimica sofisticate.
Poiché i cristalli fullerene consistono di buckyballs, che interagiscono debolmente, le proprietà di questi solidi dipendono sostanzialmente dalla struttura e dalle proprietà delle singole molecole di buckyballs. Studiare queste molecole è, pertanto, importantissimo per capire le proprietà degli svariati materiali utili che possono essere generati dal carbonio-60. In questo lavoro, esploreremo alcune delle proprietà interessanti delle molecole buckyballs.
I sessanta atomi di carbonio del carbonio-60 si trovano nei vertici di un icosaedro tronco. Per capire cosa significa ciò diamo prima un’occhiata ai cinque solidi platonici (poliedri dalla superficie composta da poligoni regolari congrui):
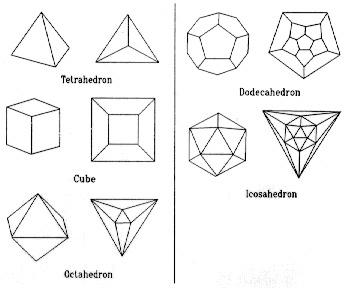
Ogni solido platonico è rappresentato in due viste. La prima è la vista normale, e la seconda è una rappresentazione "schiacciata" che ci permette di vedere tutti i vertici e gli spigoli del solido.
Per ottenere un icosaedro tronco si procede come suggerisce il nome: si tronca un icosaedro regolare come nella figura qui sotto.
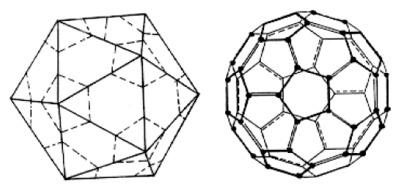
Il risultato assomiglia alla struttura di un pallone da calcio, che, come sappiamo, è identica ad una molecola buckyball. La vista "schiacciata" (che i matematici chiamano grafo, ma i chimici, che se ne servono per visualizzare molecole complesse, chiamano diagramma di Schlegel) viene mostrata qui sotto:
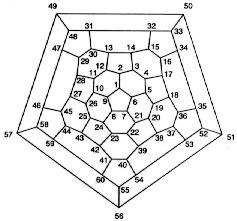
Notare che a tutti i sessanta nodi (atomi di carbonio) nel diagramma di Schlegel qui sopra è stato dato un numero dall’uno al sessanta.
Questo fatto ci permette di costruire facilmente una "matrice ad adiacenza" corrispondente a questo diagramma.
Ciò che abbiamo rappresentato sopra è di fatto una potenza N esima della matrice ad adiacenza. Prendendo potenze intere della matrice ad adiacenza, si possono conoscere il numero di percorsi (detti spesso degenerazioni) verso gli atomi inizialmente più vicini e via via ai più lontani. Avere queste informazioni è molto importante per costruire un modello realistico della molecola. Si potrebbe provare a variare il valore del parametro N, di cui sopra, per calcolare la connessione degli atomi di carbonio in una Buckyball.
essere connessi percorrendo al massimo otto spigoli (legami ) della molecola. Per convincersi che è proprio così basta rivedere il diagramma di Schlegel di una Buckyball.
Le buckyballs sono solo uno dei membri dello svariato gruppo di molecole al carbonio conosciute come fullerenes. Ecco, per esempio, un altro membro, il nanotubo carbonio:
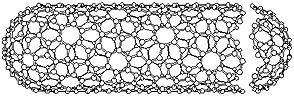
Applicazioni
Sebbene la ricerca sulle fullerenes e relativi materiali sia ancora nelle prime fasi, questi materiali dimostrano di possedere molte proprietà eccezionali, alcune delle quali porteranno certamente ad applicazioni pratiche.
Forse, una delle scoperte più affascinanti e potenzialmente più utili è stata di recente fatta da scienziati della Bell Laboratories. Si è trovato che, quando alcuni metalli alcalini ( potassio, rubidio,o cesio) vengono costretti tra le buckyballs in un reticolo, il materiale diventa superconduttore, cioè capace di condurre elettricità senza alcuna resistenza.
Tra le altre applicazioni delle buckyballs, che si stanno sviluppando, vi sono quelle relative a materiali totalmente nuovi (persino pellicole di diamante), farmaci salvavita (vaccini anti AIDS), e complesse tecniche di microfabbricazione (produzione di chips per computer).
Vista la promessa che i materiali, a base di fullerene, influenzeranno innumerevoli aspetti della tecnologia moderna, non deve sorprendere se la scienza delle buckyballs è una delle aree di ricerca più attive.
Bibliografia
M. S. Dresselhaus, G. Dresselhaus, and P. C. Eklund, Science of Fullerenes and Carbon Nanotubes, Academic Press (New York, 1996).
M. S. Dresselhaus and B. Pevzner, Recent advances in the applications of fullerenes, 21st Century Forum (Yokohama, Japan, 1996).
A. F. Hebard, Doped Fullerenes: A Soot to Superconductivity Story, Physica B Condensed Matter, 197(544), 1994.
Buckyballs – a new sphere of science
Applet Buckminster ball (C60 cage)
Tags: buckyballs, fullerene, matematica applicazioni, fisica applicazioni, chimica applicazioni, tesina, tesine maturità, matematica approfondimenti, fisica approfondimenti, molecole, buckminster fuller.
 Una Webquest è un’attività di ricerca guidata, in cui gli allievi, organizzati in gruppi cercano informazioni in Internet utili alla realizzazione di uno specifico prodotto (un ipertesto, una guida cartacea, un giornale, in questo caso l’organizzazione di una gita scolastica) che diviene il risultato di un processo di rielaborazione autonoma delle informazioni trovate.
Una Webquest è un’attività di ricerca guidata, in cui gli allievi, organizzati in gruppi cercano informazioni in Internet utili alla realizzazione di uno specifico prodotto (un ipertesto, una guida cartacea, un giornale, in questo caso l’organizzazione di una gita scolastica) che diviene il risultato di un processo di rielaborazione autonoma delle informazioni trovate.
Introduzione
Sei uno studente di una scuola secondaria di primo grado di Napoli e devi organizzare una gita in treno per visitare l’Acquario di Genova e il Museo Nazionale della Scienza e della Tecnologia di Milano.
Compito
1 Cerca su Internet le informazioni relative a:
a. orari di partenza e arrivo dei treni, tempi di viaggio, costi del viaggio,
b. alberghi a tre stelle per il pernottamento, costi degli alberghi,
c. costi per le visite dell’Acquario e del Museo,
d. costi per colazione a sacco e cena in ristorante.
2. Realizza una presentazione in PowerPoint per illustrare a tutti i partecipanti le tappe fondamentali del viaggio:
a. stazioni,
b. tratte ferroviarie,
c. alberghi,
d. luoghi da visitare.
3. Realizza un foglio Excel con i costi del viaggio.
4. Realizza un volantino in word da consegnare ai partecipanti con
a. date di partenza e di arrivo,
b. orari dei treni,
c. destinazioni,
d. costo complessivo della gita.
Procedimento
1. Fase di ricerca
Dividete la classe in cinque gruppi che lavoreranno in maniera collaborativa: tutti i gruppi cercheranno di produrre i materiali utili nel minor tempo:
un gruppo si occuperà degli orari e dei costi dei treni,
un altro gruppo si occuperà degli alberghi,
un altro gruppo della ristorazione,
un altro gruppo si occuperà dell’Acquario di Genova
un altro del Museo della Scienza di Milano.
All’interno di ciascun gruppo ci saranno le seguenti mansioni:
il coordinatore della ricerca fa il punto della situazione, dà incarichi, verifica la qualità del lavoro, riduce le perdite di tempo, evita che si esca fuori tema;
il responsabile della navigazione utilizza mouse e tastiera del computer collegato alla rete Internet, è responsabile della ricerca di siti, della navigazione nei siti, preleva testi e immagini che potrebbero servire, evita che gli altri componenti del gruppo si distraggano durante la navigazione, evita i siti con contenuti dannosi per il computer;
il responsabile della pubblicazione archivia i files, salva le immagini, copia i testi e li conserva su supporti di memoria (floppy disk e memorie a penna);
il responsabile del diario di bordo registra lo stato di avanzamento dei lavori lezione per lezione, annota i siti visitati, i siti da cui è stato copiato il testo, i siti da cui sono state prese le immagini.
2. Fase di produzione
Dividete nuovamente la classe in gruppi di quattro persone, i gruppi lavoreranno in maniera competitiva cercando di produrre i materiali migliori rispettando il tempo assegnato. All’interno di ciascun gruppo ci saranno le seguenti mansioni:
il redattore è responsabile del contenuto dei documenti e ne fa una prima stesura;
il correttore di bozze è responsabile dell’editing del testo, della sua correttezza grammaticale e della sua chiarezza;
il grafico è responsabile delle immagini, cura l’aspetto grafico generale dei documenti da produrre, decide le immagini da inserire, gli sfondi e tutti gli altri elementi grafici come disegni, tabelle e clipart;
il responsabile del diario di bordo registra lezione per lezione lo stato di avanzamento dei lavori, cura i riferimenti bibliografici, la bibliografia e la sitografia da allegare ai documenti, ha la responsabilità di indicare i siti da dove sono state prese le informazioni e le immagini;
il responsabile dei calcoli controlla le tabelle orarie, ipotizza eventuali ritardi dei treni e prevede treni alternativi; calcola i costi dei trasporti, soggiorni, ristorazione, costo dei musei e delle guide;
il revisore dei calcoli verifica la correttezza dei calcoli e predispone il foglio Excel;
il responsabile della pubblicazione fa la stesura definitiva dei documenti;
il relatore presenta all’insegnante e agli altri gruppi i lavori prodotti.
Se le mansioni sono maggiori del numero di elementi del gruppo, uno stesso membro può svolgere più mansioni. Il redattore può coincidere con il responsabile della pubblicazione ma non con il correttore di bozze. Il responsabile dei calcoli non può essere il revisore dei calcoli. I responsabili dei prodotti finali possono essere tre persone differenti: un responsabile della presentazione con PowerPoint, un responsabile del documento Word e un responsabile del documento Excel.
Risorse utili
www.trenitalia.it : sito utile per cercare i percorsi ferroviari, gli orari e i costi.
http://www.acquario.ge.it/ : sito dell’acquario di Genova, utile per la descrizione dell’acquario, cosa si potrà vedere, orari e costi, cartine per raggiungere l’acquario, servizi aggiuntivi.
http://www.museoscienza.org/ : sito del museo della Scienza di Milano, utile per la descrizione del museo, cosa si potrà vedere, orari e costi, cartine per raggiungere il museo, servizi aggiuntivi.
http://www.bookings.it/ http://www.best-hotel.it/ http://www.expedia.it/ http://www.hotels.it/ http://www.initalia.it/ siti utili per cercare alberghi e conoscerne i costi.
Autovalutazione
Valutazione del lavoro di gruppo
Valutazione del prodotto
Valutazione dell’insegnante
Scarica il file .doc per la autovalutazione
Conclusione
Se hai portato a termine il tuo lavoro hai imparato a lavorare in gruppo, hai imparato a usare attivamente gli strumenti dell’informatica e soprattutto hai capito quanto sia importante la matematica nella vita quotidiana.
Per approfondire le Webquest
http://www.apprendereonline.it/public/home.php