Sudoku facile per principianti
Autore: Antonio Bernardo
Sudoku 27032014 molto facile
Sudoku molto facile per imparare il gioco
Sudoku 26032014 estremo
Sudoku estremo per solutori particolarmente abili
Sudoku 25032014 molto difficile
Sudoku molto difficile per solutori molto bravi
Sudoku 24032014 difficile
Sudoku difficile per solutori bravi
Sudoku 23032014 medio
Sudoku medio per solutori allenati
Sudoku 21032014 molto facile
Sudoku molto facile per giocatori principianti
Idrocarburi insaturi
Test di chimica per la scuola superiore sugli idrocarburi insaturi: alcheni, carbocationi, propadiene, regola di Markovnikov…
IDROCARBURI insaturi
IDROCARBURI INSATURI
Problema 12: Capitale e Debito, Spese e Guadagni
Poniamo pari a 100 il Capitale disponibile (X) e La Spesa Effettiva (Y) nel periodo 0 di inizio della simulazione. Supponiamo che in ogni periodo il Capitale renda lo 1.0 % e che la spesa sottragga ogni periodo il 40.0% del suo importo al capitale. Supponiamo inoltre che l’entità del Capitale aumenti del 2.5% la propensione a spendere.
Dunque alla fine del primo periodo si avrà: X1 = 100 + 1 – 40 = 61 Y1 = 100 + 2.5 = 102.5. Se il Capitale diventa negativo è da intendersi che si è acceso un prestito con tasso passivo uguale a quello attivo. Se la spesa diventa negativa è da intendersi come guadagno di cui il 40% va ad accrescere il Capitale.
Costruire:
1) Il Grafo dei flussi tra le due variabili C ed S
2) La Matrice dei flussi d’influenza
3) Le equazioni ricorsive per il problema
4) Il valore numerico delle variabili C ed S (condizioni iniziali 100) per le prime 100 iterazioni
5) Il Grafico dell’andamento temporale di Spesa e Capitale
6) Il Ritratto di fase nel piano delle due variabili C (X) ed S (Y)
![]() SOLUZIONE
SOLUZIONE
La soluzione del problema nel formato XLS
In un piano è dato un segmento AB di misura 4 rispetto ad una fissata unità di misura u; trovare, rispetto ad un sistema di assi cartesiani ortogonali opportunamente scelto, l’equazione…
In un piano è dato un segmento AB di misura 4 rispetto ad una fissata unità di misura u; trovare, rispetto ad un sistema di assi cartesiani ortogonali opportunamente scelto, l’equazione del luogo dei punti P di tale piano per cui il perimetro del triangolo ABP è 14u (si consiglia di riconoscere di che luogo si tratta prima di fissare il sistema di riferimento cartesiano ortogonale).
Esercizio sui luoghi geometrici
199. La progettazione educativa fa fiorire la matematica
Gli studenti italiani non hanno successo nei test di matematica. Tutti “sanno” individuare le carenze del sistema scolastico e propongono ricette per superarle. Tra questi il ministro Francesco Profumo che ha affermato che le carenze che viziano la formazione matematica dei giovani dipendono dalle procedure di selezione del personale docente: solo chi ha la laurea specifica dovrebbe essere titolare dell’insegnamento [Bolzano – convegno sull’innovazione – settembre 2012].
Una plausibile spiegazione della “verità in tasca” che tutti presumono d’avere deriva dal loro riferimento culturale: l’insegnamento universitario. Il servizio scolastico, invece, ha una natura e un orientamento proprio: la conoscenza è strumentale rispetto alla promozione e al consolidamento delle qualità dei giovani.
199. La progettazione educativa fa fiorire la matematica
Sudoku 20032014 difficile
Sudoku difficile per solutori esperti
Sudoku 19032014 medio
Sudoku di difficoltà media per giocatori allenati
Sudoku 18032014 facile
Sudoku facile per giocatori poco esperti
Sudoku 17032014 molto facile
Sudoku molto facile per chi vuole imparare il gioco
Sudoku 16032014 difficile
Sudoku difficile per solutori esperti
Matematica: una creatura semovente?
Dovrebbe essere ormai una cognizione abbastanza scontata che il metodo scientifico consta di tre fasi concatenate. Dapprima si raccolgono i dati sperimentali riguardanti il fenomeno a cui bisogna dare una spiegazione. Successivamente, i dati sperimentali vengono trasformati in linguaggio matematico pervenendo a uno schema simbolico che rappresenta il fenomeno in modo sintetico e maneggevole, ma rigoroso ed esaustivo. Al modello così ottenuto si richiede di avere capacità predittive riguardo ulteriori esperimenti della stessa natura.
Nella pratica, tuttavia, le tre fasi non rappresentano tre momenti distinti della ricerca, non sono nettamente separate, né si verificano sempre nella stessa sequenza. La letteratura scientifica testimonia che, non di rado, le conclusioni di una ricerca rappresentano il manifestarsi di leggi matematiche che, in modo quasi prepotente, emergono (o riemergono) per dare ordine e coerenza.
Il mondo della matematica è davvero molto bizzarro da questo punto di vista. Le idee, a volte immediatamente riconoscibili come geniali a volte meno, sembrano avere vita propria. Appaiono e scompaiono in maniera inaspettata e, attraverso percorsi imprevedibili, si ripresentano rivitalizzate e pregne di strabilianti novità.
I concetti e le relazioni che i matematici studiano per ragioni puramente teoriche, senza alcuna prospettiva pratica, si rivelano a distanza di decenni, o anche secoli, come soluzioni inaspettate a problemi della realtà fisica. I casi in cui questo è accaduto sono numerosi.
Alcuni esempi sono riportati nel libro di Mario Livio “Dio è un matematico”, nel quale l’autore si domanda se la matematica sia un qualcosa di già insito nelle dinamiche della vita e dell’universo.
Il primo esempio che l’autore propone è quello di Godfrey Harold Hardy, eccentrico matematico inglese, talmente orgoglioso del fatto di essersi esclusivamente occupato di matematica pura che proclamava soddisfatto: “Nessuna mia scoperta ha aggiunto qualcosa né aggiungerà qualcosa direttamente o indirettamente, nel bene e nel male alle attrattive del mondo”. Fu smentito dai suoi stessi risultati! I suoi lavori trovarono sorprendente applicazione nello studio sull’evoluzione delle popolazioni con grande soddisfazione da parte dei genetisti.
A suggellare quanto detto esiste la legge di Hardy-Weinberg in onore di Hardy e del fisico Wilhelm Weinberg. Un altro esempio degno di nota riguarda Keplero e Newton che, nel confermare la forma ellittica delle orbite dei pianeti, riscoprirono una figura geometrica studiata, e poi quasi dimenticata, dal matematico greco Menecmo due millenni prima.
Le geometrie di Riemann, sorprendentemente, si rivelarono a distanza di tempo proprio lo strumento di cui aveva bisogno Einstein per la sua teoria della relatività. Il linguaggio matematico chiamato “teoria dei gruppi”, elaborato da Galois, al solo scopo di determinare la risolvibilità delle equazioni algebriche, è diventato nel corso degli anni il linguaggio adottato da fisici, ingegneri, linguisti e persino antropologi per descrivere tutte le simmetrie del mondo.
Il giovane fisico matematico Feigenbaum giocando con la sua calcolatrice si accorse casualmente che una serie di calcoli di una semplice equazione si approssimava sempre più al numero 4,669. Esaminando altre equazioni riscontrò che quel misterioso numero si ripeteva con una certa regolarità. Dopo vari approfondimenti, era giunto alla conclusione che quella scoperta rappresentava qualcosa di universale, cioè sembrava segnare il punto di transizione da un sistema ordinato a un sistema caotico. Nonostante la sua intuizione, il suo primo articolo scientifico fu rifiutato. Tuttavia, a distanza di qualche tempo alcuni esperimenti mostrarono che quando l’elio liquido viene riscaldato dal basso si comporta esattamente come previsto dalla soluzione universale proposta da Feigenbaum. Quello straordinario numero giocava un ruolo nella transazione di un fluido da un flusso ordinato a un moto turbolento e addirittura nel comportamento dell’acqua che gocciola da un rubinetto.
Le strabilianti sorprese della matematica non hanno risparmiato neanche i nodi. Un nodo matematico può essere immaginato come un comune nodo fatto con una corda i cui capi sono uniti. Un nodo matematico, in conclusione, è una curva chiusa senza estremità libere. La storia dei nodi è ancora più sorprendente se si pensa che in principio l’elaborazione di questa teoria scaturì da un errato modello dell’atomo sviluppato nel XIX secolo. Una volta che quel modello fu abbandonato, appena due decenni dopo il suo concepimento, la teoria dei nodi continuò a evolversi nella forma di una branca relativamente oscura della matematica pura.
Il fatto eccezionale è che questo studio astratto ha trovato inaspettate applicazioni in ambiti quali la struttura molecolare del DNA e la teoria delle stringhe che tenta di unificare il mondo subatomico con la gravità.
Domenico Signorelli
Italia 2014: paese di laureati, disoccupati e start up di successo
C’era una volta la favola del brillante laureato, che dopo un’intensa e impegnativa gavetta, riusciva a trovare lavoro e fare carriera. Ma questa favola appartiene al passato, nell’Italia del 2014, in piena crisi economica, i giovani laureati non se la passano di certo bene, e il titolo di studio di antico prestigio sembra aver perso quasi ogni valore, almeno come lasciapassare nel mondo del lavoro.
Il quadro dipinto è confermato dal sedicesimo rapporto di Almalaurea, realizzato su 450 mila laureati dei 64 atenei del consorzio, che ha messo in evidenza la scissione sempre più netta dell’antico binomio laurea-lavoro.
Secondo l’indagine, dal conferimento della laurea all’ingresso del mondo del lavoro per i “titolati” italiani trascorre in media un anno, ma il tempo si prolunga per i laureati del Sud Italia, ancor di più se di sesso femminile. I contratti a tempo inderminato hanno subito un netto calo, quasi il 15% in meno rispetto al 2008, il precariato, i contratti a progetto, e il lavoro occasionale, sono orami una realtà comune.
Questioni di gender, differenze tra Nord e Sud, quelli che da sempre sono temi caldi della propaganda politica, assumono contorni drammatici nello scontro con una realtà in cui il merito non è un parametro considerato.
A parità di condizioni di partenza, chi si laurea in un Ateneo del Su Italia ha il 59% di possibilità di lavorare o di frequentare uno stage pagato, a tre anni dalla laurea, percependo 1.045 euro al mese netti. Chi ha studiato al Nord, invece, nell’88,3% dei casi ha un’occupazione dopo tre anni, e la sua busta paga arriva a 1.251 euro.
Intanto, negli ultimi due anni la percentuale dei laureati italiani che hanno scelto di lasciare l’Italia per trovare lavoro all’estero ha raggiunto cifre da record.
“Stiamo perdendo tantissimo capitale umano”, affermava Giovannini dalle pagine di Repubblica lo scorso Novembre. Di contro, tra i cervelli rimasti, la voglia di combattere e affermarsi non sembra essersi affievolita del tutto. Nel 2013 oltre 110 milioni di euro sono stati investiti per finanziare nuove realtà imprenditoriali e 1.554 società italiane si sono iscritte alla sezione startup innovative del Registro delle Imprese. Numeri in crescita, così come le opportunità occupazionali per i neolaureati. Parliamo di realtà aziendali concepite in ottica contemporanea da e per i giovani.
I settori in cui si investe principalmente sono web, ICT, elettronica. I fondatori hanno in media 30 anni, il 48% di loro vive al Nord ed il 52% è in possesso di una laurea di primo livello. Nell’80% dei casi hanno avuto precedenti esperienze nell’ambito del lavoro dipendente, ed è proprio qui che hanno conosciuto i loro soci e fatto maturare il progetto imprenditoriale.
Lavoro precario, fuga dei cervelli, startup, fatti ed eventi di una generazione che ha voglia di riscatto e voglia di cambiamento. Sono loro il punto di forza di un Paese che deve rinascere, trasformando la favola, in realtà.
Per un quadro completo del fenomeno startup in Italia vi rimandiamo all’inforgrafica realizzata dalla Facoltà di Economia dell’Università “Niccolò Cusano”, consultabile al seguente indirizzo: http://www.unicusano.it/blog/universita/startup-for-beginners/

Infografica a cura dell’universita’Unicusano
Serena De Domenico
Esercizio sul rendimento di un titolo bancario
Hans e Martin, ormai pensionati, vivono con le rispettive famiglie in un Buen Retiro lunga la costa mediterranea. Hans viene a sapere dall’amico Martin che la banca A sta emettendo l’obbligazione O, di tipo step-up (cedole crescenti). Si tratta di un titolo con data di emissione 1 giugno 2014, durata 3 anni. Paga una cedola annua; il 1 giugno di 2015, 2016, 2017. Alla scadenza del 1 giugno 2017 rimborsa il capitale.
Le cedole per i tre anni sono, rispettivamente: 4,5%, 5,5%, 6,0%. Collocamento e rimborso a scadenza al valore di 100. La tassazione nel Paese in oggetto è del 25% per questa obbligazione.
Domanda 1. Aiutare Hans a verificare se questo bond è davvero interessante. Il termine di paragone è il Titolo di Stato (TdS) di pari durata residua, emesso nello stesso Paese. Questo TdS paga una cedola annua del 6% e scade alla stessa data dell’obbligazione O. La tassazione per il TdS è del 17%. Immaginiamo che in data 1 giugno 2014 il suo prezzo (Corso Secco) sia 103,50. Confrontare i due titoli sulla base del TRES lordo e netto. (TRES = Tasso di Rendimento Effettivo a Scadenza, ricavabile da una funzione di EXCEL, quale?) per decidere quale dei due titoli è migliore.
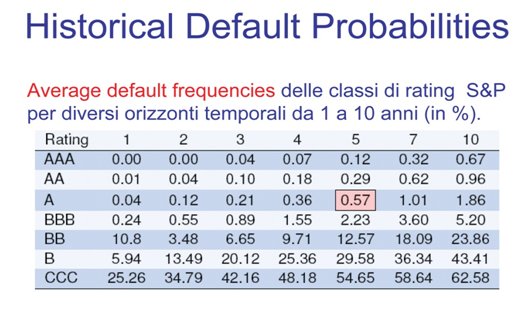
Domanda 2. Dopo aver risposto alla Domanda 1, Hans si procura, presso la banca A , il Prospetto Informativo dell’obbligazione O. Scopre che le informazioni fornite da Martin sono corrette ma incomplete. In realtà non si tratta di una normale obbligazione, bensì di un derivato. La banca A ha investito nella società manifatturiera Gamma, acquistando il bond emesso da quest’ultima per finanziare la sua espansione produttiva. Per proteggersi, almeno parzialmente, dal rischio di mancati pagamenti (cedole e/o rimborso capitale) da parte di Gamma, la banca A ha emesso il derivato O. Gli analisti della banca A, sulla base della Analisi Fondamentale della società Gamma e delle condizioni di mercato prevedibili, ritengono che la probabilità di mancati pagamenti da partedi Gamma sia del 50,5%. Questo rischio viene rimbalzato dalla banca A sugli acquirenti del derivato O, in ragione crescente della perdita eventualmente subita da A. In sostanza, se Gamma non rimborsa pienamente A, a sua volta A decurta i pagamenti agli obbligazionisti del derivato O. In questo modo il TRES di O diventa negativo. C’è però un aspetto positivo nella faccenda: i rendimenti cedolari di O non sono considerati reddito da capitale. Pertanto le tasse relative possono essere compensate dalle minusvalenze. Hans ha delle minusvalenze accumulate e potrebbe compensare integralmente le tasse su O. Il Tds già descritto alla domanda 1 ha pure esso un rischio di insolvenza (default) parziale o totale. Il suo rating è B. La relativa probabilità è contenuta nella tabella allegata (Historical DefaultProbability, fonte UNIROMA). Tenendo conto di tutte le informazioni riportate nelle domande 1 e 2 e dei TRES calcolati per la domanda 1 determinare, con la Teoria delle Decisioni, se ad Hans conviene comprare e tenere fino a scadenza il derivato O.
Nota: in tutti i calcoli si trascurino le commissioni bancarie.
![]() SOLUZIONE
SOLUZIONE
La soluzione del problema di rendimento bancario in formato XLS
Sudoku 12032014 difficile
Sudoku difficile per risolutori esperti
Sudoku 15032014 medio
Sudoku di difficoltà media per giocatori abituali
Sudoku 14032014 facile
Sudoku facile per solutori occasionali
Sudoku 13032014 molto facile
Sudoku molto facile per principianti
Sudoku 11032014 medio
Sudoku di difficoltà media per solutori allenati
198. An Introduction to Game Theory and its Applications
Game theory is formally defined as “the study of mathematical models of conflict and cooperation between intelligent rational decision-makers” (Myerson, 2001, p. 1). One alternative definition, proposed “as a more descriptive name for the discipline”, is “interactive decision theory” (Aumann, 2008, Abstract). In other words, it is the analysis (by means of mathematical reasoning) of a conflict of interest to find the optimal choices for reaching the desired outcome, under given conditions. Basically, it is the study of the ways to ‘win’ in a situation given certain circumstances.
Putting its limitations to one side, game theory has been profitably applied to many situations in the field of economics, biology, sociology, and political sciences, to predict important trends. This paper aims to offer a brief, clear overview of the main aspects of game theory and its wider applications.
TITOLO
Sudoku 10032014 facile
Sudoku facile per giocatori poco allenati.
Sudoku 09032014 molto facile
Sudoku molto facile per principianti
Sudoku 07032014 difficile
Sudoku difficile per solutori esperti
Cyberbullismo, cresce l’allarme: 1 adolescente su 10 ne è vittima
Insulti, offese, pubbliche umiliazioni: gli strumenti usati dai bulli digitali fanno male tanto quanto uno schiaffo o un pugno. Nell’era dei nativi digitali, la violenza tra coetanei trova terreno fertile in rete, sui social network, dove non esiste autorità, dove il controllo dei genitori è facilmente aggirabile. Negli ultimi mesi il cyberbullismo ha assunto proporzioni allarmanti.
aiuto da parte degli adolescenti si sono moltiplicate rapidamente. Secondo una recente indagine 1 adolescente su 10 ha subito atti di cyberbullismo o ne è stato testimone. Altri dati evidenziano come il fenomeno sia legato alla mancanza di un controllo sistematico da parte dei genitori.
L’età media in cui in Italia si ottiene il primo cellulare è attualmente 9 anni e solo il 25% delle famiglie è a conoscenza dei siti visitati e dell’attività in rete e sui social network condotta dai propri figli.
Da pericolo latente a pericolo reale, dalla violenza in rete al disagio reale, il cyberbullismo è secondo gli studiosi una delle principali cause della depressione adolescenziale, nonché una delle più grandi angosce dei giovani d’oggi.
I social network, in particolare Facebook e Twitter, hanno assunto oggi l’aspetto di una vera e propria pubblica gogna, dove il branco riesce ad azzannare le prede con disinvoltura.
In questo contesto si inserisce il progetto europeo Impact of Relationship, finanziato dalla Comunità Europea che ha lo scopo di insegnare ai giovani tra i 10 e i 17 anni l’importanza di un uso corretto dei social network, al fine di sfruttare le potenzialità della rete senza incorrere nei possibili rischi sopra menzionati.
Il progetto, il primo che coinvolge tutti gli stati dell’UE, nasce proprio dall’esigenza di porre un freno ad un fenomeno che conta migliaia di vittime tra gli adolescenti europei.
Intanto a livello nazionale sono numerose le associazioni che si occupano di fornire assistenza alle vittime del bullismo. Il messaggio dei medici e dei volontari coinvolti è forte e chiaro: se subite atti di bullismo non restate in silenzio, parlatene con un adulto.
Serena De Domenico
Tanti elettron-volt e tanto lavoro
A partire dagli anni cinquanta del ventesimo secolo, la corsa verso nuove scoperte sulle particelle elementari è stata soprattutto una corsa verso la realizzazione di acceleratori sempre più potenti. Gli Stati Uniti sfoggiavano il Cosmotron di New York e il Bevatron di San Francisco mentre la Russia rispondeva con il suo laboratorio di Dubna.
La scienza europea annaspava in quegli anni e risentiva della crisi economica causata dalla seconda guerra mondiale. Erano molti gli scienziati europei che lasciavano il proprio Paese per inseguire il sogno di fare ricerca negli Stati Uniti o altrove. Bisognerà attendere gli anni settanta perché il CERN possa affacciarsi seriamente sul panorama mondiale della fisica delle alte energie ed entrare in diretta competizione con il National Accelerator Laboratory di Chicago.
I primi acceleratori utilizzavano fasci di particelle ad alta energia per frantumare la materia in modo distruttivo: per ridurre la materia in frammenti sempre più piccoli bastava aumentare l’energia d’impatto. Questa prima generazione di acceleratori si dimostrò più che sufficiente per raggiungere tali risultati poiché per allontanare un elettrone da un atomo è richiesta un’energia relativamente piccola dato che gli elettroni sono legati all’atomo da comuni forze elettriche.
Gli stessi acceleratori si dimostrarono validi anche nell’infrangere il ben più duro nucleo i cui protoni e neutroni sono legati tra loro da un collante enormemente più intenso quale la forza forte. La successiva generazione di acceleratori, tuttavia, doveva raggiungere energie di gran lunga superiori dato che le particelle che i fisici hanno bisogno di analizzare, non esistono spontaneamente in natura e devono quindi essere appositamente create.
Per convertire l’energia in materia è necessario toccare valori molto elevati in termini di elettron-volt, in modo tale che le particelle cercate scaturiscano dal nulla nel momento stesso in cui fasci ad alta energia vengono fatti urtare contro nuclei bersaglio.
Il desiderio di conquistare il primato nella fisica delle alte energie, ha spinto i Paesi con maggiore tradizione e vocazione in questo settore a una vera e propria corsa alla realizzazione della macchina più potente.
La fisica statunitense, da sempre all’avanguardia, subì una battuta d’arresto nel momento in cui, nei primi anni novanta, furono interrotti i lavori di realizzazione del SSC (Superconducting Super Collider). Il CERN, invece, riuscì a proseguire su un proficuo sentiero che si concretizzò nella costruzione del LEP (Large Electron-Positron Collider) prima e del LHC (Large Hadron Collider) poi.
Dunque, da un lato queste colossali macchine devono assolvere al loro compito di raggiungere energie sufficientemente elevate per poter creare nuova materia, dall’altro i fisici devono mettere a punto tecniche che consentano di individuare questi neonati addensati particellari. Come riconoscere le nuove particelle? Come distinguerle dalle altre precedentemente create?
Potrebbero essere necessari miliardi di urti e collisioni prima di riuscire a individuare tracce utili e a quel punto inizia la ricerca affannosa di oggetti la cui singolare natura obbliga quasi a dover riformulare il significato stesso del termine “esistenza”: le loro dimensioni, la durata dei tempi in cui essi si manifestano e il loro modo di interagire rappresentano una manifestazione molto particolare di “esistenza”. A volte, come nel caso dei neutrini, bisogna scovare corpi che eludono i rivelatori senza lasciare traccia e la cui presenza può essere testimoniata soltanto dalla diminuzione dell’energia registrata tra gli istanti precedenti l’urto e gli istanti successivi, quando cioè essi lasciano il sistema che si sta analizzando sfuggendo attraverso la materia quasi senza nessuna resistenza da parte di quest’ultima.
A volte cercare una particella equivale a intuire in che modo essa si potrà formare in una collisione, in quali particelle potrebbe decadere, per quanto tempo potrebbe rimanere in vita una volta creata. A volte cercare una particella equivale a cercare qualcosa che non è detto esista.
Domenico Signorelli
Misure della distanza tra punti e propagazione dell’errore
Questa nota si propone di mostrare che la propagazione dell’incertezza di un’operazione di misura (per esempio la distanza tra due punti) dipende oltre che dalle ovvie incertezze dei fattori originali anche dalla forma dello spazio in cui viene svolta la misura stessa.
Questo in linea di principio permetterebbe di identificare lo spazio in cui vengono svolti esperimenti di misura analizzando i risultati in termini di propagazione degli errori. Verrà mostrato che solo le misure di distanza svolte in spazi euclidei hanno la proprietà di essere isovariabili nel senso che l’operazione di misura determina un valore della distanza che ha un’incertezza uguale a quella delle incertezze iniziali dei punti nello spazio, cosa che non vale per una geometria Riemanniana ad esempio. Introducendo il concetto di incertezza della misura e inglobando questa informazione nell’espressione della misura stessa, verrà mostrato che molte proprietà geometriche e algebriche non sono più valide.
Propagazione dell’errore
Problema 11: Evoluzione di un sistema dinamico
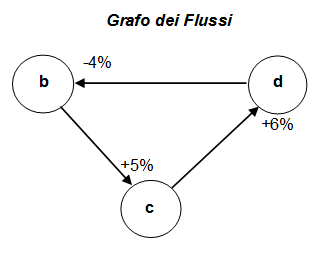
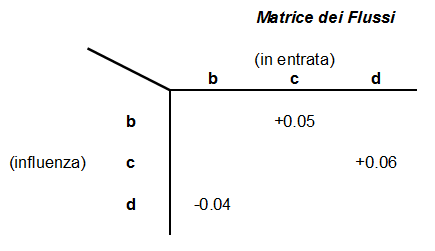
Lo studio e l’analisi di un sistema, condotto con tecniche di Brainstorming, Cross-Impact Analysis, ecc. ha portato alla identificazione di tre variabili principali (b,c,d) di cui si vuole studiare l’evoluzione nel tempo. Sotto sono riportati il grafo e la matrice dei flussi d’influenza tra le tre variabili. Ponendo pari a 100 il valore delle variabili allo istante zero:
1) Si scrivano le equazioni ricorsive di livello per le tre variabili b,c,d.
2) Si calcoli numericamente l’evoluzione delle variabili per 100 periodi di tempo.
3) Si tracci il grafico che mostra come le variabili evolvono dal periodo iniziale (0) a quello finale (100).
Scarica il file XLS con la soluzione del problema
Biologia C3
Manuale di Biologia per la secondaria di secondo grado con licenza Creative Commons BY.
Questo ebook fa parte di una collana di ebook con licenza Creative Commons per la scuola. Il titolo Biologia C3 vuole indicare che il progetto è stato realizzato in modalità Collaborativa e con licenza Creative Commons, da cui le tre “C” del titolo. Non vuole essere un trattato completo sull’argomento ma una sintesi sulla quale l’insegnante può basare la sua lezione, indicando poi testi e altre fonti per gli approfondimenti. Lo studente può consultarlo come riferimento essenziale da cui partire per approfondire. In sostanza l’idea è stata quella di indicare il nocciolo essenziale della disciplina, nocciolo largamente condiviso dagli insegnanti. La licenza Creative Commons scelta permette non solo di fruire liberamente l’ebook ma anche di modificarlo e personalizzarlo secondo le esigenze dell’insegnante e della classe.
![]() Biologia C3
Biologia C3
Manuale di Biologia per la scuola secondaria di secondo grado
Indice
Presentazione 3
1. Il trasporto attraverso la membrana plasmatica 8
1.1 La membrana plasmatica 8
1.2 Il trasporto passivo 10
1.3 Il trasporto attivo 18
Approfondimenti 22
2. Il metabolismo cellulare 23
2.1 Catabolismo e anabolismo 23
2.2 L’energia 25
2.3 ATP: il trasportatore dell’energia 26
2.4 Gli enzimi: catalizzatori biologici 27
2.5 La respirazione cellulare 31
2.6 La cattura dell’energia attraverso la fotosintesi 44
Approfondimenti 47
3. La divisione cellulare 48
3.1 Finalità della divisione cellulare 48
3.2 I cromosomi 50
3.3 Il ciclo cellulare53
3.4 Mitosi 56
3.5 Citodieresi 60
3.6 Divisione cellulare nelle cellule procariote 60
3.7 Regolazione del meccanismo di divisione cellulare 61
3.8 Riproduzione agamica e gamica 63
3.9 Meiosi 65
3.10 Un errore durante la meiosi69
3.11 Mitosi e meiosi a confronto 70
Approfondimenti 72
4. L’ereditarietà 73
4.1 Eredità per mescolanza ed eredità particolata 73
4.2 Gli esperimenti di Mendel 73
4.3 Le leggi di Mendel 77
4.4 Fenomeni ereditari complessi 86
4.5 La teoria cromosomica dell’ereditarietà 88
Approfondimenti 90
5. Struttura e duplicazione del DNA 91
5.1 Il DNA e il materiale genetico 91
5.2 La struttura della molecola del DNA 94
5.3 Duplicazione del DNA 98
5.4 La funzione dei geni102
5.5 Il codice genetico 104
5.6 RNA messaggero 107
Approfondimenti 108
6. La sintesi proteica 110
6.1 Trascrizione110
6.2 Traduzione 115
6.3 Mutazioni geniche 117
Approfondimenti 120
7. I tessuti cellulari 121
7.1 Dalla cellula all’organismo 121
7.2 Tessuti epiteliali 121
7.3 Tessuti connettivi 122
7.4 Tessuti muscolari 123
7.5 Tessuto nervoso 124
8. Sistemi e apparati 125
8.1 Il sistema tegumentario 126
8.2 L’apparato scheletrico 128
8.3 L’Apparato muscolare 131
9. Nutrizione e apparato digerente 137
9.1 Il cibo come fonte di energia 137
9.2 Rischi legati all’alimentazione sbagliata 146
9.3 Apparato digerente 148
Approfondimenti 156
10. La circolazione e la respirazione 157
10.1 Le componenti del sangue 157
10.2 La circolazione in sistemi aperti o chiusi 163
10.3 Sistema circolatorio 166
10.4 Malattie cardiache 168
10.5 Circolazione linfatica 169
10.6 Apparato respiratorio 170
Approfondimenti 176
11. Il Sistema immunitario 177
11.1 La difesa contro i microrganismi patogeni 177
11.2 Risposta immunitaria mediata da anticorpi 181
11.3 Risposta immunitaria mediata da cellule 184
11.4 Malattie legate al mal funzionamento del sistema immunitario 185
11.5 I Gruppi sanguigni 187
11.6 Vaccinazione e sieroterapia 190
Approfondimenti 192
12. Il sistema endocrino 193
12.1 I messaggeri chimici 193
12.2 Il sistema endocrino 196
Approfondimenti 206
13. Il sistema escretore 207
13.1 Il sistema escretore 207
13.2 Reni 210
13.3 Ureteri, vescica urinaria e uretra 214
13.4 Insufficienza renale 214
14. Il sistema nervoso 217
14.1 Il sistema nervoso 217
14.2 Propagazione dell’impulso nervoso 220
14.3 Sinapsi 224
14.4 Il sistema nervoso centrale 226
14.5 Il sistema nervoso periferico 232
14.6 I recettori 236
Approfondimenti 243
15. Riproduzione e sviluppo 244
15.1 Riproduzione e sviluppo 244
15.2 Apparato riproduttore maschile 245
15.3 Apparato riproduttore femminile 248
15.4 Ciclo mestruale 251
15.5 Fecondazione 254
15.6 Sviluppo embrionale 255
15.7 Metodi contraccettivi 259
15.8 Tecniche per aumentare la fertilità 262
Approfondimenti 264
Indice delle figure e fonti 265
Autori
prima stesura: Loredana Palumbo
revisione dei contenuti: Anna Rainone
revisione del testo: Elisabetta Leonetti
coordinatore editoriale: Antonio Bernardo
immagini realizzate da Ginger Lab – www.gingerlab.it
© Matematicamente.it
www.matematicamente.it – [email protected] Febbraio 2014
ISBN 9788896354599
Progetto Educationalab Mobility IT srl
Questo libro è rilasciato con licenza Creative Commons BY
Ultima revisione 28.02.2014
![]() scarica Biologia C3.
scarica Biologia C3.
Manuale di Biologia per la scuola secondaria di secondo grado
I radicali
Test sui radicali per la scuola secondaria di secondo grado, classe seconda. Operazioni con i radicali, semplificazione di radicali, razionalizzazione.
RADICALI
RADICALI
RADICALI
La Fisica a caccia di fondi
Osservando la realtà dei fatti, è del tutto evidente che il difficile rapporto tra scienziati e governi rappresenta uno degli scogli maggiori nella pianificazione di progetti di grande portata. Nessuno, a priori, può prevedere se un certo finanziamento assegnato a una ricerca darà i risultati sperati e se tali risultati avranno ricadute misurabili e concrete.
Come immaginiamo un colloquio tra uno scienziato e un’assemblea cui spetta la decisione sul finanziamento? Ci può aiutare un famoso episodio che riguarda Alvin Trivelpiece, direttore dell’Ufficio per le ricerche sull’energia, a cui erano stati concessi quindici minuti per convincere il presidente Ronald Reagan a finanziare la realizzazione dell’acceleratore più grande e più costoso che fosse mai stato concepito.
I fisici coinvolti in quel progetto sapevano benissimo che, ottenere il finanziamento, avrebbe significato sancire il dominio americano sul fronte della fisica delle alte energie. Tuttavia, la domanda cruciale era: “come spiegare le cose al presidente?”
Trivelpiece, da tutti definito come persona molto pragmatica, negli anni aveva imparato bene a relazionarsi con i politici. Pensò dunque di evitare agli astanti una noiosa lezione di fisica sulle particelle fondamentali e puntò dritto al sodo. Procedette in modo molto sbrigativo sulla descrizione del nucleo atomico e anziché soffermarsi su protoni, neutroni e quark, paragonò il nucleo a una balla di fieno al cui interno si trovano palle da biliardo. Dopo aver evocato quest’immagine nella mente del presidente e dei consiglieri, in modo altrettanto spiccio, Trivelpiece cercò di convincerli che per capire dove si trovano le palle da biliardo e misurare quanto esse sono grandi, c’è bisogno di usare una pistola, anzi meglio un bel fucile per essere sicuri che i colpi penetrino bene in profondità. Alcuni colpi attraverseranno il fieno senza incontrare ostacoli, spiegò Trivelpiece, mentre altri verranno deviati dalla loro direzione a causa delle palle nascoste all’interno. Osservando il punto in cui i proiettili entrano nel fieno e il punto da cui ne fuoriescono sarà abbastanza semplice calcolare le dimensioni delle palle e dove esse sono nascoste. “Questo è in effetti ciò che facciamo con gli acceleratori di particelle”, concluse Trivelpiece.
Vari ambiti della ricerca scientifica presentano un’intrinseca incertezza e un’ovvia impossibilità predittiva circa gli sviluppi. Il vero problema è che una ricerca può essere valutata soltanto a posteriori, cioè soltanto dopo aver verificato che i risultati ottenuti hanno prodotto un certo numero di pubblicazioni e che altri membri della comunità scientifica hanno più volte citato quegli stessi studi come riferimento significativo del settore.
Il riscontro più evidente di una ricerca rimane tuttavia, agli occhi dei più, la concretizzazione pratica che porta a ricadute nella vita quotidiana, ma come si fa a prevedere se ci saranno aziende in grado di produrre brevetti sulla base di quegli esperimenti?
Verrebbe da dire che la ricerca merita di essere finanziata sempre e comunque, perché in ogni caso da essa si acquisiranno informazioni che, se anche non concretamente utilizzabili, sposteranno gli orizzonti cognitivi di una tacca più in là.
Se a questo aggiungiamo inoltre l’intervento della serendipità che spesso ha consentito di trovare casualmente ciò che neanche si stava cercando, allora la conclusione sarebbe certamente quella di sostenere la ricerca senza esitazioni.
Tuttavia, il fascino della scoperta non è sufficiente da solo a mettere tutti d’accordo riguardo alla propensione agli investimenti e soprattutto al loro ammontare. Nei periodi difficili in cui la parola d’ordine è spending review, è davvero complicato giustificare certe decisioni.
Come se non bastasse, un’altra questione contribuisce a rendere le cose più intricate: su quali basi si seleziona una ricerca da finanziare visto che sono davvero poche le considerazione che si possono fare ex ante? Le esperienze del passato invitano alla cautela e suggeriscono di evitare troppo entusiasmo per ricerche che solo apparentemente sembrano essere gravide di risposte e al contempo non stroncare a priori ricerche che non sembrano essere foriere di buoni risultati.
Da più parti si sente dire che sono allo studio modelli probabilistici e strumenti di analisi economica per cercare di pervenire a un’analisi costi-benefici che sia di supporto in tali complesse decisioni, ma la strada è stata appena imboccata.
Domenico Signorelli
Idrocarburi (alcani)
Test di chimica per la scuola superiore sugli idrocarburi: alcani, radicale alchilico, metano, butano…
IDROCARBURI (Alcani)
IDROCARBURI (Alcani)
RoboCup Junior: in sfida dal 9 al 12 Aprile i robot progettati da ragazzi italiani
La RoboCup Junior è la sfida internazionale che nasce con lo scopo di diffondere tra gli studenti la passione per lo studio della robotica. Dal 9 al 12 Aprile si svolgerà a Pontedera la finale italiana, dove si sfideranno i robot costruiti dai ragazzi durante le lezioni di robotica, concepiti in base alle direttive specifiche della competizione.
Durante i quattro giorni della manifestazione, alla sesta edizione della RoboCup Junior sono attese a Pontedera almeno mille persone fra concorrenti, insegnanti e famiglie. La RoboCup Junior è la sezione under 19 della RoboCup una competizione, ideata nel 1993, con l’obiettivo futuristico di realizzare, entro il 2050, una squadra di robot umanoidi autonomi in grado battere la squadra di calcio campione del mondo.
Quest’anno in gara ci saranno 114 team iscritti, 90 nella Under 19 e 24 nella Under 14. Nella gara sono previste quattro tipo di specialità, che corrispondono a 4 diverse finalità di progetto. Le specialità sono: dance, rescue A, rescue B (solo per i più grandi, e soccer. La specialità DANCE vede sfidarsi robot che ballano a tempo di musica. RESCUE A e RESCUE B sono le specialità dedicate ai robot umanoidi in grado di compiere missioni di salvataggio di vario tipo. SOCCER prevede una specie di partita di calcio tra robot.
Tutte le competizioni si svolgono nel rispetto dei regolamenti internazionali e i robot in gara sono quelli costruiti a scuola durante le ore di robotica, i laboratori di meccanica e di informatica. Le squadre vincitrici di ogni singola sfida della selezione italiana prenderanno parte alla gara di livello internazionale che si svolge ogni anno. Un’ottima occasione di confronto internazionale per gli studenti italiani che metteranno in luce la loro bravura in robotica, disciplina in cui tecnica e creatività vanno di pari passo, in linea con i settori in cui il Bel Paese ha sempre prodotto risultati d’eccellenza.
Il teorema di Pitagora e la nascita del pensiero matematico
2500 anni fa, nel sud dell’Italia, in quella che oggi è la Calabria, più in particolare nella città di Crotone, qualcuno, un personaggio forse mitologico, forse realmente esistito, che aveva nome Pitagora, Pitagora da Samo, perché in origine proveniva da Samo, si trovò a fare una scoperta che è una scoperta costitutiva di ciò che oggi noi chiamiamo scienza.
Il teorema di Pitagora
Einstein e la formula di Dio di J. R. Dos Santos
Un romanzo ricco di riferimenti alla fisica, con pagine di spiegazione delle moderne teorie; nonostante questo, il ritmo della storia è incalzante e riesce a generare nel lettore una grande curiosità. Il protagonista è Tomás Noronha, un esperto di criptoanalisi e lingue antiche, che lavora alla Fondazione Gulbenkian di Lisbona.
Mentre si trova al Cairo, per lavoro, viene abbordato da Ariana Pakravan, un’iraniana a capo del gruppo di lavoro nominato dal Ministero della Scienza, Ricerca e Tecnologia della Repubblica Islamica dell’Iran. Per ordine del suo governo, Ariana chiede a Tomás se vuole lavorare per loro alla traduzione di un importante documento, un manoscritto di Einstein, “Die Gottesformel”. Gli iraniani sono convinti che il manoscritto li guiderà nella costruzione della bomba atomica.
Tomás accetta la proposta e viene subito contattato da Frank Bellamy, un agente della Cia, che lo minaccia perché lavori come spia mentre si trova in Iran, visto che nella decifrazione del manoscritto è forse implicata anche la scomparsa del prof. Siza, insegnante di fisica e amico del padre di Tomás.
Una volta giunto a Teheran, a Tomás viene negato il diritto di visionare l’intero manoscritto: gli viene comunicato solo l’enigma da decifrare e sarà autorizzato a lasciare il paese solo una volta concluso il lavoro.
La Cia organizza un furto del manoscritto e coinvolge, necessariamente, anche Tomás, il quale viene catturato e interrogato da Salman Kazemi, colonnello della Vevak, il Ministero dell’Informazione e della Sicurezza iraniano.
Il trasferimento ad un’altra prigione si rivela un’occasione fortunata: Ariana può liberarlo e espatriarlo. Rientrato a Lisbona, Tomás incontra l’assistente del prof. Siza, per avere da lui alcune informazioni: pare che l’accademico stesse cercando di formulare un’equazione che contenesse tutta la struttura dell’universo, ovvero “Die Gottesformel”, la formula di Dio.
Visitando la casa di Siza, Tomás trova una cartolina raffigurante il Potala, in Tibet: è firmata Tenzing Thubten e il messaggio dice “Cercami al monastero”. Tomás ripercorre la strada fatta da Siza, ma prima di incontrare il monaco viene rapito da Salman Kazemi.
Aiutato a fuggire ancora una volta da Ariana, Tomás incontra Tenzing Thubten, compagno di università di Siza e, insieme a lui, collaboratore di Einstein. Tomás non abbandona l’idea di decifrare il manoscritto e gli aiuti per concludere l’opera gli arrivano nel modo più inaspettato…
197. Coordinate geografiche e cartesiane. Un metodo di trasformazione
La trasformazione dalle coordinate geografiche a quelle cartesiane, sia diretta sia inversa, molto importante in geodesia. Il passaggio diretto, da coordinate geografiche a quelle cartesiane ortogonali nello spazio, non presenta particolare difficoltà ed è effettuabile mediante le note formule qui di seguito riportate:
197. Coordinate geografiche e cartesiane. Un metodo di trasformazione
Gara di Logica Matematica 2014
100 quiz in 100 giorni, gara di logica matematica e problem solving per tutti. Mantieni allenato il tuo cervello, mettiti in sana competizione con noi. Puoi vincere simpatici premi e gadget. Leggi il regolamento della gara. https://www.matematicamente.it//gare/
REGOLAMENTO
La gara di Logica Matematica e Problem Solving ha inizio il 25/02/2014 alle ore 16:00.
Nella prima parte della gara, i concorrenti dovranno risolvere un quesito al giorno di logica matematica e problema solving, fino a 100 quesiti, pubblicati in orario casuale durante la giornata.
I quesiti saranno a risposta multipla, ossia conterranno oltre alla domanda anche un certo numero di risposte (da 2 a 6) delle quali solo una è corretta. I concorrenti dovranno selezionare la risposta corretta e inviarla tramite apposito pulsante, nel più breve tempo possibile.
Se la risposta è corretta il concorrente riceverà un punteggio variabile che dipende dal punteggio base della domanda e dal tempo trascorso tra la pubblicazione del quesito e l’invio della risposta. A titolo di esempio, se un quesito vale 20 punti, il concorrente riceverà 20.000,00 punti per aver dato la soluzione corretta e un bonus massimo di 2.000 (10% del punteggio della domanda); il bonus diminuisce al passare del tempo trascorso dalla pubblicazione della domanda.
I primi 300 in classifica il 31/05/2014 alle ore 24:00 parteciperanno alla fase finale che si svolgerà in modalità diversa il 5/6/14 alle ore 22.00 fino alle 23:45.
Nella fase finale, nell’orario stabilito, saranno proposti 10 quesiti; il concorrente, dopo aver fatto login, dovrà inviare tramite apposito form presente nella stessa pagina la stringa delle soluzioni corrette (ad esempio BADEEBBAAE) nel minor tempo possibile. La classifica sarà stilata per numero di risposte corrette e successivamente per ordine di arrivo. Pertanto saranno classificati per prima quelli che hanno dato 10 risposte corrette, a seguire quelli che invieranno un numero inferiore di risposte corrette. Il punteggio della classifica della prima fase non sarà tenuto in conto.
Eventuali contestazioni vanno inviate via email a [email protected], saranno esaminate dalla giuria che deciderà in modo non ulteriormente sindacabile. La giuria potrà anche decidere l’eliminazione dei partecipanti che assumeranno atteggiamenti scorretti, anche in questo caso il giudizio della giuria è insindacabile.
Obiettivo della gara è quello di divertirsi e allenarsi rispondendo correttamente alle domande. Premi, gadget e classifica devono essere ritenuti secondari e hanno il semplice obiettivo di incentivare la partecipazione e l’impegno.
Nella fase preparatoria da febbraio a maggio il primo in classifica di ogni domenica ore 24:00 riceverà la maglietta Matematicamente.it. Il premio non è cumulabile, si può vincere una sola volta, se il primo in classifica ha già vinto la maglietta una delle settimane precedenti il premio andrà al secondo in classifica, e così via.
PREMI
1° classificato: coppa trofeo + maglietta + buono regalo MediaWorld 200,00 euro.
2° classificato: coppa trofeo + maglietta + buono regalo MediaWorld 100,00 euro.
3° classificato: coppa trofeo + maglietta +buono regalo MediaWorld 50,00 euro.
Dal 4° al 10° classificato: maglietta + buono libro IBS 20,00 euro.
Dal 11° al 20° classificato: maglietta + memoria pendrive 8 GB
Dal 21° al 50° classificato: maglietta Matematicamente.it Winner.
Tutti i primi devono essere richiesti a [email protected]
Avvio alla chimica organica
Test sulla chimica organica per la scuola superiore: composti organici, catena carboniosa, isomeri, cis, trans, isomeri ottici, enantiomeri, miscela racemica
Descrizione del test
Avvio alla chimica organica
Avvio alla chimica organica
Concorso per giovani scienziati: fino al 28 febbraio aperte le iscrizioni
Sono aperte le iscrizioni per le selezioni del concorso “I giovani e le scienze”, promosso da Commissione, Consiglio e Parlamento europei, nell’ambito del concorso European Union Contest for Young Scientists, con l’obbiettivo di avvicinare i giovani alla ricerca scientifica, al confronto internazionale, premiare le eccellenze e stimolarne la crescita in ambito scientifico.
A gestire la selezione italiana dei giovani scienziati sarà la Fast, Federazione delle associazioni scientifiche e tecniche.
Il concorso è aperto ai giovani tra i 14 e i 21 anni, che frequentano le scuole secondarie di 2° grado o il 1° anno di università in Italia e conoscono l’inglese.
È possibile iscriversi fino alle ore 17 del 28 Febbraio attraverso il modulo d’iscrizione presente sul sito della Fast e si può partecipare alla competizione anche con un progetto realizzato in gruppo (max 3 persone).
I progetti e gli studi presentati per accedere alla competizione dovranno essere originali e innovativi e relativi a qualsiasi campo scientifico: dalle scienze della terra, alla fisica, alle scienze ambientali, dell’informazione e sociali.
Gli elaborati non possono superare le 10 pagine di testo, sono concesse ulteriori 10 pagine dove inserire grafici, disegni, foto, e diagrammi. A corredo del testo italiano dovrà essere inserita una sintesi del progetto in inglese.
Sulla pagina dedicata alla selezione sul sito Fast sono indicate le modalità ottimali per sviluppare il progetto da presentare.
Un’apposita e competente giuria stabilirà i 30 progetti che verranno esposti nella mostra aperta al pubblico a Milano presso il Centro congressi Fast, dal 2 al 5 maggio 2014.
Un’ulteriore selezione individuerà i destinatari degli altri premi, tra cui una borsa di studio del valore di 7.000 euro e la partecipazione a fiere scientifiche e forum internazionali.
Per il modulo d’iscrizione e il bando di concorso vi rimandiamo alla pagina dedicata sul sito Fast al seguente indirizzo: http://www.fast.mi.it/gs2014/gs2014.htm
Lezione di calcolo delle probabilità per la scuola superiore
La nascita dello studio sistematico del calcolo delle probabilità si fa risalire al 1654, quando il matematico e filosofo Blaise Pascal, per soddisfare una richiesta del cavaliere De Meré, accanito giocatore di dadi, cominciò a dedicarsi allo studio dei meccanismi che regolano i giochi d’azzardo, intrattenendo a tale scopo anche un’interessante corrispondenza con il matematico Pierre de Fermat.
Calcolo delle probabilità
Scarica la lezione in PowerPoint
196. Programmare giochi in 3D
In questo contributo presenterò delle attività realizzate nel mondo virtuale 3D Edmondo con la classe III A Sistemi Informativi Aziendali dell’I.I.S. “A. Guarasci” sez. Tecnico Economico di Rogliano (Cs) nell’ambito della sperimentazione d’informatica sulla land Scriptlandia. Si tratta di alcuni giochi classici di cui sono stati studiati gli algoritmi risolutivi e di cui è stata fatta la codifica in LSL (Linden Scripting Language), il linguaggio di programmazione simile a C, C#, Java, utilizzato nei mondi virtuali. Il percorso didattico si colloca nell’ambito della Teoria dei Giochi di cui sono stati trattati alcuni elementi durante le ore curricolari d’informatica, con collegamenti interdisciplinari in economia aziendale e matematica. La moderna teoria dei giochi può essere fatta coincidere con l’uscita del libro “Theory of Games and Economic Behavior” di John von Neumann e Oskar Morgenstern nel 1944 e questa disciplina rappresenta un buon modello per descrivere le interazioni strategiche tra agenti economici. Molti risultati economici coinvolgono l’interazione strategica come ad esempio l’andamento di mercati non perfettamente competitivi, l’andamento nelle aste, l’andamento nelle negoziazioni economiche. La teoria dei giochi [3] ha applicazioni nel campo strategico-militare, nella politica, nella sociologia, nella psicologia, nell’informatica, nella biologia, nello sport. Lo studio e la costruzione di giochi si rivela un’attività didattica significativa e motivante per gli studenti. Di seguito saranno presentati un gioco di strategia e due giochi di sorte.
196. Programmare giochi in 3D
Problema 10: Cross impact analysis
Non esiste ovviamente un metodo o una procedura unica e generale per risolvere i problemi. Si possono però avere procedure abbastanza generali per inquadrare situazioni problematiche di natura anche molto diversa. Queste analisi consentono spesso di poter iniziare la ricerca della soluzione del problema con un grado di conoscenza notevolmente ampliato.
Si consideri il grafo riportato sotto e si costruisca a partire da esso la matrice di adiacenza (matrice che ha su righe e colonne i nodi del grafo, e nelle celle della matrice il valore 1 se esiste un arco tra i due nodi ed il valore 0 se tale arco non esiste).
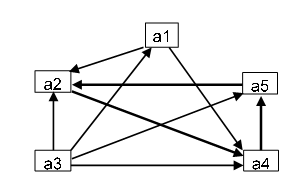
Problema 10.1: Analisi di un sistema o di un processo. Si consideri il grafo riportato sopra e la corrispondente matrice di adiacenza interpretandoli come il risultato dell’analisi di un sistema (o di un processo) in cui si sono individuate 5 componenti fondamentali (a1, …, a5) e i legami di influenza tra di esse. Cosa si può evincere sulla natura del sistema in studio dall’analisi del grafo e della corrispondente matrice?
Problema 10.2: Analisi delle preferenze di un decisore. Ad un decisore sono state presentate 5 alternative (a1, …,a5) o soluzioni possibili ad uno specifico problema. Utilizzando i confronti a coppie tra le varie alternative (ad esempio l’arco orientato tra a1 —–>> a2 sta a sgnificare che l’alternativa a1 è stata giudicata preferibile all’alternativa a2) si è potuto costruire il grafo sopra riportato e la corrispondente matrice di adiacenza. E’ possibile costruire una funzione di utilità tradizionale di questo decisore? Si può comunque trovare una gerarchia di preferenze tra le 5 alternative?
![]() SOLUZIONI DEL PROBLEMA 10
SOLUZIONI DEL PROBLEMA 10
Scarica il file XLS del problema Cross Impact Analysis
La Relatività generale a portata di mano
Secondo la teoria della relatività generale di Einstein, gli oggetti massivi creano la gravità curvando lo spazio attorno a essi. Nei primi anni successivi alla sua pubblicazione, nonostante la teoria non avesse ancora una solida base empirica, spiegava correttamente l’irregolare precessione del perielio del pianeta Mercurio.
Tutti i pianeti risentono di alterazioni delle loro orbite, anche a causa dall’interazione gravitazionale con gli altri pianeti, ma le anomalie di Mercurio sono particolarmente significative e la spiegazione einsteiniana attribuisce le ragioni di ciò al fatto che Mercurio è il pianeta più vicino al Sole e avverte in modo rilevante gli effetti della curvatura spazio-temporale che quest’ultimo provoca.
Benché la relatività generale si allontani notevolmente dalla teoria di Newton, per quanto riguarda i principi, i riscontri pratici tra i due impianti concordano così tanto da rendere molto difficile trovare delle sensibili differenze tra l’una e l’altra. Una di queste differenze è proprio l’orbita di Mercurio.
Un’altra importante differenza è lo spostamento verso il rosso dei raggi spettrali della luce provenienti da stelle di massa considerevole. A parte questi due esempi, per confermare i quali c’è bisogno di specifiche analisi e misurazioni molto accurate, il 29 maggio 1919 l’astrofisico Arthur Eddington intuì che sarebbe stata proprio la natura stessa a fornire un modo molto comodo per verificare la teoria della relatività generale di Einstein e a tale scopo aveva pensato a un ingegnoso piano per dimostrarlo.
S’imbarcò per raggiungere la piccola isola di Principe al largo della costa occidentale dell’Africa con l’obiettivo di giungervi in tempo per assistere a un’eclissi totale di Sole. La nostra stella è, naturalmente, l’oggetto con maggiore massa nel sistema solare, ragion per cui attorno a esso orbitano tutti gli altri pianeti. Secondo Eddington dunque, il Sole avrebbe dovuto curvare lo spazio. Durante l’eclissi, sarebbe stato possibile approfittare del fatto che per un breve intervallo di tempo la Luna avrebbe oscurato il Sole e ciò avrebbe consentito di osservare le stelle che altrimenti non sarebbero state visibili. Insomma, Eddington riteneva che questo fatto si sarebbe dovuto manifestare sotto forma di uno spostamento della normale posizione delle stelle.
Era chiaro che non erano certo le stelle a spostarsi dalla loro posizione bensì la luce proveniente da esse che, nel seguire la curvatura dello spazio attorno al Sole, le avrebbe fatte sembrare in una posizione apparente diversa da quella reale. Le osservazioni di Eddington vennero pubblicate un anno più tardi e fecero scalpore in tutto il mondo come la prima evidenza inoppugnabile della teoria di Einstein.
Domenico Signorelli
Manuale completo di relatività
Test d’ammissione 2014: il 12 febbraio si aprono le iscrizioni
Nonostante le polemiche e i continui ricorsi da parte di studenti e associazioni la macchina del numero chiuso non si ferma. Chi vorrà iscriversi ad un corso di laurea ad accesso programmato, quali Medicina e Chirurgia, Odontoiatria, Veterinaria, Architettura, e Professioni sanitarie, anche per l’anno accademico 2014-15 dovrà sostenere i test d’ammissione.
A regolare i test d’ingresso è il Ddl, firmato dal Ministro Carrozza, e pubblicato lo scorso 5 Febbraio. Il Decreto conferma l’abolizione del bonus maturità e l’anticipo dei test d’ammissione a numero a chiuso ad Aprile, piuttosto che a settembre come negli anni scorsi. Solo il test d’ingresso di Professione sanitarie verrà svolto dopo l’estate.
Definite le modalità d’iscrizione alle prove che si apriranno il 12 febbraio. Ciascun candidato deve presentare la richiesta di partecipazione al test selettivo per l’accesso alle facoltà a numero chiuso esclusivamente in modalità online sul portale Universitaly (www.universitaly.it ). Data ultima per l’iscrizione è il 11 marzo 2014.
Sul portale Universitaly i candidati troveranno un modulo telematico in cui dovranno indicare i loro dati anagrafici (nome, cognome, residenza, ecc..), utili anche per l’eventuale procedura di immatricolazione in caso di esito positivo del test, alla luce della graduatoria nazionale.
Sempre attraverso la procedura di iscrizione online il candidato indicherà, in ordine di preferenza le sedi per cui intende concorrere. La sede in cui si svolgerà il test sarà quella indicata come prima preferenza. Non sarà possibile modificare le preferenze dopo l’11 marzo 2014, è fondamentale, quindi, che il candidato abbia ben chiaro in quale città vorrà svolgere i propri studi universitari, e valutare le alternative.
Una volta effettuata l’iscrizione online la candidatura va completata con il pagamento del contributo per la partecipazione al test secondo le regole disposte dall’Università in cui il candidato sceglierà di sostenere la prova. Tale procedura di pagamento deve in ogni caso concludersi entro il 18 marzo 2014.
Furio Honsell, Giorgio Tomaso Bagni, Curiosità e divertimenti con i numeri, Aboca Edizioni
Luca Pacioli (1445-1517) fu uno dei matematici più noti del Rinascimento e i suoi scritti lo mostrano costantemente impegnato nell’insegnamento e nella diffusione della sua disciplina. Dopo il De divina proportione e la Summa di aritmetica, geometria, proportioni et proportionalità, Pacioli prosegue la sua opera di insegnamento con il De viribus quantitatis. Costituito da 306 carte, il manoscritto è diviso in tre parti: la prima dedicata all’aritmetica, la seconda alle geometria e la terza a indovinelli di vario genere e ad applicazioni pratiche.
L’obiettivo, come ci dice lo stesso Pacioli nel prologo all’opera, non è di esporre dottrine matematiche, ma di ricavare applicazioni pratiche.
Bagni presenta il contenuto delle prime due parti in due colonne, per evidenziare il sommario proposto da Pacioli a sinistra e l’effettivo contenuto del manoscritto a destra: nella seconda parte le differenze tra le due colonne sono minori, rispetto alla prima, forse perché la prima colonna rappresenta una traccia in parte seguita dall’autore nella realizzazione dell’opera.
Dopo l’elenco, Bagni presenta il commento ad alcuni problemi originali: la divisione di un certo numero di oggetti tra due persone, il prodotto di due numeri che hanno come risultato numeri costituiti dalla stessa cifra ripetuta, i quadrati magici e un gioco di divinazione binaria che evidenzia come uno degli obiettivi di Pacioli non sia di semplificare il gioco, ma di rendere il procedimento meno trasparente per amplificare l’effetto di sorpresa.
Nella seconda parte, ci sono alcuni risultati di geometria euclidea, come la costruzione di alcuni poligoni regolari con riga e compasso – pur trattandosi di costruzioni approssimate – oppure i giochi topologici e i giochi di prestigio. Nello snodarsi dell’opera, Pacioli si presenta come un insegnante che coinvolge efficacemente i lettori, evitando loro la noia della ripetizione degli esercizi, ma mostrando grande chiarezza matematica e Bagni mette efficacemente in evidenza tutte le strategie usate dal matematico rinascimentale.
La terza parte è quella meno semplice da interpretare: il contenuto e l’impostazione non seguono i canoni tradizionali della trattazione scientifica del periodo. I proverbi e gli acrostici tratti da De viribus quantitatis, in quanto scritti sia in latino che in volgare, non sono sempre di chiara interpretazione.
L’ultima parte dell’opera contiene una selezione di indovinelli e giochi di parole in latino e, in particolare, la sezione “Problemata vulgari a solicitar ingegno et a solazzo” contiene 222 indovinelli numerati: la parte viene descritta ampiamente da Furio Honsell nell’introduzione.
Nonostante l’ambiguità del linguaggio, al centro della scena ci sono ancora la matematica, la biologia, la semantica e la psicologia e gli indovinelli non ci offrono solo uno sguardo sul passato, ma sono uno strumento pedagogico attraverso il quale Pacioli cerca di insegnarci qualcosa.
Pacioli ci impartisce la sua lezione a partire dalle domande: non sono solo le risposte giuste che ci fanno fare un passo avanti, ma anche e soprattutto quelle sbagliate, perché una volta comprese ci fanno fare un passo avanti. Secondo Honsell, “il capitolo XXXIII è un gioiello di originalità”.
Chimica C3
Manuale di Chimica per la scuola secondaria di secondo grado.
Questo ebook di chimica per la scuola secondaria di secondo grado fa parte di una collana di ebook con licenza Creative Commons per la scuola. Il titolo Chimica C3 vuole indicare che il progetto è stato realizzato in modalità Collaborativa e con licenza Creative Commons, da cui le tre “C” del titolo. Non vuole essere un trattato completo sull’argomento ma una sintesi sulla quale l’insegnante può basare la sua lezione, indicando poi testi e altre fonti per gli approfondimenti. Lo studente può consultarlo come riferimento essenziale da cui partire per approfondire. In sostanza l’idea è stata quella di indicare il nocciolo essenziale della disciplina, nocciolo largamente condiviso dagli insegnanti. La licenza Creative Commons scelta permette non solo di fruire liberamente l’ebook ma anche di modificarlo e personalizzarlo secondo le esigenze dell’insegnante e della classe. Chiunque può contribuire a migliore questo ebook, segnalando integrazioni, modifiche e sviste al coordinatore del progetto [email protected].
INDICE
1. La mole e i modelli atomici 1.1 La materia 1.2 La mole 1.3 la teoria atomica 1.4 Le particelle subatomiche 1.5 I modelli atomici di Thomson e Rutherford 1.6 Il numero delle particelle negli atomi 25 1.7 Gli isotopi Approfondimenti
2. Gli elettroni nell’atomo 2.1 La natura ondulatoria della luce 2.2 Quanti e fotoni, la natura corpuscolare della luce 2.3 Spettri di emissione e assorbimento 32 2.4 Il modello atomico di Bohr 34 2.5 Energia di ionizzazione 35 2.6 Modello atomico a strati 35 2.7 L’energia nucleare 37 Approfondimenti 38
3. Atomo: modello ad orbitali 3.1 La duplice natura dell’elettrone 3.2 Il principio di indeterminazione di Heisenberg 40 3.3 L’orbitale atomico e i numeri quantici 40 3.4 Il numero quantico di spin 42 3.5 La configurazione elettronica 43 3.6 Il riempimento degli orbitali (principio dell’Aufbau) 44 Approfondimenti 48
4. Il sistema periodico degli elementi 4.1 Dalla legge della periodicità alla tavola periodica degli elementi 4.2 La tavola periodica moderna 4.3 Le proprietà periodiche 52 4.4 Il raggio atomico 52 4.5 L’energia di ionizzazione 53 4.6 L’affinità elettronica 53 4.7 L’elettronegatività 54 Approfondimenti 56
5. I legami chimici 5.1 Il legame chimico 58 5.2 La regola dell’ottetto 58 5.3 Il legame ionico 60 5.4 Il legame covalente 60 5.5 Polarità del legame covalente 62 5.6 Il legame covalente dativo 62 5.7 Risonanza 63 5.8 Il legame metallico 64 Approfondimenti 65
6. Geometria molecolare e forze intermolecolari 6.1 Geometria molecolare: modello VSEPR 67 6.2 Molecole con coppie elettroniche condivise 67 6.3 Molecole con coppie elettroniche libere 69 6.4 La teoria VSEPR per i legami multipli 69 6.5 Teoria del legame di valenza 70 6.6 Orbitali ibridi 72 6.7 Teoria degli orbitali molecolari 73 6.8 Le forze intermolecolari 75 6.9 Forze dipolo-dipolo 75 6.10 Forze di London 76 6.11 Legame a idrogeno 77 Approfondimenti 78
7. Solidi, liquidi e gas 7.1 I solidi 80 7.2 I liquidi 81 7.3 Evaporazione ed ebollizione 83 7.4 I gas 83 Approfondimenti 86
8. Avvio della stechiometria delle soluzioni 8.1 Miscele e soluzioni 88 8.2 La concentrazione 90 8.3 La solubilità 92
9. Come e perché avvengono le reazioni chimiche 9.1 Le reazioni chimiche 93 9.2 Fattori che influenzano la velocità di una reazione 94 9.3 Bilanciamento di una reazione chimica 95 Approfondimenti 96
10. Classificazione e nomenclatura dei composti chimici 10.1 Valenza e numero di ossidazione 99 10.2 Classificazione dei composti inorganici 100 10.3 Ossidi: composti binari con ossigeno 100 10.4 Idruri e idracidi: composti binari con idrogeno 102 10.5 I composti ternari 104 Approfondimenti 109
11. Completamento della stechiometria delle soluzioni 11.1 Miscele omogenee: soluzioni 110 11.2 Miscele eterogenee: miscugli 110 11.3 Il ruolo dell’acqua (dissociazione e ionizzazione) 111 11.4 Reazioni in soluzioni acquose: calcoli stechiometrici 113 11.5 Reazioni in soluzione acquosa: equazioni ioniche 113 11.6 Le proprietà colligative 113 11.7 Abbassamento della tensione di vapore 114 11.8 L’innalzamento ebullioscopico 114 11.9 L’abbassamento crioscopico 115 11.10 Pressione osmotica 116 11.11 Proprietà colligative di soluzioni elettrolitiche 117 11.12 I colloidi 118 Approfondimenti 119
12. Cinetica chimica 12.1 Come avviene una reazione chimica 120 12.2 Velocità di reazione 121 12.3 Fattori che influenzano la velocità di reazione 122 12.4 Il ruolo dei catalizzatori 123 12.5 La legge cinetica 124 12.6 L’andamento di una reazione chimica: l’energia di attivazione 126 12.7 Reazioni multistadio: gli stadi elementari 127 Approfondimenti 128
13. Termodinamica 13.1 Reazioni chimiche ed energia 129 13.2 I sistemi 129 13.3 Il lavoro in termodinamica 129 13.4 Il calore 130 13.5 Il calore di formazione e calore di combustione 131 13.6 Il primo principio della termodinamica 132 13.7 Applicazione del primo principio della termodinamica 133 13.8 Entalpia di formazione ed entalpia di reazione 134 13.9 La legge di Hess 135 13.10 L’entalpia di legame 136 Approfondimenti 137
14. Il secondo principio della termodinamica 14.1 Spontaneità ed entalpia 138 4.2 Entropia e disordine 138 4.3 L’interpretazione molecolare dell’entropia 139 4.4 Energia libera 140 Approfondimenti 141
15. Equilibri 15.1 L’equilibrio chimico 142 15.2 Costante di equilibrio 144 15.3 Equilibri eterogenei 145 15.4 Il principio di Le Chatelier 145 15.5 Gli equilibri di solubilità 146 15.6 Variazione della solubilità: effetto dello ione comune 147 Approfondimenti 148
16. Acidi e basi 16.1 Proprietà degli acidi e della basi 149 16.2 Acidi e basi secondo Arrhenius 149 16.3 Acidi e basi secondo Brönsted e Lowry 150 16.4 Acidi e basi secondo Lewis 151 16.5 Autoprotolisi dell’acqua 153 16.6 Soluzioni neutre, acide e basiche 154 16.7 Il pH 154 16.8 Misura e importanza del pH 155 Approfondimenti 157
17. Reazioni acido-base 17.1 Acidi forti e acidi deboli 158 17.2 Acidi poliprotici 159 17.3 Basi forti e basi deboli 159 17.4 Acidi e basi: calcolo del pH 160 17.5 Il pH della soluzione di un sale 163 17.6 Le soluzioni tampone 164 17.7 Calcolo del pH delle soluzioni tampone 165 17.8 La titolazione 166 Approfondimenti 167
18. Le ossidoriduzioni 18.1 Ossidazione e riduzione 168 18.2 Ossidante e riducente 169 18.3 Il numero di ossidazione 170 18.4 Bilanciamento delle reazioni di ossido-riduzione 170 Approfondimenti
19 Avvio alla chimica organica 19.1 La chimica organica 178 19.2 I legami del carbonio nei suoi composti 178 19.3 Catene carboniose e classificazione degli atomi di carbonio 181 19.4 Le diverse tipologie di formule in chimica organica 182 19.5 Isomeria 184 19.6 Configurazione assoluta e proiezioni di Fischer 186 Approfondimenti 187
20 Idrocarburi 20.1 Idrocarburi 188 20.2 Alcani 189 20.3 Radicale alchilico 190 20.4 Proprietà fisiche degli alcani 192 20.5 Proprietà chimiche degli alcani 193 20.6 Preparazione degli alcani 193 20.7 I cicloalcani 194 Approfondimenti 196
21 Idrocarburi insaturi 21.1 Alcheni 197 21.2 Proprietà chimiche e fisiche degli alcheni 197 21.3 Isomeria geometrica degli alcheni (cis-trans) 199 21.4 Preparazione degli alcheni 201 21.5 Polieni 201 21.6 Alchini 201 21.7 Proprietà chimiche e fisiche degli alchini 202 Approfondimenti 202
22 Idrocarburi aromatici 22.1 Il benzene 203 22.2 Nomenclatura degli idrocarburi aromatici 204 22.3 Proprietà chimiche e fisiche dei composti aromatici 205 Approfondimenti 208
23 Le diverse classi di composti organici 23.1 I gruppi funzionali 209 23.2 Alogenoderivati 210 23.3 Proprietà degli alogenoderivati 210 23.4 Alcoli 211 23.5 Proprietà fisiche e chimiche degli alcoli 212 23.6 Fenoli 213 23.7 Tioli 213 23.8 Eteri 214 23.9 Aldeidi e chetoni 214 23.10 Proprietà di aldeidi e chetoni 216 23.11 Tautomeria cheto-enolica 216 23.12 Acidi carbossilici 218 23.13 Proprietà degli acidi carbossilici 219 23.14 Acidi policarbossilici 219 23.15 Derivati degli acidi carbossilici 220 Approfondimenti
24 Le biomolecole 24.1 Le molecole biologiche 223 24.2 I carboidrati 223 24.3 Monosaccaridi 224 24.4 Oligosaccaridi 226 24.5 Polisaccaridi 227
25 I lipidi 25.1 Classificazione dei lipidi 229 25.2 Lipidi semplici 229 25.3 Lipidi complessi 233 Approfondimenti 233
26 Le proteine 26.1 Classificazione delle proteine 234 26.2 Gli amminoacidi 234 26.3 Il legame peptidico 238 26.4 Struttura delle proteine 239 26.5 Gli enzimi 240
27 Gli acidi nucleici 27.1 DNA ed RNA 243 27.2 Costituenti degli acidi nucleici 243 27.3 Differenze tra DNA ed RNA 246 27.4 Nucleotidi non contenuti negli acidi nucleici 246 Indice delle immagini Creative Commons utilizzate 248
Autori Anna La Guardia, Loredana Palumbo, Anna Rainone Revisione del testo: Elisabetta Leonetti Coordinamento editoriale: Antonio Bernardo Immagini realizzate da Ginger Lab – www.gingerlab.it © Matematicamente.it www.matematicamente.it – [email protected] Dicembre 2013
Questo libro è rilasciato con licenza Creative Commons BY
![]() scarica Chimica C3
scarica Chimica C3
Manuale di Chimica Creative Commons BY

