Risolvere una disequazione
Risolvere un problema con una equazione
Risolvere e discutere un’equazione letterale
Risolvere una disequazione di primo grado frazionaria
Risolvere un sistema coni l metodo di Cramer
Dimostrare un teorema sui quadrilateri
Risolvere una disequazione
Risolvere un problema con una equazione
Risolvere e discutere un’equazione letterale
Risolvere una disequazione di primo grado frazionaria
Risolvere un sistema coni l metodo di Cramer
Dimostrare un teorema sui quadrilateri
 We consider a particular circles chain where, each circle belonging to it, is tangent to the two previous ones and to a common straight line. Such a chain allows to express the number PI by means of a series expansion of inverse tangent functions related to Fibonacci numbers only. – Si prende in considerazione una particolare catena di cerchi dove ogni cerchio è tangente ai due precedenti e ad una retta in comune. Tale catena consente di ricavare uno sviluppo in serie per il numero (PI) dove ogni termine è dato da funzioni arcotangente il cui argomento è espresso unicamente mediante numeri di Fibonacci.
We consider a particular circles chain where, each circle belonging to it, is tangent to the two previous ones and to a common straight line. Such a chain allows to express the number PI by means of a series expansion of inverse tangent functions related to Fibonacci numbers only. – Si prende in considerazione una particolare catena di cerchi dove ogni cerchio è tangente ai due precedenti e ad una retta in comune. Tale catena consente di ricavare uno sviluppo in serie per il numero (PI) dove ogni termine è dato da funzioni arcotangente il cui argomento è espresso unicamente mediante numeri di Fibonacci.
 Indovinate il misterioso ‘special coffee’ nel minor tempo possibile. Lo ‘special coffee’ è un caffe composto da 3 elementi differnetemente colorati: piattino, tazzina e cucchiaino. VAI al gioco >>>
Indovinate il misterioso ‘special coffee’ nel minor tempo possibile. Lo ‘special coffee’ è un caffe composto da 3 elementi differnetemente colorati: piattino, tazzina e cucchiaino. VAI al gioco >>>
Visita il sito dell’autore www.salardicristian.blogspot.com
Gli esercizi che seguono riguardano la ricerca del dominio e lo studio di continuità e derivabilità di funzioni integrali, talvolta anche con quesiti che coinvolgono il calcolo della derivata di tali funzioni.
 Vogliamo esporre una dimostrazione del noto teorema di Pappo contenuto nelle proposizioni 138 e 139 della sua ‘’Collezione matematica’’. Crediamo di fare cosa gradita al lettore per il fatto che la dimostrazione prende spunto dalla geometria proiettiva, parte della matematica che, sebbene oggi alquanto trascurata, emerge con prepotenza quando si vogliano affrontare le questioni delle trasformazioni lineari nel piano che vanno sotto il nome di omotetie, affinità, omologie etc. La dimostrazione del teorema di Pappo vuole inserirsi in questo contesto culturale. Poche nozioni di geometria proiettiva permettono di dimostrare il teorema in un modo che sorprende per la sua semplicità e brevità.
Vogliamo esporre una dimostrazione del noto teorema di Pappo contenuto nelle proposizioni 138 e 139 della sua ‘’Collezione matematica’’. Crediamo di fare cosa gradita al lettore per il fatto che la dimostrazione prende spunto dalla geometria proiettiva, parte della matematica che, sebbene oggi alquanto trascurata, emerge con prepotenza quando si vogliano affrontare le questioni delle trasformazioni lineari nel piano che vanno sotto il nome di omotetie, affinità, omologie etc. La dimostrazione del teorema di Pappo vuole inserirsi in questo contesto culturale. Poche nozioni di geometria proiettiva permettono di dimostrare il teorema in un modo che sorprende per la sua semplicità e brevità.
 Analisi storico-critica del pensiero del matematico Bernhard Riemann sulla geometria. 1. Le oscurità della geometria. 2. Ipotesi e molteplicità. 3. Superfici a strati sovrapposti. 4. Gauss e Herbart: Il molteplice tra matematica e filosofia. 5. Pregiudizi tradizionali.
Analisi storico-critica del pensiero del matematico Bernhard Riemann sulla geometria. 1. Le oscurità della geometria. 2. Ipotesi e molteplicità. 3. Superfici a strati sovrapposti. 4. Gauss e Herbart: Il molteplice tra matematica e filosofia. 5. Pregiudizi tradizionali.
La geometria di Bernhard Riemann (*)
1. LE «OSCURITÀ» DELLA GEOMETRIA
«Da Euclide a Legendre, per nominare il più famoso dei moderni revisori della geometria, questa oscurità non è stata chiarita né dai matematici né dai filosofi»
Il celebre scritto Sulle ipotesi che stanno a fondamento della geometria (1) ha un’origine circostanziata: è infatti la conferenza (Habilitationsvortrag) che Bernhard Riemann pronuncia il 10 giugno 1854 per il conseguimento del titolo di «Privatdozent». La conferenza, da tenersi di fronte a un pubblico più di filosofi che di matematici, deve dimostrare la capacità del ricercatore di collegare le ricerche scientifiche del proprio settore con più ampie istanze culturali. È infatti tendenza della cultura tedesca di questo periodo cercare di ripristinare un percorso unitario del sapere, da contrapporre alla frantumazione e settorialità emersa nella Francia postrivoluzionaria (2).
Per la propria conferenza, Riemann propone al consiglio dell’Università tre temi: due su elettricità e magnetismo, uno sulla geometria. Gauss, contrariamente alle aspettative del suo allievo, sceglie l’ultimo. Scopo del lavoro è collegare le più avanzate ricerche matematiche con il problema filosofico dello spazio.
Quando Riemann tiene la conferenza, in matematica sono già avvenuti importanti cambiamenti. Tra la fine del secolo XVIII e la prima metà del XIX, si assiste a un mutamento nel rapporto sia tra matematica ed esperienza, sia tra le diverse branche della matematica. In geometria sono state introdotte delle sconcertanti novità riguardo al postulato delle parallele. Fino a tutto il secolo XVIII, i matematici avevano continuato a chiedersi se il postulato delle parallele dovesse essere assunto come assioma o come teorema. I tentativi di darne una dimostrazione sembravano progredire ma rimaneva sempre qualche difficoltà. La negazione del postulato non conduceva a proposizioni assolutamente inaccettabili ma a proposizioni indipendenti da esso e che al più potevano essere ritenute bizzarre.
Nei primi decenni dell’Ottocento, si ha un vero e proprio capovolgimento del problema. Matematici come F. K. Schweikart, F. A. Taurinus, Gauss, Lobacevskij e J. Bolyai si pongono il problema non tanto della dimostrabilità del postulato, quanto quello della sua validità, poiché ritengono che il postulato delle parallele sia logicamente indipendente dagli altri postulati e che, sostituendolo, si possano sviluppare nuove geometrie. Pertanto si rendono conto che, dal punto di vista logico-matematico, un postulato sulle parallele non è univocamente determinabile; Gauss e Lobacevskij propongono di determinare quello relativo allo spazio fisico per mezzo di misurazioni su larga scala.
Tali idee vengono accolte con indifferenza e sono ancora sconosciute alla maggior parte dei matematici, quando Riemann tiene la propria conferenza. Tuttavia esse non sono il risultato di qualche isolata ricerca, né una semplice rinuncia a una dimostrazione che sembrava irraggiungibile, quanto piuttosto il segno di profondi cambiamenti prodotti da molteplici fattori.
Fino all’alba dell’Ottocento, l’idea di sottoporre il postulato di Euclide a una verifica empirica è del tutto estranea alla cultura occidentale. I più agguerriti empiristi considerano i postulati della geometria come intuizioni sensibili e quindi come principi indubitabili. Nelle applicazioni alla fisica, la geometria è legata al calcolo infinitesimale ed utilizzata nella meccanica, secondo le idee di Newton. Dalla fine del Settecento ai primi decenni dell’Ottocento fisici e matematici francesi (Laplace, Ampère, Fourier, Fresnel, Poisson, Carnot, per citare i più importanti) ottengono nuovi e importanti risultati dall’applicazione del calcolo differenziale ai più disparati campi della fisica: meccanica, idrodinamica, termodinamica, ottica, elettricità, magnetismo. Emerge anche un nuovo ruolo del rapporto matematica-esperienza. Secondo Laplace, per esempio, la matematica non deve fornire principi necessari ed evidenti, che garantiscano a priori il valore scientifico dei risultati, né limitarsi a una sistemazione estetica dei dati fenomenologici, bensì fornire gli strumenti essenziali per una graduale e sempre migliore conoscenza dei fenomeni naturali (3).
Contestualmente alle nuove applicazioni emerge la tendenza a riorganizzare l’analisi, definendo in modo più rigoroso i concetti di base, liberandola da concetti e intuizioni più o meno vaghi provenienti dalla geometria e dalla meccanica, individuando un campo di indagine ben definito e chiarendone il ruolo nella fisica. L’analisi matematica si presta ad essere applicata alla fisica, non perché ha origine nelle osservazioni dei fenomeni fisici ma solo perché in alcuni fenomeni si possono riscontrare quelle condizioni di continuità cui soddisfano gli enti matematici. Quanto più queste condizioni sono soddisfatte, tanto più le previsioni matematiche si verificano sperimentalmente.
Questa esigenza di rigore e di autonomia comincia a penetrare anche nella geometria. Il metodo geometrico che meglio si adatta a questo processo è quello della geometria proiettiva. Nata da problemi pratici di disegno, la geometria proiettiva viene ritenuta da Poncelet (4) in grado di raggiungere il livello di rigore e autonomia dell’analisi, e di liberarsi dal supporto algebrico assegnatole da Descartes e Fermat. Inoltre, attraverso Chasles e Steiner, viene progressivamente liberata dal ricorso alle figure e quindi dalla rappresentazione intuitiva. Infine Staudt (5) elimina il concetto di distanza dai principi basilari di questa scienza e rompe il diretto legame con l’esperienza.
Si viene così a delineare un indirizzo di studi che perverrà a un’interpretazione della geometria come un sistema ipotetico deduttivo nel quale si debbono solo esplicitare i rapporti fra gli enti implicitamente definiti dagli assiomi. Giò costituisce un allontanamento dalla concezione newtoniana della geometria come parte della fìsica e da quella kantiana che la considera scienza delle intuizioni.
Altre novità nello studio della geometria vengono introdotte da Gauss, che si occupa praticamente di tutti i settori della matematica e della fisica matematica. I suoi studi sul calcolo delle probabilità, astronomia, geodesia, elettricità e magnetismo costituiscono una naturale continuazione dell’opera dei francesi. I risultati che egli ottiene testimoniano, però, che, per l’avanzamento della matematica, non è necessario separare le varie discipline e purificarle dal ricorso alla fisica. Aritmetica, geometria, analisi e fisica nei lavori di Gauss si compenetrano e si scambiano problemi, metodologie e risultati ed evidenziano la necessità di sempre nuove impostazioni metodologiche.
Le idee di Gauss sul postulato delle parallele divengono note a un pubblico ampio solo dopo la sua morte. Egli era in corrispondenza con diversi matematici impegnati nella risoluzione del problema delle parallele ed è credibile supporre che le sue idee fossero note anche nell’ambiente matematico di Gottinga. Essenzialmente Gauss ritiene che non sia possibile fondare la geometria in modo interamente a priori e che pertanto essa non vada posta accanto all’aritmetica, che è effettivamente a priori, ma sullo stesso piano della meccanica (6).
Oltre che dei citati studi sugli sviluppi di nuove geometrie, diverse da quelle di Euclide, ma fondate sullo stesso apparato metodologico, Gauss è anche autore di un nuovo metodo, messo a punto in uno scritto del 1828 (7), per trattare la geometria differenziale. Tale metodo consiste nell’applicare i risultati dell’analisi infinitesimale allo studio delle curve e delle superfici. È un indirizzo di studi che certamente non ha origine con Gauss ma che solo con la sua opera diviene pienamente attuabile.
Un altro approccio alla geometria, di cui Gauss è generalmente riconosciuto iniziatore, è quello dell’Analysis situs. Esso consiste nello studio di quelle proprietà delle figure geometriche che non dipendono dal concetto di distanza, cioè di quelle proprietà che permangono quando le figure si trasformano per continuità. Gauss non ha dedicato uno scritto specifico a questo argomento; alcuni risultati sono però espressi in articoli nei quali si applica all’Analysis situs ai problemi del potenziale elettrico e magnetico, nonché alla risoluzione delle equazioni algebriche (8). Sarà il suo allievo Listing a scrivere nel 1847 un intero trattato di topologia (9).
Per completare il quadro, va ricordato che nel 1844 viene pubblicato uno scritto di H. Grassmann (10) in cui si indica un ulteriore metodo per lo studio della geometria. Questo scritto rimane a lungo poco conosciuto, perché ritenuto oscuro e eccessivamente filosofico; esso tuttavia contiene le prime idee di quello che diverrà il calcolo vettoriale e dà origine a un modo nuovo di trattare la geometria, attraverso la struttura algebrico-operazionale dei suoi enti. Per Grassmann, la geometria non fa parte della matematica pura ma della meccanica, perché a suo giudizio la geometria non è un prodotto del pensiero puro e si riferisce a oggetti reali esistenti. Per questa ragione Grassmann traccia una teoria dell’estensione, che è un sistema generale e astratto, indipendente dalla geometria, e della quale la teoria dello spazio costituisce solo un caso particolare.
Come si può vedere anche attraverso questa rapida sintesi, quando si cerca di sviluppare nella geometria un programma di autonomia e di revisione analogo a quello in atto nell’analisi, si produce, già nella prima metà del secolo, il proliferare di numerosi nuovi metodi geometrici. Accanto al classico indirizzo deduttivo euclideo e a quello algebrico cartesiano, si fanno strada rapidamente la geometria proiettiva, che si divide in sintetica (Staudt) e analitica (Pluker), la geometria differenziale, la topologia e il calcolo vettoriale. Ma soprattutto viene a rompersi, o quantomeno a complicarsi, lo stretto rapporto tra grandezze numeriche e grandezze geometriche, che sin dai pitagorici aveva costituito la base fondamentale della trattazione unitaria della matematica.
Per quanto concerne la filosofia della geometria, lo spazio assoluto di Newton e Va priori kantiano avevano sancito l’inattaccabilità della geometria euclidea. Per altro verso, anche alcuni empiristi, per esempio Locke, Berkeley e Hume, avevano riconosciuto che la nozione di spazio si costruisce ad opera dell’intelletto, attraverso un processo di astrazione e riflessione sulle percezioni sensoriali. Lo stesso Comte, pur affermando che la matematica non è una scienza di concetti ma di fatti, non offre contributi significativi per ciò che concerne più direttamente la geometria. J. S. Mill, invece, precisa la propria posizione: la geometria si costruisce per deduzione logica da definizioni e assiomi, i quali riguardano gli oggetti reali. Deve però riconoscere che definizioni e assiomi non sono esattamente conformi agli oggetti e si ottengono per induzione dall’evidenza dei nostri sensi: l’esperienza ci mostra linee che posseggono sempre meno spessore e sempre maggiore rigidità, da qui per induzione ricaviamo la definizione di retta come limite delle linee realmente esistenti (11).
Un elemento nuovo viene introdotto da Herbart, il quale ammette che l’esperienza non è unicamente costituita da dati sensoriali bruti: i dati si presentano sotto forme e rapporti. Tali forme dell’esperienza si possono comprendere con lo studio della psicologia, la quale ci può mostrare l’effettiva origine empirica della nostra rappresentazione dello spazio. Lo spazio è una specie di sedimento lasciato dal flusso delle nostre sensazioni. Perciò la geometria non deve supporre lo spazio come qualcosa di dato ma deve costruirlo insieme con tutte le sue determinazioni, eliminando le contraddizioni che l’esperienza presenta (12).
In queste posizioni empiriste sullo spazio fisico, quindi, pur riconoscendo che la geometria si costruisce attraverso l’esperienza, si ammette che la sola esperienza non basta per fondarla. Di conseguenza esperimenti del tipo di quelli effettuati da Gauss e Lobacevskij non sono ritenuti cruciali per una fondazione empirica di questa scienza.
Stabilire i reali rapporti tra progressi della geometria e filosofia geometrica, è piuttosto difficile. Si può affermare che i filosofi generalmente pongono scarsa attenzione alle nuove ricerche e non credono che la matematica possa apportare un reale contributo alla conoscenza dello spazio. Tra i matematici vi è una situazione più articolata. Un gran numero di essi presta molta attenzione alle nuove ricerche filosofiche ma non manca chi, come Gauss, è convinto che tra matematici e filosofi si sia ormai creato un forte divario di conoscenze.
«Voi vedete il medesimo genere di cose (l’incompetenza matematica) nei filosofi contemporanei Schelling, Hegel, Nees von Essenbeck, e nei loro seguaci; non vi fanno drizzare i capelli con le loro definizioni? […] Ed anche con lo stesso Kant spesso le cose non vanno molto meglio; secondo me, la sua distinzione fra proposizioni analitiche e sintetiche è una di quelle cose che cadono nella banalità o sono false» (13).
2. IPOTESI E MOLTEPLICITÀ
«Questi fatti (i fatti più semplici con cui si possono determinare le relazioni metriche dello spazio), come tutti i fatti, non sono necessari ma hanno solo certezza empirica, essi sono ipotesi».
Nelle linee principali, la conferenza di Riemann si può così riassumere. In geometria si presuppongono già dati, sia il concetto di spazio, sia i concetti fondamentali con i quali si costruiscono le figure geometriche. Le definizioni di tali concetti sono nominali e le regole per le costruzioni geometriche, invece di chiarire il significato dei concetti fondamentali, vengono presentate sotto forma di assiomi. Nonostante gli sforzi di matematici e filosofi, il significato profondo dei fondamenti della geometria rimane perciò nell’ombra. Non siamo in grado di affermare né se, o fino a che punto, le relazioni tra i concetti elementari della geometria sono necessarie, né addirittura se sono possibili.
Per comprendere il significato di queste relazioni, Riemann pensa che si debba risalire allo studio generale della nozione di grandezza molteplicemente estesa, o meglio, di molteplicità (14) (Mannigfaltigkeit) dei modi di determinazione (Bestimmungsweisen) di un concetto generale qualsiasi. Le molteplicità possono essere continue o discrete. Vi sono una quantità ragguardevole di esempi di questo secondo caso, mentre è molto più limitata la possibilità di formulare concetti i cui modi di determinazione formino una molteplicità continua: i casi più semplici sono le posizioni degli oggetti sensibili e i colori. Le molteplicità continue trovano, invece, un gran numero di applicazioni nella matematica superiore. Per questa ragione, il loro studio può essere affrontato con gli strumenti dell’analisi matematica e costituisce la base per il campo di ricerca denominato Analysis situs.
Lo studio delle molteplicità continue si fonda su due elementi: il numero di dimensioni della molteplicità e l’assegnazione delle coordinate ad ogni punto di essa. L’assegnazione delle coordinate è un’operazione arbitraria, fatta eccezione per due aspetti: il numero delle coordinate deve necessariamente corrispondere alle dimensioni della molteplicità e l’assegnazione deve essere continua.
Questa parte dello studio delle molteplicità riguarda esclusivamente il modo in cui i punti di una molteplicità continua sono disposti. È però possibile introdurre nelle molteplicità continue la nozione di distanza tra i suoi punti e determinare al loro interno relazioni metriche. Si ottiene così la possibilità di misurare le parti di una molteplicità continua e di conseguenza di fondare analiticamente la geometria.
Per compiere operazioni di misura, si devono assumere certe grandezze come unità e supporre che queste spostandosi non subiscano deformazioni. Il caso più semplice in cui è possibile spostare segmenti senza deformarli è quello descritto dal teorema di Pitagora: il suo significato analitico è che un elemento infinitesimo di linea si esprime come la radice quadrata di un’espressione differenziale di secondo grado.
L’espressione dell’elemento di linea può essere modificata nella sua formulazione matematica: dobbiamo perciò dedurre che è possibile applicare a una stessa molteplicità metriche diverse e, conseguentemente, che sono individuabili diversi modi di misurare le distanze. Elemento determinante per riconoscere tra tutte le metriche possibili quelle che effettivamente comportano delle differenze sulla molteplicità è la nozione di cuvatura. Riemann non si riferisce evidentemente al concetto geometrico e intuitivo di curvatura ma introduce una nozione del tutto nuova, astratta e analitica (15). Nel caso più semplice in cui è possibile spostare segmenti senza deformarli, la molteplicità ha curvatura nulla. Nel caso in cui sia possibile spostare parti pluridimensionali senza deformarle, la molteplicità avrà una curvatura costante ma non necessariamente nulla.
Altra questione è quella di stabilire quale, fra le molteplicità geometricamente possibili, sia adattabile allo spazio fisico. Per risolvere questo problema, è necessario caratterizzare con delle proprietà semplici ciascuna singola molteplicità; tali proprietà devono però esprimere affermazioni la cui validità possa essere sottoposta a verifica sperimentale. Una soluzione di questo problema è, a parere di Riemann, impossibile, perché esistono diversi modi per individuare i fatti semplici che sono alla base delle proprietà metriche dello spazio ma nessuno di essi si impone con il carattere della necessità. Ne consegue che allo spazio fisico possono indifferentemente essere applicate proprietà metriche diverse. L’applicazione di una certa metrica allo spazio fisico, altro non è che una semplice ipotesi.
Tutto ciò che dello spazio fisico si può dire è che esso è una molteplicità continua, illimitata e a tre dimensioni. Se, come Euclide, si assume l’ipotesi che la forma dei corpi nello spazio fisico non dipende dalla loro posizione, si deve concludere che lo spazio fisico ha curvatura costante. Anche in questo caso comunque restano indecise tre diverse possibilità a seconda che la curvatura sia costantemente nulla, positiva o negativa. Nel primo caso la somma degli angoli interni di un triangolo misurerà 180°, nel secondo avrà una misura maggiore e nel terzo una minore.
Quando si passa a verificare sperimentalmente quale di queste tre possibilità risulti valida, occorre valutare i risultati sperimentali in base alle seguenti osservazioni. Se assumiano lo spazio fisico come una molteplicità discreta, i risultati sperimentali potrebbero fornire dati esatti ma non sarebbe possibile conoscerli tutti, perché di numero elevatissimo. Se assumiamo lo spazio fisico come una molteplicità continua i risultati sperimentali risultano solo approssimativi. Ne consegue che, né il procedimento analitico, né l’approccio sperimentale possono risolvere il problema di individuare la natura della geometria della fisica.
Le misure compiute a livello astronomico hanno stabilito che lo spazio ha curvatura nulla e quindi che la geometria dell’astronomia è quella di Euclide (16). Queste misurazioni, però, sono solo approssimative, per cui, osserva Riemann, esse non possono farci conoscere nulla sulla curvatura dello spazio a livello microscopico, per altro verso, i concetti su cui si basano le misure macroscopiche, cioè corpo indeformabile e raggio di luce, perdono ogni significato a livello microscopico. Estendere la validità delle misure astronomiche a livello microscopico, significa ipotizzare che lo spazio conservi sempre la stessa curvatura. Riemann pensa invece che le relazioni metriche dello spazio nell’infinitamente piccolo possano non essere conformi ai presupposti della geometria euclidea e che si dovrebbero cambiare questi presupposti qualora si riuscisse a spiegare in modo più semplice i fenomeni naturali. Questa questione riguarda però la fisica.
Analizzando la conferenza, tenendo presente l’originalità dell’approccio riemanniano, si può affermare che in essa il problema dei fondamenti della geometria viene sviluppato secondo quattro problematiche: analisi, geometria, fisica e filosofia.
Per ciò che riguarda l’analisi matematica Riemann si propone di trovare una base per lo studio dell ‘analysis situs e fornire nuovi strumenti matematici per la teoria delle funzioni complesse e delle equazioni differenziali; a giudicare dal suo lavoro del 1857 sulle funzioni abeliane, ritiene di aver superato questo problema (17).
In geometria si propone di mostrare come uno studio dei fondamenti di questa scienza si può sviluppare seguendo una nuova via. Invece di porre alla base della geometria nuove definizioni e nuovi assiomi da sostituire a quelli di Euclide, si possono dedurre sia la geometria di Euclide, sia ogni altra geometria possibile, dal concetto generale di molteplicità e di metrica.
Per ciò che riguarda la natura dello spazio fisico riconosce che non è un problema matematico. La matematica deve fornire gli strumenti per formulare ipotesi, tenendo il più lontano possibile pregiudizi inveterati. Per questo scopo, l’approccio tradizionale alla geometria, che è di tipo assiomatico, è inadatto. Lo spazio va studiato non nella sua globalità ma nel suo comportamento locale e quindi nella sua struttura infinitesima:
dal punto di vista matematico solo l’analisi può garantire un tale studio. Inoltre, la teoria del potenziale, che sembra ricca di sviluppi in fisica e in matematica, è fondata sul calcolo analitico; in fisica, le proprietà degli oggetti si possono cogliere, secondo Riemann, attraverso il loro modo di essere nell’infinitamente piccolo. Riemann è perciò convinto che le ipotesi per lo spazio fisico vanno elaborate in termini di analisi matematica. La verifica sperimentale delle ipotesi e la loro connessione con le leggi generali dei fenomeni sono argomento esclusivo della fisica.
A conferma di ciò, e per meglio comprendere il ruolo che l’ipotesi ha nel pensiero di Riemann, va osservato che nella conferenza di abilitazione il termine «Hypothesen» è utilizzato, oltre che nel titolo, solo in un passaggio del testo, dove ha il significato di ipotesi fisica nel senso sopra precisato. Nel resto del saggio, dove si fa riferimento ad ipotesi della geometria, del tipo di quelle ammesse da Euclide con i suoi postulati, Riemann usa il termine « Voraussetzungen», cioè più «presupposti» che non «ipotesi».
In campo filosofico, alla controversa questione se lo spazio sia a priori o di origine empirica, la risposta di Riemann sembra essere che lo spazio non è completamente a priori, lo è solo per ciò che riguarda le grandezze molteplicemente estese. Le grandezze numeriche infatti sono argomento dell’analisi matematica e godono di un grado di validità che va al di là delle osservazioni sperimentali. Le altre caratteristiche dello spazio, e in primo luogo il concetto di distanza, non si impongono necessariamente.
L’implicazione più sconvolgente delle idee di Riemann, almeno sul piano filosofico, è l’aver sostanzialmente negato una posizione privilegiata al problema dello spazio fisico e di aver inserito l’aspetto a priori della geometria nell’analisi matematica e quello empirico nella fisica.
In sintesi, la geometria ha un suo fondamento nell’analisi. Sono analiticamente pos-sibili geometrie diverse; le misurazioni empiriche non sono in grado di determinare con precisione le caratteristiche geometriche dello spazio fisico.
Si tratta di affermazioni che modificano radicalmente gli schemi interpretativi della geometria. È perciò utile, per comprendere le sue affermazioni nel loro più ampio significato, ripercorrere brevemente la sua formazione culturale e le ricerche che aveva svolto in precedenza.
3. SUPERFICI A STRATI SOVRAPPOSTI
«Tali ricerche sono divenute necessarie in diverse parti della matematica, specialmente per trattare le funzioni analitiche a più valori e la loro mancanza è proprio il motivo principale per cui il noto teorema di Abel e i contributi di Lagrange, Pfaff, Jacobi alla teoria generale delle equazioni differenziali sono rimasti così a lungo infruttuosi».
Riemann ha studiato nelle Università di Berlino e di Gottinga, rispettivamente con Dirichlet, Jacobi e Eisenstein prima, Gauss e Weber dopo. A Berlino, dove prevale l’indirizzo analitico rigorista, entra in contatto con le recenti ricerche sulle funzioni di variabile complessa, le equazioni differenziali alle derivate parziali, la risoluzione di integrali, le funzioni abeliane ed ellittiche. A Gottinga prevale invece un indirizzo geo-metrico intuitivo, più attento alle applicazioni della matematica alla fisica. Sotto il profilo metodologico, l’opera di Riemann risulta particolarmente influenzata da quest’ultimo indirizzo.
La dissertazione dottorale, presentata alla fine di novembre del 1851 all’Università di Gottinga, è dedicata ai Grundlagen fur eine allgemeine Theorie der Funktionen einer veranderlichen complexen Grosse (Fondamenti per una teoria generale delle funzioni di una grandezza variabile complessa). Eisenstein, seguendo l’indirizzo di Lagrange, aveva identificato un ramo di una funzione complessa (18) con una serie convergente. Riemann si pone da un altro punto di vista: fondare l’intera teoria delle funzioni complesse sull’equazione di Laplace. Vengono così messi in luce gli stretti rapporti che intercorrono tra funzioni complesse e teoria del potenziale. Servendosi dei teoremi relativi alla teoria del potenziale, e in particolare del principio di Dirichlet, stabilisce che le funzioni complesse si possono caratterizzare per mezzo dei valori che esse prendono sul contorno di un certo dominio e delle singolarità presenti all’interno del dominio. Da queste premesse si evince il modo di procedere di Riemann: tenere costantemente collegate analisi, geometria e fisica, per utilizzare le metodologie dell’una nell’altra. Quest’aspetto è di fondamentale importanza per comprendere la sua opera di matematico.
Nello studio delle funzioni complesse si presentano inevitabilmente funzioni a più valori. Ciò comporta serie difficoltà per l’applicazione dei metodi analitici delle funzioni reali alle funzioni complesse. L’analisi reale infatti, così come era stata riorganizzata da Cauchy, pone alla base della definizione di funzione la condizione che si stabilisca una relazione tra un valore della variabile e un unico valore della funzione. Riemann riesce a trasformare le funzioni complesse a più valori in funzioni a un solo valore, servendosi di una metodologia di tipo geometrico. Prima di tutto utilizza la rappresentazione, realizzata da Gauss, dei numeri complessi mediante un piano; in questo modo le funzioni di variabile complessa divengono funzioni che trasformano un piano in un altro. Introduce un ente geometrico del tutto nuovo: una superficie a strati sovrapposti (aufeinander liegenden Flachenteile). Considera come dominio delle funzioni a più valori non il piano ma una superficie a più strati. Tale superficie è costruita in base al numero di valori della funzione, in modo che ad ogni punto del piano corrispondano tanti punti sulla superficie quanti sono gli strati; in ognuno di questi punti dello strato la funzione assume uno dei valori possibili. Può comunque accadere che per certi punti del piano la funzione assuma un solo valore, allora i valori della funzione, che generalmente sono distribuiti su più strati, in questi punti devono confluire in un unico valore: tali punti sono detti di ramificazione (Verzweigungspunkt). Di conseguenza gli strati della superficie debbono collegarsi proprio in questi punti e in un modo che non è semplice da rappresentare. Infatti, quando la variabile compie un giro completo intorno a un punto di diramazione, deve poter passare con continuità da uno strato all’altro della superficie, e dopo aver compiuto un numero di giri pari agli strati della superficie, deve poter ritornare allo strato di partenza.
Questa superficie, in seguito detta superficie di Riemann, non può essere visualizzata nemmeno per i casi più semplici; se ne può immaginare l’andamento in alcune zone ma non se ne può avere una rappresentazione globale. Si tratta di un oggetto di natura geometrica che sfugge al modo di procedere delle normali costruzioni geometriche; la sua costruzione, infatti, richiede una concezione astratta dello spazio della variabile. Essa, qualora ne venga accettata l’esistenza, evidenzia che la geometria ordinaria è troppo angusta per gli sviluppi conseguiti dall’analisi: è perciò necessario che la geometria analitica subisca un processo di ampliamento per essere posta nella condizione di svolgere adeguatamente la propria funzione all’interno delle problematiche dell’intera matematica. Riemann, rendendo uniformi le funzioni multiformi, spinge l’analisi complessa verso un processo di geometrizzazione ma, al tempo stesso, crea le premesse per una totale revisione della geometria.
Il tema della geometrizzazione dell’analisi viene ripreso in un altro passaggio della tesi di Riemann, quando si prova che il teorema integrale di Cauchy non è sempre valido. L’integrale di una funzione complessa calcolato lungo una curva chiusa posta su una superficie assume valori diversi in base alle caratteristiche geometriche della superficie. Ispirandosi alle idee embrionalmente esposte da Euler e Gauss, introduce la nozione di ordine di connessione (Zusammenhangsordnung) di una superficie. Una superficie è semplicemente connessa quando con un taglio si divide sempre in due parti separate; molteplicemente connessa nel caso in cui occorrano più tagli. I diversi valori dell’integrale di Cauchy dipendono, conclude Riemann, dall’ordine di connessione del dominio della funzione. La nozione di connessione è di natura puramente topologica, ossia non dipende dal concetto di distanza ma esclusivamente dal modo in cui la superficie è disposta. Riemann, quindi, si rende conto che per l’analisi matematica è importante uno studio delle figure geometriche indipendente e più generale di quello affrontato dalla geometria analitica. Esso deve essere indipendente dal concetto di distanza che invece si inserisce automaticamente nell’approccio cartesiano alla geometria.
4. GAUSS E HERBART: IL MOLTEPLICE TRA MATEMATICA E FILOSOFIA
«Nel tentare di risolvere inizialmente il primo di questi problemi, lo sviluppo del concetto di grandezza molteplicemente estesa, […] non ho potuto assolutamente servirmi di nessuno studio precedente, eccetto alcuni cenni molto brevi che Gauss ha dato su questo argomento […] e di alcune ricerche filosofiche di Herbart».
Riemann indica come base filosofica del suo modo di affrontare il problema dello spazio il concetto di grandezza molteplicemente estesa. Per quanto detto nel primo paragrafo, è abbastanza normale che egli si preoccupi più di indicare gli autori ai quali si è ispirato per la formulazione di questo concetto matematico e filosofico, che non di indicare l’origine dei teoremi che sottostanno alla sua trattazione.
Riemann cita esplicitamente gli scritti di Gauss in cui è abbozzato il concetto di molteplicità. Il primo di questi scritti è la memoria sui residui biquadratici (19). Gauss dimostra che i numeri complessi possono essere interpretati come una molteplicità a due dimensioni, e dà quindi una rappresentazione geometrica di questi numeri. Gauss ritiene in questo modo di avere posto nuova luce sulla vera metafisica dei numeri complessi. Il secondo scritto di Gauss tratta invece delle equazioni algebriche (20). Gauss, per dimostrare il teorema fondamentale dell’algebra, si serve di una metodologia che, come egli stesso afferma, appartiene all’analysis situs, perciò pone una distinzione tra geometria della posizione e geometria delle grandezze. Secondo i più recenti studi storici (21), ciò che ha maggiormente orientato Riemann è il seguente passo di Gauss:
«Il vero contenuto di tutta l’argomentazione appartiene a un dominio superiore, indipendente dalla geometria dello spazio, la teoria generale astratta delle grandezze, il cui argomento è costituito dalle combinazioni di grandezze connesse tra di loro in modo continuo, un dominio che è ancora poco coltivato e nel quale non ci si può muovere senza un linguaggio preso in prestito dal contesto della geometria dello spazio» (22).
Il concetto di molteplicità ha quindi origine in questi pochi riferimenti di Gauss. Esso, sicuramente, era già stato compreso da Riemann nella stesura della tesi di dottorato. In essa si era infatti servito dell’idea di Gauss di rappresentare i numeri complessi mediante un piano. Gauss, tuttavia, non parla di un «piano» dei numeri complessi, poiché si rende conto che non si tratta di un vero e proprio piano nel senso usuale del termini, usa l’espressione «molteplicità bidimensionale» (zweidimensionalen Mannigfaltigkeit). Riemann nella sua tesi usa inizialmente il termine «dominio di grandezze bidimensionali» (Grofiengebietes von zwei Dimensionerì) e successivamente quello di «piano» (Ebene). La superficie a più strati, pur essendo una parte di questo dominio e quindi non una vera e propria superficie, viene chiamata ugualmente «superficie» (Flàche). È chiaro però che Riemann usa questi termini in modo generico, senza precisarli e quando parla di superficie ha già in mente una molteplicità bidimensionale di grandezze numeriche. Per tutti questi concetti Riemann trova una precisa collocazione matematica nella teoria generale delle molteplicità (23).
Nella seconda parte della conferenza di abilitazione, dove si introduce il concetto di metrica, Riemann sostiene di servirsi dei risultati ottenuti da Gauss nella memoria sulle superfici curve (24). Non vi è dubbio che Riemann sviluppa lo studio delle molteplicità pluriestese come generalizzazione dei risultati ottenuti da Gauss per le superfici curve. Una breve analisi di questo processo di generalizzazione può essere utile a capire la portata innovativa della memoria di Riemann.
Solitamente nello studio delle superfici si tiene conto di termini che si riferiscono a punti e linee che giacciono interamente sulla superficie e di termini che si riferiscono a punti e linee che giacciono in parte sulla superficie e in parte fuori di essa. Secondo questo modo di procedere non sarebbe stato possibile studiare le molteplicità senza pensarle immerse nello spazio geometrico. Gauss, però, ha fatto vedere che tutti i termini del secondo tipo possono essere eliminati e che quindi è possibile studiare una superficie senza necessariamente pensarla come parte dello spazio. Da questo risultato, con un ardito passaggio, Riemann si convince che sia possibile anche uno studio delle molteplicità senza fare alcun riferimento al concetto di spazio.
Fino alla memoria di Gauss, le superfici dello spazio tridimensionale venivano solitamente trattate per mezzo di equazioni che legano tra di loro le tre coordinate spaziali, oppure esprimendo una delle tre coordinate per mezzo delle altre due: è la rappresentazione di una superfice nella geometria cartesiana. Euler aveva introdotto però l’idea che, poiché una superficie ha due dimensioni, per determinare le coordinate dei suoi punti sono sufficienti due parametri: le tre coordinate si possono ottenere tramite questi due parametri. Gauss, che, prima di occuparsi di geometria differenziale, si era interessato di problemi relativi alla misurazione e rappresentazione della superficie terrestre mediante carte, si rende conto dell’utilità di una rappresentazione di questo tipo rispetto a quella cartesiana e si propone di servirsene per il proprio studio sistematico delle superfià.
La rappresentazione parametrica consiste nel riferirsi a sistemi di assi curvilinei che giacciono sulla superficie: essa è quindi una rappresentazione intrinseca alla superficie. Le coordinate in questo caso vengono dette coordinate curvilinee. Il vantaggio è evidente nel caso si consideri la superficie terrestre. Per individuare un punto sulla superficie terrestre infatti è più conveniente dare una longitudine e una latitudine piuttosto che dare tre coordinate in un sistema di riferimento posto nello spazio. Nel primo caso infatti, si fa riferimento a posizioni della superficie terrestre; nel secondo, bisogna immaginarsi fuori dalla superficie.
In sostanza le coordinate curvilinee permettono di individuare i punti della superficie senza fare riferimento allo spazio in cui tale superficie si sviluppa. La generalizzazione che compie Riemann consiste nel ritenere che sia possibile assegnare coordinate ai punti della molteplicità senza fare alcun riferimento ad assi cartesiani dello spazio geometrico.
Il passo successivo è quello di introdurre dei metodi per misurare le distanze sulle molteplicità. Anche qui Riemann si serve dei risultati di Gauss. Gauss ha fatto vedere in che modo sia possibile effettuare misure su una superficie senza fare riferimento allo spazio esterno. Si è servito delle coordinate curvilinee delle superfià e ha ottenuto un’espressione differenziale del secondo ordine che permette di calcolare la misura di un tratto infinitesimo delle curve giacenti sulla superficie. Da questo modo di misurare le distanze segue immediatamente che la geometria di una superficie curva non è una geometria euclidea. Infatti, se consideriamo la superficie di una sfera, è possibile calcolare in due modi la distanza tra due dei suoi punti. Si può misurare il percorso più breve che li unisce; esso attraversa la superficie e giace nello spazio interno. In questo caso la geometria della sfera è la stessa di quella dello spazio. Se invece ci imponiamo di non uscire dalla superficie, il percorso più breve tra i due punti è un arco di circonferenza. In questo caso le misure sono intrinseche alla superficie ma la geometria che ne segue non è euclidea.
La generalizzazione compiuta da Riemann per ciò che concerne la misura delle distanze è duplice e va ben al di là del lavoro di Gauss. Riemann per compiere le misure sulla molteplicità si serve della formula trovata da Gauss, sviluppa però il suo lavoro sulla convinzione che sia anche possibile alterare i coefficienti che compaiono nella formula della distanza. Ottiene come conseguenza modi diversi di effettuare le misure nella stessa molteplicità. Per le problematiche concernenti la geometria dello spazio, ciò comporta che nell’usuale spazio tridimensionale la stessa superficie può avere, oltre a una metrica che consegue da quella dello spazio, metriche di tipo diverso e del tutto arbitrarie. Non solo, anche la metrica dello spazio usuale può essere arbitrariamente alterata. È questo, probabilmente, il contributo più rilevante che Riemann dà al problema della geometria dello spazio.
Un altro risultato importante ottenuto da Riemann riguarda il movimento dei corpi solidi nello spazio. Riemann riconosce che la possibilità di effettuare misure nello spazio è strettamente legata alla possibilità di muovere i corpi senza che si deformino. Questo risultato influirà in maniera determinante sugli studi successivi dei fondamenti della geometria e diverrà il punto di partenza per la nozione di gruppo di trasformazioni. La matrice di questa idea si può rintracciare in un risultato matematico ottenuto da Gauss. Se si muove una parte di una superficie facendola scorrere sulla stessa superfìcie cui appartiene, essa aderirà perfettamente in ogni momento solo se la sua curvatura è punto per punto identica a quella della superficie, ossia se quest’ultima ha sempre la stessa curvatura. Una tale proprietà discende dal teorema, da Gauss detto «theorema egregium», che stabilisce che se due superfici possono essere messe in corrispondenza punto per punto, in modo che l’elemento di distanza abbia in entrambe la stessa espressione, allora le due superfici sono dette isometriche e hanno la stessa geometria: in particolare nei punti corrispondenti hanno la stessa curvatura.
La generalizzazione compiuta da Riemann consiste nel ritenere che lo stesso teorema valga per le molteplicità e in particolare per lo spazio tridimensionale. In questo caso le parti di superficie considerate da Gauss divengono parti tridimensionali dello spazio, ossia corpi. Applicando il teorema di Gauss si ottiene che per muovere un corpo senza che si deformi la curvatura dello spazio deve essere costante. Di conseguenza, se effettuare misure nello spazio comporta il trasportare un corpo scelto come unità di misurarle misure hanno valore se il corpo non si deforma durante questo movimento; ciò può accadere solo se lo spazio ha curvatura costante, anche se non necessariamente nulla. L’utilizzazione da parte di Riemann dei risultati matematici ottenuti da Gauss è quindi evidente ed è anche evidente che per il concetto di molteplicità si è servito di qualche idea avanzata da Gauss.
È invece molto discusso dagli storici il reale apporto che la filosofia di Herbart ha potuto avere sulla formulazione delle idee esposte nella conferenza; del resto lo stesso Riemann non fa riferimento a precise opere di Herbart ma genericamente alle ricerche filosofiche di quest’ultimo. Fino a qualche decennio fa, era luogo comune che Riemann si fosse servito delle idee di Herbart e tutti gli storici hanno intravisto in qualche aspetto della filosofia di Herbart il nocciolo filosofico delle idee di Riemann. Russell aveva creduto di trovare ben sei punti della filosofia di Herbart utilizzati da Riemann (25). Più recentemente Torretti ha dimostrato invece che su quasi tutti i punti vi è discordanza tra i due autori (26). Secondo alcuni studi storici ancora più recenti, Herbart ha avuto ben poca influenza diretta sulla matematica di Riemann, mentre ha influito sulle sue idee filosofiche, che però Riemann ha sviluppato in pochi scritti inediti. In particolare Scholz ritiene che il concetto di molteplicità di Riemann non ha alcuna connessione con il pensiero geometrico di Herbart e che esso sia stato elaborato esclusivamente in ambito matematico (27). G. Nowak ritiene che la filosofia dello spazio abbia influenzato Riemann senza che questi la condividesse completa-mente (28).
Tuttavia, per comprendere meglio il rapporto tra filosofia e matematica nella memoria di Riemann, va osservato, come già si è detto, che è una tendenza generale della cultura tedesca di quel momento cercare di unificare conoscenze provenienti dalla scienza con quelle provenienti dalla filosofia, nonché della tendenza abbastanza diffusa tra i matematici di affermare di essersi ispirati a qualche filosofo. Non va poi dimenticato che era proprio nello spirito della conferenza di abilitazione porre il collegamento tra ricerche matematiche e ricerca filosofica. Infine, come osserva lo storico Nowak, è molto probabile che, quando Riemann tiene la conferenza, tra gli ordinari di Gottinga sia presente Lotze. Lotze era succeduto a Herbart ed era indiscutibilmente un kantiano, e pur apprezzando l’opera di Herbart dissentiva da questi proprio in materia di filosofia della geometria. Pertanto Riemann, prudentemente, invece di criticare apertamente Kant si dichiara influenzato da Herbart, e cioè, invece di affermare che le sue ricerche matematiche hanno provato l’insostenibilità della posizione kantiana, ha voluto dire che sono state le nuove dottrine filosofiche a influire sulle sue ricerche matematiche.
5. PREGIUDIZI TRADIZIONALI
«Tali studi, che, come quello condotto qui, partono da concetti generali, possono solo servire a che questo compito (la soluzione del problema della validità dei postulati della geometria) non sia ostacolato dalla limitatezza dei concetti e che il progresso nella conoscenza delle connessioni delle cose non sia ostacolato da pregiudizi tradizionali».
La conferenza di Riemann, sebbene accolta con molto entusiasmo da parte di Gauss (29), rimane inedita fino a un anno dopo la morte del suo autore. La stessa indifferenza, almeno inizialmente, era toccata alle opere di Lobacevskij e Bolyai. Dopo la morte di Gauss, prima il necrologio del suo collega Sartorius von Waltershausen, poi la pubblicazione tra il 1860 e il 1863 della corrispondenza tra Gauss e Schumacher, rendono pubbliche le convinzioni del grande matematico tedesco sul postulato di Euclide e contribuiscono ad accendere il dibattito sul tema dei fondamenti della geometria.
L’inizio vero e proprio del dibattito è opera però di un costante e lungo lavoro di alcuni geometri minori; i quali, più che portare nuovi risultati, contribuiscono a rendere noti quelli di Gauss, Lobacevskij, Bolyai e Riemann. In Germania R. Baltzer, nella seconda edizione del suo libro Elemente der Mathematik del 1867, sostituisce la definizione euclidea di retta parallela con quella derivata dalle nuove concezioni sulla geometria; giustifica questa innovazione affermando che la nuova definizione è più generale di quella ordinaria. Nello stesso tempo, Baltzer richiama l’attenzione del francese J. Houell sulle nuove geometrie. Houell da tempo si interessa di questioni di geometria elementare. Nel 1866 traduce dal tedesco l’opuscolo di Lobacevskij e un estratto della corrispondenza fra Gauss e Schumacher; nel 1867 traduce lo scritto di Bolyai sulle geometrie non euclidee. In Italia le traduzioni di questi scritti sono opera di A. Forti e G. Battagliai (30).
Il problema della posizione da prendere nei confronti delle nuove geometrie è in questo periodo di scottante attualità per la cultura italiana, perché direttamente connesso con quello dell’insegnamento della geometria nelle scuole del nuovo Regno. Una proposta di riforma di questo insegnamento fatta da Cremona e Brioschi prevede infatti l’adozione degli Elementi di Euclide come testo per l’insegnamento della geometria nelle scuole classiche. A questo indirizzo si contrappone l’opera di G. Battaglini che a Napoli nel 1867 fonda e dirige il Giornale di Matematica. La nuova rivista diviene ben presto il giornale della geometria non euclidea e vi collaborano matematici di livello europeo. Si scatena così un furibondo clima di polemiche, nel quale le nuove geometrie vengono definite da alcuni come geometrie del soprasensibile e da manicomio (31).
Nel 1867 sulle Abhandlungen der Koniglichen Gesellschaft der Wissenschaften zu Gòt-tingen viene pubblicata a cura di Dedekind la conferenza di abilitazione di Riemann; nel 1870 viene pubblicata la traduzione francese a cura di Houell e nel 1873 quella inglese a cura di W. Clifford.
La pubblicazione della conferenza di Riemann convince Beltrami a pubblicare nel 1868 il famoso Saggio di interpretazione della geometria non-euclidea (32). Il saggio era stato redatto da più di un anno (33) e si serve di alcune intuizioni geometriche presenti anche nella conferenza di Riemann (34). Riemann, infatti, aveva dato dei modelli per visualizzare le superfici a curvatura costante positiva e negativa. Quelle a curvatura positiva, afferma Riemann, si possono immaginare come sfere di raggio uguale a uno, diviso per la radice quadrata della curvatura; quelle a curvatura negativa hanno la forma della parte interna rivolta verso l’asse della superficie di un anello. Beltrami comprende la portata di questi modelli per il dibattito allora in corso sull’accettazione delle nuove geometrie e dimostra che è possibile dare un substrato reale agli spazi a curvatura costante negativa previsti da Lobacevskij e Bolyai. Beltrami mostra come, all’interno della geometria euclidea, sia possibile costruire una superficie che abbia tutte le caratteristiche della geometria di Lobacevskij. In questo modo, anche se non in maniera completa (35), la non contraddittorietà dei postulati della geometria di Lobacevskij viene ricondotta a quella dei postulati della geometria ordinaria, e, da un punto di vista puramente logico, le due geometrie divengono assolutamente equivalenti.
Il saggio di Beltrami diviene subito noto a livello internazionale e fornisce la chiave giusta per risolvere, da un punto di vista logico-matematico, il problema del V postulato di Euclide. Tra gli anni Settanta e Ottanta il problema della validità logica delle geometrie non euclidee viene definitivamente risolto. I modelli di Beltrami, Klein e Poincaré, provenienti anche da problematiche diverse della matematica, riducono la validità logica delle geometrie non euclidee a quella della geometria euclidea: poiché nessuno dubita della validità della geometria euclidea, tutte le geometrie vengono accettate come matematicamente possibili e valide. Infine nel programma di Erlangen del 1872 Klein stabilisce definitivamente che la geometria euclidea e quelle non euclidee derivano da un’unica geometria, quella proiettiva (36).
Conseguentemente alla organizzazione delle geometrie concepita da Klein, i manuali di geometria ma anche gli altri testi che si occupano di questo argomento, riportano, accanto alla geometria euclidea, la geometria iperbolica, o geometria di Lobacevskij, e la geometria ellittica, o geometria di Riemann. Riemann e Lobacevskij vengono considerati come i fondatori delle due geometrie non euclidee.
Secondo questa schematizzazione, il contributo originale di Riemann consiste nel l’aver provato la possibilità di un tipo di geometria per lo spazio, quella a curvatura positiva, che era stata ritenuta da Lobacevskij improponibile. Lobacevskij ritiene infatti che lo spazio in quanto infinito non può avere curvatura positiva. Riemann invece, senza tenere conto dello scritto di Lobacevskij, che probabilmente non conosceva, mette in luce che la caratteristica dello spazio di essere finito dipende dalla metrica, mentre quella di essere illimitato è una caratteristica intrinseca allo spazio. Ciò che generalmente sappiamo, afferma Riemann, è che lo spazio si estende in maniera illimitata in ogni direzione, nonostante ciò esso può essere finito. Un esempio è la superficie di una sfera, che pur essendo finita è illimitata.
Il lavoro di Riemann, inserito nel dibattito sulle geometrie non euclidee, viene però ridimensionato nella sua portata innovatrice. Le ipotesi di Riemann vengono intese come ipotesi matematiche da sostituire agli assiomi della costruzione euclidea. Tutto il saggio appare ad alcuni come un modo tortuoso e poco chiaro per dire ciò che Gauss già sapeva e che Lobacevskij aveva già pubblicato. Veronese, per esempio, nel suo scritto Fondamenti di geometria afferma:
«Le ipotesi di Riemann non soltanto confermano quella di Lobacevskij, ma egli stesso ha fatto rilevare che lo spazio sebbene illimitato può essere finito. E questo è a mio parere il risultato più importante della memoria di Riemann, per quanto ad esso si possa giungere in un modo molto più semplice» (37).
Le implicazioni filosofiche della conferenza vengono invece riscoperte da Helmholtz. Helmholtz non si occupa della validità matematica delle nuove geometrie, bensì dei fondamenti della geometria dal punto di vista filosofico-psicologico; sviluppa le sue ricerche nell’ambito della fisiologia e psicologia degli organi di senso e perviene alla problematica dei fondamenti della geometria nel corso dei suoi studi sulla vista e, più precisamente, sulla localizzazione degli oggetti percepiti visivamente. Scrive un primo saggio sui fondamenti della geometria nel 1866, Nel 1868 si accinge a scriverne un secondo, quando viene a conoscenza che Riemann si era occupato di questo problema. Ricevuta una copia della memoria di Riemann, Helmholtz conclude nel mese di giugno il suo studio Sui fatti che stanno a fondamento della geometria (38).
Il titolo è chiaramente in contrapposizione con quello di Riemann: la tesi di Helmholtz è che le condizioni che Riemann chiama ipotesi siano invece dei fatti. Per Riemann lo studio dello spazio fisico deve essere condotto in maniera analoga allo studio della fisica: si avanzano alcune ipotesi sul tipo di metrica dello spazio e si verifica sperimentalmente quale nel contesto della teoria fisica in atto funziona meglio. Per Helmholtz la percezione del fatto che in natura esistono dei corpi rigidi, e cioè dei corpi che muovendosi rimangono inalterati nella forma, è la condizione che da sola, senza ulteriori ipotesi, ci consente di stabilire la natura dello spazio nel quale percepiamo i corpi. Il punto di partenza utilizzato da Riemann, e cioè il concetto di metrica e il suo stretto legame con il movimento dei corpi è, secondo Helmholtz, effettivamente alla base del processo biologico-psicologico di costruzione dello spazio.
Attraverso questo recupero della conferenza di Riemann, viene a delinearsi una nuova impostazione per il problema filosofico-matematico dello spazio, noto come problema di Riemann-Helmholtz: il fatto che in natura esistano corpi rigidi che possono liberamente muoversi è da solo in grado di determinare la natura geometrica dello spazio in cui organizziamo le nostre percezioni?
Riemann viene riconosciuto come l’autore della formulazione matematica del problema ed Helmholtz di quella filosofica (39). Si tratta evidentemente di un parziale recupero delle conclusioni di Riemann, conclusioni che peraltro non convergono con quelle di Helmholtz. Infatti Helmholtz inizialmente ritiene che l’esistenza dei corpi rigidi caratterizzi univocamente la geometria dello spazio fisico come geometria euclidea, sarà però costretto a ricredersi per un’obiezione mossagli da Beltrami: come aveva affermato Riemann, l’esistenza dei corpi rigidi ci assicura solo che lo spazio ha curvatura costante e non necessariamente nulla.
Il saggio di Helmholtz diviene dal punto di vista filosofico un superamento di quello di Riemann (40). Helmholtz è infatti impegnato a dare un effettivo collegamento tra la filosofia di Kant, Fichte, Herbart e le scienze empiriche. Già nel saggio del 1855 Uber das Sehen des Menschen, Helmholtz aveva mostrato come Va priori kantiano non fosse altro che una specie di legge empirica che agisce a livello di psicologia e fisiologia degli organi di senso. Così anche il problema dello spazio fisico trova il suo collegamento con la filosofia, e quindi con la teoria della conoscenza, non per il tramite della fisica, bensì della biologia. Tuttavia Riemann aveva in sostanza negato che il problema dello spazio fisico potesse essere risolto sul piano filosofico e che esso potesse avere una sua «dignità gnoseologica» (41). Helmholtz invece riafferma questa dignità.
Una forte rivalutazione del lavoro di Riemann, dal punto di vista filosofico, fisico e matematico si ha a partire dal secondo decennio del nuovo secolo. L’impostazione di Riemann dello studio delle molteplicità, o varietà come verranno poi chiamate, trova terreno fertile tra i matematici italiani. Ricci Curbastro e Levi-Civita, attraverso gli studi di Beltrami e L. Bianchi, pervengono nel 1899 a un nuovo e più generale calcolo differenziale. In questa memoria vengono poste le basi del calcolo differenziale assoluto, che è un algoritmo rivolto a trattare le proprietà delle varietà riemanniane a un numero qualunque di dimensioni, mediante operatori invarianti e covarianti rispetto alle trasformazioni che conservano l’elemento di linea. Tale memoria, assieme a quella del 1917 di Levi-Civita, pone le basi per l’applicazione del nuovo metodo di calcolo alla teoria della relatività generale di Einstein. Nella teoria di Einstein, la struttura metrica del continuo spazio-temporale è messa in relazione punto per punto con il tensore massa-energia attraverso le equazioni del campo e la curvatura dello spazio risulta variabile e dipendente dalla distribuzione della massa-energia.
Le varietà riemanniane divengono tra gli oggetti più studiati in matematica. In filosofia il problema dello spazio acquista una posizione centrale nel dibattito sul valore delle conoscenze empiriche e il passo della conferenza di Riemann:
«[…] la base delle relazioni metriche deve essere cercata al di fuori delle molteplicità, nelle forze di legame che in esse agiscono».
diviene una «visione profetica», «un’anticipazione di alcune idee centrali della gravitazione di Einstein» (42). Rimane così l’equivoco, in qualche trattazione sull’argomento, che la geometria ellittica di Riemann sia la geometria accettata da Einstein nella teoria della relatività generale.
S. Donato di Lecce
ANTONIO BERNARDO
(*) Articolo pubblicato su "Cultura e scuola", N. 122, 1992, pp. 252-269.
(1) B. RIEMANN, Uber die Hypothesen, welche der Geometrie zu Grmde liegen, in «Abhandlungen der Kòniglichen Gesellschaft der Wissenschaften zu Gòttingen», voi. 13 (1866/1867), Gòttingen. Ripubblicata in Bernhard Riemann’s Gesammelte Mathematiche Werke Und Wissenschaftlicher Nachlass, Leipzig, Teub- ner, 1876. Traduzione italiana in A. EINSTEIN, Relatività: esposizione divulgativa, e scritti classici su Spazio Geometria Fisica (a cura di B. CERMIGNANI), Torino, Boringheri, 1977.
(2) Cfr. S. POGGI, Introduzione a II Positivismo, Bari, Laterza, 1987.
(3) Cfr. P. S. LAPLACE, Essai philosophique sur les probabilités, Courcier, Parigi, 1814. Trad. it. Opere di Pierre Simon Laplace, a cura di O. PESENTI CAMBURSANO, Torino, UTET, 1967, pp. 241-404.
(4) Cfr. J. V. PONCELET, Traité des propriétès projectives des figures, Paris, Bachelier, 1822.
(5) Cfr. K. G. C. VON STAUDT, Geometrie der Lage, Niirnberg, Bauer-Raspe, 1847.
(6) Cfr. Lettera del 28 aprile 1817 a Olbers, in C. F. GAUSS, Werke, Leipzig, Teubner, 1900, voi. VILI, p. 177. Parzialmente tradotta in italiano in P. PARRINI, Fisica e geometria dall’ottocento a oggi, Loescher, Torino, 1979.
(7) Cfr. C. F. GAUSS, Disquisitiones generales circa superficies curvas, in Werke, cit., voi. IV.
(8) Sui contributi di Gauss alla nascita della topologia confrontare J. C. PONT, La Topologie, Algé- brique des origines à Poincaré, Paris, Presses Universitaires de France, 1974, pp. 31-38.
(9) Cfr. J. B. LISTING, Vorstudien zur Topologie, Gòttinger Studien, 1847.
(10) Cfr. H. GRASSMANN, Die Wissenschaft der extensiven Gròsse oder die Ausdehnungslehre, eine neue mathematische Disciplin. Erster Theil, die lineale Ausdehnungslehre, Leipzig, Otto Wigand, 1844.
(11) Si tratta evidentemente di una schematizzazione di posizioni ben più diversificate e complesse, e che spesso anche per uno stesso autore sono andate evolvendo. Per uno studio più approfondito si rinvia ai testi ormai classici di M. JAMMER, Concepts of Space. The History of the Theories of Space in Physics, Cambridge, Harvard University Press, 1954 (trad. it. Storia del concetto di spazio, Milano, Feltrinelli, 1974) e di E. CASSIRER, DOS Erkenntnisproblem in der Philosophie und Wissenschaft der neueren Zeit, IV: Von Hegels Tod bis zur Gegenwart (1832-;1932), Kohlhammer, Stuttgart, 1957 (trad. it. Storia della fi-losofia moderna, IV: Il problema della conoscenza nei sistemi posthegeliani, Torino, Einaudi, 1961).
(12) La teoria psicologica dello spazio è presentata da HERBART in Psychologie als Wissenschaft neu gegrmdet auf Erfahrung, Metaphysik und Mathematik (1824/25) in J. F. HERBART, Sàmmtliche Werke, Leipzig, Leopold Voss, voi. VI, pp. 114-150. Confronta anche G. F. HERBART, Introduzione alla filosofia, Bari, Laterza, 1927 (l’edizione originale è del 1813), p. 270.
(13) Cfr. Lettera a Schumacher dell’I novembre 1844. Citata in E. T. BELL, I grandi matematici, Firenze, Sansoni, 1850, p. 244.
(14) Il termine «Mannigfaltigkeit» è stato riferito, con il passare del tempo, a un concetto che è andato evolvendosi e precisandosi fino ad indicare un tipo particolare di struttura matematica chiamata «varietà». Secondo il significato di Riemann, tale termine è più vicino a quello attuale di «insieme». Lo stesso Cantor, del resto, quando formula la sua teoria degli insiemi, usa inizialmente il termine «Mannigfaltigkeit», in seguito usa il termine «Mengenbegrift».
(15) Il procedimento con cui Riemann introduce questo concetto è generalmente ritenuto oscuro. Confronta per esempio P. LIBERMANN, Géométrk différentielle, in J. DIEUDONNÉ, Abrégé d’histoire des matte- matiques 1700-1900, Paris, Hermann, 1978, p. 199.
(16) Probabilmente Riemann si riferisce alle misure effettuate da Gauss degli angoli di un triangolo formato da tre cime di monti intorno ad Hannover. Non è possibile stabilire se Riemann conoscesse i lavori di Lobacevskij, e quindi le misure che questi aveva effettuato sugli angoli del triangolo avente per vertici la Terra, il Sole e la stella Sirio. Inoltre, è attualmente controverso se le misure effettuate da Gauss avessero lo scopo di verificare il tipo di geometria dello spazio fisico. Confronta a questo proposito A. I. MILLER, The Myth of Gauss’ Experiment on the Euclidean Nature of Physical Space, in «ISIS», 63 (1972), pp. 345-348; i commenti a questo articolo di G. Goe e B. L. van der Waerden e la replica di A. I. Miller nel numero 65 della stessa rivista.
(17) Cfr. E. SCHOLZ, Geschichte des Mannigfaltigkeitsbegriffs von Riemann bis Poincaré, Basel, Birkhàu- ser, 1980, p. 90; M. MONASTRYRSKY, Riemann, Topology and Physics, Boston, Birkhàuser, 1987, p. 28.
(18) È da intendersi «funzione di variabile complessa».
(19) Cfr. C. F. GAUSS, Theoria residuorum biquadraticorum, commentatio secunda, (1831), in Werke, cit. voi. 2.
(20) Cfr. C. F. GAUSS, Beitràge zur Theorie der algebraischen Gleichmgen, (1849) in Werke, cit., voi. III.
(21) Cfr. E. SCHOLZ, Geschichte… cit., p. 54; G. NOWAK, Riemann’s Habilitationsvortrag And the Syn- thetic A priori Status of Geometry, in AA. W., The History of Modem Mathematics, New York, Academic Press, 1989, voi. I, pp. 27-28.
(22) Cfr. C. F. GAUSS, Beitràge… cit., p. 79.
(23) Cfr. E. SCHOLZ, Geschichte… cit., p. 57.
(24) Cfr. C. F. GAUSS, Disquisitiones… cit.
(25) Cfr. B. RUSSEL, An Essay on the Foundations of Geometry, Cambridge, University Press, 1897; traduzione italiana, I fondamenti della geometria, Roma, Newton Compton editori, 1975, p. 74.
(26) Cfr. R. TORRETTI, Philosophy of geometry from Riemann to Poncaré, Dordrecht, Reidei, 1978 pp 107-108.
(27) Cfr. E. SCHOLZ, Herbart’s Influence on Bernhard Riemann, in «Historia Mathematica», voi. 9 di Herbart (1982), pp. 413-440. Questo saggio contiene anche alcuni appunti inediti di Riemann sulla filosofia di Herbart. (
28) Cfr. G. NOVAK, Riemann’s… cit.
(29) Cfr. R. DEDEKIND, Bernhard Riemann’s Lebenslauf] in B. RIEMANN, Gesammelte… cit., pp. 509-526.
(30) Cfr. R. BONOLA, La geometria non-euclidea. Esposizione storico-critica del suo sviluppo, Bologna, Zanichelli, 1906. (31) Cfr. U. BOTTAZZINI, Il flauto di Hilbert. Storia della matematica moderna e contemporanea, Torino, UTET, 1990.
(32) E. BELTRAMI, Saggio di interpretazione della geometria non euclidea, in «Giornale di matematiche ad uso degli studenti», voi. 6 (1868), pp. 284-312.
(33) Cfr. U. BOTTAZZINI, Il flauto di Hilbert… cit., p. 185.
(34) Riemann, durante il soggiorno in Italia, si incontra con Beltrami nel 1860; non è da escludere perciò che Beltrami conoscesse le idee di Riemann sulla geometria prima della pubblicazione della conferenza.
(35) Sarà F. KLEIN nel saggio del 1871, ùber die sogennante Nicht-Euklidische Geometrie, a darne una dimostrazione completa. Cfr. F. KLEIN, Gesammelte mathematische Abhandlungen, Berlin, Spinger, 1921-1923, voi. I, pp. 254-305.
(36) Cfr. F. KLEIN, Vergleichende Betrachtungen iiber neuere geometrische Forscungen, in F. KLEIN, Gesammelte… cit., voL I, pp. 460-497.
(37) Cfr. G. VERONESE, Fondamenti di geometria a più dimensioni e a più specie di unità rettilinee, esposti in forma elementare, Padova, Tipografia del seminario, 1891, p. 577.
(38) Cfr. Opere di Hermann von Helmholtz, a cura di V. CAPPELLETTI, Torino, UTET, 1967, pp. 415-420.
(39) Il problema viene risolto dal punto di vista matematico da S. Lie. Cfr. S. LIE, Theorie der Transformationsgruppen, Leipzig, Teubner, 1893.
(40) È questa un’opinione condivisa da diversi studiosi. Per esempio, secondo H. Freudental, nel secolo XIX gli spazi di Riemann vennero al più accettati come una teoria matematica astratta, come filosofia dello spazio non ebbero alcuna influenza e le idee rivoluzionarie di Riemann vennero «eclissate» da quelle di Helmholtz. Cfr. la voce Riemann, in Dictionary of Scientific Biography, New York, Charles Scribner’s Sons, 1975. Secondo H. Reichenbach, mentre Riemann preparò la strada all’applicazione della geometria alla realtà fisica mediante la formulazione matematica del concetto di spazio, Helmholts gettò i fondamenti filosofici. Cfr. H. REICHENBACH, The Philosophy of Space and Time, New York, Dover, 1958; trad. it. Filosofia dello spazio e del tempo, Milano, Feltrinelli, 1977, p. 61. M. Kline ritiene invece che Riemann sia il più profondo filosofo di geometria. Cfr. M. KLINE, Mathematica! Thought from Ancient to Modem Times, New York, Oxford University Press, 1972, p. 889.
(41) L’espressione è di E. Cassirer. Cfr. E. CASSIRER, Storia della filosofia moderna… cit., p. 52.
(42) Cfr. M. JAMMER, Concepts of Space… cit., p. 140.
 In un articolo apparso su questa stessa rivista viene illustrato un interessante rapporto tra geometria e origami, essendo quest’ultimo, come tutti ben sanno, la celebre arte giapponese di piegare la carta. In particolare, l’ultima sezione è dedicata ad un breve cenno circa i legami tra origami e costruzioni con riga e compasso: l’uso degli origami permette infatti di risolvere alcuni dei problemi dell’antichità notoriamente impossibili da risolvere con riga (non graduata) e compasso. In questo articolo presentiamo alcuni aspetti di questi studi.
In un articolo apparso su questa stessa rivista viene illustrato un interessante rapporto tra geometria e origami, essendo quest’ultimo, come tutti ben sanno, la celebre arte giapponese di piegare la carta. In particolare, l’ultima sezione è dedicata ad un breve cenno circa i legami tra origami e costruzioni con riga e compasso: l’uso degli origami permette infatti di risolvere alcuni dei problemi dell’antichità notoriamente impossibili da risolvere con riga (non graduata) e compasso. In questo articolo presentiamo alcuni aspetti di questi studi.
 “Fra tutte le invenzioni dell’intelletto, nell’immanente, quella dell’Infinito è, forse, la più affascinante. Tanto più che nella REALTÀ del mondo fisico, nulla parla d’Infinito”. A partire da questa affermazione, Zichichi ci presenta, nella prima parte del libro, la realtà del mondo che ci circonda: la mente umana ha sempre cercato di misurarsi con l’infinito, ma il mondo reale non ce ne parla: poeti, pittori, musicisti ci parlano di infinito, a dimostrazione che “la creatività artistica e la razionalità matematica si fondono nel fascino di questa invenzione dell’intelletto umano”. Eppure, la velocità della luce, l’enorme spazio cosmico, il tempo, la massa, le cariche elettriche e subnucleari sono tutti in quantità finita: il loro numero è grandissimo, ma non ci parla dell’infinito.
“Fra tutte le invenzioni dell’intelletto, nell’immanente, quella dell’Infinito è, forse, la più affascinante. Tanto più che nella REALTÀ del mondo fisico, nulla parla d’Infinito”. A partire da questa affermazione, Zichichi ci presenta, nella prima parte del libro, la realtà del mondo che ci circonda: la mente umana ha sempre cercato di misurarsi con l’infinito, ma il mondo reale non ce ne parla: poeti, pittori, musicisti ci parlano di infinito, a dimostrazione che “la creatività artistica e la razionalità matematica si fondono nel fascino di questa invenzione dell’intelletto umano”. Eppure, la velocità della luce, l’enorme spazio cosmico, il tempo, la massa, le cariche elettriche e subnucleari sono tutti in quantità finita: il loro numero è grandissimo, ma non ci parla dell’infinito.
Nella seconda parte del libro, Zichichi parte da un’antica favola per portare il lettore alla scoperta dei concetti fondamentali su cui si basa la costruzione dell’infinito. Un Imperatore, alla ricerca di un metodo per incassare più tasse, indice un concorso: sarebbe risultato vincitore colui che avesse raggiunto il massimo numero di cose in suo possesso. Il Conte Alberto con i suoi piccoli cubetti d’oro, il Marchese Augusto con le sue pietre preziose e il Notaio Luigi con i suoi numeri risultano vincitori a pari merito. Riuniti in tre commissioni diverse, i contabili dell’imperatore non riescono a stabilire il vincitore nonostante numerosi conteggi, ma la principessa Cristina escogita un metodo matematico: la corrispondenza biunivoca. “Prendete i fogli numerati del Notaio. A destra di ciascun foglio mettete un cubetto d’oro. A sinistra, una pietra preziosa.”: alla prima conta risulta chiaro che cubetti d’oro, pietre preziose e numeri sono esattamente uguali. E non c’è bisogno di ulteriore verifica, visto che non c’è pericolo di errore.
La Principessa si domanda cosa succederebbe se l’insieme dei cubetti d’oro fosse infinito. Ragionando, ella dimostra ai tre vincitori che se è possibile stabilire una corrispondenza biunivoca tra l’insieme dei cubetti d’oro e l’insieme del numerabile, allora i due insiemi infiniti sono equipotenti. I quattro, riuniti in un’Accademia, si impegnano in una serie di ragionamenti sull’infinito e scoprono che è assurdo applicare a insiemi infiniti concetti e metodi tipici degli insiemi finiti: con l’infinito, il tutto è uguale ad una sua parte e sommando infiniti o moltiplicando due infiniti tra loro, otteniamo sempre lo stesso infinito.
La principessa Cristina informa l’Accademia che il Veggente di Corte le ha detto che il 12 dicembre del 1873 un uomo, Georg Cantor, scoprirà che esiste un infinito più infinito del numerabile, ovvero l’infinito del continuo. Basta pensare, come esempio, al numero di punti che c’è tra due estremi di un segmento: tale numero è infinito, per quanto piccolo possa essere questo segmento, ma non infinito in modo tale da essere numerabile. Scopriamo così che il numerabile, il primo livello dell’infinito, è meno potente del continuo.
La nostra Accademia viene informata, inoltre, che la grande scoperta di Cantor non avrà successo tra i contemporanei: verrà definita priva di senso da uno dei più grandi matematici del XIX secolo, Leopold Kronecker. Resta irrisolta per lungo tempo l’ipotesi del continuo, ovvero la domanda se tra i due livelli di infinito ce ne sia di mezzo un altro oppure no. Secondo Cantor, tra numerabile e continuo – detto diversamente, tra il livello aleph-zero e il livello aleph-uno – non c’è alcun livello intermedio, ma ancora nel 1900 un altro grande matematico, David Hilbert, porrà in prima linea, tra i grandi problemi da risolvere, l’ipotesi del continuo. Saranno scritte centinaia di memorie matematiche, prima che Kurt Gödel riesca a far crollare ogni certezza matematica nel 1931 e dimostri, nel 1940, che per gli insiemi infiniti costruibili a partire da regole ben precise vale l’ipotesi del continuo. Dopo di lui, nel 1963, Paul Cohen dimostra che per gli insiemi infiniti non costruibili, non è possibile accettare l’ipotesi del continuo. In altre parole, nascono due tipi di matematica: la matematica cantoriana e quella non-cantoriana, nella prima vale l’ipotesi del continuo, mentre nella seconda no.
Abbandonati principessa, marchese, conte e notaio, Zichichi ci parla direttamente delle scoperte matematiche del secolo scorso e si arriva così alla terza parte, dove si analizzano le radici di questa grande conquista dell’intelletto umano. L’autore ci accompagna in questa “affascinante avventura intellettuale”, con una scansione cronologica delle scoperte che hanno guidato il genere umano verso la classificazione degli infiniti. A partire dalla logica e dai paradossi degli antichi Greci – nel VI sec. a.C. – attraverso la dimostrazione di Euclide che prova che non può esistere il più grande “numero primo” – III sec. a.C. – fino ad arrivare a Galilei, che si accorse che l’insieme dei quadrati dei numeri interi è equipotente all’insieme dei numeri interi per concludere con Cantor, Hilbert, Gödel, Cohen.
Come in un percorso circolare, Zichichi torna alla fisica, dicendoci che qualsiasi esperimento ci darà solo risultati razionali, ribadendo che nel mondo reale non c’è traccia di infinito, quell’infinito che da Cantor ad oggi ha appassionato i più grandi matematici.
Daniela Molinari
 "Vediamo ora come funziona la mente. A mio parere, sono tre le funzioni principali: analizzare, sintetizzare/immaginare, valutare. Nelle forme applicate del pensiero efficace (decison making, problem solving), tutte e tre queste funzioni sono al lavoro…"
"Vediamo ora come funziona la mente. A mio parere, sono tre le funzioni principali: analizzare, sintetizzare/immaginare, valutare. Nelle forme applicate del pensiero efficace (decison making, problem solving), tutte e tre queste funzioni sono al lavoro…"
La parola ‘analisi’ deriva da un verbo greco che significa ‘sciogliere’ e indica l’atto di scomporre un intero nelle sue parti costituenti… Il pensiero analitico è strettamente correlato al ragionamento logico o passo passo… La logica ha due componenti principali: la deduzione e l’induzione (vedi Peirce). Deduzione significa letteralmente sottrarre o togliere. E’ il processo di ricavare una conclusione da ciò che si conosce o si presuppone. Nello specifico, si tratta di una inferenza dal generale al particolare. L’induzione funziona nell’altra direzione. E’ il processo di inferire o verificare una legge o un principio generale dall’osservazione di casi particolari: il nucleo del pensiero scientifico" (da Bacone e Galilei in poi).
"Non è facile dare un’unica definizione della seconda funzione. Sintetizzare (un altro termine che deriva dal greco) significa comporre diverse cose per creare un intero. E’ il processo opposto dell’analizzare. Potete sintetizzare cose con le vostre mani: è ciò che fate ogni volta che assemblate o create qualcosa. Tutti i prodotti o servizi sono il risultato di una sintesi. Tuttavia, potete anche farlo mentalmente. Questo succede quando entra in gioco un’altra facoltà: l’immaginazione. Ora l’immaginazione lavora per immagini e un’immagine è un intero che rappresenta più della somma delle parti… Il collegamento tra la creatività e il processo di sintesi diventa evidente quando si considera il modo in cui funziona la natura. Un bambino nasce completo e cresce. La natura è olistica."
"La terza funzione entra in gioco in attività mentali come definire criteri di successo, valutare, stimare le prestazioni e giudicare le persone, ad esempio nel corso di un colloquio di selezione. La critica che (dal termine greco che indica un giudizio) è una forma di valutazione. Per inciso il termine ‘critica’, nel suo senso comune, molto spesso suggerisce disapprovazione: una qualche sorta di giudizio negativo.
Tuttavia nel suo utilizzo più formale, può suggerire un’analisi di tipo neutrale o perfino una valutazione che implica approvazione. il giudizio non è sempre sfavorevole. In tutte le valutazioni vi è un elemento oggettivo (al di fuori di noi) e uno soggettivo. Tutti noi nasciamo con la capacità di valutare. Ciò che effettivamente apprezziamo (i nostri valori) dipendono in larga misura dal nostro ambiente e dalla sua cultura". John Adair (1934), Decision making & Problem solving, Franco Angeli 2008.
Secondo Adair i tre passi principali per prendere una decisione o per risolvere un problema sono fondamentalmente gli stessi:
1) Definire l’obiettivo o il problema (principalmente analisi).
2) Generare le opzioni realizzabili (principalmente sintesi).
3) Scegliere la linea d’azione o la soluzione ottimale (principalmente valutazione).
Egli sostiene che non vi è niente di più soddisfacente che affrontare una sfida mentale e superarla. Più difficile è il problema, più euforia proverà la persona o il gruppo di lavoro che lo ha risolto. E’ importante divertirsi con il decision making e il problem solving: come in ogni attività umana più ci si diverte, più la si vuole fare e più la si fa, più si diventa bravi a svolgerla.
All’interno delle organizzazioni i problemi da risolvere appartengono a due famiglie: quelli relativi al funzionamento dei sistemi e quelli relativi ai progetti e alle decisioni innovative. Un sistema è formato da un insieme di parti che interagiscono tra loro, di solito allo scopo di raggiungere un determinato obiettivo (sistema di marketing, sistema produttivo, sistema logistico, sistema amministrativo, ecc.). Un problema dei sistemi è essenzialmente una deviazione rispetto alla norma o allo standard che può essere rilevato da allarmi, procedure di verifica, carte di controllo, uffici della qualità ecc. Maggiore è lo scostamento tra le prestazioni normali (come ci si aspetta che il sistema funzioni) e le prestazioni effettive (ciò che sta accadendo realmente), più grande è il problema.
Gli ostacoli che insorgono alla realizzazione di un progetto o alla attuazione di una decisione costituiscono lo 80% delle difficoltà che i manager debbono affrontare, ma è necessario tener presente anche i problemi relativi ai sistemi sono l’altro 20%. Naturalmente se non si è generalisti, ma specialisti (professional) in ambito tecnico, amministrativo ecc., queste proporzioni sono invertite e la maggior parte del tempo lavorativo verrà dedicato a problemi relativi ai sistemi.
Il processo del pensiero creativo: 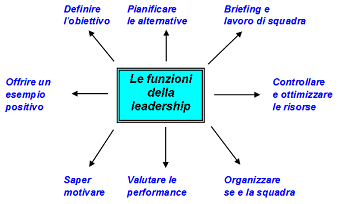
1) Preparazione: il lavoro duro. Dovete raccogliere e ordinare le informazioni rilevanti, analizzare il problema nel modo più approfondito ed esplorare le possibili soluzioni.
2) Incubazione: questa è la fase della mente profonda. Il lavoro mentale sul problema (analizzare, sintetizzare e valutare) prosegue nella mente subconscia. Le parti del problema si separano e nuove combinazioni si formano. queste possono coinvolgere altri ingredienti immagazzinati nella vostra memoria.
3) Intuizione: il momento "eureka" (vedi Archimede). Una nuova idea emerge nella vostra mente conscia, gradualmente o improvvisamente, come un pesce che guizza fuori dall’acqua. Questi momenti spesso si verificano quando non si sta pensando al problema ma si è in un atteggiamento mentale di rilassamento.
4) Convalida: a questo punto entra in gioco la facoltà di valutazione. Una nuova idea, illuminazione, intuizione, impressione o soluzione deve essere accuratamente verificata. Questo è particolarmente vero se deve operare come base per un qualche tipo di azione.
Blocchi mentali: 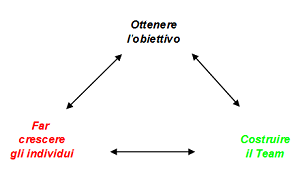
1) Mancanza di dati: se non siete certi di avere tutti i dati rilevanti, è naturale che si esiti a impegnarsi. Eseguite altre ricerche, questo dovrebbe rimettervi in movimento.
2) Mancanza di convinzione: forse vi trovate in difficoltà perché non siete convinti del valore di questo esercizio (compito) o del modo in cui vi è stato chiesto svolgerlo. Ridefinite un obiettivo utile.
3) Mancanza di un punto di partenza: magari il problema sembra così grande che non sapete da dove cominciare. In questo caso, stabilite un punto di partenza qualsiasi. Potrete sempre cambiarlo più avanti. L’ispirazione arriva dopo aver iniziato, non prima.
4) Mancanza di prospettiva: forse siete troppo vicini al problema, sopratutto se è da troppo tempo che lo tollerate o ve ne siete occupati incessantemente. Provate ad abbandonarlo per una settimana. Consultate altre persone. Anche solo spiegare loro il problema potrebbe essere d’aiuto. Potrebbero vedere nuovi aspetti.
5) Mancanza di motivazione: desiderate a sufficienza che avvenga? Il pensiero creativo richiede perseveranza di fronte alle difficoltà. Se vi lasciate scoraggiare troppo facilmente, questo potrebbe essere un segno che, nel profondo, vi manca la necessaria motivazione. Rafforzate la vostra determinazione.
 Una delle mie più fortunate letture dell’anno è stato il libro di Gabriele Lolli "Discorso sulla matematica" (Bollati Boringhieri 2011). Lolli si propone di mostrare, a mio avviso con mirabile successo, che i metodi e gli atteggiamenti che sottendono all’attività matematica creativa sono analoghi a quelli della produzione letteraria e poetica.
Una delle mie più fortunate letture dell’anno è stato il libro di Gabriele Lolli "Discorso sulla matematica" (Bollati Boringhieri 2011). Lolli si propone di mostrare, a mio avviso con mirabile successo, che i metodi e gli atteggiamenti che sottendono all’attività matematica creativa sono analoghi a quelli della produzione letteraria e poetica.
E lo fa passando in rassegna il paradigma di Calvino: Leggerezza, Rapidità, Esattezza, Visibilità, Molteplicità (Italo Calvino, "Lezioni americane", Garzanti 1988).
Il libro assolve così, innanzitutto, un compito utile: quello di far vedere come la matematica non sia solo l’apparato meccanicistico noioso e burbero che tutti si ricordano dai tempi della scuola, ma anche e soprattutto un’attività creativa.
Mi sono trovato più volte, nelle mie lezioni universitarie e nei miei libri sull’abusato concetto di Complessità (che in questa epoca viene impiegato da alcuni per aggredire il metodo scientifico), a dover spiegare che la matematica non è un’Arancia Meccanica.
Molti la vedono così perché tutto quel che ricordano della materia sono formule astruse e manipolazioni simboliche fine a sé stesse: ricordano una sequela di passi che dovevano essere pedantemente seguiti per giungere a un risultato predefinito.
Ma quella non è altro che la grammatica della matematica: a scuola devono necessariamente far fare esercizi, sennò gli studenti non apprendono la grammatica! Lo stesso succede con le lingue. Lo scopo della letteratura è leggere e gustarsi le opere letterarie, ma se non conosciamo la grammatica non possiamo farlo, né tantomeno possiamo esprimerci in modo comprensibile: ed ecco il senso dei noiosi esercizi di italiano o di inglese o di latino.
Lo scopo è l’apprendimento della lingua, non gli esercizi in sé. Così, il bello della matematica non sono i calcoli (che lasciamo comunque sbrigare ai computer) o le manipolazioni simboliche fine a sé stesse, ma
A) i passi logici che portano a una dimostrazione e
B) l’appropriarsi delle tecniche di modellazione della realtà, ossia l’imparare a descrivere un fenomeno reale mediante un modello matematico, per indagarlo e conoscerlo meglio.
Sia (A) sia (B) implicano una cospicua attività creativa: e il libro di Lolli si occupa di questa.
C’è un passo stupendo nel quale la dimostrazione del Pons Asinorum viene assimilata alla composizione di un poema cavalleresco o alla narrazione di una fiaba. Il Pons Asinorum è il teorema che afferma l’uguaglianza degli angoli alla base di un triangolo isoscele, ed era chiamato così nel Medioevo perché era un esercizio di logica molto selettivo.
La dimostrazione di Euclide inizia col disegnare un triangolo CAB. Poi nella narrazione compaiono due oggetti: i punti F e G presi sui prolungamenti dei lati CA e CB, alla stessa distanza da C. E «all’improvviso la storia si anima, perché i due oggetti, magici naturalmente, vogliono collegarsi con il maggior numero di oggetti possibile: il primo assioma di Euclide afferma che due punti possono […] essere collegati da un segmento; nel fare questo si orginano nuove figure [triangoli, NDR] entro le quali è assorbita quella originaria. I triangoli vogliono essere confrontati, e dai triangoli si discende ai lati e agli angoli, e in particolare a quelli che interessano» (pag. 94).
Il cono per rappresentare l’universo insiemistico V, invece, diventa una specie di Inferno dantesco. La dimostrazione, magnificamente sintetica, del Teorema di Pitagora del Chou Pei Suan Ching (200 a.C.), ci porta al cuore dell’idea senza dire parole, e può essere data modellando un cartoncino o un tovagliolo, senza una sola formula: «Dare giustificazioni sarebbe come spiegare il senso di una barzelletta a chi non l’ha capita, e perdere tempo».
Il libro è un esercizio sopraffino di "terza cultura", ossia una dimostrazione che per la persona veramente colta non esistono barriere tra le attività intellettuali umane e che per capire qualcosa del mondo ci serve un apparato cognitivo che superi, unendole, la sola logica, al sola intuizione, la sola curiosità, la sola creatività.
Ma il libro è anche una scoppiettante sequela di preziose gemme per il lettore curioso. Problemi matematici. Eroi dell’avventura intellettuale. Quiz stuzzicanti. E accenna da par suo all’attualissima discussione intorno al valore delle immagini nella didattica e nella formazione. E’ possibile che alla lingua scritta dell’alfabeto si sostituisca una lingua iconica, scaturita dall’uso prolungato di interfacce uomo-macchina sempre più evolute? Secondo Lolli, gli studenti di matematica non apprezzano e non sfruttano come potrebbero l’utilità e la potenza delle figure (geometriche, algebriche), e ciò potrebbe indicare che l’odierno vivere di immagini ed esprimersi per immagini si riferisca in realtà alle sterili «immagini prefabbricate» di cui parlava Italo Calvino. Appare dunque necessaria un più consapevole e mirato utilizzo del linguaggio delle immagini nella didattica della matematica.
 Questo articolo intende raccogliere una serie di curiosità relative al mondo degli scacchi e si può dividere sostanzialmente in tre parti. In primo luogo, vi sono partite o problemi scacchistici che presentano qualche particolarità degna di nota; poi vengono descritti alcuni tra i numerosissimi possibili giochi legati alla scacchiera e al movimento dei pezzi del “nobile giuoco”. La terza parte riguarda alcune varianti degli scacchi poco conosciute. In conclusione, dopo le soluzioni ai giochi proposti in precedenza, si riporta un sonetto che descrive una delle più celebri partite del ‘700.
Questo articolo intende raccogliere una serie di curiosità relative al mondo degli scacchi e si può dividere sostanzialmente in tre parti. In primo luogo, vi sono partite o problemi scacchistici che presentano qualche particolarità degna di nota; poi vengono descritti alcuni tra i numerosissimi possibili giochi legati alla scacchiera e al movimento dei pezzi del “nobile giuoco”. La terza parte riguarda alcune varianti degli scacchi poco conosciute. In conclusione, dopo le soluzioni ai giochi proposti in precedenza, si riporta un sonetto che descrive una delle più celebri partite del ‘700.
 Sono un insegnante di matematica in pensione dal 1999 e, all’inizio di quest’anno scolastico, desidero sottoporre ai colleghi docenti di questa disciplina nelle scuole medie superiori alcune considerazioni che, mi auguro, possano favorire un dibattito sull’aspetto metodologico-diattico dell’insegnamento della nostra materia. Per ciò ho ritenuto possa essere interessante prendere le mosse dal Resoconto del professore Vinicio Villani, del Convegno internazionale di Cagliari del 31-10-1981, sul tema: “Metodiche attuali nell’insegnamento della Geometria nell’arco di studi pre-universitari”.
Sono un insegnante di matematica in pensione dal 1999 e, all’inizio di quest’anno scolastico, desidero sottoporre ai colleghi docenti di questa disciplina nelle scuole medie superiori alcune considerazioni che, mi auguro, possano favorire un dibattito sull’aspetto metodologico-diattico dell’insegnamento della nostra materia. Per ciò ho ritenuto possa essere interessante prendere le mosse dal Resoconto del professore Vinicio Villani, del Convegno internazionale di Cagliari del 31-10-1981, sul tema: “Metodiche attuali nell’insegnamento della Geometria nell’arco di studi pre-universitari”.
 Il pensiero verticale è selettivo, il pensiero laterale è produttivo. Il pensiero verticale si mette in moto solamente se esiste una direzione in cui muoversi, il pensiero laterale si mette in moto allo scopo di generare una direzione. Il pensiero verticale è analitico, il pensiero laterale è stimolante. Il pensiero verticale è consequenziale, il pensiero laterale può procedere a salti. Con il pensiero verticale si deve essere corretti a ogni passo, con il pensiero laterale si può non esserlo. Con il pensiero verticale si usa la negazione allo scopo di bloccare alcuni percorsi; con il pensiero laterale non esiste alcuna negazione. Con il pensiero verticale ci si concentra e si esclude ciò che è irrilevante, con il pensiero laterale si accolgono favorevolmente le intrusioni del caso. Con le categorie del pensiero verticale classificazioni e definizioni sono fissate, con il pensiero laterale non lo sono. Edward de Bono (Malta, 1933), Creatività e pensiero laterale: manuale di pratica della fantasia.
Il pensiero verticale è selettivo, il pensiero laterale è produttivo. Il pensiero verticale si mette in moto solamente se esiste una direzione in cui muoversi, il pensiero laterale si mette in moto allo scopo di generare una direzione. Il pensiero verticale è analitico, il pensiero laterale è stimolante. Il pensiero verticale è consequenziale, il pensiero laterale può procedere a salti. Con il pensiero verticale si deve essere corretti a ogni passo, con il pensiero laterale si può non esserlo. Con il pensiero verticale si usa la negazione allo scopo di bloccare alcuni percorsi; con il pensiero laterale non esiste alcuna negazione. Con il pensiero verticale ci si concentra e si esclude ciò che è irrilevante, con il pensiero laterale si accolgono favorevolmente le intrusioni del caso. Con le categorie del pensiero verticale classificazioni e definizioni sono fissate, con il pensiero laterale non lo sono. Edward de Bono (Malta, 1933), Creatività e pensiero laterale: manuale di pratica della fantasia.
"… Stiamo annegando nella complessità. Un esempio: pochissimi utilizzano più di un decimo delle istruzioni per l’uso di un videoregistratore. Cioè il 95% della popolazione non usa il 90% delle funzioni di un normale elettrodomestico. Le pare tollerabile questo spreco? Quando dobbiamo comprare un computer ci troviamo nella stessa situazione. Quando gli scienziati della NASA investirono una fortuna per inventare una penna a sfera che scrivesse nello spazio in assenza di gravità, i loro colleghi russi, per mancanza di soldi, pensarono che si potessero usare più semplicemente le matite. Eppure dire semplice, nel linguaggio comune, significa dire sempliciotto, banale, ma così non è. 
Il pensiero è un’abilità che si può imparare. Ho cercato di dimostrare questo assunto attraverso i miei lavori su creatività e pensiero laterale come pensiero generativo, esplorativo, capace di fare salti invece che procedere per sequenze logiche. Un po’ come è nel gioco degli scacchi la mossa del cavallo. Non si può perseverare sempre con lo stesso approccio. Da qui il pensiero laterale come forma strutturata di creatività. Lo stesso vale per la semplicità.
Convivere con la complessità (Edgar Morin) è solo una perdita di tempo. Non esiste alcuna giustificazione per mantenere complesse cose che possono essere semplici. Semplice non equivale a facile, anche se la semplicità facilita la vita. Il pensiero semplice non è una filosofia contemplativa, ma interviene nell’agire quotidiano. E’ importante che la semplicità sia considerata un valore desiderabile e un atteggiamento mentale permanente.
Perchè esistono i nemici della semplicità. Tra di essi vi sono sicuramente insegnanti e uomini d’impresa. Alcuni semplicemente adorano la complessità e odiano la semplicità. Il modo più facile per sentirsi superiori è quello di fingere di capire quel che gli altri non sono in grado di capire. Per questo c’è bisogno di complessità. Gli argomenti vissuti come complessi creano un ruolo per gli attori della complessità. Mentre gli argomenti semplici lo negano, lo rendono inutile. Ma la semplicità è impegnativa sopratutto per chi non conosce a fondo un argomento. Per semplificare qualcosa bisogna conoscerla a fondo. Senza lo sforzo di capire la semplicità è semplicismo. Unita alla comprensione è vera semplicità… de Bono, intervista di Walter Passerini (Corriere Università, 30 Giu 2000).
Nel suo libro "Il Meccanismo della Mente", Edward de Bono ha in primo luogo descritto come la rete nervosa del cervello si comporti come un sistema auto-organizzato. È partendo da queste basi che il Dott. de Bono ha modellato le sue metodologie del pensiero. È l’inventore del termine "pensiero laterale" e l’ideatore del Programma di Pensiero CoRT (Cognitive Research Trust) per le scuole, che è il programma maggiormente utilizzato a livello internazionale per l’insegnamento delle abilità di pensiero.
Il problema dei tre interruttori può aiutare a comprendere le differenze tra pensiero laterale e pensiero verticale. In una stanza di un castello vi sono tre interruttori, ma non si sa quale dei tre controlla la lampada di una altra stanza non contigua. Le condizioni iniziali sono: i tre interruttori in posizioni off e la lampadina spenta. Supponendo di poter accendere e spegnere gli interruttori quante volte si vuole, ma avendo una sola opportunità di andare a controllare lo stato della lampadina, è possibile stabilire con certezza quale interruttore ne determina l’accensione? La risposta del pensiero verticale è no. La soluzione sarebbe stata facile se gli interruttori fossero stati solo due (accendere un interruttore a caso, andare a verificare nella stanza lo stato della lampadina, se è accesa è quello l’interruttore determinante se è spenta lo è l’altro). Nella situazione dei tre interruttori si può ancora accenderne uno a caso, ma solo se si è fortunati (probabilità 33%) si troverà la lampadina accesa e il problema risolto. Se la lampadina è spenta si potrà solo cercare di indovinare (con una probabilità di successo del 50%) qual è l’interruttore determinante. Il Pensiero laterale suggerisce di uscire dagli schemi (thinking out of the box), in questo caso del pensiero binario (acceso o spento), e di procedere nella seguente maniera: accendere due interruttori (es. 1 e 2), lasciar passare 3 minuti, spegnere un interruttore (es. 2) e recarsi a controllare lo stato della lampadina.
a) lampadina accesa: il collegamento è con l’interruttore N°1.
b) lampadina spenta, ma calda: il collegamento è con l’interruttore N°2.
c) lampadina spenta, ma fredda: il collegamento è con l’interruttore N°3.
In questo esempio il pensiero laterale ha consentito l’uscita dallo schema "acceso e spento" utilizzando una ulteriore variabile risolutiva per il problema: la temperatura della lampadina. 
"Sei Cappelli per pensare" propone un buon esercizio per affrontare i problemi da ottiche differenti. In pratica in una riunione, in un corso, in un dibattito ciascun interlocutore dovrebbe assumere ruoli (cappelli, vedi figura) definiti allo scopo di: dichiarare le sue posizioni, uscire dai suoi pregiudizi, considerare punti di vista alternativi; naturalmente per stimolare l’ampiezza delle soluzioni e delle critiche è auspicabile che in una discussione ciascuna persona accetti di indossare cappelli (ruoli) diversi. Di seguito i ruoli che ciascun cappello implica:
1) Cappello bianco (Neutrale): analisi dei dati, di informazioni, di eventi precedenti, analogie ed elementi che sono raccolti senza esprimere giudizi.
2) Cappello blu (Razionale): stabilisce priorità, metodi, sequenze funzionali, pianifica, organizza, stabilisce le regole del gioco. Conduce il gioco.
3) Cappello nero (Negativo): l’avvocato del diavolo che rileva gli aspetti negativi, le ragioni per cui la cosa non può andare.
4) Cappello giallo (Positivo): l’avvocato dell’angelo, rileva gli aspetti positivi, i vantaggi, le opportunità che si aprono.
5) Cappello rosso (Emotivo): emotività, esprime di getto le proprie intuizioni, come suggerimenti o sfoghi liberatori, come se si ridiventasse bambini, emozioni, sentimenti.
6) Cappello verde (Creativo): indica sbocchi creativi, nuove idee, analisi e proposte migliorative, visioni insolite.
Secondo De Bono affrontare i problemi con gli abituali metodi razionali produce risultati limitati dalla rigidità dei modelli logici. Per trovare soluzioni davvero innovative bisogna uscire dagli schemi prefissati, mettere in dubbio le presunte certezze e affidarsi ad associazioni di idee inedite. I saggi di De Bono sull’arte del pensiero creativo sono loro stessi talmente fuori dagli schemi che i librai non sanno mai se metterli nella sezione Scuola, Business o Religione. Il suo metodo si insegna già in Israele, Canada, Australia, Russia, Venezuela ed ora in Cina stanno valutando se inserirlo nelle scuole di ogni livello (dalle elementari al liceo) per rendere il paese sempre più competitivo e capace di conquistare nuovi mercati.
 Prendete un comune foglio di carta quadrettata, e con una penna tracciate a mano libera una pista qualsiasi, con una linea di partenza ed una di arrivo. Non ha alcuna importanza che nel tracciare la pista seguiate le righe o le colonne della quadrettatura, e che il percorso abbia sempre la stessa larghezza. Se preferite potete tracciare anche un percorso chiuso in modo che la linea di partenza coincida con quella di arrivo, oppure un percorso intrecciato, o infine se siete perfezionisti, potete riprodurre il tracciato di una delle piste classiche della formula uno.
Prendete un comune foglio di carta quadrettata, e con una penna tracciate a mano libera una pista qualsiasi, con una linea di partenza ed una di arrivo. Non ha alcuna importanza che nel tracciare la pista seguiate le righe o le colonne della quadrettatura, e che il percorso abbia sempre la stessa larghezza. Se preferite potete tracciare anche un percorso chiuso in modo che la linea di partenza coincida con quella di arrivo, oppure un percorso intrecciato, o infine se siete perfezionisti, potete riprodurre il tracciato di una delle piste classiche della formula uno.
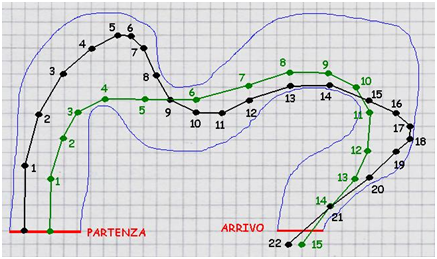
Immaginiamo per esempio di aver tracciato la pista sopra, e di giocare con un amico, il percorso nostro è quello verde, e quello del nostro amico è quello nero. Le mosse non sono stabilite dal lancio di dadi o da un altro dispositivo casuale, ma sono liberamente determinate da ciascun giocatore rispettando i punti seguenti:
1) Ogni mossa viene determinata tracciando un pallino sulla intersezione di una quadrettatura, ed unendo con un segmento questo pallino con quello della mossa precedente.
2) Il punto iniziale con cui si inizia la corsa deve essere diverso per ciascun giocatore. 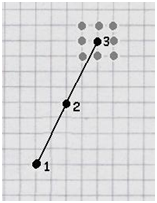
3) Supponendo (vedi figura a fianco) di aver già effettuato una mossa dal punto 1 al punto 2, la mossa successiva può essere effettuata o nel punto 3 (ripetendo così le modalità della mossa precedente) oppure, simulando una accelerazione o un rallentamento, in uno degli otto punti immediatamente adiacenti, ed indicati in grigio nella figura. La scelta è assolutamente libera. Dopo qualche prova ci si accorgerà che per effettuare una curva occorre prevedere in tempo una graduale decelerazione ed un cambiamento di direzione, altrimenti si finisce inesorabilmente fuori pista.
4) I punti di ciascuna mossa e i relativi segmenti che li uniscono devono sempre essere interamente contenuti entro il tracciato della pista.
5) Due auto non possono occupare lo stesso punto nello stesso istante: ciò equivarrebbe ad uno scontro fra le auto.
Vince la gara chi taglia per primo il traguardo.
Nella prima figura si può notare come l’auto verde raggiunga il traguardo dopo 15 mosse e seguendo un percorso piuttosto regolare. L’auto nera invece prende la prima curva troppo larga e quando la gara finisce si trova nella posizione 15, ancora molto lontana dal traguardo. Inoltre, se avesse proseguito ancora fino al raggiungimento del traguardo, avrebbe sbandato pericolosamente durante le mosse 17 e 18, evitando per un pelo di finire fuori strada, e riuscendo a completare il percorso in 22 mosse.
Il gioco è stato liberamente tratto da un articolo di Martin Gardner di circa trentacinque anni fa.
 In questa guida sono discussi alcuni comandi e alcune funzioni utili agli studenti degli ultimi anni di corso delle scuole medie superiori e agli studenti universitari del primo anno di facoltà scientifiche. Si rimanda, per ogni approfondimento, al testo del Prof. J.W.Eaton, che si trova nella sezione documentazione di Octave. Queste pagine possono costituire un ausilio didattico nei corsi introduttivi di algebra lineare, di analisi, di calcolo numerico, di programmazione e statistica. Chi ha già affrontato questi corsi impiegherà pochissimo tempo ad usare Octave.
In questa guida sono discussi alcuni comandi e alcune funzioni utili agli studenti degli ultimi anni di corso delle scuole medie superiori e agli studenti universitari del primo anno di facoltà scientifiche. Si rimanda, per ogni approfondimento, al testo del Prof. J.W.Eaton, che si trova nella sezione documentazione di Octave. Queste pagine possono costituire un ausilio didattico nei corsi introduttivi di algebra lineare, di analisi, di calcolo numerico, di programmazione e statistica. Chi ha già affrontato questi corsi impiegherà pochissimo tempo ad usare Octave.
Che cos’è GNU Octave Octave
E’ un software open-source scritto da John W. Eaton e molti altri. Non è di pubblico dominio perché esistono delle restrizioni sulla sua ridistribuzione. Queste restrizioni sono pensate per assicurare a tutti di avere gli stessi diritti di usare e ridistribuire Octave. Ciò significa che chiunque può ottenere e usare il codice sorgente, può modificarlo e ridistribuirlo nei termini della licenza GNU General Public Licence come descritta e pubblicata dalla Free Software Foundation in cui sono espresse le precise condizioni sul copyright. Octave è un linguaggio interpretato ad alto livello orientato al calcolo numerico: moltiplica e inverte matrici, determina radici di equazioni lineari e non lineari, manipola polinomi, integra, differenzia e disegna grafici. Il suo insieme di funzioni ne comprende molte orientate all’ottimizzazione, alla statistica, alla matematica finanziaria, all’interpolazione, alla teoria del controllo e allo studio dell’audio e delle immagini. Octave, in linea di massima, è compatibile con Matlab di Mathworks (laboratorio di matrici) ma non permette la manipolazione simbolica degli oggetti matematici.
 In questo numero, Gabriella D’Agostino e Antonio Guglielmi ci parlano di tassi di mercato delle attività finanziarie, di politiche di gestione del rischio dei tassi di interesse… questioni di particolare attualità. Andreana Zucco ci presenta tre congetture di Erdös riguardanti insiemi composti da un numero finito di punti nel piano. Gianluca Salvalaggio ci descrive il fascino dei numeri primi e la loro più classica applicazione alla crittografia a chiave pubblica. Michele Mazzucato fa una scheda sintetica della moltiplicazione nella sua evoluzione storica, i metodi antichi e più moderni per moltiplicare due numeri interi. Domenico Lenzi e Ilario Marra fanno alcune riflessioni sull’insegnamento delle frazioni nella scuola dell’obbligo e presentano alcune metodologie innovative. Bruno Sanchini ci dà una possibile descrizione analitica del reticolo della dama. Paolo Bonicatto ci introduce alla Teoria dei modelli.
In questo numero, Gabriella D’Agostino e Antonio Guglielmi ci parlano di tassi di mercato delle attività finanziarie, di politiche di gestione del rischio dei tassi di interesse… questioni di particolare attualità. Andreana Zucco ci presenta tre congetture di Erdös riguardanti insiemi composti da un numero finito di punti nel piano. Gianluca Salvalaggio ci descrive il fascino dei numeri primi e la loro più classica applicazione alla crittografia a chiave pubblica. Michele Mazzucato fa una scheda sintetica della moltiplicazione nella sua evoluzione storica, i metodi antichi e più moderni per moltiplicare due numeri interi. Domenico Lenzi e Ilario Marra fanno alcune riflessioni sull’insegnamento delle frazioni nella scuola dell’obbligo e presentano alcune metodologie innovative. Bruno Sanchini ci dà una possibile descrizione analitica del reticolo della dama. Paolo Bonicatto ci introduce alla Teoria dei modelli.
Il matematico in giallo” di Carlo Toffalori
Anna Cerasoli, Io conto, Feltrinelli
 La matematica […] ha mostrato che l’essere e il divenire, ossia quelle che credevamo inconciliabili caratteristiche di scienza e umanesimo, sono soltanto due visioni, complementari e non contraddittorie, di una stessa realtà. Questa è la tesi di fondo sostenuta da Odifreddi in questo libro ed espressa già nelle prime pagine.
La matematica […] ha mostrato che l’essere e il divenire, ossia quelle che credevamo inconciliabili caratteristiche di scienza e umanesimo, sono soltanto due visioni, complementari e non contraddittorie, di una stessa realtà. Questa è la tesi di fondo sostenuta da Odifreddi in questo libro ed espressa già nelle prime pagine.
 La filosofia è nata in stretta connessione con la matematica e, come mostrato da Gödel con il suo lavoro, “con una buona motivazione filosofica si può fare della buona scienza e per fare buona filosofia ci vuole un buon metodo scientifico.
La filosofia è nata in stretta connessione con la matematica e, come mostrato da Gödel con il suo lavoro, “con una buona motivazione filosofica si può fare della buona scienza e per fare buona filosofia ci vuole un buon metodo scientifico.
In letteratura alcuni autori erano matematici di professione e altri hanno usato la matematica per costruire le loro opere: basta pensare al Paradiso dantesco, il racconto di un viaggio attraverso un mondo tolemaico dalla rigida struttura geometrica, oppure ad “Alice nel paese delle meraviglie”, scritto da un logico-matematico e dalla struttura solo apparentemente caotica ma in realtà matematicamente ordinata, oppure ancora alle opere di Italo Calvino, che seppe “coniugare la complessità strutturale con il valore letterario”.
In musica i rapporti musicali si possono esprimere con rapporti numerici, come spiegato dallo stesso Pitagora e buona parte della musica classica ha trovato la sua essenza e la sua struttura nei metodi matematici. Inoltre Keplero e Newton hanno scoperto rispettivamente la terza legge del moto dei pianeti e la legge della gravitazione universale, sfruttando analogie musicali.
Per Galilei la matematica è, come è noto, il linguaggio della natura, mentre Kandinkskij vede nella matematica il linguaggio dell’arte ed Escher si mostra particolarmente attratto dalla geometria, con i solidi regolari, perché “simboleggiano in maniera impareggiabile l’umana ricerca di armonia e ordine, ma allo stesso tempo la loro perfezione ci incute un senso di impotenza”. Come avviene per la musica, anche nel caso della pittura la matematica può intervenire profondamente e nascostamente, regolandone la struttura stessa.
Si parla, quindi, erroneamente di due culture: nella realtà, non ha alcun senso mettere i due ambiti in contrapposizione. Secondo Odifreddi, la matematica è come il corpo calloso: all’interno del cervello, esso collega i due emisferi, esattamente come la matematica collega le due culture, visto che “è umanistica nei contenuti, perché descrive e inventa mondi possibili, ma scientifica nel metodo, perché usa la logica”.
Vista la grande diffusione dei computer e considerato che la matematica è il linguaggio della scienza e della tecnologia, essa dovrebbe essere il linguaggio di tutto il mondo occidentale contemporaneo: eppure gli studenti dell’ultimo anno delle superiori mostrano un livello medio-basso di conoscenze e i nomi dei grandi matematici sono praticamente sconosciuti al grande pubblico. Inoltre, la grande produttività del Novecento potrebbe indurre a pensare che non siano più rimasti problemi da risolvere e che i matematici siano “destinati a un prepensionamento forzato”, come avvalorato dalla congettura di Keplero – proposta nel 1611 e dimostrata nel 1998 – e dalla vittoria sull’Ultimo Teorema di Fermat – enunciato nel 1637 e dimostrato nel 1995. Ma la matematica è viva e vegeta: “risolve problemi che si è posta, si pone problemi che risolverà”. Nuove branche sono nate recentemente: la teoria dei giochi e la teoria della complessità, ad esempio, a dimostrazione del fatto che la matematica trova applicazioni in aree apparentemente lontane, si avvicina ad aree in cui troverà applicazioni e costituisce una rete di collegamento fra le scienze più differenti.
Odifreddi ci invita a scoprire una matematica diversa da quella nota ai più: la matematica non è solo precisione e rigore, visto che non è certo immune dai paradossi. I paradossi sono “verità che stanno a testa in giù e gambe in su per attirare l’attenzione” e la storia della matematica ne è costellata: le apparenti difficoltà create da queste contraddizioni sono state un’occasione di crescita, come dimostrato, ad esempio, dall’incommensurabilità fra diagonale e lato del quadrato che ha portato, nella sua soluzione, all’introduzione dei numeri reali, o dalla topologia, nata dallo studio di alcune curve e superfici paradossali, come la striscia di Moebius e la curva di Koch.
In totale, i campi esplorati in termini matematici sono: politica, religione, arte, letteratura, giochi, filosofia, logica, aritmetica, geometria, scienza e tecnica.
“La geometria, l’aritmetica e la logica non sono altro che le forme astratte dello spazio, del tempo e della ragione: del nostro modo, cioè, di combinare i sensi e il pensiero in una visione del mondo. La conoscenza umana non può, dunque, che essere strutturata in termini matematici.”
Dimostrare che l’equazione $xcos(/pi y)-y+e^x=0$ definisce implicitamente in un intorno del punto (0; 1) una e una sola funzione y=f(x) di cui si chiede il poli-nomio di Mac Laurin di 2° grado.
Nella notte tra 8 e 9 novembre 2011, alle 00:28 ora italiana, l’asteroide 2005 YU55 passerà tra noi e l’orbita lunare, ad una distanza di soltanto 320.000 Km dalla superficie terrestre, un’inezia intermini astronomici. L’asteroide si avvicinerà più alla Luna che alla Terra e sfiorerà il nostro satellite a circa 240.000 Km.
Scoperto sei anni fa l’asteroide appare di forma grossomodo sferica con un diametro di circa 400 m. Impiega più o meno 20 ore per ruotare intorno a se sesso e la sua superficie è scurissima, più nera del carbone.
Trattandosi di un passaggio radente, non ci sarà nessun rischio per la popolazione terrestre. Anche il contributo gravitazionale dell’asteroide è assolutamente ininfluente per la Terra.
Il passaggio sarà monitorato, oltre che dai più grandi telescopi del mondo, anche dai radiotelescopi di Goldstone (California) e Arecibo (Puerto Rico), che dovrebbero permettere una mappatura radar della sua superficie con una risoluzione di 2 metri/pixel.
Per approfondimenti e per vedere l’animazione
http://www.sidereus-nuncius.info/2011/10/31/un-asteoride-sta-per-sfiorarci/
 Nel presente articolo viene illustrato un efficiente algoritmo di esponenziazione, noto nella letteratura tecnica con il seguente nome: right – to – left binary method for exponentiation. Di questo algoritmo si danno due applicazioni per ciascuna delle quali è stato realizzato un programma in linguaggio Qbasic. Pertanto come corredo al presente articolo sono disponibili per il lettore anche i due relativi Eseguibili
Nel presente articolo viene illustrato un efficiente algoritmo di esponenziazione, noto nella letteratura tecnica con il seguente nome: right – to – left binary method for exponentiation. Di questo algoritmo si danno due applicazioni per ciascuna delle quali è stato realizzato un programma in linguaggio Qbasic. Pertanto come corredo al presente articolo sono disponibili per il lettore anche i due relativi Eseguibili
Prima applicazione
Questa applicazione è relativa al calcolo dell’elevazione a potenza di un numero intero, cioè del calcolo di xq con i valori sia di x che di q numeri interi positivi. Per questo tipo di applicazione si può utilizzare:
• Una aritmetica a doppia precisione disponibile nel software adoperato per cui i valori di x e di q non possono essere molto grandi; in effetti, come si può notare dagli esempi riportati più avanti, i valori numerici che superano la soglia di 1015 sono dati in virgola mobile e mostrati con mantissa ed esponente. In questa rappresentazione dei numeri vi è quindi un troncamento del risultato numerico alla 16-ma cifra; in compenso viene dato con la parte seguente l’ordine di grandezza del numero. Questo però se non viene superato il valore numerico di 21024 pari a (1.797693134862315) · 10308, in quanto oltre tale valore si andrebbe in overflow.
• Una aritmetica a precisione multipla per cui la notevole limitazione di calcolo utilizzando solo l’aritmetica a doppia precisione può essere superata, L’utilizzo di tale tipo di aritmetica permette di avere risultati di calcolo esatti per qualsiasi valore numerico non eccedente il valore di 1014000 , vale a dire per valori numerici aventi fino a 14000 cifre Si possono così gestire ed elaborare con un apposito programma numeri composti anche da diverse centinaia di cifre. Il valore limite 1014000 è imposto dalle limitazioni inerenti il software del linguaggio utilizzato (QBasic).
Seconda applicazione
Questa applicazione è dedicata al calcolo di xp (mod p) con valori interi di x, q , p sia piccoli che grandi, costituiti ognuno anche da decine o addirittura da qualche centinaio di cifre.
Le due applicazioni indicate, ma soprattutto la seconda, risultano importanti in diversi campi della teoria dei numeri, in particolare nel campo della Crittografia.
Questo Programma – Eseguibile è realizzato facendo riferimento a quanto illustrato ed esposto nell’articolo: Un efficiente algoritmo per il calcolo di xq e di xq (mod p)” ed è rivolto in particolare al calcolo del valore esatto di x elevato alla q-esima potenza, cioè di xq con x e q numeri interi positivi. Per svolgere i calcoli nel modo più valido viene utilizzato l’algoritmo noto con il nome di “the Right to Left Binary Algorithm”che risulta essere uno dei più efficienti metodi di esponenziazione. Poiché nel calcolo di xq si devono effettuare operazioni aritmetiche in modo esatto su numeri interi formati anche da centinaia di cifre, si utilizza una aritmetica a precisione multipla. Date le limitazioni insite nel software del linguaggio utilizzato, con il presente Eseguibile non si possono ottenere per xq valori formati da un numero di cifre superiore a 14000. Pertanto si può calcolare in modo esatto un qualsiasi valore numerico di xq non eccedente il valore di 1014000.Viene qui infine data l’informazione che l’eseguibile offre due opzioni per la presentazione del numero xq; opzioni che vengono illustrate chiaramente sullo schermo prima dell’inizio dei calcoli.
Il presente Programma-Eseguibile è realizzato facendo riferimento a quanto illustrato ed esposto nel seguente l’articolo: Un efficiente algoritmo per il calcolo di xq e di xq (mod p)” Il Programma-Eseguibile è rivolto al calcolo del valore esatto di xq (mod p ) vale a dire del resto o residuo della divisione per il numero intero p di x elevato alla q-esima potenza, con x, q e p numeri interi positivi. Per svolgere i calcoli nel modo più efficiente viene utilizzato l’algoritmo noto come “the Right to Left Binary Algorithm” che è uno dei più validi metodi di esponenziazione. Poiché nel calcolo di xq (mod p) si devono effettuare operazioni aritmetiche in modo esatto su numeri interi formati anche da varie centinaia di cifre, si è utilizzata una aritmetica a precisione multipla. L’utilizzazione del presente Eseguibile risulta essenziale per il calcolo in modo esatto e veloce di xq (mod p) in vista delle sue importanti applicazioni nel campo della crittografia.
Un semplice schema per la manutenzione del PC su sistema operativo Windows
 Sognavo una macchina amichevole alla quale delegare quelle operazioni che sono causa di fatica mentale e di errori, una macchina che sapesse imparare e poi eseguire docilmente, che immagazzinasse dati e istruzioni semplici e intuitive, il cui uso fosse alla portata di tutti, che costasse poco e fosse delle dimensioni degli altri prodotti per ufficio ai quali la gente era abituata. Dovevo creare un linguaggio nuovo, che non avesse bisogno dell’interprete in camice bianco. Piergiorgio Perotto (1930 – 2002)
Sognavo una macchina amichevole alla quale delegare quelle operazioni che sono causa di fatica mentale e di errori, una macchina che sapesse imparare e poi eseguire docilmente, che immagazzinasse dati e istruzioni semplici e intuitive, il cui uso fosse alla portata di tutti, che costasse poco e fosse delle dimensioni degli altri prodotti per ufficio ai quali la gente era abituata. Dovevo creare un linguaggio nuovo, che non avesse bisogno dell’interprete in camice bianco. Piergiorgio Perotto (1930 – 2002)
Quando lavorava alla Olivetti di Adriano, mio padre, discutendo con colleghi e collaboratori diceva: il giorno che con l’elettronica si riuscirà a fare 2+2 senza ricorso alla elettromeccanica e a meccanismi in movimento il nostro vantaggio competitivo per le macchine da calcolo sarà terminato.
In tempi recenti mi raccontava che forse, se l’ingegner Adriano non fosse scomparso prematuramente (1960), la divisione elettronica della Olivetti non sarebbe stata venduta (1964).
Sul Corrire della Sera del 28 Giugno 2011 Aldo Grasso ha scritto l’articolo: L’incredibile storia della nascita del pc: "Che storia incredibile e che rammarico! Il personal computer l’abbiamo inventato noi, cioè l’Olivetti, ma a trarne vantaggi e a rivoluzionare il mondo della comunicazione sono stati gli americani della Silicon Valley: «Quando Olivetti inventò il pc», documentario di Alessandro Bernard e Paolo Ceretto (History Channel, canale 407 di Sky, domenica scorsa, ore 23).
Era il 4 ottobre del 1965 quando New York Times, Wall Street Journal, Business Week e New York Herald Tribune titolano a piena pagina: «The first desk top computer of the world». Un team di giovani ricercatori dell’Olivetti di Ivrea, diretti dall’ingegnere Piergiorgio Perotto, aveva presentato alla fiera di New York il primo Personal computer: la Programma 101 (un curioso femminile!), un calcolatore grande come una macchina da scrivere, pensato per il singolo utente senza l’intervento di un tecnico programmatore, in un’epoca in cui i calcolatori erano enormi, complicati e inaccessibili. La Hewlett Packard ne comprò un centinaio di esemplari e poco tempo dopo lanciò un modello di computer identico alla 101. Accusata di aver violato il brevetto Olivetti, la HP sarà condannata a risarcire 900 mila dollari all’azienda di Ivrea.
Ma facciamo un passo indietro: nel 1964, a causa di una dura crisi finanziaria, l’Olivetti aveva ceduto la divisione elettronica a General Electric, come condizione perché Fiat e a Mediobanca intervenissero a salvare l’azienda. Adriano era morto da quattro anni, vantandosi di non aver mai fatto ricorso a una banca. Il figlio Roberto dovette invece fare il gran passo. La squadra di Perotto aveva però nascosto il progetto sotto il cappello della divisione calcolatrici rimasta a Ivrea e riuscì così a portare a termine il suo lavoro. Attraverso le interviste ad alcuni protagonisti, prende corpo una storia tanto sconosciuta quanto emozionante." 
"La Olivetti presentò nell’Ottobre 1965 a New York, alla mostra internazionale per le macchine per ufficio, due nuovi prodotti per il calcolo: la Logos 27 e il Programma 101. La Logos 27 era il prodotto di bandiera che doveva segnare, dopo l’abbandono della elettronica, la rentrée in forze sul mercato con un prodotto meccanico di alte prestazioni: era una supercalcolatrice, probabilmente quanto di più sofisticato un genio della tecnologia della meccanica poteva concepire. Il Programma 101 che costituì il primo personal computer nella storia del calcolo venne presentato per dimostrare che, si, la Olivetti aveva ceduto il settore elettronico, ma manteneva purtuttavia un occhio attento alle future tecnologie.
Alla mostra di New York avvenne però un fatto sconvolgente e per nulla previsto: folle sterminate si assieparono attorno al piccolo box del P101, dedicando solo una distratta attenzione alla Logos 27 e il successo si propagò alla stampa e si ripeté nelle successive presentazioni a Mosca (dicembre 1965), in Italia e in altre capitali europee" P.G. Perotto, "Il Darwinismo manageriale", Edizioni Sole 24 Ore, dic. 1988, pag 126,127.
"… Varianza viene di solito utilizzato, negli studi organizzativi, come sinonimo di fonte di disturbo dei processi lavorativi; qui viene invece utilizzato nel senso di rottura di prassi consolidate, invenzione di nuovi spazi di azione ecc. La creatività diffusa, la capacità di generare varianze e la presenza dei relativi germi attivi distribuiti costituiscono un indicatore della robustezza genetica di una organizzazione, essi la rendono più adatta a reagire positivamente e a resistere contro tutti i fenomeni di turbolenza che possono rappresentare un attacco verso l’azienda, ma sopratutto la mettono in condizioni di attaccare." Ibidem, pag. 90, 91. "
E’ interessante riportare a questo proposito alcuni principi organizzativi introdotti all’INTEL:
1) Rapida e diretta comunicazione di qualsiasi difficoltà o problema. Questo deve avvenire prontamente e senza particolare riguardo ai livelli organizzativi.
2) La dottrina dell’assunzione di responsabilità. Se un impiegato identifica un problema o una opportunità, egli deve assumersi la responsabilità della soluzione senza aspettare che qualcuno glielo dica o lo autorizzi a farlo.
3) La crociata aziendale. In certe circostanze occorre mobilitare l’intera azienda e suscitare un eccezionale sforzo per risolvere problemi eccezionali.
4) Riduzione del tempo necessario a portare un prodotto sul mercato. E’ uno dei problemi fondamentali per una azienda che operi sul fronte della innovazione.
5) Deregulation interna. La deregulation all’interno di una azienda mette una grande organizzazione in condizione di essere più competitiva, al prezzo di un maggior apparente disordine…" Ibidem, pag. 91, 92
"…In Italia è prevalente il caso di persone che semplicemente non esprimono quanto potrebbero e si ritirano sempre più nella rassegnazione, riservando a qualche hobby casalingo l’espressione della propria creatività. In America le persone più creative, dopo qualche tentativo aziendale infruttuoso, se ne vanno e tentano da qualche altra parte…" Ibidem, pag. 138, 139
"…Il costo della non qualità deve tendere a zero… Accertato quindi che non possiamo fare del solo profitto l’obiettivo esclusivo di una strategia, risulta chiaro che l’obiettivo primario è quello di creare e distribuire prodotti portatori di utilità, innovazione, ricchezza reale per il mercato." ibidem, pag. 146
"… Sempre più mercati richiedono soluzioni di problemi ossia offerte del tipo problem solver, più che prodotti o sistemi. Quindi è importante creare vantaggio competitivo non solo con prodotti dotati di elevati rapporti prestazioni/prezzo, ma saper offrire prodotti adatti a risolvere in modo ottimale sempre più specifiche esigenze applicative…" ibidem, pag. 184
 Si definisce satellite un qualsiasi oggetto, naturale o artificiale, orbitante attorno ad un corpo celeste. La stessa Terra è un esempio di satellite, in quanto orbita attorno al Sole; così come la Luna, che orbita attorno alla Terra. Il moto dei satelliti artificiali segue le stesse leggi fisiche del moto dei satelliti naturali, con la differenza però che mentre questi ultimi si muovono su orbite relativamente semplici e totalmente predeterminate, le orbite dei satelliti artificiali possono essere “progettate” e sono soggette a controllo ed eventuali mutazioni. Per approfondire Marco Giancola, SATELLITI ARTIFICIALI, e-book € 4,99
Si definisce satellite un qualsiasi oggetto, naturale o artificiale, orbitante attorno ad un corpo celeste. La stessa Terra è un esempio di satellite, in quanto orbita attorno al Sole; così come la Luna, che orbita attorno alla Terra. Il moto dei satelliti artificiali segue le stesse leggi fisiche del moto dei satelliti naturali, con la differenza però che mentre questi ultimi si muovono su orbite relativamente semplici e totalmente predeterminate, le orbite dei satelliti artificiali possono essere “progettate” e sono soggette a controllo ed eventuali mutazioni. Per approfondire Marco Giancola, SATELLITI ARTIFICIALI, e-book € 4,99
 Questo testo presenta e descrive una tabella che raggruppa un’ampia varietà di dati relativi a formule, giochi e curiosità matematiche. Gli appassionati potranno utilizzarla come una sorta di prontuario agile e facilmente consultabile. I dati sono ordinati per argomento e riguardano sia aspetti più specificamente matematici (costanti, numeri interi, calcolo combinatorio, figure geometriche), sia applicazioni legate al campo della matematica ricreativa.
Questo testo presenta e descrive una tabella che raggruppa un’ampia varietà di dati relativi a formule, giochi e curiosità matematiche. Gli appassionati potranno utilizzarla come una sorta di prontuario agile e facilmente consultabile. I dati sono ordinati per argomento e riguardano sia aspetti più specificamente matematici (costanti, numeri interi, calcolo combinatorio, figure geometriche), sia applicazioni legate al campo della matematica ricreativa.
Stefano Borgoni, Formule, curiosità, giochi matematici… tutto in una tabella (534KB)
 Adam Smith va rivisto! … Se tutti ci proviamo con la bionda, ci blocchiamo a vicenda. E alla fine… nessuno di noi se la prende. Allora ci proviamo con le sue amiche, e tutte loro ci voltano le spalle, perché a nessuno piace essere un ripiego. Ma se invece nessuno ci prova con la bionda, non ci ostacoliamo a vicenda, e non offendiamo le altre ragazze. È l’unico modo per vincere. …L’unico modo per tutti di scopare!…Adam Smith ha detto che il miglior risultato si ottiene quando ogni componente del gruppo fa ciò che è meglio per sé, giusto? Incompleto. Incompleto! Perché il miglior risultato si ottiene… quando ogni componente del gruppo farà ciò che è meglio per sé, e per il gruppo! Dinamiche dominanti, signori. Dinamiche dominanti! Adam Smith si sbagliava!
Adam Smith va rivisto! … Se tutti ci proviamo con la bionda, ci blocchiamo a vicenda. E alla fine… nessuno di noi se la prende. Allora ci proviamo con le sue amiche, e tutte loro ci voltano le spalle, perché a nessuno piace essere un ripiego. Ma se invece nessuno ci prova con la bionda, non ci ostacoliamo a vicenda, e non offendiamo le altre ragazze. È l’unico modo per vincere. …L’unico modo per tutti di scopare!…Adam Smith ha detto che il miglior risultato si ottiene quando ogni componente del gruppo fa ciò che è meglio per sé, giusto? Incompleto. Incompleto! Perché il miglior risultato si ottiene… quando ogni componente del gruppo farà ciò che è meglio per sé, e per il gruppo! Dinamiche dominanti, signori. Dinamiche dominanti! Adam Smith si sbagliava!
"Negli anni 20 Emile Borel incominciò a studiare i giochi a due persone e a somma zero, in cui cioè quando qualcuno vince l’altro perde, cercando di dimostrare l’esistenza di equilibri. Si era reso conto che si trattava di una questione importante, ma pur essendo un matematico molto famoso e competente, non era più giovanissimo e non riuscì a risolverla. Chi lo fece fu Von Neumann, che ne parlò a un seminario a Gottingen e un paio di anni dopo pubblicò il suo famoso lavoro del 1928 in cui si dimostra l’esistenza di un equilibrio che può essere interpretato come un minMax: ogni giocatore ha una strategia perfettamente difensiva e la sceglie in maniera ottimale contro la strategia difensiva dell’altro giocatore.
Von Neumann e Morgestern generalizzarono il risultato a un numero qualunque di giocatori, ma sempre per giochi a somma zero. Nella mia tesi io estesi poi la generalizzazione a giochi qualunque, e i cosiddetti equilibri di Nash si riducono ai minMax di Von Neumann e Morgestern non appena si specifica che il gioco in questione è a somma zero."
"…. Alcuni dei miei metodi sono stati quasi subito recepiti da Kenneth Arrow e Gerard Debreu. Più che fra le teorie, la relazione è fra i metodi di dimostrazione: sia Arrow che Debreu usarono il teorema del punto fisso di Kakutani, che io avevo già usato un anno o due prima per dimostrare l’esistenza di quello che oggi si chiama ‘Equilibrio di Nash’ . A me l’aveva suggerito David Gale: agli inizi io pensavo invece di usare il teorema del punto fisso di Brouwer."
"… In un articolo degli anni 30 Von Neumann aveva effettivamente usato il teorema del punto fisso di Brouwer: fu proprio quell’articolo a stimolare Shizuo Kakutani a sviluppare la sua versione , che poi io ho usato nella mia tesi".
A proposito di Von Neumann, lei lo ha mai incontrato? "Si a Princeton. Andai da lui, quando ormai la mia tesi era a buon punto. Lui ascoltò l’enunciato del mio teorema e mi chiese immediatamente se nella dimostrazione usavo un punto fisso. All’epoca rimasi sorpreso, ma quello che ho appena detto spiega, almeno in parte, la reazione di von Neumann.
E conferma anche la sua proverbiale velocità di pensiero? "Si. Ma non tanto quanto la storia che si racconta, a proposito del problema di calcolare la distanza percorsa da un ape che va avanti e indietro tra due treni che si avvicinano a velocità costanti note. Il trucco sta nel calcolare prima il tempo che i due treni impiegano ad incontrarsi, e poi la distanza percorsa dall’ape in quel tempo, ma dicono che von Neumann calcolò a mente in un attimo la somma della serie infinita dei percorsi dell’ape".
Che cos’è invece la disuguaglianza di Nash? "Ha a che fare con un mio lavoro di analisi degli anni 50, relativo ad un problema aperto sulle equazioni differenziali parziali ellittiche. Io ho avuto l’idea di collegarlo al problema analogo delle equazioni paraboliche, riuscendo a risolvere entrambi i casi. Nel corso di questo processo ho usato alcune disuguaglianze, che poi sono state chiamate col mio nome. Ma, nel frattempo, alla soluzione del problema per le equazioni ellittiche era gia arrivato indipendentemente Ennio De Giorgi, che mi ha battuto nell’obiettivo".
John Nash (1928), Intervistato da P.G. Odifreddi in "I matematici solitari". Mondadori 2009.
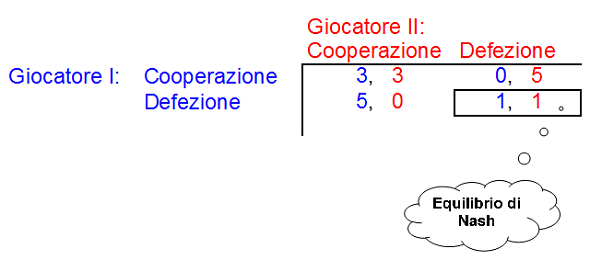
Il dilemma del prigioniero (Flood e Dresher, 1950) è forse il gioco di strategia più famoso e più diffuso dalle società di consulenza, dalle business school e dalle università americane, per descrivere le problematiche della competizione e della cooperazione. Due ladri vengono sorpresi, fermati, incarcerati ed interrogati in attesa del processo (pena prevista 5 anni). Sanno che se entrambi (cooperazione) negheranno ogni addebito per se e per il compare avranno entrambi uno sconto di pena pari a 3 anni; se, dichiarando la propria innocenza, si accuseranno reciprocamente (defezione) avranno uno sconto di solo 1 anno. Se uno solo decide di coprire il compare cooperando non avrà nessuno sconto di pena mentre l’altro che lo accusa avrà l’intera pena condonata. La matrice, riportata in figura, riassume la situazione problematica del dilemma. Il gioco (che non è a somma zero) ha un punto di equilibrio di Nash nella defezione di entrambi i giocatori (1,1). Se un solo giocatore proverà a scostarsi da esso cooperando cadrà nella situazione peggiore in cui non si ha alcuno sconto di pena. L’aspetto inquietante del gioco è dato dal fatto che proprio il punto di equilibrio stabile (1,1) è l’unico a non essere Pareto-ottimale cioè è l’unico ad essere dominato da un altro punto (3,3 che è migliore per entrambi i giocatori). Dunque la cooperazione, che è migliore per tutti, non è in questo gioco un punto di equilibrio. E’ stato simulato al computer (R. Axelrod, The Evolution of Cooperation, Basic Books, New York 1984) che, nel Dilemma del prigioniero iterato, la strategia vincente non è ne quella di Defezione ad oltranza (1,1) ne quella di Cooperazione ad oltranza (3,3), ma è quella denominata "Tit for Tat" ovvero "Occhio per occhio, dente per dente": alla prima mossa collabora, alle successive copia la precedente del tuo avversario. (R. Chiappi, Il foglio elettronico come strumento per il problem solving, F.Angeli 2008).
Chi volesse approfondire gli aspetti teorici dei giochi o conoscerne le principali applicazioni può, in questo sito, leggere sul primo numero del Magazine l’articolo di F. Patrone: "Matematica d’oggi: la teoria dei giochi" oppure consultare sull’argomento il Forum da lui diretto.
 Secondo un’originale definizione la Teoria dei Modelli è «Algebra universale più Logica», dove per Algebra universale si intende lo studio delle strutture e per Logica si intende lo studio delle formule logiche e delle regole di inferenza. Un’altra definizione ancora più recente suggerisce invece di vedere la Teoria dei Modelli come «Geometria algebrica meno campi». E’ in effetti difficile definire esattamente che cosa significhi Teoria dei Modelli; risulta ancora più arduo demarcare netti confini oltre i quali essa non si spinga. Obiettivo di questo articolo è cercare di introdurre il lettore a questa teoria fornendo gli strumenti di base e poi dimostrando il cosiddetto Teorema di Löwenheim-Skolem all’ingiù.
Secondo un’originale definizione la Teoria dei Modelli è «Algebra universale più Logica», dove per Algebra universale si intende lo studio delle strutture e per Logica si intende lo studio delle formule logiche e delle regole di inferenza. Un’altra definizione ancora più recente suggerisce invece di vedere la Teoria dei Modelli come «Geometria algebrica meno campi». E’ in effetti difficile definire esattamente che cosa significhi Teoria dei Modelli; risulta ancora più arduo demarcare netti confini oltre i quali essa non si spinga. Obiettivo di questo articolo è cercare di introdurre il lettore a questa teoria fornendo gli strumenti di base e poi dimostrando il cosiddetto Teorema di Löwenheim-Skolem all’ingiù.
 75 problemi svolti di matematica su vari argomenti: geometria piana, geometria solida, goniometria, progressioni, analisi matematica, calcolo combinatorio, curve nel piano, problemi storici, equazioni di terzo grado, problemi vari, fisica. Un ebook gratuito di 206 pagine.
75 problemi svolti di matematica su vari argomenti: geometria piana, geometria solida, goniometria, progressioni, analisi matematica, calcolo combinatorio, curve nel piano, problemi storici, equazioni di terzo grado, problemi vari, fisica. Un ebook gratuito di 206 pagine.
INDICE
Prefazione 5
Geometria piana 6
1. Triangolo rettangolo circoscritto ad una circonferenza 7
2. Triangolo isoscele circoscritto ad una semicirconferenza 9
3. Punto intersezione delle diagonali di un trapezio scaleno 11 Geometria solida 14
4. Sulla diagonale di un parallelepipedo retto 15
5. Fusione di un blocco di stagno a forma di piramide 16
6. Piramide retta avente per base un rombo 17
7. Piramide regolare quadrangolare con elementi assegnati 18
8. Piramide retta a base circoscritta ad un cerchio 19
9. Piramide sovrapposta ad un prisma retto 20
10. Cono sovrapposto ad un cilindro 21
11. Tronco di piramide quadrangolare regolare 22
12. Maturità magistrale giugno 1994 23
13. Maturità scientifica, anno 1995 25 Goniometria 27
14. Funzioni goniometriche inverse 28
15. Prima identità goniometrica 30 Progressioni 32
16. Progressioni aritmetiche 33
17. Progressioni geometriche 34
18. Problema su una progressione geometrica 36
19. Problema su una progressione geometrica 38
Analisi matematica 41
20. Primi limiti 42 21. Limite di una funzione per x 46
22. Limiti notevoli di forme algebriche indeterminate 48
23. Studio di un particolare problema differenziale 50
24. Limite I di una forma indeterminata 55 25. Limite II di una forma indeterminata 56
26. Limite III di una forma indeterminata 57
27. Limite IV di una forma indeterminata 57
28. Limite V di una forma indeterminata 58
29. Limite di una funzione per x 59
30. Calcolo elementare della derivata di una funzione 60
31. Cono di sup. laterale minima circoscritto ad una sfera 61
32. Punti estremanti di una funzione parametrica razionale 67
33. Integrale di una particolare forma indeterminata 70
34. Altro integrale notevole 74
35. Punti estremanti di una parabola cubica 77
Calcolo combinatorio 80
36. Disposizioni semplici e permutazioni 81
37. Combinazioni semplici 84 Curve nel piano 87
38. Centro di curvatura ed evolvente di una curva 88
39. Asintoti curvilinei
91 ASINTOTI PARABOLICI 92 ASINTOTI CUBICI 92
40. Problema geometrico. 96
41. Studio di quartica bicircolare 100
42. Altra quartica bicircolare 104
43. Ricerca dell’equazione polare di una quartica 108
44. Teoria su tacnodi e cuspidi di specie superiore 113
45. Esercizio 7R ( L’origine O è un tacnodo di specie ) 115
46. Applicazioni delle trasformazioni per raggi vettori reciproci 124
47. Ancora sulla trasformazione per raggi vettori reciproci 127
48. Equazioni parametriche della cardioide 131
49. Involuzione dei diametri coniugati di una conica 132
50. Costruzione dei diametri coniugati di una conica 135
51. Approfondimenti sul primo teorema di Steiner-Chasles 137
52. Altra dimostrazione del teorema di Pascal 142
53. Centro di collineazione di due fasci proiettivi di rette 144
Problemi storici 146
54. Concoide del cerchio o Lumaca di Pascal 147
55. Su un problema di Apollonio 149
56. La trisettrice di Ippia 152
57. Trisezione di un angolo: altra dimostrazione 158
Equazioni di terzo grado 160
58. Teoria delle equazioni di terzo grado 161
59. Equazione di terzo grado con discriminante positivo 163
60. Equazione di terzo grado con discriminante nullo 164
61. Equazione di terzo grado con tre radici reali 165
62. L’ equazione di terzo grado nel “casus irriducibilis” 168
63. Risoluzione grafica delle equazioni di terzo grado 172 Problemi vari 174
64. Un problema sulle età di due persone 175
65. Il problema del cane e della lepre 176
66. Quando si viaggiava in carrozza 178
67. Un problema sull’uso delle frazioni 182
68. Un problema difficile per la Camera dei Comuni 184
69. Problema del trifoglio 185
70. Problema sul numero dei polli, galline e pulcini 187
71. Le età di tre persone 189
72. Somma dei primi n numeri triangolari 190
73. Problema sulle politropiche 191
Fisica 195
74. Esercizi sui moti relativi. 196
75. Moto rettilineo uniforme visto da una piattaforma ruotante 202
N. Magnarelli, Problemi di matematica generale
 Ci proponiamo di decifrare una pagina del codice Hammer, noto anche come codice Leicester. Come molte pagine dei manoscritti di Leonardo, è piuttosto malridotta. Cominciamo ad analizzare il testo ricordandoci che Leonardo aveva l’abitudine di scrivere da destra verso sinistra, cioè in verso contrario a quello corrente, sia perché era mancino, sia perché in questo modo la sua scrittura rimaneva indecifrabile per ogni occhio indiscreto, ricordiamoci al suo tempo erano quasi tutti analfabeti, e per i pochi che sapevano leggere questo semplice artificio rappresentava un ostacolo quasi sempre insuperabile.
Ci proponiamo di decifrare una pagina del codice Hammer, noto anche come codice Leicester. Come molte pagine dei manoscritti di Leonardo, è piuttosto malridotta. Cominciamo ad analizzare il testo ricordandoci che Leonardo aveva l’abitudine di scrivere da destra verso sinistra, cioè in verso contrario a quello corrente, sia perché era mancino, sia perché in questo modo la sua scrittura rimaneva indecifrabile per ogni occhio indiscreto, ricordiamoci al suo tempo erano quasi tutti analfabeti, e per i pochi che sapevano leggere questo semplice artificio rappresentava un ostacolo quasi sempre insuperabile.
 Mostre, laboratori, conferenze ma anche fisica, musica, chimica, matematica e atronomia, dal 1 al 15 ottobre a Torino. Torino apre le porte alla terza edizione di «Ottobre Scienza», il grande evento che unisce esperti e appassionati, per intraprendere un affascinante viaggio alla scoperta delle discipline scientifiche. Decine di esperimenti, mostre interattive, conferenze e laboratori animeranno le sale del Museo di Scienze Naturali e del centro culturale Pier Giorgio Frassati (via delle Rosine 15), oltre a piazza Valdo Fusi.
Mostre, laboratori, conferenze ma anche fisica, musica, chimica, matematica e atronomia, dal 1 al 15 ottobre a Torino. Torino apre le porte alla terza edizione di «Ottobre Scienza», il grande evento che unisce esperti e appassionati, per intraprendere un affascinante viaggio alla scoperta delle discipline scientifiche. Decine di esperimenti, mostre interattive, conferenze e laboratori animeranno le sale del Museo di Scienze Naturali e del centro culturale Pier Giorgio Frassati (via delle Rosine 15), oltre a piazza Valdo Fusi.
Note, ritmo e melodie diventano oggetto di analisi scientifica al Museo Regionale di Scienze Naturali nella mostra “Il suono e l’armonia” che prende in esame onde sonore e variazioni di timbro degli strumenti musicali classici, elettrici ed elettronici. Diapason e tamburi, ma anche computer e campionatori, saranno gli strumenti utilizzati per allenare la percezione a riconoscere intervalli, sequenze ritmiche ed armonie. Ma non ci saranno solo acustica, tecnologia ed elettronica: uno spazio sarà anche dedicato alla fisiologia della percezione sonora. L’allestimento, a cui hanno collaborato gli studenti dell’Accademia Albertina guidati dal prof. Belgioioso ed il gruppo Isaac Team del Politecnico coordinati dalla dott. Mara Sola, è una delle sei mostre scelte dal Festival della Scienza di Genova per presentare il programma della manifestazione 2011 alla stampa. Dopo Torino, quindi, “Il suono e l’armonia” andrà a Genova, ospitata nei locali del Palazzo del Principe.
Le reazioni a livello molecolare sono, invece, il tema della mostra “La chimica ai tempi di Garibaldi… e oltre”, che ripercorre gli ultimi centocinquant’anni, in cui grandi cambiamenti politici e sociali si sono intrecciati con scoperte scientifiche rivoluzionarie. Ricercatori italiani ed europei saranno ricordati attraverso il loro lavoro, con exhibit e semplici esperimenti, che hanno però cambiato il corso della storia.
E ancora, quattro laboratori per provare “sul campo” quanto imparato sui banchi di scuola: dalla nascita della prima calcolatrice (rabdologia) alle applicazioni pratiche della matematica, tra dati e previsioni, c’è anche spazio per un corso “avanzato” di ritmica e produzione musicale con il corpo. L’osservazione del Sole, che avverrà in piazza Valdo Fusi tutti i giorni, sarà anche possible sabato 1 e domenica 2 ottobre in piazza Castello con il Gruppo Astrofili dell’associazione Polaris di Pinerolo.
Le visite, sempre guidate, a mostre e laboratori e la partecipazione alle conferenze devono essere prenotate sul sito www.ottobrescienza.it. Occorre sostenere unicamente il costo degli animatori (3-‐5€ per i singoli; a partire da 30€ per i gruppi organizzati).
Nata nel 2007 grazie al lavoro congiunto di studenti e professori provenienti da trenta scuole della provincia di Torino, la manifestazione «Ottobre Scienza» è il momento conclusivo dell’attività di raccolta e rielaborazione del ricco patrimonio d’idee presente negli istituti. Il progetto di coinvolgere insegnanti e giovani delle scuole superiori nel lavoro creativo d’ideazione delle esibizioni nasce dalla convinzione che essi possano diventare protagonisti nel panorama della divulgazione scientifica. L’offerta di una formazione di alto livello è anche un’occasione per stimolare nei ragazzi un’ulteriore motivazione ad intraprendere studi in tale ambito e, più in generale, la curiosità verso il mondo delle scienze.
La precedente edizione nel 2009 di «Ottobre Scienza» ha visto la partecipazione di oltre 7000 studenti e anche quest’anno i presupposti fanno sperare in un’alta adesione alle attività da parte del pubblico.
Per informazioni inviare una mail all’indirizzo [email protected] oppure contattare il numero +39 349 82 52 791. Inaugurazione al Museo Regionale di Scienze Naturali in via Giolitti 36 venerdì 30 settembre alle 16,30. Interverranno Ermanno De Biaggi, direttore del Museo Madaski, tasterista del gruppo Africa Unite Gianna Pentenero, consigliere regionale del Piemonte con la partecipazione del Coro della scuola elementare D’Assisi, diretto dalla maestra Pia Barbanera.
 Progetto realizzato per il corso di “Progettazione di Sistemi Microelettronici” (corso di Laurea Magistrale in Ingegneria Elettronica), con il supporto del Prof. Luca Fanucci, Università di Pisa, Facoltà di Ingegneria. Obiettivo del progetto: progettare un generatore di sequenze pseudo-casuali per trasmissioni CDMA. Il progetto contiene la descrizione dell’algoritmo, possibili applicazioni, possibili architetture.
Progetto realizzato per il corso di “Progettazione di Sistemi Microelettronici” (corso di Laurea Magistrale in Ingegneria Elettronica), con il supporto del Prof. Luca Fanucci, Università di Pisa, Facoltà di Ingegneria. Obiettivo del progetto: progettare un generatore di sequenze pseudo-casuali per trasmissioni CDMA. Il progetto contiene la descrizione dell’algoritmo, possibili applicazioni, possibili architetture.
.
Scarica il progetto di E. Molinari su Pseudo noise sequence generator
 Per lungo tempo il problem solving sarà più importante dello studio della teoria. La creatività non è una dote innata. Ogni ingegnere può imparare ad essere inventivo. Studiare il pensiero creativo è equivalente ad imparare a gareggiare nello sport. Perciò voi dovete focalizzarvi principalmente sulla pratica allo scopo di acquisire i metodi e le tecniche per affrontare i problemi del lavoro e della vita. Lo sviluppo di tutti i sistemi tecnici è governato da leggi oggettive. Genrich Saulovich Altshuller (1926, 1998).
Per lungo tempo il problem solving sarà più importante dello studio della teoria. La creatività non è una dote innata. Ogni ingegnere può imparare ad essere inventivo. Studiare il pensiero creativo è equivalente ad imparare a gareggiare nello sport. Perciò voi dovete focalizzarvi principalmente sulla pratica allo scopo di acquisire i metodi e le tecniche per affrontare i problemi del lavoro e della vita. Lo sviluppo di tutti i sistemi tecnici è governato da leggi oggettive. Genrich Saulovich Altshuller (1926, 1998).
Ogni oggetto che svolge una funzione è un sistema tecnico. Gli esempi di sistemi tecnici includono automobili, penne, libri, coltelli etc. Ogni sistema tecnico è composto da uno o più sottosistemi. Un automobile è composto dal sottosistema motore, un sottosistema di governo, un sottosistema frenante, una carrozzeria, etc. La gerarchia dei sistemi tecnici si estende dai meno complessi, con solo due elementi, ai più complessi con molti elementi interagenti. L’invention Machine è un sistema di problem solving che si basa sul metodo Triz elaborato in Unione Sovietica negli anni quaranta dall’ingegnere ebreo Genrich Altshuller. Triz è un acronimo russo che significa "teoria per il problem solving inventivo" relativo alle nuove tecnologie ed ai brevetti. Per Altshuller effettuare ricerca, sviluppo e innovazione tecnologica significa cercare soluzione ai problemi senza alcuna barriera tra le varie discipline. Quando era stato prigioniero nei campi di Stalin, allo scopo di sollevare il morale degli intellettuali detenuti (scienziati, filosofi, avvocati, architetti, etc.) e di colmare le sue lacune conoscitive, aveva attivato dei corsi di 12-14 ore al giorno di cui lui era l’unico studente. Gli intellettuali ebbero una motivazione per la sopravvivenza e lui ottenne lo scopo di ottenere per se una istruzione superiore e una cultura interdisciplinare. Aveva applicato a se stesso il principio "triznicko" di convertire una situazione negativa e minacciosa (la detenzione) in una opportunità di crescita e miglioramento.
Secondo Althshuller il progresso e lo sviluppo tecnologico, indipendentemente dall’epoca e dal luogo in cui prosperano, hanno alcuni modelli evolutivi che si ripetono. Dal momento che ogni problema tecnico può essere visto come la soluzione di una contraddizione si può creare una matrice o tabella delle contraddizioni in cui da un lato figurano 39 parametri tecnici esprimenti contraddizioni da superare, dall’altro 40 principi del problem solving individuati e codificati analizzando migliaia di brevetti. La matrice non è altro che uno strumento di consultazione (una specie di check list bidimensionale) che costringe il progettista ad analizzare il suo problema per inserirlo nel modo corretto in una delle 39 famiglie disponibili. Si va poi alla ricerca del principio di problem solving (tra i 40 elencati) che meglio si adatta al caso in esame. All’incrocio della matrice appaiono una serie di suggerimenti che Altshuller aveva raccolto in molti volumi, una libreria di tutte le possibili soluzioni tecniche. Questi suggerimenti sono vagliati dai tecnici che alla fine scelgono quelli che meglio si adattano al caso in esame. Poiché le soluzioni segnalate appartengono a tutti i campi della scienza e della tecnica, gli ingegneri e i tecnici si trovano di fronte ad ipotesi a cui difficilmente sarebbero arrivati data la natura interdisciplinare delle soluzioni proposte.
L’ingegneria tradizionale dice ‘dobbiamo realizzare queste funzioni e perciò dobbiamo costruire questi apparecchi’. Il metodo di Altshuller formalizzato nel Triz propone ‘dobbiamo realizzare queste funzioni senza introdurre nuovi meccanismi nel sistema’. La legge di tendenza all’ideale stabilisce che ogni sistema tecnologico, tende a divenire più affidabile, semplice ed efficace in una parola più ideale. Ogni volta che si migliora un sistema tecnologico esso costa meno, richiede meno spazio, consuma meno energia, si avvicina cioè alla idealità. Si può valutare un lavoro creativo di ricerca dal suo grado di idealità. Più un sistema è complicato, pesante, ingombrante, costoso più lontano si trova dalla soluzione ideale, quando un sistema tecnologico tende alla idealità il meccanismo fisico tende a scomparire, ma la funzione per cui è predisposto continua ad essere assicurata. La soluzione dei problemi secondo il metodo Triz passa attraverso 7 passi, composti a loro volta da sub-step e collegati da circuiti di feed-back (Es. riformulazione del problema), che consentono un procedimento per affinamenti successivi:
1) Analisi del problema,
2) Analisi del modello del problema,
3) Formulazione della soluzione ideale,
4) Risoluzione delle contraddizioni tra situazione reale e ideale,
5) Analisi qualità/costi delle modalità che hanno risolto le contraddizioni,
6) Analisi dell’effetto della soluzione sui sistemi circostanti,
7) Registrazione del processo seguito, utile per problemi futuri.
Althshuller ha fondato in Russia l’ Istituto Pubblico di Creatività Inventiva (IPCI). L’obiettivo dello Istituto era di preparare gli inventori professionisti, i ricercatori, i lettori, gli esperti in metodologie creative e gli organizzatori ed incubatori delle attività inventive. Il programma durava due anni ed i principali argomenti dei corsi erano:
1) Metodologie creative (TRIZ ed altre tecniche usate in occidente),
2) Sviluppo della immaginazione creativa,
3) Psicologia della creatività,
4) Teoria dei Sistemi,
5) Teoria della Informazione,
6) Cibernetica,
7) Teoria delle Decisioni,
8) Studio dei Brevetti,
9) Tecniche Previsionali,
10) Storia dello Sviluppo Scientifico e Tecnologico.
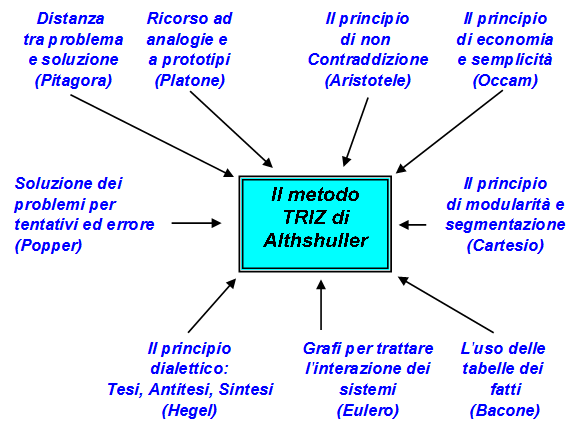
 Animazione interattiva sulle leve: teoria, simulazioni, semplici esercizi per la secondaria di primo grado.
Animazione interattiva sulle leve: teoria, simulazioni, semplici esercizi per la secondaria di primo grado.
Visita il sito dell’autore http://www.matematicainterattiva.it/
 Animazione interattiva sulle equazioni di primo grado: un programmino semplice che fa vedere come risolvere le equazioni.
Animazione interattiva sulle equazioni di primo grado: un programmino semplice che fa vedere come risolvere le equazioni.
Visita il sito dell’autore http://www.matematicainterattiva.it/
 Al contrario di quello che molti credono, Galileo non fu esattamente l’inventore del cannocchiale ma ebbe il grande merito di trasformare quello che era poco più d’un giocattolo in uno strumento scientifico e di comprenderne l’eccezionale importanza. 1. Gli studi di Galileo – 2. Altre notizie e aneddoti su Galileo – 3. La sentenza di condanna e l’atto di abiura – 4. Alla fine dell’800 c’era ancora chi minimizzava. Un ebook di 19 pagine su Galileo.
Al contrario di quello che molti credono, Galileo non fu esattamente l’inventore del cannocchiale ma ebbe il grande merito di trasformare quello che era poco più d’un giocattolo in uno strumento scientifico e di comprenderne l’eccezionale importanza. 1. Gli studi di Galileo – 2. Altre notizie e aneddoti su Galileo – 3. La sentenza di condanna e l’atto di abiura – 4. Alla fine dell’800 c’era ancora chi minimizzava. Un ebook di 19 pagine su Galileo.
 Lo scopo di queste pagine è quello di dimostrare la formula chiusa per la successione di Lucas facendo uso dell’algebra lineare e della formula di Binet per i numeri di Fibonacci.
Lo scopo di queste pagine è quello di dimostrare la formula chiusa per la successione di Lucas facendo uso dell’algebra lineare e della formula di Binet per i numeri di Fibonacci.
 “L’ultimo teorema di Fermat – L’avventura di un genio, di un problema matematico e dell’uomo che lo ha risolto dopo tre secoli” di Simon Singh
“L’ultimo teorema di Fermat – L’avventura di un genio, di un problema matematico e dell’uomo che lo ha risolto dopo tre secoli” di Simon Singh
La storia dell’Ultimo Teorema di Fermat è inestricabilmente connessa alla storia della matematica e tocca tutti i temi più rilevanti della teoria dei numeri. Per questo motivo, il libro di Simon Singh non è solo la storia della dimostrazione del teorema: è innanzi tutto una storia della matematica, che parte dalla Grecia Antica arrivando ai giorni nostri, attraverso la vita delle menti più brillanti che si sono dedicate alla dimostrazione del teorema, provando nuovi teoremi in ambiti apparentemente lontani dalla teoria dei numeri.
Pitagora (VI sec. a.C.) ebbe il merito di capire che l’esistenza dei numeri è indipendente dal mondo sensibile e che i fenomeni naturali sono governati da leggi descritte con equazioni matematiche, perciò proclamò: “Tutto è numero”.
Euclide (III sec. a.C.) dimostrò l’esistenza dei numeri irrazionali e Diofanto di Alessandria (III-IV sec. d.C.) compilò l’Arithmetica, una grande opera sulla teoria dei numeri, nella quale ritroviamo l’intera conoscenza dei numeri costruita dai suoi predecessori: la sua specialità era affrontare quesiti che richiedevano una soluzione con numeri interi.
Nel millennio successivo alla matematica greca, la matematica occidentale entrò in una fase di stallo e continuò la propria evoluzione solo grazie ai contributi provenienti dall’India e dall’Arabia: i matematici orientali copiarono le formule dei manoscritti greci, reinventarono molti teoremi ormai perduti e aggiunsero nuovi elementi. Nel 1453, quando i Turchi saccheggiarono Costantinopoli, i dotti di Bisanzio fuggirono in Occidente con tutti i testi che riuscirono a preservare e cominciò così un periodo di rinascita in Europa.
Padre Marino Mersenne (1588-1648) giocò un ruolo importante nella matematica del Seicento e fu forse l’unico matematico con il quale Fermat mantenne contatti regolari. Pierre de Fermat (1601-1665), solerte funzionario pubblico, si dedicò alla matematica come dilettante: creava nuovi teoremi e sfidava i contemporanei a trovare soluzioni ai problemi che lui stesso risolveva. Leggendo l’Arithmetica di Diofanto, troviamo, tra le sue annotazioni a bordo pagina, la scritta “… cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet” (… teorema di cui ho scoperto una meravigliosa dimostrazione. Ma questo margine è troppo piccolo per contenerla). Tale affermazione si riferisce alla congettura – meglio nota come Ultimo Teorema di Fermat – secondo la quale l’equazione an + bn = cn non ammette soluzioni intere per n > 2.
Nel secolo successivo, Leonhard Euler (1707/1783) compie i primi progressi per la dimostrazione dell’Ultimo Teorema di Fermat: con la dimostrazione del caso per n = 3 si addentra nel campo dei numeri immaginari.
All’inizio del XIX secolo, l’Ultimo Teorema di Fermat è noto come il problema più famigerato della teoria dei numeri. Sophie Germain (1776-1831) dà alla sua dimostrazione un contributo superiore a quello di tutti gli uomini che l’avevano preceduta; il primo marzo del 1847, Gabriel Lamé (1795-1870) e Augustin Louis Cauchy (1789-1857) annunciano di averlo dimostrato, ma tre mesi dopo Ernst Kummer (1810-1893) trova un errore nella dimostrazione: hanno usato una proprietà dei numeri nota come fattorizzazione unica, ma coinvolgendo anche i numeri immaginari. Nel 1908, Paul Wolfskehl destina una quota del suo patrimonio a chi fosse riuscito a dimostrare l’Ultimo Teorema di Fermat entro il 13 settembre 2007.
I matematici ancora alle prese con l’Ultimo Teorema di Fermat nel secondo dopoguerra hanno cominciato ad impiegare i computer per aggredire il problema, affidandosi ad una versione computerizzata dell’impostazione ottocentesca di Kummer.
Nel 1954, Goro Shimura (1930-) e Yutaka Taniyama (1927-1958), appassionati dello studio delle forme modulari – oggetti matematici con simmetria infinita – enunciano una congettura, sostenendo di essere in grado di unificare il mondo modulare con quello ellittico. Nel 1986 Ken Ribet dimostra il legame tra la congettura di Taniyama-Shimura e l’Ultimo Teorema di Fermat: chi dimostra la prima ha dimostrato anche il secondo. Nello stesso anno, Andrew Wiles (1953-) comincia a lavorare alla dimostrazione della Congettura, grazie alla sua ottima conoscenza delle equazioni ellittiche. Nel marzo del 1988, Yoichi Miyaoka dimostra l’Ultimo Teorema di Fermat, ma c’è una lacuna logica: la sua esperienza nella geometria non gli ha consentito di essere completamente rigoroso nella teoria dei numeri.
Nel 1993, il 23 giugno, dopo sette anni di studio, Wiles completa la dimostrazione della congettura di Taniyama-Shimura, ma due mesi dopo viene rilevato un grave errore. Il 19 settembre del 1994, Wiles completa definitivamente la dimostrazione.
Dopo una breve presentazione delle funzioni periodiche f e g con le loro proprietà, riferendoci ad un articolo della rivista Scienze, si passa ad un’applicazione di dette funzioni. Altre applicazioni sono nell’ambito geometrico e trigonometrico. Di dette funzioni sono riportati i grafici per mostrare il loro andamento relativo ai vari angoli e sono dati anche i valori differenziali ed integrali i cui passaggi matematici sono riportati in un’appendice che conclude il lavoro.
 Scopo di questa tesi è quello di descrivere gli attuali dispositivi microelettronici a stato solido di tipo bulk, dispositivi privi di nanostrutture confinanti per i portatori di carica mobile, come pozzi, fili e punti quantici, adatti a rivelare elettricamente un segnale luminoso incidente di una certa intensità e frequenza. Presenteremo una panoramica sulle tecniche di fotorivelazione più utilizzate, spiegando la fisica che sta alla base dell’optoelettronica ed accennando alle applicazioni di maggiore interesse: telecomunicazioni su fibra ottica, rilevamenti telemetrici, vari tipi di “mapping” per la diagnostica medica, terminando con i fotomoltiplicatori di ultima generazione candidati ad essere utilizzati nella tomografia ad emissione di positroni PET.
Scopo di questa tesi è quello di descrivere gli attuali dispositivi microelettronici a stato solido di tipo bulk, dispositivi privi di nanostrutture confinanti per i portatori di carica mobile, come pozzi, fili e punti quantici, adatti a rivelare elettricamente un segnale luminoso incidente di una certa intensità e frequenza. Presenteremo una panoramica sulle tecniche di fotorivelazione più utilizzate, spiegando la fisica che sta alla base dell’optoelettronica ed accennando alle applicazioni di maggiore interesse: telecomunicazioni su fibra ottica, rilevamenti telemetrici, vari tipi di “mapping” per la diagnostica medica, terminando con i fotomoltiplicatori di ultima generazione candidati ad essere utilizzati nella tomografia ad emissione di positroni PET.
TESI DI LAUREA IN INGEGNERIA ELETTRONICA
TITOLO: Tecnologia della fotorivelazione basata su dispositivi a semiconduttore
CANDIDATO: Enrico MOLINARI
ANNO ACCADEMICO 2009-2010
E. Molinari Tecnologia della fotorivelazione basata su dispositivi a semiconduttore (PDF)
Scarica la presentazione della tesi (PPT)
INTRODUZIONE
Lo scopo di questa tesi è di descrivere gli attuali dispositivi microelettronici a stato solido (a semiconduttore inorganico) di tipo bulk, ovvero dispositivi privi di nanostrutture confinanti per i portatori di carica mobile, come pozzi, fili e punti quantici (“quantum wells, quantum wires, quantum dots”), adatti a rivelare elettricamente un segnale luminoso incidente, caratterizzato da una certa intensità e frequenza. Presenteremo una panoramica sulle tecniche di fotorivelazione più utilizzate, riservando amplio spazio alla fisica che sta alla base dell’optoelettronica ed accennando brevemente alle applicazioni di maggior interesse, come ad esempio le telecomunicazioni su fibra ottica, i rilevamenti telemetrici o vari tipi di “mapping” per uso di diagnostica medica, terminando con i fotomoltiplicatori, di ultima generazione, candidati ad essere utilizzati nella tomografia ad emissione di positroni (in inglese PET – “Positron Emission Tomography”). Questi ultimi sono noti, in ambito tecnico – scientifico, con il nome di SiPMs (“Silicon Photon Multipliers” – fotomoltiplicatori al silicio). Dei dispositivi per fotorivelazione che prenderemo in esame descriveremo i principi di funzionamento, richiamando alcuni concetti fondamentali di fisica dei semiconduttori e alcune loro proprietà ottiche, le principali caratteristiche e le proprietà in base a cui vengono classificati (ad esempio l’efficienza quantica, l’efficienza di rivelazione dei fotoni, il rapporto segnale/rumore, il guadagno, il range dinamico, la responsività, la risoluzione temporale ecc…) e citeremo brevemente alcune tecnologie e passi di processo importanti che ne consentono l’integrazione a livello sub – micrometrico. Analizzeremo i dispositivi optoelettronici, ad omogiunzioni ed eterogiunzioni, più utilizzati, come i PIN (semiconduttore drogato p/semiconduttore intrinseco/semiconduttore drogato n), gli APDs (“Avalanche Photo Diodes” – fotodiodi a valanga), i SAM – APDs (“Separate Absorption and Multiplication APDs” – fotodiodi a valanga a regioni di assorbimento e moltiplicazione separate), i SAGM – APDs (“Separate Grading Absorption and Multiplication APDs” – SAM a variazione graduale del gap di energia), i GM – APDs (“Geiger Mode APDs” – APDs funzionanti in modalità Geiger) ed i SiPM. Vedremo come il loro impiego consenta di risolvere alcuni dei problemi che interessano i dispositivi a tubo (noti come PMTs – “Photon Multipliers Tubes” – fotomoltiplicatori a tubo), ampiamente usati in passato e tutt’oggi. Infine, una volta chiarite la fisica e la topologia dei suddetti fotorivelatori, illustreremo (in appendice D), a livello di principio, il contesto strumentale nel quale vanno inseriti, al fine di acquisire immagini computerizzate nell’ambito della PET.
INDICE
1) Introduzione
2) La tomografia ad emissione di positroni (“Positron Emission Tomography” – PET)
2.1) Il principio fisico alla base della PET
2.2) Il principio su cui si basa la rivelazione fotonica in ambito PET
3) Il tubo fotomoltiplicatore (PMT – “Photon Multiplier Tube”) 3.1) Concetti generali riguardanti un fotorivelatore
3.2.1) Il tubo fotomoltiplicatore classico (PMT): estrazione elettronica per effetto fotoelettrico
3.2.2) Il tubo fotomoltiplicatore classico (PMT): struttura di base
3.2.3) Il tubo fotomoltiplicatore classico (PMT): funzionamento in condizione di buio
3.2.4) Il tubo fotomoltiplicatore classico (PMT): funzionamento in condizione di illuminazione
3.3) Il fotodiodo ibrido (HPD – “Hybrid Photodiode”)
4) Concetti basilari del fotodiodo ad omogiunzione pn
4.1.1) La omogiunzione pn in condizione di equilibrio
4.1.2) La omogiunzione pn in condizione di equilibrio: richiami di fisica dei semiconduttori e della giunzione pn
4.2.1) La omogiunzione pn in condizione di polarizzazione inversa
4.2.2) I fenomeni di breakdown
4.3) Generalit{ sull’interazione fra luce e semiconduttore ……………………………………………………………….. 42 4.4.1) Un esempio di omogiunzione pn al silicio integrata, utilizzata come fotorivelatore, vista in sezione ……………………………………………………………………………………………………………………………………………. 48 4.4.2) Un caso particolare di interazione fra luce e silicio …………………………………………………………………. 49
4.5) Fotodiodi classici e fotodiodi a valanga …………………………………………………………………………………………. 55 5) I fotodiodi PIN 5.1.1) Le principali modalità di interazione fra luce e semiconduttore: descrizione qualitativa ……………………………………………………………………………………………………………………………… 56 5.1.2) Le principali modalità di interazione fra luce e semiconduttore: calcolo dei rispettivi rates …………………………………………………………………………………………………………………………………………….. 61 5.2) L’equazione di continuit{ completa per un sistema di elettroni (semplificato) in un semiconduttore …………………………………………………………………………………………………………………………………………… 66 5.3.1) Un modello semiclassico per l’interazione fra luce e semiconduttore …………………………………. 67
5.3.2) Calcolo del profilo spaziale dell’intensit{ luminosa all’interno di un fotorivelatore a semiconduttore ………………………………………………………………………………………………………………. 70
5.3.3.1) Calcolo dell’espressione generale del coefficiente di assorbimento ottico specifico α(ν,x) e dell’andamento spaziale dell’intensit{ luminosa Iν(x) per alte potenze ottiche incidenti……………………………………………………………………………………………………………………………….71 5.3.3.2) Calcolo del profilo spettrale del coefficiente di assorbimento ottico specifico α0(ђω)……74 5.3.3.3) Stima delle variazioni spettrali del coefficiente di assorbimento ottico specifico α0(ђω) causate dagli eccitoni……………………………………………………………………………………………………………79 5.4) I problemi di efficienza quantica e di risoluzione temporale, di un fotorivelatore a giunzione pn, legati alla larghezza della zona di svuotamento …………………………………………………………………………….. 87 5.5) L’andamento spaziale del campo elettrico e del potenziale all’interno di un fotorivelatore PIN asimmetrico …………………………………………………………………………………………………………………………………………. 91 5.6) L’andamento spaziale del campo elettrico, del potenziale e delle bande di energia all’interno di un fotorivelatore PIN simmetrico ……………………………………………………………………………………………………….. 94 5.7) Potenza assorbita ed efficienza quantica per un PIN …………………………………………………………………… 97 5.8) Un possibile criterio di progetto per la larghezza della zona di svuotamento di un PIN……101 5.9.1) Il grafico della compatibilità reticolare fra semiconduttori: utilità, descrizione ed interfacciamento tra semiconduttori di costante reticolare diversa………………………………………104 5.9.2) Il grafico della compatibilità reticolare fra semiconduttori: la legge di Vegard ……………….. 111 5.9.3) Il grafico della compatibilità reticolare fra semiconduttori: esempio di progettazione del PIN di terza finestra InP/In(0.57)Ga(0.43)As/InP a struttura “MESA” ………………………………………………….. 118 5.10) L’impossibilit{ di sfruttare, in un PIN, la moltiplicazione a valanga ai fini della fotorivelazione ………………………………………………………………………………………………………………………………………….. 130 5.11) Un esempio di PIN al silicio commerciale: l’elettronica di front – end, le caratteristiche del dispositivo e i passi di processo per la sua integrazione …………………………………………………………………… 131 5.12) La proporzionalit{ inversa tra l’energia di gap Egap e la parte reale nr’(ω) dell’indice di rifrazione di un semiconduttore: spiegazione formale ……………………………………………………………………… 135 6) I fotodiodi a valanga (APDs – “Avalanche Photodiodes”) 6.1) Le caratteristiche I – V di un fotorivelatore a valanga, sottoposto ad illuminazione; rivelazioni fotovoltaiche e fotoconduttive……………………………………………………………………………………………. 137 6.2) Le correnti di rumore di un fotodiodo a valanga: origine fisica delle fluttuazioni stocastiche e relative densità spettrali di potenza di rumore ……………………………………………………………………………….. 139 6.3.1) Modellizzazione matematica della fotorivelazione intrinseca di un APD …………………………. 144 6.3.2) Calcolo del limite quantico per il SNR in uscita da un fotorivelatore …………………………………. 146 6.4) Modellizzazione matematica della fotomoltiplicazione per un APD ed effetto del breakdown a valanga sul SNRAPD ………………………………………………………………………………………………………………………………… 148 6.5) Il fattore di rumore in eccesso di un APD ……………………………………………………………………………………. 151 6.6) Il rapporto segnale/rumore per PIN e APD in condizioni di funzionamento reali (le espressioni complete) ……………………………………………………………………………………………………………………………… 153 6.7.1) La “Responsivity” di un fotorivelatore: descrizione generale ……………………………………………… 156 6.7.2) La “Responsivity” di un fotorivelatore: una possibile spiegazione fisica …………………………. 158 7) I fotodiodi SAM (“Separate Absorption and Multiplication” APDs) 7.1.1) Il fotodiodo a valanga SAM n+/p/π/p+ al silicio: struttura di base, grafici spaziali delle grandezze elettriche, regioni di assorbimento e di moltiplicazione ……………………………………………….. 160 7.1.2) Il fotodiodo a valanga SAM n+/p/π/p+ al silicio: profilo della densità di corrente di elettroni nella regione di moltiplicazione e valor medio M del guadagno di fotorivelazione ……. 163 7.1.3) Il fotodiodo a valanga SAM n+/p/π/p+ al silicio: la dipendenza spaziale della “probabilit{ di trigger” ……………………………………………………………………………………………………………………………………………………….. 165 7.1.4) Il fotodiodo a valanga SAM n+/p/π/p+ al silicio: controllo e collimazione del breakdown a valanga mediante trench integrata, fattore geometrico, efficienza quantica ……………………………….. 166 7.1.5) Il fotodiodo a valanga SAM n+/p/π/p+ al silicio: crescita epitassiale dello strato di assorbimento π e profilo spaziale della concentrazione di drogante all’interfaccia π/p+ ………….. 168 7.1.6) Il fotodiodo a valanga SAM n+/p/π/p+ al silicio: il sistema antiriflesso ……………………………… 171 7.2.1.1) Il fotodiodo a valanga SAM p+/n/n-/n+ ad eterostruttura: le ragioni del suo utilizzo ed il suo funzionamento …………………………………………………………………………………………………………………………………… 173 7.2.1.2) Il fotodiodo a valanga SAM n+/p/π/p+ ad eterostruttura GaAs/GaAs/Cd(x)Hg(1-x)Te/Si utilizzato per la fotorivelazione di radiazioni ottiche nel medio – lontano infrarosso…………175 7.2.2) Il fotodiodo a valanga SAM p+/n/n-/n+ ad eterostruttura graduata: esempio di “Mesa – Etched” SAGM – APD commerciale ………………………………………………………………………………………………………… 179 7.3) Un esempio di eterostruttura graduata a basso fattore di rumore in eccesso ……………………… 180 8) I fotomoltiplicatori al silicio (SiPMs – “Silicon Photon Multipliers”) 8.1) La modalità di funzionamento Geiger e la disposizione matriciale dei SAM – APDs n+/p/π/p+ al silicio ………………………………………………………………………………………………………………………………………………………. 182 8.2) Il range dinamico e l’efficienza di rivelazione dei fotoni per un SiPM …………………………………… 183 8.3.1) Il resistore di quenching: la sua disposizione sull’ossido di microcella e due possibili tecniche di integrazione ………………………………………………………………………………………………………………………….. 186 8.3.2) Il resistore di quenching: il funzionamento …………………………………………………………………………….. 188 8.4) Il circuito equivalente di un SiPM sottoposto ad un impulso luminoso ………………………………… 190 8.5) La frequenza di eventi di buio (“dark count rate”) di un SiPM ……………………………………………….. 193 8.6) Il crosstalk ottico all’interno di un SiPM ……………………………………………………………………………………… 196 8.7) La risoluzione temporale di un SiPM: il problema degli “after pulses” relativo alla scarica Geiger ed i ritardi legati alla carica Geiger …………………………………………………………………………………………… 197 8.8) La proporzionalità inversa fra range dinamico e fattore geometrico in un SiPM ……………….. 199 8.9) Il cristallo di scintillazione LYSO accoppiato ad un SiPM per applicazioni PET ………………….. 199
Appendici
A) L’epitassia da fasci molecolari (MBE – “Molecular Beam Epitaxy”) ………………………………………….. 202
B) Una possibile tecnica per la rivelazione di luce appartenente al lontano infrarosso ……………. 211
C) Una possibile scelta di semiconduttori III – V per la rivelazione di frequenze ottiche comprese fra il visibile e l’ultravioletto ………………………………………………………………………………………………………………….. 212
D) Schema di principio dell’elettronica di lettura per la TOF PET
BIBLIOGRAFIA
Testi:
1) B. G. Streetman, S. K. Banerjee: “Solid State Electronic Devices”, Prentice – Hall International Editions
2) G. Ghione: “Dispositivi per la Microelettronica”, McGraw – Hill
3) R. S. Muller, T. I. Kamins: “Device Electronics for Integrated Circuits”, J. Wiley & Sons
4) S. Wolf, R. N. Tauber: “Silicon Processing for the VLSI Era”, vol. 1, Lattice Press
5) S. M. Sze: “Dispositivi a Semiconduttore”, Hoepli
6) G. S. May, S. M. Sze: “Fundamentals of semiconductor fabrication”, J. Wiley & Sons
7) P. S. Kireev: “Semiconductor Physics”, Mir Publishers
8) J. F. Gibbons: “Semiconductor Electronics”, McGraw – Hill
9) A. Pirovano, C. Monzio Compagnoni: “Dispositivi optoelettronici integrati”, Societ{ Editrice Esculapio
10) T. Tamir: “Guided – wave optoelectronics”, Springer Verlag
11) H. A. Haus: “Waves and fields in optoelectronics”, Prentice – Hall International Editions
12) D. L. Lee: “Electromagnetic principles of integrated optics”, J. Wiley & Sons
13) L. D. Hutcheson: “Integrated optical circuits and components”, Marcel – Dekker
14) H. Nishihara, M. Haruna, T. Suhara: “Optical Integrated Circuits”, McGraw – Hill
15) C. Kittel: “Introduzione alla Fisica dello Stato Solido”, Boringhieri
16) B. E. A. Saleh, M. C. Teich: “Fundamental of Photonics”, J. Wiley & Sons
17) J. Singh: “Optoelectronics: An Introduction to Materials and Devices”, McGraw – Hill
18) J. Singh: “Semiconductor Devices: An Introduction”, McGraw – Hill
19) M. Dagenais, R. F. Leheny, J. Crow: “Integrated Optoelectronics”, Academic Press
20) E. J. Murphy: “Integrated Optical Circuits and Components”, Marcel – Dekker
21) J. Singh: “Electronic and Optoelectronic Properties of Semiconductor Structures”, Cambridge University Press
22) K. Konishi, G. Paffuti: “Meccanica Quantistica: nuova introduzione”, Edizioni PLUS – Pisa University Press
23) C. Hamaguchi: “Basic Semiconductor Physics”, Springer
24) B. E. A. Saleh, M. C. Teich: “Fundamentals of photonics”, J. Wiley & Sons
25) A. Bogoni, L. Potì: “Elementi di comunicazioni ottiche”, Pitagora
26) M. Luise: “Sitemi di trasmissione su fibra ottica”, Edizioni ETS, Pisa
27) W. R. Fahrner: “Nanotechnology and Nanoelectronics”, Springer
Pubblicazioni:
1) J. Haba: “Status and perspectives of Pixelated Photon Detectors” (2008), Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 595 (1), pp. 154 – 160 2) M. Mazzillo, G. Condorelli, D. Sanfilippo, A. Piazza, G. Valvo, B. Carbone, G. Fallica, G. Bonanno, (…): “Silicon photomultipliers for nuclear medical imaging applications” (2008), Proceedings of SPIE – The International Society for Optical Engineering 7003, art. no. 70030I 3) M. Petasecca, B. Alpat, G. Ambrosi, P. Azzarello, R. Battiston, S. Haino, A. Papi, (…): “Thermal and electrical characterization of silicon photomultipliers” (2008), IEEE Transactions on Nuclear Science 55 (3), art. no. 4545198, pp. 1686 – 1690 4) E. Levin, E. Shelegeda, C. Sitarsky, (…): “Advances in the development of solid state photomultipliers for medical imaging” (2008), Progress in Biomedical Optics and Imaging – Proceedings of SPIE 6913, art. no. 69130J 5) G. Laurenti, G. Levi, E. Foschi, C. Guandalini, M. Zuffa, (…): “Time Of Flight Detectors: from phototubes to SiPMs” (2008), Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 588 (1-2), pp. 267 – 271 6) G. Llosà, N. Belcari, M. G. Bisogni, A. Del Guerra, G. Collazuol, S. Marcatili, S. Moehrs, C. Piemonte: “Silicon photomultipliers and SiPM matrices as photodetectors in nuclear medicine” (2007), IEEE Nuclear Science Symposium Conference Record 3, art. no. 4436825, pp. 3220 – 3223 7) C. Piemonte: “A new silicon photomultiplier structure for blue light detection” (2005), Nuclear Instruments and Methods in Physics Research, 568 (A), pp. 224 – 232 8) D. Renker: “Photodetectors” (2004), Nuclear Instruments and Methods in Physics Research, 527 (A), pp. 15 – 20 9) V. Golovin, V. Saveliev: “Novel type of avalanche photodetector with Geiger mode operation” (2003), Nuclear Instruments and Methods in Physics Research, 447 (A), pp. 486 – 490 10) R. Battiston, M. G. Bisogni, M. Boscardin, G. Collazuol, F. Corsi, G. F. Dalla Betta, A. Del Guerra, N. Dinu, G. Levi, S. Marcatili, S. Moehrs, C. Marzocca, C. Piemonte, A. Pozza, C. Sbarra, L. Quadrani, G. Llosà: “Novel silicon photomultipliers for PET applications” (2006), IEEE Transactions on Nuclear Science (3), pp. 1875 – 1879 11) G. Collazuol: “Optical Materials” (2007) 12) P. Buzhan, B. Dolgoshein, L. Filatov, A. Ilyin, V. Kaplin, (…): “Silicon photomultiplier and its possible applications” (2003), Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 504 (1-3), pp. 48 – 52 227 13) E. A. Georgievskya, S. N. Klemin, L. Filatov, P. Buzhan, B. Dolgoshein, A. Ilyin, (…): “The solid – state silicon photomultiplier for a wide range of applications” (2002), Proceedings of SPIE – The International Society for Optical Engineering 5126, pp. 37 – 42 14) G. B. Bondarenko, P. Buzhan, V. Golovin: “Microcell Si avalanche photodiode with limited Geiger mode gain” (2000), IEEE Nuclear Science Symposium and Medical Imaging Conference 1, pp. 7 – 27 15) C. Piemonte, R. Battiston, M. Boscardin, G. F. Dalla Betta, A. Del Guerra, N. Dinu, A. Pozza, N. Zorzi: “Characterization of the First Prototypes of Silicon Photomultiplier Fabricated at ITC – irst” (2007), IEEE Transactions on Nuclear Science, vol. 54, art. no. 1 16) G. Llosà, N. Belcari, M. G. Bisogni, G. Collazuol, A. Del Guerra, N. Dinu, C. Piemonte, (…): “Evaluation of the First Silicon Photomultiplier Matrices for a Small Animal PET Scanner” (2008), IEEE Transactions on Nuclear Science
Ulteriori fonti:
1) A. Diligenti (Prof. Ordinario, Facoltà di Ingegneria, Università di Pisa): “Appunti del corso di Dispositivi e Tecnologie Elettroniche” (a.a. 2006/2007), SEU – Servizio Editoriale Universitario di Pisa 2) P. E. Bagnoli (Prof. Ordinario, Facoltà di Ingegneria, Università di Pisa): “Appunti dei corsi di Optoelettronica e Fotonica”, Edizioni “il Campano” 3) F. Giannetti (Prof. Associato, Facoltà di Ingegneria, Università di Pisa): “Comunicazioni Ottiche”, Edizioni “il Campano” 4) M. Morganti, F. Cei ( Facoltà di Scienze Matematiche Fisiche e Naturali, Università di Pisa): “Appunti di meccanica quantistica”, reperibili online sul sito web del Dott. Cei 5) S. Bassi: “Tesi di Laurea Specialistica in Fisica Medica sulla Caratterizzazione Spettroscopica di Fotorivelatori al Silicio SiPM” (a.a. 2007/2008)
La giuria ha giudicato vincitrici del concorso le seguenti tesine:
Miglior tesina area umanistia
La parola, il suo significato e il suo potere di Valentina Bianchin (Montebelluna)
Miglior tesina area scientifica
Applicazione delle serie di Fourier di Manuel Zambelli (Verona)
Miglior tesina area tecnica
Linee di desiderio di Marco Fenucci (Santa Maria a Monte, Pisa)
Miglior tesina area umanistia
La parola, il suo significato e il suo potere di Valentina Bianchin (Montebelluna)
Il lavoro presentato offre una esaustiva trattazione dell’argomento scelto. L’esposizione risulta nel complesso originale e l’individuazione di autori solitamente non trattati nei programmi curriculari, per supportare le argomentazioni di fondo, evidenziano una buona capacità critica e una autonomia nella individuazione e nella maturazione di itinerari di riflessione personali e nella estrinsecazione di contenuti originali. Il registro linguistico usato è appropriato e le competenze disciplinari trasversali emergono in maniera articolata. La struttura generale del lavoro, anche dal punto di vista della redazione dello stesso è più che adeguata.Tesina
Miglior tesina area scientifica
Applicazione delle serie di Fourier di Manuel Zambelli (Verona)
La tesina espone una dettagliata applicazione della matematica nel riconoscimento dei suoni e nella compressione delle immagini digitali. Il lavoro, in parte pubblicato sulla rivista online MatematicaMente della sezione veronese della Mathesis (la coincidenza del nome della rivista della Mathesis con il nome del sito che ha bandito la gara è del tutto casuale) è nato da una collaborazione con la Facoltà di Scienze dell’Università degli Studi di Verona. L’autore ha poi proceduto in modo autonomo nella parte applicativa e sperimentale utilizzando software come “Mathematica” e LATEX usati prevalentemente nella ricerca universitaria.Tesina
Miglior tesina area tecnica
Linee di desiderio di Marco Fenucci (Santa Maria a Monte, Pisa)
L’autore ha realizzato un’applicazione informatica che permette di analizzare la domanda di mobilità relativa agli studenti di una scuola al fine di fornire proposte motivate agli amministratori pubblici e alle aziende di trasporto per pianificare il trasporto pubblico urbano per studenti. Come caso studio l’autore ha applicatolo strumento elaborato ai dati degli studenti della propria scuola. Il lavoro si presenta ben strutturato, curato, completo e descritto con chiarezza.Tesina
I vincitori sono pregati di contattare [email protected] per i premi
 “Nelle pagine seguenti userò il termine ‘teoria’ in senso lato, includendovi credenze comuni (per esempio la credenza nell’esistenza di oggetti materiali), miti (per esempio il mito dell’eterno ritorno), credenze religiose ecc. In breve designerò come teoria qualsiasi punto di vista sufficientemente generale concernente questioni di fatto”. I problemi dell’empirismo (P. Feyerabend, 1971).
“Nelle pagine seguenti userò il termine ‘teoria’ in senso lato, includendovi credenze comuni (per esempio la credenza nell’esistenza di oggetti materiali), miti (per esempio il mito dell’eterno ritorno), credenze religiose ecc. In breve designerò come teoria qualsiasi punto di vista sufficientemente generale concernente questioni di fatto”. I problemi dell’empirismo (P. Feyerabend, 1971).
“I razionalisti vogliono che ci si comporti sempre in modo razionale, ossia che si prendano decisioni secondo regole e criteri che essi e i loro amici considerano importanti e fondamentali. L’esempio della scienza indica che un tale comportamento non conduce ad alcun risultato: il mondo fisico è troppo complesso per poter essere dominato e compreso con l’ausilio di metodi razionali. Ma il mondo sociale, il mondo del pensiero e del sentimento umano, della fantasia umana, il mondo della filosofia, della poesia, delle scienze, il mondo della convivenza politica è ancora più complicato. Ci si deve forse attendere che i razionalisti abbiano successo in questo mondo, dopo aver fallito nel mondo fisico ?”.
Scienza in una società libera
“La scienza non ha portato alla liberazione, ma ad una servitù anche peggiore di quelle che ha contribuito ad abbattere… essa è oggi tanto oppressiva quanto le ideologie contro cui ha dovuto combattere …”.
Discorso contro la scienza, Università del Sussex 1974.
“….una scienza gestita da gente libera sarebbe più attraente della scienza di oggi che è praticata da schiavi, di istituzioni e schiavi della ragione. … Ovviamente gli scienziati non svolgeranno alcun ruolo predominante nella società da me prospettata. Essi saranno più che controbilanciati da maghi, o preti, o astrologi. Una tale situazione è intollerabile per molte persone vecchie e giovani, di destra e di sinistra. Quasi tutti voi avete la ferma convinzione che almeno una qualche sorta di verità sia stata trovata, e che debba essere conservata. …. Il compito più duro ha bisogno della mano più leggera, altrimenti il suo assolvimento non condurrà alla libertà, ma ad una tirannia molto peggiore di quella che sostituisce."
Come difendere la società contro la scienza.
"La verità è piuttosto un oceano, sempre crescente di alternative reciprocamente incompatibili (e forse anche incommensurabili): ogni singola teoria, ogni favola, ogni mito che fanno parte di questa collezione costringono le altre a una maggiore articolazione, e tutte contribuiscono, attraverso questo processo di competizione, allo sviluppo della nostra coscienza. Nulla è mai deciso, nessuna concezione può mai essere lasciata fuori da una esposizione generale”. " L’idea di un metodo che contenga princìpi fermi, immutabili e assolutamente vincolanti come guida dell’attività scientifica si imbatte in difficoltà considerevoli quando viene messa a confronto con i risultati della ricerca storica. Troviamo infatti che non c’è una singola norma, per quanto plausibile e per quanto saldamente radicata nell’epistemologia, che non sia stata violata in qualche circostanza. Diviene evidente anche che tali violazioni non sono eventi accidentali, che non sono il risultato di un sapere insufficiente o disattenzioni che avrebbero potuto essere evitate. Al contrario, vediamo che tali violazioni sono necessarie per il progetto scientifico. In effetti, uno dei caratteri che più colpiscono delle recenti discussioni sulla storia e la filosofia della scienza è la presa di coscienza del fatto che eventi e sviluppi come l’invenzione dell’atomismo nell’antichità, la rivelazione copernicana, l’avvento della teoria atomica moderna …., il graduale emergere della teoria ondulatoria della luce si verificano solo perché alcuni pensatori o decisero di non lasciarsi vincolare da certe norme metodologiche ‘ovvie’, o perché involontariamente le violarono."
Contro il metodo.
Accanto all’assenza di restrizioni metodologiche Feyerabend (Vienna, 1924 -1994) teorizza il principio di proliferazione delle teorie e la tesi della controinduzione, secondo cui l’incremento della conoscenza è frutto dell’elaborazione di punti di vista teorici alternativi e reciprocamente incompatibili e del capovolgimento di teorie saldamente acquisite. Egli giunge così non solo a sostenere la pari dignità delle differenti tradizioni all’interno della scienza, ma anche a negare la superiorità della conoscenza scientifica rispetto ad altre forme di sapere come ad esempio l’arte e l’astrologia.
Imre Lakatos (ungherese) fu grande amico di Feyerabend. Entrambi, filosofi della scienza, erano stati allievi di Popper ed insieme progettarono un libro a quattro mani "A favore e contro il metodo" che non vide mai la luce a causa della prematura scomparsa di Imre Lakatos, che rappresentava la voce in qualche modo più favorevole al metodo, avrebbe voluto riconciliare il razionalismo critico di Popper con l’epistemologia storicistica di Kuhn, mentre Feyerabend (il più contestatore dei due) prese posizioni fortemente critiche sia nei confronti di Popper che di Kuhn.
In seguito ai commenti iniziali di Contro il metodo,che erano principalmente negativi, nel 1975 Feyerabend cadde in profonda depressione.
"Restai depresso per più di un anno; la depressione per me era come un animale, qualcosa di ben definito e localizzabile. Mi potevo svegliare, aprire gli occhi, ascoltare… C’è o non c’è? Nessun segno di essa. Forse dorme. Forse oggi mi lascerà in pace. Con prudenza, con molta prudenza, mi alzo dal letto. È tutto tranquillo. Vado in cucina e comincio a fare colazione. Nessun suono. In TV c’è Good Morning America, David non-ricordo-il-nome, un tipo che non sopporto. Mangio e guardo gli ospiti. Lentamente il cibo riempie il mio stomaco e mi dà forza. Ora una corsa in bagno e poi via per la mia passeggiata mattutina – ed eccola, la mia fedele depressione: "Pensavi di poter restare senza di me?" .
Nonostante ciò, egli continuò a difendere la sua controversa posizione filosofica e a sostenerla viaggiando incessantemente. Col passare del tempo Contro il metodo si dimostrò un successo clamoroso in tutto il mondo.
La posizione di Feyerabend, favorevole ad una sorta di anarchismo metodologico, al fine di trovare nuove teorie per risolvere problemi e cercare la verità, ha riscontro nelle prassi seguita da alcune organizzazioni che non si vogliono limitare, per affrontare i loro problemi, ai confini della scienza: psicologia, sociologia, empirismo, razionalismo, metodi quantitativi, ecc.. Nelle organizzazioni (multinazionali, industriali, di servizi, di credito, statali, municipali, no-profit, non governative ecc.) è sempre più diffuso, per addestrare le persone a risolvere e gestire i problemi, l’uso dell’arte, della storia, del teatro, della letteratura, della poesia delle fiabe, dei miti, e della religione. Alcune imprese per selezionare e coltivare talenti ricorrono anche alla magia, all’astrologia, alla filosofia new age, alle palestre e all’outdoor training.
 Perché di notte è buio? Cominciamo ponendoci un problema che sembrerebbe non avere alcuna attinenza con l’astronomia: supponiamo di trovarci al centro di una foresta di raggio R, e tentiamo di determinare quale debba essere il valore minimo del raggio R della foresta affinchè non sia possibile al nostro sguardo uscire fuori dalla foresta stessa.
Perché di notte è buio? Cominciamo ponendoci un problema che sembrerebbe non avere alcuna attinenza con l’astronomia: supponiamo di trovarci al centro di una foresta di raggio R, e tentiamo di determinare quale debba essere il valore minimo del raggio R della foresta affinchè non sia possibile al nostro sguardo uscire fuori dalla foresta stessa.
 Il Convegno, che è anche corso di formazione e aggiornamento, in collaborazione con il gruppo “Polymath” di Torino, è il quarto della serie “Matematica in classe”. Il primo si è tenuto a Idro (Brescia 2008), il secondo a Roma nel 2009, il terzo a Riccione l’anno scorso. Quest’anno si svolgerà a Frascati presso l’Auditorium del Museo delle Scuderie Aldobrandini, in piazza Marconi 5, con l’eccezione di venerdì pomeriggio quando i lavori si apriranno presso l’Hotel Cacciani in via Armando Diaz 15.
Il Convegno, che è anche corso di formazione e aggiornamento, in collaborazione con il gruppo “Polymath” di Torino, è il quarto della serie “Matematica in classe”. Il primo si è tenuto a Idro (Brescia 2008), il secondo a Roma nel 2009, il terzo a Riccione l’anno scorso. Quest’anno si svolgerà a Frascati presso l’Auditorium del Museo delle Scuderie Aldobrandini, in piazza Marconi 5, con l’eccezione di venerdì pomeriggio quando i lavori si apriranno presso l’Hotel Cacciani in via Armando Diaz 15.
La quarta edizione di “Matematica in classe” privilegerà i temi della Probabilità e della Statistica, entrati da tempo nell’uso comune e riconosciuti nella loro importanza strategica ormai da tutti i programmi e le indicazioni nazionali. Il riconoscimento è basato sulla pervasività dei linguaggi probabilistico e statistico nella vita di tutti i giorni, sulla possibilità quindi che questi linguaggi offrono per approfondire la matematizzazione della realtà, sulle numerose applicazioni nelle scienze naturali e fisiche ma anche in quelle economiche e sociali, sulle prospettive che aprono nello sviluppo di alcuni significativi strumenti matematici.
Anche questa edizione è l’occasione di incontrare all’inizio dell’anno, in un ambiente piacevole e sereno“antichi” e nuovi colleghi e discutere con loro idee, esperienze e progetti. Da un punto di vista più strettamente disciplinare, il Corso ripercorrerà degli “snodi” fondamentali nell’insegnamento di Probabilità e Statistica (anche alla luce delle recenti indicazioni nazionali), presenterà l’opportunità di avvalersi delle moderne tecnologie di calcolo per elaborare dati e rappresentare i risultati ottenuti sotto forma di grafici e tabelle, introdurrà infine ad una lettura critica delle più usuali modalità d’insegnamento/apprendimento che invero nascerà in modo molto naturale dalle relazioni previste e dalle competenze e esperienze dei partecipanti al Convegno.
PROGRAMMA
Il Convegno/Corso di formazione contiene al suo interno un mini-corso di 8 ore di Probabilità, un mini-corso di Statistica (5 ore) e 3 conferenze/lezioni di 1 ora. Le lezioni si svolgeranno venerdì 14 dalle 15.00 alle 19.00 presso l’hotel Cacciani in via Aramndo Diaz 15, sabato 15 dalle 9.00 alle 13.00 e dalle 15.00 alle 19.00 e domenica 16 dalle 9.00 alle 13.00 presso l’Auditorium del Museo della Scuderie Aldobrandini in piazza Marconi 5. La loro calendarizzazione verrà precisata in seguito.
Il mini-corso di probabilità sarà tenuto dal prof. Giuliano Spirito del Liceo Scientifico “Cavour” di Roma e si svilupperà secondo la seguente traccia:
• Punti di forza e limiti delle definizioni classiche, frequentistica e soggettivistica di probabilità
• Le formule fondamentali del calcolo delle probabilità
• Probabilità e calcolo combinatoria
• Esempi e applicazioni Il mini-corso di Statistica sarà tenuto dal prof. Walter Racugno dell’Università di Cagliari e si svilupperà sulla seguente traccia:
• Statistica univariata: dai dati osservati alle sintesi statistiche (tabelle di frequenza, rappresentazioni grafiche, indici sintetici di posizione e di dispersione di una distribuzione di frequenza). Osservazioni critiche.
• Statistica bivariata: tabelle a doppia entrata, rappresentazioni grafiche.
• Studio descrittivo della dipendenza statistica tra due variabili e dipendenza lineare: gli scarti come risorsa. Osservazioni critiche.
• Un cenno al concetto e all’uso di “significatività statistica”.
Le conferenze/lezioni di 1 ora saranno tenute dai proff. Franca Abazia dell’Istituto “Leonardo Da Vinci” di Firenze (“Esperienze didattiche al primo anno di un Istituto professionale e nell’ultimo anno di un Istituto Tecnico”), Gian Italo Bischi dell’Università di Urbino (“Bruno de Finetti: la probabilità non esiste”), Nando Geronimi del Centro PRISTEM (“La probabilità nei giochi matematici”).
Per ulteriori informazioni
http://matematica.unibocconi.it/articoli/frascati-14-16-ottobre-2011
 Materiali: scacchiera 6X6, otto pedine bicolore, un dado colorato con 3 facce chiare e 3 facce scure. Obiettivo del gioco: la partita si sussegue in un certo numero di sfide basate sulla rapidità del pensiero logico. Ad ogni sfida, ciascun giocatore deve battere sul tempo l’avversario nell’individuare una “sequenza magnetica” utile a rovesciare una o più pedine avversarie trasformandole in proprie. Vince la partita il giocatore che per primo riesce a rovesciare tutte le pedine dello sfidante.
Materiali: scacchiera 6X6, otto pedine bicolore, un dado colorato con 3 facce chiare e 3 facce scure. Obiettivo del gioco: la partita si sussegue in un certo numero di sfide basate sulla rapidità del pensiero logico. Ad ogni sfida, ciascun giocatore deve battere sul tempo l’avversario nell’individuare una “sequenza magnetica” utile a rovesciare una o più pedine avversarie trasformandole in proprie. Vince la partita il giocatore che per primo riesce a rovesciare tutte le pedine dello sfidante.
![]() Scarica il pdf completo della descrizione del gioco magnetic brain
Scarica il pdf completo della descrizione del gioco magnetic brain
Consulta il blog dell’autore
E’ noto che gli esseri umani usano, ormai da secoli, il sistema di numerazione po-sizionale in base dieci poiché hanno dieci dita delle mani. In una sala vi sono 175 sedie, arriva un marziano e, dopo averle contate, scrive 106; quante dita delle mani ha il marziano?
Francesco Camia, Sui sistemi di numerazione posizionali in base qualunque
“ Il percorso frazionario ” è un gioco da tavolo che si sviluppa su una serie di caselle dove sono state già scritte delle frazioni. I giocatori, preferibilmente da due a quattro, spostano i loro segnalini lanciando il dado uno alla volta con l’obiettivo di arrivare primi al traguardo conclusivo. Se il giocatore arriva su una frazione propria deve indietreggiare di una casella, se giunge su una frazione impropria deve avanzare di una casella, se, infine, va a finire su una frazione apparente deve avanzare di tante caselle quante ne indica il numero naturale uguale alla frazione stessa.
Ci sono, poi, alcune caselle caselle come il recinto , la ruota bucata , le faccine , l’aeroplano, per le quali sono previste istruzioni particolari.
I giocatori possono poi arrivare sulle caselle identificate dal punto interrogativo ; si tratta degli imprevisti che vengono superati soltanto rispondendo bene alle domande che si trovano sulle carte.
Il gioco è provvisto, oltre che dal tabellone stampabile preferibilmente su carta colorata in formato A3, anche di alcuni allegati, come “Le regole del gioco” e le carte “IMPREVISTI” (da ritagliare ed incollare su cartoncino insieme alle copertine).
Didatticamente può essere usato come esercizio di gruppo per il recupero ed il potenziamento delle competenze sui numeri razionali (la frazione come operatore, tipi di frazioni, semplici problemi con i numeri razionali, ecc.)
L’approccio è, ovviamente, ludico ed al tempo stesso laboratoriale, favorendo anche un’educazione del tipo “peer to peer”, cioè tra pari.
La valenza del gioco aumenta considerevolmente se si considera che il docente può rimodulare le domande degli “IMPREVISTI”, o aggiungere altre carte, se intende recuperare o potenziare alcuni aspetti o argomenti particolari sui quali i propri alunni risultano particolarmente deboli. Destinatari sono i ragazzi di prima media o di seconda che comunque abbiano già affrontato lo studio dei numeri razionali.
Autore: Prof. Angelo Gagliardi, docente di matematica e scienze presso l’IC Catanzaro Casalinuovo Sud di Catanzaro
Scarica il tabellone e le carte da gioco, attenzione sono nel formato A3 doppio foglio A4
Scarica le regole del gioco, formato A4
 L’ontologia applicata al DJIA trova conferma nei dati storicamente rilevati per le variabili del sistema e per la nuova variabile “utile futuro annuo atteso d” che, evidenziando, dopo un tempo sufficientemente lungo, attraverso vari cicli economici, il comportamento unidimensionale del Dow, ricodnuce al modello matematico della parabola di M. J. Feigenbaum che fa emergere le caratteristiche caotiche e non lineari tipiche di un sistema fisico dispersivo; consente inoltre di connettere il concetto di PE (punto di quasi equilibrio) con la nozione di equilibrio macroeconomico di sottoccupazione di J. M. Keynes, evidenziando l’insensatezza dei presupposti dei modelli della Reh secondo cui il mercato sia sempre prossimo alla condizione di equilibrio.
L’ontologia applicata al DJIA trova conferma nei dati storicamente rilevati per le variabili del sistema e per la nuova variabile “utile futuro annuo atteso d” che, evidenziando, dopo un tempo sufficientemente lungo, attraverso vari cicli economici, il comportamento unidimensionale del Dow, ricodnuce al modello matematico della parabola di M. J. Feigenbaum che fa emergere le caratteristiche caotiche e non lineari tipiche di un sistema fisico dispersivo; consente inoltre di connettere il concetto di PE (punto di quasi equilibrio) con la nozione di equilibrio macroeconomico di sottoccupazione di J. M. Keynes, evidenziando l’insensatezza dei presupposti dei modelli della Reh secondo cui il mercato sia sempre prossimo alla condizione di equilibrio.
Scarica l’articolo di Giacomo de Laurentis (ing.) Ontologia applicata al DJIA: conseguenze
BIBLIOGRAFIA
1) John R. Searle, The construction of Social Reality , free press, New York 1995; traduzione italiana di Andrea Bosco, La costruzione della realtà sociale, Edizioni di << Comunità>>, Milano 1996;
2) Ilya Prigogine e Isabelle Stangers, La nuova alleanza. Metamorfosi della scienza ; edizioni Einaudi 1999; trad. it. Napolitani P. D.; collana Piccola Biblioteca Einaudi. Nuova serie, pag. 288;
3) Peter Coveney e Roger Highfield, La freccia del tempo, edizione Rizzoli 1991
4) Peter William Atkins, Il secondo principio, Zanichelli editore 1988
5) Giulio Casati, Il caos Le leggi del disordine, Le Scienze Spa Editore 1991
6) René Thom, Stabilità strutturale e morfogenesi, Giulio Einaudi Editore 1980
7) René Thom, Modelli matematici della morfogenesi, Giulio Einaudi Editore 1985
8) B. H. Lavanda, Termodinamica dei Processi Irreversibili, Liguori Editore, Napoli, 1980
9) Adriano Sacco, Fondamenti di chimica generale e inorganica, Adriatica Editrice –Bari
10) Fabrizio Galimberti, Economia e pazzia, Editori Laterza 2002
11) Roman Frydman e Michael Goldberg, Imperfect Knowledge Economics, Princeton University Press 2007
12 ) Rampa Giorgio, Introduzione all’equilibrio economico generale Editore: Unicopli
13) De Girolamo Umberto, L’equilibrio di sottoccupazione nell’analisi di Keynes: alcune considerazioni, Levante 1989.
 “Prima di morire, il 20 settembre 1996, all’età di ottantatre anni, Erdős riuscì a pensare a più problemi di qualunque altro matematico della storia. Scrisse da solo o in collaborazione 1475 saggi accademici, molti monumentali e tutti consistenti. E non era solo la quantità di lavoro a essere impressionante in lui, ma anche la qualità.” Collaborò con più persone di qualunque altro matematico della storia (ben 485) dimostrando che la matematica non è soltanto un gioco da ragazzi. Strutturò la sua vita per massimizzare il tempo da dedicare alla matematica, nonostante facesse la spola tra i quattro continenti a un ritmo frenetico, spostandosi da un’università o un centro di ricerca all’altro.
“Prima di morire, il 20 settembre 1996, all’età di ottantatre anni, Erdős riuscì a pensare a più problemi di qualunque altro matematico della storia. Scrisse da solo o in collaborazione 1475 saggi accademici, molti monumentali e tutti consistenti. E non era solo la quantità di lavoro a essere impressionante in lui, ma anche la qualità.” Collaborò con più persone di qualunque altro matematico della storia (ben 485) dimostrando che la matematica non è soltanto un gioco da ragazzi. Strutturò la sua vita per massimizzare il tempo da dedicare alla matematica, nonostante facesse la spola tra i quattro continenti a un ritmo frenetico, spostandosi da un’università o un centro di ricerca all’altro.
Rinunciando al piacere fisico e ai beni materiali – quel poco che guadagnava, lo dava via – consacrò tutta la vita alla scoperta della verità matematica. Cominciò a far matematica a tre anni e dopo la morte della madre, negli ultimi venticinque anni della sua vita, dedicava alle sue ricerche 19 ore al giorno, tenendosi in piedi con anfetamine e caffè: “Un matematico è una macchina per trasformare caffè in teoremi”.
Il suo più grande interesse erano i numeri primi, suoi “amici intimi”, ma aprì anche nuovi campi nella matematica, grazie alla sua abilità nel formulare problemi e nel dedurre soluzioni brevi e brillanti. Uno dei suoi più fondamentali contributi alla matematica fu la scoperta di una potente nuova forma di dimostrazione di esistenza, detta metodo probabilistico, introdotta nel 1947. Inoltre, diede un grande contributo alla teoria computazionale, nonostante rifuggisse i computer.
Nato a Budapest il 26 marzo 1913, figlio di due insegnanti di matematica delle superiori, nel 1934, per ragioni politiche, dovette lasciare l’Ungheria: andò in Inghilterra, per una borsa di studio post-laurea di quattro anni a Manchester. Più avanti, cacciato da Princeton per il suo comportamento maleducato e anticonformista, fu invitato da Ulam a unirsi allo sforzo bellico a Los Alamos, ma non venne accettato, visto che aveva sottolineato la possibilità di tornare a Budapest dopo la guerra.
Tornò in Ungheria, ma alla chiusura delle frontiere da parte di Stalin, ripartì in tutta fretta e passò qualche anno tra Inghilterra e Stati Uniti. A causa di uno scambio epistolare con Hua, teorico dei numeri cinese – le lettere che si scambiavano vennero considerate messaggi cifrati visti gli impenetrabili simboli matematici ivi contenuti – gli americani impedirono a Erdős di rientrare nel paese. Erdős non accettava che gli venissero posti dei vincoli, ma poté rientrare negli Stati Uniti solo nel 1963, a seguito di una raccolta di più di duecento firme.
Nel marzo del 1997 – l’anno dopo la morte di Erdős – all’Università di Memphis, ci fu la 919^ Assemblea dell’American Mathematical Society – si svolgeva annualmente e coincideva con il compleanno di Erdős – e Ralph Faudree, principale organizzatore del convegno, invitò tutti a fermarsi a casa sua per una “festa dei sopravvissuti”, durante la quale si scambiarono aneddoti su Erdős. Il ritratto che ne emerse lo descrive molto bene: “benché fosse un disastro nelle cose materiali, con la gente era sempre gentile”, “era una persona piena di attenzioni”, “si prendeva a cuore le cose che stavano a cuore a te, anche cose che a lui non piacevano”. Una persona eccentrica, ma estremamente generosa, che aveva a cuore la scoperta della verità e con la frase “La mia mente è aperta” invitava i matematici a lui più vicini a collaborare con lui.
 La produttività nello sviluppo dei programmi applicativi era fortemente condizionata dalla necessità per i programmatori di seguire i legami di collegamento prestabiliti tra i vari set di dati. Inoltre non era possibile fare anche solo piccoli cambiamenti nella struttura della base dei dati senza dover rivedere e correggere tutti i programmi applicativi che facevano riferimento alla vecchia struttura. Come risultato di tutto questo molte ore di lavoro di programmatori ed analisti erano impiegate nella continua ed inevitabile manutenzione dei programmi. La principale motivazione che condusse alla formulazione del modello relazionale fu l’obiettivo di stabilire in modo netto e chiaro una linea di demarcazione tra la struttura fisica e logica dei dati.
La produttività nello sviluppo dei programmi applicativi era fortemente condizionata dalla necessità per i programmatori di seguire i legami di collegamento prestabiliti tra i vari set di dati. Inoltre non era possibile fare anche solo piccoli cambiamenti nella struttura della base dei dati senza dover rivedere e correggere tutti i programmi applicativi che facevano riferimento alla vecchia struttura. Come risultato di tutto questo molte ore di lavoro di programmatori ed analisti erano impiegate nella continua ed inevitabile manutenzione dei programmi. La principale motivazione che condusse alla formulazione del modello relazionale fu l’obiettivo di stabilire in modo netto e chiaro una linea di demarcazione tra la struttura fisica e logica dei dati.
Non sorprende che i tentativi fatti dagli enti di standardizzazione, quali il CODASYL a lo ANSI, di sviluppare separatamente il linguaggio di strutturazione dei dati (DDL, Data Definition Language) e quello di manipolazione degli stessi (DML, Data Management Language) hanno portato a molti fraintendimenti e incompatibilità. L’approccio relazionale tende a considerare tutte le relazioni come operatori logici. Il suo scopo principale è quello di evitare dei loop (stallo circolare del computer), un requisito fondamentale per gli utenti finali e un evidente modo per incrementare la produttività di chi scrive programmi applicativi. Edgar F. "Ted" Codd (1923 – 2003), informatico britannico: Relational Database: A Practical Foundation for Productivity (1982)
Edgar Codd scrisse le dodici regole dell’esecuzione analitica online (OLAP: OnLine Analytical Processing) di programmi su data base relazionali. Se ne riassumono alcune tra le più significative:
R1 e R2) Tutte le informazioni comprese in un data base relazionale sono rappresentate in modo univoco mediante un indicatore di riga ed un indicatore di colonna che fa riferimento ad una specifica tabella bidimensionale.
R3) Come in statistica è necessario distinguere i valori NULL (assenza di informazione) dal valore zero (che è un particolare valore numerico). Qualunque campo di un D.B può avere valore NULL.
R4 e R5) Un sistema di gestione di D.B. relazionali deve supportare, per gli utenti finali, un linguaggio d’interrogazione (SQL, Structured Query Language) e per gli specialisti un linguggio per la gestione del sistema (RDBMS, Relational Data Base Management System).
R6 e R7) Per qualunque vista del D.B: debbono essere facilitate le operazioni di aggiornamento (Update), inserimento (Insert) e cancellazione dei dati (Delete).
R8) Indipendenza fisica dei dati: i mutamenti nella struttura fisica di memorizzazione dei dati (vettori, liste indicizzate, ecc.) non devono implicare la necessità di un cambiamento nei programmi applicativi.
R9) Indipendenza logica dei dati: i mutamenti nella struttura logica dei dati (tabelle, colonne, righe, campi chiave, ecc.) non devono implicare la necessità di un cambiamento nei programmi applicativi.
R10) I sistemi volti a garantire la sicurezza e l’integrità dei dati debbono essere generalizzati ed indipendenti dagli specifici programmi applicativi.
R11) L’eventuale distribuzione geografica di parti (o della totalità) del data base su diversi sistemi o reti deve essere invisibile agli utenti finali e ai programmatori.
Quando iniziai a lavorare a metà degli anni 70 si usavano ancora, per archiviare i dati, i files tradizionali (sequenziali o indicizzati) ed ogni programma gestionale (generalmente scritto in linguaggio COBOL) necessitava in input un nuovo file organizzato secondo le esigenze della specifica applicazione; i dati venivano quindi continuamente duplicati. Con l’introduzione dei Data Base questa esigenza venne a cessare, i dati erano archiviati una sola volta nel D.B. e gli applicativi accedevano direttamente ad essi. Vi poteva essere un unico referente responsabile che amminstrava i dati per tutti (Data Base Administrator). I Data Base erano organizzati in tabelle (vedi figura)
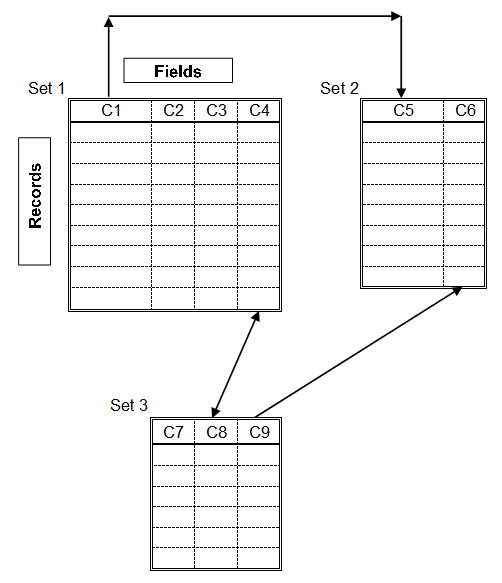
chiamate data set strutturate in righe e colonne. Le ricerche e le selezioni dei dati venivano fatte sulla base di campi chiave che servivano anche come collegamento tra i diversi set. Le due strutture principali per collegare i set di dati erano quella gerarchica (set padri, set figli, ecc.) o quella reticolare (adottata dallo IMS della IBM).
Il nostro gruppo aziendale, che allora disponeva di uno dei più grandi e moderni centri di elaborazione dati in europa, scelse di adottare come DBMS il System 2000, potente, snello e, sebbene gerarchico, con alcune caratteristiche dei sistemi relazionali che ancora non erano sviluppati e diffusi commercialmente. System 2000 era dotato di un linguaggio d’interrogazione (NL Natural Language) e aggiornamento assai semplice che risolveva molti problemi che gli utenti finali avevano nell’interagire con le basi di dati. Si potevano digitare semplici frasi in Inglese del tipo: List C1,C2, C3, C6; Ordered By C1,C7; Where (C3 > 100 AND C1 = Null) OR C2 = "Castoro Sei". Cioè: listami il contenuto dei campi C1,C2,C3,C6; ordinandoli come prima chiave per C1 e come seconda per C7; Selezionami solo i record che abbiano, o C3 > 100 e C1 mancante, o C2 uguale a "Castoro Sei". La società passò negli anni successivi ad ARTEMIS (data base relazionale che disponeva anche di una banca metodi orientata alla gestione dei progetti) e poi a SAP, ma non ho mai più trovato un linguaggio per interagire con il DB semplice, ed orientato all’utente finale, come quello di System 2000.
Codd alla fine degli anni 60, mentre lavorava per l’IBM, creò il modello relazionale per la gestione delle basi di dati, pubblicando "A Relational Model of Data for Large Shared Data Banks" (un modello relazionale di dati per gestire grandi banche dati condivise). Con suo grande disappunto l’IBM, che voleva continuare a commercializzare il suo prodotto reticolare (IMS), tardò a sfruttare le sue idee innovative fino a quando la concorrenza cominciò ad implementarle. Ad esempio, Larry Ellison costruì, sulla base delle idee di Codd, il database Oracle che fu il primo DB commerciale basato sul modello relazionale. La principale forza di questo modello fu e rimase quella di poter stabilire dinamicamente i legami tra i set di dati (purchè avessero un campo comune) al momento della ricerca, senza dover sottostare a strutture rigide progettate a priori come accadeva nei sistemi gerarchici e in quelli a rete.
 Questo studio riguarda alcune funzioni matematiche sui numeri interi. Si tratta di funzioni molto semplici ma che hanno importanti applicazioni pratiche. L’idea di fondo è quella di raccogliere una serie di dati e informazioni sul tema, affrontandolo con un approccio un po’ diverso dal solito. Il testo è corredato da una tabella relativa ai primi 200 numeri interi, che riporta per ciascun numero il valore relativo alle diverse funzioni esaminate.
Questo studio riguarda alcune funzioni matematiche sui numeri interi. Si tratta di funzioni molto semplici ma che hanno importanti applicazioni pratiche. L’idea di fondo è quella di raccogliere una serie di dati e informazioni sul tema, affrontandolo con un approccio un po’ diverso dal solito. Il testo è corredato da una tabella relativa ai primi 200 numeri interi, che riporta per ciascun numero il valore relativo alle diverse funzioni esaminate.
Scarica tutto l’articolo di Stefano Borgoni, Funzioni sui numeri interi, curiosità e applicazioni.
Un estratto dell’articolo.
NUMERI PERFETTI In primo luogo, s (n) richiama i cosiddetti “numeri perfetti”, definiti – per l’appunto – come numeri equivalenti alla somma dei propri divisori. In altre parole, un numero n è perfetto se vale la relazione n = s (n). I numeri perfetti furono studiati sin dall’antichità: un teorema enunciato da Pitagora e dimostrato poi da Euclide afferma che se 2n – 1 è un numero primo, allora m = 2n-1 (2n – 1) è un numero perfetto. Successivamente, Eulero dimostrò che tutti i numeri perfetti pari devono avere tale forma. Ma i numeri esprimibili come 2n – 1 con n primo sono i ben noti “numeri primi di Mersenne” , per cui si può dire che ciascuno di essi dà sicuramente origine a un numero perfetto. Al momento, si conoscono solo 47 numeri primi di Mersenne e, di conseguenza, 47 numeri perfetti; il più grande tra questi è formato da quasi 26 milioni di cifre! Aggiungiamo l’elenco dei primi cinque numeri perfetti: 6, 28, 496, 8.128 e 35.550.336. Tra le altre proprietà dei numeri perfetti, si può ricordare che essi sono anche triangolari, visto che si possono scrivere nella forma k (k+1) / 2, che è appunto la formula per trovare il k-esimo numero triangolare. Inoltre, è facile dimostrare che tutti i numeri perfetti del tipo sopra indicato terminano per 6 o per 8.
NUMERI AMICHEVOLI Sempre a partire dalla funzione s (n) si ottengono i cosiddetti “numeri amichevoli” , ossia coppie di numeri tali che la somma dei divisori dell’uno è uguale all’altro e viceversa. Sinteticamente, a e b sono numeri amichevoli se a = s (b) e b = s (a).
NUMERI SOCIEVOLI Un’estensione immediata dei numeri amichevoli è data dai “numeri socievoli” (in inglese “sociables”), gruppi di numeri che formano una catena di relazioni tale per cui il primo è pari alla somma dei divisori del secondo, il secondo è pari alla somma dei divisori del terzo e così via fino all’ultimo, che chiude il cerchio.
NUMERI FIDANZATI Infine, applicando la stessa regola dei numeri amichevoli ma non considerando l’1 nella somma dei divisori, si ottengono i “numeri fidanzati”.
Numeri difettivi Si tratta dei numeri maggiori della somma dei propri divisori. In altre parole, un numero n è difettivo se n > s (n). E’ facile verificare che tutti i numeri primi e le loro potenze sono numeri difettivi. Inoltre, tutti i divisori propri dei numeri difettivi e dei numeri perfetti sono a loro volta difettivi. Esempi di numeri difettivi sono 9, 17, 26, 76, 133.
Numeri abbondanti Al contrario di quanto appena visto, i numeri abbondanti sono quelli inferiori alla somma dei propri divisori, cioè i numeri per cui vale la relazione n < s (n).
Numeri altamente composti I numeri altamente composti sono numeri che hanno più divisori di qualsiasi intero positivo minore. Riprendendo quanto detto nel paragrafo 1.1 a proposito della fattorizzazione, se n = p1a p2b … pnz, allora la somma dei divisori di n sarà (a+1) (b+1) … (z+1).