Dire se l’applicazione lineare
$f:((x),(y),(z))->((-11y+9z),(x-3z),(x-3y))$
è diagonalizzabile.
Svolgimento:
la matrice associata all’applicazione lineare è
$A=((0,-11,9),(1,0,-3),(1,-3,0))$;
calcolando il polinomio caratteristico di $A$ trovi che gli autovalori sono:
$\lambda_1=3;\lambda_2=-1;\lambda_3=-2$.
La matrice è diagonalizzabile in quanto ci sono 3 autovalori distinti.
Sostituendo $\lambda_1$ nella matrice $A-\lambdaI$ si trova la matrice:
$A-3I=((-3,-11,9),(1,-3,-3),(1,-3,-3))$
il ker di questa matrice è generato dal vettore $((3),(0),(1))$.
Se fai la stessa cosa con gli altri due autovalori troverai che la matrice $M$
le cui colonne sono gli autovettori della matrice $A$ è:
$M=((3,2,1),(0,1,1),(1,1,1))$
in particolare
$((2),(1),(1))$ è autovettore relativo all’autovalore $\lambda_2=-1$
e
$((1),(1),(1))$ è autovettore relativo all’autovalore $\lambda_3=-2$.
E’ buona regola, alla fine di un esercizio,
fare la verifica dei risultati che abbiamo trovato:
$((0,-11,9),(1,0,-3),(1,-3,0))((3),(0),(1))=((9),(0),(3))=3*((3),(0),(1))$
$((0,-11,9),(1,0,-3),(1,-3,0))((2),(1),(1))=((-2),(-1),(-1))=(-1)*((2),(1),(1))$
$((0,-11,9),(1,0,-3),(1,-3,0))((1),(1),(1))=((-2),(-2),(-2))=(-2)*((1),(1),(1))$.

 Ipotesi
Ipotesi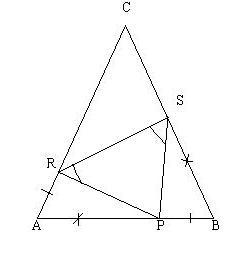 Ipotesi
Ipotesi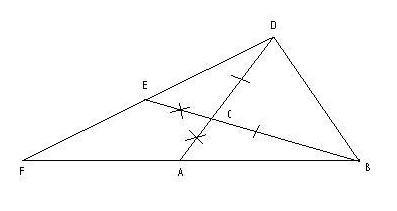 Ipotesi
Ipotesi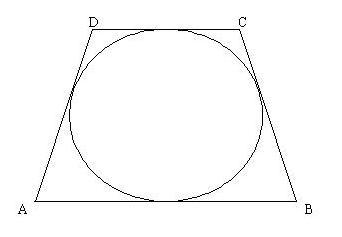 Dati
Dati 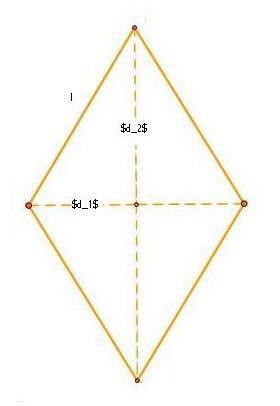 Dati
Dati Ipotesi
Ipotesi
 Dati
Dati  Dati
Dati Dati
Dati