
Commento audio dell’esercizio




 Attualmente non è difficile eseguire con i computer domestici calcoli sia numerici che simbolici utilizzando programmi potenti come Mathematica, Matlab, Octave. In questo articolo vogliamo presentare il programma bc e dimostrare che, se da una parte non ha la pretesa di competere con i programmi professionali, dall’altra permette, in modo opportuno, di eseguire calcoli di una certa complessità. Come esempio di applicazione illustreremo la valutazione di un integrale tridimensionale col metodo di Monte Carlo per arrivare ad una stima di pi greco.
Attualmente non è difficile eseguire con i computer domestici calcoli sia numerici che simbolici utilizzando programmi potenti come Mathematica, Matlab, Octave. In questo articolo vogliamo presentare il programma bc e dimostrare che, se da una parte non ha la pretesa di competere con i programmi professionali, dall’altra permette, in modo opportuno, di eseguire calcoli di una certa complessità. Come esempio di applicazione illustreremo la valutazione di un integrale tridimensionale col metodo di Monte Carlo per arrivare ad una stima di pi greco.
 Secondo alcuni, le migliori soluzioni ai problemi si trovano se la mente non ha sempre il perfetto controllo di se. In proposito Lucio Anneo Seneca, nato a Cordoba nel 4 a.C., scriveva nel De tranquillitate animi:
Secondo alcuni, le migliori soluzioni ai problemi si trovano se la mente non ha sempre il perfetto controllo di se. In proposito Lucio Anneo Seneca, nato a Cordoba nel 4 a.C., scriveva nel De tranquillitate animi:
"E non bisogna nemmeno tenere la mente sempre sotto tensione, ma concederle degli svaghi. Socrate non si vergognava di giocare con i bambini; Catone si ristorava con un bicchiere di vino l’animo affaticato dai pubblici impegni; Scipione si dava alle danze con quel suo fisico da trionfatore e da Soldato… Ci furono grandi uomini che si concedevano regolarmente delle vacanze mensili; altri invece dividevano ogni giornata tra riposo ed affari. Ricordo che faceva così il grande oratore Asilio Pollione: niente lo tratteneva al lavoro dopo le quattro del pomeriggio; passata quell’ora non leggeva neppure le lettere, per timore che gli venissero dei problemi, ma in quelle due ore scaricava tutta la stanchezza della giornata…. A volte ci aiuterà un viaggio, un cambiamento d’aria un pranzo, qualche bicchiere in più… Se vogliamo credere al poeta greco (Solone nato nel 640 a.C…) "a volte è piacevole fare qualche pazzia"; o a Platone, "invano bussa alla porta della poesia chi è sempre padrone di sè"; o ad Aristotele, "non c’è mai stato un grande ingegno senza un granello di follia". Occorre una certa eccitazione della mente, perchè questa riesca a fare qualcosa di grande e straordinario…. Finché la mente ha sempre controllo di sè, non può esprimere niente di sublime e di elevato…."
Forse proprio per migliorare le prestazioni nella soluzione dei problemi alcune organizzazioni offrono oggi ai loro dipendenti: cucina dietetica, palestra, piscina, yoga e meditazione, teatro, biblioteca dei classici, spazi per la danza e intrattenimenti romantici, training outdoor (vela, montagna, tennis, giochi di squadra), viaggi premio, ecc.
"Niente ci appartiene Lucilio, solo il tempo… dunque Lucilio caro, fai quello che mi scrivi: metti a frutto ogni minuto; sarai meno schiavo del futuro se ti impadronirai del presente".
Seneca, riprende in questo passo il pensiero di Teofrasto, un allievo di Aristoltele che sosteneva: "Il tempo è la cosa più preziosa del mondo" e anticipa il celebre slogan di Benjamin Franklin: "Il tempo è denaro", ma anche i pensieri di Charles Darwin (L’uomo che osa sprecare anche un’ora del suo tempo non ha scoperto il valore della vita) e di Italo Calvino (Il contrario della rapidità è la fretta).
Lo slogan di un recente convegno internazionale (Ipma Roma 2008) sulla gestione dei progetti è stato: "Project management to run" scelto forse per ricordare che dopo l’importanza data in passato al controllo dei costi e della qualità è forse il momento di dare il giusto peso anche al controllo dei tempi. In Italia il problema è particolarmente sentito nella pubblica amministrazione dove le opere infrastrutturali (a causa di burocrazia, permissistica e inefficienze) hanno tempi di realizzazione tre o quattro volte superiori a quanto previsto dai programmi. Qualcuno, forse pensando alla sanità pubblica o a fenomeni di corruzione, ha anche capovolto lo slogan di Franklin sostenendo che: "Il denaro è tempo".




 Nella sezione Studio del Grafico di funzione puoi trovare decine di esercizi svolti sullo studio di funzione, alcuni anche con il commento audio. Funzioni polinomiali, razionali, irrazionali, logaritmiche, esponenziali, goniometriche, con valore assoluto e miste. Nel Formulario trovi gli appunti su come fare lo studio di una funzione.
Nella sezione Studio del Grafico di funzione puoi trovare decine di esercizi svolti sullo studio di funzione, alcuni anche con il commento audio. Funzioni polinomiali, razionali, irrazionali, logaritmiche, esponenziali, goniometriche, con valore assoluto e miste. Nel Formulario trovi gli appunti su come fare lo studio di una funzione.
 La strategia per vincere questo finale è portare il re verso un angolo dello stesso colore delle case su cui si muove l’alfiere, quindi dare matto con l’alfiere avendo controllato la casa adia-cente col cavallo.
La strategia per vincere questo finale è portare il re verso un angolo dello stesso colore delle case su cui si muove l’alfiere, quindi dare matto con l’alfiere avendo controllato la casa adia-cente col cavallo.
Per giocare a scacchi con gli altri iscritti a Matematicamente.it


 È detto percorso Euleriano su un grafo un percorso che si ottiene senza mai staccare la matita dal foglio e che percorre tutti i lati del grafo esattamente una volta. Il più celebre problema associato ai percosi Euleriani è quello dei ponti di Koenigsberg. Estendendo la definizione ad un solido, un percorso Euleriano è un percorso che passa una e una sola volta su tutti gli spigoli di un poliedro. In questo documento ci occupiamo di mostrare come si possono determinare tutti i percorsi Euleriani indipendenti su un ottaedro regolare.
È detto percorso Euleriano su un grafo un percorso che si ottiene senza mai staccare la matita dal foglio e che percorre tutti i lati del grafo esattamente una volta. Il più celebre problema associato ai percosi Euleriani è quello dei ponti di Koenigsberg. Estendendo la definizione ad un solido, un percorso Euleriano è un percorso che passa una e una sola volta su tutti gli spigoli di un poliedro. In questo documento ci occupiamo di mostrare come si possono determinare tutti i percorsi Euleriani indipendenti su un ottaedro regolare.
 Mathematica, sviluppato da Wolfram Research, è un software completo per il calcolo, lo sviluppo, la didattica e la progettazione. Grazie alla perfetta integrazione di tutte le sue funzionalità offre fluidità del lavoro, coerenza, affidabilità e innovazione. Piuttosto che richiedere diversi tool per differenti lavori, Mathematica è stato sviluppato dalle origini con un unico obiettivo: creare l’ambiente di calcolo e sviluppo definitivo.
Mathematica, sviluppato da Wolfram Research, è un software completo per il calcolo, lo sviluppo, la didattica e la progettazione. Grazie alla perfetta integrazione di tutte le sue funzionalità offre fluidità del lavoro, coerenza, affidabilità e innovazione. Piuttosto che richiedere diversi tool per differenti lavori, Mathematica è stato sviluppato dalle origini con un unico obiettivo: creare l’ambiente di calcolo e sviluppo definitivo.
In tutto il mondo, ingegneri, scienziati, analisti finanziari, ricercatori, professori e studenti usano Mathematica per risolvere problemi complessi e per effettuare calcoli di ogni tipo. Con Mathematica è possibile risolvere singoli problemi, come un sistema di equazioni differenziali, o progettare e sviluppare un prototipo, intere soluzioni o applicazioni tecnico-scientifiche.
Con la nuova versione 7 di Mathematica, Wolfram Research continua a perseguire l’obiettivo di integrare e automatizzare nuove funzionalità come caratteristiche del core di Mathematica, aggiungendo funzionalità per l’elaborazione delle immagini e il calcolo parallelo ad alte prestazioni (HPC), nuovi dati collezionati e accuratamente controllati e altre innovazioni computazionali recentemente sviluppate. In totale più di 500 nuove funzioni e 12 nuove aree applicative!
Elaborazione delle immagini L’elaborazione delle immagini è una delle nuove integrazioni chiave. Funzioni a elevate performance e potenza industriale, per la composizione, trasformazione, arricchimento e segmentazione delle immagini, si combinano con l’attuale infrastruttura di Mathematica di linguaggio di alto livello, con la possibilità di costruire automaticamente delle interfacce, con i documenti notebook interattivi e con l’enorme potenza di calcolo, per creare una soluzione di elaborazione delle immagini estremamente versatile.
Calcolo Parallelo Le capacità di calcolo parallelo built-in sono un’altra nuova area chiave dell’integrazione di Mathematica 7. Per la prima volta, ogni copia di Mathematica (così come il tool per la distribuzione di applicazioni Mathematica Player Pro 7) viene fornita di default con la tecnologia per eseguire in parallelo i calcoli distribuendoli su core multipli o su licenze network di Mathematica installate su di un grid. Ogni copia di Mathematica 7 dispone di quattro processi di calcolo. Ulteriori processi, così come le capacità di networking, possono essere aggiunte facilmente. Il calcolo parallelo è un importante passo in avanti per aumentare le performance di calcolo tecnico, dato che tutti i computer stanno diventando multicore. Il calcolo parallelo di Mathematica è tipicamente accessibile in due semplici modi: automaticamente, utilizzando certe funzioni native, e su richiesta dell’utente applicando al proprio codice o ai propri calcoli la superfunzione Parallelize. Mathematica automaticamente distribuisce il compito sui processi disponibili, ottimizzandolo per l’hardware installato. Integrare la tecnologia parallela offre numerosi vantaggi chiave rispetto al fatto di aggiungerla come add-on. In particolare, permette agli sviluppatori software di poter sfrutture per il calcolo parallelo i propri client abilitati con Mathematica o con il tool add-on Mathematica Player Pro.
Dati integrati e calcolati Le sorgenti dati computabili, introdotte con Mathematica 6, sono un’innovazione unica e popolare grazie alla facilità con cui i dati possono essere utilizzati in Mathematica. Mathematica 7 viene fornito con aggiunte importanti quali il genoma umano completo, dati metereologici, astronomici, GIS e geodetici. Esempi di uso includono il trovare, analizzare e visualizzare sequenze genetiche,utilizzando le potenti capacità di ricerca stringhe di Mathematica, di pattern matching e statistiche. Similarmente, sono inclusi in Mathematica 7 i dati real-time e storici di oltre 16.000 stazioni metereologiche, fornendo informazioni accurate a coloro, dal climatologo all’economista, che vogliono utilizzarle nelle analisi o nelle applicazioni.
Altre aree di innovazione in Mathematica 7
§ Grafici e visualizzazione delle informazioni
§ Visualizzazione di campi vettoriali
§ Supporto spline globale, incluso NURBS
§ Calcolo Booleano di potenza industriale
§ Analisi di modelli statistici
§ Dati geodetici e GIS integrati
§ Molte innovazioni nel calcolo simbolico, incluso il calcolo discreto, il riconoscimento di sequenze e le radici di equazioni trascendenti
Mathematica è disponibile per i sistemi operativi Windows, Mac OS X, Linux, Unix e sistemi compatibili.
———————————————–
Adalta è distributore unico ufficiale per l’Italia dei software Wolfram Research. Nel sito www.Adalta.it/wolfram i dettagli del software.
———————————————–
Per maggiori informazioni o richiesta di un kit DEMO per effettuare la recensione: web : www.adalta.it email [email protected] – [email protected] Tel. 0575 333 297 Fax 0575 333 284
==============================
Da una comunicazione giunta in redazione
![]() E’ tornato nei nostri cieli, a far bella mostra di sé, Saturno, il più spettacolare dei pianeti del sistema solare. Nonostante il cielo velatissimo e le nubi sparse di queste sere, non sono riuscito a contenere l’irrefrenabile voglia di dargli un’occhiatina al telescopio, regalandomi uno spettacolo rarissimo, in quanto il pianeta ora si mostra in maniera del tutto differente rispetto agli anni passati.
E’ tornato nei nostri cieli, a far bella mostra di sé, Saturno, il più spettacolare dei pianeti del sistema solare. Nonostante il cielo velatissimo e le nubi sparse di queste sere, non sono riuscito a contenere l’irrefrenabile voglia di dargli un’occhiatina al telescopio, regalandomi uno spettacolo rarissimo, in quanto il pianeta ora si mostra in maniera del tutto differente rispetto agli anni passati.

Nelle foto che vi ho proposto ci sono diverse riprese di Saturno, che ho effettuato in anni differenti, e si vede come cambia l’inclinazione dei suoi anelli, dovuta alla diversa prospettiva da cui noi lo osserviamo, mentre esso viaggia nella sua orbita intorno al Sole.
Saturno compie una rivoluzione intera in 29,45 anni circa e, poiché il suo asse di rotazione mantiene la medesima inclinazione, noi vediamo i suoi anelli a volte dal lato “superiore”, a volte da quello “inferiore”, alternativamente ogni 14,7 anni circa.
 Questo significa anche che vedremo i suoi anelli “di taglio” una volta ogni 14,7 anni circa, esattamente come sono apparsi ai miei occhi in queste sere. Questo accade perché la Terra attraversa il suo piano orbitale.
Questo significa anche che vedremo i suoi anelli “di taglio” una volta ogni 14,7 anni circa, esattamente come sono apparsi ai miei occhi in queste sere. Questo accade perché la Terra attraversa il suo piano orbitale.
Se volete cimentarvi nell’osservazione in questi giorni è utile sapere che Saturno sorge abbastanza presto a est, già verso le 21:30, anche se per poterlo osservare meglio occorre attendere almeno un’oretta, il tempo che sia sufficientemente alto nel cielo, in maniera da evitare il deleterio effetto dovuto all’estinzione atmosferica. Lo troverete in prossimità della zampa posteriore del Leone.
Tuttavia, sebbene già oggi appaia bellissimo, questi giorni non rappresentano ancora il periodo migliore per osservarlo, in quanto non siamo ancora in fase opposizione. Cioè non abbiamo ancora raggiunto il perfetto allineamento Sole-Terra-Saturno che lo porterà alla minima distanza da noi e quindi ci permetterà di goderne appieno.
Molto presto però raggiungeremo l’opposizione, nella prima decade di marzo 2009, quindi tra meno di due mesi.
Non appena le condizioni meteo me lo permetteranno proverò ad effettuare qualche ripresa del pianeta che, ovviamente, non mancherò di condividere con voi.


 In questo articolo viene presentato un criterio di divisibilità per un qualunque numero purché sia coprimo di 10. Di questo criterio si offre una dimostrazione basata sulla soluzione di un’equazione diofantea lineare. Il metodo per risolvere l’equazione offre un esempio significativo di utilizzo del foglio di calcolo elettronico.
In questo articolo viene presentato un criterio di divisibilità per un qualunque numero purché sia coprimo di 10. Di questo criterio si offre una dimostrazione basata sulla soluzione di un’equazione diofantea lineare. Il metodo per risolvere l’equazione offre un esempio significativo di utilizzo del foglio di calcolo elettronico.




 Dunque era quello l’appuntamento fisso delle sei. Metallica, ogni giorno, metteva a disposizione del Centro di Servizi per il Volontariato un’ora del suo tempo. E in quell’ora faceva matematica. Sia che si trattasse di spiegazioni a bambini in ospedale, sia che si trattasse di doposcuola a ragazzi stranieri o in difficoltà, lei era a disposizione. Sono tornato a casa pensando che se non fossi passato per quella piazza non avrei mai saputo del suo impegno civile. Tutto nel suo stile: fare senza apparire.
Dunque era quello l’appuntamento fisso delle sei. Metallica, ogni giorno, metteva a disposizione del Centro di Servizi per il Volontariato un’ora del suo tempo. E in quell’ora faceva matematica. Sia che si trattasse di spiegazioni a bambini in ospedale, sia che si trattasse di doposcuola a ragazzi stranieri o in difficoltà, lei era a disposizione. Sono tornato a casa pensando che se non fossi passato per quella piazza non avrei mai saputo del suo impegno civile. Tutto nel suo stile: fare senza apparire.
 L’argomento proposto in questo articolo è un classico problema di ottimizzazione, ideato dal fisico R. Feynman, che prelude al principio di Fermat e alla legge di Snell; ragion per cui è particolarmente indicato per la classe conclusiva delle scuole superiori. Il problema viene affrontato con diversi metodi e da diversi punti di vista, in particolare viene usato il free-software di geometria dinamica GeoGebra.
L’argomento proposto in questo articolo è un classico problema di ottimizzazione, ideato dal fisico R. Feynman, che prelude al principio di Fermat e alla legge di Snell; ragion per cui è particolarmente indicato per la classe conclusiva delle scuole superiori. Il problema viene affrontato con diversi metodi e da diversi punti di vista, in particolare viene usato il free-software di geometria dinamica GeoGebra.
 Per l’a.a. 2008-2009 l’Università del Salento, in collaborazione con l’Università di Udine (sede amministrativa) ed altre otto università italiane, ha avviato il Corso di Perfezionamento "Innovazione Didattica in Fisica e Orientamento 2 (IDIFO2)". Il Corso, che comporta l’acquisizione di 15 CFU (crediti formativi universitari), intende formare una figura professionale di insegnante perfezionato culturalmente e professionalmente in Innovazione didattica in Fisica e Orientamento. Scadenza delle domande 26 gennaio, durata del corso: 150 ore in modalità blended da gen09 a dic09, costo 300 euro, disponibilità massima: 5posti. Per informazioni scrivere a [email protected]
Per l’a.a. 2008-2009 l’Università del Salento, in collaborazione con l’Università di Udine (sede amministrativa) ed altre otto università italiane, ha avviato il Corso di Perfezionamento "Innovazione Didattica in Fisica e Orientamento 2 (IDIFO2)". Il Corso, che comporta l’acquisizione di 15 CFU (crediti formativi universitari), intende formare una figura professionale di insegnante perfezionato culturalmente e professionalmente in Innovazione didattica in Fisica e Orientamento. Scadenza delle domande 26 gennaio, durata del corso: 150 ore in modalità blended da gen09 a dic09, costo 300 euro, disponibilità massima: 5posti. Per informazioni scrivere a [email protected]
Il Corso intende formare una figura professionale di insegnante perfezionato culturalmente e professionalmente in Innovazione didattica in Fisica e Orientamento, con competenze sul Problem Solving per l’Orientamento Formativo (PSOF) e competenze qualificanti su una delle seguenti tematiche (a scelta dell’interessato):
A. Meccanica Quantistica
B. Relatività
C. Superconduttività (C1) e/o fisica statistica e della materia (C2)
D. Tempo
E. Energia
F. Fisica ed Arte
Il corso, erogato in modalità blended (per la Puglia presso l’ateneo salentino), ha una durata complessiva di 150 ore, con inizio nel gennaio 2009 e termine entro dicembre 2009. Per il raggiungimento degli obiettivi del Corso è prevista una prova finale che consisterà nella discussione di un Project work sul Problem Solving per l’Orientamento Formativo (PSOF) e sul tema prescelto da ciascun corsista. Il manifesto degli studi.
Per informazioni scrivere a [email protected].
 Il salto del cavallo è un problema che si può esprimere in termini di grafi euleriani e grafi hamiltoniani. In questo articolo si presenta il problema e si esaminano le sue possibilità di soluzione. Si spiega perché si può disegnare un cammino chiuso, in cui tutte le possibili mosse siano tracciate una sola volta, nel caso in cui il cavallo si muove su una scacchiera n × n con n = 3; perché il cavallo può occupare tutte le caselle di una scacchiera ritornando sulla casella da cui è partito solo nel caso n > 5 e pari; perché nel caso n = 5 il cammino non è chiuso. Infine quanti possibili cammini chiusi può descrivere il cavallo muovendosi su di una scacchiera n × n con n pari. Vedi anche il gioco on line del salto del cavallo.
Il salto del cavallo è un problema che si può esprimere in termini di grafi euleriani e grafi hamiltoniani. In questo articolo si presenta il problema e si esaminano le sue possibilità di soluzione. Si spiega perché si può disegnare un cammino chiuso, in cui tutte le possibili mosse siano tracciate una sola volta, nel caso in cui il cavallo si muove su una scacchiera n × n con n = 3; perché il cavallo può occupare tutte le caselle di una scacchiera ritornando sulla casella da cui è partito solo nel caso n > 5 e pari; perché nel caso n = 5 il cammino non è chiuso. Infine quanti possibili cammini chiusi può descrivere il cavallo muovendosi su di una scacchiera n × n con n pari. Vedi anche il gioco on line del salto del cavallo.
 Matematicamente.it, comunità di studenti, insegnanti e appassionati di matematica, si propone di recuperare e valorizzare, rendendole patrimonio comune, le tesi di laurea, tesi di master, tesi di dottorato e tesi di specializzazione SSIS (nel seguito tutte indicate con il termine generico Tesi) realizzate a partire dall’A.A. 2000-2001 relativamente ai seguenti temi:
Matematicamente.it, comunità di studenti, insegnanti e appassionati di matematica, si propone di recuperare e valorizzare, rendendole patrimonio comune, le tesi di laurea, tesi di master, tesi di dottorato e tesi di specializzazione SSIS (nel seguito tutte indicate con il termine generico Tesi) realizzate a partire dall’A.A. 2000-2001 relativamente ai seguenti temi:
• didattica della matematica;
• didattica della fisica;
• applicazioni delle nuove tecnologie alla didattica disciplinare (di qualsiasi disciplina).
Consulta le tesi pervenute >
Scadenza La Tesi deve essere inviata a [email protected] entro il 31 maggio 2009 per la pubblicazione sul sito Matematicamente.it.
Premi Vincono un Apple iPhone 3G ciascuno, del valore attuale di 499,00 euro, gli autori di
• migliore Tesi in didattica della matematica;
• migliore Tesi in didattica della fisica;
• migliore Tesi in applicazioni delle nuove tecnologie alla didattica disciplinare (di qualsiasi disciplina).
Regolamento[*]
1) Il concorso è riservato agli iscritti a Matematicamente.it che hanno redatto una Tesi sui temi oggetti del bando e che hanno spedito entro il 31 maggio 2009 la propria Tesi per la pubblicazione sul sito Matematicamente.it.
2) L’autore della Tesi si assume la responsabilità dell’autenticità e originalità del proprio lavoro.
3) La Tesi deve essere spedita in formato elettronico a [email protected], indicando nell’oggetto della mail la dicitura “Concorso Tesi”; nel caso la Tesi sia corredata di allegati superiori ai 10MB è opportuno chiedere un parere preventivo alla redazione di Matematicamente.it, utilizzando lo stesso indirizzo e-mail del concorso.
4) Le Tesi pervenute saranno pubblicate nel giro di pochi giorni in una apposita sezione del sito, gli autori potranno verificarne la corretta pubblicazione.
5) Un gruppo di collaboratori del sito selezionerà le dieci ‘migliori’ Tesi per ciascun tema, basandosi anche sul numero di consultazioni delle Tesi e sui giudizi degli iscritti alla community; le trenta Tesi finaliste saranno sottoposte a una giuria qualificata che assegnerà i seguenti premi a suo insindacabile e inappellabile giudizio:
• all’autore della ‘migliore’ Tesi in didattica della matematica un Apple iPhone 3G;
• all’autore della ‘migliore’ Tesi in didattica della fisica un Apple iPhone 3G;
• all’autore della ‘migliore’ Tesi in applicazioni delle Nuove Tecnologie alla didattica disciplin-are un Apple iPhone 3G;
• tutti gli autori delle trenta Tesine finaliste riceveranno la t-shirt di Matematicamente.it.
Il giudizio di ‘migliore Tesi’ è da intendersi esclusivamente come giudizio soggettivo delle com-missioni che valuteranno le Tesi.
6) Inviando la Tesi si accetta automaticamente il regolamento.
[*] Il concorso in oggetto, secondo quanto indicato nel nuovo regolamento concernente la revisione organica della dis-ciplina dei concorsi e delle operazioni a premio, nonché delle manifestazioni di sorte locali ai sensi dell’ art. 19, comma 4, della legge 27 dicembre 1997, n. 449 (G.U. 13 dicembre 2001, n. 289), D.p.r. 430/2001, non è classificato come "concorso a premi" in base all’art. 6 (esclusioni) comma 1-a. (i concorsi indetti per la produzione di opere letterarie, artistiche o scientifiche, nonché per la presentazione di progetti o studi in ambito commerciale o industriale, nei quali il conferimento del premio all’autore dell’opera prescelta rappresenta (…) il riconoscimento del merito personale…").
– – – – – – – – – – – – – – – – – – – – – – – – –
Segnalato su www.soldissimi.it il portale dei concorsi a premi!"
 Auguri a tutti da Marco De Angelis e dalla Redazione di Matematicamente.it
Auguri a tutti da Marco De Angelis e dalla Redazione di Matematicamente.it
PER UN 2009 FELICE E CON TUTTI I RISULTATI GIUSTI !
"Il biglietto di auguri non è strettamente "matematico", ma invita a fare i calcoli giusti per il futuro…" M. De Angelis

 Cosa c’è di meglio, per la Befana, di organizzare un concorso di bellezza? Banale? Volgare? Non “politically correct”? Niente di tutto questo. In effetti si tratta di un “concorso di bellezza” molto particolare. C’entra solo il nome, che è semplicemente la traduzione in italiano di “beauty contest”. I curiosi troveranno una decente giustificazione per il nome originario, leggendo più avanti.
Cosa c’è di meglio, per la Befana, di organizzare un concorso di bellezza? Banale? Volgare? Non “politically correct”? Niente di tutto questo. In effetti si tratta di un “concorso di bellezza” molto particolare. C’entra solo il nome, che è semplicemente la traduzione in italiano di “beauty contest”. I curiosi troveranno una decente giustificazione per il nome originario, leggendo più avanti.
Ma passiamo a descrivere direttamente il gioco. Il perché e percome del nome, come detto, a dopo.
“Materiali” necessari:
– un gruppo di amici, più ce n’è meglio è;
– foglietti e penne quanti sono i partecipanti al gioco;
– volendo, un premio da offrire al vincitore (o da dividersi tra i vincitori).
Preparazione Davvero facile, basta leggersi le istruzioni. Semmai è la preparazione alla discussione, che può portare via un po’ di tempo.
Svolgimento Vengono lette le istruzioni. Al termine della lettura, e sviscerati eventuali dubbi, ognuno scrive su un foglietto di carta il numero che ritiene più opportuno.
N.B.: i partecipanti al gioco non possono consultarsi tra di loro su quale numero scegliere.
Quando tutti hanno scritto, vengono raccolti i foglietti. Si fanno i (pochi) calcoli necessari e si nomina il vincitore o i vincitori se ci sono dei “pari merito”. Poi si discute del perché e percome.
Istruzioni Ognuno dei partecipanti al gioco deve scrivere su un foglio un numero intero (senza la virgola…) da 1 a 100 (compresi). Oltre al numero, scriverà sul foglietto il suo nome o, comunque, un suo identificativo. Quando tutti i partecipanti hanno scritto il loro numero, si raccolgono i fogli e si calcola la somma di tutti i numeri che sono stati scritti. Il risultato trovato si divide per il numero dei foglietti raccolti (insomma, si calcola il valore medio del numero scritto dai partecipanti). Il risultato trovato si moltiplica prima per 2 poi si divide per 3. Il vincitore (o i vincitori, non è escluso che ci possano essere dei pari merito) è chi ha scritto il numero che più si avvicina al risultato dei calcoli precedenti.
Esempio 1. Supponiamo di avere 10 partecipanti. I numeri scritti siano i seguenti: 8, 64, 22, 31, 99, 1, 100, 44, 70, 100. La somma fa 539. Diviso per il numero di foglietti, cioè per dieci, viene 53.9. Moltiplicando per 2 fa 107.8 e dividendo per 3 si ottiene 35.933… ed evidentemente il numero più vicino tra quelli scritti è 31, quindi il vincitore è colui che ha scritto 31 sul suo foglietto.
Esempio 2. I giocatori siano 4 e i numeri scritti siano: 10, 10, 11, 32. La somma fa 63. Diviso 4 viene 15.75. Moltiplicato per 2 fa 31.5 e diviso per tre viene 10.5. Abbiamo quindi ben tre vincitori: i due che hanno scritto 10 e chi ha scritto 11.
Varianti e chiacchiere finali Moltiplicare il valor medio per 2 e dividere il risultato per 3 è parte essenziale del giochetto. Per il giochino in sé non c’è ragione particolare per cui i numeri debbano essere proprio 2 e 3. Volendo ci si può sbizzarrire con altre scelte (ad esempio, dividere semplicemente per 3, senza moltiplicare per 2). Diciamo che quella presentata qui è la “variante classica” del gioco.
Nulla vieta di giocare più volte. Anzi, si innesca un interessante processo di apprendimento, che dovrebbe portare abbastanza rapidamente al fatto che (quasi) tutti scrivano 1 sul loro foglietto. Ma fare previsioni dettagliate non è facile!
Spiegazione Esattamente come per il giochino “Tombola!”, anche qui siamo di fronte ad un classico degli studi sperimentali di teoria dei giochi. Si tratta del cosiddetto “beauty contest”, che mostra quanto forte sia l’assunzione di estrema intelligenza e di “common knowledge” (“conoscenza comune”) di questa intelligenza, ipotesi che fa parte del nucleo classico della teoria dei giochi.
Provo ad essere un po’ più esplicito, anche se questo comporta un po’ da scrivere e da leggere: spero non sia troppo.
Nella teoria dei giochi classica si assume che i giocatori siano “infinitamente” intelligenti. Ma non c’è solo questa assunzione, riguardo all’intelligenza. Ad esempio, c’è l’ipotesi che ogni giocatore sappia che gli altri sono infinitamente intelligenti o, il che è lo stesso, ogni giocatore creda che gli altri giocatori siano infinitamente intelligenti e questa sua credenza sia vera. Non solo, ogni giocatore sa che gli altri sono infinitamente intelligenti. E così via, costruendo catene sempre più lunghe di “ognuno sa che ognuno sa … che ognuno sa che tutti i giocatori sono infinitamente intelligenti”. Questa bella famigliola di ipotesi viene condensata dicendo che si assume essere “common knowledge” il fatto che i giocatori siano mostruosamente intelligenti. Una ipotesi simile viene fatta sulla razionalità dei giocatori e sulle preferenze dei giocatori rispetto all’esito del gioco. In questo gioco, tutto questo si riduce all’assumere che sia “common knowledge” il fatto che uno preferisca vincere anziché perdere e che faccia le sue scelte di conseguenza.
Si tratta evidentemente di ipotesi piuttosto ardite. E il giochino qui presentato serve proprio a mettere in evidenza la differenza esistente tra le assunzioni teoriche, le previsioni che ne derivano e i risultati sperimentali.
La previsione della teoria dei giochi classica è che ogni giocatore scriva “1” sul foglietto. Perché?
Tanto per cominciare, visto che il massimo numero che si può scrivere è 100, il risultato che viene fuori dai conti (calcolo del valor medio, moltiplicato poi per 2 e diviso per 3) al massimo potrà essere 100•(2/3) = 66.666… Quindi non ha senso scrivere un numero maggiore di 67, visto che la scelta di scrivere 67 (o un numero minore) è sempre meglio di quella di scrivere un numero più alto.
Fin qui, basta solo la ipotesi di razionalità e intelligenza dei giocatori (si noti che l’intelligenza non ha da essere neppure “mostruosa”): non c’è bisogno di nessuna ipotesi su “come sono fatti” gli alti giocatori. Ma, ed ecco qui il punto chiave, se assumo che tutti i giocatori siano razionali ed intelligenti, allora nessuno scriverà un numero maggiore di 67. Se un giocatore sa che gli altri sono intelligenti e che preferiscono vincere anziché perdere (ed è a sua volta intelligente e preferisce vincere piuttosto che perdere), allora gli è noto che nessuno scriverà un numero maggiore di 67. Insomma, il numero più alto che si possa aspettare di vedere scritto è 67, quindi il risultato dei conti al massimo sarà 67•(2/3) = 44.666… Ma allora non ha senso scrivere un numero maggiore di 45.
Non penso occorra molta fantasia per immaginare come la storia possa andare avanti, grazie alle ipotesi di “common knowledge”. Otteniamo questa successione di numeri:
100 66,667
67 44,667
45 30,000
30 20,000
20 13,333
13 8,667
9 6,000
6 4,000
4 2,667
3 2,000
2 1,333
1
Come si vede, la scelta da fare è inequivocabilmente quella di scrivere “1” sul foglietto.
E’ però altrettanto evidente come le ipotesi di “common knowledge” formulate siano toppo forti, troppo lontane dal descrivere una situazione reale. In effetti, in miei pseudo-esperimenti fatti in varie occasioni, su un totale complessivo di 277 risposte avute le risposte “1” sono state solo 24 (e nessuno ha mai vinto, scrivendo “1”). Non solo, 13 volte è stato scritto un numero maggiore di 67, il che “prova sperimentalmente” che era errata la presunzione che questi giocatori fossero intelligenti o che preferissero vincere anziché perdere. Sembra essere molto plausibile che questi giocatori non avessero voglia o ragione di impegnarsi seriamente nel gioco. S
ono molto interessanti, comunque, le risposte che si otterranno. E soprattutto sarà interessante discutere le motivazioni dietro tali risposte. Si potranno osservare approcci significativamente diversi ad un problema non banale, e reso ancor più difficile dal fatto che si tratta di un problema inconsueto.
L’espressione “beauty contest”, contrariamente a quanto si potrebbe immaginare, ha una origine “importante”: si riferisce al termine usato da J.M. Keynes nel descrivere il comportamento di chi opera in borsa, da lui assimilato al comportamento di chi partecipava a dei concorsi in cui occorreva scegliere la più bella fra le donne illustrate in una pagina di giornale. L’aspetto importante di questi concorsi è che chi inviava al giornale la sua scelta poteva partecipare a una lotteria a premi solo se la sua scelta risultava tra le prime classificate. Insomma, come in questo giochino, era decisivo fare le ipotesi giuste su cosa avrebbero scelto gli altri.
Per dettagli (in inglese), vedasi: http://www.psychol.ucl.ac.uk/ljdm/Studentconference/beauty.pdf
![]() Scarica l’articolo Concorso di Bellezza in formato pdf (107 KB)
Scarica l’articolo Concorso di Bellezza in formato pdf (107 KB)
 Con "crisi dei fondamenti della matematica" si indica l’ampio dibattito che ha coinvolto la comunità dei matematici, e dei filosofi, nel primo trentennio del XX secolo, incentrato sulla natura della matematica, cioè su quali siano, se ci sono, gli enti primitivi indimostrabili che costituiscono il punto di partenza di questa disciplina. In sintesi, ci si chiedeva qual è la risposta giusta alla domanda cos’è la matematica?
Con "crisi dei fondamenti della matematica" si indica l’ampio dibattito che ha coinvolto la comunità dei matematici, e dei filosofi, nel primo trentennio del XX secolo, incentrato sulla natura della matematica, cioè su quali siano, se ci sono, gli enti primitivi indimostrabili che costituiscono il punto di partenza di questa disciplina. In sintesi, ci si chiedeva qual è la risposta giusta alla domanda cos’è la matematica?
Tale dibattito fu di dimensioni così vaste che portò praticamente tutti gli uomini di scienza a pronunciarsi in proposito. Le posizioni filosofiche più innovatrici diedero vita a vere e proprie scuole matematiche, come l’Intuizionismo, il Formalismo e il Logicismo, che furono tutte in rottura con le dottrine classiche, come il Kantismo . Dalle nuove impostazioni epistemologiche derivò addirittura la nascita di nuove discipline, come la "teoria della dimostrazione" o "metamatematica", ed il consolidamen-to di quelle emergenti, come la logica matematica.
Nonostante le questioni fondazionali abbiano monopolizzato l’interesse della comunità scientifica per diversi decenni, si deve constatare che non si è mai giunti a conclusioni soddisfacenti, cioè universalmente accettate. Almeno da una cinquantina d’anni i matematici hanno quasi del tutto rinunciato a portare avanti il dibattito, o per lo meno lo considerano di interesse esclusivamente filosofico. La matematica contemporanea è sempre più prolifica di risultati tecnici, anche grazie alla recente commistione con l’informatica e al rapidissimo sviluppo del calcolo delle probabilità e della statistica, e pare ormai allontanarsi quasi del tutto dalle investigazioni epistemologiche, così che la crisi dei fondamenti può considerarsi chiusa nella pratica. Nei prossimi paragrafi cercheremo di fare un resoconto chiaro della crisi, analizzando le possibili cause, le diverse scuole di pensiero, le opere più importanti. Tutto ciò in modo abbastanza sintetico, quindi senza alcuna pretesa di completezza.
Tratto da: G. Di Saverio, Dal paradiso di Hilbert all’inferno di Gödel, Tesi di Laurea, Facoltà di Scienze Matematiche Fisiche e Naturali, Università degli Studi di Perugia, Perugia 2003.
Indice del saggio
Precisazione: cosa vuol dire essere platonista?
La nascita dell’analisi moderna
La scoperta delle geometrie non euclidee
La nascita della logica matematica
L’aritmetizzazione dell’analisi e la nascita della teoria degli insiemi
La logicizzazione dell’aritmetica
La formalizzazione della geometria
La crisi
Paradossi logici
Paradossi semantici
Il logicismo di Russell
L’Intuizionismo di Brouwer
Il Formalismo di Hilbert
Uno sguardo oltre
Sitografia
U. BARTOCCI, Elementi di Matematica (un libro di matematica online “kantiano”), in progress dal 2003, http://www.cartesio-episteme.net/mat/elementi.htm; Breve profilo storico della matematica, 2003-2004,
http://www.cartesio-episteme.net/mat/profilo.htm; Una breve presentazione (critica) del teorema di incompletezza di Gödel, 2005 http://www.cartesio-episteme.net/mat/teor-goed.pdf
Scarica il saggio La crisi dei fondamenti della matematica (pdf 422 KB)
 21a selezione italiana per il concorso dell’unione europea dei giovani scienziati. Ragazze e ragazzi delle scuole superiori e del primo anno universitario hanno tempo fino a venerdì 27 febbraio 2009 per presentare i loro lavori al concorso “I giovani e le scienze”.
21a selezione italiana per il concorso dell’unione europea dei giovani scienziati. Ragazze e ragazzi delle scuole superiori e del primo anno universitario hanno tempo fino a venerdì 27 febbraio 2009 per presentare i loro lavori al concorso “I giovani e le scienze”.
I giovani e le scienze è la selezione italiana, organizzata dalla Fast e autorizzata dalla Commissione europea, per partecipare al concorso European Union Contest for Young Scientists.
Il concorso dell’Unione europea per giovani scienziati è la vetrina annuale delle migliori scoperte scientifiche da parte di ragazze e ragazzi che hanno così l’opportunità di confrontarsi con colleghi con simili interessi ed attitudini.
Attraverso la manifestazione, la Commissione cerca di valorizzare gli sforzi fatti in tutti i paesi che partecipano alla gara, ed invogliare i giovani ad intraprendere le carriere scientifiche.
Possono partecipare al concorso solo i giovani che vengono selezionati dalle rispettive giurie nazionali. In ogni paese il National organizer – per l’Italia Fast (Federazione delle Associazioni Scientifiche e Tecniche), p.le R. Morandi, 2 – 20121 Milano; [email protected] – è responsabile della scelta dei progetti e dei partecipanti alla finale comunitaria.
I lavori possono essere elaborati sia da singoli che da gruppi di non più di 3 ragazzi.
Gli studenti, giudicati in base al lavoro scritto, all’allestimento dello stand e tramite interviste con la giuria, concorrono per 9 riconoscimenti principali:
3 primi premi da 5000 euro ciascuno,
3 secondi premi da 3000 euro e
3 terzi premi da 1500 euro.
Ci sono altre rilevanti opportunità, quali soggiorni studio o inviti ad iniziative di qualità come la cerimonia per il conferimento dei premi Nobel a Stoccolma.
I migliori contributi italiani vengono invitati a all’esposizione del 19-21 aprile a Milano. Tra questi la giuria decide chi deve rappresentare l’Italia ai seguenti eventi principali (ma altri ne seguiranno): finale del 21° concorso dell’Unione europea a Parigi; 12^ esposizione scientifica internazionale di Milset a Nabuel in Tunisia; 20^ settimana Scienza e natura a Zurigo e sulle Alpi svizzere; 51° forum internazionale giovanile della scienza di Londra: 16° premio internazionale dell’acqua per i giovani a Stoccolma; 61^ fiera internazionale della scienza e dell’ingegneria a San Josè in California; conferenza internazionale sui cambiamenti climatici in Danimarca; esposizioni scientifiche di organizzazioni internazionale; visite a centri di ricerca e a industrie innovative.
I candidati devono presentare studi o progetti originali e innovativi in qualsiasi campo scientifico. A titolo di esempio: acqua, scienze della terra, chimica, fisica, matematica, farmacologia, medicina, salute, scienze biologiche, scienze ambientali, energia (in particolare fonti rinnovabili e tecnologie dell’idrogeno), tecnologie dell’informazione.
"Scegli un argomento che ti interessa (l’idea deve essere originale, naturalmente); aggiungi un po’ di curiosità e conoscenza tecnica; un tocco di perseveranza e caparbietà; qualche consiglio da parte di esperti; un pizzico di ingenuità, critica ed entusiasmo; spirito intraprendente in abbondanza; ma l’ingrediente principale è la parte migliore della tua immaginazione". Contribuirai al progresso scientifico e tecnologico, e ti darà anche personale gratificazione. Ci sarà pure rischio di insuccesso, ma le difficoltà verranno presto superate, se ti domanderai quali sono state le cause. Quindi, qual è un progetto vincente? Essere scelti dalla giuria non è il fatto più rilevante. La cosa più importante arriva alla fine della giornata: quel personale senso di orgoglio nell’aver superato difficoltà enormi nello sviluppare un’idea originale e aver dato il massimo per migliorare te stesso e la tua conoscenza, e per aver contribuito al bene della comunità."
Una mini guida con i comandi più usati del software opensource Geogebra
GeoGebra è un programma adatto per l’apprendimento di geometria, algebra e analisi. Sviluppato da Markus Hohenwarter presso la Florida Atlantic University, per la didattica della matematica nella scuola, è un sistema di geometria dinamica con il quale è possibile eseguire costruzioni con punti, vettori, segmenti, rette, coniche e funzioni e successivamente modificarle dinamicamente. Ma GeoGebra può gestire contemporaneamente variabili numeriche, vettori e punti, calcolare derivate e integrali di funzioni e dispone di comandi come Radice o Estremo. I due punti di vista, quello puramente geometrico e quello algebrico-analitico, sono caratteristici di GeoGebra: un’espressione nella finestra algebra corrisponde a un oggetto nella finestra geometria e viceversa.
La finestra del software all’avvio
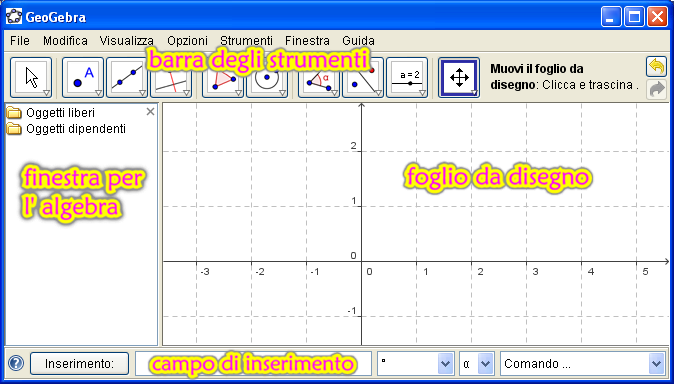
Input geometrico
| Icona 1: muovi | ||
| Muovi |
Consente di trascinare e rilasciare oggetti liberi con il mouse. Dopo aver selezionato un oggetto in modalità Muovi è possibile eliminarlo premendo il tasto Canc o muoverlo utilizzando i tasti freccia. La modalità Muovi si attiva anche premendo il tasto Esc. |
|
| Ruota intorno a un punto |
Dopo aver selezionato il centro di rotazione, è possibile ruotare gli oggetti liberi intorno a questo punto, trascinandoli con il mouse. |
|
| Icona 2: punti | ||
| Nuovo Punto |
Per creare un nuovo punto, fare clic sul foglio da disegno. Le coordinate del punto vengono fissate quando il pulsante del mouse viene rilasciato. Facendo clic su un segmento, una retta, una curva si crea un punto vincolato su questo oggetto. Facendo clic sull’intersezione di due oggetti si genera il punto di intersezione. |
|
| Intersezione di due oggetti |
I punti di intersezione di due oggetti possono essere determinati in due modi: |
|
| Punto medio o centro |
Fare clic su: due punti per ottenerne il punto medio; un segmento per ottenerne il punto medio; una conica per ottenerne il centro. |
|
| Icona 3: segmenti | ||
| Retta per due punti |
Selezionando due punti A e B viene tracciata la retta per A e B. Il vettore direzione della retta è (B-A). |
|
| Segmento tra due punti |
Selezionare due punti A e B per creare il segmento di estremi A e B. Nella finestra algebra viene visualizzata la lunghezza del segmento. |
|
| Segmento di data lunghezza da un punto |
Fare clic su un punto A, primo estremo del segmento. Nella finestra che viene visualizzata di seguito specificare la lunghezza desiderata. |
|
| Semiretta per due punti |
Selezionando due punti A e B viene generata la semiretta uscente da A e passante per B. Nella finestra algebra viene visualizzata l’equazione della retta corrispondente. |
|
| Vettore tra due punti |
Selezionare il punto di applicazione e il punto finale del vettore. |
|
| Vettore da un punto |
Selezionare un punto A e un vettore v per creare il punto B = A + v e il vettore da A a B. |
|
| Icona 4: costruzioni | ||
| Retta perpendicolare |
Selezionando una retta g e un punto A viene tracciata la retta per A perpendicolare a g. |
|
| Retta parallela |
Selezionando una retta g e un punto A viene tracciata la retta per A parallela a g. |
|
| Asse di un segmento |
L’asse di un segmento viene tracciato selezionando un segmento s o due punti A e B. |
|
| Bisettrice |
La bisettrice di un angolo può essere tracciata in due modi: selezionando tre punti A, B, C si genera la bisettrice dell’angolo da essi definito, in cui B è il vertice; selezionando due rette si generano le due bisettrici degli angoli da esse formati. |
|
| Tangenti |
Le tangenti a una conica possono essere tracciate in più modi: selezionando un punto A e una conica c vengono tracciate tutte le tangenti a c, passanti per A; selezionando una retta g e una conica c vengono tracciate tutte la tangenti a c che sono parallele a g; selezionando un punto A e una funzione f viene generata la retta tangente a f in x=x(A). |
|
| Polare o diametro |
Questa modalità genera la polare o il diametro di una conica. E’ possibile selezionare un punto e una conica per ottenere la polare oppure selezionare una retta o un vettore e una conica per ottenerne il diametro. |
|
| Luogo |
Selezionare il punto B di cui si desidera visualizzare il luogo dipendente da un altro punto A, quindi fare clic sul punto A. Il punto B deve essere un punto su un oggetto (ad es. retta, segmento, circonferenza). |
|
| Icona 5: poligoni | ||
| Poligono |
Selezionare almeno tre punti, che saranno i vertici del poligono. Quindi fare nuovamente clic sul primo punto per chiudere il poligono. Nella finestra algebra viene visualizzata l’area del poligono. |
|
| Poligono regolare |
Selezionando due punti A e B e digitando un numero n nel campo di testo della finestra di dialogo che viene visualizzata, si ottiene un poligono regolare con n vertici (inclusi i punti A e B). |
|
| Icona 6: curve | ||
| Circonferenza di dato centro |
Selezionando un punto M e un secondo punto P si definisce la circonferenza di centro M e passante per P. Il raggio della circonferenza è la distanza MP. |
|
| Circonferenza dati centro e raggio |
Dopo aver selezionato il centro M è necessario inserire la misura del raggio nella finestra di dialogo visualizzata. |
|
| Circonferenza per tre punti |
Selezionando tre punti A, B, C viene tracciata la circonferenza per questi tre punti. Se i tre punti sono allineati, la circonferenza degenera nella retta per i tre punti. |
|
| Semicirconferenza per due punti |
Selezionando due punti A e B si ottiene la semicirconferenza di diametro AB. |
|
| Arco circolare di dato centro per due punti |
Selezionando tre punti M, A e B si ottiene un arco di circonferenza di centro M, con punto iniziale A e punto finale B. |
|
| Arco circumcircolare per tre punti |
Selezionando tre punti si ottiene un arco di circonferenza per questi tre punti. |
|
| Settore circolare di dato centro per due punti |
Selezionando tre punti M, A e B si ottiene un settore circolare di centro M con punto iniziale A e punto finale B. |
|
| Settore circumcircolare per tre punti |
Selezionando tre punti si ottiene un settore circolare per questi tre punti. |
|
| Conica per cinque punti |
Selezionando cinque punti viene generata la conica passante per questi. E’ sufficiente che almeno quattro dei cinque punti non sono allineati affinché la conica sia definita. |
|
| Icona 7: misure | ||
| Angolo |
Questo strumento può creare: l’angolo tra tre punti; l’angolo tra due segmenti; l’angolo tra due rette; l’angolo tra due vettori; tutti gli angoli interni di un poligono. Se si vuole limitare la misura massima dell’angolo a 180°, deselezionare nella Finestra delle Proprietà la voce Permetti angolo concavo. |
|
| Angolo di data misura |
Selezionare due punti A e B e digitare la dimensione dell’angolo nella casella di testo della finestra che viene visualizzata. Questo modo genera un punto C e un angolo α, dove α è l’angolo ABC. |
|
| Distanza o lunghezza |
Questo strumento fornisce la distanza tra due punti, tra due rette o tra un punto e una retta. Inoltre può fornire la lunghezza di un segmento o la misura di una circonferenza. |
|
| Pendenza |
Questo modo fornisce la pendenza di una retta come testo dinamico nella finestra geometria. |
|
| Icona 8: trasformazioni | ||
| Simmetrico rispetto a una retta |
Selezionare l’oggetto di cui si desidera ottenere il simmetrico. Quindi fare clic sulla retta che funge da asse di simmetria. |
|
| Simmetrico rispetto a un punto |
Selezionare l’oggetto di cui si desidera ottenere il simmetrico. Quindi fare clic sul punto che funge da centro di simmetria. |
|
| Ruota intorno a un punto di un angolo |
Selezionare l’oggetto che deve essere ruotato, quindi fare clic sul punto che funge da centro di rotazione. Verrà visualizzata una finestra in cui si deve specificare l’angolo di rotazione. |
|
| Trasla di un vettore |
Selezionare l’oggetto da traslare, quindi fare clic sul vettore di traslazione. |
|
| Dilata da un punto di un fattore |
Selezionare l’oggetto da dilatare. Quindi fare clic sul punto che funge da centro di dilatazione. Verrà visualizzata una finestra in cui si deve specificare il fattore di dilatazione. |
|
| Icona 9: testo | ||
| Slider |
In GeoGebra uno slider è la rappresentazione grafica di un numero o di un angolo liberi. Fare clic in una qualunque area libera del foglio da disegno per creare uno slider relativo ad un numero o ad un angolo. La finestra che viene visualizzata permette di specificare l’intervallo [min, max] del numero o dell’angolo, come pure l’allineamento e l’ampiezza dello slider (in pixel). E’ possibile creare uno slider a partire da qualsiasi numero o angolo liberi già esistenti, mostrando l’oggetto dal Menu contestuale. |
|
| Casella di controllo per mostrare nascondere oggetti |
Facendo clic sul foglio da disegno viene creata una casella di controllo (variabile Booleana) che consente di mostrare o nascondere uno o più oggetti. Nella finestra di dialogo che viene visualizzata è possibile specificare quali oggetti devono essere controllati dalla casella di controllo. |
|
| Testo |
Con questo strumento è possibile creare testi statici e dinamici o formule LaTeX nella finestra geometria. Facendo clic sul foglio da disegno viene creato un nuovo testo nella posizione specificata. Facendo clic su un punto viene creato un nuovo testo la cui posizione è collegata al punto. Successivamente viene visualizzata una finestra di dialogo per l’immissione del testo. |
|
| Inserisci immagine |
Questo strumento permette di aggiungere un’immagine alla costruzione. Facendo clic sul foglio da disegno si posiziona il vertice inferiore sinistro dell’immagine. Facendo clic su un punto si specifica questo punto come vertice inferiore sinistro dell’immagine. Verrà quindi visualizzata una finestra di dialogo, nella quale si potrà selezionare il file immagine da inserire. |
|
| Relazione tra due oggetti |
Selezionare due oggetti per ottenere informazioni sulla loro relazione. Per esempio, si può sapere se due rette sono parallele, … |
|
| Icona 10: visualizzazione | ||
| Muovi il foglio da disegno |
Trascinare e rilasciare il foglio da disegno per spostare l’origine del sistema di coordinate. E’ possibile muovere il foglio da disegno premendo il tasto Shift e trascinandolo con il mouse. Questo modo consente anche di modificare la scala di ciascuno degli assi, trascinandolo con il mouse. |
|
| Zoom avanti |
Fare clic in un punto qualsiasi del foglio da disegno per ingrandire. |
|
| Mostra/nascondi oggetto |
Gli oggetti geometrici possono essere visualizzati graficamente (mostra) oppure resi invisibili (nascondi). Per modificarne lo stato si utilizza lo strumento Mostra / nascondi oggetto o il Menu. L’icona alla sinistra di ogni oggetto nella finestra algebra mostra lo stato di visualizzazione corrente ( “mostrato” o “nascosto”). |
|
| Mostra/nascondi etichetta |
Le etichette associate a un oggetto geometrico possono essere nascoste o rese visibili con questo strumento. |
|
| Copia stile visuale |
Questo strumento permette di copiare le proprietà di visualizzazione grafica come colore, dimensione, stile, etc. da un oggetto ad altri. Scegliere l’oggetto le cui proprietà devono essere copiate, quindi fare clic su tutti gli altri oggetti a cui si desiderano applicare le stesse proprietà. |
|
| Cancella oggetti |
Attivare questo strumento e fare clic sugli oggetti da cancellare. |
|
Il menu contestuale
Il menu contestuale si attiva facendo clic con il tasto destro del mouse su un oggetto.
|
|
Mostra oggetto – permette di mostrare o nascondere l’oggetto. Mostra etichetta – permette di mostrare o nascondere l’etichetta associata all’oggetto. Traccia on – i questa modalità, gli oggetti geometrici possono lasciare una traccia sullo schermo, quando vengono utilizzati dinamicamente. Per eliminare tutte le tracce utilizzare il comando Ripristina la videata dal menu Visualizza. Rinomina – per rinominare l’oggeto. Ridefinisci – La ridefinizione di oggetti è uno strumento molto versatile per modificare una costruzione. Esempi: Per posizionare un punto libero A su una retta h, scegliere Ridefinisci nel menu contestuale del punto A e immettere Punto[h]nel campo di inserimento della finestra di dialogo che viene visualizzata. Per rimuovere il punto dalla retta e renderlo nuovamente libero, ridefinirlo assegnandogli coordinate libere Per convertire una retta h passante per due punti A e B in un segmento, scegliere Ridefinisci e immettere Segmento[A,B]nel campo di inserimento della finestra di dialogo che viene visualizzata. Cancella – per cancellare l’oggetto. Proprietà – La finestra di dialogo Proprietà permette di modificare le proprietà degli oggetti (ad es., colore, stile della linea). |
Input algebrico
Nella finestra algebra, posta sul lato sinistro, vengono visualizzati valori, coordinate ed equazioni di oggetti liberi e dipendenti. Gli oggetti liberi non dipendono da alcun altro oggetto e possono essere modificati direttamente.
E’ possibile creare e modificare oggetti utilizzando il campo di inserimento testo, in basso nella schermata di GeoGebra.
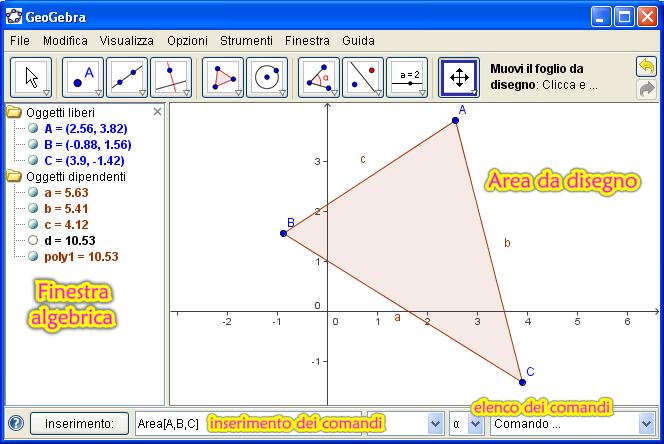
I comandi più frequenti
| Angolo[vettore v1, vettore v2] | Angolo tra due vettori v1 e v2 (tra 0 e 360°) |
| Angolo[retta g, retta h] | Angolo tra i vettori direzione di due rette g e h (tra 0 360°) |
| Angolo[punto A, punto B, punto C] | Angolo compreso tra BA e BC (tra 0 e 360°). Il punto B è il vertice. |
| Angolo[punto A, punto B, angolo alpha] | Angolo di misura alpha tracciato da A con vertice B. |
| Angolo[conica c] | Angolo di inclinazione dell’asse maggiore di una conica c. |
| Angolo[vettore v] | Angolo tra l’asse x e il vettore v. |
| Angolo[punto A] | Angolo tra l’asse x e il vettore posizione di A. |
| Angolo[numero n] | Converte un numero n in un angolo (compreso tra 0 e 2pi). |
| Angolo[poligono poly] | Tutti gli angoli interni di un poligono poly |
| ArcoCircolare[punto M, punto A, punto B] | Arco di circonferenza con centro M tra due punti A e B. Il punto B non deve necessariamente giacere sull’arco. |
| Area[punto A, punto B, punto C, …] | Area del poligono definito dai punti A, B, e C |
| Area[conica c] | Area della conica c (circonferenza o ellisse) |
| Asintoto[iperbole h] | Entrambi gli asintoti di un’iperbole h |
| Baricentro[poligono poly] | Baricentro di un poligono poly |
| Bisettrice[punto A, punto B, punto C] | Bisettrice dell’angolo (A, B, C), dove B è il vertice dell’angolo. |
| Bisettrice[retta g, retta h] | Entrambe le bisettrici di g e h. |
| Centro[conica c] | Centro di una conica c (es. circonferenza, ellisse, iperbole) |
| Circonferenza[punto M, numero r] | Circonferenza di centro M e raggio r. |
| Circonferenza[punto M, segmento s] | Circonferenza di centro M e raggio = Lunghezza[s]. |
| Circonferenza[punto M, punto A] | Circonferenza di centro M e passante per A. |
| Circonferenza[punto A, punto B, punto C] | Circonferenza per i tre punti A, B e C |
| Conica[punto A, punto B, punto C, punto D, punto E] | Conica per cinque punti A, B, C, D, e C. I punti devono essere a quattro a quattro non allineati. |
| Curva[espressione e1, espressione e2, parametro t, numero a, numero b] | Curva in forma parametrica con espressione e1 per la x ed e2 per la y (dipendenti dal parametro t) nell’intervallo dato [a, b] Esempio: c = Curva[2 cos(t), 2 sin(t), t, 0, 2 pi] |
| Derivata[funzione f] | Derivata della funzione f(x). È possibile utilizzare f’(x) invece di Derivata[f] |
| Derivata[funzione f, numero n] | n-esima derivata della funzione f(x). È possibile utilizzare f’’(x) invece di Derivata[f, 2]. |
| Diametro[retta g , conica c] | Diametro della conica c parallelo alla retta g. |
| Diametro[vettore v, conica c] | Diametro della conica c con vettore direzione v. |
| Distanza[punto A, punto B] | Distanza tra due punti A e B. |
| Distanza[punto A, retta g] | Distanza di un punto A da una retta g. |
| Distanza[retta g, retta h] | Distanza tra le rette g e h. La distanza tra due rette incidenti è 0. Questa funzione è utile per le rette parallele. |
| Ellisse[punto F, punto G, numero a] | Ellisse di fuochi F, G e lunghezza del semiasse maggiore a. Condizione: 2a > Distanza[F,G]. |
| Ellisse[punto F, punto G, segmento s] | Ellisse di fuochi F, G e lunghezza del semiasse maggiore uguale a quella del segmento s (a = Lunghezza[s]). |
| Funzione[funzione f, numero a, numero b] | restituisce una funzione uguale a f nell’intervallo [a, b] e non definita al di fuori di [a, b]. |
| Integrale[funzione f, numero a, numero b] | Integrale definito di f(x) tra a e b. Nota: Questo comando disegna anche l’area tra il grafico della funzione e l’asse x. |
| Integrale[funzione f, funzione g, numero a, numero b] | Integrale definito di f(x)-g(x) da a a b. Nota: Con questo comando viene tracciata anche l’area tra i grafici delle funzioni f e g. |
| Intersezione[retta g, retta h] | Punti di intersezione di due rette g e h. |
| Intersezione[retta g, conica c] | Tutti i punti di intersezione di g e c (max. 2). |
| Intersezione[retta g, conica c, numero n] | n-esimo punto di intersezione di g e c. |
| Intersezione[conica c1, conica c2] | Tutti i punti di intersezione di c1 e c2 (max. 4). |
| Intersezione[conica c1, conica c2, numero n] | n-esimo punto di intersezione di c1 e c2. |
| Intersezione[polinomio f1, polinomio f2] | Tutti i punti di intersezione di f1 e f2. |
| Intersezione[polinomio f1, polinomio f2, numero n] | n-esimo punto di intersezione di f1 e f2. |
| Intersezione[polinomio f, retta g] | Tutti i punti di intersezione tra il polinomio f e la retta g. |
| Intersezione[polinomio f, retta g, numero n] | n-esimo punto di intersezione tra il polinomio f e la retta g. |
| Intersezione[funzione f, funzione g, punto A] | Punto di intersezione tra le funzioni f e g con punto iniziale A (per il metodo di Newton). |
| Intersezione[funzione f, retta g, punto A] | Punto di intersezione tra la funzione f e la retta g con punto iniziale A (per il metodo di Newton). |
| Iterazione[funzione f, numero x0, numero n] | Itera la funzione f n volte utilizzando il valore di avvio immesso x0. Esempio: Dopo aver definito f(x) = x^2 il comando Iterazione[f, 3, 2] restituisce il risultato $(3^2)^2=81$. |
| Lunghezza[vettore v] | Lunghezza di un vettore. |
| Lunghezza[punto A] | Lunghezza del vettore posizione di A. |
| Lunghezza[funzione f, numero x1, numero x2] | Lunghezza del grafico della funzione f tra i numeri x1 e x2. |
| Lunghezza[funzione f, punto A, punto B] | Lunghezza del grafico della funzione f tra i due punti A e B sul grafico. |
| Lunghezza[curva c, numero t1, numero t2] | Lunghezza della curva c tra i numeri t1 e t2. |
| Lunghezza[curva c, punto A, punto B] | Lunghezza della curva c tra i due punti A e B sulla curva. |
| Lunghezza[lista L] | Lunghezza della lista L (numero di elementi nella lista). |
| Luogo[punto Q, punto P] | Restituisce il luogo del punto Q al variare del punto P. Nota: Il punto P deve essere un punto su un oggetto (ad es. retta, segmento, circonferenza). |
| Parabola[punto F, retta g] | Parabola di fuoco F e direttrice g. |
| Pendenza[retta g] | Pendenza di una retta g. Con questo comando viene tracciato anche il triangolo di pendenza, le cui dimensioni possono essere modificate dalla finestra di dialogo delle proprietà. |
| Perimetro[poligono poly] | Perimetro di un poligono poly. |
| Perpendicolare[punto A, retta g] | Retta per A perpendicolare a g. |
| Perpendicolare[punto A, vettore v] | Retta per A perpendicolare a v. |
| Poligono[punto A, punto B, punto C, …] | Poligono definito dai punti immessi A, B, C,… |
| Poligono[punto A, punto B, numero n] | Poligono regolare di n vertici (inclusi i punti A e B). |
| Polinomio[funzione f] | Espande la funzione polinomiale f. Esempio: Polinomio[ (x – 3)^2] produce $x^2 – 6x + 9$. |
| PolinomioTaylor[funzione f, numero a, numero n] | sviluppo in serie di potenze di ordine n della funzione f con centro nel punto x=a. |
| Punto[retta g] | Punto su una retta g. |
| Punto[conica c] | Punto su una conica c (es circonferenza, ellisse, iperbole). |
| Punto[funzione f] | Punto su una funzione f. |
| Punto[poligono poly] | Punto su un poligono poly. |
| Punto[vettore v] | Punto su un vettore v. |
| Punto[punto P, vettore v] | Costruisce il punto P+v. |
| PuntoMedio[punto A, punto B] | Punto medio tra A e B. |
| PuntoMedio[segmento s] | Punto medio del segmento s. |
| Simmetrico[punto A, punto B] | Simmetrico del punto A rispetto al punto B. |
| Simmetrico[retta g, punto B] | Simmetrico della retta g rispetto al punto B. |
| Simmetrico[conica c, punto B] | Simmetrico della conica c rispetto al punto B. |
| Simmetrico[poligono poly, punto B] | Simmetrico del poligono poly rispetto al punto B. |
| Simmetrico[punto A, retta h] | Simmetrico del punto A rispetto alla retta h. |
| Simmetrico[retta g, retta h] | Simmetrico della retta g rispetto alla retta h. |
| Simmetrico[conica c, retta h] | : Simmetrico della conica c rispetto alla retta h. |
| Simmetrico[poligono poly, retta h] | Simmetrico del poligono poly rispetto alla retta h. |
| Successione[espressione e, variabile i, numero a, numero b] | Elenco di oggetti generato utilizzando l’espressione e e l’indice i, che varia dal numero a al numero b. Esempio: L = Successione[(2, i), i, 1, 5] crea un elenco di punti le cui ordinate variano da 1 a 5. |
| Vettore[punto A, punto B] | Vettore tra A e B Vettore[punto A]: Vettore posizione di un punto A |
 Gnuplot è un programma che consente di tracciare grafici di funzioni o di dati a due o tre dimensioni. È gratuito e i sorgenti sono disponibili, ma non è open source in senso stretto poiché non è consentito diffonderne versioni modificate. Il software può essere utile per anche per gli studenti della scuola secondaria. Si ottengono grafici di funzioni, curve e superfici di ottima qualità. E’ adatto anche per la computer art o math-art.
Gnuplot è un programma che consente di tracciare grafici di funzioni o di dati a due o tre dimensioni. È gratuito e i sorgenti sono disponibili, ma non è open source in senso stretto poiché non è consentito diffonderne versioni modificate. Il software può essere utile per anche per gli studenti della scuola secondaria. Si ottengono grafici di funzioni, curve e superfici di ottima qualità. E’ adatto anche per la computer art o math-art.
.
Introduzione
Esistono versioni di gnuplot per molte piattaforme, anche se gli ultimi rilasci vengono collaudati estensivamente solo su Unix/Linux, Windows e OSX.
Quale che sia la piattaforma, il programma è sempre a linea di comando.
Su Unix/Linux viene eseguito digitando gnuplot in una finestra xterm (o equivalenti); appare quindi il prompt "gnuplot> ", dopo il quale vanno digitati i comandi. Il programma può essere eseguito anche indicando il nome di un file di testo contenente una successione di comandi, che vengono eseguiti in sequenza. Si opera analogamente su OSX, eseguendo gnuplot dal Terminal, da suoi sostituti come iTerm, oppure da xterm.
Per Windows esiste un eseguibile wgnuplot.exe che apre una finestra dotata di menù; in questa viene però comunque proposta l’interfaccia a riga di comando con lo stesso prompt.
Il comando help propone un’estesa guida in linea, tanto estesa che non è facile orientarsi per chi si avvicini le prime volte al programma.
Speriamo che questa breve intriduzione aiuti ad acquisire quel minimo di familiarità necessario per poter poi sfruttare appieno, secondo necessità, la ricca messe di comandi e di opzioni.
.
Installazione
Molte distribuzioni Linux comprendono già gnuplot; se non risulta già disponibile, lo si può installare usando il package manager della propria distribuzione (rpm per RedHat, YaST per Suse, APT per Debian, ecc.). Chi desidera scaricare e compilare i sorgenti, può scegliere uno dei siti indicati nell’apposita pagina del sito ufficiale.
Dagli stessi siti si possono scaricare le versioni già compilate per Windows, riconoscibili per la presenza di "win" nel nome del file (ad esempio, gp422win32.zip da quest’elenco). Per l’installazione è sufficiente scompattare il file in una qualsiasi cartella. Su OSX si può installare il programma con Fink, usando il comando apt-get install gnuplot oppure l’interfaccia grafica FinkCommander, ma si possono anche scaricare e compilare i sorgenti come su Linux.
Lanciare dalla cartella Bin il file wgnuplot.exe. Può essere utile memorizzare la cartella in una qualsiasi cartella dell’hard disk e creare sul desktop un collegamento al file eseguibile.
.
Grafici bidimensionali
Appena eseguito il programma, viene proposto un prompt dal quale è subito possibile costruire grafici.
Ad esempio: gnuplot> plot sin(x) traccia il grafico della funzione seno.
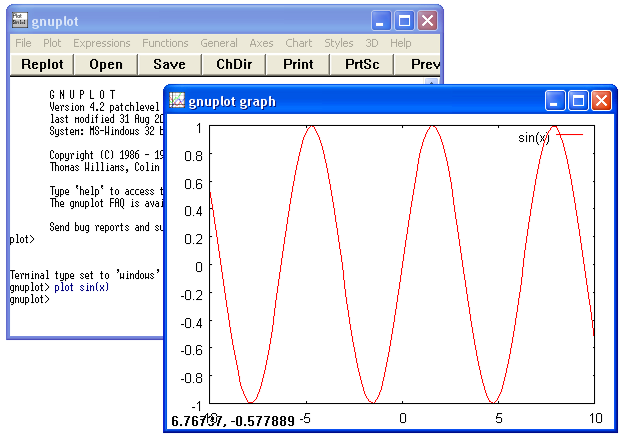
L’insieme delle funzioni disponibili è molto ampio, tanto che preferiamo riviare al manuale, qui ne indichiamo solo qualcuna: abs(x), exp(x), log(x), sqrt(x), tan(x).
Sottolineamo, piuttosto, che è possibile definire nuove funzioni a partire da quelle disponibili (ne vedremo qualche esempio più avanti).
Il grafico che si ottiene viene prodotto adottando valori di default per un gran numero di opzioni (per vederle tutte, si può usare il comando show all). Ad esempio:
Anche plot ha sue opzioni, che consentono di definire tipo, colore e spessore delle curve tracciate nel grafico. Va forse sottolineato che tra queste c’è un’opzione title diversa da quella appena menzionata. Per default, un comando come plot sin(x), oltre a tracciare il grafico della funzione seno, scrive "sin(x)" in alto a destra seguito da un segmento tracciato con le stesse opzioni usate per tracciare la curva. Questo è utile quando si tracciano più funzioni, ad esempio con il comando plot sin(x), cos(x): le curve verranno tracciate in modo diverso (per default, linee continue di colore diverso) e la legenda in alto a destra consente di individuarle.
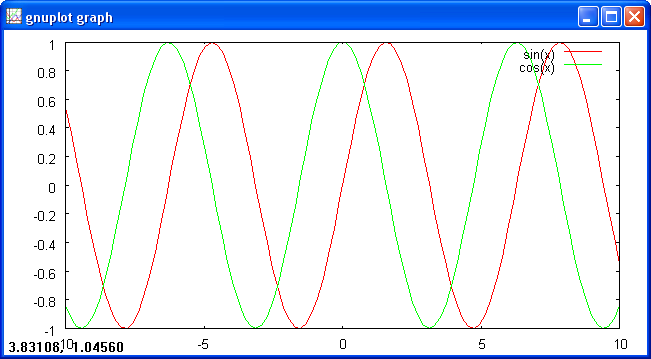
Si può assegnare un nome diverso alle singole curve indicandolo dopo ciascuna funzione (ad esempio: plot sin(x) title "seno", cos(x) title "coseno"), oppure non mostrarne alcuno scrivendo notitle.
In sostanza, set title imposta il titolo del grafico, che viene scritto per default sopra il grafico, plot
.
Coordinate cartesiane
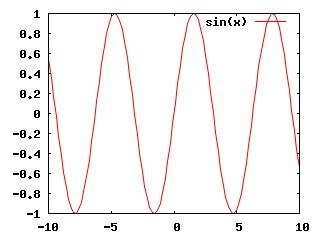
Il grafico della figura che segue è stato prodotto con il solo comando: plot sin(x)
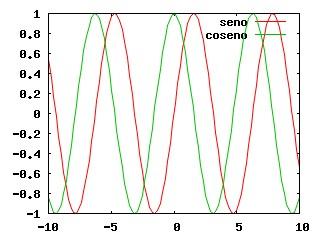
Il grafico della figura che segue è stato prodotto con il comando: plot sin(x) title "seno", cos(x) title "coseno"
Il grafico della figura che segue è stato prodotto con i comandi:
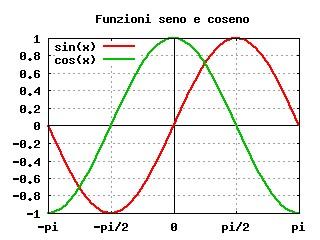 set title "Funzioni seno e coseno"
set title "Funzioni seno e coseno"
set xrange[-pi:pi]
set xtics ("-pi" -pi, "-pi/2" -pi/2, "0" 0, "pi/2" pi/2, "pi" pi)
set zeroaxis lt rgb "black"
set zeroaxis lt 2
set grid
set key top left
plot sin(x) lw 2, cos(x) lw 2
Il primo imposta il titolo del grafico. Il secono imposta il campo di variazione della variabile indipendente da -π a π (la costante π si indica con "pi"; vedremo tra breve come scriverla meglio su un grafico), il successivo suddivide l’asse delle ascisse in intervalli larghi π/2.
I due comandi set zeroaxis tracciano gli assi delle ascisse e delle ordinate in nero e con un tratto continuo (per default, ovvero dando il comando senza opzioni, vengono tracciati con linee punteggiate).
Il comando set grid fa sì che venga tracciata una griglia di linee punteggiate secondo i "tic" (gli estremi degli intervalli) definiti sui due assi.
Il comando set key top left sposta la legenda in alto a sinistra, in modo che non si sovrapponga ai grafici delle funzioni. L’ultimo comando traccia i grafici del seno e del coseno, entrambi con una linea continua di spessore 2.
.
Coordinate polari
Il grafico della figura che segue è stato prodotto con i comandi: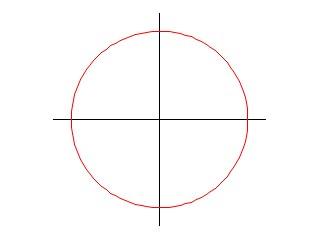
set polar
set xrange[-1.2:1.2]
set yrange[-1.2:1.2]
set size ratio 1
unset border
unset tics
set zeroaxis lt rgb "black"
set zeroaxis lt 2
plot 1 notitle
Il primo comando imposta le coordinate polari, i due successivi definiscono il campo di variazione delle variabili. Il comando set size ratio 1 fa sì che, quali che siano le dimensioni della finestra di output, i due assi coordinati abbiano la stessa scala. I due comandi unset eliminano sia il rettangolo che per default delimita il grafico (come negli esempi visti fin qui), sia i "tic" definiti lungo gli assi coordinati. I tre comandi finali sono analoghi ad altri già visti. Si può magari sottolineare che, avendo impostato le coordinate polari, per tracciare il cerchio è sufficiente indicarne il raggio (in questo caso, 1).
Il grafico della figura seguente è stato prodotto con i comandi:
set polar set trange[0:38]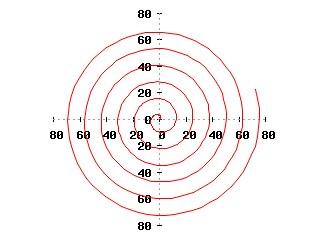
set size square
unset border
set zeroaxis
set xtics axis
set ytics axis
set samples 400
plot 2*t notitle
Una volta impostate le coordinate polari, la variabile indipendente viene chiamata t e si usa il comando set trange per impostarne il campo di variazione. set size square è identico al già visto set size ratio 1. L’opzione axis dei comandi che governano i "tic" fa sì che questi vengano tracciati sugli assi coordinati invece che sul rettangolo che delimita il grafico. Il comando set samples consente di aumentare la "risoluzione" del grafico, in modo da ottenere grafici più accurati (più simili a curve vere e proprie che a spezzate).
Nella figura seguente (adattata da http://gnuplot.sourceforge.net/demo_4.0/polar.html ) si usano due funzioni per comporre un’unica figura:
set polar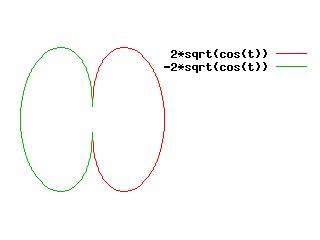
set size square
unset border
unset tics
set key outside
set samples 400
plot 2*sqrt(cos(t)),-2*sqrt(cos(t))
Il comando set key outside pone la legenda fuori del rettangolo che delimita la figura, anche se, avendo usato unset border, il rettangolo non viene disegnato.
.
Funzioni parametriche
Per usare funzioni parametriche si usa il comando set parametric, dopo il quale le funzioni vanno definite in termini della variabile t per disegni bidimensionali, delle variabili u, v per disegni tridimensionali
Una funzione parametrica bidimensionale va definita mediante una coppia di funzioni. Ad esempio, la retta di equazione $y=x-2$ viene rappresentata con le due equazioni parametriche $x=4+t$, $y=2+t$ (da queste si ha, infatti, $t=x-4=y-2$, ovvero $y=x-2$). Le due funzioni di t vanno indicate nel seguente ordine: prima quella per x, poi quella per y.
La figura che segue mostra il grafico di due rette per mettere in evidenza l’importanza dell’ordine con cui vengono indicate le due funzioni di t. È stata prodotta con i comandi: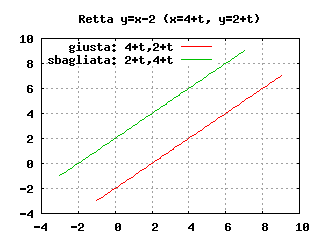
.
set parametric
set title "Retta y=x-2 (x=4+t, y=2+t)"
set grid
set key top left
plot 4+t,2+t title "giusta: 4+t,2+t", 2+t,4+t title "sbagliata: 2+t,4+t"
.
Come si vede, il comando plot 4+t,2+t produce il grafico della retta y=x-2, mentre plot 2+t,4+t produce il grafico di una retta traslata in alto (y=x+2).
.
La figura seguente mostra un cardioide. I comandi con i quali è stata ottenuta sono: 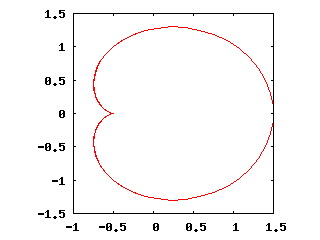
.
set parametric
set size square
plot cos(t)+0.5*cos(2*t),sin(t)+0.5*sin(2*t)
notitle
.
.
.
.
La figura seguente, adattata da http://gnuplot.sourceforge.net/demo_4.0/param.html , mostra alcune sezioni coniche ottenute parametrizzando rispetto a t.
Sono state ottenute con i seguenti comandi: 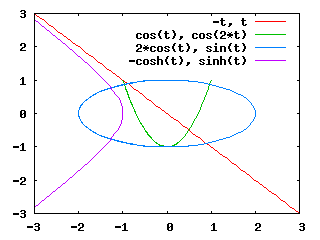
.
set parametric
set xrange[-3:3]
set yrange[-3:3]
plot -t,t,cos(t),cos(2*t),2*cos(t),sin(t),-cosh(t),sinh(t)
.
.
.
.
.
Grafici tridimensionali
Produrre grafici tridimensionali è piuttosto semplice: basta usare splot (surface plot) invece di plot. Vi sono, tuttavia, interessanti differenze. Ad esempio, quando si usa il terminale di default (cioè lo schermo), le immagini sono "animabili", nel senso che cliccando col tasto sinistro del mouse e tenendolo premuto si può cambiare come si desidera la prospettiva.
Vi sono poi apposite opzioni per una resa migliore rispetto a quelle già viste. Quelle che più si distinguono sono quelle che consentono di colorare le superfici e di eliminare le linee nascoste. Vengono infatti spesso tracciate superfici, rese normalmente con griglie di linee (o punti) più o meno fitte, ed è possibile sia rappresentarle come vere e proprie superfici colorate, invece che tratteggiate, sia evitare la visualizzazione di porzioni di superfici che rimangono nascoste da altre.
Le tre figure che seguono sono adattate da http://gnuplot.sourceforge.net/demo_4.0/
La figura che segue è stata prodotta con i comandi: 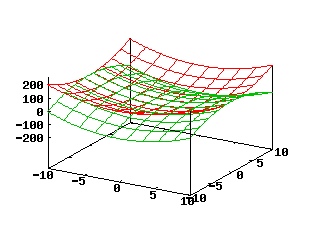
.
set zrange[-200:250]
set ztics ("-200" -200, "-100" -100, "0" 0, "100" 100, "200" 200)
splot x**2+y**2 notitle, x**2-y**2 notitle
.
Si può notare che splot e plot si usano in modo molto simile, con l’ovvia differenza che le funzioni vengono espresse in termini delle due variabili x e y. Vi sono inoltre comandi come set zrange e set ztics per l’asse z.
Le superfici che rappresentano le due funzioni sono tracciate ciascuna con una griglia di linee e sono "trasparenti", nel senso che si vedono anche porzioni che resterebbero nascoste se le superfici fossero compatte.
.
Eliminazione delle linee nascoste
La figura che segue mostra un grafico tracciato con equazioni parametriche. Per ottenere il grafico è stato usato il comando set hidden3d che elimina le linee nascoste: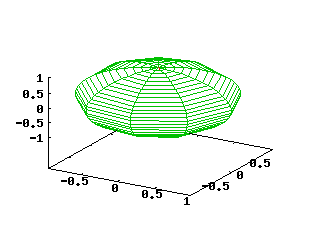
.
set parametric
set isosamples 30,10
set hidden3d
set xtics -1, .5, 1
set ytics -1, .5, 1
set ztics -1, .5, 1
set urange [ -1.57080 : 1.57080 ]
set vrange [ 0.00000 : 6.28319 ]
splot cos(u)*cos(v),cos(u)*sin(v),sin(u) notitle
Quando vengono tracciati grafici a due dimensioni, le curve sono in realtà linee spezzate che appaiono come curve vere e proprie tanto più quanto più si aumenta la risoluzione con il comando set samples.
I grafici a tre dimensioni vengono tracciati con segmenti che uniscono i punti di curve di livello (isoline); la risoluzione del grafico può essere aumentata in due direzioni: il primo numero dopo set isosamples governa la distanza tra le curve di livello, il secondo determina il numero dei punti che compongono le singole curve di livello. Si può dire che i due numeri regolano, rispettivamente, la risoluzione "verticale" e quella "orizzontale" del grafico (a spese del tempo richiesto per tracciarlo).
La figura di prima mostra anche un altro uso dei comandi set [x|y|z]tics: si può modificare l’intervallo dei "tic" indicando il primo, l’incremento e l’ultimo.
.
Colorazione delle superfici
La figura che segue mostra ancora un grafico tracciato con equazioni parametriche, ma viene usato il comando set pm3d (palette mapped 3d) per colorare le superfici: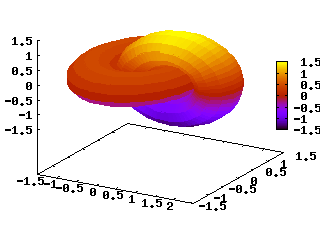
.
set parametric
set isosamples 50,20
set pm3d depthorder
set view 60, 30, 1.1, 1.33
unset key
set xtics -1.5, .5, 2.5
set ytics -1.5, .5, 1.5
set ztics -1.5, .5, 1.5
splot cos(u)+.5*cos(u)*cos(v),sin(u)+.5*sin(u)*cos(v),.5*sin(v) with pm3d,
1+cos(u)+.5*cos(u)*cos(v),.5*sin(v),sin(u)+.5*sin(u)*cos(v) with pm3d
Le diverse sfumature di colore rendono la distanza lungo l’asse z dal piano xy. Viene mostrata anche una colonna con la scala dei colori (può essere eliminata con unset colorbox).
Non si usa il comando set hidden3d, ma l’opzione depthorder di set pm3d; le superfici vengono colorate tenendo conto della loro profondità rispetto al punto di vista dell’osservatore e si ha, così, un effetto analogo a quello dell’eliminazione delle linee nascoste.
Il punto di vista dell’osservatore viene definito con il comando set view, che accetta quattro parametri: rotazione intorno all’asse x (da 0 a 180, 60 per default), rotazione intorno all’asse z (da 0 a 360, 30 per default), scala dell’intero grafico e scala dell’asse z (entrambi 1 per default).
Il comando usato per tracciare la figura precedente aumenta del 10% la dimensione dei due tori e li "allunga" del 30% in verticale. Normalmente i grafici vengono comunque tracciati come griglie di linee; per eliminarle ed ottenere solo superfici colorate si deve dare l’opzione with pm3d dopo ciascuna delle funzioni che si chiede a splot di tracciare.
.
Creazione di file
Finora abbiamo ipotizzato che i grafici venissero prodotti sul terminal di default, che è x11 per Unix/Linux, windows per Windows e aqua per OSX. Per creare un file sono sufficienti i comandi:
set terminal <tipo>
…
set output
Con set terminal si sceglie il tipo di terminale e, se si desidera creare un file, il tipo di file, ad esempio jpeg o png. Possono essere indicate diverse opzioni, la più usata delle quali, size, determina le dimensioni del grafico. Con set output "<nome file>
Le figure usate in questa introduzione sono state tutte create in questo modo, a volte come file jpeg, altre come file png. Per l’ultima figura, quella dei due tori, si è creato un file di testo "tori.gp" contenente i comandi:
set terminal png size 320, 240
set output "tori.png"
set parametric
set isosamples 50,20
set pm3d depthorder
set view 60, 30, 1.1, 1.33 unset key
set xtics -1.5, .5, 2.5
set ytics -1.5, .5, 1.5
set ztics -1.5, .5, 1.5
splot cos(u)+.5*cos(u)*cos(v),sin(u)+.5*sin(u)*cos(v),.5*sin(v) with pm3d,
1+cos(u)+.5*cos(u)*cos(v),.5*sin(v),sin(u)+.5*sin(u)*cos(v) with pm3d
set output
e si è poi eseguito gnuplot indicando il nome del file sulla riga comandi:
$ gnuplot tori.gp
.
Testo "enhanced"
Sia quando si tracciano grafici sullo schermo, sia, e soprattutto, quando si creano file, può essere utile scrivere testi che abbiano un formato più ricco di quello standard. Ciò si ottiene usando l’opzione enhanced quando si sceglie il dispositivo di output.
Il dispositivo più flessibile è il terminal postscript, per usare il quale è buona norma definire, con set fontpath, la collocazione dei font nel proprio sistema.
La figura che segue è stata costruita nel modo seguente.
1. Per prima cosa si è creato un file di testo "gaussiana.gp" con i comandi:
set fontpath "/usr/share/fonts/default/ghostscript"
set terminal postscript eps enhanced font "arial,28"
set output "gaussiana.eps"
set xrange [-5:5]
set yrange [0:.5]
set key spacing 1.3 e = exp(1)
plot 1/sqrt(2*pi)*e**(-x**2/2) title "(2{/Symbol p})^{(-1/2)}e^{-x^2/2}"
set output
2. Si può notare che, nell’opzione title di plot si è indicato il pi greco con "{/Symbol p}" e si è usato l’accento circonflesso, "^", per gli esponenti; si è poi creato il file "gaussiana.eps" dalla riga comandi, con:
$ gnuplot gaussiana.gp
3. Si è infine trasformato il file "gaussiana.eps" in un file di tipo png usando Ghostscript:
gs -dNOPAUSE -sDEVICE=png16 -sOutputFile=gaussiana.png -g500x350 -dBATCH gaussiana.eps
.
Conclusioni
In questa breve introduzione abbiamo cercato di dare un’idea delle potenzialità di gnuplot e dei comandi di uso più frequente. Speriamo che gli esempi proposti possano essere utili per chi voglia cominciare a creare i propri grafici, ma ciascuno di essi dovrebbe essere visto solo come una prima indicazione circa l’uso di comandi che, in realtà, hanno insiemi di opzioni molto più vasti di quanto qui illustrato.
Crediamo opportuno, quindi, rinviare sia al sito ufficiale, sia ad altri siti Internet; in particolare:
dalla pagina http://www.gnuplot.info/screenshots/index.html si accede ad una ricca messe di esempi;
la pagina http://www.gnuplot.info/docs/gnuplot.html contiene la documentazione completa di Gnuplot;
la pagina http://www.gnuplot.info/faq/faq.html contiene risposte alle domande più frequenti circa l’uso del programma;
la pagina http://t16web.lanl.gov/Kawano/gnuplot/index-e.html contiene moltissime informazioni utili, corredate da numerosi esempi.
 L’ONU ha proclamato l’anno 2009 “Anno Internazionale dell’Astronomia”, accogliendo così la mozione che l’UNESCO aveva già avanzato nel dicembre 2005. Questa proclamazione è anche un successo italiano, poiché è stato proprio il nostro Paese il primo a farsene promotore fin dal 2003. Uno risultato raggiunto anche grazie al fatto che nel 2009 ricorre il IV centenario dalla prima osservazione del cielo con un cannocchiale, da parte di Galileo Galilei. Moltissime le attività organizzate in tutto il pianeta in ambito astronomico, in Italia sarà l’INAF (Istituto Nazionale di Astrofisica), sia autonomamente sia in collaborazione con altri enti, università e associazioni culturali, ad organizzare eventi su tutto il territorio nazionale. Lo scopo di questa iniziativa è quello di offrire a tutti la possibilità di avvicinarsi all’astronomia con un approccio semplice, accessibile ed alla portata di chiunque.
L’ONU ha proclamato l’anno 2009 “Anno Internazionale dell’Astronomia”, accogliendo così la mozione che l’UNESCO aveva già avanzato nel dicembre 2005. Questa proclamazione è anche un successo italiano, poiché è stato proprio il nostro Paese il primo a farsene promotore fin dal 2003. Uno risultato raggiunto anche grazie al fatto che nel 2009 ricorre il IV centenario dalla prima osservazione del cielo con un cannocchiale, da parte di Galileo Galilei. Moltissime le attività organizzate in tutto il pianeta in ambito astronomico, in Italia sarà l’INAF (Istituto Nazionale di Astrofisica), sia autonomamente sia in collaborazione con altri enti, università e associazioni culturali, ad organizzare eventi su tutto il territorio nazionale. Lo scopo di questa iniziativa è quello di offrire a tutti la possibilità di avvicinarsi all’astronomia con un approccio semplice, accessibile ed alla portata di chiunque.
Tra i progetti su scala mondiale segnaliamo:
• 100 ore di astronomia, in occasione delle quali saranno organizzate diverse attività pratiche di osservazione del cielo con strumenti astronomici che messi a disposizione del grande pubblico, sia da parte di osservatori astronomici istituzionali, sia da parte di associazioni culturali locali.
• Il galileoscopio, che prevede l’osservazione del cielo con uno strumento molto simile al rudimentale cannocchiale utilizzato da Galileo, questo anche allo scopo di comprendere le notevoli capacità di osservazione dello scienziato toscano, considerando la rudimentalità dello strumento utilizzato all’epoca.
• Il portale dell’Universo, attraverso il quale sarà resa disponibile una grande mediateca online che conterrà notizie, immagini, filmati e moltissimo altro materiale.
• Dark Sky Awareness, che si propone di proteggere il cielo stellato notturno dal continuo dilagare dell’inquinamento luminoso, prodotto dagli impianti di illuminazione artificiale spesso concepiti e installati male.
• Astronomy and World Heritage è invece un’iniziativa volta ad individuare e valorizzare tutti quei siti astronomici di una certa rilevanza culturale.
• Galileo, programma di formazione per i docenti che insegnano l’astronomia. Il programma prevede corsi per l’utilizzo della strumentazione astronomica e dei software astronomici di manipolazione delle immagini digitali.
• La percezione dell’Universo, che ha l’obiettivo di avvicinare i bambini svantaggiati alla percezione dell’Universo, attraverso giochi, canzoni, attività manuali, cartoni animati ecc.
• L’Universo dalla Terra invece è un progetto che mostrerà le più belle immagini astronomiche riprese dai telescopi spaziali in orbita intorno al nostro Pianeta. I luoghi delle mostre saranno i più inusuali, dai giardini ai parchi pubblici, dai musei ai centri commerciali…
• Sviluppare l’Astronomia in una prospettiva globale, prevede una serie di iniziative in ambito astronomico realizzate in sinergia tra università, enti di ricerca, e scuole.
La data ufficiale di apertura dell’Anno Internazionale dell’Astronomia sarà il 15 gennaio 2009, la manifestazione si terrà a Parigi. La manifestazione di chiusura sarà tenuta invece in Italia, il 6 gennaio 2010, data particolarmente densa di significato per noi italiani, il 2010 infatti è l’anno in cui fu pubblicato il famoso “Sidereus Nuncius”, un trattato scientifico che Galileo Galilei pubblicò in 550 copie a Venezia, in esso erano riportate le sue scoperte riguardanti i satelliti di Giove, la corrugata superficie della Luna, un gran numero di stelle non visibili ad occhio nudo e altro: un trattato destinato a stravolgere le conoscenze astronomiche della sua epoca e a gettare le basi della moderna astronomia.
Tra le innumerevoli iniziative programmate in Italia vi segnalo l’importante appuntamento con il “Festival dello Spazio” che si terrà domenica 29 marzo 2009 presso le sale dello Sheraton Nicolaus Conference Center di Bari. E’ una manifestazione a livello nazionale nel cui ambito sarà allestito un planetario itinerante, dove i partecipanti potranno immergersi nella ricostruzione fedele e realistica del cielo visto da qualsiasi località geografica ed in qualsiasi epoca; sarà presente anche una Galleria delle Scienze, nella quale saranno eseguiti in pubblico esperimenti scientifici; sono previsti diversi importanti ospiti, tra i quali l’astronauta italiano Umberto Guidoni, già intervenuto in due delle precedenti edizioni; un’esposizione di astrofotografie, un modello in scala 1:1 dello “Sputnik”, un’esposizione dei “Vettori Americani” (Gemini, Redstone e Saturn V), del “Modulo MLPL” (fornito dall’Agenzia Spaziale Italiana) e della ricostruzione in scala 1:48 dell’Atterraggio di Apollo 11; una mostra di meridiane, orologi solari e calendari astronomici, una mostra di meteoriti provenienti da tutto il mondo, tra cui alcuni rarissimi frammenti di breccia lunare e di basalto marziano. Numerose anche le conferenze a carattere divulgativo.
Per approfondimenti si può consultare il sito internet della manifestazione www.festivaldellospazio.it .
Tra i siti specifici per questa iniziativa segnalo Anno Internazionale dell’Astronomia 2009 http://www.astronomy2009.it/ .
Ulteriore iniziativa è la nascita del blog Sidereus Nuncius che si propone di offrire aggiornamenti continui e quotidiani nell’ambito dell’astronomia, dell’astrofisica e dell’astronautica, sempre riportati in maniera semplice ed accessibile anche ai non addetti ai lavori. Troverete il blog all’indirizzo: www.sidereus-nuncius.info .
Il video di presentazione dell’iniziativa
 Scopo del gioco è quello di riempire le caselle bianche con numeri da 1 a 9, in modo tale che in ogni riga, in ogni colonna e in ogni regione quadrata con bordi in neretto, siano presenti tutte le cifre da 1 a 9 senza ripetizioni. Ma questa è solo la regola. Per risolvere effettivamente il gioco ci vuole logica e inventiva. Qualcuno il metodo infallibile l'ha trovato: riempire ogni casella con i numeri da 1 a 9 e poi cancellarli man mano. Sarà pure una tecnica risolutiva ma è di un noia mortale. D'altra parte ci sono tanti software che risolvono i sudoku, basta dare in pasto al computer i numeri noti ed ecco la soluzione da ricopiare. Anche questa è una tecnica risultiva ma no è certo un bel modo di giocare. Dov'è il divertimento? Allora immaginiamoci seduti su una sdraio vicino al mare, fa caldo, ma c'è l'ombra e c'è un piacevole venticello che viene dal mare. Prendiamo la matita, il foglio del sudoku …
Scopo del gioco è quello di riempire le caselle bianche con numeri da 1 a 9, in modo tale che in ogni riga, in ogni colonna e in ogni regione quadrata con bordi in neretto, siano presenti tutte le cifre da 1 a 9 senza ripetizioni. Ma questa è solo la regola. Per risolvere effettivamente il gioco ci vuole logica e inventiva. Qualcuno il metodo infallibile l'ha trovato: riempire ogni casella con i numeri da 1 a 9 e poi cancellarli man mano. Sarà pure una tecnica risolutiva ma è di un noia mortale. D'altra parte ci sono tanti software che risolvono i sudoku, basta dare in pasto al computer i numeri noti ed ecco la soluzione da ricopiare. Anche questa è una tecnica risultiva ma no è certo un bel modo di giocare. Dov'è il divertimento? Allora immaginiamoci seduti su una sdraio vicino al mare, fa caldo, ma c'è l'ombra e c'è un piacevole venticello che viene dal mare. Prendiamo la matita, il foglio del sudoku …
METODOLOGIE RISOLUTIVE
Riduci il campo di gioco a tre righe orizzontali per volta, comincia da quelle dove ci sono più numeri. Nell'esempio sotto sono partito dalle prime tre righe, quelle con sfondo grigio. Osserva che il numero 7 è già in quetti e tre i riguadri e in tutte e tre le righe, quindi non se ne possono mettere altri. Il numero 1 invece è presente solo in 2 riquadri, manca allora nel terzo riquadro e nella seconda riga. Quindi l'1 sarà lì: nel terzo riquadro nella seconda riga. Ci sono però due posizioni libere, quella sotto il 6 e quella sotto il 5. L'1 non può stare sotto il 6 perché nella stessa colonna c'è già l'1, quindi deve stare sotto il 5.
Messo l'1 possiamo fissare l'ultima fascia verticale, come in figura. Osserviamo che l'1 c'è in ogni riquadro e in ogni colonna, quindi non ce ne vogliono altri. L'8 invece manca nella prima colonna e nell'ultimo riquadro. Può stare in un solo posto nella prima colonna in grigio sopra L'1 e sotto il 4.
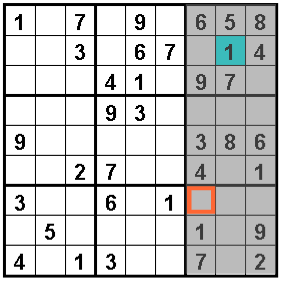
Nella settima colonna, indica con la riga arancione, mancano solo due numeri, è facile capire quali sono, il 2 e il 5. Segnamoli a matita e proviamo a capire quale va escluso. Nel riquadro in alto a destra è già presente il 5, quindi nella casella celeste non può esserci il 5, cancello il 5 e rimane soltanto il 2.
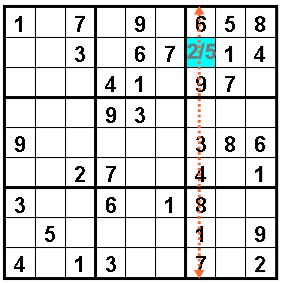
Nella settima colonna, ora è rimasta una sola cella libera; è facile capire di quale numero si tratta perché è l'unico che manca nella colonna, il 5.
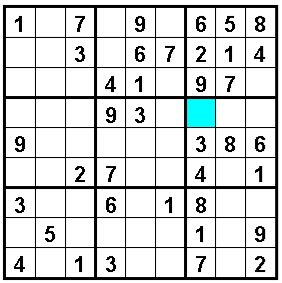
 Qualità, competenza e studi approfonditi debbono essere effettuati nella progettazione delle opere mentre nella realizzazione non sono ammessi ritardi poiché i tempi di completamento debbono essere certi. E se, quando l’opera sarà completata, le spese non supereranno le stime ci saranno complimenti ed onori. Ma se le supereranno del 25% vi saranno penali per il costruttore. (Vitruvio – De Architectura – circa 25 a.C.).
Qualità, competenza e studi approfonditi debbono essere effettuati nella progettazione delle opere mentre nella realizzazione non sono ammessi ritardi poiché i tempi di completamento debbono essere certi. E se, quando l’opera sarà completata, le spese non supereranno le stime ci saranno complimenti ed onori. Ma se le supereranno del 25% vi saranno penali per il costruttore. (Vitruvio – De Architectura – circa 25 a.C.).
I Guru del project management fanno coincidere la nascita della moderna disciplina con il presidio della pianificazione e del controllo di tempi, costi e qualità dei progetti, ma tutto è in realtà già contenuto nei pensieri sopra riportati.
Fra gli autori latini pochi furono quelli che scrissero qualcosa sulle opere d’ingegneria, l’organizzazione adottata e le infrastrutture realizzate dalla Roma antica. Fra di essi il più importante fu Vitruvio Pollione vissuto al tempo di Giulio Cesare ed Augusto. La sua opera principale, De Architectura, reca tracce evidenti degli ingegneri alessandrini, cita infatti esplicitamente il nome di Ctesibio e parecchie sue invenzioni (la pompa, una balestra ad aria compressa, l’argano idraulico, ecc.).
Stupisce che la civiltà romana abbia risolto brillantemente molti problemi ingegneristici, costruttivi ed organizzativi senza lasciare consistenti tracce scritte, come invece fece per il diritto che è rimasto dominante nel mondo occidentale almeno sino all’epoca napoleonica. Anfiteatri, fori, templi, terme, archi, ponti e soprattutto la grande rete stradale e la grande rete degli acquedotti, che per essere compiute hanno richiesto una forte capacità di risolvere problemi pratici, testimoniano che molti servizi pubblici furono meglio organizzati allora che nell’Europa, poniamo del Settecento.
L’impero aveva centomila chilometri di strade, l’Italia sola possedeva circa quattrocento grandi arterie e la loro pavimentazione aveva consentito a Cesare di percorrere millecinquecento chilometri in otto giorni. Il telegrafo era sostituito da segnalazioni luminose attraverso fari posati sulle alture, ed è rimasto sostanzialmente identico sino ai tempi di Napoleone.
Il prosciugamento del Fucino fu un autentico capolavoro: furono gli egiziani a scoprire i principi dell’idraulica, ma furono i romani a concretarli in acquedotti e fognature, e a loro si deve anche lo zampillo delle fontane della Roma di oggi.
In tempi moderni è stato verificato che la costruzione della cupola del Pantheon di Roma, ma anche delle campate di alcuni archi e ponti, è congruente con quello che si sarebbe realizzato oggi sulla base del calcolo infinitesimale e della moderna scienza delle costruzioni.
I Romani, benché nel I° secolo a.C. gli alessandrini avessero scoperto il mulino ad acqua, non furono mai interessati alla ricerca di nuove fonti di energia, ma il fatto è spiegabile considerando che lo sfruttamento sistematico delle fonti di energia naturale apparivano più costose di quella animale e umana: cento schiavi costavano meno di una turbina, e la meccanizzazione avrebbe creato un insolubile problema di disoccupazione.
 Si è concluso il primo trofeo di scacchi di Matematicamente.it. Il vincitore è Nato_pigro (Giorgio Ricca, prov. Imperia), secondo Amandy (Andrea Mandelli, Pesaro), terzo Pisolo (Paolo Monti, Milano). Complessivamente sono state giocate 1923 partite per oltre 9000 mosse e più di 500 partecipanti. Nell’articolo tutti i vincitori. Molto presto partirà il trofeo di scacchi 2009 con nuovi e accattivanti premi. A giorni i dettagli.
Si è concluso il primo trofeo di scacchi di Matematicamente.it. Il vincitore è Nato_pigro (Giorgio Ricca, prov. Imperia), secondo Amandy (Andrea Mandelli, Pesaro), terzo Pisolo (Paolo Monti, Milano). Complessivamente sono state giocate 1923 partite per oltre 9000 mosse e più di 500 partecipanti. Nell’articolo tutti i vincitori. Molto presto partirà il trofeo di scacchi 2009 con nuovi e accattivanti premi. A giorni i dettagli.
I vincitori dell’edizione 2008
1. Nato_pigro, Giorgio Ricca (prov. Imperia), vincitore di giugno e vincitore del trofeo, riceverà la coppa della foto
2. Amandy , Andrea Mandelli (Pesaro), vincitore di agosto, ha ricevuto la maglietta Winner
3. Pisolo, Paolo Monti (Milano), vincitore di novembre, ha ricevuto la maglietta Winner
4. Martino, vincitore di dicembre, riceverà la maglietta Winner
5. Patrizio20, Patrizio Monatti (Firenze), vincitore di settembre, ha ricevuto la maglietta Winner
6. Luca_92, vincitore di ottobre, riceve la maglietta Winner
7. Battista_l, vince la maglietta Winner come 2° classificato
8. Rickytravel, vince la maglietta Winner come 3° classificato
13. shah.ruhk, vincitore di luglio, vince la maglietta Winner
16. Lorenzo93, vince la maglietta Winner per aver concluso il maggio numero di partite
Tamerlano, vincitore di maggio, riceverà la maglietta Winner.
Tutti i vincitori sono pregati di inviare una mail a [email protected] nella quale indicheranno il recapito presso cui ricevere la maglietta (se non l’hanno già ricevuta), nella mail indicheranno la taglia della maglietta e se acconsentono a pubblicare accanto al nick il nome reale e la provincia di residenza.
La classifica al momento è congelata, le nuove partite che si concluderanno in seguito non daranno diritto a punteggio.
Molto presto partirà il nuovo trofeo, con qualche integrazione al software.
I punteggi ELO saranno tutti azzerati, tutti gli iscritti partiranno con lo stesso punteggio.
Quest’anno ci sarà qualche premio in più.
 1. Riprogrammazione cellulare: ottenere linee cellulari su misura riprogrammando le cellule estratte da persone malate in modo da riportarle a uno stadio di staminali simil-embrionali. A questa ricerca hanno partecipato anche gruppi italiani. Nel 2008 si sono ottenuti risultati in grado di aprire la strada a terapie per malattie oggi inguaribili come Alzheimer, Parkinson, distrofie, diabete.
1. Riprogrammazione cellulare: ottenere linee cellulari su misura riprogrammando le cellule estratte da persone malate in modo da riportarle a uno stadio di staminali simil-embrionali. A questa ricerca hanno partecipato anche gruppi italiani. Nel 2008 si sono ottenuti risultati in grado di aprire la strada a terapie per malattie oggi inguaribili come Alzheimer, Parkinson, distrofie, diabete.
2) Pianeti extrasolari: nel 2008, per la prima volta, sono stati osservati quattro pianeti orbitanti al di fuori del nostro sistema solare. Questa ‘osservazione’ è stata ottenuta per mezzo di speciali telescopi in grado di distinguere la debole luce proveniente dai pianeti da quella molto più intensa proveniente dalle stelle intorno a cui orbitano.
Le altre otto scoperte sono tutte valutate ex equo.
Catalogo dei geni tumorali: ampliamento dei geni implicati nei tumori, in particolare nel tumore al pancreas e nel glioblastoma sono state individuate diverse mutazioni la cui presenza favorisce lo sviluppo del cancro.
Nuovi superconduttori: un gruppo di ricercatori della Florida ha scoperto una nuova classe di materiali che conducono elettricità senza resistenza a temperatura particolarmente elevate, finora erano noti solo materiali superconduttori a temperature molto basse.
Proteine osservate al lavoro: un gruppo di biochimici è stato in grado di osservare le proteine mentre si legano ai recettori, modificano lo stato metabolico delle cellule e determinano le caratteristiche dei tessuti.
Energie rinnovabili: nuove tecniche promettenti per immagazzinare l’eccesso di energia generato da impianti solari ed eolici, utilizzando un nuovo catalizzatore formato da cobalto e fosforo, per separare ossigeno e idrogeno.
Il video degli embrioni in formazione: Un gruppo tedesco di ricercatori è stato in grado di osservare e filmare le prime fasi di sviluppo di un embrione di un piccolo pesce d’acqua usato come modello per gli studi di biologia.
Grasso buono: un nuovo modo per distinguere il cosiddetto ‘grasso bruno’ da quello più conosciuto ‘grasso bianco’. Una scoperta che può costituire un significativo progresso nella lotta all’obesità in quanto il grasso bruno può bruciare il grasso ‘bianco’ per generare energia per l’organismo.
La massa del protone: un gruppo internazionale di fisici ha messo a punto un modello matematico in grado di predire la massa di neutroni e protoni.
Mappatura del DNA: le tecniche per mappare il DNA sono diventate molto più rapide ed economiche rispetto ai primi grandi sforzi per mappare la sequenza del primo genoma umano.
 C’è un giochino che capita di fare durante le vacanze natalizie, ed in particolare la vigilia di Natale: la tombola. Qui vi do un’idea per il pre-tombola, che dovrebbe rendere un po’ più frizzantino il gioco. Si tratta di raccogliere i soldi per i premi con un sistema di “offerte volontarie”, una colletta insomma, ma non una colletta banale. Una raccolta di fondi inusuale che vi permetterà anche di accendere una discussione interessante.
C’è un giochino che capita di fare durante le vacanze natalizie, ed in particolare la vigilia di Natale: la tombola. Qui vi do un’idea per il pre-tombola, che dovrebbe rendere un po’ più frizzantino il gioco. Si tratta di raccogliere i soldi per i premi con un sistema di “offerte volontarie”, una colletta insomma, ma non una colletta banale. Una raccolta di fondi inusuale che vi permetterà anche di accendere una discussione interessante.
“Materiali” necessari:
– un organizzatore del gioco: solitamente è colui/colei che ospita gli amici;
– un gruppo di amici;
– buste, foglietti e penne quanti sono i partecipanti al gioco;
– chi organizza il gioco deve controllare di avere a portata di mano un bel po’ di euro, per integrare le offerte, come previsto dal gioco.
Preparazione
Piuttosto facile, basta leggersi le istruzioni. Svolgimento L’organizzatore legge le istruzioni che si trovano nella prossima sezione. Dopo averle lette ed aver fornito le eventuali precisazioni richieste, può far partire il gioco: ogni giocatore sarà invitato a scrivere sul suo foglietto, segretamente, la sua offerta. I foglietti devono essere numerati, in modo che alla fine del gioco sia possibile identificare le offerte di ciascuno.
Istruzioni
La proposta è la seguente: chi vuole partecipare alla tombola mette dentro una busta (senza essere visto dagli altri) un foglio il quale indica la sua offerta, da 0 a 10 euro a sua scelta, per i premi da assegnare a chi vince alla tombola. Al ricavato complessivo l’organizzatore aggiungerà di tasca sua una cifra pari alla somma raccolta.
I partecipanti devono essere almeno tre, ma più sono meglio è!
Varianti e chiacchiere finali
Il range da 0 a 10 euro può naturalmente essere allargato o ristretto, a seconda di come si ritenga più opportuno. Non c’è nessun problema a fissare come limite massimo 5, o anche 3. Volendo, si può organizzare questa colletta per ogni partita di tombola. Oppure invece di soldi si può trattare di caramelle, o di altro. Non è obbligatorio usare soldi. Anziché alla tombola, lo si può applicare ad un acquisto di gruppo: i fuochi d’artificio o i botti (legali, s’intende!) per fine d’anno. O per comprare beveraggi. O per fare un’opera di beneficenza… o vedete voi.
Fa parte del divertimento discutere alla fine di quanto uno ha messo, del perché e percome.
Spiegazione
Questa non è altro che una delle tante possibili versioni di un gioco critico, molto studiato sperimentalmente in teoria dei giochi, e che va sotto il nome del problema delle “voluntary contributions”. Esso mostra le difficoltà di natura “fondamentale” che si frappongono alla realizzazione partecipata di un progetto pubblico.
Dal punto di vista della “spiega” tecnica, del giochino, il fatto cruciale è il seguente, che descriviamo con un esempio (il matematico, se presente, potrà tradurre in formule generali, a richiesta).
Cosa succede se uno offre 0 (zero). Immaginiamo che ci siano in tutto 8 giocatori e che la cifra raccolta, grazie alle offerte fatte, sia 36. Con l’integrazione dell’organizzatore, il premio totale per chi vincerà è di 72 euro. Visto che le probabilità di vincere sono uguali per tutti, ogni partecipante avrà un guadagno atteso pari a 72/8, e quindi pari a 9. Cosa sarebbe successo se, invece di offrire 0, il tizio avesse offerto, poniamo, 4? La somma totale raccolta sarebbe salita a 40, e quindi il premio a 80 euro: pertanto la quota attesa di premio da ognuno sarebbe salita a 80/8, cioè 10. Il discorso è quindi semplice: offrendo 4 euro anziché 0 uno si aspetta mediamente un guadagno di 10 anziché 9. Un bel “guadagno”, non c’è che dire. Insomma, individualmente, meno ci si mette meglio è. Però…
Però, se tutti offrono 0, ricavano 0. Se tutti offrono 10, ricavano mediamente 20, grazie al contributo generosamente offerto dall’organizzatore!
Siamo quindi di fronte a un caso tipico in cui si ha un conflitto tra interesse individuale e interesse collettivo. E’ un problema che si incontra nel contesto del finanziamento di beni pubblici. Un maggior contributo all’opera darebbe un “ritorno” individuale maggiore: il guaio è che, per la caratteristica tipica delle opere pubbliche, ne usufruiscono in ugual misura chi ha contribuito (poco o tanto che sia) così come chi non ci ha messo niente. Da qui l’interesse per questo gioco, che a suo tempo è stato dibattuto un bel po’ anche sul forum di matematicamente.it, nella sezione di teoria dei giochi.
![]() Scarica l’articolo nel formato PDF.
Scarica l’articolo nel formato PDF.
Discuti di questo gioco sul Forum di Teoria dei giochi.
Se hai sperimentato il gioco raccontaci come è andata. Scrivici la tua opinione.
 Numeri al posto di lettere.
Numeri al posto di lettere.
Pagina Web creata con Crossword Compiler.
Scarica il gioco in formato RTF.
 Cruciverba con i numeri al posto delle lettere.
Cruciverba con i numeri al posto delle lettere.
Pagina Web creata con Crossword Compiler.
Scarica il gioco in formato pdf.
 Cruciverba tematico piuttosto impegnativo con molte definizioni prese nell’ambito della matematica.
Cruciverba tematico piuttosto impegnativo con molte definizioni prese nell’ambito della matematica.
 Hai buona memoria geometrica? Osserva il poligono che ti viene proposto su una lavagna e prova a ridisegnarlo a memoria. Attenzione non è importante la posizione quanto la forma e gli angoli.
Hai buona memoria geometrica? Osserva il poligono che ti viene proposto su una lavagna e prova a ridisegnarlo a memoria. Attenzione non è importante la posizione quanto la forma e gli angoli.
 I vincitori del premio Peano, il trio di Rudi Mathematici ci riprova con un nuovo libro che racconta di matematica in modo originale. Un viaggio in Svizzera tra le montagne è l’occasione per i tre autori di parlare di cosa scrivere nel libro, il tema è la teoria dei giochi e tutte le sue implicazioni nella vita sociale, economica e quant’altro. Alla fine del viaggio il taccuino degli appunti è stracolmo, basta metterlo in forma elettronica. Sara andata così?
I vincitori del premio Peano, il trio di Rudi Mathematici ci riprova con un nuovo libro che racconta di matematica in modo originale. Un viaggio in Svizzera tra le montagne è l’occasione per i tre autori di parlare di cosa scrivere nel libro, il tema è la teoria dei giochi e tutte le sue implicazioni nella vita sociale, economica e quant’altro. Alla fine del viaggio il taccuino degli appunti è stracolmo, basta metterlo in forma elettronica. Sara andata così?
Un’idea per fare un regalo di Natale ad amici amanti della matematica
http://www.ibs.it/code/9788895526126/clerico-rodolfo/rudi-ludi.html
 Diario di bordo di un’esperienza didattica relativa al progetto M@tabel. I nodi concettuali a cui questa esperienza fa riferimento sono: • I numeri naturali e le loro proprietà • Traduzione dal linguaggio naturale al linguaggio dell’algebra; formalizzazione • Congetture • Calcolo automatico con Excel • Differenza tra verifica in un numero finito di casi e dimostrazione in generale • Ricerca di controesempi.
Diario di bordo di un’esperienza didattica relativa al progetto M@tabel. I nodi concettuali a cui questa esperienza fa riferimento sono: • I numeri naturali e le loro proprietà • Traduzione dal linguaggio naturale al linguaggio dell’algebra; formalizzazione • Congetture • Calcolo automatico con Excel • Differenza tra verifica in un numero finito di casi e dimostrazione in generale • Ricerca di controesempi.
Scarica il file direttamente da qui https://www.matematicamente.it//didattica/Todisco-diario_bordo.pdf
 Nato a Siracusa nel 287 a.C. Archimede è considerato uno dei più grandi matematici di tutti i tempi (Es. studi sulle aree e sui volumi – Noli turbare circulos meos.) anche se molti sono i suoi contributi alla fisica (Es. trattato sui galleggianti – Eureka!), alla meccanica (Es. il principio della leva – da mihi ubi consistam et terram movebo.) e all’ingegneria (Es. la vite senza fine per sollevare l’acqua).
Nato a Siracusa nel 287 a.C. Archimede è considerato uno dei più grandi matematici di tutti i tempi (Es. studi sulle aree e sui volumi – Noli turbare circulos meos.) anche se molti sono i suoi contributi alla fisica (Es. trattato sui galleggianti – Eureka!), alla meccanica (Es. il principio della leva – da mihi ubi consistam et terram movebo.) e all’ingegneria (Es. la vite senza fine per sollevare l’acqua).
Alla fine del 1800 ricomparve un suo palinsesto (Codice C) poi nuovamente scomparso per riapparire alla fine dello scorso secolo e ribattezzato da Netz e Noel nel loro libro : "Il Codice perduto di Archimede".
Sembra che Archimede non solo anticipasse, con il metodo di esaustione, il calcolo infinitesimale di Newton e Leibnitz, ma che anche anticipasse concetti della teoria degli insiemi (la corrispondenza biunivoca degli elementi e l’infinito in atto di Cantor) e, nello Stomachion, il calcolo combinatorio.
Resta da comprendere perché gli studi e gli eccezionali risultati ottenuti da Archimede ebbero qualche successo solo con gli scienziati e gli ingegneri alessandrini (Ctesibio, Erone, ecc.), ma in generale non ebbero seguito né nel mondo romano, né nel medio evo né nel rinascimento italiano (la matematica di Leonardo da Vinci era molto inferiore a quella di Archimede).
Alla fine dello scorso secolo per il collegamento tra la Calabria e la Sicilia fu proposto un progetto denominato "Il ponte di Archimede". Si trattava di tre grossi tubi (due per le auto e uno per i treni) da ancorare sul fondo del mare in modo da collegare la Calabria con la Sicilia: la soluzione sarebbe stata meno rischiosa e a minor impatto ambientale del ponte sullo stretto e meno costosa di un passaggio subalveo del tipo dell’Eurotunnel sotto la Manica.
Il canale che collega in Scozia Glasgow ad Edinburgo per superare vari dislivelli funzionava, come molti altri canali, con una serie di chiuse a scala. Nel 2002 è entrata in funzione una gigantesca ruota ad acqua bilanciata, funzionante in base al principio della leva di Archimede: il sistema consente un più veloce transito dei battelli ed un notevole risparmio energetico.
Gli specchi ustori, con cui si racconta Archimede tenesse a bada la flotta romana che assediava la sua città, ebbero un revaival negli ultimi anni con le ricerche (tra i pionieri l’italiano Carlo Rubbia) sul solare termodinamico. In pratica specchi parabolici concentrano i raggi solari su tubi in cui scorrono nitrati di sodio e potassio che raggiungono la temperatura di 550° C. Attraverso degli scambiatori di calore viene generato del vapore acqueo che fa funzionare le turbine per generare elettricità.
Nel 2006 in Sardegna (Olbia) fu ritrovata una ruota dentata epicicloidale appartenente ad un ingranaggio del III secolo a.C. che faceva parte, probabilmente, di una macchina per il calcolo delle posizioni dei pianeti (astrolabio). La forma arrotondata (e non triangolare) dei denti ha fatto comprendere che ad Archimede e agli ellenisti fosse nota una matematica ritenuta, in precedenza, solo moderna. Probabilmente i copisti medioevali non riproducevano quello che non capivano e questo spiegherebbe perché tanta matematica fu reinventata solo con la rivoluzione scientifica del 1600.
 La Terra rallenta, il Naval Observatory di Washington e International Earth Rotation and Reference Systems Service hanno deciso di allungare di un secondo quest’anno. Esattamente il 31 dicembre 2008 ci sarà da contare un secondo in più. Come faremo il conteggio alla rovescia per stappare lo spumante e sparare per primi i fuochi d’articificio? Tenendo conto che quest’anno è stato anche bisestile … e che le cose non stanno andando tanto bene, probabilmente il 2008 passerà alla storia come l’anno più lungo.
La Terra rallenta, il Naval Observatory di Washington e International Earth Rotation and Reference Systems Service hanno deciso di allungare di un secondo quest’anno. Esattamente il 31 dicembre 2008 ci sarà da contare un secondo in più. Come faremo il conteggio alla rovescia per stappare lo spumante e sparare per primi i fuochi d’articificio? Tenendo conto che quest’anno è stato anche bisestile … e che le cose non stanno andando tanto bene, probabilmente il 2008 passerà alla storia come l’anno più lungo.
Le Coordinate Universali del tempo (UTC) saranno le seguenti:
31 DEC 2008 23 HOURS 59 MINUTES 59 SECONDS
31 DEC 2008 23 HOURS 59 MINUTES 60 SECONDS
01 JAN 2009 00 HOURS 00 MINUTES 00 SECONDS
L’aggiunta di un ulteriore secondo è stata effettuata l’ultima volta alla fine del mese di Dicembre 2005; la prossima volta che si presentarà tale "anomalia" sarà il 31 Dicembre 2008, dunque l’anno 2008 durerà esattamente 366 giorni (il 2008 è bisestile) composti da 24 ore ciascuno + 1 secondo che verrà conteggiato dall’orologio atomico, nel seguito denotato con UTC, alle ore 23:59:59 del 31 Dicembre 2008, facendo seguire alle 23:59:59 le 23:59:60 e quindi le 0:00:00 del 1 Gennaio 2009.
La necessità di tale aggiustamento è dovuta al fatto che il secondo, nel corso degli anni, ha avuto dei cambiamenti di definizione.
Infatti storicamente il secondo è definito come la 86.400-ma parte del giorno solare medio. Varie altre definizioni più accurate sono state date nel corso degli anni, fino alla definizione attualmente in uso data nel 1967 al "Thirteenth General Conference on Weights and Measures": il secondo viene definito come la durata 9.192.631.770 periodi di emissione di radiazione corrispondenti alla transizione tra due livelli dello stato fondamentale dell’atomo di cesio 133.
Il pianeta Terra è invece continuamente sottoposto a accelerazioni e decelerazioni della propria rotazione e dunque la definizione storica di secondo diventa meno attendibile rispetto a quella atomica. A causa di ciò ogni tanto si necessita di un aggiustamento della durata dell’anno per aggiustare l’eventuale differenza che si accumula giorno per giorno che è appunto dovuta ad una definizione di secondo che non tiene più conto della rotazione terrestre. A
ttualmente la Terra viaggia con un ritardo pressochè costante, rispetto al tempo misurato con l’UTC, di 2 milli-secondi al giorno, per cui ogni 500 giorni circa si necessita di un aggiustamento di circa 1 secondo da aggiungere all’anno in corso.
La prima aggiunta del secondo è stata introdotta nel 1972. Vi sono anche altre unità di misura di tipo temporale che non vengono aggiustate nel corso degli anni; ad esempio il TAI, che ha come unità di misura 1 secondo UTC al livello del mare, non viene aggiustata come l’UTC. Il sistema GPS ancora è un esempio di sistema che è stato sincronizzato con l’orologio UTC ma che non viene aggiustato con il secondo aggiuntivo. Per maggiori dettagli si veda http://tycho.usno.navy.mil/leapsec.html.