Equazioni differenziali del primo ordine
Definizione. Una equazione differenziale del primo ordine è una relazione tra una variabile indipendente $ x $, una funzione incognita $ y $ e la sua derivata prima $ y’ $: \[ f(x; y; y’) = 0 \]
Esempi di equazioni differenziali
Sono equazioni differenziali del primo ordine le seguenti equazioni
- \( y’ + 2x = 1 \)
- \( y’ = y\sin x + \sin x \)
- \( y’ – y = 1 \)
- \( y’ = 2xy – x \)
Osserviamo che non è necessario che compaia anche la funzione incognita $ y $.
Poiché la derivata di una funzione si può espremere come il rapporto di differenziali, l’equazione differenziale:
\( y’ + 2x = 1 \)
diventa:
\( \frac{dy}{dx} + 2x = 1 \)
Equazioni differenziali del secondo ordine
Definizione. Una equazione differenziale del secondo ordine è una relazione tra una variabile indipendente $ x $, una funzione incognita $ y $, la sua derivata prima $ y’ $ e la sua derivata seconda $ y’’ $.
Un’equazione differenziale del secondo ordine, quindi, è del tipo: \[ f(x; y; y’; y”) = 0 \]
Esempi di equazioni differenziali del secondo ordine
- \( 5x + y” = y’ \)
- \( y” – 4y + 4x = 0 \)
- \( y” – 3y = e^{3x} \)
Notiamo che, anche in questo caso, non è necessaria la presenza del termine $ y $, affinché si possa parlare di equazione differenziale del secondo ordine; è invece necessario, ovviamente, che compaia la derivata seconda della funzione da cercare.
Equazioni differenziali dell’ennesimo ordine
In generale, possiamo definire equazioni differenziali di qualsiasi ordine come relazioni tra una variabile indipendente x, una funzione incognita $ y $ e le sue derivate successive fino a quella di ordine $ n $: \[ f(x; y; y’; \ldots; y^{(n)}) = 0 \]
Notiamo, quindi, che l’ordine di un’equazione differenziale è dato dall’ordine della derivata di ordine massimo che vi compare.
In particolare, un’equazione differenziale è considerata del primo ordine se al suo interno compare il termine $ y’ $, mentre non è necessario che compaiano anche $ x $ e $ y $; allo stesso modo, un’equazione del secondo ordine è tale se vi compare $ y’’ $, mentre i termini $ x $, $ y $, $ y’ $ possono non comparire.
Inoltre, come nelle equazioni algebriche, anche nelle equazioni differenziali possono comparire, oltre alle lettere che indicano la variabile indipendente e le incognite, altre lettere, che costituiscono dei parametri, cioè delle costanti il cui valore può non essere specificato.
Integrale di una equazione differenziale
Consideriamo una generica equazione differenziale di ordine $n$: \[ f(x; y ; y’; \ldots; y^{(n)}) = 0 \]
Una funzione di equazione $ y = f(x) $ si dice soluzione, o integrale particolare dell’equazione se, sostituendo la sua espressione a quella delle derivate nell’equazione differenziale, si ottiene un’identità.
Esempio di soluzione di una equazione differenziale
L’equazione differenziale \( y’ – 6x = 0 \) ha per soluzione la funzione \( y = 3x^2 \). Infatti \( y = 3x^2 \rightarrow y’ = 6x \), andando a sostituire questo $ y’ $ nella equazione assegnata si ha che l’equazione è verificata.
Tuttavia, la soluzione non è unica, infatti sono soluzione anche le funzioni \( y = 3x^2 + 1 \), \( y = 3x^2 + 2 \), ecc. Sono, cioè, soluzioni tutte le funzioni del tipo \( y = 3x^2 + c \) con $ c $ un numero reale qualsiasi.
La soluzione generale, o integrale generale, di un’equazione differenziale è un’equazione del tipo: \[ y = f(x; c_1; c_2; \ldots; c_n) \]
per la quale, qualunque siano i valori reali che si sostituiscono ai parametri $ c_1, c_2, \ldots, c_n $, l’equazione che si ottiene da essa è quella di una funzione che è soluzione dell’equazione differenziale di partenza, e viceversa: se l’equazione di ogni funzione dell’equazione differenziale si può ottenere dalla precedente per determinati valori dei parametri $ c_1, c_2, \ldots, c_n $.
In generale, per esprimere le soluzioni di un’equazione differenziale di ordine n, occorrono $ n $ parametri.
In particolare, l’integrale generale di un’equazione differenziale del primo ordine si può esprimere da un’equazione del tipo: \[ y = f(x; c) \]
mentre, per quanto riguarda le equazioni differenziali del secondo ordine, le soluzioni generali sono della forma: \[ y = f(x; c_1; c_2) \]
Osserviamo che la soluzione generale di un’equazione differenziale è data in funzione di alcuni parametri. Per individuare i valori numerici di questi parametri e di conseguenza trovare la funzione specifica per risolvere l’equazione, sarà necessario conoscere delle condizioni cui deve soddisfare la soluzione. In particolare, poiché per gli integrali del primo ordine vi è un solo parametro, si ha bisogno di una sola informazione, mentre per quelli del secondo ordine, in cui sono presenti due parametri, sono necessarie almeno due condizioni.
Si dice che la curva del grafico di una funzione che è soluzione di un’equazione differenziale è una curva integrale di tale equazione.


 Si dice che la curva $ f(x) $ ha nel punto $ P $ di coordinate $ (c ; f(c)) $
Si dice che la curva $ f(x) $ ha nel punto $ P $ di coordinate $ (c ; f(c)) $  Si dice che la curva $ f(x) $ ha nel punto $ P $ di coordinate $ (c ; f(c)) $ concavità rivolta verso il semiasse negativo delle $ y $ se esiste un intorno del punto $ c $ per tutti i punti del quale (escluso il punto $ x = c $) le ordinate dei punti sulla curva sono minori delle ordinate dei corrispondenti punti sulla tangente in $ P $.
Si dice che la curva $ f(x) $ ha nel punto $ P $ di coordinate $ (c ; f(c)) $ concavità rivolta verso il semiasse negativo delle $ y $ se esiste un intorno del punto $ c $ per tutti i punti del quale (escluso il punto $ x = c $) le ordinate dei punti sulla curva sono minori delle ordinate dei corrispondenti punti sulla tangente in $ P $.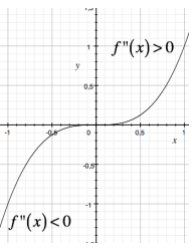 La funzione in questione, quindi, nei due intorni di $ c $ (destro e sinistro), volge concavità differenti: verso il basso da una parte, e verso l’altro dall’altra. Il punto $ c $ che ha queste proprietà viene definito
La funzione in questione, quindi, nei due intorni di $ c $ (destro e sinistro), volge concavità differenti: verso il basso da una parte, e verso l’altro dall’altra. Il punto $ c $ che ha queste proprietà viene definito 