Modulo per il calcolo dell’intervallo di tempo in giorni fra due date del calendario.
Scarica il file in formato XLS
Modulo per il calcolo dell’intervallo di tempo in giorni fra due date del calendario.
Scarica il file in formato XLS
Modulo per il calcolo approssimato degli istanti dell’alba e del tramonto solare.
Scarica il file in formato XLS
Modulo per il calcolo del giorno secondo il calendario giuliano.
Scarica il file in formato XLS
Calcolo della distanza tra due punti della Terra.
Scarica il file in formato XLS
Il procedimento con il quale le coordinate geografiche (latitudine e longitudine) sono trasformate da una sfera tridimensionale in una mappa piana bidimensionale è chiamato proiezione cartografica. La branca della scienza che si occupa della effettuazione di tali proiezioni prende il nome di cartografia.
Le dimensioni dei continenti, degli oceani, dei paesi e le loro distanze vengono tutte modificate quando sono trasformate in quelle corrispondenti su di una superficie piana.
Un metodo comune di classificazione delle proiezioni su mappe bidimensionali è quello di raggrupparle secondo il tipo di superficie sulla quale la sfera è stata proiettata: cilindrica, conica e azimutale. Questa classificazione fornisce un vantaggioso sistema per visualizzare e comprendere il processo di trasformazione.
Nelle proiezioni cilindriche, le distorsioni diventano sempre più considerevoli con l'aumentare della distanza dei punti considerati dall'equatore, come mostrato nel seguente disegno. Si noti come le aree trasformate risultano più grandi man mano che ci si sposti verso latitudini più alte.
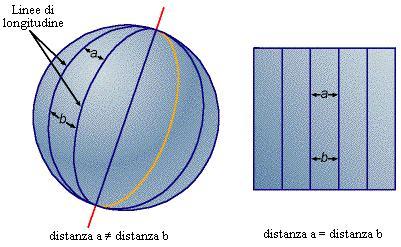
Una proiezione azimutale viene spesso usata per mappe con forme circolari o quadrate. E' costruita proiettando punti della sfera su un piano tangente alla sfera in un punto, spesso situato ad uno dei due poli della Terra.
Una proiezione conica è particolarmente adatta per mostrare aree situate alle latitudini medie, con estensione da est a ovest (per esempio gli Stati Uniti). Questa proiezione si ottiene sviluppando su un piano la superficie laterale di un cono retto, tangente alla sfera lungo un parallelo o secante questa secondo due paralleli.
Tutte queste varie proiezioni possono essere rappresentate con semplicità, riportando latitudine e longitudine (coordinate sferiche) su di un piano XY (coordinate Cartesiane). E' davvero facile costruirle con Mathcad.
Per prima cosa, leggiamo un ampio insieme di dati (circa 7000 punti!) di longitudini e latitudini nella variabile
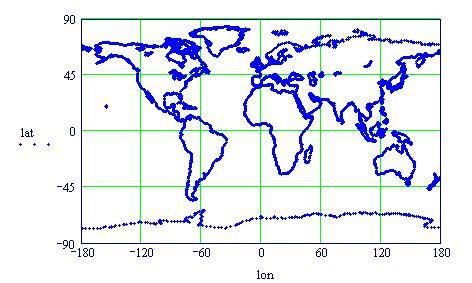
Siccome latitudine e longitudine di un luogo sono solamente le sue coordinate sferiche, per disegnare i nostri dati sulla superficie di un globo in tre dimensioni, abbiamo bisogno di convertirli da coordinate sferiche a coordinate Cartesiane (x,y,z):
Se volessimo far ruotare il globo attorno all'asse, che unisce Polo Nord e Polo Sud, possiamo utilizzare una matrice di rotazione con parametro:
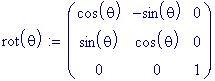
Variando il valore dell'angolo di rotazione q vedremo il globo ruotare

Indice
1 Meridiane Solari: un’interpretazione geometrica
1.1 Che cos’è una meridiana solare
1.2 Arco diurno solare
1.3 Tipi di meridiane
1.3.1 L’ombra proiettata dallo stilo e le diverse numerazioni orarie
1.3.2 Meridiane Orizzontali con gnomone parallelo all’asse terrestre
1.3.3 Meridiane Orizzontali con gnomone perpendicolare a terra
1.3.4 Meridiane Verticali con gnomone parallelo all’asse terrestre
1.3.5 Meridiane Verticali con gnomone perpendicolare al muro
1.3.6 Declinazione parete e piano inclinato
2 Simulazione di meridiana con Matlab
3 Un esempio di meridiana reale
4 Qualche motto
Bibliografia
1.1 Che cos’è una meridiana solare
Per meridiana solare intendiamo un orologio in grado di indicare l’ora, giorno per giorno, anno per anno sfruttando l’ombra di uno stilo proiettata su di un piano (verticale, orizzontale o inclinato) dal Sole durante il suo moto apparente diurno (e annuale) nella Sfera Celeste.
Fin dall’antichità l’uomo ha cercato di misurare il tempo per i motivi più svariati come individuare specifici periodi dell’anno: per effettuare la semina, il raccolto, per fare previsioni di eclissi, di inondazioni, oroscopi,… sfruttando le tecniche più disparare, si pensi ai monoliti di Stonehenge del II millenio a.C. che permettevano di segnalare i cambi di stagione, agli obelischi egizi, ai giganteschi gnomoni indiani e cinesi che venivano usati anche per prevedere le eclissi.
Gli annali cinesi raccontano infatti che nel 2169 a.C. gli astronomi imperiali Ho e Hi sotto il regno di Ciu-Kang vennero giustiziati mediante decapitazione per non essere stati in grado di prevedere l’eclissi di Sole verificatasi quell’anno (la prima che sia stata registrata nella storia dell’astronomia).
Non bisogna dimenticare il ruolo divino ricoperto dal Sole presso molte popolazioni per la sua luce, il suo calore e le caratteristiche fisiche che hanno impressionato tutti i popoli dell’antichità facendo sbocciare veri e propri culti religiosi.
Le meridiane possono essere solari, lunari o astronomiche; tutte servono per scandire il corso del tempo, nella trattazione che segue ci occuperemo delle meridiane solari.
Il termine tempo deriva dal greco t’emno e dal latino temperare, entrambi significano l’atto con cui qualcosa è diviso secondo ordine e misura.
Scarica l’articolo completo sulle meridiane
Laurea specialistica in matematica
Lo studio del gruppo delle trecce e delle sue applicazioni inizia negli anni venti del Novecento, a opera di Emil Artin. Il gruppo delle trecce Bn, presentato in termini di n generatori e opportune relazioni, è un gruppo non abeliano di ordine infinito e pertanto lo studio delle sue rappresentazioni richiede l’impiego di tecniche più sofisticate di quelle utilizzate per i gruppi finiti. Il presente lavoro riguarda proprio l’analisi comparativa di diverse rappresentazioni di Bn e il loro utilizzo per costruire invarianti polinomiali dei nodi. Il gruppo delle trecce compare infatti in modo naturale nella teoria matematica dei nodi, in quanto ogni nodo immerso nello spazio t ridimensionale può essere ottenuto come chiusura di una treccia aperta – rappresentata geometricamente come una collezione di n stringhe intrecciate, i cui estremi superiori e inferiori sono fissati su due dischi paralleli (teorema di Alexander).
Il problema di maggior interesse, rimasto irrisolto per molti decenni, riguarda la linearità dei gruppi delle trecce, vale a dire la ricerca di una rappresentazione fedele di Bn in un gruppo di matrici su un anello commutativo. Nel 1935 Werner Burau introdusse una rappresentazione (n−1)-dimensionale lineare non banale, che per lungo tempo fu considerata un buon candidato per una rappresentazione fedele (si mostra infatti che questa rappresentazione è fedele per n <= 3). Solo alla fine degli anni Novanta è stato realizzato che la rappresentazione di Burau non è fedele per n >= 5 (lasciando aperto l’unico caso n = 4).
Ruth Lawrence nel 1990 ha introdotto una rappresentazione del gruppo delle trecce, dipendente da due variabili, che nel 2000 Daan Krammer ha dimostra-to essere fedele per n = 4 (in realtà la costruzione di Krammer è di tipo algebrico, mentre quella della Lawrence è di tipo topologico). Nel 2001 Stephen Bigelow è riuscito a provare, attraverso una nuova costruzione di natura topologica, che la rappresentazione di Lawrence-Krammer è fedele per ogni n e, quindi, il gruppo delle trecce risulta essere lineare. Il problema a lungo rimasto aperto ha trovato cos’ı una soluzione definitiva.
Questa tesi si ispira al contributo fondamentale di Stephen Bigelow ed è finalizzata a chiarire i legami tra le costruzioni algebrica e topologica della rappresentazione di Lawrence-Krammer e a mettere in luce aspetti relativi alla costruzione di invarianti polinomiali dei nodi.
Dopo aver introdotto la definizione di gruppo delle trecce, le sue relazioni con il mapping class group e con il gruppo libero su n generatori, nel secondo capitolo viene richiamata la rappresentazione di Burau nonché i risultati sulla sua non fedeltà.
Nel terzo capitolo si analizzano in modo critico i risultati riguardanti la rappresentazione di Lawrence-Krammer. In particolare nel paragrafo 3.6 viene presentato uno schema generale in cui si inseriscono le rappresentazioni di Burau e Lawrence-Krammer; tale schema si basa sul fatto che il gruppo delle trecce Bn agisce fedelmente come gruppo degli automorfismi del gruppo libero su uno stesso numero di generatori.
Nel capitolo 4, sulle algebre di Hecke, viene riconosciuto come la rappresentazione di Burau sia in relatà una rappresentazione del gruppo delle trecce in un’opportuna algebra di Hecke. Sull’algebra si introduce una funzione traccia che, nel caso della rappresentazione di Burau, risulta corrispondere all’invariante di Alexander per i nodi.
Nel capitolo 5, l’algebra di Birman-Murakami-Wenzl (BMW) è dapprima considerata relativamente al suo legame con l’algebra di Hecke: si costruisce infatti una decomposizione di tale algebra, che contiene una sottoalgebra isomorfa all’algebra di Hecke. Nella seconda parte del capitolo si mostra, riprendendo i lavori di Matthew Zinno, che la rappresentazione regolare dell’algebra BMW è irriducibile e coincide con la rappresentazione di Lawrence-Krammer del gruppo delle trecce, discussa nel terzo capitolo.
Nel capitolo finale si forniscono i minimi prerequisiti per comprendere il legame tra trecce e nodi (collezione di curve chiuse e semplici nel 3-spazio). Le costruzioni algebriche delle tracce sulle algebre di Hecke e BMW, esaminate nei capitoli precedenti, vengono esplicitamente legate al polinomio HOMFLY (traccia sull’algebra di Hecke) e al polinomio di Kauffman (ricavato dalla funzione traccia sull’algebra BMW). Entrambi questi polinomi dipendono da due variabili e si riferiscono rispettivamente a nodi orientati e non orientati. Viene proposta un’analisi originale delle relazioni tra questi due tipi di invarianti, mettendo in luce il ruolo della rappresentazione di Lawrence-Krammer, non sufficientemente chiarito in letteratura.
La tesi è corredata di un’appendice con richiami sulla teoria delle rappresentazioni del gruppo simmetrico, la cui algebra di gruppo è il punto di partenza per le costruzioni delle rappresentazioni del gruppo delle trecce nelle algebre di Hecke.
In questo lavoro non vengono affrontate le numerose applicazioni della teoria delle rappresentazioni del gruppo delle trecce, che in realtà sono estremamente importanti in Fisica teorica ed in particolare nella teoria quantistica dei campi. Rappresentazioni unitarie del gruppo delle trecce compaiono infatti nelle teorie di campo conforme bidimensionale (holonomy representations e rappresentazioni basate sulla matrice R) e nella teoria di campo topologica tridimensionale del tipo Chern-Simons1. In tali teorie, il polinomio HOMFLY, valutato per opportuni valori delle variabili, risulta essere la più generale osservabile fisica, ottenuta come valore di aspettazione quantistico di operatori chiamati “Wilson loops”.
Si osservi infine che problemi algoritmici legati al gruppo delle trecce (problema della parola, problema della coniugazione) sono ingredienti fondamentali di sistemi crittografici, come ad esempio il BCKE (Braid Group Commutator Key Exchange); si stanno attualmente analizzando protocolli che utilizzano le matrici della rappresentazione di Lawrence-Krammer.
Scarica la tesi
https://www.matematicamente.it//tesi/Paganini-Gruppo_trecce.pdf
Laurea in Informatica
La matematica si è sempre interessata allo studio dei numeri primi, cercando di evidenziarne le proprietà e accentuarne le differenze con gli altri numeri inteti, detti composti.
Oggi, molte di queste caratteristiche sono ancora da formalizzare e rimangono delle congetture. Recentemente è stato risolto un problema, noto in letteratura come "PRIMES" e che consiste nel trovare un algoritmo efficiente per testare la primalità di un numero. In realtà, l'interesse sull'efficienza computazionale si è diffuso solo negli anni sessanta con l'avvento dei calcolatori elettronici, ma da parecchi secoli, i matematici si sono cimentati nella produzione di algoritmi di primalità più o meno veloci.
Scarica la tesi
https://www.matematicamente.it//tesi/Durso-Test_primalita.pdf
Laurea in Fisica
Nei rilevatori utilizzati negli esperimenti di fisica nucleare il segnale generato dal passaggio di una particella ionizzante appare come un impulso in tensione o in corrente l’ampiezza di tale impulso è proporzionale all’energia rilasciata dalla particella dentro il rivelatore. Durante l’analisi del segnale si deve prestare attenzione a tutti quei fenomeni che possono modificare la misura dell’ampiezza e del tempo.
Scarica la tesi
https://www.matematicamente.it//tesi/Alberto-Filtraggio_digitale.pdf
Scarica la presentazione PowerPoint
https://www.matematicamente.it//tesi/Alberto-Filtraggio_digitale.pps
Laurea in Ingegneria delle Telecomunicazioni
1.1 Genomic Signal Processing
E’ risaputo che molte delle scoperte scientifiche e tecnologiche che avverranno nel corso del XXI secolo dipenderanno in larga scala dall’essere in grado di processare e interpretare un’enorme quantità di dati.
In questi ultimi anni si è resa necessaria una capacità di gestione e catalogazione sempre maggiore che l’uomo non è più riuscito a garantire: di qui l’importanza del data processing, una nuova frontiera, un nuovo approccio informatico che permette di trattare studi ed esperimenti che generano grandi moli di dati.
Nel campo della genetica, ad esempio, settore di ricerca molto vasto e interdisciplinare che va dalla medicina alla biologia, dall’ingegneria all’agricoltura, sta nascendo un nuovo filone atto a gestire e sondare il libro della vita: il Genomic Signal Processing(GSP), il quale deriva dal Digital Signal Processing (DSP). Si tratta di una disciplina ingegneristica che studia il DNA come un segnale qualsiasi: il segnale genomico.
Considerando il ruolo fondamentale, giocato nella genetica, dai segnali di trascrizione, è naturale che la teoria del Signal Processing debba essere utilizzata per ottenere una comprensione sia della parte strutturale che di quella funzionale del fenomeno in questione.
L’obiettivo del GSP è quello di integrare la teoria e i metodi del SP con una globale comprensione della genomica funzionale e con particolare enfasi sulle regolazioni genomiche; in particolar modo abbraccia svariate tecniche di espressione come la scoperta, la predizione, la classificazione, il controllo e la modellizzazione statistica e dinamica delle reti di geni (gene networks).
Nello studio della genetica, il GSP è diventato una disciplina fondamentale checostituisce un modello strutturale basato su analisi e sintesi che sta alla base del rigore matematico ingegneristico [B.2].
Esempi di tecniche mutuate dall’Ingegneria delle Telecomunicazioni sono:
• Digital Signal Processing (sequence spectral analysis, filtering, prediction, image processing);
• Information theory(entropy, source coding, channel coding);
• Networks theory.
Nei capitoli che seguono ci occupiamo dell’analisi di sequenze di DNA mediante tecniche di Teoria dell’Informazione come misurazioni di entropia, numeri medi calcolati con gli algoritmi di Huffman e Lempel-Ziv applicati a sottosequenze individuate con il metodo della sliding window. Ricerchiamo sequenze ridondanti e periodiche ed infine eseguiamo un’analisi spettrale (Power Spectral Density) delle porzioni di DNA considerate. L’obiettivo è individuare le caratteristiche del segnale genetico, come ad esempio la delimitazione tra aree codificanti (che servono per costruire le proteine) e non codificanti.
Nei due paragrafi che seguono vengono introdotti il Progetto Genoma ed i concettidi base della genetica per fare un po’ di luce in questo nuovo campo di applicazione dell’ingegneria.
Scarica la tesi
https://www.matematicamente.it//tesi/Alberto-Studio_proprieta.pdf
Scarica la presentazione PowerPoint
https://www.matematicamente.it//tesi/Alberto-Studio.zip
Laurea in matematica
Scopo di questa tesi è dare una breve ma esaustiva spiegazione del funzionamento dell’algoritmo crittografico Advanced Encryption Standard.
Nei quattro capitoli vedremo, rispettivamente, la “storia” di AES ed i motivi per i quali venne adottato, le basi matematiche richieste per comprendere al meglio l’implementazione e le operazioni dell’algoritmo, la descrizione dettagliata di tutte le operazioni svolte all’interno di AES e, infine, la sua rappresentazione polinomiale.
E’ inoltre presente un’appendice utile come ripasso di alcuni concetti utilizzati nella spiegazione delle basi matematiche, quali le definizioni e le proprietà principali riguardanti anelli, campi e polinomi.
Scarica la tesi
https://www.matematicamente.it//tesi/Capitani-Advanced_Encryption_Standard.pdf
Laurea in Economia marittima e dei trasporti
Questo lavoro tratta sinteticamente alcuni aspetti del problema del cammino minimo in reti urbane. La ristrettezza degli spazi concessi ha fatto sì che il lavoro sia limitato ad un aspetto topico del problema, a mio giudizio importante, ma non unico.
Poiché, secondo le più comuni interpretazioni della riforma dei corsi di laurea, appare che questo “breve elaborato scritto” debba rappresentare una forma di relazione finale con cui lo studente “chiude” il proprio ciclo di studi, ho ritenuto adeguato seguire, durante l’elaborazione di questa tesi, le linee guida apprese dal mio corso di studi.
Ho scelto di trattare una materia matematica per via del personale interesse verso la materia, trovando un ottimo mezzo per unire l’utile al dilettevole.
La ricerca operativa mi ha permesso di unire la mia passione verso la matematica al corso di studi svolto, applicando la stessa al settore dei trasporti.
Ho scelto altresì di fornire un’adeguata introduzione storica all’argomento, ritenendo particolarmente importante questa dimensione della matematica, spesso erroneamente trascurata.
Il primo capitolo introduce la materia, la teoria dei grafi ed il problema del cammino minimo, passando, dall’analisi del problema banale, attraverso l’introduzione di ipotesi e vincoli, allo studio di un problema che rappresenti, in modo il più possibile verosimile, la situazione reale.
Nel secondo capitolo, sono analizzati nel dettaglio tre algoritmi proposti da due ricercatori del dipartimento di ingegneria civile dell’università del Maryland; nel momento in cui questa tesi è scritta, il lavoro dei ricercatori americani è in fase di pubblicazione sul “European Journal of operational research”. Gli algoritmi in questione possiedono un certo grado di sofisticatezza matematica, tale
da richiedere un’analisi approfondita; per questo motivo, e perché lo stesso lavoro rappresenta l’ultimo ritrovato in materia, ho preferito incentrarmi su que-sta “promessa di pubblicazione”. L’innovazione proposta dai due scienziati è stata l’introduzione dell’analisi multicriterio in reti stocastiche e variabili rispetto al tempo.
Nel terzo capitolo sono passato ad analizzare il lavoro svolto da Paola Modesti e Anna Sciomachen nel 1998, che tratta un problema simile da un punto di vistaleggermente diverso.
La mia tesi si risolve quindi con l’analisi delle criticità dei due lavori, con un confronto tra gli stessi e con le considerazioni personali sul problema dell’analisi multicriterio. Questa rappresenta infatti il fulcro del mio lavoro, in cui sono gettati i presupposti per possibili nuovi sviluppi dell’argomento, considerata l’opera di sintesi svolta attraverso la discussione dei lavori analizzati.
Con la speranza che questa conclusione possa tradursi nell’inizio di una nuova affascinante esperienza in ambito matematico.
Scarica la tesi
https://www.matematicamente.it//tesi/Villa-Cammino_minimo.pdf
Laurea specialistica Ingegneria delle Telecomunicazioni
Era generalmente accettata la definizione del telerilevamento come l'insieme di tecniche, strumenti e mezzi interpretativi che permettono di estendere e migliorare le capacità percettive dell'occhio umano, fornendo informazioni qualitative e quantitative su oggetti posti a distanza dal luogo d'osservazione. Le moderne tecniche di telerilevamento hanno ampliato il campo di indagine ben oltre alle informazioni legate allo spettro elettromagnetico comprendendo misure di campi di forze (gravitazionali, magnetico , elettrico) e utilizzando una grande quantità di strumenti (sistemi laser, ricevitori a radio frequenza, sistemi radar, sonar, dispositivi termici, sismografi, magnetometri, gravimetri, scintillatori). Oggi il telerilevamento comprende tecniche di analisi della radiazione elettromagnetica e dei campi di forze finalizzate ad acquisire ed interpretare dati geospaziali presenti sulla superficie terrestre, negli oceani e nell'atmosfera.
Le informazioni raccolte possono distare dall'osservatore da alcuni metri (Proximal Sensing) fino a migliaia di chilometri (Remote Sensing), come nel caso delle osservazioni effettuate dai satelliti. Il veicolo di informazione del telerilevamento generalmente è l'energia elettromagnetica, sia essa proveniente dal sole, emessa dalla terra o generata da strumenti radar o laser. L'energia elettromagnetica che trasporta le informazioni più utili nel campo del telerilevamento applicato allo studio del territorio è quella delle bande del visibile, infrarosso e delle microonde.
Solitamente il rilievo di una superficie effettuato con tecniche di telerilevamento prevede tre fasi distinte: la ripresa dei dati (da aereo, satellite o da terra), la loro elaborazione e l'analisi. Gli strumenti di rilievo utilizzati possono essere distinti in due categorie e cioè quelli che forniscono delle misure, come radiometri, spettrofotometri, scatterometri o altri, e quelli che forniscono delle immagini, cioè macchine fotografiche, dispositivi digitali di scansione, termocamere ecc.. Tutti gli strumenti da ripresa nel gergo tecnico vengono chiamati sensori. Una distinzione che può essere fatta è quella fra strumenti passivi e attivi: gli strumenti passivi misurano le radiazioni (siano esse emesse o riflesse) provenienti dalle superfici investigate mentre gli strumenti attivi provvedono essi stessi alla illuminazione delle superfici, captando poi la radiazione riflessa.
L'insieme di questi strumenti parallelamente alle moderne tecniche di analisi (interferometria SAR, analisi spettrale, alta risoluzione spaziale, etc.) rappresentano un metodo pratico, sistematico ed economico di mantenere ed aggiornare le informazioni sul mondo che ci circonda ed in particolare nei seguenti campi di applicazione:
· Agricoltura: gestione dei processi produttivi, verifiche di dettaglio di appezzamenti e tipologie di colture, inventario e previsione dei raccolti, controllo delle proprietà, valutazione dei danni post-calamità, etc;
· Scienze Forestali: cartografia forestale, gestione demaniale, monitoraggio aree deforestate o percorse da incendi, etc.;
· Geologia e Geologia Applicata: cartografia geologica, esplorazioni marine e terrestri, valutazioni di impatto ambientale, monitoraggio di attività estrattive, subsidenze, movimenti franosi, etc.;
· Topografia e Cartografia Tematica: realizzazione gestione ed aggiornamento della cartografia, pianificazione territoriale, catasto,
controllo dell'abusivismo edilizio, etc. ;
· Ambiente: classificazione multitemporale di uso e coperture del suolo, controllo e gestione dell'ecosistema, valutazioni di impatto ambientale, monitoraggio inquinamento, discariche e rifiuti urbani e industriali, gestione della rete idrica e aree umide, etc.;
· Gestione del Rischio: monitoraggio di frane, subsidenze, alluvioni, vulcani e terremoti e valutazione dei danni, localizzazione di aree
inquinate, pianificazione delle strutture di pronto soccorso, etc.;
· Difesa del territorio: monitoraggio di obiettivi strategici, pianificazione e preparazione di missioni, verifica della pianificazione e degli accordi, controllo dell'industria estrattiva, etc.;· Mare e Aree Costiere: gestione delle coste, fenomeni di erosione costiera, monitoraggio aree glaciali, pianificazione e controllo delle rotte nautiche, presenza di alghe, etc.;
· Telecomunicazioni: pianificazione e supporto delle reti di trasporto e navigazione a scala urbana e internazionale, etc.;
· Media e Turismo: cartografia, pubblicità, educazione, analisi di proprietà, valorizzazione del territorio, etc..
Attualmente, nell'ambito del telerilevamento a microonde, i SAR rappresentano senza dubbio i sensori attivi più affidabili e maggiormente diffusi. Il SAR o Radar ad Apertura Sintetica, sfruttando lungo l'intera rotta di volo i ritorni provenienti da un generico punto a terra, simula di fatto un'antenna di grandi dimensioni fisiche, o, più precisamente, un allineamento di antenne di dimensioni reali posizionate lungo la direzione di volo, consentendo di raggiungere risoluzioni in azimuth molto spinte. Sensori di questo tipo sono stati, infatti, montati sui satelliti ERS1 ed ERS2 (in orbita, rispettivamente, dal 1991 e dal 1995) e sul satellite ENVISAT
nell'ambito del progetto Osservazione della terra, gestito e finanziato da ESA (European Space Agency).
Allo stesso modo la missione COSMO Sky Med, concepita da Alenia Spazio, gestita e finanziata da ASI (Agenzia Spaziale Italiana) e finalizzata al lancio diuna costellazione di sette satelliti con i quali è stato effettuato il telerilevamento ottico e radar su una vasta area del Mediterraneo, ha previsto l'utilizzo di SAR.
L'attività di ricerca nel settore del telerilevamento a microonde ha condotto negli anni scorsi alla ideazione e sviluppo di modelli elettromagnetici appropriati alla simulazione di segnali SAR (Radar ad Apertura Sintetica) e alla relativa stesura di codici numerici di simulazione per diverse modalità operative e per diversi tipi di scena osservata (scene terrestri naturali, urbane, oceaniche). Infatti il progetto di un SAR richiede innanzitutto la presenza di un simulatore numerico che riesca anzitutto a riprodurre il segnale trasmesso dal sensore e diffuso dalla superficie (mappa di riflettività) e poi ad elaborare il segnale diffuso per simulare il reale segnale grezzo ricevuto dal sensore. Per tale motivo la simulazione del segnale grezzo SAR si basa su tre modelli:Modello di superficie, che consente di descrivere la scena a terra;
· Modello di scattering, che essenzialmente consente di ricavare la mappa di riflettività;
· Modello radar, che invece, permette di stimare la funzione risposta impulsiva del sistema SAR, e quindi di calcolare il segnale grezzo tramite una opportuna serie di operazioni con la mappa di riflettività.
In questa tesi non ci si è soffermati sul modello radar e sulle tecniche di acquisizione ed analisi delle immagini telerilevate, bensì sui modelli di superfici naturali e sui modelli di diffusione elettromagnetica trattati entrambi nel capitolo 2; di solito le superfici naturali vengono descritte statisticamente in termini di processi aleatori bidimensionali stazionari con assegnata densità di probabilità (pdf) e funzione di autocorrelazione. In realtà una tale descrizione ha condotto a dei risultati non troppo coerenti con quelli ricavati da misure reali ed è per tale motivo che sono stati introdotti i modelli frattali come l’fbm (moto frazionario browniano) e WM (Weierstrass-Mandelbrot). Per quanto riguarda, invece, i modelli di scattering, ne sono stati sviluppati diversi, basati sulle approssimazioni di Kirchhoff e delle piccole perturbazioni e sul metodo delle condizioni al contorno estese (EBCM), per la valutazione della diffusione da superfici descritte tramite il moto frazionario Browniano o la funzione di Weierstrass-Mandelbrot.
Nel capitolo 2, inoltre, viene evidenziato anche l’uso congiunto dei modelli di superficie e di scattering, che come detto precedentemente stanno alla base di un qualsiasi simulatore numerico (non solo SAR) e che permettono di risolvere quello che va sotto il nome di problema diretto: noti il profilo altimetrico della scena e le caratteristiche elettromagnetiche del terreno (costante dielettrica e conducibilità), viene ricavato il ritorno elettromagnetico (e quindi il coefficiente di backscattering) e successivamente il segnale grezzo tramite un opportuno modello radar.
La ricerca sta ora proseguendo secondo due linee: da un lato, per il calcolo del campo diffuso da tali superfici si cerca di utilizzare nuovi metodi con ambiti di validità più ampi, come ad esempio il metodo dell'equazione integrale (IEM); dall'altro, si stanno valutando i regimi di validità dei modelli già sviluppati.
Una ulteriore linea di ricerca prevede l’impiego dei modelli di diffusionesviluppati nella determinazione di tecniche per la stima dei parametri dielettrici e di rugosità del suolo a partire da misure di campo diffuso: questo è, invece, il problema inverso. In quest’ultimo caso, quindi, a partire ad esempio dalla misura del coefficiente di backscattering si deve risalire, tramite l’implementazione di opportuni algoritmi, ai parametri superficiali. Questo aspetto viene trattato nei capitoli 3 e 4; nel terzo vengono elencati e discussi i principali modelli teorici, empirici e semi-empirici di recupero dei parametri dielettrici e di rugosità presenti in letteratura, mentre nel quarto viene proposto un algoritmo di recupero di parametri classici e frattali da misure di campo diffuso. In particolare la procedura implementata viene applicata in primo luogo a dati simulati con e senza rumore per testarne l’efficienza e poi a dati sperimentali in nostro possesso ed i differenti risultati ottenuti rispettivamente nel caso classico e frattale sono presentati.
Scarica la tesi
https://www.matematicamente.it//tesi/DeRosa-Inversione_parametri.pdf
Scarica la presentazione PowerPoint
https://www.matematicamente.it//tesi/DeRosa-Inversione.ppt
Laurea triennale in Ingegneria delle Telecomunicazioni
Quando una radiazione elettromagnetica incide sulla superficie di un materiale, possono verificarsi fenomeni di riflessione per cui la radiazione stessa può essere rinviata del tutto o in parte nello stesso mezzo dall’interfaccia che separa i due mezzi considerati, fenomeni di diffrazione per cui l’onda elettromagnetica incidente penetra nella zona d’ombra dell’ostacolo stesso a causa ad esempio dell’incidenza su spigoli che provoca onde da cammini multipli, e fenomeni di diffusione per cui la radiazione viene dispersa in tutte le direzioni a causa di particelle sospese presenti nel mezzo attraversato. Tale radiazione dispersa non è altro che il campo diffuso. La conoscenza del campo diffuso è di notevole importanza per lo studio dell’impatto sull’ambiente delle interazioni elettromagnetiche. Negli ultimi anni sono state sviluppate numerose tecniche di telerilevamento che hanno costituito e costituiscono tuttora una risorsa
importantissima per avere notizie su fenomeni naturali di varia natura e di pari rilevanza. Uno dei sistemi piu’ noti per telerilevare i dati è il SAR , acronimo per radar ad antenna sintetica, grazie al quale è possibile poter lavorare in qualsiasi condizione climatica ed indipendentemente dall’ora del giorno e ricavare le proprietà fisiche di una porzione della superficie terrestre a partire dalla
conoscenza del campo diffuso.
Consci di questo fatto, affronteremo in questa tesi un rilevante problema di diffusione elettromagnetica. Come in ogni problema di questo tipo, vanno stabiliti due modelli:
-modello di superficie;
-modello elettromagnetico.
Per quanto riguarda il modello di superficie, sono stati sviluppati modelli classici che descrivono superfici naturali rugose attraverso processi stocastici bidimensionali che presentano una data densità di probabilità (di solito gaussiana) e funzione di correlazione (anch’essa gaussiana per superfici molto rugose o esponenziale per superfici poco rugose o una combinazione di esse). Tali modelli
si scontrano però con la realtà dal momento che sono incapaci ed inadeguati per descrivere le superfici naturali che sono autosimilari, cioè presentano proprietà di invarianza di scala. Per tale motivo viene introdotta la geometria frattale. I modelli frattali piu’ noti per superfici naturali sono il modello WM (Weierstrass-Mandelbrot) e il modello fBm (Fractional Brownian motion). L’fBm è un processo continuo non differenziabile in alcun punto ad incrementi stazionari. Il vantaggio derivante da quest’ultimo è dovuto al fatto che permette di ricavare in forma chiusa e semplice la densità di potenza diffusa (e quindi il coefficiente di backscattering o retrodiffusione) sia sotto l’approccio di Kirchhoff sia con l’utilizzo del modello elettromagnetico SPM (Small perturbation method), sotto particolari limiti di validità da non violare. Lo svantaggio principale è dovuto al fatto che esso non fornisce un’espressione analitica della superficie. Per risolvere tale problema può essere usata un’altra particolare funzione frattale, la WM a banda limitata, che bene approssima l’fBm. Per quanto riguarda il modello elettromagnetico, viene usato il metodo EBCM, acronimo per ”Metodo delle condizioni al contorno estese”.
La tesi è suddivisa in tre capitoli. Nel primo si evidenzia l’importanza della geometria frattale e vengono descritti i vantaggi e gli svantaggi dei due modelli di superfici frattali sopra citati, l’fBm e la WM. Nel secondo viene affrontato il problema della diffusione elettromagnetica da una superficie monodimensionale che separa due mezzi con permittività e permeabilità diverse. Gli esempi numerici vengono mostrati in relazione a una situazione in cui il profilo superficiale separa lo spazio libero da un mezzo dielettrico di permittività dielettrica r e , con le stesse permeabilità. Utilizzando la proprietà della WM di essere quasi-periodica, il campo diffuso e quello trasmesso risultano scritti come sovrapposizione finita di modi di Floquet espressi in termini di matrici di dimensioni infinite. Per poter avere una soluzione numerica del problema bisogna troncare le matrici in gioco.
Viene così mostrato un criterio di troncamento suffragato da varie considerazioni che ne evidenziano la fondatezza e l’efficienza. I risultati cui giungiamo sono in linea con le aspettative teoriche. Nel terzo capitolo, invece, viene affrontato lo stesso problema nel caso bidimensionale, nell’ipotesi in cui lo spazio dielettrico sia sostituito da un conduttore elettrico perfetto. Anche in tal caso il campo diffuso risulta scritto come sovrapposizione di modi e i risultati sperimentaliconfermano l’efficienza del modello usato.
In fondo, invece, vengono riportate delle appendici in cui sono mostrati i programmi realizzati col software Matematica 5.0, usati per testare e avvalorare il metodo implementato.
Scarica la tesi
https://www.matematicamente.it//tesi/DeRosa-Diffusione_da_superfici_frattali.pdf
Scarica la presentazione PowerPoint
https://www.matematicamente.it//tesi/DeRosa-Diffusione.ppt
Laurea in Ingegneria
La sempre maggiore diffusione di dispositivi wireless e il crescente bisogno di sicurezza esigono l’utilizzo di sistemi crittografici che possano soddisfare le stringenti limitazioni imposte, in termini di consumo energetico, utilizzo di banda e capacità elaborativa. L’introduzione della Crittografia basata su Curve Ellittiche (ECC, Elliptic Curve Cryptography) è relativamente recente ma negli ultimi dieci anni tale tecnica si è rapidamente imposta come alternativa ai sistemi crittografici a chiave pubblica già largamente utilizzati come RSA e DSA. La principale attrattiva dell’ ECC è che al momento non esistono algoritmi sufficientemente veloci che risolvano il problema matematico sul quale si basa. Ciò significa che l’ECC offre lo stesso livello di sicurezza dei sistemi tradizionali (RSA, DSA, Diffie-Hellman) utilizzando chiavi di dimensione inferiore, richiedendo così elaborazioni più veloci, consumi energetici contenuti e un risparmio di utilizzo della banda. Tali caratteristiche, quindi, rendono l’ECC particolarmente adatta all’utilizzo in ambienti con limitata disponibilità di risorse: palmari, telefoni cellulari, smart cards.
Obbiettivi e Organizzazione della Tesi. Verrà presentata la Crittografia basata su Curve Ellittiche, analizzando sia gli aspetti teorici che i protocolli utilizzati e soprattutto confrontando questa tecnica con le attuali soluzioni a chiave pubblica.
Considerata la natura dell’argomento, l’esposizione sarà caratterizzata da un taglio necessariamente matematico e formale. Il primo capitolo riprende i concetti base della Crittografia. Il Capitolo 2 presenta i principali sistemi asimmetrici e introduce brevemente l’ECC mentre il terzo descrive le Curve Ellittiche e l’aritmetica ad esse abbinata. Il Capitolo 4 affronta lo studio del problema matematico sul quale si basa l’ ECC, ossia l’Elliptic Curve Discrete Logarithm Problem (ECDLP). Nel Capitolo 5 si analizzano i principali protocolli crittografici basati sulle curve ellittiche. L’ultimo capitolo infine confronta l’ECC con gli altri sistemi a chiave pubblica. In Appendice A sono raccolte le nozioni matematiche fondamentali per la comprensione dell’argomento, l’Appendice B contiene le formule matematiche relative alla regola di addizione su Curve Ellittiche.
Scarica la tesi
https://www.matematicamente.it//tesi/Salvalaggio-Crittografia_basta_su_curve_ellittiche.pdf
Laurea in matematica
Anche se si tratta di un argomento ben noto, ricordiamo l’idea centrale del “programma di Erlangen” di Felix Klein. Un tipo di geometria è assegnato quando sono dati un insieme X (non vuoto) e un gruppo G di trasformazioni su X.
Noti X e G, ci si propone di studiare le proprietà dei sottoinsiemi di X, le quali sono invarianti rispetto alle trasformazioni di G. Spesso X è dotato di una struttura, che determina il gruppo G. Per esempio, se X è dotato della struttura di spazio topologico, è naturale assumere come G il gruppo degli omeomorfismi di X e chiamare topologiche le proprietà dei sottoinsiemi di X invarianti per gli omeomorfismi di G. Si noti che così si inquadra nel “programma di Erlangen” lo studio di un singolo spazio topologico, non lo studio di tutti gli spazi topologici, cosa che si fa invece abitualmente in topologia generale.
Anche assegnato uno spazio ambiente, ci si può porre, però, oltre al problema indicato sopra, anche un problema leggermente diverso. Assegnamo ancora uno spazio topologico X; consideriamo tutti i suoi sottoinsiemi (non vuoti) e tutti i possibili omeomorfismi tra tali sottoinsiemi (non soltanto le restrizioni degli omeomorfismi dell’intero spazio X).
Gli omeomorfismi che consideriamo ora non formano più gruppo; si può parlare di un gruppoide di trasformazioni.
Per le proprietà di sottoinsiemi di X, abbiamo ora due tipi di invarianza:
1) invarianza rispetto ai soli omeomorfismi di X;
2) invarianza rispetto a tutti gli omeomorfismi tra sottoinsiemi di X.
La seconda invarianza implica la prima (tra gli omeomorfismi tra sottoinsiemi di X ci sono, in particolare, le restrizioni degli omeomorfismi di X), ma non viceversa.
Per esempio, si può considerare come X lo spazio euclideo tridimensionale e come proprietà quella di una curva chiusa semplice di essere annodata (con linguaggio più tecnico: la proprietà di un nodo di essere intrecciato). Si tratta di una proprietà invariante nel primo senso, ma non nel secondo. Chiameremo “punto di vista di Klein” lo studio dell’invarianza nel primo caso, “punto di vista di von Staudt” lo studio dell’invarianza nel secondo. L’uso di questo secondo termine è forse un po’ arbitrario: conviene precisare in quale senso sia stato adottato da alcuni autori, nell’ambito della geometria proiettiva.
Nel 1847, venticinque anni prima del “programma di Erlangen”, von Staudt dimostrò che, nel piano proiettivo reale, esiste una e una sola proiettività tra due rette, che trasforma una terna ordinata di punti distinti della prima in una terna ordinata di punti distinti della seconda. È stato poi dimostrato:
a) in un qualunque piano proiettivo P, esiste almeno una proiettività tra due rette che trasforma una terna ordinata di punti distinti della prima in una terna ordinata di punti distinti della seconda;
b) si ha l’unicità se e solo se P è il piano proiettivo su un campo.
Per “punto di vista di von Staudt” si intende, propriamente, lo studio dei legami tra le proprietà di un piano proiettivo P e le proprietà del gruppo delle proiettività su una retta di P. In modo esteso, il termine è stato usato per strutture di incidenza diverse dai piani proiettivi. Con un’estensione ulteriore, e forse eccessiva, nella tesi useremo il termine anche nel senso indicato nel capoverso precedente.
Più in particolare, il contenuto della tesi è il seguente. I primi due capitoli riguardano il “programma di Erlangen” del Klein. Si
tratta di un argomento che si trova spesso esposto nei testi universitari; pertanto, non si è voluto darne una trattazione completa e si è preferito portare l’attenzione su due gruppi di trasformazioni degli spazi euclidei, meno frequentemente citati: il gruppo delle applicazioni bilipschitziane e il gruppo delle trasformazioni cremoniane intere. Entrambi contengono, come sottogruppo, il gruppo delle affinità.
Di conseguenza si inizia l’esposizione, nel primo capitolo, analizzando alcune proprietà invarianti rispetto al gruppo delle affinità, con particolare attenzione alla proprietà che lega la misura di Lebesgue di un insieme alla suddetta collezione.
In seguito, dopo alcuni richiami sulle applicazioni lipschitziane, si introduce la famiglia delle applicazioni bilipschitziane e si studia l’invarianza della dimensione di Hausdorff di un insieme.
Il secondo capitolo è dedicato alle trasformazioni cremoniane, in particolare alle trasformazioni cremoniane intere: alla caratterizzazione di alcune proprietà invarianti, segue la presentazione della “congettura dello jacobiano”.
Si passa poi al “punto di vista” di von Staudt. È sembrato opportuno incominciare con alcuni richiami di geometria proiettiva; questi
rappresentano il contenuto del capitolo successivo: si descrivono tre diverse impostazioni della geometria proiettiva, a cui si fa riferimento per definire le proiettività, le collineazioni e le involuzioni.
La costruzione grafica di un’involuzione permette di caratterizzare le quaterne armoniche: nel quarto capitolo, dopo una breve presentazione di carattere storico, si enuncia un risultato, noto come teorema di Staudt, che lega le proiettività alle corrispondenze staudiane, cioè alle corrispondenze biunivoche che mutano ogni quaterna armonica in una quaterna armonica.
Il quinto capitolo è dedicato alla discussione di alcune proprietà, prevalentemente topologiche, per le quali è possibile distinguere tra “punti di vista” di Klein e di von Staudt.
A conclusione della tesi, si presentano alcune situazioni di invarianza in altri ambiti della Matematica, con casi particolari in cui i due punti di vista coincidono.
Scarica la tesi
https://www.matematicamente.it//tesi/Paganini-Trasfromazione_geometriche.pdf
Laurea in matematica per le scienze dell'ingegneria
Il lavoro di tesi nasce nel contesto della progettazione di reti ottiche di telecomunicazioni di tipo IP (Internet Protocol). Il problema di Network Design consiste essenzialmente nell’ottimizzare la topologia di una rete, ciè nel determinare l’installazione di cavi tra coppie di nodi della rete che minimizzi il costo complessivo e che consenta di soddisfare un insieme di richieste di traffico.
Lo sviluppo di reti di telecomunicazioni di tipo IP è attualmente un problema di grande interesse, in connessione con la corrente e continua espansionedi Internet, nel numero di utenti utilizzatori e di servizi offerti.
Il futuro non può che prevedere sempre maggiori richieste da parte degli utenti, e dunque sarà importante progettare reti sicure e veloci, oltre che in grado di fornire servizi sempre più all’avanguardia.
La strategia di instradamento più utilizzata nelle reti IP è quella OSPF (Open Shortest Path First), secondo la quale ogni pacchetto di dati viene instradato su uno dei cammini minimi fra il nodo di partenza e quello di destinazione, e conseguentemente ogni flusso, costituito da tanti pacchetti di dati, viene suddiviso in parti uguali su tutti i cammini minimi possibili.
La formalizzazione matematica in un modello di Programmazione Lineare Misto-Intera di problemi di Network Design è stata affrontata ampliamente in un precedente lavoro di tesi [5], in cui tra l’altro si è tenuto conto anche della possibilità di studiare reti robuste, ovvero in grado di resistere ad eventuali malfunzionamenti di alcuni archi. In questa tesi si è considerato un modello relativamente più semplice, ma ciononostante sempre di notevole complessità computazionale, ed in particolare si è tentato l’approccio risolutivo con un metodo che si colloca in posizione intermedia fra il Branch and Bound esatto ed i metodi euristici. Si tratta del metodo del Local Branching, descritto ampiamente in [1], che consiste in una successione di soft variable fixing: non vengono scelte manualmente le variabili da fissare, ma è l’algoritmo stesso che decide quali sia più conveniente mantenere costanti e quali invece far variare.
Questo tecnica può essere implementata in Programmazione Lineare grazie all’inserimento di un particolare tipo di taglio, detto taglio di Local Branching, in grado di ridurre ad un piccolo sottoinsieme del politopo originale lo spazio di ricerca delle soluzioni.
Il metodo che ne deriva, pur essendo in linea di principio esatto, si comporta essenzialmente come una meta-euristica, e dunque è in grado di trovare in tempi brevi soluzioni molto prossime all’ottimo, ma senza poterne garantire l’ottimalità. Si propone allora in questa tesi un confronto tra questo metodo innovativo ed il più tradizionale Branch and Bound applicato al problema in esame.
I risultati rispecchiano la grande complessità del problema, che può essere risolto con queste tecniche solo per istanze di 6, 7 nodi, ancora troppo lontane da istanze reali, che dovrebbero tenere in conto almeno 15, 20 nodi. Il Local Branching, opportunamente settato, può però risultare nettamente migliore del Branch and Bound classico, soprattutto quando la ricerca è volta a determinare la migliore soluzione possibile in tempi brevi.
Scarica la tesi
https://www.matematicamente.it//tesi/Cimolin-Ottimizzazione_topologica_reti.pdf
Scarica la presentazione PowerPoint
https://www.matematicamente.it//tesi/Cimolin-Ottimizzazione.ppt
Per definire una funzione ricorsiva bisogna definire il valore iniziale usando l'indice 0.
La nota che le orchestre usano per accordare gli strumenti è il La . Essa corrisponde alla frequenza di 440 Hz. Sotto c'è una rappresentazione di una tastiera con le frequenze relative alla scala armonica che inizia dal Do dell'ottava di mezzo.
Quando calcolate i successivi saldi su un conto corrente, il saldo per l'ennesimo anno è calcolato in termini del saldo dell'anno (n – 1)-simo.
Prima definiamo l'intervallo di variazione dell'indice:
Il saldo dopo 1 anno è , il saldo dopo 2 anni è
e il saldo dopo 10 anni è
.
Per vedere la variazione del bilancio in 16 anni clicchiamo qui
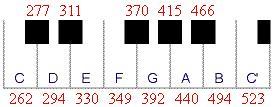
La differenza in frequenza tra le note è basata sulla scala temperata. Un'ottava è divisa in 12 semitoni (7 tasti bianchi e 5 tasti neri sul pianoforte), in cui il rapporto tra le frequenze di 2 semitoni successivi è:
Ci sono 88 tasti su un pianoforte e ciascun tasto corrisponde a un diverso semitono. Il tasto più basso è Do, con una frequenza di 27,500 Hz. Scriviamo una funzione ricorsiva che generi le frequenze di ciascun tasto e quindi troviamo la frequenza di 2 Do su due ottave successive (tasti 13 e 25), il Sol sull'ottava di mezzo (tasto 47) e il Do più alto (tasto 88).
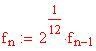
Perciò i due Do sulle ottave successive hanno frequenze: e
. Il So l sull'ottava di mezzo è
e il Do più alto ha frequenza
.
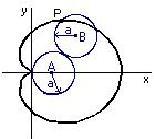
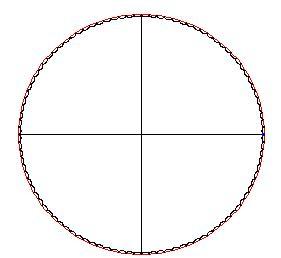
Le curve nel piano sono descritte spesso come punti che si muovono seguendo certe condizioni. Per esempio, la cardioide è generata da un punto P sulla circonferenza di un cerchio A che rotola su un altro cerchio B avente lo stesso raggio a. Essa è un caso particolare dell'epicicloide in quanto si ottiene da essa imponendo che i raggi dei due cerchi siano uguali tra loro.
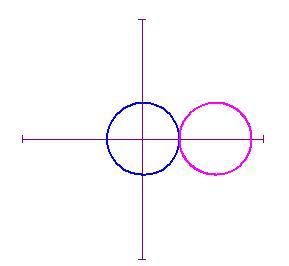
Incominciamo disegnando due cerchi di raggio a e b tangenti esternamente con a=b .
Useremo le equazioni parametriche in funzione di per disegnare il cerchio fisso ed
per quello mobile
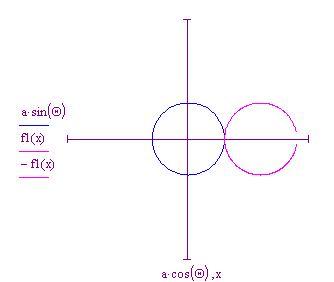
Il cerchio mobile inizia a rotolare in senso antiorario lungo la circonferenza del cerchio fisso. Se teniamo il nostro occhio fermo sul punto della circonferenza del cerchio mobile, vediamo che esso traccia una curva man mano che il cerchio rotola partendo dal punto
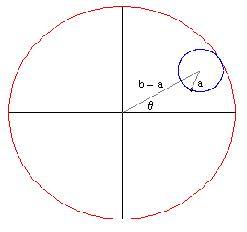
Metteremo a punto un'animazione che ci mostrerà la curva descritta dal cerchio ruotante. Con un pò di trigonometria ed il disegno qui sotto,
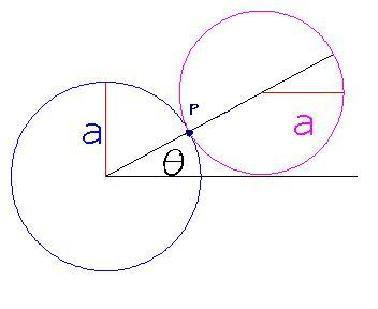
possiamo trovare le equazioni parametriche per la curva tracciata da un punto del cerchio mobile;
dove è l'angolo formato dalla linea che congiunge l'origine con il centro del cerchio mobile e l'asse
. La curva sarà
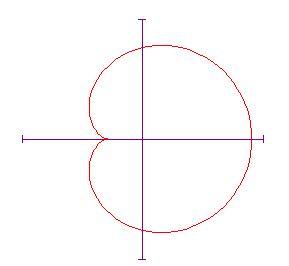
Ci piacerebbe animare il disegno della curva facendo in modo che l'angolo vari. Abbiamo bisogno di poter disegnare il cerchio rotante in qualsiasi posizione
.
Troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in una posizione qualsiasi
Cambiando qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata da esso. (Tutti gli angoli sono misurati in radianti)
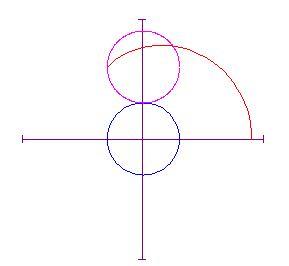
Ripetiamo l'impostazione data usando la variabile k come parametro per far variare l'angolo .
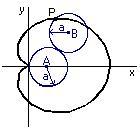
Esempio : Trova l'area racchiusa dalla curva e la lunghezza della curva stessa conoscendo la lunghezza a del raggio delle circonferenze A e B
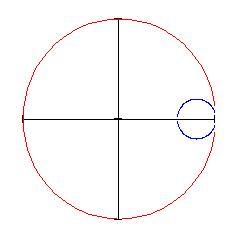
Le curve nel piano sono descritte spesso come punti che si muovono sottoposti a certe condizioni. Per esempio, l'epicicloide è generata da un punto sulla circonferenza di un cerchio che rotola su un altro cerchio ed esternamente a questo.
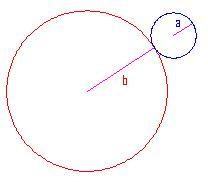
Incominciamo disegnando un piccolo cerchio di raggio all'esterno di uno più grande di raggio
.
Useremo per disegnare il cerchio più grande in forma parametrica ed
per quello più piccolo.
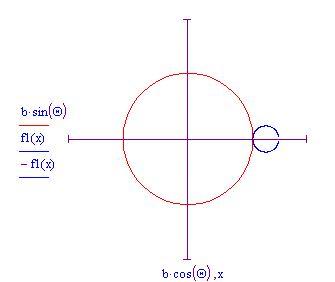
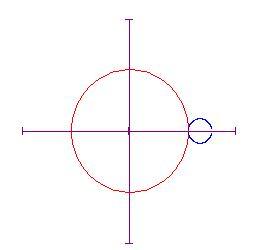
Il cerchio più piccolo inizia a rotolare in senso antiorario lungo la circonferenza del cerchio più grande. Se teniamo il nostro occhio fermo su un punto del cerchio di raggio a , esso traccia una curva man mano che il cerchio rotola partendo dal punto
Metteremo a punto un'animazione che ci mostrerà la curva descritta dal cerchio ruotante. Con un pò di trigonometria ed il disegno qui sotto,
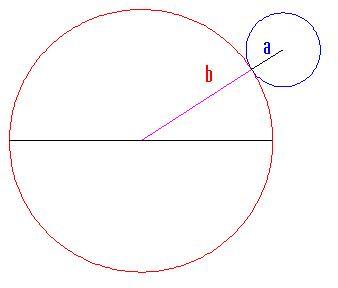
possiamo trovare le equazioni parametriche per la curva tracciata da un punto del cerchio di raggio a ;
dove è l'angolo formato dalla linea che congiunge l'origine con il centro del cerchio esterno e l'asse
. La curva sarà:
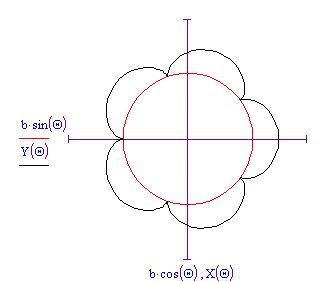
Ci piacerebbe animare il disegno della curva facendo variare i valori dell'angolo . Dobbiamo disegnare il cerchio ruotante in qualsiasi posizione
.
Troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in ogni posizione
Cambiando qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata da esso. (Tutti gli angoli sono misurati in radianti.)
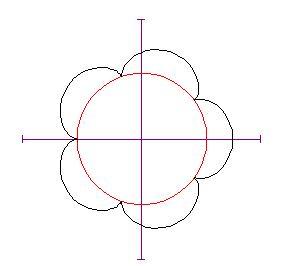
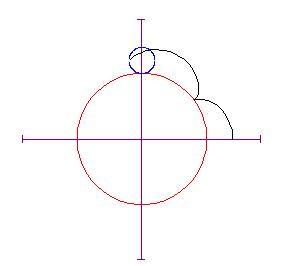
Ripetiamo l'impostazione data usando la variabile k come parametro per far variare l'angolo .
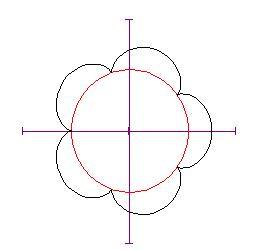
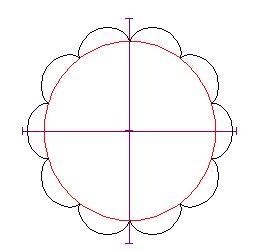
Se il valore di non è un intero, il punto sul cerchio ruotante non tornerà al punto di partenza e se lo fai continuare a girare (poni
maggiore di 2 p ) vedrai un comportamento diverso della curva
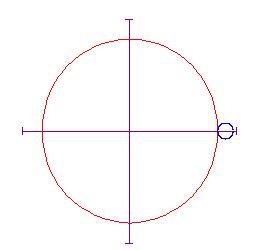
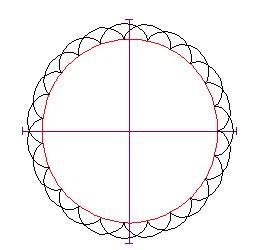
Le curve nel piano sono descritte spesso come punti che si muovono seguendo certe condizioni. Per esempio, la ipocicloide è generata da un punto sulla circonferenza di un cerchio che rotola internamente alla circonferenza di un cerchio più grande.
Incominciamo disegnando un piccolo cerchio di raggio all'interno di uno più grande di raggio
.
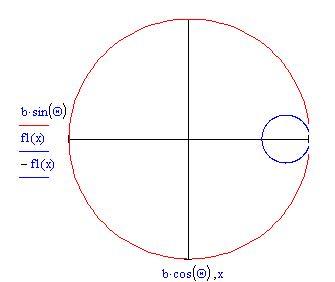
Il cerchio più piccolo inizia a rotolare in senso antiorario lungo la circonferenza del cerchio più grande. Se teniamo il nostro occhio fermo sul punto del cerchio interno, esso traccia una curva man mano che il cerchio rotola partendo dal punto
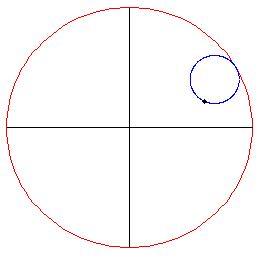
Metteremo a punto un'animazione che ci mostrerà la curva descritta dal cerchio ruotante. Con un pò di trigonometria ed il disegno qui sotto,
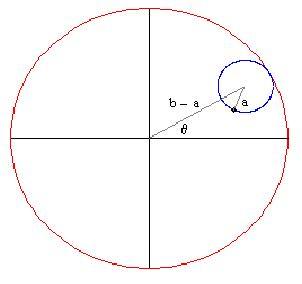
possiamo trovare delle equazioni parametriche per la curva tracciata da un punto del cerchio interno;
dove è l'angolo formato dalla linea che congiunge l'origine ed il centro del cerchio interno e l'asse
. La curva sarà
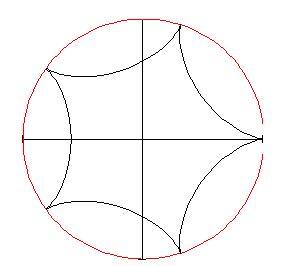
Ci piacerebbe animare il disegno della curva facendo in modo che variano i valori dell'angolo . Abbiamo bisogno di poter disegnare il cerchio rotante in qualsiasi posizione
.
Troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in ogni posizione
Cambiando qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata da esso. (Tutti gli angoli sono espressi in radianti.)
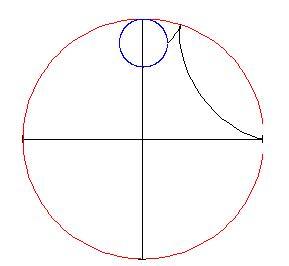
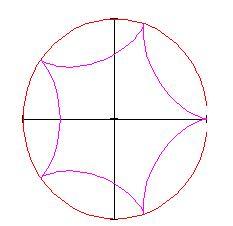
Se il valore di non è un intero, il punto sul cerchio rotante non tornerà al punto di partenza e se lo fai continuare a girare (poni
maggiore di 2 p ) vedrai un comportamento del genere:
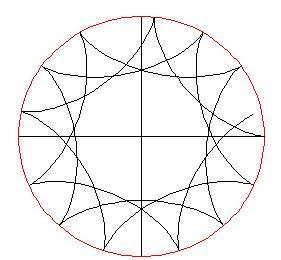
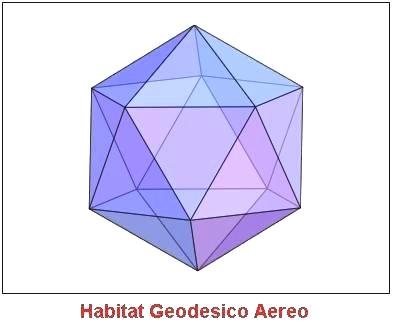
Parecchi anni fa un gruppo di ricercatori avanzò la proposta di vivere in una sfera geodesica sospesa nell'atmosfera. Questa sfera sarebbe stata trattenuta in aria mediante una differenza di temperatura tra l'interno e l'esterno della sfera in modo tale che la densità media della struttura fosse minore della densità dell'atmosfera circostante
La proposta apparve affascinante. Di seguito vengono illustrati una serie di ipotesi e calcoli che i ricercatori fecero per verificare la fattibilità di un tale modello. Non si trattava di uno studio completo, ma di un semplice progetto per vedere quali potessero essere i parametri fondamentali di una tale struttura.
La sfera avrebbe ricevuta una spinta ascensionale poiché avrebbe avuto un'atmosfera interna meno densa dell'atmosfera esterna. La differenza di densità avrebbe compensato sia il peso dell'aria interna sia il peso della struttura geodesica. Per dimostrare come ciò potesse accadere i ricercatori considerarono le equazioni relative al peso e alla forza ascensionale:
dove è l'accelerazione di gravità,
è la forza di gravità che trattiene la sfera a terra e
è la forza ascensionale. Il principio di Archimede assicura che la forza verso l'alto della sfera deve essere uguale al volume della sfera (il volume dell'aria spostata) per la densità dell'aria circostante per l'accelerazione di gravità g . La sfera geodesica incomincerà a galleggiare quando
Bisogna calcolare la densità dell'aria e la massa dell'aria all'interno della sfera più la massa della sfera geodesica stessa . Incominciamo con la densità dell'aria esterna
Sarà necessario calcolare la densità media dell'atmosfera alla TPS (temperatura e pressione standard) per conoscere la densità massima della sfera galleggiante. Si assuma che l'atmosfera consista solo dei seguenti gas: ossigeno, azoto e argo e che siano presenti nelle seguenti proporzioni : 21% O 2 , 78% N 2 , e 1% Ar.
Usando la costante del volume molare e i pesi molecolari di questi tre gas, calcolare la TPS nell'atmosfera. Il volume molare di un gas ideale alla TPS è:
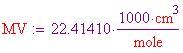
Per calcolare le densità dei tre gas più abbondanti, che compongono l'atmosfera terrestre e l'atmosfera all'interno della sfera, bisogna dividere il peso molecolare per il volume molare al fine di ottenere le densità in grammi per centimetro cubo.
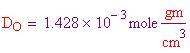
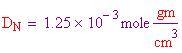
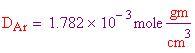
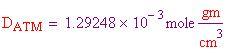
Ora si deve trovare il volume dell'aria spostata, che è pari al volume della sfera. Il volume dipende dal raggio, perciò ne prendiamo uno a caso . Il volume è
Ora che si sono stabilite le densità dei gas fuori e dentro la sfera, si deve determinare la massa della singolare sfera. Una sfera geodesica è formata da un icosaedro proiettato su una sfera. Ogni triangolo dell'icosaedro è composto da un certo numero di triangoli più piccoli. Questo dato è utile per calcolare il numero dei montanti da usare per costruire la sfera e il suo peso approssimativo.
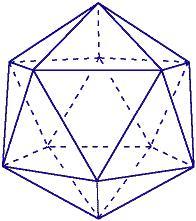
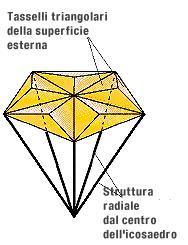
Realizzeremo i supporti interni come montanti radiali per ogni vertice dell'icosaedro tassellato. Per ottenere la lunghezza di questi raggi, prendiamo alcune sezioni della struttura e disegniamole in modo tale che sia agevole applicare i teoremi della geometria e della trigonometria .
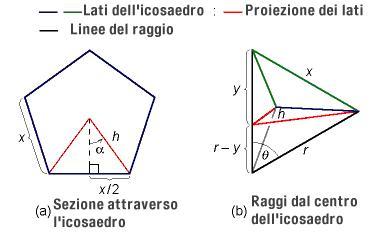
Infine ricaveremo l'angolo formato da due raggi dell'icosaedro uniti da uno stesso lato (nel diagramma è mostrato con la lettera ). Per fare ciò, dapprima si deve trovare la lunghezza
. Il seno dell'angolo
è pari al lato opposto fratto l'ipotenusa del triangolo indicato in(a) e, dato un pentagono regolare, si sa che questo angolo è pari a p-greca/5. Perciò,
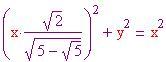
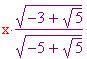
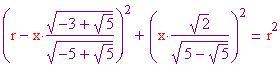
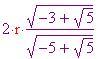
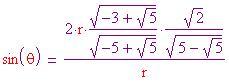
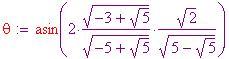
Ora occorre determinare il grado di tassellazione. Il numero di punti che suddividono ciascun lato di ciascun triangolo dell'icosaedro è . Pertanto il numero di lati ( o meglio montanti) nella sfera geodesica è
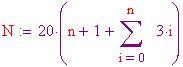
La lunghezza approssimativa di un montante della sfera geodetica, dati il raggio ed il numero di suddivisioni :
Prendiamo un'area ragionevole per la sezione di un montante: . Così, i montanti della sfera sono ognuno approssimativamente lunghi
metri con una sezione di 25 cm quadrati. Potrebbero essere realizzati in un materiale leggero ma resistente, come ceramica a base di alluminio. Questo materiale ha un modulo di elasticità alto, il che significa che la struttura sarà molto rigida. E' anche abbastanza robusto (paragonato all'acciaio, al carbonio) e non molto pesante, che forse è il fattore più importante per il nostro particolare problema. La ceramica a base di allumina ha una densità di
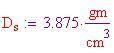
E adesso l'idea. Creeremo un gradiente termico dall'interno all'esterno della sfera riscaldando l'aria interna.
Assumeremo che la pressione interna ed esterna siano uguali, e che il volume della sfera non cambierà (da ricordare che abbiamo scelto un materiale rigido per i montanti). Ciò significa che, quando si riscalda l'interno della sfera, dovremo avere una valvola per far fuoriuscire un pò d'aria, per mantenere pressione e volume costanti mentre si sta riscaldando la temperatura. Servendoci della legge universale dei gas ideali e le nostre assunzioni su pressione e volume costante, possiamo arrivare ad una equazione per la massa dell'aria dentro la sfera, che dipende solamente dalla densità del gas esterno e dalle due temperature:
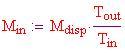
sia un numero positivo. Da un altro punto di vista, la capacità massima di spinta per la temperatura e il raggio dati è
Così, in questo caso, la nostra sfera dovrebbe galleggiare abbastanza bene, e potrebbe pesare anche il doppio di quanto abbiamo stimato e continuare a galleggiare. Questo margine è importante, poiché non abbiamo preso in considerazione la pannellatura di chiusura della sfera, né il peso delle partizioni interne, gli arredi e la gente.
I parametri di ingresso per determinare se una sfera galleggerà sono il raggio , le temperature
e
il numero di suddivisioni nell'icosaedro
(che a sua volta determina il numero di montanti
), la sezione dei montanti
e la densità
del materiale che forma i montanti, Se
, allora la sfera galleggerà. Altrimenti si può tornare indietro e modificare uno qualsiasi dei parametri di ingresso finché non si ottiene la condizione di forza ascensionale.
Si potrebbero approfondire altre idee, come sapere a che altezza galleggerà la sfera. Se la sfera è sigillata quando viene imposta la condizione di differenziale termico, si innalzerà fino a quando la densità esterna abbia raggiunto un equilibrio con la densità interna. Ciò solleva ulteriori domande. Nell'atmosfera, la sfera esploderà se esiste un differenziale di pressione? Esistono altri materiali con cui costruire la sfera? Come si potrebbe mantenere uniforme la temperatura interna? Cosa succede se si prende in considerazione il differenziale di temperatura nell'atmosfera? Provate a dare una risposta ad alcune di queste domande per conto vostro.
"La ricerca metodologico-disciplinare nella costruzione modulare"
Struttura Modulare: contesti, relazioni, problematiche
La Progettazione Modulare: modalità, scopi, definizioni
Modularità e Ricerca Metodologica Disciplinare (della D.B.)
Curriculum esplicito e curriculum implicito : mediatori didattici e variabili formative
“Logica” Pluridimensionale della RMD
Progetto dintervento didattico modulare multidisciplinare
Struttura Modulare: contesti, relazioni, problematiche
La Progettazione Modulare:
modalità, scopi, definizioni
La "progettazione modulare " è la risposta alla complessità ed alla flessibilità del problema educativo in termini didattici.
« La progettazione modulare prevede "l’impiego flessibile di segmenti di itinerari di insegnamento-apprendimento – i moduli – che hanno struttura, funzioni e ampiezza variabili, ma formalmente e unitariamente definite." In tale ottica "ciascun modulo viene a costituire una parte significativa, altamente omogenea ed unitaria di un esteso percorso formativo disciplinare o pluri, multi, interdisciplinare programmato, una parte del tutto, ma in grado di assolvere ben specifiche funzioni e di far perseguire ben specifici obiettivi cognitivi verificabili, documentabili e capitalizzabili."» – Gaetano Domenici
In una struttura modulare "mediatori didattici" (contenuti compresi) e "variabili formative" pur presentando una struttura fondamentalmente complessa sono comunque "facilmente" gestibili, più controllabili e tra l’altro più rispondenti alle diverse esigenze didattico-educative; progettare infatti un percorso formativo mediante moduli didattici significa assicurare all’allievo non solo adeguati livelli di formazione – con particolare riferimento al biennio ed all’assolvimento di quello che è l’obbligo scolastico -, ma anche competenze specifiche a livello professionale, mediante la definizione per ciascun modulo di obiettivi propri finalizzati ai bisogni degli allievi.
" La struttura modulare, permette di graduare i moduli in modo da passare da compiti semplici a compiti più complessi di tipo progettuale-autonomo, muovendosi da un livello minimo di autonomia ad un livello massimo di complessità" .
Modularità e Ricerca Metodologica Disciplinare (della D.B.)
La RMD è una risorsa per il miglioramento dell’offerta formativa; in particolare passando attraverso una codifica della struttura e della funzione di tutti gli "elementi" oggetto di ricerca rapportati alla dimensione educativa e formativa, si possono definire i seguenti livelli rispetto ai quali sviluppare la RMD .
Curriculum esplicito e curriculum implicito : mediatori didattici e variabili formative
Nello schema seguente si può osservare come alcune variabili formative siano presenti in diversi contenuti, riferiti non solo alla stessa disciplina ma anche a discipline diverse (costanti formative); le variabili formative infatti si può dire che dipendono dalla struttura del contenuto e pertanto vanno ricercate ed opportunamente rilevate per un utilizzo adeguato in un percorso curricolare.

Le costanti formative vanno definite in funzione degli obiettivi specifici e trasversali sia cognitivi che operativi, in rapporto:
| disciplinare | |
|
pluridisciplinare
multidisciplinare |
| interdisciplinare |
| esplicito | |
|
|
| implicito |
Nel diagramma di seguito riportato vengono evidenziati alcuni aspetti strutturali d’interazione tra i due diversi curricoli rapportati alle dimensioni educative "cognitivo" e "non cognitivo", che ritengo fondamentale per una RMD finalizzata alla costruzione di un Modulo Didattico Multidisciplinare;
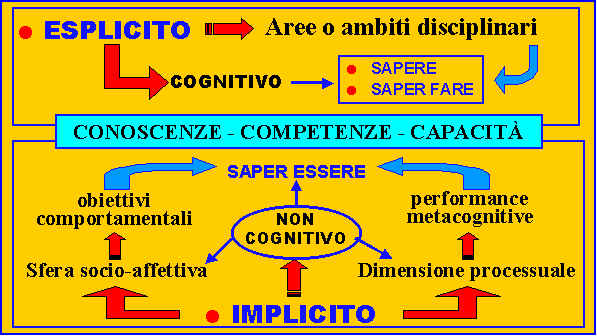
Una defizione della " logica " della ricerca in relazione ai diversi piani : strutturale, processuale, topologico, funzionale permette una destrutturazione dei contenuti in termini di mediatori metacognitivi favorendo il processo formativo dell’allievo.
Per condurre un’indagine significativa sui diversi piani è evidente che i caratteri distintivi dei contenuti devono trovare risposta a forme dichiarative e procedurali codificabili nel modo seguente:
che cosa è …, come è fatta …, è simile a …, è diversa da …; codifica della procedura di indentificazione dell’oggetto; ricerca e riconoscimento delle parti o degli elementi costituenti; ricerca di analogie formali e sostanziali;
sul piano processuale:
a cosa serve …, come funziona e fino a che punto …, come si applica …, come si può modellare in funzione di (destrutturazione) …, definizione di procedure dirette ed inverse (funzionale all’applicazione), in che modo si sviluppa: in termini sequenziali, selettivi, iterativi o ciclici (diagrammi di flusso, algoritmi, diagrammi a blocchi), in termini "problematici" (ipotesi, analisi, deduzioni, verifica, sintesi)
dove si trova …, quando serve …, dove si applica …; con che cosa è compatibile (o incompatibile) sia a livello sintattico che a livello semantico; in quali modelli o strutture o sequenze l’oggetto può essere inserito (funzione procedura all’interno di un "ragionamento");
a che cosa serve … (per la presentazione del contenuto, per lo sviluppo o il potenziamento di capacità o abiltà, verifica delle conoscenze o delle capacità o abilità operative strumentali e processuali); cosa implica … ( ipo t esi di soluzione in termini qualitativi, definizione della logica procedurale (top-down, bottom-up), rilettura dati e definzione del modello risolutivo, strutturazione della procedura risolutiva, sviluppo dell’algoritmo, sintetizzazione della soluzione).
Soggetti destinatari
: alunni classi prime e seconde di Istituti e Scuole superiori.
Operatori scolastici implicati
: componenti dei rispettivi consigli di classe.
Finalità
: riduzione del rischio di abbandono e/o del calo di motivazione allo studio e/o di interesse per il sapere disciplinare.
Considerazioni-premessa di ordine semantico
E’ il caso di precisare alcuni aspetti riguardanti il concetto e la struttura di
modularità disciplinare : riorganizzazione dei contenuti disciplinari che tiene conto delle finalità e degli obiettivi generali ma che risponde ai bisogni formativi in termini di sapere, saper fare, saper essere mediante specifiche performances connesse ad argomenti e temi sui quali si sviluppano le unità modulari che garantiscono conoscenze, competenze, capacità (capitalizzabili) certificabili; le diverse unità modulari sono connesse tra loro in una logica sia spaziale (livello e complessità di approccio) che temporale (collocazione nel "curricolo" che può essere determinata dalle proprietà intrinseca dei moduli o dal bisogno formativo che ne ha determinata la progettazione).
Per quanto riguarda i concetti di modularità pluri-, multi-, inter-, (disciplinare) si richiamano i concetti di pluridisciplinarità, multidisciplinarità, interdisciplinarità che possono essere modulati in un cotesto di organizzazione modulare didattica e quindi dare un’adeguata interpretazione dal punto operativo:
Pluridisciplinarità : concorrenza di più discipline i cui contesti o ambiti disciplinari di riferimento sono ben definiti e gli argomenti sono confinati nei suddetti contesti o ambiti non necessariamente interagenti.
Multidisciplinarità : quando non sono distinguibili i confini degli ambiti o dei contesti disciplinari di riferimento in cui gli argomenti si sviluppano ed è quindi possibile riscontrare nella struttura dei contenuti una transdisciplinare che ne permette la riorganizzazione modulare.
Interdisciplinarità : quando, indipendentemente da tematiche o argomentazioni che possono definirsi come ambiti o contesti di riferimento in relazione a contenuti riguardanti una o più discipline, si evidenziano o vengono privilegiate implicazioni di natura epistemologica o strutturale che permettono l’evolversi dei contenuti in modo tale che concorrano alle stesse finalità, alla costruzione o allo sviluppo di modelli mentali analogici, allo sviluppo di abilità di transfer e processi di generalizzazione.
Il Modulo Multidisciplinare
Metodologie e strategie didattiche d’approccio
Operazionalizzazione degli obiettivi
|
1. – potenziamento delle capacità linguistico – espressive ; |
|
conoscenze-competenze (sapere e saper fare) |
1.1 – acquisizione di un sufficiente bagaglio lessicale (specifico); 1.2 – interpretazione dei linguaggi specifici (disciplinari);
|
|
2. – potenziamento delle abilità logico-operative e di metodo di lavoro ; |
|
Capacità – Abilità (saper essere) |
|
|
|
|
Saper essere |
|
|
Contenuti
|
( scelti opportunamente in rispetto del curriculum esplicito riferito alle discipline concorrenti e funzionali agli obiettivi individuati ) |
Metodologie e strategie didattiche d’approccio
Le strategie d’intervento in genere strutturate in modo complesso tengono conto del carattere diacronico dei moduli d’intervento per il raggiungimento (a medio termine) degli obiettivi programmati nelle diverse aree formative/educative: cognitiva, metacognitiva, socio-affettiva-relazionale.
In particolare puntando sull’utilizzo dei mediatori didattici: mappe concettuali, parole-chiave, concetti fondamentali, linguaggio specifico e tentare il coinvolgimento diretto in termini operativi dello studente verificando costantemente attraverso appositi fogli d’appoggio o schede test i livelli di conoscenza e la capacità di utilizzo delle stesse mediante produzione divergente.
L’azione didattica si articolerà principalmente e costantemente in tre momenti significativi :
- momento della presentazione o dell’analisi di un caso esempio;
- momento di riflessione stimolata (feedback) o di lavoro guidato;
- momento di approfondimento o di lavoro autonomo (studio personale);
in relazione ad ogni momento ed obiettivo vanno scandite operazioni e comportamenti del docente e dell’alunno.
Per quanto riguarda l’insegnante operazioni (cosa si propone) e comportamenti (come si pone) funzionali all’obiettivo saranno riferiti principalmente ad aspetti:
- di natura progettuale : scelta e destrutturazione dei contenuti, strutturazione di macrologiche di orientamento o di organizzazione del lavoro, costruzione di fogli d’appoggio o schede di supporto all’attività didattica, modalità interattive legate ai diversi momenti, modelli e tecniche di schematizzazione o sintesi ;
- di natura gestionale-organizzativa : definizione della sequenza temporale delle operazioni d’intervento (presentazioni, consegne, modalità di lavoro: individuali o di gruppo, somministrazione di fogli e schede di approfondimento o di verifica), individuazione dei mediatori didattici o delle logiche procedurali (esplicite ed implicite) di riferimento dettati dalla complessità del contenuto .
Per quanto riguarda l’alunno operazioni (cosa deve fare) e comportamenti (come deve fare) saranno quelli opportuni alle diverse situazioni di compito che si moduleranno in funzione dei diversi momenti (presentazione, lavoro guidato, lavoro autonomo) dell’azione didattica.
Nella prassi didattica un’adeguata declinazione di ciascun sottobiettivo in obiettivi specifici corrispondenti ad opportune operazioni di compito permetterà una più agevole e controllabile attività oltre ad una coerente gestione dell’attività di verifica e valutazione.
Da ogni obiettivo specifico infatti vanno definiti indici e livelli di prestazione o di performance da raggiungere in relazione ai diversi criteri stabiliti.
Operazionalizzazione degli obiettivi
In relazione ad ogni sotto-obiettivo si possono definire opportuni obiettivi specifici che sono riferibili trasversalmente a tutte le discipline e pertanto ogni docente del consiglio di classe che aderisce al progetto dovrà oppprtunamente riferire a specifici contenuti disciplinari in coerenza con la propria programmazione:
1.1 – acquisizione di un sufficiente bagaglio lessicale (specifico) :
1.1.1 – riconoscere le parole chiave;
1.1.2 – individuare il lessico specifico;
1.1.3 – definire interazioni lessicali o costruire mappe concettuali.
1.2 – interpretazione dei linguaggi specifici (disciplinari):
1.2.1 – associare significati ai termini (specifici) o unità lessicali;
1.2.2 – definire concetti elementari o fondamentali;
1.2.3 – analizzare strutture semplici o complesse in relazione ad aspetti semantico-concettuali.
1.3 – Produzione di semplici testi scritti o orali mediante l’uso di un linguaggio chiaro, preciso e corretto :
1.3.1 – sintetizzare scalette o diagrammi di flusso come guida alla produzione di un testo scritto o parlato o per una qualunque operazione complessa di pensiero;
1.3.2 – descrivere situazione, fatti e fenomeni evidenziandone caratteri o elementi fondamentali che li contraddistinguono;
1.3.3 – esporre quanto appreso con chiarezza e precisione di linguaggio;
1.3.4 – raccontare di avvenimenti o di situazioni utilizzando forme e modelli testuali adeguati;
1.3.5 – sostenere coerenti forme di dialogo, dando risposte adeguate e mirate.
Il corrispondente piano delle attività va corredato di opportuni strumenti di verifica che rispondano ai principi di valutazione e di autovalutazione e quindi la costruzione di apposite schede di indagine che fanno ricorso a modalità, criteri e tecniche adeguati per la valutazione e quindi la definizione di opportuni indicatori ed indici.
Mario Quarta
POF ED ANALISI DEL CONTESTO
Dall’analisi dei dati alle scelte dell’offerta formativa
a cura di Mario Quarta
Nota introduttiva
Il presente lavoro mira a dare un modello di analisi di contesto a livello locale che interessa alcune variabili significative relative alla dispersione scolastica. Ritengo sia interessante notare il rapporto tra dati locali e dati nazionali proprio per stimolare una riflessione all’interno delle singole istituzioni scolastiche per un’analisi della propria utenza e avere la possibilità di rapportare i dati ottenuti con quelli locali e modulare opportunamente la propria offerta formativa.
Inoltre, tra le variabili considerate nell’analisi, sarà possibile individuare opportunamente degli indicatori di qualità dell’offerta formativa in termini di efficacia e quindi variabili da monitorare nel processo di valutazione dell’azione educativa.
La ricerca, l’elaborazione e la presentazione dei dati è stata curata personalmente dall’autore utilizzando le diverse fonti disponibili in particolare gli archivi del Provveditorato agli studi di Lecce.
Premessa
La formazione degli adolescenti si sviluppa in una logica interistituzionale oltre che sistemica: scuola, extrascuola, soggetto educando. Pertanto per un’adeguata offerta formativa vanno analizzati elementi e dati riguardanti il soggetto rapportati non solo al sistema scuola, ma anche e soprattutto all’extrascuola, in relazione alle diverse sfere educative: cognitiva, metacognitiva, socio-affettiva, relazionale.
Una eventuale lettura di dati va sviluppata in una logica sistemica definendo ruoli e compiti dei diversi enti ed istituzioni educative e formative che supportano l’azione della scuola o interagiscono con essa per garantire lo sviluppo dei processi che permettono lo sviluppo formativo del soggetto e della sua integrazione sociale. Ora premesso e sintetizzato che
Un indice dell’efficacia dell’azione educativa della scuola a livello locale può essere ottenuto confrontando i dati relativi agli indicatori di scolarizzazione di livello nazionale (vedi grafico 1 seg.) con quelli provinciali. A riguardo sono interessanti i risultati relativi al tasso di passaggio (scuola media – scuola superiore) – grafico 2 – ed al tasso di maturità – grafico 3 – interpretati alla luce delle ultime innovazioni: l’innalzamento dell’ "obbligo scolastico " da una parte e l’introduzione del "nuovo esame di stato " dall’altra.
sommario
Gli indici di scolarizzazione: tassi di passaggio e tassi di maturità
Distribuzione degli iscritti in rapporto alla tipologia d’istituti
Il rapporto tra ripetenze e abbandoni
Gli indici di scolarizzazione: tassi di passaggio e tassi di maturità
Si può rilevare come il numero di licenziati di scuola media ormai si attesti intorno al 100% dei frequentanti, fatto salvo un punto percentuale circa che è ritenuto fisiologico nel tasso di scolarizzazione, questo vale a livello sia nazionale che provinciale; il dato non va letto ovviamente come efficacia della risposta educativa – spesso disattesa o comunque non adeguata – ma come bisogno culturale sociale che l’istituzione scolastica deve garantire al di là dei risultati specifici, pertanto i suddetti dati vanno analizzati con molta attenzione. Si riportano i grafici per un confronto più immediato ed una sintesi più ampia dell’analisi dei dati presi in considerazione al di là della parziale lettura fatta in questo contesto. Nel "grafico 1" sono riportati gli indici di scolarizzazione a livello nazionale, mentre nei "grafici 2 e 3" sono sintetizzati i dati a livello provinciale che sono stati comparati, almeno relativamente ad alcuni indicatori con quelli nazionali.
GRAFICO 1
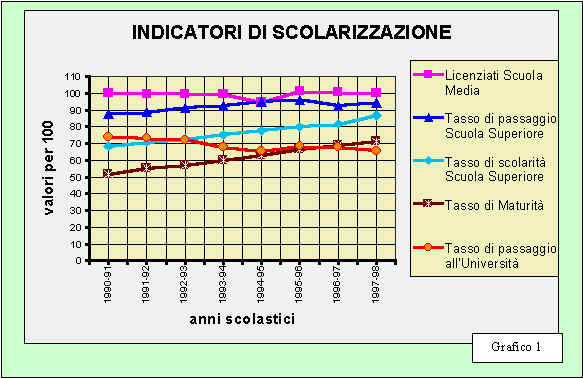
Fonte Isfol su dati Istat
Come si può vedere dal "grafico 2"seguente, nel trend del "tasso di passaggio " dalla scuola media alla scuola superiore pur mantenendo sostanzialmente un analogo andamento, tra il dato nazionale e quello provinciale, vi è una differenza in media di due punti percentuale; tale dato va considerato come margine di miglioramento nell’ambito del sistema scolastico nella fase di interazione tra i diversi ordini in una logica di continuità educativa e di orientamento. Inoltre va ripensato il progetto educativo in funzione dei bisogni degli adolescenti in modo tale che gli stessi trovino nella scuola superiore il punto di riferimento o l’ambiente adatto in cui si possano coltivare le proprie aspirazioni attraverso un riequilibrio culturale ed un processo d’integrazione sociale.
GRAFICO 2
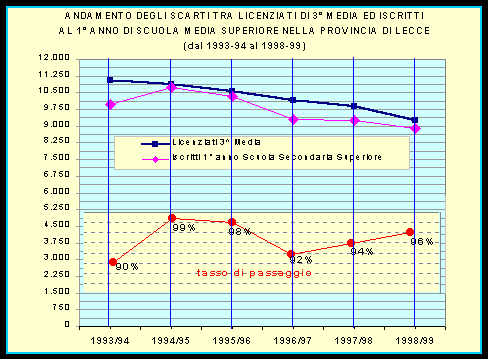
Fonte dati "Provveditorato agli studi di Lecce"
Dall’analisi dei dati riguardanti il tasso di dispersione risulta significativo l’andamento anno per anno relativamente al quinquennio di un corso dal momento dell’ingresso all’uscita, confrontato quindi con il "tasso di maturità ". A tal proposito in questo contesto si riportano i dati riguardanti la provincia di Lecce (vedi tabella seg.), relativi ai due quinquenni: (93-94/97-98) e (94-95/98-99). Tali dati si ritengono significativi proprio per l’alta variazione che si presenta nel valore percentuale tra il primo ed il secondo quinquennio. Ora confrontando i dati e quelli relativi al "tasso di maturità " con quelli nazionali riportati nel "grafico 1" precedente si può evidenziare come il valore provinciale, pur restando nella media nazionale – tra il 70 ed il 71% -, tra i maturati del 97/98 e quelli del 98/99 vi è uno scarto di circa 14 punti che, confrontati con i frequentanti dell’ultimo anno – scarto pari al 10% -, si può osservare questo dato sia collegabile all’introduzione del "nuovo esame di stato" che potremmo definire come un vero e proprio "effetto aberrazione " .
TAVOLA 1
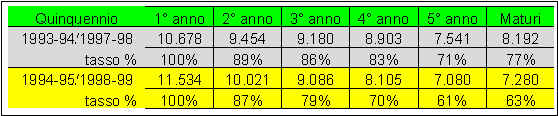
Il dato più preoccupante è proprio il trend crescente della percentuale di dispersione che se pur indicativa come dato storico è comunque non trascurabile, nella valutazione dell’efficacia dell’azione formativa, che va senz’altro rivista mediante un’innovazione totale delle proposte didattiche a livello sia culturale che professionale, visto che lo scarto tra gli studenti in entrata (frequentanti il primo anno) e quelli in uscita (frequentanti il 5° anno) passa dal 29% del quinquennio 1993-1998, al 39% del quinquennio successivo (1994-1999), (come da tabella precedente e grafici successivi).
GRAFICO 3
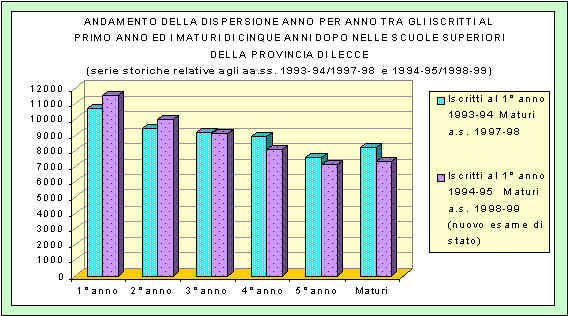
Pertanto se tali variabili vengono assunte quali indicatori da monitorare per una valutazione qualitativa e quantitativa dell’offerta formativa, nel grafico seguente, si può vedere come si possa concretizzare in termini grafici il margine di miglioramento esistente, per poter quindi attraverso un’azione didattico-educativa mirata ridurre lo scarto tra studenti in uscita e studenti in entrata.
GRAFICO 4
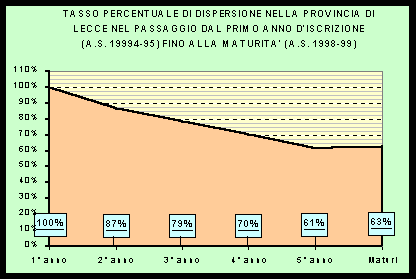
Dall’analisi dei dati si configura pertanto una scuola che ha perso la sua vocazione orientativa o che comunque non è in grado di rispondere alla domanda formativa in relazione alle scelte professionali o di prolungamento dell’istruzione, quindi è sempre più urgente rimodulare l’offerta formativa attraverso una approfondita analisi dei bisogni in rapporto al territorio ed alle aspirazioni degli utenti.
Ora prima di passare ad un’analisi se pur limitata di alcuni dati riguardanti la distribuzione degli iscritti in relazione alla tipologia d’istituti, è il caso di leggere se pur attraverso un semplice istogramma (grafico 5 seg. – DAL 29° RAPPORTO CENSIS – 1995 ) alcuni dati "storici" che mettono a confronto la realtà provinciale con quella regionale e quella nazionale e rapportarli alla situazione attuale tracciata attraverso i dati precedentemente presentati.
GRAFICO 5
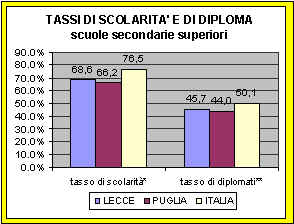
Distribuzione degli iscritti in rapporto alla tipologia d’istituto
A livello provinciale un altro dato significativo è quello relativo agli iscritti al primo anno. Dall’analisi di tali dati risulta, almeno a partire dall’anno scolastico 1995-96 (confronta TAVOLA 2 successiva), che vi è una equa distribuzione degli iscritti in rapporto alle diverse tipologie di scuole o istituti: professionali ed istituti d’arte, tecnici, licei e magistrali; in particolare salvo una leggera flessione degli istituti professionali, sostanzialmente tecnici e licei/magistrali si equivalgono, al contrario degli anni scolastici precedenti in cui gli istituti tecnici hanno registrato un flusso di iscrizioni sempre maggiore fino a raggiungere il 39% degli iscritti contro il 29-30% nei licei/magistrali.
Il fenomeno del livellamento del flusso d’iscrizioni va analizzato prendendo in considerazione sicuramente una pluralità di fattori; in ogni caso vanno evidenziati almeno due fattori più significativi:
– una sorta di ricerca da parte dell’utenza di essere più sicuri nel soddisfare i bisogni culturali, visti come maggiori opportunità di "scelte" dopo l’istruzione superiore;
– non trascurabile la non più tanto evidente diversificazione dell’offerta formativa che in precedenza era sicuramente più caratterizzante e più adeguata ai tempi.
A questo punto vanno meditate delle scelte educative/formative, che non sono sicuramente facili e, che oltre a tenere presente quanto espresso nei punti "a" e "b", rispondano istituzionalmente al problema posto dall’innalzamento dell’obbligo scolastico. Va sicuramente effettuato un cambiamento di rotta nell’offerta formativa ; va elaborata, un’offerta che sia in grado di assicurare ed accelerare un processo di orientamento che possa stimolare nei giovani scelte consapevoli e coerenti in relazione alle loro conoscenze, capacità e competenze. Una proposta educativa che tenga conto degli scenari sociali e quindi delle opportunità presenti sul territorio sia nel proseguimento degli studi sia per un eventuale inserimento nel mondo del lavoro, specie per quanto riguarda le opportunità offerte dall’avvento e dalla diffusione delle nuove tecnologie. Questo significa che bisogna prevedere un considerevole aumento dell’offerta formativa nei campi comunicativo, tecno-scientifica, socioeconomico e tecnologico, partendo dal principio che i cittadini di domani non possono sottrarsi alla rete dello sviluppo tecnologico ed al processo di globalizzazione e quindi al confronto con lo scenario "virtuale". In particolare per quel che riguarda il biennio, l’offerta formativa deve rispondere ad una sorta di riequilibrio culturale oltre che ad un riorientamento che garantisca la revisione delle scelte attraverso opportune proposte educative/formative che investono le aree linguistico-epressiva, logico-matematica e la tecnologia dell’informazione e della comunicazione (TIC).
SERIE STORICA DEGLI STUDENTI ISCRITTI AL 1° ANNO (nelle scuole statali)
PER TIPOLOGIA D’ISTITUTO NELLA PROVINCIA DI LECCE
TAVOLA 2
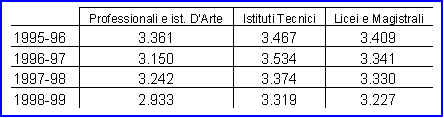
GRAFICO 6
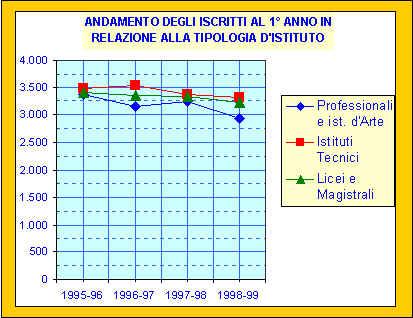
Fonte dati: annuari del "Sistema informativo" del Ministero Pubblica Istruzione
Variazione percentuali studenti iscritti al 1° anno confrontati
tra le diverse tipologie d’istituto riferiti agli ultimi aa.ss.
GRAFICO 7
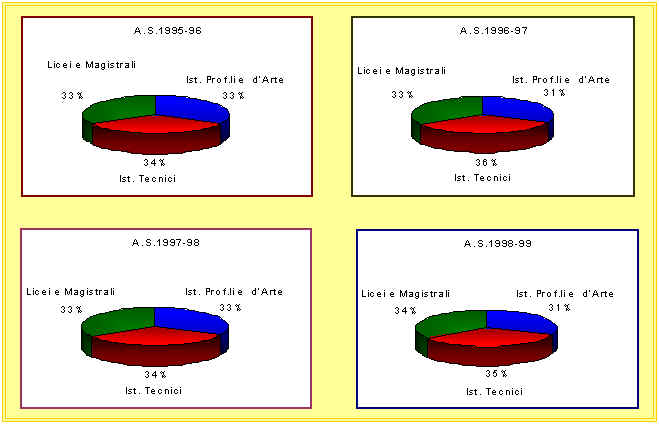
Il rapporto tra ripetenze e abbandoni
La conferma di una "efficacia mancata" dell’azione educativa/formativa viene da un ulteriore analisi di dati riguardanti le ripetenze e gli abbandoni, indicatori da non trascurare sia in fase diagnostica sia in fase di verifica (autovalutazione) a livello di istituto. Al di là dell’effettivo numero di abbandoni, può essere significativo in questo contesto riflettere sulla presenza del "desiderio" di abbandonare gli studi che è sicuramente un indicatore dello stato di disagio dello stare a scuola e delle difficoltà del vivere il tempo scuola. Come si può desumere dai due grafici seguenti, in un gran numero di studenti si manifesta «… un trend di disagio che cresce con l’età e con la permanenza a scuola . Ciò vuol dire che il sistema scolastico non è in grado di assorbire e contenere il disagio che i ragazzi esprimono e che paradossalmente aumenta con l’avvicinarsi della conclusione del ciclo di studi. È il caso di dire che lo stare a scuola spegne l’entusiasmo dell’esserci . …».
GRAFICO 8
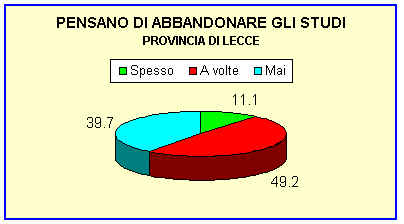
A tal proposito «…è interessante soffermarsi sulle diverse fasce d’età. La prima fascia riguarda l’ingresso nella scuola superiore, l’impatto con tale sistema. Nel primo anno di frequenza la quota di ragazzi che dichiara di non aver mai pensato all’abbandono è più elevata rispetto alle altre fasce d’età: c’é quindi in ingresso una fiducia in se stessi e/o nell’istituzione, un entusiasmo che prevale sulle difficoltà di inserimento.
Nella seconda fascia d’età si riduce la quota di ragazzi che non hanno mai pensato all’abbandono e prevale la quota di ragazzi che lo hanno pensato "a volte".
Infine, nella terza fascia d’età, quella superiore ai 18 anni, quindi tra coloro i quali frequentano l’ultimo anno o sono ripetenti, è evidente il grado di malessere che traspare dall’aumento di quanti hanno spesso pensato di abbandonare e la diminuzione di quanti non lo hanno mai pensato . …» .(fonte dati "Laboratorio permanente per i giovani" – provincia di Lecce).
GRAFICO 9
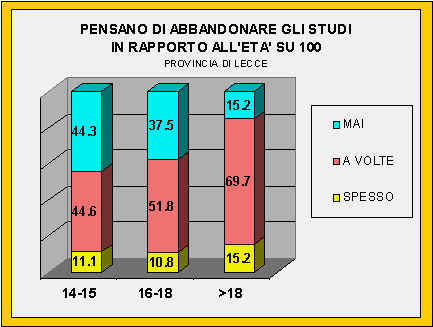
"Il passaggio dalla scuola media inferiore alla superiore richiede ai ragazzi di rivisitare e rivedere le modalità di relazione con insegnanti e compagni oltreché i modelli cognitivi di apprendimento. La nuova realtà scolastica esige l’investimento di notevoli energie psicologiche, cognitive, emotive, impone la sperimentazione di nuove strategie cognitive e relazionali, induce a vivere sentimenti contrastanti circa la possibilità di dimostrarsi all’altezza della nuova situazione ed in grado di far fronte alle richieste dell’istituzione scolastica ".
Osservando il seguente grafico sull’andamento del tasso delle ripetenze anche se si può rilevare un trend decrescente della percentuale di ripetenti, specie negli istituti tecnici e nei licei (nei professionali risulta sostanzialmente stabile), in realtà prendendo in considerazione anche i dati relativi al tasso di dispersione in relazione al quinquennio di studi (vedere grafico) si può desumere che vi è una sorta di autoselezione dovuta sicuramente all’impatto con la nuova dimensione scolastica e la "nuova" proposta culturale-formativa che spesso si rivela incomprensibile a livello comunicativo e trova gli stessi ragazzi impreparati ad affrontare le difficoltà dovute ad aspetti strutturali: strumentali e logici.
GRAFICO 10
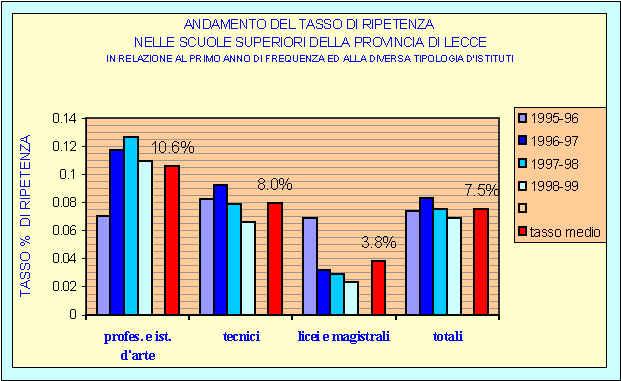
Fonte dati "Provveditorato agli studi di Lecce"
Sarà sicuramente interessante un’analisi formale dei dati confrontando la media con i dati parziali oppure i tassi fra le diverse tipologie d’istituto per una prima diagnosi; è comunque evidente che confrontando i dati con la riposta formativa – sicuramente non soddisfacente – si può facilmente dedurre come da parte del corpo docente più che intensificare e rimodulare l’azione formativa, si ha la sensazione, che da parte dello stesso vi sia una formale rinuncia alla risoluzione dei problemi, favorendo una fittizia riduzione del tasso di ripetenza; d’altronde attraverso una diagnosi non approfondita delle situazioni e un accomodamento dei casi problematici si medita e si concretizza di fatto una sorta di differimento prima e di delega poi dell’azione educativa rapportata ai bisogni.
Pertanto dal punto di vista professionale va rivisto o meglio riflettuto il ruolo ed il compito della funzione docente, perché la stessa si sviluppi e si realizzi in una logica di coerenza nell’ambito della dimensione istituzionale del sistema educativo scuola.
Calcolo del liquido contenuto in una cisterna cilindrica
Carmine Iorio (22/05/04)
Chiunque abbia una cisterna , che contenga scorta d'acqua, gasolio per riscaldamento, ecc. sa che, almeno nella maggior parte dei casi, la sua forma è un cilindro a base circolare e che è installata " orizzontalmente " come nella figura.
Il problema che si incontra in questi casi è quello di calcolare il liquido contenuto nella cisterna con oscendo soltanto l'altezza h del “liquido” (ovviamente devono essere note anche il raggio R e la lunghezza L . 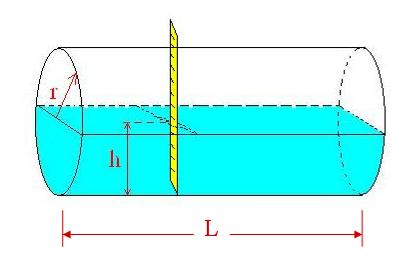
La formula che ci dà il risultato è la seguente:
![]()
Dimostrazione
Equazione generale della circonferenza con coordinate del centro del raggio C(0;0):
x2 +y2 =r2
Per comodità consideriamo quella di una qualsiasi circonferenza che poggia sull’asse delle x (in modo che l’altezza h del segmento corrisponda al valore di y):
(y-r)2 +x2 =r2
e risolvendo rispetto ad x, otteniamo le due soluzioni dell’equazione:
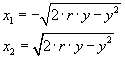
di cui ognuna è una semi-circonferenza. Noi adotteremo la seconda (quella sul quadrante positivo degli assi x;y) e la moltiplichiamo per 2 (per avere appunto un'intera circonferenza.:
Integrando la precedente espressione per i limiti inferiore e superiore di h (e quindi di y)
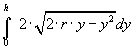
svolgendo i vari calcoli, si ottiene l’equazione del segmento circolare:
![]() .
.
| BUSY PHONE CALL (a symmetric problem) |
Mi è capitato circa 8267 volte (o forse 8268) di telefonare ad una persona e trovare occupato.
Poco male, fai il 5 e buonanotte!
In un certo senso sì, buonanotte. Ma non mi sono potuto tirare indietro quando ho capito che si trattava di una LOS (Linea Occupata Simmetricamente – vocabolo desmatronico).
In breve, se la persona sta parlando con altrui essere umano diverso da voi che chiamate, benissimo fate il 5.
Ma come fate ad essere sicuri che stia intrattenendo una conversazione con un'altra persona? E se stesse invece cercando di chiamarvi a sua volta e trova occupato perché voi fate la stessa cosa?
In questo caso la domanda sarà:
"Qual è la migliore strategia da seguire?"
E non è molto facile scoprirlo visto che supponiamo fin d'ora che entrambi svolgano il medesimo ragionamento.
Ad esempio, una strategia (fallace) potrebbe essere "attacco la cornetta e aspetto che arrivi la telefonata" . Anche un bambino capirebbe che i due facendo lo stesso ragionamento, sarebbero indotti ad attendere un tempo tra l'infinito ed infinito più uno.
Insomma, la chiave della soluzione dove sta?
Risiede nel fatto che dobbiamo far svolgere ai due un comportamento diverso. E tutto ciò semplicemente con le sole informazioni che disponiamo.
Sostanzialmente abbiamo bisogno che uno attacchi il telefono e che l'altro chiami.
Questo è possibile.
Innanzitutto immaginiamo che chi chiama non conosce il proprio numero.
Se i due avessero a disposizione un computer per la generazione di numeri random e prendessero il primo numero che viene loro mostrato dal pc, supponiamo in un range umano di 30 secondi ed attendessero esattamente un numero di secondi pari al numero propostogli dal computer, avremmo discrete chances di metterci in contatto.
In questo caso la probabilità di ritrovare occupato al primo tentativo è 1 su 30, ma già al secondo tentativo è così irrisoria (0,1%) che si può ritenere sicuro il 'contatto'.
Gli inconvenienti principali di questo metodo sono sostanzialmente due e tutti voi lettori avrete già sentito puzza di poca praticità. Innanzitutto il pc; cavolo saranno pure piccoli i portatili al giorno d'oggi, ma portarsene sempre dietro uno è ben lungi dal definirsi pratico e comodo. Mi direte che ci sono i palmari, ma tutti hanno a disposizione un palmare? A noi interessa coprire il maggior numero di casi ed anche una semplice calcolatrice programmabile potrebbe esser di poco aiuto e soprattutto di poca diffusione. Inoltre c'é da considerare un fatto: se a me esce il numero 24 attenderò 24 secondi prima di rifare il numero, ma se all'altro chiamante esce il 25? O il 26 o il 23? Di certo rischieremmo (anche con la discreta velocità del tasto R) di non riuscire a fare il numero in un secondo o due e peggio ancora se stiamo telefonando da un cellulare che dovrà cercare la banda!
Comunque il nostro passetto in avanti lo stiamo per compiere, perché una delle informazioni che i due hanno sicuramente a disposizione è il numero di telefono che stanno facendo.
Ed è oltretutto un'ottima distribuzione di numeri random che non saranno mai uguali al 100%.
Allora cosa si potrebbe fare? Si potrebbe ad esempio prendere la prima cifra A ed attendere esattamente A secondi prima di ritentare la telefonata. La probabilità che l'altra persona abbia la stessa cifra è del 10% e se consideriamo che spesso si chiama verso lo stesso distretto o prefisso di cellulare, questa percentuale salirà di molto. Ma allora perché non partire dal fondo? E' molto più probabile che siano differenti i numeri in coda che quelli in testa rappresentati dallo stesso distretto se non addirittura dallo stesso prefisso cittadino.
Le probabilità d'incontrare un numero uguale per entrambi i numeri di telefono sarà del 10% in maniera molto più 'forte' della precedente, al secondo tentativo sarà dunque dell'1% e diverrà irrisoria al terzo tentativo: 1 su 1000.
Rimarrà però purtroppo il problema dell'uno/due secondi di range per fare materialmente il numero. Ad esempio, il numero che voglio chiamare termina per 5 e quello mio per 4. La persona che voglio chiamare attenderà 4 secondi, farà il numero e prima di prendere la linea saranno passati magari 6/7 secondi (4+2 o 4+3 non 6 o 7 secondi dalla fine del conteggio!) durante i quali io stesso avrò terminato la mia attesa e starò componendo il numero dell'altro. Senza contare il problema della precisione di calcolo di questi secondi; li conto a mente (caso peggiore)? Lo strumento che ho a disposizione ha la stessa precisione di quello dell'altro? Forse quest'ultimo inconveniente è superabile dal fatto che per tempi così brevi, tutti gli orologi o cronometri possono ritenersi ugualmente precisi, ma possiamo anche 'sgarrare' nel momento di partenza: quando inizia il conteggio?
A questo punto un buon metodo potrebbe essere quello di prendere il quintuplo della cifra che abbiamo ed attendere esattamente questi secondi. Se dopo tre tentativi troviamo ancora occupato, possiamo ragionevolmente ritenere che l'altra persona sia impegnata in una conversazione diversa dalla nostra.
Ma attendere il quintuplo di una cifra vicina al 9 può essere estenuante.
Ad esempio, supponiamo che Guidalcisio voglia chiamare il suo amico Brepustene al cellulare le cui ultime 4 cifre sono 2348. Al primo tentativo (il tentativo ZERO) Guidalcisio troverà occupato e si domanderà se sia incappato o meno in una LOS. Allora comincerà con l'attendere 40 secondi e poi farà di nuovo il numero. Non conoscendo il suo stesso numero di telefono per poter capire quanti e quali secondi stia aspettando eventualmente Brepustene continuerà, in caso trovi ancora occupato, ad attendere altri 20 secondi (4 per 5) e poi ancora 15. A questo punto noi gli consigliamo di riprovare tra un'oretta, ma se invece sapesse quale sia il proprio numero, le cose cambierebbero in meglio.
Infatti dovrebbe semplicemente prendere la prima cifra diversa dal suo numero partendo dal fondo. Questo proprio perché nel caso di una LOS, Brepustene adotterebbe la stessa strategia.
Immaginiamo i due numeri come di seguito:
Guidalcisio deve fare il: 705462561 63842348Brepustene deve fare il: 704526252 63842348
Guidalcisio attenderà 5 secondi e farà nuovamente il numero di Brepustene. A sua volta Brepustene attenderà 10 secondi prima di rifare il numero di Guidalcisio e con molta probabilità prima che passino questi 10 secondi riceverà la chiamata di Guidalcisio.
Appare comunque evidente che c'é un 'di più' a questo punto della strategia perché seguendo entrambi lo stesso ragionamento e conoscendo entrambi il proprio numero, sapranno sicuramente in partenza chi chiamerà per primo, ovvero Guidalcisio.
Ricordo che nel caso in cui i due non conoscano il proprio numero di telefono (molto comune tra gli esseri umani), la probabilità (visto questo esempio) che abbiano 8 cifre uguali è dello 0,000001%, ovvero 1 su 100 milioni.
E' più facile che 2 italiani che s'incontrano all'estero si conoscano.
Ora, abbiamo detto che attendere il quintuplo di una cifra da 0 a 9 possa risultare poco pratico, anche nel caso in cui uno dei due stia o meno intorno ai 20 secondi (cifra 4 dunque).
Esiste un metodo migliore di queste estenuanti attese?
Beh direi di sì, ma solo nel caso che Guidalcisio e Brepustene conoscano il proprio numero di telefono.
Uno dei due compone il numero dell'amico e trova occupato.
Sarà una LOS o una LOA (Linea Occupata Asimmetricamente, ovvero terzo ricevente tra i piedi)?
E' sufficiente prendersi tutto il tempo che si vuole (peraltro breve) per osservare quale tra i due numeri sia il più grande. Seguendo la regola dell'Anziano, chi ha il numero di telefono più grande si riposa e attende la chiamata dell'altro.
Esempio
| SOLVING LOS PROBLEM | Guidalcisio | Brepustene | Chi chiama | Chi attende |
| Numero di telefono | 192.745.198 .831.234.1 | 192.745.197 .831.234.1 | – | – |
| Numero di telefono da chiamare | 192.745.197.831.234.1 | 192.745.198.831.234.1 | – | – |
| Numero più grande | 192.745.198 .831.234.1 | – | Brepustene | Guidalcisio |
Dalla tabella si capisce che colui che deve chiamare è colui che, scorrendo da sinistra, ha il primo numero diverso più piccolo. Abbastanza veloce d'afferrare.
Esaminiamo invece il caso in cui uno solo dei due stesse chiaccherando con una terza persona; l'altro applicherebbe il metodo dell'Anziano e troverebbe occupato se fosse lui il più giovane. Allora capirebbe che era solo una LOA.
Se invece fosse lui l'Anziano e la telefonata non arriva diciamo entro venti secondi, potrebbe ritenere anche quà di aver beccato una LOA.
Nel caso in cui Guidalcisio o Brepustene decidano di chiamare rispettivamente Brepustene o Guidalcisio senza conoscere quale sia il proprio numero di telefono è sufficiente applicare il metodo del 5 e cioé dei quintupli.
Ma riassiumiamo il tutto con due esempi.
Esempi
Faccio parte di quell'80% circa (fonte dati: A.P.R.I. – Approssimazione Percentuale per Rendere l'Idea) di persone che conoscono il proprio numero oltre a quello che stanno chiamando.
Chiamo.
Trovo occupato.
Attacco la cornetta. LOS o LOA?
Esamino subito i due numeri e so che la stessa cosa sta facendo l'altra persona, dunque non ho fretta.
A) Il mio è minore, continuo a chiamare.
B) Il mio è maggiore, attendo.
Se invece facessi parte di quel simpaticissimo 20% e si presuppone che io sappia di non sapere :-) …
applicherei il metodo del 5.
A) parto dall'ultima cifra, la moltiplico per 5 e conto (decisamente a mente)
Se siete degli speranzosi incalliti, provate pure con la quarta cifra, ma per ottenere un ottimo del problema ritengo che lo 0,1% sia sufficiente a farvi desistere.
Perciò riassumendo, nella maggior parte dei casi sarà applicato l'Anziano.
Per quelle persone che non conoscono il proprio numero applicate pure il 5.
Memorizzatevi quei piccoli casi e ricordatevi che:
1) l'Anziano riposa
2) se non vi mettete in contatto entro 20 secondi è una LOA
3) anche con il metodo del 5 in un tempo massimo di 2 minuti e dieci secondi (45+45+40) capirete se è una LOS o una LOA
Facendo una media del metodo del 5 potremmo accontentarci di un 130 secondi diviso tre.
Dunque 43 secondi circa per venire a capo del problema.
Not too bad.
Rimarrebbe il caso in cui noi siamo a conoscenza del metodo e l'altra persona no.
In questo caso ci allontaneremmo dal presupposto che i due ragionino alla stessa maniera o meglio, applichino lo stesso algoritmo o strategia.
Ma anche quì siamo sostanzialmente salvi poiché si possono verificare due sole situazioni critiche sui 4 casi possibili:
1) io sono l'Anziano, attendo e la stessa cosa inconsciamente farà l'altra persona
2) io non sono l'Anziano, chiamo l'altra persona che continuerà imperterrita a digitare il mio numero
Sembrerebbero due situazioni di stallo, ma non è così.
Infatti io ragiono con una strategia, l'altro no. E questa è una distribuzione diversificata delle azioni, indistinguibilmente diverse tra loro (lo abbiamo preso proprio come caso particolare).
Perciò nel primo caso avremo un'attesa assolutamente asimmetrica in quanto io avrò pianificato di attendere e dunque non chiamerò più per un bel pò. L'altro invece è in "modalità random" e dunque al 99% dei casi alzerà la cornetta molto prima che io ritenti.
Nel secondo caso io, con la mia strategia penserei che l'altra persona stia parlando con un terzo interlocutore, abbasserò il telefono e come prima, non ritenterò per un tempo t sicuramente maggiore al 99% del tempo random t' dell'altra persona.
E adesso scusate…
…..ma devo fare una telefonata ;-)
Definiamo la frontiera della regione del piano x-y :
A ssumiamo e
per ogni x .
I ntegrali Doppi variabili calcolati numericamente ( Carlo Elce )
Partendo da una funzione, che rappresenta un piano variabile parallelo al piano x-y su cui è definito un dominio quadrato, viene evidenziato come un integrale doppio calcoli il volume di un parallelepipedo. Facendo poi variare la funzione e il dominio piano viene mostrato come l'integrale doppio calcoli il volume di un solido delimitato da una superficie più generale .
.
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
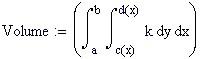
Definiamo una nuova funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
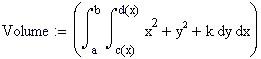
Definiamo una terza funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
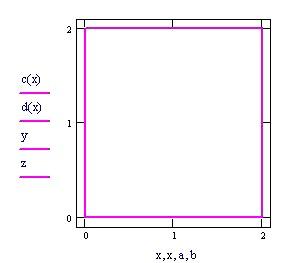
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
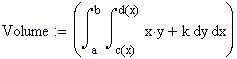
Definiamo una nuova frontiera della regione del piano x-y :
assumiamo e
per ogni x .
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
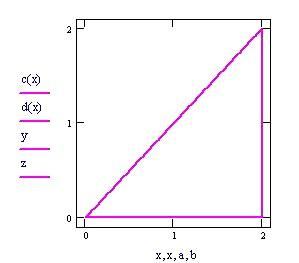
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
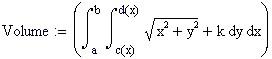
Definiamo una nuova frontiera della regione del piano x-y :
assumiamo e
per ogni x .
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
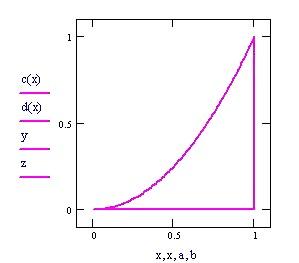
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
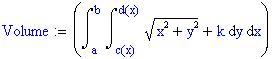
Definiamo una nuova frontiera della regione del piano n x-y :
assumiamo e
per ogni x.
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
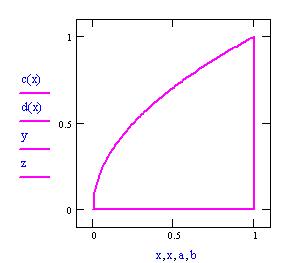
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L' integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l'animazione clicca sul grafico seguente
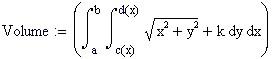
Scarica il file in formato PDF
Una superficie di rotazione intorno all'asse z è definita da una equazione del tipo
![]() Poniamo
Poniamo ![]() e consideriamo la funzione
e consideriamo la funzione
La sua curvatura meridiana è quella della linea meridiana e vale
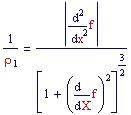
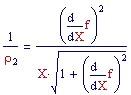
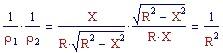
Ma per i punti della pseudosfera , essendo tutti iperbolici, le due curvature hanno segno contrario, quindi la curvatura totale risulta negativa. Se assumiamo R come parametro,che chiamiamo k, avremo una superficie parametrica variabile al variare di k con curvature principali variabili ma, per ogni superficie, la curvatura totale sarà costante per ogni punto della superficie. Per vedere l'animazione cliccate sul grafico seguente, che è stato ottenuto per k=5 e considerando solo il ramo superiore.
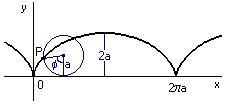
 Quando è nata la Terra? Il metodo di datazione qui proposto ci permette di vedere quando è stata “fatta” la materia che compone la terra e viene proposto agli studenti della quarta Liceo Socio-Psico-Pedagogico come applicazione “interessante” delle equazioni esponenziali e logaritmiche
Quando è nata la Terra? Il metodo di datazione qui proposto ci permette di vedere quando è stata “fatta” la materia che compone la terra e viene proposto agli studenti della quarta Liceo Socio-Psico-Pedagogico come applicazione “interessante” delle equazioni esponenziali e logaritmiche
Scarica il file in formato PPS
Risoluzione di un'equazione di 3° grado a una incognita a coefficienti complessi per mezzo di un foglio Excel.
Scarica il file in formato XLS