Autore: Antonio Bernardo
Alcuni software di geometria statica e dinamica
Trasformazioni geometriche
Relazione e proprietà
Potenzialità grafiche di Derive
Funzioni e loro rappresentazione grafica
Dai numeri naturali ai numeri reali
L’incredibile motore differenziale di Babbage
Il motore differenziale N.2 di Charles Babbage pesava tre tonnellate, non aveva parti elettroniche e calcolava i valori dei polinomi del settimo grado con la precisione di 31 cifre decimali. Questo calcolatore meccanico aveva più di 4.000 componenti ed era azionato a mano. Se tutto ciò può stupire, è incredibile sapere che è stato progettato nel 1 847!
La motivazione primaria per la costruzione di un simile strumento era l'incredibile numero di errori presenti nelle tabelle matematiche del tempo, che descrivevano valori di vari polinomi per sequenze di dati di ingresso . In una selezione casuale di 40 libri c'erano 3,700 errori rilevati; inoltre le correzioni stesse contenevano altri errori. Questi errori derivavano sia da calcoli sbagliati sia da errori di stampa. Il motore differenziale venne progettato per correggere ambedue le cose.
Il calcolo dei valori dei polinomi viene fatto meccanicamente dal motore differenziale che si basa sul metodo delle differenze finite. Per capire come funziona matematicamente questo metodo prendiamo come esempio di polinomio e troviamo le sequenze di differenza per i primi cinque valori,
. La prima serie di differenze,
, viene elencata sotto
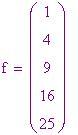
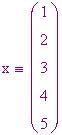
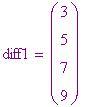
La seconda serie di differenze viene acquisita dalla prima serie in maniera simile. Ciò prosegue fino alla -sima differenza, dove
rappresenta l'ordine del polinomio(in questo caso 2). Il risultato dalla differenza ennesima sarà una costante, come si può vedere in
.
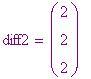
La costante rimasta alla fine della catena di differenze risulta . Attenti a cosa accade più in generale. Le differenze vengono determinate come:
Succede che se è un polinomio di grado
, allora la colonna
in una tabella di differenze sarà costituita da una costante diversa da zero. Come si è appena visto sopra nel polinomio di secondo grado
, la terza fila, costituita dalla seconda serie di differenze, era costantemente 2. Si può riconoscere sopra la sequenza di numeri davanti ai
come coefficienti di binomi alternanti oppure come le immissioni nel Triangolo di Pascal:
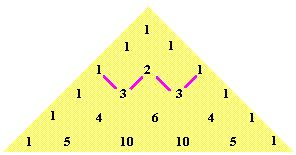
La esima entrata nell'
esima colonna è
. Usando questa espressione, possiamo calcolare l'intera matrice delle differenze per un dato polinomio. Di nuovo, x 2 sarà usato come esempio. Nota cosa succede: i termini del polinomio di varia potenza si cancellano, eccetto che per le costanti, che non sono uniformi nei termini
, e così via, come nell'esempio seguente:
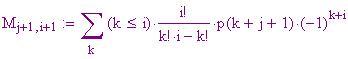

Dato un qualunque polinomio, sapreste determinare quale sarà la fila di costanti diverse da zero? Suggerimento: provate , poi
, poi
, e
.
Data questa informazione, il metodo può essere capovolto per trovare tutti gli altri valori del polinomio nei punti di numero intero; operatore unico è l'addizione. Questa procedura viene illustrata nella tabella che segue per . Questo procedimento deve iniziare con i primi
valori consecutivi
, cioè
. Da lì, verranno trovate le prime quattro differenze. La quarta differenza (o quinta colonna) sarà una colonna di costanti. Usando questa costante possiamo ricostruire termini aggiuntivi usando l'addizione, come si dimostra nella tabella sottostante.
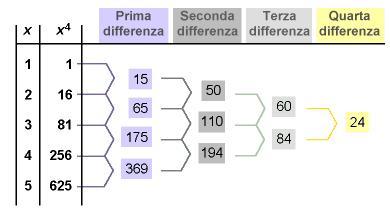
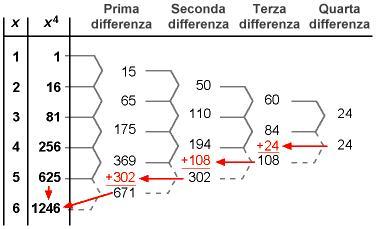
La quarta differenza viene usata per aggiungere un'ulteriore immissione alla terza differenza. Usiamo questo nuovo numero per trovare la successiva immissione nella fila delle seconde differenze. Si continua così fino a che non si trova una nuova immissione nella prima fila dei valori di costante, cioè, un valore per .
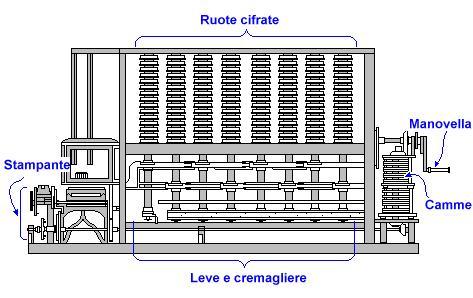
Meccanicamente, questo calcolo inizia girando la manovella a lato del motore differenziale nell'illustrazione all'inizio di questo documento. Ciò fa entrare in azione 14 paia di camme, che controllano la sincronizzazione dell'intero meccanismo.
Ci sono otto colonne di ingranaggi, ognuna delle quali contiene 31 ruote numerate, usate per fissare i valori di inizio del calcolo. Il motore deve essere preimpostato con numeri di inizio calcolati a mano, come si diceva sopra. Le ruote sono sbloccate e ruotate fino al valore iniziale corretto.
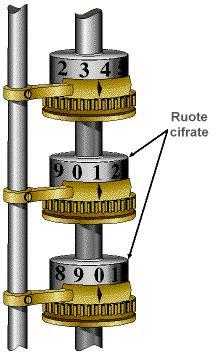
Le camme sono collegate alle otto colonne da cremagliere e bracci. Ogni giro del manubrio alza, abbassa e fa girare l'asse della colonna delle ruote numerate che compiono l'addizione delle differenze.
Il risultato finale del calcolo è contenuto nell'ultima colonna di ruote, collegata ad una macchina stampante. Questa macchina stampa un valore di trenta cifre per il polinomio ad ogni giro di manovella. Ad ogni giro il valore di immissione è aumentato automaticamente di uno ( ).
Questo metodo richiede un numero specifico di valori diversi di inizio basati sull'ordine del polinomio. Se l'equazione è di ordine , ci devono essere
valori calcolati (il polinomio stesso e le
differenze) per poter arrivare alle valutazioni polinomiche successive. Simuleremo ora il metodo delle differenze finite per
come veniva impiegato meccanicamente per trovare valori di f
. Diamo alla simulazione la serie di valori calcolati, che equivale a predisporre le ruote numerate.
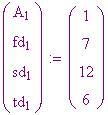
Vettore della prima risposta ad ogni colonna di differenze. Va notato che, per un polinomio di grado 3, sono necessari quattro valori iniziali .
Qui, corrisponde alla
esima immissione nella fila delle prime differenze. Nello stesso modo ,
corrisponde alle seconde differenze e
alle terze.
Una iterazione distribuita in un vettore emula il motore differenziale molto bene. Il meccanismo non poneva in memoria i numeri, ma li stampava man mano che venivano calcolati. L'ultima serie di risposte veniva conservata in registri per utilizzarla nella successiva serie di calcoli.
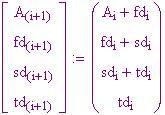
La seguente tabella e grafico fanno vedere le risposte calcolate con questo metodo. La tabella è sfalsata per far vedere le giuste relazioni delle differenze:
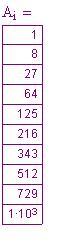
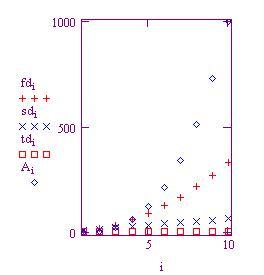
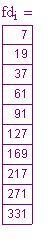
IL grafico mostra dieci valori per la funzione e ogni differenza. Va ricordato che ogni differenza riduce il grado di uno. Così, , la fila di valori di funzione è di terzo grado poiché
.
è di quarto grado, così il suo grafo è una parabola.————- di primo grado, così è lineare . Poiché
è un polinomio di grado zero – una costante – ciò spiega perché il grafo è una linea piatta.
Dato un qualunque polinomio . Il motore differenziale potrebbe trovare valori per
per ogni numero intero, se si avesse abbastanza pazienza e un braccio robusto. L'esempio che segue calcola
per i primi cento valori interi positivi di
.
Sei valori iniziali che corrispondono ad una equazione di quinto grado.
Le colonne delle differenze quinte(rappresentata dalla sesta colonna) dovrebbero essere costante
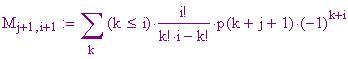
Questi sono i primi sei valori del polinomio (prima colonna) con la tabella delle differenze.

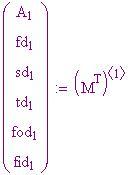
I valori di cui abbiamo bisogno per dare il via al procedimento iterativo rappresentano la prima fila della matrice qui sopra.
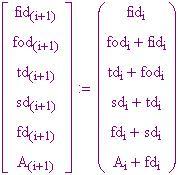
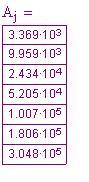
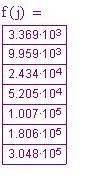
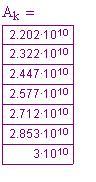

Da notare che il calcolo fa uso di logaritmi e funzioni esponenziali per determinare i valori di nei vari valori di
. La macchina di Babbage, invece, si serve solo della addizione!
Charles Babbage non vide mai la sua prodigiosa macchina pienamente operativa. Il suo Motore No.1 (una versione primitiva della No.2) era finanziata dal governo Britannico, che però abbandonò il progetto nel 1842 dopo aver speso 17,470 sterline e completando 12000 delle 25000 parti previste. Per avere un confronto, basti pensare che una delle prime locomotive a vapore costruita nel 1831 costò 784 sterline.
Avrebbe mai funzionato? Grazie al museo della scienza di Londra, un modello funzionante in scala 1:1 venne completato il 29 novembre 1991 per un costo di $500,000. Un'ultima nota finale: Babbage progettò anche il Motore Analitico, che era un computer programmabile tutto fare. Qualunque tipo di calcolo poteva esservi programmato, aveva una memoria, poteva accettare numeri fino a 50 cifre, dare risultati fino a 100 cifre e poteva stampare, perforare o tracciare il risultato prodotto. Se la tecnologia del silicio fosse stata a sua disposizione, chissà cosa avrebbe saputo creare Babbage.
La pseudosfera di Beltrami

La pseudosfera di Beltrami
Verso la fine degli anni sessanta del XIX secolo, il dibattito sulle geometrie non euclidee è particolarmente acceso.
Lobacevskj nel 1829 e Bolyai nel 1832 avevano scritto dei saggi in cui dimostravano la possibilità di geometrie differenti da quella di Euclide, in particolare geometrie nelle quali il famoso quinto postulato sulle parallele era diverso da quello euclideo: per un punto esterno a una retta passa più di una parallela alla retta data.
Le ricerche di questi matematici erano rimaste pressoché ignorate fino a che con la morte di Gauss (1855) e la pubblicazione del suo epistolario si viene a sapere che anche il sommo Gauss aveva avuto la stessa idea. L’interesse per questo problema fa emergere una memoria che Riemann , allievo di Gauss, aveva scritto nel 1854 ed era rimasta inedita: Sulle ipotesi che stanno a fondamento della geometria. 
La memoria pubblicata nel 1867 forniva un nuovo modo di intendere la geometria. Da un lato presentava la geometria come un caso particolare di un nuovo concetto matematico, la varietà pluridimensionale ; dall’altro presentava un secondo caso di geometria non euclidea, la geometria ellittica, nella quale non esistono rette parallele.
Incoraggiato dalle pubblicazioni di personaggi così celebri, il giovane matematico italiano Eugenio Beltrami si decide a dare alle stampe un suo manoscritto redatto qualche anno prima e messo da parte per paura delle aspre critiche che coinvolgevano chi si occupava di geometrie ‘astrali’ o ‘da manicomio’. Il suo Saggio di interpretazione della geometria non euclidea segna un punto di svolta nella ricerca geometrica su questo millenario problema.
 Beltrami aveva trovato un ‘substrato reale’ per la geometria di Lobacevskj, ossia aveva trovato all’interno della geometria euclidea, una superficie di rotazione, la pseudosfera , che poteva essere interpretata come un modello euclideo di geometria non euclidea. In questo modo dimostrava che la geometria di Lobacevskj ha lo stesso diritto logico-matematico della classica geometria di Euclide. Alla superficie aveva dato il nome di pseudosfera perché ha curvatura costante come una sfera ma di segno negativo.
Beltrami aveva trovato un ‘substrato reale’ per la geometria di Lobacevskj, ossia aveva trovato all’interno della geometria euclidea, una superficie di rotazione, la pseudosfera , che poteva essere interpretata come un modello euclideo di geometria non euclidea. In questo modo dimostrava che la geometria di Lobacevskj ha lo stesso diritto logico-matematico della classica geometria di Euclide. Alla superficie aveva dato il nome di pseudosfera perché ha curvatura costante come una sfera ma di segno negativo.
Per capire come avviene questa ‘traduzione’ occorre introdurre la nozione di geodetica . Nel piano il percorso più breve che unisce due punti si trova sulla retta passante per i due punti. Estendendo questo concetto alle superfici, il percorso più breve che unisce due punti della superficie si trova su di una linea, generalmente curva, detta geodetica. Per esempio, dovendosi muovere sulla superficie di una sfera, il percorso più breve non è quello rettilineo, perché non esistono percorsi di questo tipo, ma è l’arco di cerchio massimo, che in questo caso è una geodetica.
 La ‘traduzione’ si ottiene interpretando la superficie pseudosferica come piano di Lobacevski, le rette di questo piano sono le geodetiche della superficie.
La ‘traduzione’ si ottiene interpretando la superficie pseudosferica come piano di Lobacevski, le rette di questo piano sono le geodetiche della superficie.
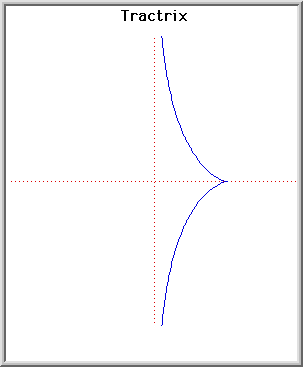
Tuttavia, alcuni matematici hanno perplessità circa la validità del ragionamento di Beltrami. Il punto più debole dell’argomentazione sta nel fatto che il modello ha valore locale e non può rappresentare globalmente la geometria non euclidea. Infatti, tra le infinite forme che una superficie pseudosferica può assumere si conosce l’espressione analitica solo di qualche caso particolare. Beltrami l’aveva ottenuta dalla rotazione di una curva studiata da F. Minding, la trattrice . Questa curva ha il difetto di avere un punto cuspidale, che ruotando dà origine a un cerchio di punti singolari della superficie: la superficie ottenuta dalla rotazione della trattrice quindi non è regolare e non può rappresentare interamente il piano non euclideo.
Il problema è allora se tra tutte le superfici, delle quali non si conosce l’espressione analitica, ne esiste almeno una che sia regolare. Beltrami ne è convinto ma non riesce a provarlo.
"Ho avuto un’idea bizzarra", scrive Beltrami a un suo amico matematico francese, Hoüel, "ho voluto tentare di costruire materialmente la superficie pseudosferica sulla quale si realizzano i teoremi della geometria non euclidea". Il modello materiale costruito in cartone aveva il diametro di 1,04 m; oggi è custodito presso il dipartimento di matematica dell’Università di Pavia.
 Soltanto nel 1901 Hilbert dimostra rigorosamente che il modello descritto da Beltrami ha un valore esclusivamente locale e non può essere accettato come prova matematica. Nel frattempo però altre dimostrazioni erano state già ottenute.
Soltanto nel 1901 Hilbert dimostra rigorosamente che il modello descritto da Beltrami ha un valore esclusivamente locale e non può essere accettato come prova matematica. Nel frattempo però altre dimostrazioni erano state già ottenute.
Il modello di Beltrami, pur non essendo un modello rigoroso, ha avuto un grande ruolo storico perché ha fornito la chiave per interpretare le nuove geometrie non euclidee.
Beltrami E., Saggio di interpretazione della geometria non-euclidea, in "Giornale di matematiche", (6) 1868, pp. 284-312.
Beltrami E., Sulla superficie di rotazione che serve di tipo alle superficie pseudosferiche, in "Giornale di matematiche", (10) 1872, pp. 147-159.
Beltrami E. Opere matematiche , Hoepli, Milano, 1902.
Bonola R., Il modello di Beltrami di superficie a curvatura costante negativa, in "Bollettino di bibliografia e storia delle scienze matematiche, 1906, pp. 33-38.
Capelo A.C., Ferrari M., La cuffia di Beltrami: storia e descrizione, in "Bollettino di storia delle scienze matematiche", 1982, pp. 233-247.
Nella rete
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Beltrami.html http://www.britannica.com/bcom/eb/article/2/0,5716,15522+1,00.html
http://chronomath.irem.univ-mrs.fr/chronomath/Beltrami.html
http://chronomath.irem.univ-mrs.fr/chronomath/DisqueBeltrami.html
http://chronomath.irem.univ-mrs.fr/chronomath/tractrice.html
L’immagine è presa da The MacTutor History of Mathematics archive
traduzione
superficie pseudosferica —> regione di piano non euclideo
punto della superficie —> punto del piano
geodetica arco di geodetica —> retta del piano, segmento del piano
due punti determinano una geodetica —> due punti determinano una retta del piano
per un punto esterno a una geodetica passano infinite geodetiche che non si incontrano con quella data —>
per un punto esterno a una retta passano infinite rette parallele alla retta data
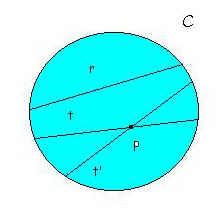
Un disegno nel piano del modello di Beltrami. La regione C colorata è il modello. Per il punto P esterno alla retta r passano almeno due rette, t e t’, che non incontrano la retta r.
Appunti su uno studio più vivo dell’analisi matematica
Un desiderio anzitutto: vorrei non essere preso sul serio, sia dagli studenti che dai docenti. Sono uno che fa un mestiere ben diverso dal pedagogista e quindi non ho le carte in regola per dare consigli a nessuno. Queste mie annotazioni sono frutto di un reinnamoramento estivo che però covava da tempo. Avete presente quando dopo una vita si reincontra l’oggetto, maturo anch’esso, di un lontanissimo amore giovanile?
Può essere devastante, se non si è serenamente appagati dalla vita che poi si è scelto di fare, ma se si è tranquilli, può essere fonte di sensazioni piacevoli, che non necessariamente devono portare a qualcosa di pericolosamente travolgente.
Per uno come me, sposato con soddisfazione reciproca alla scienza medica, riprendere in mano un libro di analisi matematica dopo trenta anni, mi ha dato quelle sensazioni piacevoli di cui prima parlavo. Il fatto poi che il libro l’abbia preso in prestito da un neodiplomato (che peraltro mi ha confessato di aver odiato profondamente la matematica) e che tale decisione sia stato il frutto di un proposito a lungo coltivato, mi ha spinto a prendere carta e penna per esporre ciò che mi frullava in testa: cosa, devo ammettere, che costa tempo e fatica, ma che poi si rivela sorprendentemente piacevole e appassionante. Lo stesso potrebbe non essere per chi legge.
Il problema è che a furia di veder rappresentati su un piano di assi cartesiani tanti parametri biologici, mi sono sempre più convinto che anche tanti stati d’animo, tanti andamenti biologici e perché no psichici possono in tal maniera essere rappresentati, forse troppo schematicamente ma comunque in maniera efficace.
Ma ve l’immaginate il significato di un’iperbole e di un suo asintoto? Potrebbe rappresentare l’amor platonico o per chi ha fede una vita verso la santità, insomma l’immagine di una tensione verso qualcosa che si potrà raggiungere solo all’infinito.
E perché non pensare a due parabole che toccano in un solo punto tangente come la rappresentazione di un rapporto occasionale; che se poi i punti sono due (di più non possono essere!) vuol dire che c’è stato un reincontro.
Se poi si vuol rappresentare la vita di due persone che stanno insieme, quale peggiore errore pensare a due rette coincidenti! La vita a due non può significare l’annullamento delle singole personalità e delle proprie esperienze di vita. Quale migliore rappresentazione schematica di due sinusoidi che si allontanano e si avvicinano fino ad intersecarsi. La vita a due, per durare, non può essere una coincidenza che vuol dire annullamento, ma un insieme di incontri e distacchi, perché sono per definizione utili per creare quelle tensioni (di allontanamento e di avvicinamento) che tengono vivo il rapporto. Questi punti di incontro possono essere al di sopra e al di sotto della linea delle ascisse, perché gli incontri si possono verificare quando due sono su di giri per festeggiare o giù di corda per consolarsi; la cosa più bella si verifica quando le due sinusoidi da piani opposti tendono ad avvicinarsi fino ad incontrarsi, perché allora vuol dire che c’è stato da parte di entrambi una voglia di andarsi incontro, l’uno risalendo da uno stato di depressione, l’altro rinunciando ad una parte del suo benessere per amore. Fantastica immagine!
L’intensità del rapporto intuitivamente sarà dato dalla densità di incontri (numero per un determinato periodo di tempo): avremo così modi diversi di rappresentare un rapporto tra due persone tranquille (mi verrebbe di dire anziane, ma ho conosciuto coppie arzille di settantenni che la danno abbondantemente a coppie giovani) rispetto a una coppia di persone focose. Peraltro non basta dire numero di incontri nel tempo, perché un elevato numero di incontri nello stesso intervallo di tempo può avvenire perché le due curve si allontanano pochissimo e quasi si confondono (pensiamo a due sposini in viaggio di nozze, felice) oppure con curve che si allontanano bruscamente, ma dopo aver raggiunto notevoli lontananze, altrettanto rapidamente si avvicinano fino ad incontrarsi (insomma un rapporto tumultuoso ma travolgente). Alla luce di queste considerazioni è importante quindi per una più veritiera rappresentazione del rapporto di coppia andare a valutare da derivata della sinusoide, cioè il coefficiente angolare della retta tangente alla curva nel momento che andiamo ad esaminare, configurando curve a più basso coefficiente angolare rapporti di coppia più tranquilli e rarefatti (prossimi alla pace dei sensi), e viceversa rapporti di coppia da odi et amo curve con derivata maggiore.
Che se poi vogliamo dirla tutta, se è vero come è scritto sui sacri testi che l’integrale definito di una funzione in un determinato intervallo rappresenta l’area del trapezoide sotteso tra il grafico della funzione e l’asse delle ascisse, dobbiamo immaginare che esso possa rappresentare il cumulo di esperienze, positive e/o negative che porta all’allontanamento e all’avvicinamento reciproco dei due componenti la coppia.
Certamente l’ideale per una società monogamica è la presenza per ogni piano di assi cartesiani di una sola coppia di sinusoidi chiuse che si incontrano tra di loro e solo tra di loro. Il problema è la rappresentazione di tutta quella serie di rapporti multipli e irregolari che sono sempre più frequenti attualmente: credo che bisognerebbe ricorrere a funzioni irregolari, aperte, a più variabili e ovviamente non basterebbe più un banale piano di assi cartesiani ma si dovrebbe ricorrere a spazi tridimensionali e forse ….immaginari!
Non voglio tediarvi ulteriormente con questo avvilupparsi immaginario di curve, tangenti e via discorrendo, ma mi chiedo e vi chiedo: è possibile rendere più vivo lo studio della matematica e in tal maniera affascinare qualche giovane apatico non parlando solo di punti, rette, curve, funzioni, ma di momenti di vita che si modificano in continuazione, in “funzione” di qualcosa o di qualcuno? Per esempio considerare l’asse delle ascisse come uno stato di neutralità, impossibile da mantenere, spesso attraversato, e comunque utile per potersi orientare tra momenti positivi e negativi? La mia abitudine a rappresentare mentalmente in maniera quasi automatica tanti eventi della vita come su un piano di assi cartesiani, è l’effetto dei miei studi giovanili di matematica e non può essere trasmesso a tanti ragazzi che odiano tale materia?
Tutti sanno che le nuove idee nascono in ambienti non verbali e non logici e solo più tardi vengono tradotti nei linguaggi simbolici. Meglio non parlare dei sentimenti che difficilmente, con estrema fatica e solo in minima parte riescono ad essere espressi dalla comunicazione verbale (pensate alla “fatidica” dichiarazione d’amore!). Trascurando queste forme preverbali di pensiero probabilmente si frustano le capacità inventive di molti studenti. Oltretutto i matematici e molti studiosi di scienze fisiche, come ha testimoniato lo stesso Einstein, raggiungono intuizione visuali, muscolari e tattili e solo “in un secondo tempo devono essere laboriosamente cercate parole convenzionali e/o altri segni”. In pratica le cose scoperte sensitivamente, emozionalmente, intuitivamente e privatamente devono essere trasformate in espressioni pubbliche usando il linguaggio delle rispettive discipline.
Alla luce di queste considerazioni due quindi devono essere gli obiettivi da raggiungere:
– fornire ai giovani una ricca gamma di strumenti creativi, come l’usare immagini, astrazioni, modelli, analogie;
– allenarli ad acquisire le capacità di tradurre ciò che hanno imparato grazie a questi strumenti in linguaggi formali, simbolici, come le parole, i simboli matematici, la musica, la danza (a tal proposito non è strano che un gruppo di fisici a Parigi elaborò ed eseguì una danza per capire come ci si sente nell’interagire come elettroni!!).
Per ottenere tutto ciò c’è bisogno di un grande sforzo di immaginazione e di empatia, che non deve interessare, come è sempre stato concepito, solo i docenti di materie letterarie, di filosofia, di arte, di musica, ma può e deve essere perseguito anche da professori di materie scientifiche, che, con l’utilizzo di ponti interdisciplinari, devono “elevarsi” ad un insegnamento “volgare” della matematica, delle categorie formali in essa usate, affabulando e coinvolgendo gli studenti.
Molti avranno letto il libro di … ”Flatlandia” (ed. Adelphi) in cui si immagina un mondo a due dimensioni: chi non l’ha fatto è invitato a farlo. Ebbene il fascino e il gusto di una tale lettura è stato per me direttamente proporzionale alle solide basi di matematica formale trasmessemi dal mitico prof. V. Lorusso; ma mi sono molto rammaricato di non aver avuto la possibilità, con la mente e gli studi freschi di qualche decennio fa, di immaginare da me un mondo del genere.
Dr. Onofrio Caputi-Lambrenghi
Ciao, chi sei?

| Ciao, chi sei? | ||
| Studente superiori | 486 | 33,7% |
| Studente università | 417 | 28,9% |
| Docente | 151 | 10.5% |
| Appassionato | 108 | 7,5% |
| Studente medie | 100 | 6,9% |
| Ho sbagliato sito | 94 | 6,5% |
| Curioso | 70 | 4,9% |
| Ricercatore | 10 | 1.1% |
Geometrie non euclidee
Le geometrie non euclidee
Le geometrie non euclidee partono da postulati opposti a quello di Euclide sulla rette parallele, in particolare dalle due negazioni possibili del V postulato .
Un modo equivalente per esprimere questo postulato di Euclide è il seguente:
P1) In un piano, per un punto esterno a una retta data esiste un’unica retta passante per il punto dato e parallela alla retta data.
Un teorema che consegue da questo postulato è il seguente:
T1) In un triangolo, la somma degli angoli interni è 180°.
Nel 1829, N. Lobacevskij , e più o meno contemporaneamente l’ungherese J. Bolyai , costruirono una geometria, risultata poi altrettanto coerente matematicamente di quella di Euclide, secondo la quale
P2) per un punto esterno a una retta data passa più di una retta parallela (se ne esiste più di una ne esistono infinite).
Come conseguenza,
T2) in un triangolo, la somma degli angoli interni è minore di 180°
Nel 1854, B. Riemann , in uno studio globale sulla geometria, ipotizzo la possibilità di una terza geometria, nella quale
P3) per un punto esterno a una retta data non passa alcuna parallela.
Come conseguenza,
T3) in un triangolo, la somma degli angoli interni è maggiore di 180°.
Le tre geometrie sono state più correttamente definite da F. Klein , rispettivamente, geometria parabolica, iperbolica ed ellittica.
Per immaginare le due geometrie distinte da quella euclidea si può fare ricorso a dei ‘modelli’.
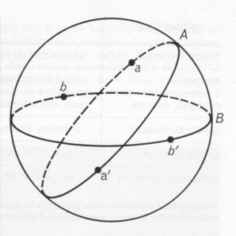
Per la geometria ellittica o riemanniana, Invece del piano consideriamo la superficie di una sfera e traduciamo gli elementi geometrici del piano in corrispondenti elementi geometrici sulla superficie della sfera.
I punti del piano corrispondono a punti della superficie della sfera. Le rette del piano corrispondono alle circonferenze massime della superficie sferica. In generale, si fanno corrispondere alle rette del piano le linee geodetiche di una superficie curva. Queste ultime infatti conservano la principale caratteristica delle rette e precisamente sono le linee più brevi che sulla superficie congiungono due punti dati. Sulla superficie della sfera le geodetiche sono proprio le circonferenze massime, cioè quelle circonferenze che si ottengono intersecando la superficie della sfera con piani passanti per il centro della sfera. Esempi familiari sono i meridiani e l’equatore, non lo sono i paralleli.
Sulla superficie della sfera non esistono ‘rette’ o meglio geodetiche che non si incontrano, quindi non esistono parallele.
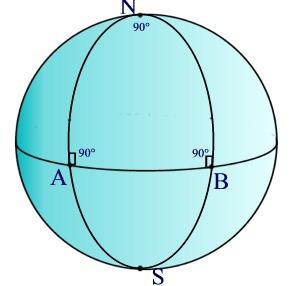 Nella figura sono rappresentati due meridiani perpendicolari all’equatore e che si incontrano perpendicolarmente al polo Nord. Si vede che la somma degli angoli interni del triangolo curvilineo ABN è 270°. In generale la somma degli angoli interni di un triangolo di questo tipo è sempre maggiore di 180° e non è costante per tutti i triangoli. Mentre nella geometria euclidea la somma degli angoli interni di un triangolo è sempre 180°, nella geometria ellittica la somma degli angoli interni del triangolo è variabile e dipende dalla grandezza del triangolo.
Nella figura sono rappresentati due meridiani perpendicolari all’equatore e che si incontrano perpendicolarmente al polo Nord. Si vede che la somma degli angoli interni del triangolo curvilineo ABN è 270°. In generale la somma degli angoli interni di un triangolo di questo tipo è sempre maggiore di 180° e non è costante per tutti i triangoli. Mentre nella geometria euclidea la somma degli angoli interni di un triangolo è sempre 180°, nella geometria ellittica la somma degli angoli interni del triangolo è variabile e dipende dalla grandezza del triangolo. 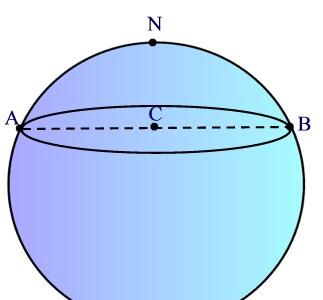
Un’altra caratteristica di questo tipo di geometria è che il rapporto tra circonferenza e raggio è minore di PIGRECO.
Infatti, la circonferenza di diametro AB non ha centro in C ma in N, ricorda che siamo sulla superficie della sfera, mentre C è posto dentro la sfera. Poiché evidentemente l’arco AN è maggiore del segmento AC, il rapporto tra la circoferenza AB e il suo raggio AN è minore di PIGRECO.
Un modello intuitivo, dadatticamente utile per la geometria iperbolica o di Lobacevskj è un po’ più complesso. In particolare, non esiste un modello che rappresenti globalmente una geometria di questo tipo. Si può prendere una superficie a forma di sella, o meglio la pseudosfera (vedi scheda sulla pseudosfera di Beltrami ).
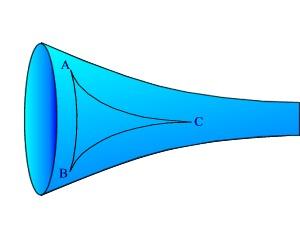
Il triangolo curvilineo ABC su un pezzo di pseudosfera è il corrispondente di un triangolo rettilineo del piano euclideo, perché è composto da linee geodetiche. La somma degli angoli interni di questo triangolo è minore di 180° e dipende dalla grandezza del triangolo.
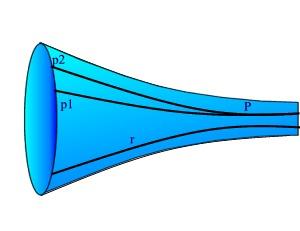
Per il punto P, esterno alla geodetica r, passano più geodetiche (p1 e p2) che non incontrano la geodetica r e che quindi sono parallele a r.
Antonio Bernardo
P. Parrini, Fisica e geometria dall’Ottocento a oggi , Loescher, Torino, 1979
P. Freguglia, Fondamenti storici della geometria, Feltrinelli, Milano,1982
R. Bonola, La geometria non euclidea, esposizione storico critica del suo sviluppo, Zanichelli, Bologna, 1906
R Trudeau, La geometria non euclidea, Bollati Boringheri, Torino, 1991
Cinque modi per moltiplicare due numeri
Cinque modi per moltiplicare due numeri
Chi te domanda affinche fa 1234 fia 56789 fa per li cinqe modi qui sottoscritti
 |
E’ il classico algoritmo utilizzato ancora oggi |
 |
E’ una semplice variante del precedente |
 |
E’ una variante del precedente. I risultati parziali della moltiplicazione non si fanno scalare di un posto ma si riscrivono allineati. Per ottenere il risultato si somma lungo le diagonali del reticolo. Il risultato si legge lungo i bordi partendo da quello orizzontale. |
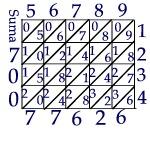 |
E’ la moltiplicazione detta a graticola. Nelle caselle della grata si scrivono i risultati ottenuti dalla moltiplicazione delle cifre: 1×9=09, 2×9=18. Infine si somma lungo le diagonali, partendo dal basso a destra: |
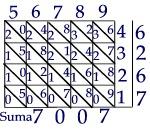 |
E’ una variante del precedente. |
Questi algoritmi di calcolo sono presi da Larte del Labbacho , di autore ignoto e stampato a Treviso nel 1478, praticamente a soli 23 anni dalla prima stampa a caratteri mobili, inventata da Gutemberg.
Nel testo sono usati i simboli e il sistema di numerazione posizionale arabo. Il sistema di numerazione romano era stato abbandonato da tempo perché poco pratico rispetto a quello importato dall’oriente. Già nel 1348, l’Università di Padova aveva raccomandato di esporre tutti i prezzi delle merci con i numeri arabi.
Questo sistema di numerazione era stato importato da Fibonacci e riportato nel suo Liber Abbaci , 1202. Fibonacci l’aveva definito indiano.
Gli algoritmi presentati qui costituiscono un enorme semplificazione nel calcolo rispetto ai sistemi di numerazione non posizionali e privi dello zero, come quello romano.
Il penultimo metodo, detto a graticola, non è più usato ma risulta a volte molto più semplice di quello in uso attualmente e può essere utilizzato a scopo didattico.
E’ detto a ‘graticola’ o a ‘gelosia’. Nella Summa de Arithmetica , 1494, di Luca Pacioli è spiegato l’uso del termine: gelosia intendiamo quelle graticelle che si costumano mettere alle finestre de le case dove habitano done, acio che non si possino facilmente vedere.
Il libro Larte del Labbacho è stato ristampato in copia anastatica dall’Editore Zoppelli nel 1969.
Antonio Bernardo
Eratostene e la misura della Terra
Eratostene e la misura della Terra
Non sempre si riesce, nell’insegnamento della matematica, a trovare situazioni problematiche reali che introducano le tecniche di calcolo da studiare. Un esempio può essere questo classico problema: come fecero gli antichi scienziati a calcolare la grandezza della Terra?
Gli obiettivi specifici che si possono raggiungere riguardano la risoluzione di problemi usando proprietà geometriche delle figure e, più in generale, esplorare, descrivere e rappresentare lo spazio . I nuclei trasversali: misurare, argomentare e congetturare, risolvere e porsi problemi . Il processo del misurare è trasversale a tutte le discipline di tipo tecnico. L’argomentare riguarda il passaggio dai livelli operativi e manuali a forme di pensiero astratto, da forme di nozioni intuitive all’argomentazione o dimostrazione matematica. Nel caso della misura della Terra da parte degli antichi scienziati, gli allievi constatano l’impossibili di procedere in modo manuale e riconoscono la necessità di un processo mentale superiore. L’ultimo nucleo essenziale colma il passaggio dalle conoscenze acquisite in forma di nozioni alla loro applicazione in situazioni concrete.
Altre competenze trasversali riguardano la collocazione nel tempo e nello spazio degli eventi, la capacità di costruire ragionamenti, formulare ipotesi e congetture, generalizzare i risultati, comprendere il senso dell’invenzione matematica, stabilire relazioni tra fatti apparentemente indipendenti, osservare il processo che va dal porsi il problema al raggiungere la soluzione.
Il fatto
Collocazione storica. Eratostene vive nel III secolo a.C., studia ad Atene e successivamente si trasferisce ad Alessandria per dirigere la più grande biblioteca fino allora mai esistita. La città di Alessandria era stata fondata da Alessandro Magno che aveva esteso i territori greci conquistando un immenso impero e contestualmente aveva posto le basi per l’espansione della cultura greca. Proprio ad Alessandria la cultura scientifica greca raggiunge livelli elevatissimi.
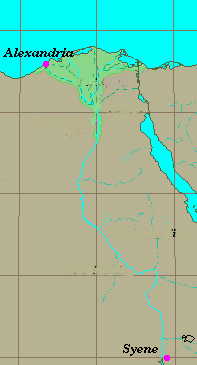
 Collocazione geografica . Il fatto si svolge tra Alessandria, che si trova alla foce del Nilo e l’attuale Assuan, allora chiamata Syene. I due luoghi si trovano in una posizione geografica che è cruciale per l’esperienza in questione: Syene si trova ‘quasi’ sul Tropico del Cancro e Alessandria si trova a nord di Syene, ‘quasi’ sullo stesso meridiano terrestre.
Collocazione geografica . Il fatto si svolge tra Alessandria, che si trova alla foce del Nilo e l’attuale Assuan, allora chiamata Syene. I due luoghi si trovano in una posizione geografica che è cruciale per l’esperienza in questione: Syene si trova ‘quasi’ sul Tropico del Cancro e Alessandria si trova a nord di Syene, ‘quasi’ sullo stesso meridiano terrestre.
Il problema . Era già noto che la Terra avesse una forma sferica. Una tale convinzione derivava dal fatto che durante le eclissi di Luna, la forma dell’ombra terrestre appare sempre come un arco di circonferenza. Il problema più stimolante non era quello qualitativo di accertarne la forma ma quello quantitativo di misurarne la grandezza. In altre parole assodato che la Terra ha una forma sferica quanto misura la sua circonferenza? Come si poteva misurare questa grandezza se le distanze in gioco erano enormi per quei tempi e gli oceani costituivano un ostacolo insormontabile?
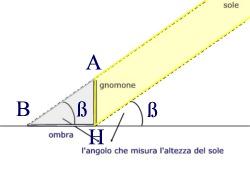
 La strumentazione tecnica . Lo strumento di cui si serve Eratostene è incredibilmente semplice, un banale bastone piantato verticalmente in un terreno perfettamente pianeggiante: lo gnomone . Studiando l’ombra che si genera si possono seguire i movimenti del Sole. Durante il giorno, il momento in cui l’ombra è più corta corrisponde a mezzogiorno. Lo gnomone permette di seguire anche il cambio delle stagioni: il giorno in cui a mezzogiorno l’ombra è più corta è il solstizio d’estate ; sei mesi dopo, l’ombra a mezzogiorno è la più lunga ed è il solstizio d’inverno . Infine si può stabilire in ogni momento l’altezza del Sole, ossia l’angolo ß che i suoi raggi formano con la linea dell’orizzonte, confrontando semplicemente la lunghezza del bastone AH con la sua ombra BH.
La strumentazione tecnica . Lo strumento di cui si serve Eratostene è incredibilmente semplice, un banale bastone piantato verticalmente in un terreno perfettamente pianeggiante: lo gnomone . Studiando l’ombra che si genera si possono seguire i movimenti del Sole. Durante il giorno, il momento in cui l’ombra è più corta corrisponde a mezzogiorno. Lo gnomone permette di seguire anche il cambio delle stagioni: il giorno in cui a mezzogiorno l’ombra è più corta è il solstizio d’estate ; sei mesi dopo, l’ombra a mezzogiorno è la più lunga ed è il solstizio d’inverno . Infine si può stabilire in ogni momento l’altezza del Sole, ossia l’angolo ß che i suoi raggi formano con la linea dell’orizzonte, confrontando semplicemente la lunghezza del bastone AH con la sua ombra BH.
Nella città di Syene, il giorno del solstizio d’estate, a mezzogiorno, il bastone non dà ombra, il che significa che i raggi del Sole cadono perpendicolarmente al terreno: il Sole si dice che è allo zenit .
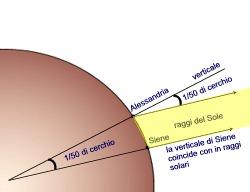
L’argomentazione . A mezzogiorno d’estate Eratostene misura l’altezza del Sole nella città di Alessandria. Poiché sa che in quel momento il Sole è perfettamente perpendicolare a Syene, ottiene l’angolo tra la verticale ad Alessandria e la verticale a Syene. Questo angolo è esattamente quello formato dal raggio della Terra che ha per estremo Alessandria e dal raggio che ha per estremo Syene. L’angolo risulta essere 1/50 dell’intera circonferenza, in gradi 7° e 12′. Quindi , Eratostene deduce che la circonferenza della Terra doveva essere 50 volte la distanza tra Alessandria e Syene. Poiché la distanza tra le due città era misurata in 5.000 stadi (circa 800 km attuali), dedusse per la circonferenza terrestre la misura di 250.000 stadi (circa 40.000 km attuali).
Congetture nascoste . Questa argomentazione richiede in realtà l’assunzione di altre ipotesi: che la Terra sia perfettamente sferica, che il Sole sia così distante dalla Terra da poter considerare paralleli i raggi del Sole ad Alessandria con quelli a Syene, che le due città siano esattamente sullo stesso meridiano terrestre, che sia possibile misurare correttamente la distanza tra le due città. Tutte queste circostanze rendono la misura di Eratostene, così incredibilmente vicina a quella reale di 40.009, una fortuita coincidenza.
R.Osserman, Poesia dell’universo. L’esplorazione matematica del cosmo, Longanesi & C., Milano, 1996.
L.Russo, La rivoluzione dimenticata. Il pensiero scientifico greco e la scienza moderna, Feltrinelli, Milano 1996.
http://www.vialattea.net/eratostene/
http://www.cd-astro.org/quaderni/eratostene/eratostene.html
http://www.bpchamp.com/part/tlaurent/pedago/eratosthene/eratosthene.htm
Equazione di terzo grado
La formula risolutiva per l’equazione di terzo grado
 La storia del rinvenimento della formula risolutiva dell’equazione di terzo grado si sviluppa nella prima metà del 1500. Come tutte le storie, soprattutto quelle in cui sono coinvolte più persone, è piuttosto intricata e difficile da ricostruire. I personaggi sono tutti italiani: Scipione dal Ferro, il suo allievo Antonio Maria Fior, Niccolò Fontana, detto Tartaglia, e Gerolamo Cardano.
La storia del rinvenimento della formula risolutiva dell’equazione di terzo grado si sviluppa nella prima metà del 1500. Come tutte le storie, soprattutto quelle in cui sono coinvolte più persone, è piuttosto intricata e difficile da ricostruire. I personaggi sono tutti italiani: Scipione dal Ferro, il suo allievo Antonio Maria Fior, Niccolò Fontana, detto Tartaglia, e Gerolamo Cardano.
La difficoltà storica di attribuire la paternità di una formula è legata alle motivazioni socio-economiche che spingono questi matematici verso la ricerca scientifica. Da un lato c’è l’urgenza di scoprire le leggi della balistica, dall’altro la bravura di un matematico si misura con sfide pubbliche, delle vere e proprie gare di matematica. In entrambi i casi, la scoperta di una formula che permettesse di risolvere i problemi allora in voga era un segreto da custodire gelosamente.
Il 22 febbraio 1535 si tiene una sfida tra Tartaglia e Fior: ciascuno propone all’altro trenta problemi da risolvere nel più breve tempo possibile. Tartaglia risolve rapidamente i problemi di Fior, mentre quest’ultimo non riesce a risolverne nessuno.
 Tutti i problemi si risolvevano per mezzo di equazioni di terzo grado; quelli proposti da Fior potevano essere ricondotti tutti all’unico tipo che conosceva di equazione di terzo grado, la cui formula risolutiva gli era stata rivelata dal suo maestro Scipione dal Ferro. La schiacciante vittoria di Tartaglia dimostrava che questi aveva trovato un metodo per risolvere tutte le equazioni di terzo grado.
Tutti i problemi si risolvevano per mezzo di equazioni di terzo grado; quelli proposti da Fior potevano essere ricondotti tutti all’unico tipo che conosceva di equazione di terzo grado, la cui formula risolutiva gli era stata rivelata dal suo maestro Scipione dal Ferro. La schiacciante vittoria di Tartaglia dimostrava che questi aveva trovato un metodo per risolvere tutte le equazioni di terzo grado.
La notizia giunge a Cardano, medico, scienziato e astrologo dalla fama internazionale. Cardano cerca di convincere Tartaglia a rivelargli la formula, lo lusinga, lo minaccia, gli fa promesse. Dopo numerose insistenze Tartaglia cede richiedendo che la formula restasse segreta.
Occorre precisare che proprio in questo periodo comincia a svilupparsi il simbolismo matematico del calcolo letterale. I matematici arabi, da cui gli italiani avevano appreso il calcolo algebrico e i metodi per risolvere le equazioni, usavano un linguaggio geometrico, in parte in uso ancora oggi: il cubo, il quadrato, il lato. Per esempio l’equazione x3 +6x=20 veniva scritta "il cubo e sei volte il lato è uguale a venti".
Tartaglia invia a Cardano i seguenti versi
Quando che ‘l cubo con le cose appresso $x^3 +px$
Se agguaglia a qualche numero discreto: $= q$
Trovami dui altri, differenti in esso; $u-v = q$
Dapoi terrai, questo per consueto,
Che ‘l loro produtto, sempre sia eguale $u*v =$
Al terzo cubo delle cose netto; $(p/3)^3$
El residuo poi suo generale,
Delli lor lati cubi, ben sottratti $
oot{3}{u} –
oot{3}{v}$
Varrà la tua cosa principale. $= x$
In el secondo, de cotesti atti;
Quando che ‘l cubo, restasse lui solo,
Tu osserverai quest’altri contratti,
Del numer farai due tal part’ a volo,
Che l’ una, in l’ altra, si produca schietto,
El terzo cubo delle cose in stolo;
Delle quali poi, per commun precetto,
Terrai li lati cubi, insieme gionti,
El cotal somma, sarà il tuo concetto;
El terzo, poi de questi nostri conti,
Se solve col secondo, se ben guardi
Che per natura son quasi congionti,
Questi trovai, et non con passi tardi
Nel mille cinquecent’ e quattro e trenta;
Con fondamenti ben saldi, e gagliardi;
Nella Città del mar ‘intorno centa.
Nel 1545, contravvenendo alla promessa verso Tartaglia, Cardano pubblica nell’Ars magna la formula risolutiva delle equazioni di terzo grado. Invece di trattare la formula generale con il complesso linguaggio che ne sarebbe derivato, Cardano affronta un caso particolare, un esempio diremmo oggi, sottintendendo che il metodo si può applicare a qualsiasi caso.
Partiamo dall’equazione $x^3+6x=20$ applicando il procedimento di Tartaglia si ha
1) $u-v=20$
2) $uv = frac{216}{27}=8$
sostituendo la 1) nella 2) si ottiene
3) $(20+v)cdot v = 8$ da cui $v^2+20v-8=0$
Infine $x=
oot{3}{sqrt{108}+10}-
oot{3}{sqrt{108}-10}$
oot{3}{sqrt{(frac{p}{3})^3+(frac{q}{2})^2}+frac{q}{2}}-
oot{3}{sqrt{(frac{p}{3})^3+(frac{q}{2})^2}-frac{q}{2}}$
Qualche decennio dopo, Ludovico Ferrari perviene alla risoluzione, con radicali quadratici e cubici, dell’equazione generale di 4° grado, riducendola al 3° grado.
Si pensò che si potessero risolvere le equazioni algebriche di ogni ordine. Tuttavia, già l’equazione di 5° grado divenne un ostacolo insormontabile. Solo nel 1799 Paolo Ruffini e nel 1828 il norvegese Niels Abel, indipendentemente l’uno dall’altro, dimostrarono che per una equazione algebrica di grado superiore al 4° non è possibile esprimere le radici per mezzo di un numero finito di operazioni razionali e di estrazioni di radici.
Alcuni problemi posti da Fior
-Trovare un numero che, sommato alla sua radice cubica, dia come risultato sei.
-Un ebreo presta un capitale a condizione che alla fine dell’anno gli venga pagata come interesse la radice cubica del capitale. Alla fine dell’anno, l’ebreo riceve ottocento ducati, tra capitale e interessi. Qual era il capitale?
Alcuni problemi posti da Tartaglia
-Un vascello sul quale si trovano quindici turchi e quindici cristiani viene colpito da una tempesta e il capitano ordina di gettare fuori bordo la metà dei passeggeri. Per sceglierli si procederà come segue: tutti i passeggeri verranno disposti in cerchio e, cominciando a contare a partire da un certo punto, ogni nono passeggero verrà gettato in mare. In che modo si devono disporre i passeggeri perché solo i turchi siano designati dalla sorte per essere gettati a mare?
-Suddividere un segmento di lunghezza data in tre segmenti con i quali sia possibile costruire un triangolo rettangolo.
-Una botte è piena di vino puro. Ogni giorno se ne attingono due secchi, che vengono sostituiti con due secchi d’acqua. In capo a sei giorni, la botte è piena per metà d’acqua e per metà di vino. Qual era la sua capacità?
Bibliografia essenziale
C. B. Boyer, Storia della matematica, Mondadori, Milano, 1980, pp. 328-331.
G. Loria, Storia delle matematiche, Hoepli, Milano, 1950, pp. 302-303.
M. Klein, Mathematical thought from ancient to modern times, Oxford University Press, New York, 1972, pp. 263-270.
Su Internet
http://www.unife.it/tesi/A.Montanari/algebra.htm
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Ferro.html
http://www.lib.virginia.edu/science/parshall/algebra.html#CARD
http://www.mbservice.it/scuola/tartaglia/le_equazioni_di_terzo_grado.htm
http://www.dmf.bs.unicatt.it/~paolini/divulgazione/matopin/NGB/articolo.html
Analisi funzionale
Cos'è l'analisi funzionale
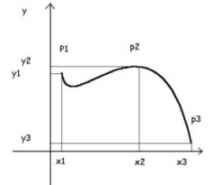 |
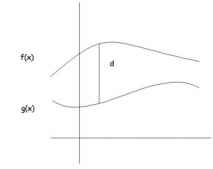
La rappresentazione grafica di una funzione fa ormai parte della cultura comune: il grafico della temperatura in un certo posto al passare del tempo, il grafico dei profitti e delle perdite di una società, il grafico della temperatura di un malato. Si dice che una certa grandezza y è funzione di un'altra grandezza x, se per ogni valore di x la funzione determina in modo univoco un valore di y. (fig. 1) Lo studio delle funzioni è stato sviluppato nel calcolo infinitesimale classico da Newton , Leibnitz , Cauchy , Weierstrass . L'Analisi Funzionale nasce alla fine del XIX secolo e si sviluppa nel XX; il nome è dovuto al matematico francese Hadamard . Tra i più celebri matematici italiani che hanno contribuito alla sua nascita è da ricordare Vito Volterra . Questa nuova e più astratta analisi non studia le singole funzioni o un numero finito di esse bensì una famiglia infinita di funzioni. Il suo problema principale è quello di organizzare questa famiglia in maniera da poterne studiare le proprietà. Si parla perciò di spazio funzionale , attribuendo alla parola spazio un significato più ampio di quello comunemente inteso. Il primo passo che bisogna compiere per organizzare lo spazio delle funzioni è quello di fissare un metodo per misurare la distanza tra una funzione e un'altra, o in modo equivalente quello di stabilire quanto una funzione si differenzia da un'altra. Osserviamo, intanto, che il modo di misurare le distanze non è univoco. Prendiamo un esempio banale. Che distanza c'è tra Lecce e Torino? Se ne può misurare la distanza in linea d'aria ma se andiamo in automobile questa informazione non ci interessa, ci interessa sapere quanta strada bisogna percorrere per arrivare a Roma. Se invece andiamo in treno non ci interessa quanta strada il treno deve percorrere ma quanto tempo ci vuole per arrivare. Se andiamo in aereo ci interessa essenzialmente il costo del biglietto. Assegnare una distanza in senso lato significa attribuire ai due enti, Lecce e Torino nell'esempio, un numero. Questo numero ci permette di fare confronti tra le varie coppie di enti, per esempio ci può servire per confrontare Lecce-Torino con Lecce-Milano o con Palermo-Venezia. In termini matematici parliamo di un spazio metrico. In che modo possiamo misurare la distanza tra una funzione e un'altra? Un modo semplice può essere quello di considerare il massimo scarto tra le due funzioni: si considerano tutte le differenze f(x)-g(x) e si individua quella che in valore assoluto è la maggiore (fig. 2) Vediamo un esempio pratico. f(x) rappresenta i ricavi di un'azienda e g(x) le sue spese, la distanza in questo caso è data dal guadagno massimo registrato in un giorno. Un altro esempio. f(x) rappresenta la temperatura di Lecce e g(x) quella di Torino; la distanza, in questo caso, è data dalla differenza massima di temperatura registrata nello stesso giorno a Lecce e a Torino. Se invece si è più interessati a una distanza media, si deve considerare l'area racchiusa tra i due grafici (fig. 3). In questo caso sapremo per esempio la differenzia media di temperatura tra Lecce e Torino. E' evidente però che il modo di misurare la distanza tra due enti, pur essendo arbitraria, deve sottostare a delle limitazioni, alcune delle quali molto evidenti. Proprietà triangolare : andare direttamente da Roma a Milano deve necessariamente essere più conveniente che passare per un'altra città; al più può essere indifferente se quest'ultima città si trova sul nostro percorso. Usando un pizzico di simbolismo d(A,B) < oppure = d(A,C) + d(C,B) Una seconda proprietà, o assioma, è fin troppo ovvia per il modo usuale di ragionare. Tuttavia i matematici, abituati a snidare mostruosità logiche proprio nelle cose apparentemente ovvie, ci tengono a esplicitarla. Un elemento ha distanza nulla da se stesso . La terza proprietà sembra ovvia a prima vista ma riflettendoci un po' su non lo è. Si richiede infatti che la distanza da A a B sia la stessa di quella da B a A . Un semplice esempio. A si trovi al livello del mare e B a 500 m di altezza. Dovendo andare in bicicletta è evidente che il percorso BA è più piacevole e più 'breve' del percorso AB. Nel caso in cui valga quest'ultima proprietà si parla di distanze simmetriche , nel caso opposto si parla di distanze asimmetriche . Di gran lunga più complesso è il problema di estendere il concetto di dimensione tipico dello spazio geometrico allo spazio funzionale. Vi sono diversi modi per individuare le dimensioni di un ente geometrico. Per esempio, se siamo in autostrada possiamo andare solo avanti o indietro; questo fatto ci dice che siamo in uno 'spazio' a una dimensione. Se siamo in campagna possiamo andare avanti e indietro, a destra e a sinistra: questa doppia possibilità di scelta ci dice che siamo in uno 'spazio' a due dimensioni. Se siamo sott'acqua, o siamo in aereo, possiamo andare avanti-indietro, destra-sinistra, su – giù: tre possibilità di muoverci corrispondono a tre dimensioni. Un altro modo è il seguente. Un segmento di un metro scomposto in centimetri si divide in 100 parti. Un quadrato di lato un metro scomposto in quadrati di lato un centimetro si divide in 1002 parti. Un cubo di lato un metro scomposto in cubi di lato un centimetro si scompone in 1003 parti. L'esponente del numero 100 ci dice qual è il numero di dimensioni dell'oggetto considerato. Gli spazi funzionali più interessanti dal punto di vista matematico e applicativo hanno purtroppo dimensione infinita . Si parla in questi casi di spazi di Hilbert . Uno spazio a una dimensione ha bisogno di una coordinata per individuare i suoi punti. Uno spazio a due dimensione ne ha bisogno di due, e così via. Uno spazio a infinite dimensioni necessita di una quantità infinita di coordinate. In uno spazio così mostruoso l'intuizione matematica non può fare a meno di un severo controllo logico, il quale a sua volta necessità un simbolismo astratto piuttosto complesso. Una delle applicazioni più importanti di questa branca di studi è il calcolo delle variazioni . Si tratta dell'estensione naturale della ricerca di massimi e minimi per una funzione. Invece di cercare i punti in cui la funzione assume valori massimi o minimi; si cercano, tra le tante possibili, quelle funzioni che rendono minima o massima una certa condizione. Uno dei problemi classici del calcolo delle variazioni è quello delle superfici minime: assegnata una curva dello spazio, determinare la superficie di area minima avente come bordo la curva assegnata. Un altro problema classico è quello delle geodetiche , ossia la determinazione dei percorsi più brevi su una superficie curva. Altre applicazioni importanti del calcolo delle variazioni riguardano la minimizzazione di costi (teoria dell'ottimizzazione ), la minimizzazione di certi funzionali dell'energia di sistemi fisici soggetti a vincoli naturali, per esempio i cristalli liquidi, i problemi di transizione di fase nei materiali composti, problemi di omogeneizzazione e di rilassamento dei materiali. Antonio Bernardo N.Bourbaki, Elementi di storia della matematica, Feltrinelli, Milano, 1963 E. De Giorgi, Sviluppi dell'Analisi Funzionale del Novecento , in AA.VV. Morte di un matematico napoletano , Ubulibri, Milano, 1992. C.F.Manara e G.Giorello, La m atematica nel XX secolo, in Storia delle Scienze , a cura di E.Agazzi, Città Nuova Editrice, Roma, 1984. F.Severi e F.Conforto, Caratteri e indirizzi della matematica moderna, in Enciclopedia delle matematiche elementari , a cura di L. Berzolari, Hoepli, Milano, 1962. In rete: http://gruppiindam.cs.unibo.it/gnafa/ Gruppo nazionale per l'analisi funzionale e le sue applicazioni. http://calvino.polito.it/ricerca/gruppi/gruppo8.html Gruppo di ricerca in analisi funzionale del Politecnico di Torino http://www.unict.it/mathesis/bollet7/marino.htm Un articolo del prof. M.Marino su Teoria della misura: da Cavalieri ai nostri tempi. |
|
fig.1 grafico di una funzione |
|
 |
|
|
fig.2 primo esempio di distanza |
|
 |
|
| fig. 3 distanza media | |
 |
|
| fig. 4 Vito Volterra |
Le origini di @
Alle origini di @
La @ chiocciola, il più moderno simbolo della comunicazione umana ha cinquecento anni di vita e ha origini italiane. Lo sostiene il prof. Giorgio Stabile, docente di Storia della Scienza presso l'Università La Sapienza di Roma, che ne ha trovato traccia negli scritti mercantili veneziani del cinquecento.
Il simbolo @ rappresentava un'anfora e aveva il significato di unità di peso e di capacità. Da Venezia questo simbolo si era esteso in tutto il mediterraneo.
Più tardi è entrato nell'alfabeto commerciale inglese con il significato di "at", "al prezzo di".
E' stato l'ingegnere Ray Tomlinson a sceglierlo come simbolo per separare il nome dall'indirizzo di posta elettronica.
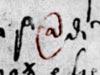
http://www.regione.veneto.it/videoinf/periodic/precedenti/num37/chiocciola.htm
http://www.wmsociety.org/bacheca/messages/185.html
Medaglie fields
Le medaglie Fields
|
|
Il chimico svedese A. B. Nobel fece una enorme fortuna con l'invenzione della dinamite. Nel testamento lasciò parte di questa fortuna a una fondazione: il premio Nobel. Cinque premi annuali di uguale valore assegnati, a partire dal 1901, dalla Reale Accademia delle Scienze di Svezia. Il premio viene attribuito allo scienziato che sia pervenuto alle più importanti scoperte inerenti la fisica, la chimica, la medicina, all'autore dell'opera letteraria più rappresentativa e a chi si è meglio adoperato per la pace nel mondo. Nel 1969 la banca di Svezia ha istituito anche un premio per le scienze economiche. Non è ben noto il motivo storico che ha portato Nobel a escludere dalla sua fondazione le scienze matematiche. Secondo alcuni pettegolezzi, la causa è da ascriversi ai litigi personali scoppiati tra Nobel e il matematico Mittag-Leffler suo connazionale: gelosia per colpa di donne, eccessiva intraprendenza di Mittag-Leffler? Secondo altri storici, Nobel si interessava completamente di matematica. Il premio Nobel per la matematica non è mai stato istituito. Esiste però un premio equivalente: la medaglia Fields. Nel 1924, il matematico canadese J. C. Fields per organizzare il congresso internazionale dei matematici a Toronto riesce a raccogliere una notevole quantità di contributi finanziari. Chiuso il convegno rimane una somma piuttosto significativa che Fields decide di utilizzare per due medaglie da assegnare ai successivi congressi internazionali di matematica. Poco prima del congresso di Zurigo del 1932, Fields viene colpito da una grave malattia. Le prime due medaglie vengono assegnate solo nel 1936 al Congresso di Oslo. A causa della guerra non ci sono stati altri congressi fino a quello di Harvard nel 1950. Da allora, ogni quattro anni le medaglie vengono assegnate regolarmente a giovani matematici di età non superiore ai quaranta anni. Antonio Bernardo |
|
A. B. Nobel |
|
|
|
|
|
J. C. Fields |


- 1936
-
Lars Valerian AHLFORS
Jesse DOUGLAS -
- 1950
- Laurent SCHWARTZ
Atle SELBERG - 1954
- Kunihiko KODAIRA
Jean-Pierre SERRE
Klaus Friedrich ROTH
René THOM
Lars HÖRMANDER
John Willard MILNOR
Michael Francis ATIYAH
Paul Joseph COHEN
Alexander GROTHENDIECK
Stephen SMALE
Alan BAKER
Heisuke HIRONAKA
Serge NOVIKOV
John Griggs THOMPSON
Enrico BOMBIERI
David Bryant MUMFORD
Pierre René DELIGNE
Charles Louis FEFFERMAN
Gregori Alexandrovitch MARGULIS
Daniel G. QUILLEN
Alain CONNES
William P. THURSTON
Shing-Tung YAU
Simon K. DONALDSON
Gerd FALTINGS
Michael H. FREEDMAN
Vladimir DRINFELD
Vaughan F.R. JONES
Shigefumi MORI
Edward WITTEN
Jean BOURGAIN
Pierre-Louis LIONS
Jean-Christophe YOCCOZ
Efim ZELMANOV
Richard E. Borcherds
W. Timothy Gowers
Maxim Kontsevich
Curtis T. McMullen
Andrew J. Wiles
2002
Laurent Lafforgue
Vladimir Voevodsky
2006
Andrei Okounkov,
Wendelin Werner,
Terence Tao,
rifiutata da Grigori Perelman
http://www.kva.se/eng/index.html : la fondazione Nobel
http://www.math.toronto.edu/fields.html : ritratto di Fields
http://www.mat.uniroma3.it/studenti_orientamento/fields/fieldsindex.htm : le medaglie fields
http://www-emis.cwi.nl/mirror/IMU/medals/
http://www-history.mcs.st-and.ac.uk/history/Societies/FieldsMedal.html
http://www.cs.unb.ca/~alopez-o/math-faq/mathtext/node19.html
Curva di koch
Curva di Koch
Questa curva è stata 'inventata' dal matematico svedese H. von Kock nel 1906. E' un esempio di curva chiusa non differenziabile, di area finita ma di perimetro infinito. Si ottiene come limite di una serie di curve spezzate, definite in modo ricorsivo.
Si comincia con un triangolo con lati di lunghezza 1. A metà di ciascun lato si aggiunge un nuovo triangolo il cui lato misura 1/3 di quello precedente. La sua area è finita, sicuramente minore di quella del cerchio circoscritto alla curva. Il suo perimetro è infinito. Infatti, il perimetro del primo triangolo è 3; quello della seconda figura si ottiene sommando i 12 lati di lunghezza 1/3, quindi 12·1/3, ossia 4; quello della terza 48·1/9; e così via. Il perimetro si ottiene dalla formula 3·4/3·4/3·4/3·…

Carl Friedrich Gauss: la geometria intrinseca
Carl Friedrich Gauss: la geometria intrinseca
Il matematico tedesco C. F. Gauss si è occupato di numerosi campi di ricerca matematica e fisica. Riguardo al problema della dimostrabilità o meno del V postulato di Euclide , quello sulla parallela, non ha pubblicato dei contributi chiari e precisi, ha scritto, però, alcune lettere indirizzate ad amici matematici che si occupavano della questione.
Fino alla fine del Settecento la geometria euclidea sembrava avere un unico neo: un postulato che Euclide era stato in qualche modo costretto ad aggiungere alla sua organizzazione logico-deduttiva della geometria. Questo postulato era necessario? era dimostrabile a partire dagli altri? da dove derivava la sua necessità? da questione logiche o empiriche?
Il 16 dicembre 1799 scrive a W. Bolyai, padre di Janos uno dei scopritori delle geometrie non euclidee ,
Mi dispiace molto di non aver sfruttato la nostra maggiore vicinanza di un tempo per conoscere più a fondo i tuoi lavori sopra i primi fondamenti della geometria; certamente mi sarei in tal modo risparmiato una serie di inutili fatiche … Io stesso ho fatto molti progressi nei miei lavori su tale argomento, nonostante che le mie altre occupazioni, del tutto eterogenee, mi lascino poco tempo per esso; solo che la via che ho imboccato conduce non già allo scopo che si desidera e che tu sostieni di aver raggiunto (la dimostrazione del V postulato di Euclide), ma piuttosto a mettere in dubbio la verità della geometria.
Il 28 aprile 1817 scrive a Olbers
Mi persuado sempre di più che la necessità della nostra geometria non possa essere dimostrata, non, per lo meno, dall’intelletto umano o per l’intelletto umano, Può darsi che in una diversa vita noi si giunga, sulla natura dello spazio, ad idee diverse, le quali ci sono per ora inattingibili. Ma fino ad allora è necessario porre la geometria non accanto all’aritmetica, la quale è puramente a priori, ma all’incirca sullo stesso piano della meccanica.
Il 27 gennaio 1829 scrive a Bessel
In qualche ora libera sono talvolta tornato a riflettere su un altro argomento che per me è già vecchio di quasi quarant’anni; intendo parlare dei primi fondamenti della geometria; non so se Le ho già parlato delle mie idee in proposito. Anche su tale argomento ho ulteriormente consolidato alcuni punti, e la mia convinzione che non sia possibile fondare la geometria in modo interamente a priori è divenuta se possibile, ancora più salda. Intanto lascerò passare molto tempo prima di decidermi ad elaborare per la pubblicazione le mie assai ampie ricerche sull’argomento, e forse ciò non avverrà mai durante la mia vita, perché temerei le strida dei Beoti qualora volessi esprimere compiutamente le mie idee.
I Beoti di cui parla Gauss sono quasi sicuramente i seguaci di Kant, i quali ritengono che la geometria sia una forma di conoscenza sintetica ma a priori .
Il 9 aprile 1830 scrive ancora a Bessel
Secondo la mia più profonda convinzione, la dottrina dello spazio occupa rispetto alla nostra conoscenza a priori un posto del tutto diverso da quello della teoria pura delle grandezze; infatti manca del tutto alla nostra conoscenza della prima quella completa convinzione della sua necessità (e quindi anche della sua assoluta verità), che è propria della seconda; dobbiamo umilmente riconoscere che mentre il numero è un puro prodotto del nostro spirito, lo spazio ha una realtà anche al di fuori del nostro spirito, e le sue leggi noi non le possiamo descrivere interamente a priori.
Nel maggio del 1831scrive a Schumacher
Da qualche settimana ho cominciato a mettere per iscritto qualche risultato delle mie meditazioni su questo soggetto, che risalgono in parte a quarant’anni, e di cui non avevo mai nulla redatto; cosa che mi ha costretto tre o quattro volte a ricominciare tutto il lavoro nella mia testa. Non vorrei pertanto che tutto ciò perisse con me.
Il primo novembre 1844 scrive a Schumacher
Osserverete la stessa cosa (l’incompetenza matematica) nei filosofi contemporanei Schelling, Hegel, Nees von Essembeck, e nei loro seguaci; non vi fanno rizzare i capelli sulla testa con le loro definizioni? Leggete nella storia della filosofia antica quele che i grandi uomini di quell’epoca, Platone ed altri (escludo Aristotele) davano come spiegazioni. Ed anche con lo stesso Kant spesso le cose non vanno molto meglio; secondo me, la sua distinzione fra proposizioni analitiche e sintetiche è una di quelle cose che cadono nella banalità o sono false.
Dunque, Gauss si convince sempre di più del fatto che, se l’aritmetica, e tutta la matematica che si fonda sul numero, è a priori, la geometria dello spazio fa riferimento a una realtà che è al di fuori della nostra mente, quindi una realtà da investigare empiricamente.
Per capire come sia giunto a queste convinzioni è utile tenere presente la sua attività di geodeta e i suoi studi sulla geometria differenziale delle superfici.
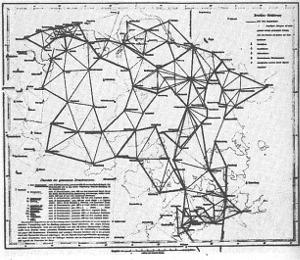
Le sue ricerche partono da un’attività pratica. Nel 1818, accetta l’incarico di eseguire la direzione di una rilevazione topografica del regno di Hannover. Lo studio della geometria di Gauss comincia proprio dall’origine storica alla quale si fa risalire il termine stesso di geometria, cioè la misura della Terra. Il procedimento classico usato nell’esecuzione di un rilievo geodetico si chiama "triangolazione". Si scelgono un certo numero di punti di riferimento nel paesaggio e si misurano con cura le distanze fra coppie diverse di punti di riferimento. La regione di cui si esegue il rilievo viene ricoperta da una rete di triangoli i cui lati e i cui angoli vengono determinati attraverso strumenti di misurazione nel modo più preciso possibile. E’ un’operazione relativamente semplice e noiosa che porta via molto tempo ed è soggetta a errori. Da questa enorme mole di dati bisogna dedurre le distanze, in linea d’aria, di
punti inaccessibili uno dall’altro. A questo punto interviene una fatto cruciale. La forma della Terra incide in maniera non trascurabile sul modo di raccordare le misure. Se la Terra fosse piana si potrebbe utilizzare al geometria euclidea, se fosse perfettamente sferica si potrebbero utilizzare le formule note della geometria sulla superficie sferica. Era già noto invece che la Terra ha approssimativamente la forma di un ellissoide, i cui assi principali erano stati dedotti da Newton dalle sue leggi sulla gravitazione. La conoscenza della forma della Terra è determinante per il lavoro di raccordo delle triangolazioni eseguite sul terreno. Gauss considera invece il problema opposto: come si possono utilizzare i rilievi geodetici per determinare la forma della Terra.
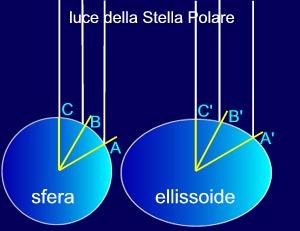
La forma della Terra si può dedurre da osservazioni astronomiche. Se la forma è sferica si osserva che, percorrendo uno stesso tratto AB = BC, l’angolo tra la verticale e la Stella Polare varia di una stessa quantità. Se la forma è ellittica, per misurare la stessa variazione dell’angolo, bisogna percorrere un tratto diverso, A’B’>B’C’.
Il problema che si pone Gauss è più complesso e profondo: se non abbiamo riferimenti esterni, come l’osservazione degli astri, possiamo dedurre dalla sola rilevazione geodetica la forma della Terra? In altre parole è possibile stabile la curvatura della Terra compiendo soltanto misurazioni sulla sua superficie?
Per capire il pensiero di Gauss esaminiamo, sia pure in modo molto superficiale i risultati teorici sullo studio delle superfici curve pubblicati in un saggio del 1827 intitolato Disquisitiones generales circa superficies curvas .
Vediamo i principali paletti teorici dei suoi studi.
Una superficie, come per esempio quella della Terra, può essere pensata immersa in uno spazio tridimensionale e studiata con i classici metodi della geometria analitica cartesiana, utilizzando tre coordinate x, y, z, ma in realtà sono sufficienti due coordinate (longitudine e latitudine) per la superficie terrestre.
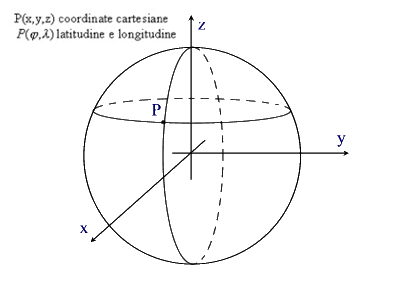
La latitudine è la distanza angolare di un punto dall’Equatore, misurata in gradi e frazioni di grado, sull’arco di meridiano passante per quel punto. Alla misura in gradi bisogna aggiungere N o S a seconda che il punto si trovi nell’emisfero boreale o in quello australe.
La longitudine è la distanza angolare di un punto dal meridiano di riferimento, o meridiano zero, che è quello passante per Greenwich, misurata in gradi e frazioni di grado, sull’arco di parallelo passante per quel punto. Alla misura in gradi bisogna aggiungere E o W a seconda che il punto si trovi a Est o a Ovest del meridiano fondamentale.
Gauss utilizza, quindi, non l’equazione cartesiana, del tipo f(x,y,z)=0, ma le equazioni parametriche x=x(u,v); y=y(u,v); z=z(u,v), dove u e v sono le coordinate curvilinee della superficie.
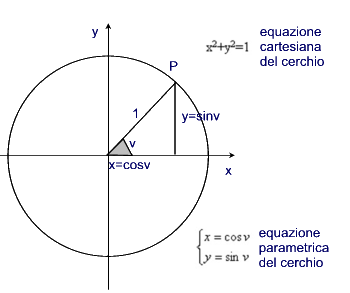
Per la superficie della sfera unitaria il procedimento è analogo. L’equazione cartesiana è
x2 +y2 +z2 -1=0, quindi del tipo f(x,y,z)=0
L’equazione parametrica è
x=cosu·cosv
y=cosu·sinv
z=sinu
dove u è la latitudine, v la longitudine.
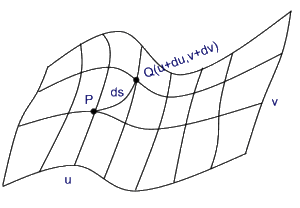
Il secondo passaggio fondamentale è quello di determinare il modo di calcolare le distanze sulla superficie.
Un’altra importante innovazione che Gauss introduce è la nozione di curvatura di una superficie.
Nel caso delle curve si parte dalla curvatura di un cerchio, che per definizione si assume come il reciproco del raggio, cioè K=1/r.
Per calcolare la lunghezza di un arco infinitesimale si serve del teorema di Pitagora
(1) ds2 =dx2 +dy2 +dz2
Dalle equazioni parametriche x=x(u,v); y=y(u,v); z=z(u,v), passando ai differenziali
dx=adu+a’dv; dy=bdu+b’dv; dz=cdu+c’dv
e sostituendo nella (1) ottiene
ds2 =Edu2 +2Fdudv+Gdv2 ,
dove
E=a2 +b2 +c2 , F=aa’+bb’+cc’, G=a’2 +b’2 +c’2
nota con il nome di prima forma fondamentale.
Questa formula esprime la distanza tra due punti infinitamente vicini sulla superficie P(u,v) e Q(u+du,v+dv), da essa, applicando il calcolo delle variazioni, si possono ottenere le curve di minima distanza ossia le geodetiche .
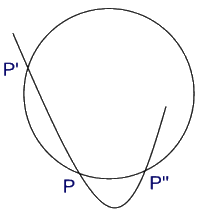
Per determinare la curvatura di una curva in un punto si considera il cerchio osculatore che è il cerchio tangente alla curva nel punto P. Il cerchio osculatore si ottiene in questo modo. Si prendono tre punti, piuttosto vicini, sulla curva: P’,P,P”; per questi tre punti passa un solo cerchio; quindi si fanno avvicinare sempre di più i punti P’ e P” a P, nella situazione limite in cui i tre punti coincidono, si ottiene il cerchio osculatore. La curvatura di questo cerchio è per definizione la curvatura della curva nel punto P.
La curva rappresentata ha nei due punti P e Q curvatura di segno opposto.
La curvatura di una retta è nulla.
L’approccio utilizzato per le curve, tuttavia, non è generalizzabile alle superfici. Gauss prende spunto da alcune tecniche utilizzate in astronomia.
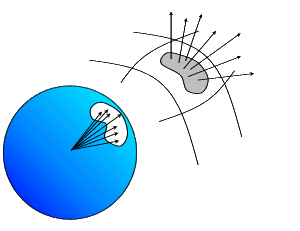
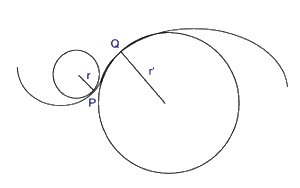
La curvatura totale di una porzione limitata di superficie si definisce attraverso la nozione di normale . La normale alla superficie in un punto P è la retta passante da P e perpendicolare al piano tangente alla superficie condotto dal punto P. Per definire la curvatura di una superficie, si serve di una sfera unitaria. A ogni punto P della superficie fa corrispondere un punto P’ sulla sfera, in modo che entrambi abbiano la stessa normale. Se si considera una piccola regione della superficie contenete P ad essa corrisponderà sulla sfera una regione contenente P’. La curvatura della superficie in P è definita come il limite del rapporto tra l’area della regione sulla sfera e l’area della regione sulla superficie, quando queste due aree tendono a ridursi ai rispettivi punti P e P’. Gauss ottiene la formula
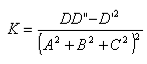
Dopo numerosi calcoli, Gauss dimostra una caratteristica particolarmente importante. In generale, i coefficienti A, B, C, D che compaiono nella formula della curvatura sembrano dipendere dalle coordinate cartesiane x,y,z. Se invece la superficie è data per mezzo di equazioni parametriche, i coefficienti di K dipendono esclusivamente dalle coordinate curvilinee u e v. Da qui un risultato fondamentale per lo studio delle superfici: la curvatura non dipende dallo spazio circostante, è una caratteristica intrinseca alla superficie stessa. In altre parole, si può stabilire se la superficie è curva o piana restando sulla superficie stessa, senza fare riferimento a un ipotetico spazio ambiente in cui è immersa. Relativamente alla superficie terrestre si può stabilire il suo grado di curvatura effettuando esclusivamente misure sulla superficie, senza fare riferimento a osservazioni astronomiche.
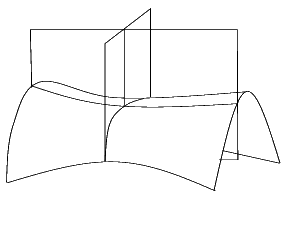
In un passo successivo dimostra che la propria definizione di curvatura corrisponde a quella data da Eulero e ripresa da Monge. Eulero aveva proceduto in questo modo: per un punto della superficie aveva costruito il piano perpendicolare alla superficie in quel punto. Questo piano determina una curva della superficie, facendo ruotare il piano si ottengono curve con differente curvatura. Tra queste ce n’è una che ha la curvatura minima R1 e una che ha la curvatura massima R2 . Gauss dimostra che la propria definizione di curvatura, K, si può ottenere dal prodotto delle due curvature principali, quella minima e quella massima K=1/R1 ·R2 .
Questa proprietà ci permette di calcolare con facilità la curvatura di alcune superfici e di classificarle in base alla loro curvatura, che può essere positiva, negativa o nulla.
Gauss ottiene infine un teorema fondamentale per la trattazione delle superfici, il teorema definito da egli stesso "egregium ": una superficie può essere sovrapposta su un’altra solo se le due superfici hanno la stessa curvatura.
Questo teorema comporta dei risultati di particolare importanza. Prima di tutto risolve l’annosa questione della rappresentazione di una superficie su un altra, in particolare della rappresentazione della superficie terrestre su una carta piana. Il teorema dimostra che ciò è impossibile perché un foglio piano ha curvatura nulla, mentre la superficie della Terra ha curvatura ovunque positiva. Tuttavia, nella parte conclusiva delle sue Disquisizioni , Gauss dimostra che il triangolo terrestre che ha per vertici le colline di Brocken, Hohehagen e Inselberg si comporta agli effetti pratici come un triangolo su un foglio piano, poiché l’errore che si commette è impercettibile.
Ma ancora più importante dal punto di vista teorico è la conclusione che un pezzo di superficie, per esempio un triangolo o un’altra figura geometrica, può essere trasportato da una parte a un’altra della superficie solo se questa ha in tutti i punti la stessa curvatura, ossia la curvatura della superficie è costante.
L’importanza di quest’ultima caratteristica delle superfici è in stretto rapporto con una delle proprietà fondamentali della geometria, la congruenza delle figure geometriche che si rileva spostando una figura su un’altra fino a farle sovrapporre. Se le figure si sovrappongono perfettamente allora sono uguali. Un’altra conseguenza è che il concetto stesso di misura si fonda sulla possibilità di trasportare l’unità di misura da una regione a un’altra senza che essa si deformi. Le superfici sulle quali si può costruire una simile geometria sono tutte quelle a curvatura costante, non solo il piano che ha curvatura costante nulla ma anche quelle che hanno curvatura costante positiva o negativa.
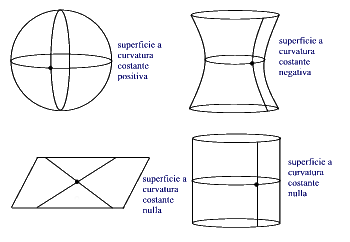
La superficie della sfera ha curvatura costante positiva, perché in ogni punto le due curvature principali sono costanti e positive. La pseudosfera ha curvatura costante negativa, perché in ogni punto le due curvature principali sono costanti ma di segno opposto. Il piano ha curvatura costante nulla perché in ogni punto le due curvature principali sono nulle. Il cilindro ha curvatura costante nulla, perché in ogni punto una delle due curvature principali è sempre nulla.
Infine, Gauss costruisce i primi elementi della geometria sulle superfici. Nel piano le costruzioni geometriche partono dalle rette; sulle superfici non vi sono rette nel senso comune del termine ma linee geodetiche, le linee della superficie che uniscono due punti per mezzo del percorso più breve. Nel piano è un segmento di retta, sulla superficie sferica è un arco di cerchio massimo, sul cilindro è un arco di elica.
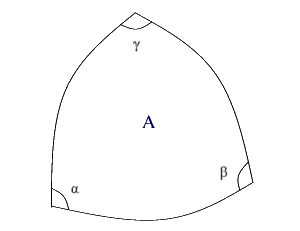
Quindi, inizia una prima trattazione dei triangoli geodetici delle superfici. Il primo risultato fondamentale è che la somma degli angoli interni di un triangolo geodetico su una superficie curva non è 180°. Lo scarto rispetto a 180° è dato dall’integrale della curvatura esteso alla superficie del triangolo.
![]()
Se la curvatura della superficie è positiva la somma degli angoli interni del triangolo geodetico supera PIGRECO di una quantità proporzionale alla sua area; se la curvatura è negativa la somma degli angoli interni è inferiore di PIGRECO.
Se la superficie ha curvatura costante, la somma degli angoli interni del triangolo geodetico differisce da PIGRECO della quantità KA, dove K è la curvatura, A è l’area del triangolo.
R. Ossermann, Poesia dell’universo , Longanesi, Milano, 1996
P. Parrini, Fisica e geometria dall’Ottocento a oggi , Loescher,Torino, 1979
M. Kline, Storia del pensiero matematico, Einauidi, Torino, 1996
Tord Hall, Carl Friedrich Gauss, a biography , The MIT Press, Cambridge, 1970
U. Bottazzini, Il flauto di Hilbert , UTET, Torino, 1990
R. Bonola, La geometria non euclidea, esposizione storico-critica del suo sviluppo, Zanichelli, Bologna, 1906
C.F.Gauss, General investigations of curved surfaces, Raven Press, New York, 1965
Bernard Riemann: la geometria come ipotesi
Bernhard Riemann: la geometria come ipotesi

Di origini modeste, G. F. B. Riemann si laurea presso l'Università di Gottinga, in Germania, discutendo una tesi sulla teoria delle funzioni di variabile complessa, ricca di nuove idee per lo studio dell'analisi, della topologia e della fisica matematica. Nel 1854, è tenuto a presentare, sempre presso l'Università di Gottinga, una dissertazione per ottenere il titolo di Privatdozent , che gli avrebbe permesso di dare lezioni private presso l'università.
Riemann aveva proposto tre temi: due su elettricità e magnetismo, uno sulla geometria. Argomenti di cui si occupava il suo maestro Gauss. Proprio Gauss, contrariamente alle aspettative del giovane Riemann, sceglie il tema più complesso e filosoficamente più impegnativo e compromettente: collegare le più avanzate ricerche matematiche con il problema filosofico dello spazio.
In una lettera al fratello, Riemann scriveva:
Con i miei lavori va ora discretamente: all'inizio di dicembre ho consegnato lo scritto di abilitazione e insieme a quello dovevo proporre tre temi per la lezione d'abilitazione, tra i quali la facoltà ne sceglie uno. I primi due li avevo pronti e speravo che si sarebbe preso uno di quelli: Gauss però aveva scelto il terzo, e così ora sono di nuovo un po' alle strette, poiché questo devo ancora prepararlo.
Il compito che deve affrontare Riemann è quello di proseguire le ricerche del maestro nel campo della geometria differenziale delle superfici (vedi la scheda su Gauss ) ed esplicitarne le implicazioni filosofiche. La relazione doveva essere presentata all'intero consiglio della facoltà di filosofia e quindi a un pubblico costituito principalmente da filosofi; ciò costringe Riemann a un ulteriore sforzo per semplificare il complesso linguaggio tecnico della geometria differenziale.
Il risultato è un capolavoro che ha aperto la strada a numerosi campi della matematica (topologia, geometria differenziale, spazi a un numero qualsiasi di dimensioni, fondamenti della geometria, geometrie non euclidee) e della fisica (molti lo considerano il punto di partenza per la teoria della relatività di Einstein).
E' noto che la geometria presuppone, come qualcosa di dato, sia il concetto di spazio, sia i primi concetti fondamentali per le costruzioni nello spazio. Di essi dà soltanto definizioni nominali, mentre le determinazioni essenziali compaiono sotto forma di assiomi.
E' l'esordio della conferenza. Nonostante lo sforzo di matematici e filosofi, continua Riemann, il significato profondo dei fondamenti della geometria rimane nell'ombra. Non siamo in grado di affermare né se, o fino a che punto, le relazioni tra i concetti elementari della geometria sono necessarie, né addirittura se sono possibili.
La ragione sta forse nel fatto che non è stato per nulla sviluppato il concetto generale di grandezze pluri-estese, in cui rientrano le grandezze spaziali.
Il primo passo è quindi quello di introdurre la nozione di grandezza molteplicemente estesa, molteplicità (Mannigfaltigkeit ) o varietà secondo l'uso attuale del termine.
Concetti di grandezza sono possibili solo là dove esiste già un concetto generale che permette diversi modi di determinazione. A seconda che tra questi modi di determinazione vi sia o no un passaggio continuo dall'uno all'altro, essi formano una varietà continua o una varietà discreta; i singoli modi si chiamano nel primo caso punti, nel secondo caso elementi, della varietà.
Vi sono numerosi esempi di varietà discrete, mentre quelle continue sono casi piuttosto limitati. I casi più semplici di varietà continue sono le posizioni degli oggetti e i colori. Esse trovano, invece, un gran numero di applicazioni nella matematica superiore.
Le varietà discrete, cioè gli insiemi finiti di elementi, si possono confrontare semplicemente contando gli elementi.
Lo studio delle varietà continue è più complesso e si fonda su due elementi: il numero di dimensioni della varietà e l'assegnazione delle coordinate ad ogni punto di essa.
Se in un concetto i cui modi di determinazione formano una varietà continua, si passa secondo modalità definite, da un modo di determinazione a un altro, i modi di determinazione attraversati formano una varietà mono-estesa, il cui carattere essenziale è che da ogni suo punto ci si può spostare con continuità soltanto in due direzioni, in avanti o indietro. Se si immagina ora che questa varietà si trasformi di nuovo in un'altra, del tutto diversa, naturalmente ancora una volta secondo modalità definite, e ciò in modo che ogni punto dell'una passi in un punto determinato dell'altra, i modi di determinazione così ottenuti formano insieme una varietà biestesa. In modo analogo si ottiene una varietà triestesa, se si immagina che una varietà biestesa si trasformi secondo modalità definite, in una del tutto diversa, ed è facile vedere come questa costruzione possa procedere oltre. […] questa costruzione può essere indicata come una composizione di una variabilità a n+1 dimensioni, formata da una variabilità a n dimensioni e da una a una sola dimensione.
Il numero di dimensioni è quindi una caratteristica della varietà. L'assegnazione delle coordinate è, invece, un'operazione arbitraria, fatta eccezione per due aspetti: il numero delle coordinate deve necessariamente corrispondere alle dimensioni della molteplicità e l'assegnazione deve essere continua.
Questa parte dello studio delle varietà riguarda esclusivamente il modo in cui i punti di una molteplicità sono disposti ed è la base dello studio dell'analisi matematica. E' però possibile aggiungere la nozione di distanza tra due punti e quindi i processi di misura. Le relazioni di estensione e di dominio sono, quindi, distinte da quelle metriche; in particolare su relazioni di estensione identiche sono concepibili relazioni metriche differenti. Si ottiene così la possibilità di misurare le parti di una varietà continua e, conseguentemente, di fondare analiticamente la geometria. I principi fondamentali dello studio 'geometrico' delle varietà sono contenuti, lo ammette lo stesso Riemann, nel trattato di Gauss sulle superfici curve.
Le determinazioni metriche richiedono che la grandezza sia indipendente dalla sua posizione: condizione che si può realizzare in diversi modi. L'ipotesi che si presenta probabilmente per prima, e che io voglio qui seguire fino in fondo, è che la lunghezza di una linea sia indipendente dalla sua posizione, e che quindi ogni linea sia misurabile per mezzo di ogni altra linea.
Per compiere operazioni di misura si devono, quindi, assumere certe grandezze come unità e supporre che queste spostandosi non subiscano deformazioni. Il caso più semplice che si presenta è quello descritto dal teorema di Pitagora: un elemento infinitesimo di linea si ottiene per mezzo di un'espressione differenziale di secondo grado ![]() . Questa espressione può essere modificata: dobbiamo perciò dedurre che è possibile applicare a una stessa varietà metriche diverse e, conseguentemente, che sono possibili diversi modi per misurare le distanze.
. Questa espressione può essere modificata: dobbiamo perciò dedurre che è possibile applicare a una stessa varietà metriche diverse e, conseguentemente, che sono possibili diversi modi per misurare le distanze.
Le varietà nelle quali, come nel piano e nello spazio, l'elemento di lineare si può ridurre alla forma ![]() costituiscono quindi solo un caso particolare delle varietà che prendiamo qui in considerazione. Esse meritano un nome particolare, perciò chiamerò piane queste varietà in cui il quadrato dell'elemento lineare si può ridurre alla somma di quadrati di differenziali totali.
costituiscono quindi solo un caso particolare delle varietà che prendiamo qui in considerazione. Esse meritano un nome particolare, perciò chiamerò piane queste varietà in cui il quadrato dell'elemento lineare si può ridurre alla somma di quadrati di differenziali totali.
Nonostante questa arbitrarietà nella scelta del modo di effettuare le misure, ogni varietà ha una caratteristica intrinseca, come ha dimostrato Gauss per le superfici. Si tratta della curvatura. Riemann introduce la nozione di curvatura estendendo quella gaussiana in un modo generalmente ritenuto piuttosto oscuro.
Le varietà il cui valore di curvatura è zero in ogni punto si possono considerare come caso particolare di quelle la cui curvatura è costante in ogni punto. Il carattere comune di queste varietà a curvatura costante si può anche esprimere dicendo che le figure che si trovano in esse possono venire mosse senza essere deformate. E' infatti evidente che le figure su di esse non si possono muovere e far girare a piacere se in ogni punto la misura di curvatura non è la stessa in tutte le direzione.
[…]
Può essere utile per un'esposizione geometrica prendere in considerazione superfici con valore di curvatura costante. Si vede facilmente che le superfici a curvatura costante positiva potranno sempre essere adattate su una sfera il cui raggio è l'unità divisa per la radice quadrata della misura di curvatura.
[…]
La superficie a curvatura zero sarà semplicemente una superficie cilindrica tangente all'equatore; le superfici con curvatura negativa saranno tangenti esternamente a questo cilindro e saranno formate come la parte interna della superficie di un anello, quella rivolta verso l'asse.
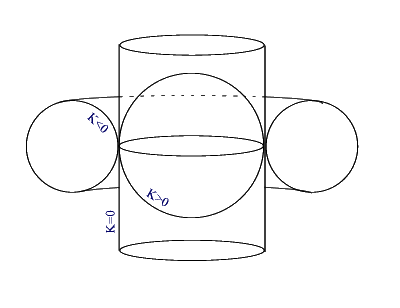
Altra questione è quella di stabilire quale, fra le molteplicità geometricamente possibili, sia adattabile allo spazio fisico. Per risolvere questo problema, è necessario caratterizzare con delle proprietà semplici ciascuna singola molteplicità; tali proprietà devono esprimere affermazioni la cui validità possa essere sottoposta a verifica sperimentale. In questo senso esse sono ipotesi . La possibilità di misurare le distanze servendosi del teorema di Pitagora ![]() è quindi semplicemente un'ipotesi.
è quindi semplicemente un'ipotesi.
Si cercano quindi sistemi di determinazioni metriche semplici dai quali le relazioni metriche dello spazio risultino completamente determinate e dai quali conseguano necessariamente tutti i teoremi intorno a queste relazioni. Rimane ora da esaminare in che grado e misura queste ipotesi sono garantite dall'esperienza.
[…] nelle seconde, invece, dove i casi possibili formano un continuo, ogni determinazione basata sull'esperienza rimane sempre inesatta, per quanto grande possa essere la possibilità che sia quasi corretta. Questa distinzione diventa importante quando si estendono queste determinazioni empiriche al di là dei limiti dell'osservazione, nell'incommensurabilmente grande e nell'incommensurabilmente piccolo.
Ne consegue che allo spazio fisico possono indifferentemente essere applicate proprietà metriche diverse. L'applicazione di una certa metrica allo spazio fisico altro non è che un'ipotesi . Tutto ciò che dello spazio fisico si può dire è che esso è una molteplicità continua, illimitata e a tre dimensioni. Se, come ha fatto Euclide, si assume l'ipotesi che la forma dei corpi nello spazio fisico non dipende dalla loro posizione, si deve concludere che lo spazio fisico ha curvatura costante. Restano però possibili tre alternative a seconda che la curvatura sia costantemente positiva, nulla o negativa. Se assumiamo che lo spazio sia una varietà continua i risultati sperimentali sono sempre approssimativi. Ne consegue che né il procedimento analitico, né l'approccio sperimentale possono risolvere il problema di individuare la natura della geometria della fisica.
Le misure compiute a livello astronomico hanno stabilito che lo spazio ha curvatura nulla e quindi che la geometria dell'astronomia è quella di Euclide. Queste misurazioni, però, non possono farci conoscere nulla sulla curvatura dello spazio a livello microscopico
Ora, sembra che i concetti empirici su cui sono basate le misurazioni spaziali, in particolare i concetti di corpo solido e di raggio luminoso, cessino di valere nell'infinitamente piccolo: di conseguenza si può benissimo concepire che nell'infinitamente piccolo le relazioni metriche dello spazio non siano in accordo con i postulati della geometria, e di fatto si sarebbe costretti a fare questa ammissione non appena essa permettesse una più semplice spiegazione dei fenomeni.
Altra questione è quella dell'incommensurabilmente grande. La nostra intuizione ci fa ritenere che le rette, o linee di minimo percorso, debbano essere infinite. Riemann distingue invece tra infinito e illimitato .
[…] Quando le costruzioni nello spazio vengono estese nell'incommensurabilmente grande, bisogna distinguere l'illimitato dall'infinito; l'uno appartiene alle relazioni di estensione, l'altro a quelle metriche. […] L'illimitatezza dello spazio ha quindi maggiore certezza empirica di qualsiasi esperienza del mondo esterno. Da questo carattere, tuttavia, non consegue in alcun modo l'infinitezza; al contrario, se si assume che i corpi siano indipendenti dalla loro posizione e si attribuisce quindi allo spazio una misura di curvatura costante, esso verrebbe a essere necessariamente finito non appena questa misura di curvatura avesse sia pure il più piccolo valore positivo. Se si prolungassero in linee di minimo percorso le direzioni iniziali, giacenti su una superficie, si otterrebbe una superficie illimitata con valore di curvatura positiva e costante, cioè una superficie che in una varietà piana triplamente estesa assumerebbe la forma di una superficie sferica, e dunque finita.
L'approccio di Riemann allo studio dei fondamenti della geometria non segue, quindi, il metodo tradizionale dello studio degli assiomi e delle definizioni. Sviluppando in modo ardito le idee di Gauss sulla geometria differenziale delle superfici, mette a fondamento della geometria una nuova nozione, quella di varietà; in seguito si parlerà, infatti, di varietà riemanniane . Per ciò che riguarda il problema dello spazio fisico, riconosce che non si tratta di un problema matematico: la matematica deve fornire gli strumenti per formulare ipotesi svincolate il più possibile da pregiudizi. Lo spazio va studiato non tanto nella sua globalità quanto nel suo comportamento locale e quindi nella sua struttura infinitesima. Pertanto, solo l'analisi può garantire un tale studio.
In sintesi, la geometria ha un suo fondamento nell'analisi. Sono analiticamente possibili geometrie diverse; le misurazioni empiriche non sono in grado di determinare con precisione le caratteristiche geometriche dello spazio fisico.
La conferenza di Riemann, accolta con molto entusiasmo da parte di Gauss, che muore l'anno seguente, rimane inedita fino alla morte del suo autore. La stessa indifferenza iniziale era toccata alle opere di Lobacevski e Bolyai sulle geometrie non euclidee.
La pubblicazione della corrispondenza di Gauss, avvenuta dopo il 1860, rende pubbliche le convinzioni del principe dei matematici sui fondamenti della geometria e contribuisce ad accendere il dibattito su questo complesso problema. L'inizio vero e proprio di questo dibattito è opera di un costante e lungo lavoro di alcuni matematici minori i quali contribuiscono a portare alla luce le idee di Gauss, Lobacevski, Bolyai e Riemann. Il francese J. Houell e l'italiano G. Battaglini ne traducono nelle rispettive lingue i più importanti saggi.
Il problema della posizione da prendere nei confronti delle nuove geometrie è, in questo periodo, particolarmente attuale per la cultura italiana, perché strettamente correlato a quello dell'insegnamento della geometria nelle scuole del nuovo Regno. La riforma di Cremona prevede che nelle scuole di indirizzo classico si studi il libro di Euclide. Battaglini invece mette in discussione la validità della scelta proprio alla luce dell'emergere delle geometrie non euclidee. Si scatena un aspro clima di polemiche, nel quale le nuove geometrie vengono bollate come geometrie del soprasensibile o da manicomio.
Nel 1868 viene pubblicata la memoria di Riemann a cura di Dedekind; nel 1870 ne viene pubblicata la traduzione francese e nel 1873 quella inglese.
In una riorganizzazione storico-didattica delle geometrie non euclidee, viene attribuita a Lobacevski la 'scoperta' della geometria a curvatura negativa e quindi quella relativa all'esistenza di più di una parallela condotta per un punto dato, a Riemann viene invece attribuita la scoperta della geometria a curvatura positiva, nella quale per un punto non passa nessuna parallela a una retta data.
A partire dalla pubblicazione del saggio di Riemann, vengono intraprese diverse ricerche nel campo della matematica pura e della fisica matematica che fanno uso del concetto di varietà. In particolare, si indaga sulla possibilità di estendere alcune discipline classiche della fisica matematica agli spazi a curvatura non nulla, nella speranza di trovare nuove soluzioni ai problemi rimasti irrisolti. La condizione indispensabile per queste ricerche è la necessità di esprimere le equazioni fondamentali della fisica matematica in una notazione generale che restasse valida per ogni tipo di spazio, euclideo e non. Da queste ricerche nasce la nozione di tensore e di calcolo tensoriale elaborata da Ricci-Curbastro e Levi-Civita verso la fine del secolo. Intorno al 1912, Einstein si serve degli strumenti matematici elaborati da Gauss, Riemann, Levi-Civita e Ricci-Curbastro per elaborare la teoria della relatività generale. Nella conferenza di Kyoto del 1922, Einstein afferma
Se tutti i sistemi sono equivalenti allora la geometria euclidea non può valere in ciascuno di essi. Abbandonare la geometria e conservare le leggi fisiche è come descrivere i pensieri senza parole. Bisogna cercare le parole prima di poter esprimere i pensieri. Che cosa si doveva cercare a questo punto? Tale problema rimase insolubile per me fino al 1912, quando all'improvviso mi resi conto che la teoria di Gauss delle superfici forniva la chiave per svelare questo mistero. Compresi che le coordinate di una superficie di Gauss avevano un profondo significato. Non sapevo però a quell'epoca che Riemann aveva studiato i fondamenti della geometria in maniera ancora più profonda. […] Mi resi conto che i fondamenti della geometria avevano un significato fisico. Quando da Praga tornai a Zurigo, vi trovai il matematico Grossmann, mio caro amico: da lui appresi le prime notizie sul lavoro di Ricci e in seguito su quello di Riemann.
Antonio Bernardo
Antinomia del bugiardo
I numeri esistono? Cosa ne pensano i filosofi (da Platone a Cartesio)
Una volta tanto ho intenzione di mettere in disparte le classiche operazioni numeriche per lasciar spazio ad un’ indagine che sta a monte delle operazioni stesse: i numeri, quelle entità con le quali facciamo addizioni, sottrazioni, moltiplicazioni, divisioni e quant’altro, esistono? E se esistono, che cosa sono? Non é certo un problema da poco! Già 2400 anni fa, circa, Platone si era posto il problema: che cosa esiste? Ecco allora che aveva tirato in ballo il concetto di dunamis (potenza) secondo il quale esisterebbe tutto ciò che può (dunatai) compiere e subire un’azione. Esisteranno, quindi, tutti gli enti materiali che ci circondano, é evidente, perché possono allo stesso tempo compiere e subire azioni: il cane corre e può essere accarezzato, ad esempio, quindi esiste. Ma con questa definizione si é costretti ad ammettere anche l’esistenza di enti immateriali: le idee, ossia quelli che noi definiamo oggetti del pensiero, dovranno avere una loro esistenza proprio perché subiscono l’azione di essere pensati; l’idea stessa di giustizia agisce anche nel senso che le cose giuste partecipano di essa: se una cosa è giusta vuol dire che ci sarà un’idea di giustizia. Di conseguenza, e qui arriviamo al dunque, in qualche misura esisteranno anche i numeri come oggetto del nostro pensiero.
Secondo l’illustre filosofo Aristotele i numeri esistono, certo, ma come pure e semplici astrazioni: egli effettua una distinzione tra sostanza (ciò che per esistere non ha bisogno di null’altro all’infuori di sé) e accidente (ciò che per esistere ha bisogno di una sostanza cui riferirsi). Così la terra o il libro saranno sostanze proprio perché dotati di esistenza autonoma, il blu o il marrone saranno accidenti perché potranno esistere solo se abbinati ad una sostanza: il blu e il marrone di per sé, sostiene Aristotele, non esistono, bensì esistono libri blu e terra marrone. Gli accidenti si trovano dunque ad avere un’esistenza che potremmo definire “parassitaria”, ossia totalmente legata ad una sostanza cui riferirsi. Ritornando al discorso dei numeri, Aristotele non esita a collocarli tra gli accidenti: il 2 o il 3, di per sé, non esistono, bensì esistono gruppi di due o tre sostanze: tre libri, due penne, due case … Non é sbagliato dire che, in un certo senso, il numero é l’ultima cosa che permane man mano che si tolgono a due o più oggetti le differenze: i due libri hanno colori diversi, tolgo il colore; hanno scritte diverse, tolgo le scritte; hanno dimensioni diverse, tolgo le dimensioni; alla fine, quando li avrò spogliati di ogni cosa, resterà solo il numero: sono due. Così ragiona Aristotele e così siamo portati a ragionare anche noi: non ci sogneremmo mai di sostenere che il 2 o il 3 esistano di per sé senza sostanze cui riferirsi.
Tuttavia, Platone, che di matematica se ne intendeva molto più di Aristotele, sosteneva l’esistenza dei numeri sganciata dalle sostanze: il 2 o il 3 per Platone esistono non solo nelle cose materiali (sostanze) che ne partecipano (2 case, 3 gatti …) , ma addirittura come enti a sé stanti: se ho un gruppo di 6 libri significa che esso partecipa all’idea del 6 (il numero ideale 6). Questa strana concezione dei numeri deriva dall’impianto metafisico stesso di Platone: per lui al quesito “che cos’è x ?” (dove x sta per bello, giusto …) la risposta a questa domanda consiste nel rintracciare l’idea in questione (per esempio l’idea di bellezza, di giustizia …).L’idea è dunque un “universale”: ciò significa che i molteplici oggetti sensibili, dei quali l’idea si predica, dicendoli per esempio belli o giusti, sono casi o esempi particolari rispetto all’idea: una bella persona o una bella pentola sono casi particolari di bellezza, non sono la bellezza. Mentre gli oggetti sensibili sono caratterizzati dal divenire e dal mutamento, soltanto delle idee si può propriamente dire che sono stabilmente se stesse; proprio questa differenza di livelli ontologici,ossia di consistenza di essere, qualifica le idee come modelli rispetto agli oggetti sensibili corrispondenti. L’attività di un artigiano, per esempio di un costruttore di letti, è descrivibile da parte di Platone come un insieme di operazioni che mirano a foggiare un determinato materiale (in questo caso il legno) secondo il modello dell’ idea del letto, alla quale egli si riferisce costantemente con il suo pensiero. L’idea è quindi dotata di esistenza autonoma, né dipende per la sua esistenza dal fatto di poter essere pensata; essa è ciò di cui gli oggetti sensibili partecipano. La partecipazione all’idea, per esempio, di bellezza rende un determinato oggetto sensibile bello. Le idee hanno quindi una quadruplice valenza : 1) ontologica: i cavalli esistono perché copiano l’idea di bellezza; 2) gnoseologica: riconosco che quello é un cavallo perché nella mia mente ho l’idea di cavallo; 3) assiologica: ogni idea è il bene cui tendere, lo scopo a cui aspirare ; 4) di unità del molteplice: i cavalli esistenti sono tantissimi e diversissimi tra loro, ma l’idea di cavallo é una sola . Ora anche i numeri sono idee e hanno pertanto le prerogative delle idee: così come quel cavallo é bello perché partecipa all’idea di bellezza, esso é uno perché partecipa all’idea di uno; così come i cavalli materiali sono una miriade ma l’idea di cavallo é una, così anche i 3 scritti sulle lavagne o sui fogli sono una miriade ma l’idea di tre é una sola, da cui tutti gli altri tre dipendono. I numeri sono sì idee come le altre, ma si tratta di idee particolarmente complesse tant’é che Platone non esita a collocarli su un livello superiore: i numeri ideali, ossia le essenze stesse dei numeri, in quanto tali, non possono essere sottoposti ad operazioni aritmetiche. Il loro status metafisico è ben differente da quello aritmetico, appunto perché non rappresentano semplicemente numeri, ma l’essenza stessa dei numeri. In effetti, non avrebbe senso sommare l’ essenza del due all’essenza del tre e così via. I Numeri ideali, quindi, costituiscono i supremi modelli dei numeri matematici. Inoltre, per Platone, i numeri ideali sono i primi derivati dai Principi primi, per il motivo che essi rappresentano, in forma originaria e quindi paradigmatica, quella struttura sintetica dell’ unità nella molteplicità, che caratterizza anche tutti gli altri piani del reale a tutti gli altri livelli. Inoltre, Aristotele ci riferisce: ” Platone afferma che, accanto ai sensibili e alle Forme (idee) , esistono enti matematici intermedi fra gli uni e le altre , i quali differiscono dai sensibili , perché immobili ed eterni, e differiscono dalle Forme, perché ve ne sono molti simili, mentre ciascuna Forma é solamente una e individua “.
Platone ha introdotto questi “enti matematici intermedi” per i seguenti motivi: i numeri su cui opera l’aritmetica, come anche le grandezze su cui opera la geometria, non sono realtà sensibili, ma intellegibili. Però, tali realtà intellegibili non possono essere Numeri Ideali né Figure geometriche ideali perché le operazioni aritmetiche implicano l’ esistenza di molti numeri uguali (pensiamo ad esempio ad un’equazione dove, per dire, il numero 6 può comparire diverse volte) e le dimostrazioni e le operazioni geometriche implicano molte figure uguali e molte figure che sono una variazione della medesima essenza (pensiamo a molti triangoli uguali e molte figure che sono variazioni della medesima essenza, ossia triangoli di vario tipo: equilatero, isoscele … ). Invece, ciascuno dei Numeri Ideali (così come ciascuna forma ideale) é unico, e inoltre i Numeri Ideali non sono operabili. Se si tiene presente questo, risultano chiare le conclusione platoniche sull’esistenza di enti matematici aventi caratteri “intermedi” fra il mondo intellegibile e il mondo sensibile. In quanto sono immobili ed eterni, gli enti matematici condividono i caratteri delle realtà intellegibili, e cioè delle idee; invece, in quanto ve ne sono molti della medesima specie sono analoghi ai sensibili. Il fondamento teoretico di questa dottrina sta nella convinzione radicatissima in Platone della perfetta corrispondenza fra il conoscere e l’ essere, per cui ad un livello di conoscenza di un determinato tipo deve necessariamente far riscontro un corrispettivo livello di essere. Di conseguenza, alla conoscenza matematica, che é di livello superiore alla conoscenza sensibile, ma inferiore alla conoscenza filosofica, deve corrispondere un tipo di realtà che ha le corrispettive connotazioni ontologiche. I numeri ideali sono superiori alle idee stesse in un certo senso perché ne regolano i rapporti numerici con cui si rapportano con la realtà. Certo oggi a noi la concezione di Platone sembra molto distante e improbabile e preferiamo quella aristotelica, tuttavia sorge un dubbio che rimette in gioco la teoria platonica: e se nessuno contasse più i numeri continuerebbero ad esistere? Con la definizione aristotelica, infatti, essi esistono solo come processo di astrazione della mente umana e, se vi fosse un improvviso annichilimento della realtà, sembra quasi che non contando più nessuno i numeri debbano sparire, ma é evidentemente ridicolo dire così: 2 + 2 = 4 é vero anche senza che io lo pensi e quindi pare aver ragione Platone: i numeri hanno esistenza autonoma.
Nel medioevo, poi, il dibattito sui numeri assumerà una vivace coloritura dovuta soprattutto alle credenze religiose: che 2 + 2 = 4 lo decide Dio o anch’ Egli deve sottostare a questa verità? In realtà tutto dipende dalla concezione stessa di Dio a seconda delle posizioni aristoteliche o platoniche: come accennavo prima, per Platone, accanto al nostro imperfetto mondo sensibile ve ne è uno immutabile ed eterno, di cui il nostro è solo una pallida copia: si tratta del mondo intellegibile delle idee, ossia degli archetipi delle cose che ci circondano. Ora per spiegare come le idee si calassero nelle cose materiali (ossia come dall’idea di cavallo derivasse il cavallo in carne ed ossa) Platone era ricorso alla figura del Demiurgo, ossia di un divino artigiano che, attenendosi alle idee, plasmava la materia in funzione di esse dando così vita agli enti materiali e non. Il Cristianesimo in buona parte mutua la sua concezione di Dio dal Demiurgo platonico, pur apportando delle notevoli differenze: Dio non si limita a plasmare materia già esistente, ma la crea nel vero senso della parola. E’ evidente, i seguaci medioevali di Platone non possono far altro che sostenere, sulla scia del padre delle idee, che Dio, pur essendo onnipotente e creatore, deve per forza attenersi all’apparato ideale che gli sta a monte: la sua onnipotenza si manifesterà nel decidere di creare l’uomo, ma questo creare sarà semplicemente un calare nella materia l’idea preesistente di uomo, cui Dio stesso deve sottostare. A pensarla così saranno i Francescani, un ordine religioso mistico e interessato più che altro ad adorare Dio; ma contrapposti a loro vi sono i Domenicani, che abbracciano non già le posizioni platoniche, ma quelle aristoteliche: per Aristotele non vi è un’idea uomo che sta a monte dell’uomo stesso: la forma uomo (o idea uomo, se vogliamo dirla con Platone) esiste incollata all’uomo stesso, è presente in tutti gli uomini e durerà fin tanto che esisteranno uomini: essa non è ante rem, come credeva Platone, ma in re. Non vi è un mondo all’infuori del nostro, né vi è quel complesso apparato di idee: di conseguenza i domenicani potranno ancora più dei francescani esaltare l’onnipotenza di Dio, il quale non è più costretto ad attenersi a delle idee per creare: la sua onnipotenza si manifesta nell’atto di creare l’uomo in carne ed ossa ma anche nell’atto di crearne l’idea. E questo implica una radicale divergenza nella concezione degli enti matematici: per i francescani 2 + 2 = 4 indipendentemente da Dio: Dio deve sottostare a questa verità e non può cambiarla, anzi deve attenersi ad essa nel creare il mondo. Per i domenicani, invece, che 2 + 2 = 4 l’ha deciso Dio di sua spontanea iniziativa perché , in assenza delle idee cui é costretto ad attenersi, Dio può tutto: ha deciso che 2 + 2 = 4 , ma avrebbe anche potuto decidere che 2 + 2 = 5 ! Sembra però che ci sia una contraddizione di fondo in questo ragionamento “matematico”: come si spiegano le leggi fisiche, alle quali pare proprio che Dio sia subordinato?
A fornire una risposta é Guglielmo da Ockham: le leggi fisiche ci sono, é evidente, ed é Dio che, nella sua illimitata onnipotenza, le ha poste con la sua potenza ordinata, ma questo non toglie che egli, proprio perché onnipotente, possa stravolgerle con la sua potenza assoluta: ha deciso che gli oggetti lasciati cadano verso il basso, ma potrebbe benissimo cambiare le carte in gioco (proprio perché non ci sono le idee cui deve attenersi) facendo cadere gli oggetti obliquamente E i miracoli non sono forse la prova di quanto dice Ockham E’ Dio che stravolge le leggi fisiche può allo stesso modo decidere che 2 + 2 = 5 anziché 4: le verità matematiche per i domenicani non sono quindi un qualcosa di immutabile e di assolutamente certo perché Dio potrebbe decidere da un momento all’altro di mutarle; per i francescani, al contrario, esse sono assolutamente inconfutabili proprio perché Dio stesso deve attenersi ad esse.
Cartesio, nel Seicento, arriverà a dire che le verità matematiche che l’uomo é riuscito ad acquisire, tramite sforzi immani e secoli di ricerca, egli le conosce alla pari di Dio: in altri termini, secondo Cartesio, che 2 + 2 = 4 lo so io esattamente come lo sa Dio: tutto quel che c’è da sapere nella verità 2 + 2 = 4 lo sappiamo, così come lo sa Dio. Sul piano qualitativo siamo dunque alla pari di Dio (ciò che sappiamo in ambito matematico lo sappiamo esattamente come lo sa Dio), su quello quantitativo siamo nettamente in svantaggio: la quantità di verità matematiche che noi conosciamo é infinitamente minore rispetto a quella conosciuta da Dio: questo vale solo per quel che riguarda la matematica, la forma di pensiero più precisa e rigorosa di cui siamo in possesso. Dunque sia noi sia Dio possiamo conoscere con certezza le verità matematiche e sia noi sia Dio dobbiamo sottostare ad esse, ossia non possiamo fare nulla per cambiarle: da notare come Cartesio sia molto più vicino alle idee francescane che non a quelle domenicane sotto questo profilo e, non é un caso, egli é un platonico. Va poi senz’altro ricordata la celebre ipotesi cartesiana del genio maligno, con la quale il pensatore francese arriva a mettere in discussione perfino le verità matematiche: chi non mi dice di essere stato creato da un genio maligno che impiega tutta la sua onnipotenza per ingannarmi di continuo? Chi non mi dice di essere stato creato da un genio maligno che mi ha costruito tale da credere e prendere per certo che 2 + 2 = 4 quando in verità 2 + 2 = 5 ? E’ interessante questa ipotesi bislacca perché in un certo senso stravolge il modo di pensare, ci toglie il terreno da sotto i piedi, ci fa crollare addosso il mondo. Tuttavia, basta dimostrare che non siamo stati creati dal genio maligno per rimettere le cose a posto e per far ritornare indiscutibili le verità matematiche e Cartesio lo fa con una certa abilità argomentativa: sono a conoscenza della mia imperfezione perché dubito perfino delle verità matematiche e ciò che dubita, evidentemente, é imperfetto; ma per dire che una cosa é imperfetta devo avere nella mia testa l’idea di perfezione (come potrei dire che una cosa é imperfetta se non so cosa é la perfezione?) ; ma chi me l’ha messa in testa? Io no, di sicuro, perché sono imperfetto: deve avermela data qualcosa di perfetto: Dio , che esiste ed é perfetto. Se Dio é perfetto, naturalmente, sarà buono e viene quindi scartata l’ipotesi del genio maligno: posso affermare con sicurezza che 2 + 2 = 4, con una tale sicurezza che Dio stesso non potrebbe smentirmi. Come tutti sapranno in un’espressione algebrica o anche nel più comune dei calcoli ( 1 + 1 = 2 ) non vi é nulla che non avvenga necessariamente, nel senso che si deve per forza arrivare ad un risultato non vi é la libertà di scelta: 5 + 4 dà 9 e non potrebbe essere altrimenti. I calcoli numerici, nella loro perfezione, esprimono dunque una necessità e dissipano ogni possibilità.
Da questa considerazione muoverà la concezione stessa di Dio del filosofo olandese del Seicento Benedetto Spinoza: Dio, che per il pensatore olandese é l’intero universo in tutte le sue manifestazioni, se é perfetto come vuole la definizione stessa di divinità non può che esprimere una necessità proprio come un calcolo del tipo 2 + 2 = 4: ciò che avviene in campo divino e quindi (proprio perché Dio non é altro che l’intero cosmo) tutto ciò che avviene nel mondo non può che avvenire necessariamente: con Spinoza viene a cadere il libero arbitrio dell’uomo, il quale, facendo parte dell’universo-Dio, é anch’egli manifestazione di Dio. Tutto nel mondo avviene in modo perfetto, e il mondo intero potrebbe essere letto come una grande espressione: non c’é possibilità che 2 + 2 dia 5 come non vi é possibilità che le cose vadano diversamente da come vanno. D’altronde il concetto stesso di libertà implica la possibilità di errore e di impotenza del soggetto, prerogativa che stona notevolmente con le istanze di Dio. Probabilmente a molti la concezione spinoziana sembrerà un po’ forzata, quasi a dimostrare un anelito del pensatore a trovare nel mondo una perfezione numerica che in molti casi pare davvero inconcepibile. Tuttavia non ci si deve stupire troppo: dobbiamo tenere a mente che Spinoza vive nel Seicento, il secolo della fisica matematizzata, il secolo in cui si cerca di ricorrere sempre e solo alla matematica; in quegli stessi anni un altro grande pensatore, Thomas Hobbes , arriva a dire che pensare significa svolgere sottrazioni e addizioni: dire che una penna é blu significa addizionare alla sostanza penna l’attributo blu per ottenere così la penna blu allo stesso modo in cui 2 + 2 mi dà 4; viceversa, dire che la penna non é blu significa sottrarre l’attributo blu alla sostanza penna, esattamente come 6 – 2 mi dà 4. Quella di Spinoza, di Hobbes, di Cartesio e di molti altri filosofi di quegli anni sembra una vera e propria esasperata corsa al numero, dettata dalla consapevolezza che la matematica costituisca il sapere più preciso di cui l’uomo disponga, talmente preciso da essere identico a quello di Dio .
Le frazioni egiziane
Euclide, questo sconosciuto!
In questo articolo noi cercheremo di presentare, con lo scopo di offrire al lettore qualche spunto di riflessione critica, alcuni aspetti riguardanti l’impostazione euclidea della geometria, con particolare riferimento alla prima parte degli Elementi di Euclide.
In this paper we shall try to present some considerations concerning the first part of euclidean Elements.
1. Premessa
Verso la fine del quarto secolo a. C. si ebbe in Grecia ad opera di Euclide, con i suoi Elementi, il periodo più significativo ed esaltante del processo di razionalizzazione della Geometria che era iniziato circa tre secoli prima con Talete, che pare abbia tratto stimoli e spunti significativi nel corso di alcuni suoi viaggi in Egitto. Sulle orme del primo grande maestro della matematica greca si era poi incamminato Pitagora, che di Talete forse fu allievo. E a proposito della Matematica del periodo ellenistico lo Struik a pagina 53 di [S] ci ricorda: “La matematica contribuì a trovare l’ordine nel caos, a disporre le idee in catene logiche, a trovare principi fondamentali. Era la più razionale di tutte le scienze”.
Prima di Euclide altri matematici greci avevano scritto degli Elementi, termine con cui di solito si intitolavano i trattati assiomatici ellenistici. Tra questi va annoverato Ippocrate di Chio; ma sono da ricordare anche Leone di Atene e Teudio di Magnesia (si veda [Pr], pp. 71 e seguenti). Purtroppo, come è noto, di quel fulgido periodo della matematica non possediamo una documentazione diretta e le notizie attualmente in nostro possesso risalgono a Proclo, il quale (cfr. [M], p. 3, nota (5)) attinse informazioni – forse in via indiretta – da Eudemo di Rodi (4° sec. a. C.).
Dello stesso Euclide si sa ben poco. E Frajese nella sua Introduzione in [E1] dice a p. 9, forse un po’ paradossalmente: “Euclide, questo sconosciuto! […] Ciò che di Euclide può dirsi è strettamente legato alla sua opera maggiore, gli Elementi.” Tuttavia, nonostante la posizione un po’ estrema di Frajese, qualche notizia è filtrata nel corso dei secoli.
Con ogni probabilità Euclide visse ad Alessandria sotto Tolomeo I (circa 300 a. C.), successore di Alessandro Magno in uno dei tre regni in cui l’immenso dominio macedone era stato smembrato dopo la morte del suo grande imperatore. Egli diede un notevole contributo alla diffusione della matematica in tutto il mondo allora conosciuto, suscitando un notevole interesse, nonostante le difficoltà che la disciplina presentava. E pare che proprio a Tolomeo – che gli chiedeva se ci fosse una via più breve per lo studio della geometria – Euclide abbia detto (si veda [Ht], p. 354) che non esisteva una via regia alla geometria.
Così come Ippocrate di Chio non è da confondere col medico suo omonimo, anche il nostro Euclide non deve essere confuso col filosofo Euclide di Megara, vissuto alcune decine di anni prima. Come ci informa Thomas Heat in [Ht] (p. 355), dove si possono attingere altre notizie sul grande matematico greco, la confusione tra i due Euclide fu molto diffusa nel Medio Evo. La prima traccia di questo inconveniente comparve in uno scritto di Valerio Massimo, vissuto al tempo di Tiberio.
2. Gli Elementi
L’eccelsa opera di Euclide è stata per lungo tempo considerata un modello di perfezione e i suoi Elementi per molti secoli hanno forse costituito, dopo la Bibbia, il libro più letto, analizzato e sviscerato. Comunque va tenuto presente che Euclide con ogni probabilità ha attinto copiosamente a quanto molti studiosi avevano già prodotto prima di lui. Frajese in [E1] a p. 9 ci ricorda: “[…] gli Elementi di Euclide costituiscono il punto di arrivo di un periodo di elaborazione trisecolare della matematica, (che) […] si suol chiamare periodo della geometria pre-euclidea […];Ma gli Elementi di Euclide rappresentano anche un punto di partenza; successori immediati di Euclide sono i sommi matematici Archimede e Apollonio […].”; e a p. 10 aggiunge: “[…] quest’opera riassume, utilizza, coordina, sistema l’opera dei matematici predecessori, offrendone una validissima sintesi, che al tempo stesso è analitica nella vastità della sua intelaiatura”. Inoltre Federico Enriques a p. 2 di [En] dice in proposito: “L’opera […] non può ritenersi costruzione originale di Euclide, ma appare riduzione in un trattato organico di ciò che il genio greco ha costruito nei tre secoli precedenti.”
Gli Elementi di Euclide sono suddivisi in tredici libri e iniziano con ventitré Definizioni che hanno lo scopo di delineare gli “oggetti”, gli enti geometrici che saranno presi in considerazione nel corso della trattazione. Dopo le Definizioni vengono cinque postulati. Tra questi è molto famoso il quinto, dalla cui negazione hanno avuto origine le Geometrie non euclidee; invece, se si prescinde da questo postulato, allora si ha la cosiddetta Geometria assoluta.
Ai cinque postulati fanno immediatamente seguito le cosiddette Nozioni Comuni (si veda [E1] pp. 58 e 73, [He] pp. 5 e 6, nonché [Sz]) e le prime fondamentali proposizioni con cui inizia la teoria vera e propria, nel corso della quale si incontrano altre definizioni.
Nel prosieguo di questo intervento le parti riportate in neretto non sono altro che la parte iniziale del primo Libro degli Elementi di Euclide, così come la si ricava da [E1], fino alle Nozioni Comuni incluse.
A un’attenta lettura degli Elementi secondo i canoni interpretativi moderni si avvertono alcune incongruenze ed ingenuità, comprensibili per quel periodo. Certo ai tempi di Euclide era ancora molto lontano quel salto di qualità che avremmo avuto soltanto dopo più di duemila anni, quando la matematica del XIX secolo avrebbe affinato i suoi strumenti di indagine critica. Poi nel XX secolo quegli strumenti si sarebbero affinati ancor più, raggiungendo un tale grado di perfezione (compatibilmente con la naturale predisposizione umana all’errore) che è difficile capire quali altri miglioramenti potranno essere conseguiti.
I limiti dell’impostazione euclidea non sfuggirono a Hilbert, che forse per questo sentì l’esigenza di una rifondazione della geometria, che egli realizzò nel suo famoso Grundlagen der Geometrie (si veda [H] e [H1]).
Da Euclide a Hilbert c’è stato un lungo percorso di circa 2200 anni durante il quale la matematica è assurta al ruolo di regina delle scienze. Questo periodo è stato illuminato da molti astri di prima grandezza nel firmamento della nostra disciplina, che ci hanno regalato risultati fondamentali nell’ambito della matematica e delle scienze esatte.
3. Le Definizioni, i Postulati e le Nozioni comuni negli Elementi
Per due punti distinti passa una e una sola retta. Questa proposizione generalmente viene considerata da molti testi scolastici come il primo postulato della geometria euclidea. Ma al riguardo c’è un equivoco di fondo, poiché negli Elementi di Euclide con il termine “rette” di fatto si intendono i nostri segmenti. E Silvio Maracchia, in accordo con diversi altri studiosi, nella nota “(48)” riportata a p. 23 di [M] scrive: “[…] per Euclide la retta non è data nella sua infinità attuale, ma solo in quella potenziale di segmento prolungabile quanto si vuole.” Inoltre, a proposito del significato da dare negli Elementi all’espressione “linea retta” (o, semplicemente, “retta”) Attilio Frajese nella parte finale della nota “3” a piè di pagina 66 di [E1] scrive: “Va infine osservato che la linea è considerata come terminata, cioè avente estremi: qui e costantemente (salvo rarissima eccezione) negli Elementi.”
Però le eccezioni di cui parla Frajese potrebbero essere più apparenti, “potenziali”, che non effettive. La prima la troviamo nella Proposizione 12 del primo Libro degli Elementi; essa viene enunciata così (si veda [E1], p. 93): Ad una data retta illimitata, da un punto dato ad essa esterno, condurre una linea retta perpendicolare. Ebbene ci pare di poter presumere che nella suddetta proposizione il termine “illimitata” venga usato nel senso di “opportunamente prolungata”. La seconda eccezione la si ritrova a p. 111 di [E1] nella costruzione che Euclide ci propone relativamente alla sua Proposizione 22, ove sembra comparire la nozione di semiretta. Infatti lì troviamo scritto: Si assuma una retta DE terminata in D ed illimitata dalla parte di E […]. In realtà in quella costruzione ciò che serve è un ben individuabile prolungamento di un segmento DF ivi considerato. Tuttavia, il fatto che nel Postulato II che vedremo in seguito si usi l’espressione “retta terminata” indurrebbe a pensare che per Euclide possano esistere anche rette non terminate (cioè, illimitate), corrispondenti in qualche modo alle rette considerate attualmente da noi. Nel contempo la mancanza della specificazione “terminata” nel Postulato I riportato più sotto può far presumere che in quel contesto – in presenza della locuzione “condurre […] da […] ad”, che di per sé lascia intendere limitatezza – la precisazione sia ritenuta inutile da Euclide. Ed egli assume questo tipo di atteggiamento anche in altre situazioni in cui evita precisazioni superflue. Ad esempio in [E1], pp. 79 e 80, nella Proposizione 2 (Applicare ad un punto una data retta uguale ad una retta data) e nella Proposizione 3 (Date due rette disuguali […]), dove l’uguaglianza e la disuguaglianza chiamate in causa si riferiscono chiaramente a segmenti. Naturalmente, i discorsi fatti sulla “illimitatezza potenziale” delle rette considerate da Euclide vanno estesi anche ai piani.
Ed ecco le 23 definizioni con cui iniziano gli Elementi di Euclide. A proposito degli enti geometrici considerati nelle Definizioni crediamo sia opportuno riportare quanto Frajese – in accordo con altri studiosi – dice in [E1] a p. 48: “[…] si tratta (per Euclide, n. d. r.) di descriverli, affinché possano essere facilmente riconosciuti attraverso una soddisfacente nomenclatura. Quegli enti geometrici, cioè, esistono già: la definizione ha per Euclide soltanto il senso di individuarli.”
I. Punto è ciò che non ha parti.
II. Linea è lunghezza senza larghezza.
III. Estremi di una linea sono punti.
IV. Linea retta è quella che giace ugualmente rispetto ai punti su di essa (cioè, ai suoi punti).
Nella nota “4” di p. 66 di [E1] Frajese considera oscura, giustamente, la Definizione IV; e lo stesso Maccioni – che insieme a Frajese ha curato l’edizione di [E1], occupandosi anche della traduzione degli Elementi in italiano – nel commento denotato con “a” collocato nella stessa pagina cerca di fornirci una spiegazione sul piano filologico, svolgendo una sottile analisi della formulazione in lingua greca della definizione, però anche lui è costretto ad arrendersi di fronte all'”oscurità” del testo.
Al giorno d’oggi non si dà alcuna definizione particolare di punto o di retta. Infatti per punti si intendono gli elementi di un dato insieme non vuoto S. Si dà quindi la nozione di spazio geometrico, intendendo con tale locuzione lo stesso insieme S munito di certi suoi sottinsiemi chiamati blocchi. Ad esempio, si possono considerare come blocchi le rette, oppure i piani dello spazio della nostra intuizione. I blocchi a loro volta sono formalmente detti rette proprio quando sono dotati di proprietà particolarmente evocative rispetto alle rette intese intuitivamente.
Tuttavia è doveroso far presente che anche la precedente posizione andrebbe meglio precisata, poiché potrebbe portare a situazioni poco soddisfacenti. Ad esempio, dati tre “oggetti” a, b e c e considerato l’insieme S i cui elementi sono a, b, c, {a} e {a, b} – che quindi svolgono il ruolo di punti – se si assumono come blocchi i sottinsiemi di S dati da {a, b}, {a, c} e {b, c}, si ha l’inconveniente che {a, b} è nello stesso tempo un punto ed un blocco. Perciò per poter parlare di insieme di punti forse si dovrebbe fare in modo che inconvenienti di questo tipo siano evitati.
Ora proseguiamo con la presentazione delle Definizioni euclidee.
V. Superficie è ciò che ha soltanto lunghezza e larghezza.
VI. Estremi di una superficie sono linee.
VII. Superficie piana è quella che giace ugualmente rispetto alle rette di essa (cioè, alle sue rette).
Come R. Trudeau sottolinea a p. 46 di [T], le Definizioni V, VI e VII sono l’analogo in due dimensioni delle precedenti Definizioni I, II e III. Inoltre il Trudeau in alcune delle prime sette Definizioni vede più il tentativo di delineare dei concetti (termini) primitivi, che non delle definizioni vere e proprie (cfr. [T], p. 45).
Per Euclide, verosimilmente, le rette/segmenti debbono godere delle usuali proprietà elementari, anche se egli non le esprime tramite assiomi. Ad esempio, le rette AC e CA coincidono; e se due rette distinte AC e AD sono prolungamenti distinti di una stessa retta AB, allora esse sono una prolungamento dell’altra. Ed ancora, dato un punto C su di una retta AB, allora i due segmenti AC e CB hanno in comune il solo estremo C; inoltre, i punti di AB sono esattamente quelli di AC e/o quelli di CB.
VIII. Angolo piano è l’inclinazione reciproca di due linee su un piano, le quali si incontrino fra loro e non giacciano in linea retta.
IX. Quando le linee che comprendono l’angolo sono rette, l’angolo si chiama rettilineo.
X. Quando una retta innalzata su una [altra] retta forma gli angoli adiacenti uguali fra loro, ciascuno dei due angoli uguali è retto, e la retta innalzata si chiama perpendicolare a quella su cui è innalzata.
Notiamo che per gli angoli “adiacenti” Euclide non dà alcuna definizione; ma si capisce che qui egli adopera il significato usuale per noi. Però altre volte – ad esempio, nella Proposizione 14 del Libro I (si veda [E1], p. 97) – “adiacenti” sta per il nostro “consecutivi”.
Sulla Definizione X si è molto discusso, anche contestando ad Euclide di non aver precisato cosa intendesse per angoli uguali. Un discorso analogo ha riguardato anche l’uguaglianza tra segmenti; dimenticando che per Euclide il concetto di uguaglianza non poteva essere che quello legato al cosiddetto trasporto rigido; ciò anche in accordo col significato concreto che, non solo allora, si attribuiva alla geometria. Il che è confermato dalle dimostrazioni di alcune delle prime proposizioni degli Elementi. Del resto il trasporto rigido di segmenti e di angoli – idealmente svolto tramite strumenti materiali quali il goniometro (anche senza tacche) e l’asta rigida, con la convenzione che essa possa identificarsi con un “lato” del goniometro – ha sempre costituito un ottimo surrogato e una notevole semplificazione di assiomi che solo da qualche decennio il mondo della matematica si è dato (si veda [H], p. 12 e sgg.). Comunque, per completezza di informazione, va detto che Euclide fa ricorso al trasporto rigido solo in rare occasioni, anche se già nelle dimostrazioni della Proposizione 4 e della Proposizione 8 del Libro I (da noi conosciute come primo e terzo criterio di uguaglianza per i triangoli).
XI. Angolo ottuso è quello maggiore di un retto.
XII. Angolo acuto è quello minore di un retto.
XIII. Termine è ciò che è estremo di qualche cosa.
Si sottolinea la genericità della Definizione XIII, che sembra più una convenzione di linguaggio relativa alla parola “termine”.
XIV. Figura è ciò che è compreso da uno o più termini.
XV. Cerchio è una figura piana compresa da un’unica linea tale che tutte le rette, le quali cadano sulla linea a partire da un punto fra quelli che giacciono internamente alla figura, sono uguali fra loro.
XVI. Quel punto si chiama centro del cerchio.
Notiamo che, allo stato attuale, un cerchio potrebbe avere più centri.
XVII. Diametro del cerchio è una retta condotta per il centro e terminata da ambedue le parti dalla circonferenza del cerchio, la quale retta taglia anche il cerchio per metà.
XVIII. Semicerchio è la figura compresa dal diametro e dalla circonferenza da esso tagliata. E centro del semicerchio è quello stesso che è anche centro del cerchio.
XIX. Figure rettilinee sono quelle comprese da rette, vale a dire: figure trilatere quelle comprese da tre rette (sono i triangoli; n. d. r.), quadrilatere quelle comprese da quattro, e multilatere quelle comprese da più di quattro rette.
XX. Delle figure trilatere, è triangolo equilatero quello che ha i tre lati uguali, isoscele quello che ha soltanto due lati uguali, e scaleno quello che ha i tre lati disuguali.
A differenza dell’uso odierno, nelle Definizioni XX e XXII che seguono i termini sono dati con un significato esclusivo; cioè, un triangolo isoscele non è mai equilatero, un rettangolo non è mai un quadrato, ecc.
XXI. Infine, delle figure trilatere, è triangolo rettangolo quello che ha un angolo retto, ottusangolo quello che ha un angolo ottuso, ed acutangolo quello che ha i tre angoli acuti.
XXII. Delle figure quadrilatere, è quadrato quella che è insieme equilatera ed ha gli angoli retti, rettangolo quella che ha gli angoli retti, ma non è equilatera, rombo quella che è equilatera, ma non ha gli angoli retti, romboide quella che ha i lati e gli angoli opposti uguali fra loro, ma non è equilatera né ha gli angoli retti. E le figure quadrilatere oltre a queste si chiamino trapezi.
XXIII. Parallele sono quelle rette che, essendo nello stesso piano e venendo prolungate illimitatamente dall’una e dall’altra parte, non si incontrano da nessuna delle due parti.
Ora diamo i primi due Postulati di Euclide, che ci permetteranno di inquadrare meglio la nozione euclidea di retta. Seguiranno gli altri tre Postulati, così come sono riportati in [E1] a p. 71, perché si possa fare una prima e immediata valutazione dell’impostazione euclidea. Per un maggior approfondimento si consiglia di consultare anche [M] (p. 22 e sgg).
I Risulti postulato: che si possa condurre una linea retta da un qualsiasi punto ad ogni altro punto.
II E che una retta terminata si possa prolungare continuamente in linea retta.
Facciamo presente che nel Postulato I deve intendersi come naturalmente sottintesa anche l’unicità della “retta (terminata)” ivi considerata. In proposito si riporta qui di seguito la “traduzione” di tale postulato fatta dal Trudeau in [T] (p. 55, Postulato 1): “Da un punto qualsiasi è possibile condurre ad ogni altro punto una e una sola retta.” E il Trudeau, aggiungendo la locuzione “una sola”, esplicita quanto con ogni probabilità era ovvio per Euclide, il cui punto di partenza negli Elementi – come in parte è stato già detto – è di tipo intuitivo, anche se l’impostazione ipotetico-deduttiva che egli dà tende a svincolarsi il più possibile dagli aspetti intuitivi. Ciò in qualche modo è confermato anche dall’enunciato del successivo quinto postulato, nel quale si intravede la nozione di semipiano (… quella parte in cui sono gli angoli minori di due retti), che tuttavia non rientra nelle definizioni già date.
Per ragioni di completezza informativa, facciamo presente che alcuni autori fanno risalire l’unicità del segmento che congiunge due punti alla successiva proposizione IX (da molti considerata come un’ulteriore Nozione Comune, ma che non è riportata da tutti i testi). Tuttavia, ciò non inficia la nostra precedente posizione, dal momento che questa difficilmente è una Nozione attribuibile ad Euclide (si veda [M], p. 25).
IX. Due linee rette non racchiudono uno spazio.
Ed ecco gli altri tre postulati.
III. E che si possa descrivere un cerchio con qualsiasi centro ed ogni distanza.
IV. E che tutti gli angoli retti siano eguali fra loro.
V. E che, se una retta venendo a cadere su due rette forma gli angoli interni e dalla stessa parte minori di due retti, le due rette prolungate illimitatamente verranno ad incontrarsi da quella parte in cui sono gli angoli minori di due retti.
Gli assiomi III e V, per come sono enunciati, si riferiscono implicitamente ad un piano. Ciò non sempre è messo in evidenza dagli esegeti euclidei. Il Trudeau lo fa con il Postulato V, che a p. 57 di [T] enuncia per rette che giacciono su di un piano. Notiamo anche che il Postulato III, preso alla lettera, risulta banale. Infatti, dato un centro B e una distanza d – o meglio, un secondo punto C – la proprietà di essere un punto F avente distanza d da B (o meglio, di determinare un segmento BF uguale a BC) è ben definita in ogni piano (e nello spazio), onde essa individua completamente la classe di punti che costituiscono il “supporto” del cerchio di cui al Postulato III. Perciò a noi sembra che nel Postulato III Euclide volesse ravvisare piuttosto quel tipo di continuità secondo cui in un piano un cerchio che abbia il suo centro in B è proprio come ce lo immaginiamo: esso lascia la sua “traccia” su ogni segmento “sufficientemente lungo” che abbia un estremo in B. Cosa questa a cui Hilbert ha dedicato il suo Assioma III 1 (si veda [H], p.12 ). Questa nostra interpretazione sembra essere confermata da come Euclide a volte usa le circonferenze. Ad esempio, nella dimostrazione della Proposizione 2 del Libro I degli Elementi (si veda [H], p. 79) egli considera un segmento BF al solo scopo di considerarne l’intersezione con un cerchio avente centro in B.
A proposito del Postulato IV il Trudeau a p. 55 di [T] tenta di darne un giustificazione così: “Sebbene […] gli angoli retti si presentano a coppie, ciò non ci costringe a credere che due angoli retti situati in una parte del piano siano uguali ad altri due posti altrove.” Tuttavia questa posizione ci trova in disaccordo. Infatti, coerentemente con quanto detto a proposito del trasporto rigido, si vede subito che, dati due angoli adiacenti $\theta$ e $\phi$, nonché due angoli adiacenti $\theta’$ e $\phi’$, le ipotesi di adiacenza fanno sì che con un trasporto rigido si possa trasferire (eventualmente in modo parziale) un lato AB di $\phi$ su di un lato A’B’ di $\phi’$ in modo tale che B si sovrapponga a B’ e il lato BC di $\theta$ che è allineato con AB si trasferisca sul lato B’C’ che è allineato con A’B’. Di conseguenza $\theta$ è minore di $\theta’$ se e solo se $\phi$ è maggiore di $\phi’$. Ciò comporta come immediato corollario il fatto che due angoli retti – anche non adiacenti – debbano essere uguali. Il che rende superfluo il Postulato IV.
Ora diamo le Nozioni Comuni. Anche esse non sono state tutte scritte da Euclide. Nel corso dei secoli gli studiosi sono stati abbastanza concordi nell’attribuire al grande matematico alessandrino le tre Nozioni seguenti:
I. Cose che sono uguali ad una stessa sono uguali anche fra loro.
II. E se cose uguali sono addizionate a cose uguali, le totalità sono uguali.
III. E se da cose uguali sono sottratte cose uguali, i resti sono uguali.
A proposito delle precedenti Nozioni a nostro modesto avviso esse sono da intendersi non tanto come proprietà di carattere generale – il che le renderebbe estremamente vaghe – ma piuttosto come una convenzione sull’uso del termine “uguale”. Infatti – dando per scontato che una cosa, un oggetto, un elemento debba dirsi eguale a se stesso – è facile verificare che un “legame” (o meglio, una relazione binaria) tra coppie di oggetti di un certo aggregato (di un insieme), che sia espresso dalla locuzione “… è eguale a …”, per il quale valga la I, gode anche della proprietà simmetrica e di quella transitiva; perciò quella relazione è un’equivalenza. Inoltre la II e la III conferiscono ad elementi equivalenti un carattere di “intercambiabilità” rispetto alle operazioni a cui essi vengono sottoposti. Cosa questa che oggidì fa usare, invece del termine “equivalenti”, i termini “eguali” oppure “congruenti”.
Nei riguardi delle altre Nozioni Comuni è sempre esistita discordanza di vedute sulla paternità delle due Nozioni denotate con VII e VIII che sono riportate qui sotto. E Maccioni nella nota a riportata a p. 73 di [E1] scrive: “[…] Proclo […] critica l’indebita pretesa di Erone di Alessandria – il massimo ingegnere e professore di ingegneria alessandrino – di riconoscerne come autentiche solo le prime tre.”
IV. E se cose uguali sono addizionate a cose disuguali, le totalità sono disuguali.
V. E doppi di una stessa cosa sono uguali tra loro.
VI. E metà di una stessa cosa sono uguali tra loro.
VII. E cose che coincidono fra loro sono fra loro uguali.
VIII. Ed il tutto è maggiore della parte.
Si fa presente che alcuni studiosi considerano le Nozioni IV, V e VI, nonché la proposizione IX esposta precedentemente, di epoca successiva rispetto a Euclide (anche se esse sono adoperate dal grande maestro alessandrino). Tra di loro è da annoverare I. L. Heiberg, a cui è dovuto un importante testo critico su Euclide (si veda [He]).
A nostro avviso tale posizione è ampiamente condivisibile. Infatti la Nozione V è chiaramente un caso particolare della II, invece la IV è una conseguenza immediata di II e III (purché si considerino addizione e sottrazione – nella loro accezione più generale, non solo numerica – come operazioni che sono l’una l’inversa dell’altra), perciò è probabile che Euclide abbia considerato superfluo riportarle esplicitamente. D’altro canto se egli avesse effettivamente inserito la VI, allora avrebbe coerentemente inserito anche una Nozione Comune che prendesse in considerazione i “terzi” di una stessa cosa, una che prendesse in considerazione i “quarti”, ecc. Anzi, ci sembra di poter addirittura accettare la posizione di Erone, piuttosto che quella di Proclo; dal momento che la Nozione VII è banale, mentre la VIII – forse la più famosa – è più una convenzione di linguaggio che non una nozione vera e propria. In definitiva, sembra che nella VIII si voglia dire che quando si considera una parte di una “totalità”, allora della prima si dice che è minore della totalità a cui si riferisce. Una precisazione, quella, con la quale forse si è voluto mettere un freno alle tante dispute accese soprattutto da parte dei sofisti. Infatti, anche quando due segmenti hanno lunghezze diverse, essi individuano insiemi di punti che hanno la stessa cardinalità, cosa ben nota ai matematici ellenici; ciononostante, se il primo dei due segmenti è un prolungamento dell’altro, allora nel contesto degli Elementi il secondo – in forza della Nozione Comune VIII – è da dirsi minore del primo, pur avendo essi la stessa cardinalità.
E in quella precisazione ci piace intravvedere un tentativo di metter freno a un atteggiamento tipico – allora come ora – della comunicazione umana, spesso caratterizzata dal “così è se vi pare”, dal “qui lo dico e qui lo nego”. Euclide, o chi per lui, sembra voler dare un senso inequivocabile alle sue parole. E in fondo si tratta di un atteggiamento tipico del matematico, che se diventasse – con un’opportuna educazione alla nostra disciplina – patrimonio comune dell’umanità, forse renderebbe meno problematici i rapporti umani.
Bibliografia
[E] Euclide (1926) Gli Elementi di Euclide e la critica antica e moderna, Vol. I, a cura di F. Enriques e altri, Stock, Roma.
[E1] Euclide (1970) Gli Elementi, a cura di A. Frajese e L. Maccioni, U.T.E.T., Torino.
[En] Enriques F. (1983) L’evoluzione delle idee geometriche nel pensiero greco: punto, linea e superficie; in: Questioni riguardanti le Matematiche elementari, a cura di F. Enriques, Zanichelli, Bologna.
[F] Frajese A. (1968) Il sesto postulato di euclide, Periodico di matematiche, 1-2, pp. 150-159.
[H] Hilbert D. (1970) Fondamenti della geometria, Feltrinelli, Milano.
[H1] Hilbert D. (1968) Grundlagen der Geometrie, B. G. Teubner, Stuttgart.
[He] Heiberg I. L. (1969) Euclides, vol. I, libri I-IV, B. G. Teubner, Stuttgart.
[Ht] Heath T. (1981) A history of greek mathematics, Dover Publications, Inc., New York.
[M] Maracchia S. (1975) La matematica come sistema ipotetico-deduttivo (profilo storico), Firenze, Le Monnier.
[Pr] Proclo (1978) Commento al primo libro degli Elementi di Euclide, a cura di M. Timpanaro Cardini, Giardini, Pisa.
[S] Struik D. J. (1981) Matematica: un profilo storico, Bologna, il Mulino.
[Sz] Szábó Á. (1960) Anfänge des Euklidischen Axiomensystems, Archive for History of Exact Sciences, I.
[T] Trudeau R. (1991) La rivoluzione non euclidea, Torino, Bollati Boringhieri.
La cicloide
Dal teorema di De Giorgi – Nash al teorema di Pitagora
Dal teorema di De Giorgi – Nash al teorema di Pitagora: un salto a ritroso di venticinque secoli segnati dalla costante ricerca della verità scientifica
Domenico Lenzi (Dip. Mat.Univ. del Salento)
Sunto: Intorno al 600 a. C., grazie a Talete (cfr. [T] a pag. 13 ed [M] a pag. 3), iniziò un lento processo di razionalizzazione della geometria, che ebbe il suo momento più alto con Euclide: nacque così la Scienza. Pitagora, da molti ritenuto allievo di Talete, fu uno dei principali artefici di quel processo. Recentemente è stata ricordata la figura di John Forbes Nash Jr., matematico americano il cui nome è legato a quello del nostro Ennio De Giorgi in un importante teorema sul calcolo delle variazioni.
Il presente articolo è dedicato a questi studiosi, che hanno segnato tappe fondamentali per la storia della matematica e della scienza.
Abstract: This paper is dedicated to theorem of De Giorgi-Nash and to theorem of Pythagoras.
 |
|
 |
1. Premessa
L’Oscar attribuito alcuni mesi fa al film “A beautiful mind” – che narra con qualche spunto arbitrario la vita di John Forbes Nash Jr., matematico americano tuttora vivente, insignito nel 1994 del premio Nobel per l’Economia, mentre per la Matematica il Nobel non è previsto – ha risvegliato attenzioni sopite da tempo nei riguardi di numeri, figure geometriche e ogni altra cosa legata a loro. E forse mai come quest’anno ci sono state tante richieste di partecipazione alle Olimpiadi di Matematica per la scuola media, organizzate da enti vari e associazioni quali Mathesis, C.I.I.M., Sc. Normale Sup. di Pisa, Universita’ “Bocconi”, ecc.
Misurare e far di conto sono sempre state attività tipiche dell’umanità. E’ vero che nella Bibbia si legge che il Padreterno nel corso della creazione contò fino a sei giorni e poi si riposò; ma Dio la matematica non la fa, Lui è la matematica, Lui è la ragione, è tutto.
Inoltre si conoscono casi in cui animali hanno mostrato una certa, anche se rozza, parvenza di attività matematica; ma – a parte alcuni fenomeni da baraccone in cui trucchi occulti l’hanno fatta da padrone – si è sempre trattato di casi estremamente elementari in cui la matematica ha fatto appena capolino e, come “etichetta”, è stata usata impropriamente.
Generalmente è considerato emblematico il comportamento del cuculo che va a deporre il suo uovo in un nido non suo, però premurandosi di sostituirlo a un altro – inquilino legittimo – che fa precipitare, per evitare che il vero proprietario del nido si renda conto dell’intrusione. Ma forse il suo è solo un fatto istintivo governato dal suo DNA e non, come qualcuno ha detto, un esempio di abilità aritmetica. Meno noto è il taglifo, un animaletto che quando ritorna alla sua tana lo fa secondo un percorso in linea retta. Conosce la geometria il taglifo? Noi non lo crediamo. Con ogni probabilità anche lui si limita semplicemente a seguire il suo istinto. Però per l’uomo le cose stanno in maniera diversa; e su di un terreno in cui intuito e istinto sono un concime basilare, spesso si innesta un’attività di tipo razionale in cui l’eccitazione (se così si può dire) di zone tipiche del cervello umano è essenziale.
Ebbene nell’ambito della disciplina matematica – purtroppo spesso mal digerita e mal sopportata da molti studenti, anche per colpa di insegnanti non adeguatamente preparati da una università che sembra andare verso il baratro (ma questo è un altro discorso) – con ogni probabilità il risultato più noto è rappresentato dal Teorema di Pitagora: Il quadrato costruito sull’ipotenusa di un triangolo rettangolo è equivalente all’unione dei quadrati costruiti sui cateti.
D’altro canto il teorema di De Giorgi-Nash ha rappresentato uno dei risultati più importanti degli ultimi cinquant’anni; cercheremo di vederne il perché.
2. Un recente passato
Come molti sapranno, Nash meritò il Nobel per i suoi risultati sulla Teoria dei Giochi.
Ma cos’è questa teoria dal nome strano, che fa pensare più a una sala fumosa dove si pratica il gioco d’azzardo che non alla stanza di lavoro – spesso disordinata e caotica (per gli altri!) – di uno scienziato?
Gianfranco Gambarelli – uno dei principali esperti italiani e fondatore della scuola italiana di Teoria dei Giochi, che ha avuto modo di collaborare con Nash (in proposito risulta molto intrigante l’ultimo capoverso di [Ga2], intitolato La busta gialla) – ha brevemente illustrato, ancora in [Ga2] (ma in proposito si può consultare anche il suo testo [Ga], di lettura facile e gradevole): La Teoria dei Giochi è la scienza matematica che analizza situazioni di conflitto e ne ricerca soluzioni competitive e cooperative. Le applicazioni e interazioni di tale teoria sono molteplici: dal campo economico a quello militare, biologico, sociologico, psicologico.
Quella di Nash è stata una vita davvero travagliata, soprattutto per la sua schizofrenia, che ha inevitabilmente determinato per lui alcune incomprensioni nell’ambito del mondo accademico e qualche delusioni professionale. Una di queste delusioni riguardò il celebre teorema di De Giorgi-Nash sul calcolo delle variazioni, dimostrato nel 1957 – alcuni mesi prima di Nash, tra l’altro in modo più semplice ed elegante – da Ennio De Giorgi (cfr. [Gi], [Gi1] ed [L]), insigne matematico pugliese morto nel 1996, che fu professore presso la Sc. Normale Sup. di Pisa ed ha attivato presso l’Università di Lecce (sua città natale) una fiorente scuola sul calcolo delle variazioni, disciplina di cui egli è stato uno degli studiosi più importanti.
Ma cosa dice il teorema di De Giorgi-Nash? Senza scendere in complicati dettagli tecnici – che esulano dallo scopo di queste brevi considerazioni e potrebbero risultare in parte incomprensibili – rinviamo a [Gi] (e agli altri interventi che accompagnano [Gi]) chiunque fosse interessato anche a un minimo di approfondimento sull’attività scientifica del nostro Ennio. Qui ci limitiamo a segnalare che questo teorema si riferisce alla regolarità di un certo tipo di funzionali.
Invece per quel che riguarda il calcolo delle variazioni, riportiamo le parole che De Giorgi stesso e due suoi allievi, Giuseppe Buttazzo e Gianni Dal Maso, hanno scritto sull’Enciclopedia Treccani del Novecento: … rientrano nel calcolo delle variazioni tutti i problemi in cui si cerca il minimo o il massimo di una certa grandezza. … In esso rientrano molte questioni sia di matematica pura sia di matematica applicata alla Fisica, all’ingegneria, alla Biologia, all’Economia.
Quanto è stato richiamato or ora in qualche modo dovrebbe far capire l’importanza del calcolo delle variazioni per la Teoria dei Giochi, poiché nelle funzioni a più variabili proprietà di minimo e nello stesso tempo di massimo sono spesso legate ai “punti di sella”, che generalmente caratterizzano situazioni di equilibrio, che hanno notevole importanza in Teoria dei Giochi (dove segnaliamo i cosiddetti “equilibri di Nash”).
A proposito delle dimostrazioni del teorema di De Giorgi-Nash, Enrico Giusti – che insieme a De Giorgi e a Enrico Bombieri [Bombieri è l’unico matematico italiano a cui sia stata assegnata (1974) la Medaglia Field] ha dato importanti contributi al calcolo delle variazioni – in [Gi] ha scritto: Il metodo di Nash, totalmente differente da quello di De Giorgi, era molto più complesso e non ha avuto sviluppi. Non così quello di De Giorgi, che è stato il punto di partenza per innumerevoli ricerche, e il cui potenziale non si è ancora esaurito.
E Antonio Leaci, anche lui allievo dell’insigne maestro salentino, in [L] ci rivela: Le loro dimostrazioni erano completamente diverse, così come lo erano i loro caratteri e i loro modi di lavorare: competitivo e individualista Nash, prodigo ed estimatore del lavoro in collaborazione De Giorgi.
Il teorema di De Giorgi-Nash è legato al 19° dei 23 fondamentali problemi di matematica presentati da David Hilbert durante il famoso Convegno dell’Unione Matematica Internazionale svoltosi a Parigi nel 1900.
Prima di De Giorgi molti altri studiosi si erano cimentati con quel 19° problema, fornendo soluzioni parziali. Con De Giorgi – e dopo alcuni mesi, in maniera indipendente, con Nash – il problema fu completamente risolto.
De Giorgi ha fornito contributi determinanti anche per lo studio del 20° e del 23° di quei problemi, anche questi sul calcolo delle variazioni.
Tornando a Nash, c’è da ricordare che la sua è stata solo una delle tante vite travagliate di matematici. Ricordiamo per tutti i grandi Renato Caccioppoli e Alan Turing, morti suicidi durante il secolo scorso, ai quali sono stati dedicati rispettivamente i film “Morte di un matematico napoletano” e il recente “Enigma”. Grandi menti le loro, ma purtroppo (come si è verificato per molti matematici eccelsi) con seri problemi.
Qualcuno ha detto che la razionalità confina con la pazzia; e forse questo è in parte vero. Probabilmente per alcuni studiosi un eccessivo chiudersi in se stessi e nei propri problemi scientifici a volte irrisolubili, coniugato con una certa mancanza di elasticità e con la continua e giustificabile lotta contro il “così è se vi pare” imperante – che pure, in piccole dosi, talora potrebbe essere una sorta di valvola di sfogo – spesso può determinare esiti dirompenti e una certa repulsione da parte degli “altri” anche sul piano personale, oltre che su quello scientifico. Perciò si dovrebbe cercare di porre preventivo rimedio, specialmente in ambito didattico, a questi inconvenienti legati alla razionalità, che tuttavia – è bene ricordarlo – caratterizza le funzioni più elevate dell’essere umano ed ha nell’attività matematica la sua massima espressione.
2. Un’intrigante dimostrazione
Il celebre teorema di Pitagora, anche se la sua origine è incerta, in qualche modo era conosciuto già prima che il grande matematico ne facesse il caposaldo della sua famosa scuola. Però prima di allora quel risultato era qualcosa di estremamente empirico, legato a particolari esigenze concrete, quali – ad esempio, prima dell’avvento dell’impero di Alessandro Magno – la costruzione di altari in India (si veda [Bt], p. 548 e segg.); invece con Pitagora esso assunse il ruolo di un teorema, con la presa di coscienza del suo valore universale e non limitato ad alcuni casi, seppur significativi. Il che caratterizzò gran parte della geometria allora conosciuta, principalmente a partire da Talete (circa 7°-6° sec. a.C.) e Pitagora – forse allievo di Talete – che diedero inizio storicamente a quel processo di razionalizzazione della geometria, che trovò la sua massima espressione negli “Elementi” di Euclide (circa 4° sec. a.C.).
Di questo teorema la storia della matematica non ci fornisce una dimostrazione che sia attribuibile a Pitagora o ad altri matematici del suo tempo, anche perché non abbiamo documenti risalenti a quel periodo. Infatti le prime informazioni sul periodo ellenico degli studi di matematica sono giunte a noi attraverso gli scritti di Proclo (circa 5° sec. d.C.), il quale – come ci ricorda Maracchia in [M] (si veda nota (5) a pié di pagina 3) – attinse, forse in via indiretta, le sue notizie da Eudemo di Rodi (4° sec. a.C.).
Comunque Proclo fa presente che Talete per la sua attività scientifica trasse spunto da quanto allora era in parte già conosciuto in Egitto; infatti egli scrive (si veda ancora [M], p. 3): Talete per primo essendo andato in Egitto, porto’ questa scienza, ed egli trovò molte cose, e di molte indicò i principi a coloro che vennero dopo di lui …. E lo stesso Aristotele conferma la possibilità della presenza di una scienza di tipo speculativo in Egitto nel periodo che precede il fiorire in Grecia della geometria (o, come sottolinea lo Struik in [S], p. 39, nella tarda tradizione egizia tramandataci dai Greci). Infatti, come si legge in [Bt], p. 547, il sommo filosofo greco scrisse: … sviluppatesi oramai le arti pratiche in modo da provvedere adeguatamente ai bisogni materiali della vita, ha potuto sorgere in Egitto una di quelle scienze che non sono rivolte a fini utilitari, essendo ivi la casta sacerdotale in possesso dell’otium necessario alla ricerca disinteressata.
Tornando al teorema di Pitagora va detto che di esso col passare dei secoli sono state “sfornate” dimostrazioni in quantità copiosa. Tra l’altro, una di queste è attribuita a J. A. Garfield, che fu presidente degli U.S.A. Carmine Mazzei, presidente della sezione Mathesis di Crotone – patria adottiva di Pitagora, ove questi giunse fuggitivo da Samo verso il 520 a.C. e ove fondò la sua famosa scuola – ha raccolto diverse centinaia di tali dimostrazioni e conta di trovarne altre ancora.
A ogni modo io ho acquisito la convinzione, per le ragioni che saranno esposte nel seguito, che Pitagora stesso non può non aver avuto la “prova provata” – come a volte si dice in altri contesti – di quel formidabile risultato, divenuto fondamentale per la geometria e per la visione del mondo che ci circonda, dato che essa era sotto i suoi occhi.
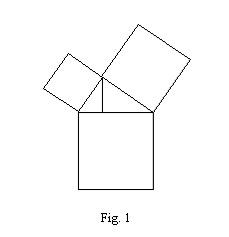
Molti si domanderanno dove sia questa dimostrazione del teorema. Ebbene, essa è qui sopra, nella figura che generalmente rappresenta – ma anche dimostra immediatamente, se la si legge in modo opportuno – quanto il teorema afferma.
Ciò che serve allo scopo sono soltanto alcune nozioni di carattere concreto che ai tempi di Pitagora erano senz’altro patrimonio strumentale ben consolidato anche per artigiani e cultori di arti quali i pittori e gli scultori. Ci riferiamo agli ingrandimenti senza deformazioni – cioè che conservano le forme – secondo un fattore di scala (in breve: le similitudini); per i quali, date due figure piane A e B che siano in un certo rapporto p, quel rapporto si mantiene tra quelle stesse figure ingrandite.
La nostra affermazione è avvalorata dal fatto che considerazioni di questo tipo venivano certo fatte in quel periodo, sia prima che dopo Pitagora, per ricavare proprietà fra le figure tramite considerazioni legate alle simmetrie e alle similitudini (cfr. [M2]); per esempio, in riferimento al rapporto costante tra cerchio e quadrato ad esso circoscritto.
Simplicio ci ha conservato un lungo brano della Storia della Geometria (non pervenutaci), che risulta essere la fonte autentica più antica di Storia della Matematica giunta fino a noi (cfr [Ti], p.44) di Eudemo di Rodi, in cui Eudemo dice di Ippocrate di Chio (da non confondere con l’omonimo a cui si attribuisce il giuramento dei medici) vissuto intorno al 450 a.C., quindi solo qualche decina di anni dopo Pitagora: Egli assumeva … : segmenti circolari simili stanno fra loro come i quadrati delle loro basi. Ciò egli provava col dimostrare che i quadrati dei diametri stanno fra loro come i loro circoli (si veda [Ti], p. 45).
Quindi Ippocrate si esprime seguendo un’impostazione che sembra incanalarsi, anche se in forma meno intuitiva e immediata, nel solco in cui io sono portato a pensare che si sia mosso Pitagora. D’altro canto è proprio quell’immediatezza che mi fa presumere che la prova del teorema sia in fig. 1, in quel disegno mal riuscito di un bambino privo di fantasia; in quella strana casetta dal tetto sghimbescio e con due grossi camini di foggia quadrata che lo ricoprono completamente; priva di porte e finestre, ma con quella linea verticale che divide il tetto, chiave di volta della dimostrazione. Infatti la figura espressa dalla casetta priva dei due camini rappresenta un ingrandimento secondo un certo fattore di scala della figura costituita dalla parte triangolare sinistra del tetto e dal camino sovrastante; potendosi dire la stessa cosa rispetto all’analoga parte situata a destra. Il che giustifica le eguaglianze riportate successivamente in (2). Allora un semplice calcolo dimostra il teorema.
Ma quale calcolo ci sarà mai stato per il nostro Pitagora? In verità forse per lui non ci fu calcolo alcuno, ma solo un’intuizione improvvisa, una visione immediata; una di quelle cose che ti danno una scarica di adrenalina e ti mozzano il fiato. Come dirlo meglio? Forse più adatte sono le parole con cui Sergio Frau descrive la formidabile intuizione che lo ha portato a concepire le Colonne d’Ercole sul Canale di Sicilia piuttosto che sullo Stretto di Gibilterra, dando così finalmente senso a molte affermazioni sulla geografia dell’antica Grecia (si veda “Le Colonne d’Ercole” Edizioni Nur Neon, 2OO2): … è stato un flash, un lampo: roba di un attimo, di quella che, però, ti buca gli occhi, ti mette gli spilli nella schiena, ti scioglie le ginocchia, ti cambia lo sguardo. E ancora: … è bastato un attimo: è stato lo spettacolo più maestoso e possente che si possa immaginare. Come raccontarlo? Inimmaginabile se non lo si vede.
Ma proviamo a raccontarla questa dimostrazione del teorema di Pitagora, però riconducendola alle aree interessate. Perciò chiamiamo T l’area del nostro triangolo rettangolo, nonché T1 e T2 le aree del triangolo sinistro e di quello destro in cui il primo è suddiviso dalla sua altezza relativa all’ipotenusa (si veda fig. 1), da cui segue la seguente eguaglianza, fondamentale per la dimostrazione che stiamo per presentare:
(1) T = T1 + T2.
Inoltre chiamiamo Q l’area del quadrato costruito su quell’ipotenusa e rispettivamente Q1 e Q2 le aree costruite sul cateto di sinistra e su quello di destra. In fine, per quanto già detto in precedenza, poniamo:
(2) p = Q/T = Q1/T1 = Q2/T2.
Allora da T = T1 + T2 si ricava subito p*T = p*T1 + p*T2; cioè:
Q = Q1 + Q2.
Tutto qui!
Appendice. Per maggior completezza osserviamo che le eguaglianze in (2) discendono in modo attualmente più esauriente dalle formule con cui si calcola l’area di quadrati e triangoli. Infatti se denotiamo con i, i1, i2 le lunghezze delle ipotenuse dei triangoli considerati e con h, h1, h2 le lunghezze delle altezze relative alle ipotenuse degli stessi, allora si ottiene:
Q/T = 2i/h, Q1/T1 = 2i1/h1, Q2/T2 = 2i2/h2.
Perciò le eguaglianze in (2) sono ovvie anche per la similitudine dei triangoli considerati.
Per concludere, si fa presente che diversi autori hanno cercato di capire quale possa essere stata la dimostrazione di Pitagora. Tra questi Sir Thomas Heat presenta in [H] (pp. 148 e 149) tre proposte delle quali la seconda si avvicina molto a quella illustrata precedentemente, poiché anch’essa si basa sull’eguaglianza (1) e sulle similitudini richiamate. Tuttavia la dimostrazione di Heath risente – come quella legata alla prima parte di quest’Appendice – della mediazione di una proprietà che, per quanto semplice, non consente di raggiungere l’immediatezza espressiva della dimostrazione qui presentata originariamente [Tale proprietà – da cui seguono subito le eguaglianze espresse in (2) – rientra nella Proposizione 19 del Libro VI di Euclide che afferma (si veda [E], p. 386): I triangoli simili stanno fra loro in rapporto duplicato di quello dei lati omologhi (cioè, dei quadrati costruiti sui lati omologhi; n.d.a.)].
Cerchiamo di spiegare meglio il senso di queste parole. Ebbene ci sono dimostrazioni, anche semplici ed elementari come le due precedenti, che pur tuttavia si riferiscono ad affermazioni che in realtà “a priori” sono delle congetture, magari altamente verosimili sulla base di indizi numerosi e significativi. Ci sono poi dimostrazioni che non sono altro che la traduzione immediata di un’intuizione, della visione di una proprietà attraverso la percezione del relativo percorso dimostrativo. Come esempio significativo ricordiamo il “teorema dei carabinieri” sulla convergenza di funzioni reali. Orbene, sulla base di quanto espresso in questo articolo, noi presumiamo che Pitagora ad un certo punto si sia trovato proprio nel secondo tipo di situazione.
Bibliografia
[Bt] Bortolotti E. (1972) Storia delle Matematiche elementari, in: Enciclopedia delle Matematiche elementari e complementi (a cura di L. Berzolari), Hoepli, Milano.
[Br] Boyer C. B. (1968) A history of mathematics, J. Wiley, N. York.
[E] Euclide (1970) Gli Elementi, a cura di A. Frajese e L. Maccioni, U.T.E.T., Torino.
[F] Frajese A. (1969) Attraverso la storia della matematica, Le Monnier, Firenze.
[Ga] Gambarelli G. (1997) Giochi competitivi e cooperativi, Padova, Cedam.
[Ga1] Gambarelli G. (1999) Una testimonianza personale su John Nash, Periodico di Matematiche, 2.
[Ga2] Gambarelli G. (2002) John Nash dal Nobel all’Oscar, Didattica delle Scienze, 219.
[Gi] Giusti E. (1998) Le equazioni alle derivate parziali e le superfici minime, in: Lettera matematica – pristem (dossier pristem), 27-28, p. XVIII.
[Gi1] Giusti E. (2000) Il contributo di Ennio De Giorgi (1928-1996) al calcolo delle variazioni, in: Per Ennio De Giorgi, a cura del Dipart. di Matematica dell’Università di Lecce, Liguori Editore, Napoli.
[H] Heath T. (1981) A history of greek mathematics (vol. I), Dover Publications, Inc., New York.
[L] Leaci A. (2002) Ennio per primo sulla cima del monte, il Corsivo (settimanale del Salento), 11.
[L1] Loria G. (1929) Storia delle Matematiche, Torino, Sten.
[M] Maracchia S. (1975) La matematica come sistema ipotetico-deduttivo (profilo storico), Firenze, Le Monnier.
[M1] Maracchia S. (1969) Sulla genesi della geometria razionale, Archimede, 1 e 2.
[M2] Maracchia S. (1971) Talete nello sviluppo della geometria razionale, Cultura e Scuola, 37.
[S] Struik D. J. (1981) Matematica: un profilo storico, Bologna, il Mulino.
[T] Trudeau R. (1991) La rivoluzione non euclidea, Torino, Bollati Boringhieri.
[Ti] Timpanaro Cardini M. (1962) Pitagorici, Testimonianze e Frammenti, Fasc. II, Firenze, La Nuova Italia.
[V] Veljan D. (2000) The 2500-old Pythagorean Theorem, Math. Magazin, 4.
http://cvgmt.sns.it/people/degiorgi/
http://www.dm.unile.it/de-giorgi.html
http://www.ams.org/notices/199709/emmer.pdf
http://www.dmf.bs.unicatt.it/~paolini/degiorgi/deg.html
http://www.clio.it/sr/ce/palmieri/annuario/degiorgi.html
http://www.quipo.it/netpaper/degiorgi1995.htm
http://www.math.unifi.it/matematicaitalia/schede_opere/97degiorgi57.html
http://matematica.uni-bocconi.it/nash/gambarellitalia.htm
http://www.nobel.se/economics/laureates/1994/nash-autobio.html
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Nash.html
http://www.consulta-salutementale.it/libri_bis.htm
http://matematica.uni-bocconi.it/nash/gambarellifilm.htm
Helmholtz: i fatti della geometria
Hermann Ludwig Ferdinand von Helmholtz: i fatti della geometria
 Hermann von Helmholtz (1821-1894) completa nel 1842 gli studi in medicina; diviene nel 1849 professore di fisiologia a Koenigsberg, nel 1855 professore di fisiologia e anatomia a Bonn, nel 1858 professore di fisiologia a Heidelberg. Negli anni Sessanta si occupa del problema dei fondamenti della geometria: una problematica che interseca diversi suoi interessi: fisica, fisiologia dell’occhio, matematica, filosofia.
Hermann von Helmholtz (1821-1894) completa nel 1842 gli studi in medicina; diviene nel 1849 professore di fisiologia a Koenigsberg, nel 1855 professore di fisiologia e anatomia a Bonn, nel 1858 professore di fisiologia a Heidelberg. Negli anni Sessanta si occupa del problema dei fondamenti della geometria: una problematica che interseca diversi suoi interessi: fisica, fisiologia dell’occhio, matematica, filosofia.
Punto di partenza per queste ricerche sullo spazio sono gli studi di ottica fisiologica. Nel 1867 ha pubblicato un’opera di oltre mille pagine che raccoglie una lunghissima serie di esperimenti sulla percezione visiva, la descrizione degli organi coinvolti nel processo di visione, le loro disfunzioni e alcune osservazioni di carattere storico e filosofico (Manuale di ottica fisiologica). Helmholtz vuole ora indagare sul modo in cui l’azione fisica dei corpi esterni, la struttura fisiologica dei nostri organi di senso e la rielaborazione psicologica delle sensazioni concorrono alla percezione e rappresentazione degli oggetti esterni.
L’attività psichica che ci porta a concludere che un determinato oggetto, con una determinata forma, si trova in una determinata posizione al di fuori di noi è, quasi sempre, un’attività di cui non siamo coscienti. La maggior parte delle nozioni che riguardano lo spazio deve essere considerata il risultato dell’esperienza e dell’abitudine. La rappresentazione della forma dei corpi e della loro localizzazione nello spazio si produce per mezzo del confronto delle immagini ricevute dai due occhi: attraverso spostamenti sia dei corpi sia dell’osservatore, ci si rende conto che qualcosa rimane inalterato.
Se non esistessero un gran numero di oggetti simili, la nostra facoltà di formare delle nozioni di specie non ci sarebbe di alcuna utilità; se non ci fossero corpi rigidi, le nostre facoltà geometriche resterebbero senza sviluppo e senza uso allo stesso modo in cui l’occhio non ci servirebbe a niente in un mondo senza luce
(Manuale di ottica fisiologica, 1867, p. 447)
Quanto allo spazio, afferma Helmholtz, vi sono due posizione: quella empirista, secondo la quale la nozione di spazio deriva direttamente dall’esperienza, e quella innatista, per la quale la nozione di spazio si costruisce attraverso un sistema di concetti innati.
Hemholtz ha appena iniziato una ricerca matematica sui fondamenti della geometria, quando viene pubblicata la memoria di Riemann “Sulle ipotesi che stanno a fondamento della geometria”. Si rende conto che Riemann ha già sviluppato in modo egregio l’argomento; decide di pubblicare delle proprie osservazioni in merito. Prende corpo una conferenza dal titolo “Sui fatti che stanno a fondamento della geometria” che presenta nel 1868.
La premessa di Helmholtz è che bisogna distinguere, in primo luogo, le proposizioni della geometria che hanno un significato fattuale da quelle che sono semplici definizioni legate al linguaggio usato per esprimersi. Quindi, trovare l’origine delle proposizioni che riguardano i fatti.
La geometria, così come è esposta nei manuali, osserva Helmholtz, presuppone tutta una serie di fatti che vengono ritenuti ovvi, sui quali non si è sufficientemente indagato, mentre proprio la loro ovvietà esprime caratteristiche ben precise del mondo reale esterno a noi. Riemann ha correttamente utilizzato lo strumento dell’analisi matematica, che occupandosi di concetti puri senza fare ricorso all’intuizione geometrica, può permetterci di distinguere quelle proprietà dello spazio che sono puramente matematiche da quelle che riguardano proprietà fattuali, il cui fondamento va cercato all’esterno della matematica.
Dopo aver ripreso il concetto riemanniano di varietà multidimensionale, passa alla caratteristica fondamentale dello spazio: la possibilità di effettuare misure. Mette così subito in chiaro la differenza tra la propria posizione e quella di Riemann.
Riemann assume la formula di Pitagora, ds2=dx2+dy2+dz2, come ipotesi e pur sostenendo che è la più semplice tra quelle possibili ritiene che si possa cambiarla liberamente. Dal suo punto di vista, è possibile avere diverse geometrie a seconda di come si sceglie la formula per calcolare le distanze: la geometria di Euclide è solo una delle tante analiticamente possibili. Per quanto riguarda la geometria dello spazio fisico, è convinto che sia compito della fisica individuare quale tra le geometrie matematicamente possibili sia quella più idonea per la fisica.
Helmholtz introduce dall’inizio la condizione che le figure spaziali possano muoversi liberamente senza alterazione della loro forma, traduce questa idea empirico-intuitiva in assiomi sull”esistenza dei corpi rigidi e dei loro movimenti, ottiene come conclusione che la formula per calcolare le distanze non è arbitraria, l’unica compatibile con l’esistenza dei corpi rigidi è quella espressa dal teorema di Pitagora: la geometria di Euclide è, quindi, l’unica possibile in quanto l’unica compatibile con il concetto di corpo rigido.
Helmholtz conclude il proprio saggio sostenendo di essere arrivato al punto di partenza delle ricerche di Riemann.
Il 24 Aprile del 1869, il matematico italiano E. Beltrami scrive una lettera a Helmholtz.
Per quanto mi è possibile penetrare nel vero significato delle vostre belle ricerche, non incontro nessuna conclusione che non possa verificare dal mio punto di vista e che io ho esposto in parte in due pubblicazioni intitolate: Saggio di interpretazione della geometria non euclidea e Teoria fondamentale degli spazi di curvatura costante, che ho avuto l’onore di inviarvi, tempo fa. C’è solo un punto sul quale debbo chiedervi delucidazioni.
Beltrami nei due saggi in questione ha studiato una superficie a curvatura costante negativa (cfr. la scheda sulla pseudosfera di Beltrami), chiamata pseudosfera, che soddisfa tutte le condizioni poste da Helmholtz per l’esistenza dei corpi rigidi.
Helmholtz si rende subito conto del proprio errore e pochi giorni dopo scrive un Supplemento al suo primo saggio, nel quale precisa:
[…], ho sostenuto in una parte non ancora pubblicata e non completamente studiata a fondo, nella quale si è insinuato un errore, che allora non conoscevo, che una certa costante che io credevo dovesse essere reale, aveva significato anche quando la si assume immaginaria. L’affermazione colà enunciata, che lo spazio, se deve essere esteso all’infinito non può che essere piano (nel senso di Riemann), è errata. Ciò risulta specialmente dall’altamente interessante e importante ricerca di Beltrami[…]; questi ha studiato la teoria delle superfici e degli spazi con curvatura costante negativa e ha dimostrato la concordanza di questa teoria con la geometria immaginaria già enunciata in precedenza da Lobacevski. In questa teoria lo spazio è infinitamente esteso in tutte le direzioni; figure congruenti a una data possono essere costruite in ogni parte; tra ogni coppia di punti è possibile individuare una linea di minor percorso ma la proposizione sulle parallele non vale.
In un secondo saggio Helmholtz afferma che la conclusione cui è pervenuto riguardo la geometria euclidea non è del tutto esatta: le proprie ricerche non costituiscono una discriminazione tra la geometria di Euclide e quella di Lobacevski.
Il tentativo di Helmholtz di dimostrare matematicamente che l’unica geometria valida per lo spazio fisico è quella di Euclide non è quindi riuscito: il concetto di corpo rigido e lo strumento logico dell’analisi matematica non sono sufficienti a individuare in modo univoco la geometria euclidea. Se si aggiunge che Riemann aveva già dato un quadro sufficientemente completo della geometria e che ancora prima Gauss aveva stabilito il teorema sulla possibilità di muovere una figura senza deformarla, si può ritenere il tentativo di Helmholtz la pretesa di dare una veste matematica a quello che era ancora un pregiudizio della cultura scientifica e filosofica.
L’obiezione di Beltrami sembrerebbe far vacillare le conclusioni di Helmholtz. Ciò è vero solo per la parte matematica, l’aspetto filosofico ne esce rafforzato. Nel 1870, presenta una seconda conferenza sulla geometria, dal titolo: Sull’origine e il significato degli assiomi geometrici. La geometria, sostiene Helmholtz, non è accumulo di dati empirici e, tuttavia, è capace di ottenere risultati applicabili al mondo reale. Kant ne ha tratto la conclusione che possiamo avere intuizione solo di quelle esperienze che hanno un contenuto organizzato secondo lo schema euclideo della geometria; Helmholtz pensa che gli assiomi dello spazio non sono una forma a priori di conoscenza ma hanno natura empirica.
Se immaginiamo, spiega Helmholtz, essere bidimensionali dotati di ragione che si muovono in un mondo bidimensionale. Essi attribuirebbero al loro spazio due dimensioni e non sarebbero in grado di rappresentarsi uno spazio con più di due dimensioni. Essi osserverebbero un punto in movimento descrive una linea, che una linea in movimento descrive una superficie e che una superficie in movimento descrive ancora una superficie. Allo stesso modo la nostra percezione dello spazio è tridimensionale perché il movimento di una superficie descrive un solido, ma il movimento di un solido non può che descrivere un altro solido. Quindi, il numero di dimensioni dello spazio ha una radice empirica, perché è una conseguenza del tipo di spazio nel quale viviamo.
Analogamente, hanno radice empirica i seguenti assiomi: per due punti passa una sola retta, per un punto esterno a una retta passa un’unica parallela. Infatti, essi non sarebbero validi per esseri bidimensionali che vivessero sulla superficie di una sfera. Occorre premettere che, per essi, la linea di minimo percorso tra due punti, cioè la retta, è un arco del cerchio massimo passante per quei due punti. Presi due poli della sfera, questi sarebbero uniti da infiniti percorsi della stessa lunghezza minima: tutti i meridiani. Non varrebbe nemmeno l’assioma delle parallele poiché tutti i circoli massimi, opportunamente prolungati si incontrano.
Infine, esseri bidimensionali viventi su una superficie a forma di uovo, osserverebbero l’impossibilità di spostare figure senza deformarle.
Già questi esempi mostrano che, secondo il tipo di spazio ambientale, esseri dotati di capacità intellettive affatto corrispondenti alle nostre formulerebbero assiomi geometrici diversi.
Gli assiomi geometrici, dunque, parlano non soltanto di rapporti spaziali ma anche del comportamento meccanico dei corpi. In questo senso, gli assiomi geometrici possiedono un contenuto reale che può essere confermato o confutato dall’esperienza. Queste intuizioni dello spazio però non sono state acquisite dall’umanità tramite precise misure geometriche ma sono conseguenza di un gran numero di esperienze quotidiane avute fin dalla prima giovinezza. Si tratta di una forma di conoscenza empirica che si forma nella nostra mente attraverso accumulo e rafforzamento di successive impressioni omogenee, non di una forma trascendentale dell’intuizione, che precede ogni esperienza.
Un altro esperimento considerato da Helmholtz è quello dello specchio convesso. Un tale specchio mostra l’immagine speculare di ogni oggetto antistante, conferendole un’apparenza corporea come se esso fosse posto in una certa posizione e a una certa distanza dietro la superficie dello specchio. Per ogni figura del mondo oggettivo viene a formarsi una corrispondente figura dietro lo specchio, nel mondo speculare. Inoltre, poiché nello specchio gli strumenti di misura si deformano allo stesso modo degli oggetti da misurare, la misura di un segmento nel mondo reale è identica a quella del mondo speculare. Di conseguenza gli uomini del mondo speculare non potrebbero scoprire che i loro corpi non sono rigidi.
Secondo Helmholtz, nello spazio pseudosferico di Beltrami ci accadrebbe la stessa cosa che accade a un portatore principiante d’occhiali. Costui inizialmente si accorgerà di vedere gli oggetti ravvicinati e che si dilatano; l’illusione scompare dopo un po’.
Il saggio si Helmholtz sugli assiomi della geometria diviene un punto di riferimento e di confronto per il dibattito filosofico e culturale sulle nuove geometrie. In esso, Helmholtz, ha saputo presentare in modo semplice una tematica complessa e trattata ancora in modo esclusivamente tecnico.
Dai suoi questi esempi sugli esseri bidimensionali prenderà spunto E. Abbott per il suo grazioso libretto Flatlandia.
-
A. Einstein, Relatività: esposizione divulgativa e scritti classici su Spazio, Geometria e Fisica, Boringheri, Torino, 1967.
Kant: geometria e verità
Kant: geometria e verità
Il filosofo tedesco Immanuel Kant (1724-1804) è autore di un attento esame delle possibilità e dei limiti conoscitivi del pensiero umano, di una severa critica della possibilità di una conoscenza puramente filosofica, di una metafisica puramente dogmatica. La sua analisi parte dalla moderna scienza della natura nell’assetto conferitogli da Newton e dalla geometria di Euclide rimasta immutata per due millenni.
Nella Critica della ragion pura (1781), Kant classifica le regole formali del pensiero, distinguendo tra giudizi a priori e empirici, che a loro volta si distinguono tra analitici e sintetici.
| Giudizi | a priori | empirici |
| analitici | analitici a priori o semplicemente analitici |
non esistono |
| sintetici | sintetici a priori | sintetici empirici o semplicemente sintetici |
I giudizi a priori sono indipendenti dall’esperienza e derivano dal pensiero in se stesso, si distinguono per la loro necessità e universalità.
I giudizi empirici o a posteriori derivano dall’esperienza, pertanto non sono universali ma contingenti, particolari, dipendono da fatti specifici.
I giudizi analitici sono quelli contenuti implicitamente nel soggetto di cui si parla, pertanto non ampliano la nostra conoscenza.
I giudizi sintetici sono quelli che aggiungono al soggetto di cui si parla qualcosa che non era già pensato in esso, pertanto ampliano effettivamente la nostra conoscenza.
Noi dunque intenderemo (…) per conoscenze a priori non conoscenze che abbiano luogo indipendentemente da questa o da quell’esperienza, ma conoscenze che non dipendano assolutamente da nessuna esperienza. Ad esse sono contrapposte le conoscenze empiriche, o tali che sono possibili solo a posteriori, cioè per esperienza.
I. Kant, Critica della ragion pura, Laterza, Bari, 1971, Introduzione, sez. 1.
Ogni enunciato analitico è sicuramente a priori, così come ogni enunciato empirico è sicuramente sintetico.
“Tutti gli scapoli non sono sposati” è un giudizio analitico a priori. Ha validità universale ma tutto sommato è inutile, in quanto il fatto di non essere sposato è un giudizio automaticamente incluso in quello di essere scapolo. E’ utile nel caso uno non conosca il termine “scapolo”: il giudizio “non è sposato” ne esplicita il significato.
“Fra gli studenti della classe 3A del Liceo “G. Galilei” di Roma – ammesso che questa classe esista – ce ne sono due nati nel 1985″ è un giudizio empirico perché la validità non può essere dedotta logicamente dall’enunciato ma dobbiamo effettivamente recarci presso la scuola indicata e acquisire le informazioni necessarie per verificare se è vero o no. Su un giudizio di questo tipo, comunque, rimane sempre un dubbio sull’affidabilità delle affermazioni delle persone e sull’autenticità dei documenti esibiti.
… 1) che per mezzo di giudizi analitici la nostra conoscenza non può estendersi punto, ma può invece essermi reso esplicito e intelligibile il concetto che già posseggo; 2) che nei giudizi sintetici io ho bisogno, oltre che del concetto del soggetto, di qualcos’altro ancora (X), su cui si appoggi l’intelletto per riconoscere che gli appartiene un predicato non compreso nel concetto.
I. Kant, Critica della ragion pura, Laterza, Bari, 1971, Introduzione, sez. 4.
L’attenzione di Kant è rivolta ai giudizi sintetici a priori. Essi rappresenterebbero una forma di conoscenza sicura e universale che arricchisce la nostra conoscenza su un dato oggetto e allo stesso tempo non ha il carattere di imperfezione della conoscenza empirica.
Per Kant, le proposizioni della matematica sono giudizi a priori e non empirici, poiché la loro necessità è di tipo logico e non dipende dall’esperienza.
Anzitutto devesi notare che le vere e proprie proposizioni matematiche sono sempre giudizi a priori e non empirici, poiché portano con sé una necessità che non può essere presa dall’esperienza. Se però non mi si vuol concedere questo, ebbene io restringo la mia affermazione alla matematica pura, il cui concetto già porta con sé che essa non contenga conoscenza empirica, ma soltanto pura conoscenza a priori.
I teoremi della geometria di Euclide invece sono dei giudizi a priori ma sintetici.
Per esempio, consideriamo il postulato relativo agli angoli retti.
Definizione 10: se una retta innalzata a partire da un’altra retta forma con essa angoli adiacenti uguali fra loro, ciascuno dei due angoli è retto e la retta si dice perpendicolare a quella su cui si è innalzata.
Postulato 4: tutti gli angoli retti sono uguali fra loro.
Questo postulato non è affatto banale. Noi siamo abituati a pensare che gli angoli retti misurano 90°, per cui ci sembra ovvio che siano tutti uguali. In realtà è vero l’inverso. Il postulato 4 garantisce il fatto che tutti gli angoli retti misurano 90°. Infatti, non è affatto ovvio che i due angoli formati dalle perpendicolari in figura siano uguali
Noi sappiamo dalla definizione che A1=A2 e che B1=B2 ma la definizione di angolo retto non ci dice nulla sull’uguaglianza tra A1=B1. D’altra parte l’uguaglianza tra gli angoli formati dalle due rette di sinistra con quelli formate dalle due rette a destra non ci viene dall’esperienza, non è un fatto empirico. Si tratta quindi di una forma di conoscenza sintetica, perché non è una conseguenza logica della definizione, a priori perché non deriva dall’esperienza.
L’esempio scelto da Kant è un’altro: “La linea retta è il cammino più breve fra due punti”. Questo non è uno dei postulati di Euclide, anche se spesso i manuali di geometria lo hanno riportato come postulato: probabilmente Kant fa riferimento al manuale su cui aveva studiato la geometria.
Che la linea retta sia la più breve tra due punti, è una proposizione sintetica. Giacché il mio concetto di ‘retta’ non contiene nulla che riguardi grandezza, ma soltanto qualità. Il concetto ‘la più breve’ adunque vi si aggiunge del tutto e non può essere tratto dall’analisi del concetto di linea retta …
Quindi, i postulati di Euclide sono giudizi sintetici a priori, di conseguenza lo sono anche tutti i teoremi della geometria.
In che modo, allora, le nostre conoscenze dello spazio sono applicabili al mondo esterno dei fenomeni fisici? Perché i postulati di Euclide ci appaiono veri e non riusciamo ad immaginarne altri?
Secondo Kant, i dati relativi allo spazio reale in cui viviamo ci giungono attraverso i sensi, la vista e il tatto, e vengono organizzati dal nostro intelletto. Quando giungono alla nostra coscienza sono stati già rielaborati. La nostra idea di spazio non si riferisce allo spazio reale esterno a noi ma a uno spazio di natura intellettiva che filtra e organizza le nostre esperienze.
I principi di Euclide descrivono, quindi, non uno spazio esterno ma questa struttura mentale che ci permette di cogliere e organizzare la percezione che abbiamo degli oggetti. Essi sono infallibili e indiscutibili proprio perché non si riferiscono all’esperienza ma al modo in cui la nostra mente dà una struttura all’esperienza.
Lo spazio non è un concetto empirico, proveniente da esperienze esterne. Infatti, affinché certe sensazioni siano riferite a qualcosa fuori di me (ossia a qualcosa che si trovi in un luogo dello spazio diverso dal mio), e affinché io possa rappresentarmele come esterne e accanto l’una all’altra – e quindi non soltanto come differenti ma come poste in luoghi diversi – deve già esserci a fondamento la rappresentazione di spazio. Conseguentemente, la rappresentazione dello spazio non può derivare, mediante l’esperienza, dai rapporti del fenomeno esterno; al contrario, l’esperienza esterna è possibile solo in virtù di detta rappresentazione.
Lo spazio è una rappresentazione a priori, necessaria, che sta a fondamento di tutte le intuizioni esterne. Non è possibile farsi la rappresentazione che non ci sia spazio, mentre si può benissimo pensare che non ci sia in esso alcun oggetto. Lo spazio va pertanto considerato come la condizione della possibilità dei fenomeni e non come una determinazione da essi dipendente; ed è una rappresentazione a priori, che sta necessariamente a fondamento dei fenomeni esterni.
AA.VV., Storia della filosofia: 4. Il Settecento, a cura di P. Rossi e C. A. Viano, Laterza, Bari, 1996, pp. 500-502.
I. Kant, Critica della ragion pura, trad. it. a cura di G. Gentile e G. Lombardo-Radice, Laterza, Bari, 1971.
L. Magnani, Le geometrie non euclidee, Zanichelli, Bologna 1978.
R. Trudeau, La rivoluzione non euclidea, Bollati Boringheri, Torino, 1991.
Il primo libro di euclide
Il primo libro degli Elementi di Euclide
I libri di testo di geometria dell'attuale biennio delle scuole medie superiori sono basati più o meno direttamente su un'opera di Euclide, Gli Elementi. Di quest'opera non ci sono pervenute copie dirette e autografe, né abbiamo notizie certe sul suo autore. La data di composizione si fa risalire al 300 a.C.
La versione attuale è stata ricostruita a partire da commenti, osservazioni e riassunti di diversi autori. L'opera di riferimento principale è quella di Teone di Alessandria, vissuto nella seconda metà del secolo IV d.C., 700 anni dopo Euclide. Questi ne semplificò il linguaggio, aggiunse qualche passo alle dimostrazioni e inserì alcuni teoremi secondari.
Circa 400 anni dopo Teone, una copia del suo manoscritto (o una copia di una copia) viene tradotta in arabo. Intorno al 1120, una copia del testo arabo (o una copia di una copia) viene tradotta in latino da Adelardo di Bath. Nel 1270, la traduzione di Adelardo fu riveduta, anche alla luce di altre fonti arabe (a loro volta derivate da altre versioni greche del manoscritto di Teone) da Campano di Novara. Questa versione (o una copia di una copia) viene stampata a Venezia nel 1482. Sono passati circa 1800 anni.
Successivamente, sono state ritrovate altre versioni greche del manoscritto di Teone e una copia greca che probabilmente è precedente a quella di Teone. La ricostruzione attuale si basa sulla versione del filologo danese J. L. Heiberg risalente al 1880 e su quella dello storico inglese T. L. Heath del 1908.
La prima edizione italiana è dovuta al matematico italiano Federigo Enriques e risale al 1935. Nel 1970 compare nei tipi della UTET un'altra versione italiana, tradotta da Lamberto Maccioni e commentata da Attilio Fraiese.
Come premessa, è necessario quindi precisare che quando si fa riferimento a Euclide e al suo pensiero ci si riferisce in realtà al contenuto della sua opera così come è stato ricostruito alla luce degli eventi storici suddetti.
Il primo dei libri di Euclide è di particolare interesse storico e filosofico perché in esso sono contenuti i principi primi da cui prende le mosse l'organizzazione euclidea della geometria. Questi principi sono organizzati in definizioni, postulati e nozioni comuni.
Nella trattazione moderna della geometria si parte da alcuni termini primitivi, per esempio punto e retta, che non vengono definiti. A noi sembra evidente che l'operazione del definire consiste nel costruire una nozione partendo da altre nozioni, le quali a loro volta devono essere definite. E' evidente che questo processo di definizione deve pur partire da alcuni termini che non devono essere definiti: questi sono appunti i termini primitivi. Una tendenza assiomatica moderna consiste nel partire da alcuni enti di cui si dà la definizione implicita, questi enti sono descritti o caratterizzati da regole o assiomi che ne stabiliscono il comportamento e il loro utilizzo.
Euclide definisce invece tutti gli enti che entrano in gioco nella trattazione.
Lo strumento 'definizione' che emerge dal testo di Euclide ha, infatti, una natura diversa. Non si tratta di costruire gli enti geometrici a partire dai mattoni di base, bensì di descriverli semplicemente affinché possano essere facilmente riconosciuti e individuati dai loro nomi: gli enti geometrici esistono già, indipendentemente dall'uomo. Essi sono forme pure che si materializzano, in modo imperfetto, negli oggetti reali. O viceversa, sono idealizzazioni di oggetti concreti.
Definizioni
1. Un punto è ciò che non ha parti.
2. Una linea è una lunghezza senza larghezza.
3. Gli estremi di una linea sono punti.
4. Una retta è una linea che giace ugualmente rispetto ai punti su di essa.
5. Una superficie è ciò che ha soltanto lunghezza e larghezza.
6. Gli estremi di una superficie sono linee.
7. Una superficie piana è quella che giace ugualmente rispetto alle rette su di essa.
8. Un angolo piano è l'inclinazione reciproca di due linee in un piano le quali, si incontrino e non giacciano in linea retta.
9. Quando le linee che comprendono l'angolo sono rette, l'angolo è detto rettilineo.
10. Quando una retta innalzata a partire da un'altra retta forma con essa angoli adiacenti uguali fra loro, ciascuno dei due angoli è retto, e la retta si dice perpendicolare a quella su cui è innalzata.
11. Dicesi angolo ottuso l'angolo maggiore di un angolo retto.
12. Dicesi acuto l'angolo minore di un angolo retto.
13. Dicesi termine è ciò che è estremo di qualche cosa.
14. Dicesi figura è ciò che è compreso da uno o più termini.
15. Dicesi cerchio una figura piana delimitata da un'unica linea tale che tutte le rette che terminano su di essa a partire da un medesimo punto fra quelli interni alla figura, siano uguali fra loro.
16. Quel punto si chiama centro del cerchio.
17. Dicesi diametro del cerchio è una retta condotta per il centro e terminata da ambedue le parti dalla circonferenza del cerchio, la quale retta taglia anche il cerchio per metà.
18. Dicesi semicerchio è la figura compresa dal diametro e dalla circonferenza da esso tagliata. E centro del semicerchio è quello stesso che è anche centro del cerchio.
19. Dicesi rettilinee le figure delimitate da rette, vale a dire: figure trilatere quelle comprese da tre rette, quadrilatere quelle comprese da quattro rette e multilatere quelle comprese da più di quattro rette.
20. Dicesi triangolo equilatero la figura trilatera che ha i tre lati uguali, triangolo isoscele quella che ha soltanto due lati uguali, e scaleno quella che ha i tre lati disuguali.
21. Dicesi inoltre triangolo rettangolo la figura trilatera che ha un angolo retto, triangolo ottusangolo quella che ha un angolo ottuso, e triangolo acutangolo quella che ha i tre angoli acuti.
22. Dicesi quadrato la figura quadrilatera che ha i lati uguali e gli angoli retti.
23. Diconsi parallele rette giacenti nello stesso piano che, prolungate illimitatamente in entrambe le direzioni, non si incontrino fra loro da nessuna delle due parti.
Postulati
Risulti postulato che:
1. E' possibile condurre una linea retta da un qualsiasi punto ad ogni altro punto.
2. E' possibile prolungare illimitatamente una retta finita in linea retta.
3. E' possibile descrivere un cerchio con qualsiasi centro e distanza (raggio) qualsiasi.
4. Tutti gli angoli retti sono uguali fra loro
5. Se (in un piano) una retta, intersecando due altre rette, forma con esse, da una medesima parte, angoli interni la cui somma è minore di due angoli retti, allora queste due rette indefinitamente prolungate finiscono con l'incontrarsi dalla parte detta.
Nozioni comuni
1. Cose uguali a un'altra medesima sono tra loro uguali.
2. Se a cose uguali si aggiungono cose uguali, allora si ottengono cose uguali.
3. Se da cose uguali si tolgono cose uguali, allora si ottengono cose uguali.
4. Cose che possono essere portate a sovrapporsi l'una con l'altra sono uguali tra loro.
5. Il tutto è maggiore della parte.
Definizioni di matematica
Definizioni di matematica
Perché la matematica è chiamata così? I peripatetici, che dicono che la retorica, la poesia e la musica popolare possono essere praticate anche senza essere studiate, ma che nessuno può capire le cose che vengono chiamate con il nome di matematica senza averle prima studiate, rispondono che per questa ragione la teoria di queste cose è detta matematica.
Anatolio. [Matema in greco significa studio, oggetto di studio]. Il testo è preso da L. Russo, La rivoluzione dimenticata,Milano, Feltrinelli, 1996.
…………
La matematica nel suo insieme consiste nell'organizzazione di una serie di sussidi per l'immaginazione nel processo del ragionamento.
(A. N. Whitehead, Universal Algebra, Cambridge, 1898, p. 12)
…………
La matematica è la scienza che tratta delle leggi generali alle quali le cose si devono uniformare nella loro essenza.
Bernhard Bolzano (1781-1848)
…………
Potremmo convenientemente assegnare alla matematica il carattere di un vero e proprio Calcolo, ossia di un metodo basato sui Simboli, le cui leggi di combinazione sono note e generali, e i cui risultati ammettono un'interpretazione coerente.
George Boole, The Mathematical Analysis og Logic, 1847, pp. 3,4.
…………
La matematica è la scienza che trae conclusioni necessarie.
Benjamin Peirce, 1870
…………
La matematica pura è la classe di tutte le proposizioni della forma "p implica q", dove p e q sono proposizioni contenenti una o più variabili, le stesse nelle due proposizioni, e né p né q contengono alcuna costante eccetto costanti logiche. […] Oltre a queste, la matematica adopera poi una nozione che non entra come costituente nelle proposizioni da essa considerate, e precisamente la nozione di verità.
B. Russell, I principi della matematica, ed. it. Longanesi, Milano, 1980, p. 35; ed. orig. 1903.
…………
La matematica come scienza ebbe inizio quando per la prima volta qualcuno, forse un greco, dimostrò delle proposizioni relative a qualsiasi cosa o a qualche cosa, senza indicare di cosa si trattasse in particolare.
Matematica, o matematiche (dal greco insegnamento) significa originariamente "disciplina" o "scienza razionale". Questo significato conferirono alla parola i filosofi della scuola italica, fondata da Pitagora (prima del 500 a. C.), che pose la scienza dei numeri a base di ogni conoscenza della natura.
F. Enriques, Enciclopedia Italiana.
…………
Come espressione della mente umana, la matematica riflette la volontà attiva, la ragione contemplativa e il desiderio di perfezione estetica. I suoi elementi fondamentali sono la logica e l'intuizione, l'analisi e la costruzione, la generalità e l'individualità.
R. Courant e H. Bobbins, What is Mathematics, New York, Oxford University Press, 1941 (trad. it.: Che cos'è la matematica?, Torino, Boringheri, 1983)
…………
[…] gran parte di ciò che oggi va sotto il nome di matematica è il risultato di uno sviluppo di pensiero che originariamente era accentrato attorno ai concetti di numero, grandezza e forma.
C. Boyer, A history of mathematics, New York, 1968 (trad. it.: Storia della matematica, Milano, Mondadori, 1976, p.1.
…………
A differenza dalle altre scienze, ciascuna delle quali si interessa di un aspetto determinato del mondo circostante, la matematica tratta le proprietà più generali inerenti a tutti i fenomeni accessibili alla ricerca scientifica. […] Ogni legge della natura ci dà una relazione fra grandezze, o più precisamente, fra numeri esprimenti queste grandezze. Sono questi numeri e le diverse relazioni che li legano a costituire l'oggetto della ricerca matematica, indipendentemente dal carattere concreto delle grandezze o delle leggi che ci hanno condotto a questi numeri e relazioni.
V. I. Smirnov, Corso di matematica superiore, ed. it. Editori Riuniti, Roma, 1999, p. 11.
…………
Insieme di discipline scientifiche aventi in comune l'uso di un elaborato linguaggio simbolico fondato sui concetti di numero e di figura geometrica, un metodo di ricerca basato sul modello ipotetico-deduttivo e la possibilità di raggiungere un elevato grado di astrazione.
Grande Enciclopedia della scienza e della tecnologia, Novara, De Agostini, 1997
…………
Scienza che si avvale di metodi ipotetico-deduttivi all'interno di un sistema derivato da un insieme coerente di assiomi per lo studio di enti (la cui natura è teoricamente irrilevante) spec. di natura geometrica e numerica.
Enciclopedia Zanichelli, Milano, Zanichelli, 1997
…………
Scienza avente per oggetto sistemi ipotetico-deduttivi concernenti enti di natura non precisata in modo esplicito ma definita per mezzo delle proprietà descritte da un sistema compatibile di assiomi.
La nuova enciclopedia delle scienze Garzanti, 1988
…………
[…] la matematica è la scienza comprendente tutte le discipline che si riferiscono alle grandezze e alle quantità, e al modo di misurarle e di calcolarle.
A. Piccato, Dizionario dei termini matematici, Milano, Rizzoli, 1987
…………
Study of relationships among quantities, magnitudes, and properties and of logical operations by which unknown quantities, magnitudes, and properties may be deduced.
ENCARTA
…………
The science of structure, order, and relation that has evolved from elemental practices of counting, measuring, and describing the shapes of objects. It deals with logical reasoning and quantitative calculation, and its development has involved an increasing degree of idealization and abstraction of its subject matter.
Enciclopedia Britannica
Cronologia matematica
| -50.000 | Traccia di conteggi da parte dell'uomo di Neanderthal |
|
| -25.000 | Disegni geometrici primitivi da parte dell'uomo di Cro-Magnon |
|
| -15.000 | Nell'attuale Libano, si sono trovate ossa di animali, risalenti a questo periodo, che mostrano intaccature riunite in gruppi di eguale cardinalità. | |
| -4241 | Presunta origine del calendario egiziano |
In Egitto e in Mesopotamia si conoscono il numero 'p greco', le quattro operazioni, le equazioni quadratiche, il calcolo dell'area di quasi tutte le figure piane. Tebe e Babilonia sono i principali centri di studio della matematica. La maggior parte dei problemi sono di natura economica. |
| -3000 | Numeri geroglifici in Egitto | |
| -1850 | Papiro di Mosca: notazione posizionale in Mesopotamia | |
| -1700 | Papiro di Rhind: rotolo lungo cinque metri, composto da quattordici fogli di papiro, contiene decine di problemi matematici di vario tipo. | |
| -600 | Il greco Talete (624-546 circa) è considerato il fondatore della geometria. Sebbene non abbiamo nessun documento certo, gli vengono attribuiti i teoremi sulla similitudine dei triangoli, in particolare quello che porta il suo nome. |
I Greci raccolgono l'eredità dei matematici babilonesi ed egiziani e trasformano una collezione di risultati empirici in una scienza organica. I due principali processi della organizzazione logica della matematica sono l'astrazione (trarre un'idea generale dalla percezione di cose diverse) e la deduzione (giungere da certe premesse a una conclusione in modo che non si possano trovare errori in alcuna parte dell'argomentazione). |
| -500 | Il greco Pitagora (580-497 circa) è il fondatore di una scuola matematica, filosofica e religiosa con sede a Crotone. Nessun documento scritto ci è pervenuto di questo pensatore. Gli si attribuisce il famoso teorema sui triangoli rettangoli che porta il suo nome. | |
| -400 |
Il greco Ippocrate (460-377) scrive il primo trattato di geometria. Democrito (460-370), Eudosso (408-353), Archita di Taranto risolvono importanti problemi di geometria e aritmetica). Zenone enuncia i famosi paradossi. |
|
| -300 |
Euclide organizza negli Elementi i teoremi di geometria e di teoria dei numeri ottenuti dalla cultura matematica greca dell'epoca. Procede per definizioni, postulati e teoremi con una esposizione che è rimasta classica per ogni tempo. Aristotele codifica le leggi del ragionamento logico. |
La matematica greca raggiunge il massimo sviluppo. Il centro della cultura matematica si sposta da Atene ad Alessandria d'Egitto.
|
| -200 |
Archimede di Siracusa (287-212) si occupa di aritmetica, algebra, geometria, fisica; risolve importanti problemi sulle equazioni cubiche; anticipa il calcolo logaritmico e il calcolo integrale. Ipparco (190-125) fonda la trigonometria piana e sferica. Apollonio studia le coniche. Eratostene effettua la prima misurazione del diametro della Terra. |
|
| -100 | Erone compie importanti studi di geometria e di fisica | |
| 100 | Tolomeo nell'Almagesto tratta problemi di trigonometria piana e sferica. | |
| 200 | Diofanto studia l'aritmetica, usa i simboli algebrici ed enuncia le regole per risolvere le equazioni di primo e secondo grado | |
| 500 |
Il latino Boezio compie ricerche di logica e geometria. |
|
| 600 | Gli Indiani usano la notazione posizionale e i numeri indù.
I Cinesi introducono l'estrazione di radice quadrata. |
Il centro della cultura matematica passa da Alessandria a a Baghdad, capitale dell'Islam. L'arabo diviene linguaggio scientifico internazionale. Gli studiosi arabi traducono i principali testi della matematica greca, creano nuovi settori di ricerca e mettono in contatto la matematica occidentale con quella indiana.
|
| 800 |
Gli Arabi diffondono la numerazione posizionale indiana, detta poi arabica. L'arabo al-Khuwarizmi compone il trattato Al-giabr wa'l mu kabala, da cui deriva il nome algebra. Dal nome di questo matematico deriva il nome algoritmo. |
|
| 1000 |
L'indiano Sridhara dà una chiara esposizione dell'uso del numero 0, affermando che a+0=a, a-0=a, a·0=0, 0·a=0. |
|
| 1200 |
L'italiano Fibonacci di Pisa (1175-1240) nel trattato Liber Abaci introduce in Europa il sistema di numerazione arabo, nonché i risultati algebrici della cultura musulmana. |
Il commercio, che le repubbliche italiane avviano con i paesi del mondo arabo, avvia il ritorno degli studi di matematica nel mondo occidentale. Si sviluppa la scuola italiana di algebra elementare che ha come obiettivo principale la risoluzione delle equazioni algebriche di terzo e quarto grado.
|
| 1500 |
L'italiano Luca Pacioli (1445-1510) scrive il primo trattato generale di aritmetica e algebra, Summa, con un accenno al calcolo delle probabilità e ai logaritmi. Gerolamo Cardano tratta le cosiddette grandezze immaginarie. Niccolò Fontana detto Tartaglia espone la regola per la risoluzione delle equazioni di terzo grado ridotte. Il francese Viète introduce l'algebra simbolica, che permette di scrivere lunghe espressioni algebriche, secondo il metodo moderno. |
|
| 1600 |
Napier e Buergi inventano, indipendentemente l'uno dall'altro, i logaritmi. Briggs pubblica le prime tavole dei logaritmi a base 10. Fermat coglie i principi essenziali della geometria analitica. Cavalieri studia il calcolo infinitesimale. Nel 1636 Descartes pubblica il Discours de la méthode che contiene i fondamenti della geometria analitica. Pascal dà le basi della geometria proiettiva e del calcolo delle probabilità. Newton crea il calcolo delle flussioni, poi detto calcolo infinitesimale. Anche Leibniz crea, indipendentemente da Newton, e con simbolismi differenti il calcolo differenziale. |
Si sviluppano due nuovi rami della matematica: la geometria analitica e l'analisi infinitesimale |
| 1700 |
Eulero introduce il calcolo delle variazioni, applicando i metodi del calcolo differenziale alle curve e alle superfici. I Bernoulli e Lagrange sviluppano la teoria delle equazioni integrali e differenziali applicandola alla geometria e alla meccanica |
Gli studi di matematica si concentrano sullo sviluppo dell'analisi. Gli oggetti principali dello studio della matematica divengono le funzioni. |
| 1800 |
Gauss dimostra il teorema fondamentale dell'algebra: ogni equazione ha tante equazioni quanto è il suo grado. Nel campo della geometria introduce lo studio della curvatura delle superfici e mette in crisi la geometria euclidea. Laplace introduce in modo rigoroso la teoria della probabilità. Cauchy e Weierstrass rendono rigoroso il calcolo infinitesimale. Monge e Poncelet fondano la geometria descrittiva e la geometria proiettiva. Lobacevskij e Bolyai, indipendentemente l'uno dall'altro, studiano una geometria che contraddice il postulato di Euclide sulle parallele. Riemann fonda le geometrie euclidee e non euclidee sul concetto di metrica. Boole applica il calcolo algebrico alla logica. Cantor formula la teoria degli insiemi. Klein dà un quadro completo, attraverso la teoria dei gruppi di trasformazioni delle varie geometrie sorte nell'Ottocento: proiettiva, metrica, euclidea, ellititica, iperbolica, topologia. Frege si propone di unificare logica e aritmetica. Peano costruisce una simbologia per il calcolo logico e per le dimostrazioni matematiche. Enriquez organizza in modo rigoroso la geometria proiettiva. |
I principali filoni di ricerca di questo secolo sono la teoria delle funzioni di variabile immaginaria, la geometria proiettiva, le geometrie non euclidee, la teoria dei gruppi, il calcolo delle matrici. |
| 1900 |
Hilbert dà una formulazione puramente assiomatica della geometria. Ricci-Curbastro e Levi-Civita creano il calcolo differenziale assoluto, strumento utilizzato da Einstein per formulare la teoria della relatività. Russell cerca di fondare la matematica su basi puramente logiche. Brouwer in contrapposizione ritiene esclusivamente intuitivi i principi della matematica. Volterra fonda il calcolo funzionale. von Newmann elabora la teoria dei giochi. Goedel dimostra che nei sistemi formali è possibile individuare proposizioni indimostrabili, ne consegue che l'aritmetica non può fondarsi su se stessa. Wiener introduce la cibernetica e la teoria dell'informazione. Thom intraprende lo studio delle catastrofi o del caos, ossia delle trasformazioni improvvise. Mandelbrot espone lo studio dei frattali, forme geometriche irregolari che appaiono simili se osservate su scale diverse. |
|
Testi consultati per la realizzazione di questa scheda
C.B. Boyer, Storia della matematica, Milano, Mondadori, 1980.
AA.VV., Scienza e tecnica dalle origini al Novecento, Milano, Mondadori, 1977.
AA.VV. Grande enciclopedia della scienza e della tecnologia, Novara, De Agostini, 1997.
A.Dahan-Dalmedico, J. Peiffer, Une histoire des mathématiques, Parigi, Editions du seuil, 1986.
Ogni errore di interpretazione dei testi è esclusivamente mio.
Antonio Bernardo





 qui andrà un articolo di rilievo.
qui andrà un articolo di rilievo.