Scarica il file in formato PDF
Scarica il file in formato PDF
Scarica il file in formato PDF
Scarica il file in formato PDF
Scarica il file in formato PDF
Scarica il file in formato PDF.
Rappresenta nel piano cartesiano i punti A(3;-3) B (3;3) C(3;-1) D(-3;-1) e congiungili nell’ ordine dato. a) classifica il quadrilatero ABCD giustificando la tua risposta b) determina perimetro e area di tale quadrilatero.
Rappresenta nel piano cartesiano i punti A(3;-3) B (3;3) C(3;-1) D(-3;-1) e congiungili nell’ ordine dato. a) classifica il quadrilatero ABCD giustificando la tua risposta b) determina perimetro e area di tale quadrilatero
 Troppe cose, che un tempo erano frutto di un lampo di genio, possono oggi essere rigorosamente calcolate. La teoria delle innovazioni di J. A. Schumpeter.
Troppe cose, che un tempo erano frutto di un lampo di genio, possono oggi essere rigorosamente calcolate. La teoria delle innovazioni di J. A. Schumpeter.
«Ogni produzione consiste nel combinare materiali e forze che si trovano alla nostra portata. Produrre altre cose o le stesse cose in maniera differente, significa combinare queste cose e queste forze in maniera diversa» Schumpeter, J.A. (1883, 1950), Teoria dello sviluppo economico.
"L’imprenditore e la sua funzione non sono difficili da concettualizzare; la caratteristica che lo definisce è data semplicemente dal fare cose nuove o dal fare cose già fatte in modo nuovo (innovazione)". L’imprenditore nell’economia di oggi.
"…. riformare o rivoluzionare il quadro produttivo sfruttando un’invenzione o, più generalmente, una nuova possibilità tecnica finora trascurata di produrre una nuova merce o di produrre in modo nuovo una merce vecchia, aprendo una nuova sorgente di rifornimento di materie prime o un nuovo sbocco ai prodotti, riorganizzando un’industria, ecc." Capitalismo, socialismo, democrazia.
"Come la teoria consente di aguzzare lo sguardo sui fatti – e questo sia detto con tutte le riserve – questi a loro volta influiscono ad ogni passo in modo fruttuoso sulla teoria: la più piccola delle osservazioni può portare ad una svolta sorprendente". L’essenza e i principi dell’economia teorica
"Il significato e la validità dei problemi e dei metodi non possono essere pienamente afferrati senza una conoscenza dei precedenti problemi e metodi, da cui i primi sono scaturiti (per tentativi). L’analisi scientifica non è semplicemente un processo logicamente coerente che abbia inizio con qualche nozione primordiale e accresca via via la somma delle cognizioni secondo uno sviluppo rettilineo. Non è semplicemente la progressiva scoperta di una realtà oggettiva come è, per esempio, la scoperta del bacino del Congo. E’ piuttosto una lotta incessante con creazioni della nostra mente e di quella dei nostri predecessori, e "progredisce" (se progredisce) a zig-zag, non secondo quello che suggerisce la logica, ma secondo l’urto di nuove idee o di nuove osservazioni o di nuove necessità, o anche secondo quello che dettano le inclinazioni e i temperamenti di nuovi uomini. Perciò un qualsiasi trattato, il quale tenti di prospettare "lo stato presente della scienza" prospetta in realtà metodi, problemi e risultati che sono sempre storicamente condizionati e hanno un significato solo in riferimento allo sfondo storico da cui emergono". Storia dell’analisi e economica.
In un’ipotetica economia basata sul modello statico (Walras), i beni vengono prodotti e venduti secondo la mutevole domanda dei consumatori ed il ciclo economico assorbe le influenze della storia, ma i prodotti scambiati rimangono sempre gli stessi, le strutture economiche non mutano, ecc. Schumpeter fa notare che questo modello di economia non corrisponde alla realtà e lo supera con l’approccio "dinamico", in cui un nuovo soggetto, l’imprenditore, introduce nuovi prodotti, sfrutta le innovazioni tecnologiche, apre nuovi mercati, cambia le modalità organizzative della produzione. L’imprenditore può fare questo in quanto dispone dei capitali messigli a disposizione dalle banche, che remunera con l’interesse, ossia una parte del profitto aggiuntivo realizzato grazie all’innovazione.
La teoria delle innovazioni consente a Schumpeter di spiegare l’alternarsi, nel ciclo economico, di fasi espansive e recessive. Le innovazioni, infatti, non vengono introdotte in misura costante, ma si concentrano in alcuni periodi di tempo – che, per questo, sono caratterizzati da una forte espansione – a cui seguono le recessioni, in cui l’economia rientra nell’equilibrio di flusso circolare. Un equilibrio però diverso dal precedente e mutato dall’innovazione. Le fasi di trasformazione, sotto la spinta di innovazioni radicali vengono definite da Schumpeter di "distruzione creatrice", alludendo al drastico processo selettivo che le contraddistingue, nel quale molte aziende spariscono, altre nascono, e altre si rafforzano.
Tre sono i punti toccati da Schumpeter che hanno notevole rilevanza per quanto riguarda gli strumenti delle organizzazioni per risolvere i problemi: l’innovazione, l’interazione tra teoria e fatti, la storia. Per quanto riguarda il primo punto, l’innovazione, si può affermare che oggi tutti riconoscono che essa sia il fattore chiave per fronteggiare il problema principale di qualunque tipo d’impresa: la sopravvivenza sul lungo periodo (cioè la sostenibilità sociale, economica e ambientale delle politiche e strategie attuate). I buoni imprenditori sono quelli che hanno capacità d’innovare i prodotti, i processi di produzione, i mercati, le fonti di approvvigionamento, le strutture organizzative ecc.
Per inciso uno studio del 2004 della società di consulenza At Kearney mostra che in Europa fatto cento il budget totale della ricerca e sviluppo risulta:
Negli Stati Uniti il budget totale è considerevolmente maggiore, ma la ripartizione percentuale è similare fatta eccezione per lo Sviluppo di nuovi prodotti che ha un paio di punti percentuali in meno. Il secondo punto è cruciale: si tratta di sapersi avvalere sia dei modelli teorici sia delle esperienze pregresse (teoria e fatti). Schumpeter pone anche l’accento sulla considerazione che queste due (la via del processo studiato a tavolino e la via della esperienza vissuta) modalità di soluzione dei problemi, oltre ad avere valenza di per se, si rinforzano a vicenda come in un circuito virtuoso.
Il terzo punto, la storia, smentisce l’immagine che molti hanno dei metodi e delle tecniche disponibili per risolvere i problemi delle organizzazioni: non si tratta semplicemente di una cassetta degli attrezzi, fornita una volta per tutte, da cui trarre lo strumento più idoneo per un certo tipo di problema. Si deve anche tenere a mente che, sia i metodi che i problemi cui sono applicati, hanno una loro storia ed un contesto che ne condiziona la validità e le potenzialità; anche da questo derivano i limiti di applicabilità degli uni agli altri.
Quest’ultimo punto fornisce una motivazione per queste schede che vogliono mostrare come, nel corso del tempo, idee e metodi sono stati prima accennati vagamente, poi ripresi, spesso consolidati e talora sorpassati dagli eventi della storia.
Rappresenta nel piano cartesiano i punti A(3;-3) B (-3;-3) C(5;-3) e congiungili nell’ordine dato. a) classifica il triangolo ABC giustificando la tua risposta b) determina perimetro e area di tale triangolo.
Rappresenta nel piano cartesiano i punti A(3;-3) B (3;3) C(3;-1) D(-3;-1) e congiungili nell’ ordine dato. a) classifica il quadrilatero ABCD giustificando la tua risposta b) determina perimetro e area di tale quadrilatero.
Rappresenta nel piano cartesiano i punti A(5;1) B (2;5) C(-1;1) D(2;-3) e congiungili nell’ordine dato. a) classifica il quadrilatero ABCD giustificando la tua risposta b) determina perimetro e area di tale quadrilatero
 "Sono convinto che Dio non giochi a dadi."; "Dio è sottile, non malizioso."; "Voglio conoscere i pensieri di Dio, il resto è un dettaglio."; "Dio non s’interessa delle nostre difficoltà matematiche. Lui integra empiricamente."
"Sono convinto che Dio non giochi a dadi."; "Dio è sottile, non malizioso."; "Voglio conoscere i pensieri di Dio, il resto è un dettaglio."; "Dio non s’interessa delle nostre difficoltà matematiche. Lui integra empiricamente."
La Fisica e l’Universo
* Ogni conoscenza della realtà ha origine dall’esperienza e nell’esperienza si conclude. Le prospettive puramente logiche sono vuote davanti alla realtà. E’ merito di Galileo l’averlo scoperto e di aver diffusa questa idea nel mondo scientifico: percò egli è considerato il padre della fisica moderna, o meglio dell’intera scienza moderna.
* Newton, che per primo creò un completo sistema di fisica teorica, credeva ancora che le idee e le leggi fondamentali del suo sistema derivassero dall’esperienza. Il suo "hipothesis non fingo" non può che essere interpretato in questo senso.
* I concetti della fisica sono libere creazioni dello spirito umano, e non sono, malgrado le apparenze, determinati unicamente dal mondo esterno.
* La fisica contemporanea è basata su concetti qualche volta analoghi al sorriso di un gatto che non c’è.
* La teoria atomica può essere compresa meglio come una visualizzazione simbolica che come un concetto che riguarda la reale costruzione della materia.
* La cosa più misteriosa dell’universo è che esso è comprensibile.
* Due sono le cose infinite: l’universo e la stupidità umana, ma non sono ancora sicuro per quanto riguarda l’universo.
* Non mi preoccupo mai troppo del futuro: tanto arriva assai presto.
* E’ più facile spezzare un atomo che un pregiudizio.
La Matematica
* Quando le leggi della matematica si riferiscono al mondo reale non sono certe e quando sono certe non si riferiscono al mondo reale.
* Certo bisogna dividere il nostro tempo tra la politica e le equazioni, ma per me le equazioni sono più importanti poiché la politica riguarda il momento attuale mentre le equazioni valgono per sempre.
* Da quando i matematici hanno invaso la teoria della relatività, non la capisco più io stesso.
* La preoccupazione dell’uomo e del suo destino devono sempre costituire l’interesse principale di tutti gli sforzi tecnici. Non dimenticatelo mai in mezzo a tutti i vostri diagrammi ed alle vostre equazioni.
* Persisto a credere alla possibilità di un modello della realtà, vale a dire di una teoria, che rappresenti le cose stesse e non soltanto le probabilità della loro esistenza.
* I concetti matematici possono essere suggeriti dall’esperienza, ma mai dedotti da questa. L’esperienza resta, naturalmente l’unico criterio per utilizzare una costruzione matematica per la fisica, ma è nella matematica che risiede il principio creatore.
* Com’è possibile che la matematica, pur essendo fondamentalmente un prodotto del pensiero umano indipendente dall’esperienza, spieghi in modo così ammirevole le cose reali?
La Conoscenza
* La cosa più importante è non cessare mai di porsi delle domande. L’esistenza ha la sua ragion d’essere nella curiosità.
* La nostra conoscenza, se paragonata alla realtà, è primitiva e infantile. Eppure è il bene più grande di cui disponiamo.
* La ricerca della verità è più preziosa del suo possesso.
* Colui che non ha mai fatto un errore, non ha mai tentato qualcosa di nuovo.
* L’immaginazione è più importante della conoscenza.
* L’unica cosa realmente di valore è l’intuizione.
* Mai memorizzare quello che puoi comodamente trovare in un libro.
* L’intera scienza non è niente più che la rifinitura del pensiero di tutti i giorni.
* L’educazione è quello che rimane quando uno ha dimenticato quello che ha appreso a scuola.
* La saggezza non è un prodotto dell’istruzione, ma del tentativo di acquisirla che dura tutta la vita.
* È un autentico miracolo che i moderni metodi di istruzione non abbiano ancora interamente soffocato la sacra curiosità della ricerca.
* Non hai veramente capito qualcosa fino a quando non sei in grado di spiegarlo a tua nonna.
* Questi pensieri non entrano in alcuna formulazione verbale. Molto raramente penso tramite parole. Un pensiero arriva, e dopo io posso provare ad esprimerlo in parole.
* Le parole o il linguaggio, scritti o parlati, non sembrano giocare alcun ruolo nel meccanismo del mio pensiero. Le entità psichiche che sembrano servire come elementi nel pensiero sono certi segni ed immagini più o meno chiare che possono essere ‘volontariamente’ riprodotte e associate. […] Gli elementi sopra citati sono, nel mio caso, di tipo visivo e in un certo senso di tipo muscolare. Le parole convenzionali o altri segni devono essere ricercati attivamente soltanto in un secondo tempo, quando il processo associativo che ho menzionato si è sufficientemente stabilito e può essere riprodotto a volontà
Il Problem Solving
* Ogni cosa deve essere resa semplice quanto possibile, ma non forzosamente semplificata.
* Non è che sono così astuto è solo che rimango con i problemi più a lungo.
* Tutti sanno che una cosa è impossibile da realizzare, finché arriva uno sprovveduto che non lo sa e la inventa.
* La follia è continuare a fare le stesse cose ed aspettarsi risultati differenti.
* Le tre regole di lavoro: 1) Esci dalla confusione, trova semplicità. 2) Dalla discordia, trova armonia. 3) Nel pieno delle difficoltà risiede l’occasione favorevole.
* Un giorno le macchine riusciranno a risolvere tutti i problemi, ma mai nessuna di esse potrà porne uno nuovo.
* Noi non possiamo risolvere i problemi usando gli stessi tipi e lo stesso livello di pensieri che usiamo quando li creiamo.
* La teoria è quando si sa tutto e niente funziona. La pratica è quando tutto funziona e nessuno sa il perché. Noi abbiamo messo insieme la teoria e la pratica: non c’è niente che funziona… e nessuno sa il perché!
* La formulazione di un problema è più importante della soluzione, che spesso può essere determinata da una semplice operazione matematica: … 55 minuti per definire il problema e solo 5 per trovare la soluzione.
* L’immagine più semplice che ci si può formare dell’origine della scienza empirica è quella che si basa sul metodo induttivo anche se i progressi veramente grandi nella conoscenza della natura si sono avuti seguendo una via quasi diametralmente opposta a quella dell’induzione.
* Il ricercatore non perviene al suo sistema teorico per via metodica, induttiva; egli, piuttosto, si avvicina ai fatti tramite una scelta intuitiva tra teorie pensabili basate su assiomi.
* E’ l’afferrare intuitivo dell’ ’essenziale di una situazione problematica che porta il ricercatore a proporre un principio ipotetico o più principi del genere.
* Dal principio egli estrae per via puramente logico-deduttiva le conseguenze nel modo più completo possibile. Successivamente le conseguenze vengono messe a confronto con le esperienze e forniscono così un criterio per la giustificazione del principio ammesso.
* Non vi è alcuna via logica che porti agli assiomi, essi possono essere raggiunti solo attraverso l’intuizione, che si basa su un’empatia con gli oggetti dell’esperienza.
* Nessuna quantità di esperimenti potrà dimostrare che ho ragione; un unico esperimento potrà dimostrare che ho sbagliato.
(Albert Einstein 1879 -1955)
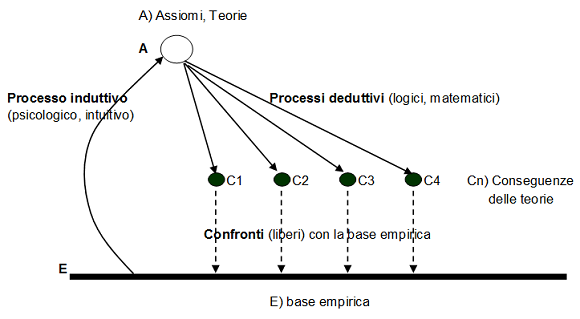
Gli ultimi sei pensieri riportati sopra sono ben rappresentati in uno schema allegato ad una lettera che Einstein scrisse all’amico Solowin. Questo schema (vedi figura) rappresenta il processo della conoscenza scientifica. La retta in basso (E) è la base empirica osservabile, la linea curva, che da E porta ad (A = teorie ed assiomi) rappresenta il processo induttivo. Questo processo, ed in questo Einstein sposa la critica di Hume all’induzione, non è logico, ma intuitivo o psicologico. Le Teorie e gli Assiomi sono i concetti più importanti, le visioni del mondo o delle situazioni problematiche; esse nel tempo possono cambiare (la fisica di Aristotele, la fisica di Galilei e Newton, la fisica di Einstein, ecc.). Dagli Assiomi, con processi deduttivi basati questa volta sulla logica e sulla matematica, si giunge alle conseguenze (C1, C2, …, Cn) delle teorie. A questo punto per avere una conferma o una corroborazione delle teorie stesse non resta che effettuare i confronti delle conseguenze (C) con la base empirica (E).
L’ultimo pensiero riportato è stato forse di ispirazione per Popper per la sua teoria della falsificazione: Einstein sapeva benissimo che, se l’esperimento svolto da Eddington al largo dell’Africa durante l’eclissi solare del 1919 non avesse confermato la curvatura dei raggi luminosi provenienti dalle stelle in vicinanza del sole, la sua teoria della relatività generale sarebbe stata falsificata.
Il primo pensiero: "Dio non gioca a dadi" merita una riflessione conclusiva sul ruolo della probabilità, dell’incertezza e del determinismo nel mondo fisico. Si deve partire dalla visione di Dio che aveva Einstein. Non si trattava del Dio personalistico delle grandi religioni monoteiste o di quelle politeiste. Si trattava piuttosto di una visione immanentista, forse vicina al Dio di Giordano Bruno e Spinoza, che faceva coincidere la divinità, con l’armonia, la regolarità e la bellezza dell’Universo: per Einstein non c’era grande differenza tra Dio e le forze intrinseche della natura. La celebre frase nacque in opposizione alla visione di Copenaghen (N. Bohr, W. Heisenberg e la maggior parte dei fisici dell’epoca) che vedevano l’incertezza come insita nel comportamento delle particelle elementari costituenti l’universo. Per Einstein non era possibile che le leggi della natura fossero intrinsecamente governate dall’incertezza: questa doveva derivare dalla nostra ignoranza dei veri processi deterministi sottostanti. Si racconta che Niels Bohr rispondesse ad Einstein: "Non dire a Dio come deve giocare". Successivamente in una discussione sul comportamento dei positroni con Feynman e Wheeler Einstein riprese, ed in parte corresse, le sue posizioni: "Non riesco ancora a credere che Dio giochi a dadi … ma forse mi sono guadagnato il diritto di commettere degli errori".
 Tra pochissimi giorni potremo assistere ad un simpatico sciame meteorico sopra i nostri cieli: le Orionidi di ottobre. Questo spettacolo andrà ad aggiungersi a quello della cometa di Hartley. Un bel modo di iniziare l’autunno!
Tra pochissimi giorni potremo assistere ad un simpatico sciame meteorico sopra i nostri cieli: le Orionidi di ottobre. Questo spettacolo andrà ad aggiungersi a quello della cometa di Hartley. Un bel modo di iniziare l’autunno!
Proprio in queste sere sui nostri cieli sta transitando la cometa 103P/Hartley, scoperta dall’astronomo inglese Malcolm Hartley, nel 1986. L’ho osservata proprio pochi minuti fa, nella costellazione del Perseo, ma appare poco luminosa; anche con l’aiuto di un binocolo ai riesce a vedere un debole batuffolino senza coda. La speranza è che nei prossimi giorni la cometa possa rendersi visibile anche ad occhio nudo, raggiungerà infatti il perielio il 28 ottobre. Le comete sono astri imprevedibili: può verificarsi infatti un improvviso outburst che le portano a diventare luminosissime, come può accadere invece l’esatto contrario. L’unica cosa che possiamo fare è seguirla lungo il suo cammino e sperare… Mal che vada potremo comunque vedere le immagini della cometa riprese da una distanza ravvicinata. Infatti la NASA, nell’ambito della missione EPOXI, ha programmato un incontro ravvicinato della sonda Deep Impact che, il prossimo 4 novembre, fotograferà la 103P/Hartley da una distanza di soli 700 Km.
Proprio come nella notte delle perseidi, dello scorso agosto, anche questo mese avremo un simpatico sciame meteorico, si tratta delle Orionidi. Il nome ci suggerisce che il radiante di questo sciame (il punto nel cielo dal quale sembrano provenire tutte le scie luminose), si trova proprio nella costellazione di Orione, una delle più belle del cielo autunnale-invernale. Lo sciame è generato dalla cometa di Halley i cui detriti, che dissemina nello spazio, intersecano l’orbita della Terra e a causa dell’attrito con la nostra atmosfera si surriscaldano regalandoci lo spettacolo delle stelle cadenti (le meteore). Il periodo di attività delle Orionidi è compreso tra il 16 ed il 27 Ottobre, ma il picco massimo di attività è previsto per la sera del 21.
Buona Osservazione!
Per approfondimenti
http://www.sidereus-nuncius.info/2010/10/14/arrivano-le-stelle-cadenti-autunnali/
http://www.sidereus-nuncius.info/2010/10/11/la-cometa-hartley-visibile-in-queste-sere/
 Esistono problemi che hanno avuto una storia curiosa. Ad esempio, quando James Joseph Sylvester nel 1893, mentre era professore all’Università di Oxford, propose su una rivista il quesito di provare che dato nel piano un insieme finito, superiore a 2, di punti non allineati esiste una retta che ne contiene esattamente 2, non poteva supporre che la soluzione sarebbe arrivata circa mezzo secolo dopo e che la paternità della soluzione sarebbe stata controversa.
Esistono problemi che hanno avuto una storia curiosa. Ad esempio, quando James Joseph Sylvester nel 1893, mentre era professore all’Università di Oxford, propose su una rivista il quesito di provare che dato nel piano un insieme finito, superiore a 2, di punti non allineati esiste una retta che ne contiene esattamente 2, non poteva supporre che la soluzione sarebbe arrivata circa mezzo secolo dopo e che la paternità della soluzione sarebbe stata controversa.
 Nella prima parte di questo articolo torniamo su certe questioni riguardanti la Proposizione 24 degli Elementi di Euclide, da noi chiamata – per l’immagine che evoca il suo enunciato – teorema del compasso. Nel primo paragrafo, rivolgiamo una fugace attenzione ai due casi che Proclo imputa a Euclide di aver tralasciato nella dimostrazione della proposizione suddetta. Nel secondo paragrafo esaminiamo la dimostrazione della Proposizione 21 degli Elementi, facendo delle osservazioni che, insieme al Teorema Mancante, valgono anche per una dimostrazione meno naif della Proposizione 24, rispetto a quella condotta da Euclide. Trattiamo questi argomenti senza alcuna pretesa di originalità, col solo intento di indurre il lettore a interessarsene, data la loro valenza sul piano storico ed epistemologico.
Nella prima parte di questo articolo torniamo su certe questioni riguardanti la Proposizione 24 degli Elementi di Euclide, da noi chiamata – per l’immagine che evoca il suo enunciato – teorema del compasso. Nel primo paragrafo, rivolgiamo una fugace attenzione ai due casi che Proclo imputa a Euclide di aver tralasciato nella dimostrazione della proposizione suddetta. Nel secondo paragrafo esaminiamo la dimostrazione della Proposizione 21 degli Elementi, facendo delle osservazioni che, insieme al Teorema Mancante, valgono anche per una dimostrazione meno naif della Proposizione 24, rispetto a quella condotta da Euclide. Trattiamo questi argomenti senza alcuna pretesa di originalità, col solo intento di indurre il lettore a interessarsene, data la loro valenza sul piano storico ed epistemologico.
 Studiare il moto di un veicolo spaziale diretto verso la Luna equivale a risolvere il problema ristretto dei tre corpi (Terra, Luna, veicolo), il quale non ammette soluzione analitica. Pertanto, una traiettoria lunare può essere calcolata con sufficiente precisione solamente mediante integrazione numerica delle equazioni del moto. In questo articolo si presenta il metodo delle coniche raccordate.
Studiare il moto di un veicolo spaziale diretto verso la Luna equivale a risolvere il problema ristretto dei tre corpi (Terra, Luna, veicolo), il quale non ammette soluzione analitica. Pertanto, una traiettoria lunare può essere calcolata con sufficiente precisione solamente mediante integrazione numerica delle equazioni del moto. In questo articolo si presenta il metodo delle coniche raccordate.
 Il celeberrimo problema isoperimetrico è il seguente: “Tra tutte le figure piane aventi lo stesso perimetro, determinare quelle aventi area massima.” Tale problema ha origini nella matematica greca antica e venne probabilmente formulato per la prima volta intorno al IX secolo a.C.; gli stessi greci “indovinarono” che le soluzioni dovessero essere i cerchi. Pur essendo la soluzione del problema “intuitivamente nota” sin dall’antichità, molti illustri matematici hanno lavorato per dare basi rigorose a tale intuizione, riuscendoci solo a partire dalla fine del 1800. In questo articolo si cerca di ricostruire la storia del problema isoperimetrico, si compendiano varie leggende in cui esso viene citato e si fornisce un resoconto dei tentativi classici e moderni verso la sua soluzione.
Il celeberrimo problema isoperimetrico è il seguente: “Tra tutte le figure piane aventi lo stesso perimetro, determinare quelle aventi area massima.” Tale problema ha origini nella matematica greca antica e venne probabilmente formulato per la prima volta intorno al IX secolo a.C.; gli stessi greci “indovinarono” che le soluzioni dovessero essere i cerchi. Pur essendo la soluzione del problema “intuitivamente nota” sin dall’antichità, molti illustri matematici hanno lavorato per dare basi rigorose a tale intuizione, riuscendoci solo a partire dalla fine del 1800. In questo articolo si cerca di ricostruire la storia del problema isoperimetrico, si compendiano varie leggende in cui esso viene citato e si fornisce un resoconto dei tentativi classici e moderni verso la sua soluzione.
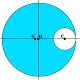 Consideriamo un disco di raggio R e pratichiamo un foro circolare di raggio r < R in modo tale che il foro sia tangente internamente al disco; il centro di massa G del disco forato si trova, per evidenti questioni di simmetria, sulla retta passante per il centro O del disco intero e per il centro C del foro. A questo punto vogliamo vedere qual è l’intervallo di r affinché il centro di massa G appartenga al disco forato, ovvero affinché G stia nella zona colorata.
Consideriamo un disco di raggio R e pratichiamo un foro circolare di raggio r < R in modo tale che il foro sia tangente internamente al disco; il centro di massa G del disco forato si trova, per evidenti questioni di simmetria, sulla retta passante per il centro O del disco intero e per il centro C del foro. A questo punto vogliamo vedere qual è l’intervallo di r affinché il centro di massa G appartenga al disco forato, ovvero affinché G stia nella zona colorata.
 La mia principale preoccupazione stava nel fatto che l’idea era così elementare, così semplice nella sua logica, che mi pareva difficile credere che nessun altro avesse pensato di metterla in pratica.
La mia principale preoccupazione stava nel fatto che l’idea era così elementare, così semplice nella sua logica, che mi pareva difficile credere che nessun altro avesse pensato di metterla in pratica.
"La peculiarità dell’uomo, la caratteristica che segna la sua differenza e la sua superiorità sugli altri esseri viventi, […] consiste, penso, nella capacità di scambiare con i suoi simili pensieri, sensazioni, desideri, ideali, preoccupazioni ed anche lamentele! Ogni cosa progettata per facilitare e sviluppare questa capacità veramente superiore deve essere – oso affermare – salutata come il mezzo per il progresso dell’umanità e la via per potenziare la tipica peculiarità dell’uomo." Guglielmo Marconi (1874 -1937)
Nel 1902, mentre Guglielmo Marconi, in una conferenza stampa spiegava le sue ultime imprese, un giornalista gli pose la seguente domanda: "Perché formò la sua prima Compagnia in Inghilterra e non in Italia? ", Guglielmo Marconi attese un attimo e poi come suo solito rispose lentamente: "Le condizioni economiche dell’Italia sono buone, ma si ha dinanzi un largo passivo. Somme ingenti vi furono e si sono spese, ad esempio, per la produzione dell’energia elettrica. Il governo italiano mi fu largo d’appoggi, ma soltanto in Inghilterra e in America ho potuto trovare i capitali necessari per l’inizio della mia impresa. Soltanto gli esperimenti sono costati cinque milioni. In Italia sarebbe stato impossibile trovare chi volesse arrischiare tale somma. Ora la Compagnia ha basi solide e vantaggi commerciali. Certamente il mio desiderio sarebbe stato di fondare la Compagnia in Italia, ma…".
“Nelle mie prime prove ho adoperato un comune oscillatore di Hertz e poi quello di Righi, come rivelatore, il coesore di Branly, in seguito rivelatosi poco stabile e sostituito da un nuovo coesore, un tubetto di vetro contenente limatura di nickel e argento. Con un tasto Morse inserito in uno dei circuiti del trasmettitore era possibile emettere attraverso lo spazio onde elettriche, brevi o lunghe, riproducendo esattamente i segnali telegrafici. Con tale apparecchio potei telegrafare alla distanza di circa mezzo miglio”
“Per quanto possa essere grande l’importanza della telegrafia senza fili per le navi e la navigazione, credo che essa sia destinata ad avere un’importanza per lo meno uguale come mezzo di comunicazione efficiente ed economico fra parti distanti del mondo. Per questa via si potrà forse un giorno trasmettere i messaggi a Paesi lontani con minimo consumo di energia e con una minima spesa” Discorso del 1909 in occasione dell’assegnazione del premio Nobel.
Ecco come Albert Einstein spiegava, con la consueta ironia, la telegrafia senza fili: "Vedete, il tradizionale telegrafo, funziona come un gatto molto, molto lungo. Voi tirate la coda a New York e la sua testa miagola a Los Angeles. Comprendete questo? La radio funziona nello stesso identico modo. Voi mandate un segnale da qui e loro lo ricevono laggiù. L’unica differenza è che nel caso della radio non c’è il gatto".
Sin da ragazzo Marconi era interessato alla ricerca e alla sperimentazione ed il primo successo lo ebbe quando mostrò a sua madre, una signora irlandese che non mancò mai d’incoraggiare il figlio, come era in grado di far suonare un campanello a distanza senza ricorrere ad alcun filo. Un passo successivo fu quello di mostrare che le onde radio non vengono fermate dagli ostacoli fisici: Marconi riuscì a far suonare il campanello posto rispetto a lui dall’altro versante di una collina.
Dopo molti altri esperimenti e successi Marconi si impose all’attenzione mondiale quando riuscì a dimostrare che le onde hertziane, grazie alla riflessione della ionosfera, non sono fermate nemmeno dalla curvatura terrestre: dalle coste inglesi della Cornovaglia trasmise più volte tre punti (nell’alfabeto Morse la lettera S) che furono ricevuti dall’altro lato dell’ Atlantico nelle coste canadesi di Terranova. L’apoteosi venne quando, ormai celebre, Marconi dal suo Yacht Elettra trasformato in laboratorio (la marina inglese era stata tra i primi sponsor di Marconi) riuscì a far accendere a Sidney in Australia le luci della esposizione universale.
Oggi i nostri politici fanno a gara per celebrare Marconi e la cosa stride parecchio in quanto oggi, come allora, la ricerca scientifica italiana è assai trascurata. A fronte dei continui tagli alla ricerca che fanno fuggire all’estero i nostri migliori ricercatori e scienziati, oggi come allora sono sempre di più i giovani che scappano all’estero per lavorare. Uno stillicidio, dal momento che prima lo stato investe tanto per prepararli e poi non riesce a dare una adeguata collocazione.
Più o meno 100 anni fa durante la guida del ministero delle Poste e Telegrafi il politico Pietro Lacava ricevette una lettera da Guglielmo Marconi in persona il quale illustrò l’invenzione del telegrafo senza fili chiedendo finanziamenti. La lettera non solo non ottenne risposta ma venne liquidata dal ministro con la scritta «alla Longara», intendendo il manicomio posto in via della Lungara a Roma. Per il ministro erano farneticazioni di un pazzo. Marconi, non avendo ottenuto risposta, andò in Inghilterra dove, presentato il suo lavoro, ottenne il brevetto e i necessari finanziamenti anche grazie all’interesse del Post Office britannico. Nel 1897 fondò a Londra la Marconi’s Wireless Telegraph Company, Ltd. che negli anni, seguenti assieme all’omonima società fondata negli USA, sviluppò prodotti e sistemi elettronici per le telecomunicazioni a partire dalle valvole termoioniche sviluppate da Fleming nel 1904 e poi televisione, radar, avionica. Le società fondate da Marconi contribuirono alla formazione della BBC in Inghilterra della Rca negli Stati Uniti dell’EIAR (Poi Rai in Italia) e della radio vaticana.
Le onde hertziane erano ben note ai fisici alla fine dell’800, ma solo Marconi intuì la possibilità di usarle per trasmettere messaggi da un capo all’altro della Terra, scavalcando montagne e oceani.
Nel 1900 Marconi riesce a risolvere il problema della sintonia, quindi a trasmettere più messaggi contemporaneamente su frequenze diverse. La radio è finalmente una tecnologia utilizzabile. Ha così creato un nuovo mercato, ma soprattutto una nuova risorsa che nessuno avrebbe mai immaginato: lo spettro radioelettrico.
Nella storia della scienza non sono molte le figure di studiosi che, dopo aver realizzato la propria invenzione, ne abbiano condotto i successivi sviluppi e le applicazioni pratiche, come ha fatto Marconi viaggiando instancabilmente da un paese all’altro. Alla sua figura di grande scienziato e abile imprenditore va associata quella di manager della scienza. Nel corso della sua lunga presidenza, dal 1927 al 1937, Marconi ha fatto del Cnr dell’epoca uno strumento moderno, capace di coniugare ricerca e applicazioni, innovazione e mondo delle imprese.
Nel 1922 Guglielmo Marconi avanzò l’idea di un radiotelemetro per localizzare a distanza mezzi mobili e nel 1933 in un incontro riservato ne propose la realizzazione a un gruppo di militari italiani tra i quali il colonnello dell’esercito Luigi Sacco; quest’ultimo, convinto della validità e dell’importanza dell’idea, la affidò all’ing. Ugo Tiberio, un giovane e brillante ufficiale delle armi navali, che negli anni seguenti portò avanti le ricerche e realizzò diversi prototipi, ma non ottenne le risorse e i fondi necessari per arrivare a un sistema radar operativo; i vertici della Marina italiana non credettero fino in fondo al progetto di Tiberio e solo dopo la disfatta di capo Matapan, dovuta anche all’uso del radar da parte degli inglesi, la ricerca sul radiotelemetro ebbe finalmente i fondi necessari per realizzare i primi sistemi radar italiani denominati GUFO e FOLAGA. Forse senza l’improvvisa scomparsa di Marconi i fondi necessari al progetto di Tiberio sarebbero arrivati prima e la Marina italiana avrebbe avuto il radar in tempo per scontrarsi ad armi pari con quella inglese.
Nella seconda metà degli anni 30 a Roma si parlò molto di un fatto avvenuto sulla via Cristoforo Colombo: tutte le auto erano rimaste bloccate per 20 minuti. Si diceva che Marconi stesse studiando un raggio (poi ribattezzato raggio della morte) in grado di fermare a distanza qualunque tipo di motore e quindi anche quello degli aerei. L’improvvisa morte dello scienziato non permise mai di accertare la reale consistenza degli eventi. Mussolini lasciò intendere che Marconi stava studiando sistemi che avrebbero potuto portare alla costruzione di armi micidiali, ma che per una promessa fatta a Pio XI non avrebbe più portato a termine le ricerche.
 Non c’è da stupirsi se oggi troviamo relazioni tra operazioni matematiche e costruzioni geometriche; già presso gli antichi greci aritmetica e geometria viaggiavano su binari paralleli, l’una serviva all’altra, anche se la geometria restava il sapere principale. Ma qui non parliamo dei soliti greci, bensì dei cinesi. Pare che proprio agli antichi cinesi venga attribuito il cosiddetto metodo della moltiplicazione grafica: un algoritmo di natura geometrica che permette di moltiplicare due interi.
Non c’è da stupirsi se oggi troviamo relazioni tra operazioni matematiche e costruzioni geometriche; già presso gli antichi greci aritmetica e geometria viaggiavano su binari paralleli, l’una serviva all’altra, anche se la geometria restava il sapere principale. Ma qui non parliamo dei soliti greci, bensì dei cinesi. Pare che proprio agli antichi cinesi venga attribuito il cosiddetto metodo della moltiplicazione grafica: un algoritmo di natura geometrica che permette di moltiplicare due interi.
 Un Learnign Object per capire come funzionano i sistemi di numerazione confrontando quello che usiamo oggi con quelli più antichi: il sistema bibilonese, quello egiziano, quello maya e quello dei romani.
Un Learnign Object per capire come funzionano i sistemi di numerazione confrontando quello che usiamo oggi con quelli più antichi: il sistema bibilonese, quello egiziano, quello maya e quello dei romani.
 Un Learnign Object per esercitarsi con i sistemi di numerazione a base 2, 5, 8, 16.
Un Learnign Object per esercitarsi con i sistemi di numerazione a base 2, 5, 8, 16.
 Le tabelline, tormentone dell’infanzia di tutti gli studenti, rappresentano un prezioso strumento di calcolo nonché una imperdibile opportunità per l’esercizio della memoria.
Le tabelline, tormentone dell’infanzia di tutti gli studenti, rappresentano un prezioso strumento di calcolo nonché una imperdibile opportunità per l’esercizio della memoria.
 Un simpatico regolo per esercitarsi con le equivalenze di misure: lunghezza, capacità, peso. Per i bambini della scuola primaria.
Un simpatico regolo per esercitarsi con le equivalenze di misure: lunghezza, capacità, peso. Per i bambini della scuola primaria.
 Scopo del Master è formare un insegnante di fisica esperto: in didattica della fisica moderna (fisica quantistica, relativistica, cosmologia); utilizzo delle tecnologie; formazione al pensiero teoretico ed alle attività sperimentali per la fisica quantistica e relativistica; progettazione e realizzazione di fisica in contesto; attività didattiche basate sulla lettura di articoli divulgativi della ricerca scientifica; didattica laboratoriale con strategie di Inquiry Learning e PEC; progettazione e realizzazione di materiali ed attività per l’orientamento formativo in fisica; analisi dei processi di apprendimento nell’innovazione didattica. Per la Puglia rivolgersi a [email protected]
Scopo del Master è formare un insegnante di fisica esperto: in didattica della fisica moderna (fisica quantistica, relativistica, cosmologia); utilizzo delle tecnologie; formazione al pensiero teoretico ed alle attività sperimentali per la fisica quantistica e relativistica; progettazione e realizzazione di fisica in contesto; attività didattiche basate sulla lettura di articoli divulgativi della ricerca scientifica; didattica laboratoriale con strategie di Inquiry Learning e PEC; progettazione e realizzazione di materiali ed attività per l’orientamento formativo in fisica; analisi dei processi di apprendimento nell’innovazione didattica. Per la Puglia rivolgersi a [email protected]
![]() Possono partecipare alla Gara di Matematica con le Tecnologie gli studenti della Scuola Media Superiore in un’unica categoria. La gara è costituita da una prova di selezione e da una prova finale; consiste nel risolvere dieci quesiti, sei a risposta multipla e 4 a risposta aperta. La prova finale si svolgerà nel mese di aprile 2011 presso il Liceo Scientifico "Vittorini" di Gela. Le spese di soggiorno, ma non di viaggio, degli studenti selezionati e di un docente accompagnatore saranno a carico dell’organizzazione.
Possono partecipare alla Gara di Matematica con le Tecnologie gli studenti della Scuola Media Superiore in un’unica categoria. La gara è costituita da una prova di selezione e da una prova finale; consiste nel risolvere dieci quesiti, sei a risposta multipla e 4 a risposta aperta. La prova finale si svolgerà nel mese di aprile 2011 presso il Liceo Scientifico "Vittorini" di Gela. Le spese di soggiorno, ma non di viaggio, degli studenti selezionati e di un docente accompagnatore saranno a carico dell’organizzazione.
 Lo sviluppo demografico di una popolazione biologica che cresce in funzione del tempo viene provocata da una o più fonti energetiche note della quale essa si nutre. Supporremo che tali fonti siano sparse in modo omogeneo e che la loro posizione possa essere, secondo i casi analizzati, palese o nascosta alla “vista”. Supporremo inoltre di essere in presenza di una popolazione omogenea composta da una singola specie che si sviluppa in un ambiente privo di limiti ambientali che non siano quelli propri dei modelli studiati. Il sito dell’autore http://sites.google.com/site/pianetagalileo/
Lo sviluppo demografico di una popolazione biologica che cresce in funzione del tempo viene provocata da una o più fonti energetiche note della quale essa si nutre. Supporremo che tali fonti siano sparse in modo omogeneo e che la loro posizione possa essere, secondo i casi analizzati, palese o nascosta alla “vista”. Supporremo inoltre di essere in presenza di una popolazione omogenea composta da una singola specie che si sviluppa in un ambiente privo di limiti ambientali che non siano quelli propri dei modelli studiati. Il sito dell’autore http://sites.google.com/site/pianetagalileo/
Come ottenre l’equazione parametrica dell’evoluta della parabola, ovvero il luogo geometrico dei centri dei cerchi osculatori.
The purpose of this study was to rewrite the formulas for the sum of powers of integers in a subsequent general mathematical formula independent of Bernoulli polynomials and numbers, starting from the formula of Faulhaber.
 Questo articolo è dedicato ai quadrati magici, un argomento che è stato trattato in lungo e in largo da generazioni di matematici (e non), e su cui esiste un’ampia letteratura. L’intenzione è quella di raggruppare e sintetizzare i principali dati e informazioni disponibili sui quadrati magici (comprese una serie di varianti al tema principale) per offrire in poche pagine una panoramica complessiva e, si spera, sufficientemente esauriente.
Questo articolo è dedicato ai quadrati magici, un argomento che è stato trattato in lungo e in largo da generazioni di matematici (e non), e su cui esiste un’ampia letteratura. L’intenzione è quella di raggruppare e sintetizzare i principali dati e informazioni disponibili sui quadrati magici (comprese una serie di varianti al tema principale) per offrire in poche pagine una panoramica complessiva e, si spera, sufficientemente esauriente.
 Un percorso didattico per la scuola primaria sui sistemi di numerazione. "Quando gli uomini vivevano ancora nelle caverne, un ometto simpatico di nome Numerix era molto bravo a cercare frutti nel bosco. Ad ogni frutto che raccoglieva faceva…"
Un percorso didattico per la scuola primaria sui sistemi di numerazione. "Quando gli uomini vivevano ancora nelle caverne, un ometto simpatico di nome Numerix era molto bravo a cercare frutti nel bosco. Ad ogni frutto che raccoglieva faceva…"
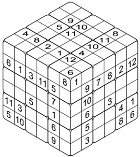 Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.
Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.
 Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.
Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.
 Le regole della variante del sudoku detta cubo di coppo.
Le regole della variante del sudoku detta cubo di coppo.
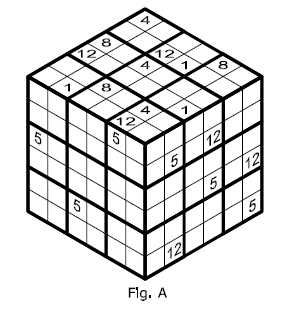 |
REGOLA A In ciascuno dei tre lati a vista del cubo 6x6x6 devono essere presenti tutti i numeri da 1 a 12 ripetuti tre volte. |
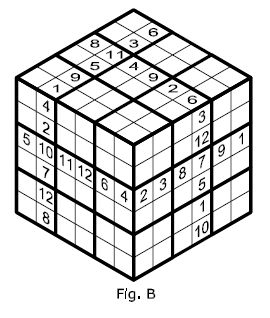 |
REGOLA B In ciascuna delle 18 file del cubo composte dalla consecuzione di ciascuna riga e/o colonna di un lato del cubo con la riga e/o colonna di un altro lato del cubo contigua alla precedente, devono essere presenti tutti i numeri da 1 a 12 senza ripetizione. |
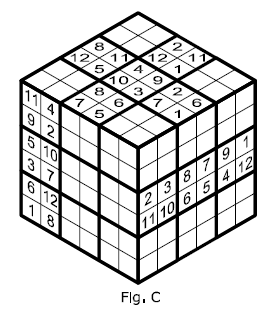 |
REGOLA C In ciascuna delle sei regioni 6×2, sia orizzontali che verticali, appartenenti a ciascun lato del cubo da 6×6, devono essere presenti tutti i numeri da 1 a 12 senza ripetizione. |
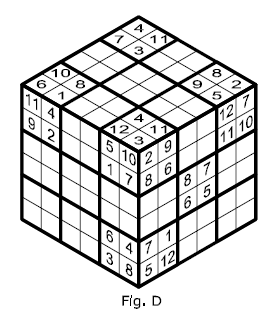 |
REGOLA D Nel cubo ad angolo del tipo 2x2x2 devono essere presenti tutti i numeri da 1 a 12 senza ripetizione. In tutti gli altri cubi 2×2 saranno presenti solo alcuni numeri da 1 a 12 senza ripetizione |
 La questione della continuità uniforme è legata alla questione dell’integrabilità di funzioni continue ed è un’arma molto utile.
La questione della continuità uniforme è legata alla questione dell’integrabilità di funzioni continue ed è un’arma molto utile.
 Uno dei linguaggi interpretativi della realtà che ci circonda è quello della scienza; la comprensione del metodo scientifico e del ragionamento logico matematico, la conoscenza dell’evoluzione storica di concetti che consideriamo acquisiti, ma che hanno richiesto secoli per essere sviluppati, la consapevolezza della portata e dei limiti delle conquiste della scienza moderna, sono aspetti diversi che contribuiscono a formare un’ampia sensibilità alle problematiche del mondo, fondamento della personalità del cittadino.
Uno dei linguaggi interpretativi della realtà che ci circonda è quello della scienza; la comprensione del metodo scientifico e del ragionamento logico matematico, la conoscenza dell’evoluzione storica di concetti che consideriamo acquisiti, ma che hanno richiesto secoli per essere sviluppati, la consapevolezza della portata e dei limiti delle conquiste della scienza moderna, sono aspetti diversi che contribuiscono a formare un’ampia sensibilità alle problematiche del mondo, fondamento della personalità del cittadino.
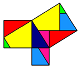 Esistono numerose dimostrazioni grafiche del ‘teorema di Pitagora’, si tratta spesso di un connubbio tra geometria e arte ed hanno un efficace valore didattico in quanto ‘fanno vedere’ intuitivamente come funziona il teorema.
Esistono numerose dimostrazioni grafiche del ‘teorema di Pitagora’, si tratta spesso di un connubbio tra geometria e arte ed hanno un efficace valore didattico in quanto ‘fanno vedere’ intuitivamente come funziona il teorema.
 Un corso universitario può interessare anche chi non deve laurearsi. Ma mentre ciò non stupisce ad esempio per Storia del Cinema, può sorprendere un po’ che qualcuno si prenda la briga di seguire il mio corso di "Metodi e modelli per la pianificazione finanziaria" presso il Dipartimento di Matematica dell’Università di Torino. Però tant’è: l’anno scorso sono venuti un informatico di Torino, un impiegato delle Poste di Alessandria, un consulente finanziario di Monza e, complice l’Alta Velocità, persino una giovane funzionaria regionale di Bologna.
Un corso universitario può interessare anche chi non deve laurearsi. Ma mentre ciò non stupisce ad esempio per Storia del Cinema, può sorprendere un po’ che qualcuno si prenda la briga di seguire il mio corso di "Metodi e modelli per la pianificazione finanziaria" presso il Dipartimento di Matematica dell’Università di Torino. Però tant’è: l’anno scorso sono venuti un informatico di Torino, un impiegato delle Poste di Alessandria, un consulente finanziario di Monza e, complice l’Alta Velocità, persino una giovane funzionaria regionale di Bologna.
Anche quest’anno il corso semestrale è incentrato sui criteri di scelta per il reddito fisso e il TFR. Per il programma ecc. si veda: http://bit.ly/bZ7qo5
L’inizio è previsto venerdì 1° o venerdì 8 ottobre 2010 e la fine nel gennaio 2011. L’orario è ancora provvisorio: orientativamente saranno 3 ore il venerdì e a partire da dicembre altre 2 ore il martedì, sempre dalle ore 16 o dalle 17.
Anche appunto chi non è studente universitario può iscriversi al corso nella forma detta "iscrizione a corso singolo". E’ richiesto un diploma di scuola media superiore e la tassa di iscrizione è di 100 euro. Maggiori informazioni sono riportate al punto 2 della pagina web: http://www.dm.unito.it/personalpages/scienza/corsi_investimenti.htm
L’iscrizione deve avvenire entro fine settembre ed è opportuno che gli interessati mi contattino prima di inscriversi, anche per ricevere indicazioni più dettagliate. Preciso subito che non c’è possibilità di seguire il corso on line né sono previste registrazioni delle lezioni o dispense; una bibliografia è riportata nella scheda del corso.
Il suddetto corso non è da confondere con quello di 4 giornate su "Gli investimenti in obbligazioni e azioni per il risparmio e la previdenza" per risparmiatori e operatori del settore: http://www.dm.unito.it/personalpages/scienza/documenti/progr-corso-investimenti-2009.htm
Beppe Scienza
Dipartimento di Matematica
via Carlo Alberto 10
10123 Torino
tel. 011-670-2906 fax 011-670-2878
 Obiettivo di questa raccolta di schede ed esercitazioni è quello di mettere il lettore nelle condizioni di affrontare problematiche ordinarie (di tipo economico, sociale, industriale, formativo…) attraverso tecniche di problem-solving informatico basate sul foglio di calcolo elettronico. L’autore si propone di far acquisire una mentalità idonea allo sfruttamento strategico e funzionale delle tecnologie.
Obiettivo di questa raccolta di schede ed esercitazioni è quello di mettere il lettore nelle condizioni di affrontare problematiche ordinarie (di tipo economico, sociale, industriale, formativo…) attraverso tecniche di problem-solving informatico basate sul foglio di calcolo elettronico. L’autore si propone di far acquisire una mentalità idonea allo sfruttamento strategico e funzionale delle tecnologie.
 In questo studio proviamo a definire il valore del limite di alcune particolari funzioni, utilizzando ripetutamente il primo ed il secondo teorema integrale di Cauchy.
In questo studio proviamo a definire il valore del limite di alcune particolari funzioni, utilizzando ripetutamente il primo ed il secondo teorema integrale di Cauchy.
In this paper we try to define the value of the limit of some particular functions, using repeatedly the First and the Second Integral Theorem of Cauchy.
Scarica il file in formato PDF
 Dalla Fisica Tecnica sappiamo che uno scambiatore di calore è un dispositivo attraverso il quale si realizza una trasmissione di calore tra fluidi, per esempio il nostro "radiatore" o termosifone di casa, attraverso il quale scambiano calore tra il liquido interno al termosifone e l’aria della stanza senza che i fluidi si miscelino tra di loro.
Dalla Fisica Tecnica sappiamo che uno scambiatore di calore è un dispositivo attraverso il quale si realizza una trasmissione di calore tra fluidi, per esempio il nostro "radiatore" o termosifone di casa, attraverso il quale scambiano calore tra il liquido interno al termosifone e l’aria della stanza senza che i fluidi si miscelino tra di loro.
 Un ebook con licenza creative commons per i piccoli della scuola primaria, contiene dieci semplici esperimenti sull’aria, che possono essere svolti con materiale povero. La scienza, cari ragazzi, è un modo di considerare le cose della realtà fisica, un modo di porre domande e determinare le risposte, riflettendo, sperimentando e studiando le esperienze e gli esperimenti degli altri. Lo scienziato cerca di comprendere e di trovare le risposte a molte domande sul mondo fisico. Anche voi potete essere degli scienziati: cominciate con questi esperimenti. Da http://scientificando.splinder.com
Un ebook con licenza creative commons per i piccoli della scuola primaria, contiene dieci semplici esperimenti sull’aria, che possono essere svolti con materiale povero. La scienza, cari ragazzi, è un modo di considerare le cose della realtà fisica, un modo di porre domande e determinare le risposte, riflettendo, sperimentando e studiando le esperienze e gli esperimenti degli altri. Lo scienziato cerca di comprendere e di trovare le risposte a molte domande sul mondo fisico. Anche voi potete essere degli scienziati: cominciate con questi esperimenti. Da http://scientificando.splinder.com
Problem solving & Decision making (metodi quantitativi per il mangement ed il project management) Milano, 12 Ottobre 2010 Sede: Fast Centro Congressi P.le R. Morandi, 2 – Milano. Questo workshop è diretto sia a persone che si accostano per la prima volta al Problem Solving sia a quelle che ne hanno già una certa esperienza. L’obiettivo è illustrare i metodi e le tecniche disponibili (Matematica applicata, Calcolo delle probabilità, Simulazione dinamica/stocastica, Programmazione lineare, non lineare e intera, Statistica e analisi delle serie storiche, Valutazioni economiche e finanziarie, Scelta degli investimenti, Tecniche di Project Management, Teoria delle decisioni, Teoria dei Grafi, Analisi del rischio, ecc.) per una gestione efficace ed efficiente, prescindendo dai diversi software e procedure usati nelle singole aziende.
Gli appuntamenti di settembre per tenersi aggiornati nella didattica della matematica.
Primi passi in aritmetica: a Fognano (Ravenna), dal 3 al 5 settembre 2010, presso la Casa di accoglienza delle suore domenicane, la società nazionale Mathesis organizza una scuola/convegno di matematica, dal titolo: Primi passi in aritmetica dalla scuola dell’infanzia ai primi anni della scuola primaria. Per i dettagli leggi tutto l’articolo.
Gruppo di Formazione Matematica della Toscana: 27° convegno sulla didattica della matematica, Viareggio Istituto Tecnico Commerciale “C. Piaggia” 9–10 Settembre 2010. Lavori di gruppo in collegamento con le lezioni in aula: congetturare in un ambiente di geometria dinamica, statistica e probabilità, topologia, Valutare le competenze: verso la costruzione di prove, esperienze astronomiche in matematica. Per i dettagli leggi tuttol’articolo.
Matematica in classe: organizzato dal Centro PRISTEM dell’Università “Bocconi” per gli insegnanti di Matematica, Fisica e Informatica delle scuole medie superiori. Riccione, dal 17 al 19 settembre, presso l’Hotel Corallo
Matematica e relatà: Hotel Oriente, Vico Equense (Napoli) 30 settembre, 1-2 ottobre 2010. Fra le novità l’estensione della sperimentazione alla scuola primaria e l’espletamento di due gare nazionali di modellizzazione (una individuale e l’altra a squadre). Quest’anno la sperimentazione è proposta in classe su “percorsi in continuità”. Per i dettagli leggi tutto l’articolo.
L’eredità di Giovanni Prodi: dai progetti degli anni ’70 ai cambiamenti della scuola di oggi, XXIX Convegno UMI-CIIM sull’insegnamento della matematica, Cetraro (Cosenza), 21 -22 ottobre.
Incontri con la matematica: XXIV convegno nazionale, Castel San Pietro Terme 5-7 novembre 2010. Per i dettagli leggi tutto l’articolo.
Associazione per la Didattica ocn le Tecnologie: convegno su Il Problem Solving in Matematica e Fisica con le nuove tecnologie, 19-20-21 novembre 2010 Istituto Professionale per i Servizi “A. Filosi” Aula Magna, Via Roma 125, Terracina (LT) .
![]() Scuola/convegno organizzato dalla Mathesis Primi passi in aritmetica, 3-5 settembre 2010
Scuola/convegno organizzato dalla Mathesis Primi passi in aritmetica, 3-5 settembre 2010
![]() 27° Convegno sulla didattica della matematica, Viareggio
27° Convegno sulla didattica della matematica, Viareggio
![]() Matematica in classe, Riccione 17-19 settembre, il programma
Matematica in classe, Riccione 17-19 settembre, il programma
http://www.matematicaerealta.it
![]() Matematica e realtà 2010-2011: la locandina del VI corso-convegno
Matematica e realtà 2010-2011: la locandina del VI corso-convegno
![]() Matematica e realtà: i percorsi didattici per il 2011
Matematica e realtà: i percorsi didattici per il 2011
![]() Matematica e realtà: le attività per il 2011
Matematica e realtà: le attività per il 2011
L’eredità di Giovanni Prodi e l’insegnamento della matematica http://umi.dm.unibo.it/ciim/index.php
![]() L’opusco del convegno Incontri con la matematica
L’opusco del convegno Incontri con la matematica
 "Quando Euclide, considerato come libro di testo, veniva attaccato per la sua verbosità o per la sua oscurità o la sua pedanteria, era uso difenderlo dicendo che la sua eccellenza logica è trascendente, e consente un invalutabile esercizio al potere giovanile di ragionamento. In realtà questa affermazione cade ad un’ispezione ravvicinata. Le sue definizioni non sempre definiscono, le sue dimostrazioni richiedono molti assiomi dei quali è del tutto inconsapevole… Il valore del suo lavoro come capolavoro di logica è stato esagerato enormemente". The Principles of Mathematics (1902).
"Quando Euclide, considerato come libro di testo, veniva attaccato per la sua verbosità o per la sua oscurità o la sua pedanteria, era uso difenderlo dicendo che la sua eccellenza logica è trascendente, e consente un invalutabile esercizio al potere giovanile di ragionamento. In realtà questa affermazione cade ad un’ispezione ravvicinata. Le sue definizioni non sempre definiscono, le sue dimostrazioni richiedono molti assiomi dei quali è del tutto inconsapevole… Il valore del suo lavoro come capolavoro di logica è stato esagerato enormemente". The Principles of Mathematics (1902).
"Io ritengo che l’abolizione della proprietà privata della terra e del capitale rappresenti un passo necessario per l’edificazione di un mondo nel quale le nazioni possano vivere in pace l’una con l’altra". 1919: Proposed Roads to Freedom.
"Compito dell’educazione è quello di guidare l’istinto in una direzione tale da permettergli di sviluppare le azioni utili anziché quelle dannose". 1929: Marriage and Morals.
"A quell’epoca cominciavo ad emergere da quel lago di idealismo germanico in cui ero stato gettato da Mc Taggart… In questo processo fui molto aiutato da Moore con cui in quel periodo ero in stretto contatto. Fu una grande emozione, dopo aver lungamente ritenuto irreale il mondo sensibile, poter ancora credere che esistessero cose come tavoli e sedie". 1969: The Autobiografy of Bertrand Russell.
"So che alla mia morte dovrò imputridire e che nulla del mio ego sopravvivrà. Non sono giovane e amo la vita, ma disdegno di abbattermi al pensiero dell’annientamento. La felicità non è meno vera, anche se deve finire. Il pensiero e l’amore non perdono il loro valore se non sono eterni. Parecchi uomini hanno affrontato il patibolo con fierezza; la stessa fierezza ci dovrebbe insegnare a riflettere senza tremare sul destino dell’uomo nell’universo. Anche se le finestre spalancate dalla scienza al primo momento ci fanno rabbrividire, abituati come siamo al confortevole tepore casalingo dei miti tradizionali, alla fine l’aria fresca ci rinvigorirà". 1927: Why I am not a Christian.
"In complesso la filosofia continentale ha aspirato a costruire sistemi di ampio respiro. Le sue argomentazioni sono di tipo aprioristico e, nel suo slancio, essa spesso non s’interessa alle questioni particolari. La filosofia britannica (oggi diremmo analitica), viceversa segue più da vicino il metodo scientifico della ricerca empirica. Si preoccupa in modo frammentario di una quantità di piccole cose e, quando propone principi generali, li mette sempre a confronto con l’esperienza diretta.
In conseguenza di questo modo diverso di affrontare i problemi, i sistemi a priori, anche se di per se stessi coerenti, cadranno in polvere se i loro pilastri verranno scossi. Invece la filosofia empirica, basata sui fatti osservati, non crollerà se in qualche punto affioreranno difetti. E’ come la differenza fra due piramidi una delle quali sia costruita a rovescio. La piramide empirica poggia sulla base e non cade se gli si toglie qualche mattone. La piramide a priori sta in equilibrio sul vertice e si sfascia qualora si faccia tanto di darle uno spintone". 1959: Wisdom of the West.
"La matematica è la sola scienza esatta in cui non si sa mai di cosa si sta parlando, ne se quello che si dice è vero". Bertrand Russell (1872-1970)
I significati fisici associati ai numeri o ai concetti geometrici non fanno parte della matematica. E’ pensando a questo che Russell disse quanto riportato nell’ultimo pensiero. All’epoca lui e Frege confidavano di poter fondare la matematica sui principi della logica. Nel 1903 Frege al termine dei suoi Grundgesetze scrisse: "Nulla di più indesiderabile può capitare ad uno scienziato del fatto che una delle fondamenta del suo edificio si incrini dopo che l’opera è finita. E’ questa la situazione in cui mi trovo in seguito ad una lettera (contenente il paradosso) inviatami dal signor Bertrand Russell proprio mentre si stava ultimando la stampa di questo volume… Non è soltanto questione del mio particolare modo di gettare le fondamenta, ma è in questione la possibilità o meno di dare all’aritmetica un qualsiasi fondamento logico".
Russell aveva trovato il paradosso considerando l’insieme di tutti gli insiemi che non sono membri di se stessi, ponendosi la domanda se essi fossero o meno membri di se stessi. Sia la risposta negativa che quella positiva da luogo ad una contraddizione. Per divulgare il paradosso Russell fece il divertente esempio di un ipotetico barbiere di un paese che, per definizione, fa la barba solo a tutti quelli che non se la fanno da se. La domanda è: chi fa la barba al barbiere? Sia la risposta "se la fa da se" che la risposta "non se la fa da se" è in contraddizione con la definizione data del barbiere.
 Tesina per la maturità scientifica 2010. Il lavoro nasce dalla curiosità suscitatami dalla Teoria della Relatività nella sua versione del 1915. Essa rappresenta una svolta fondamentale nel progresso dello studio della fisica moderna. All’alba del XX secolo, infatti, i fisici erano generalmente convinti di essere arrivati alla fine del loro percorso, riuscendo a descrivere qualunque fenomeno fisico con la meccanica Newtoniana e con l’elettromagnetismo di Maxwell, e ritenendo di dover apportare solo minime correzioni a queste due grandi teorie.
Tesina per la maturità scientifica 2010. Il lavoro nasce dalla curiosità suscitatami dalla Teoria della Relatività nella sua versione del 1915. Essa rappresenta una svolta fondamentale nel progresso dello studio della fisica moderna. All’alba del XX secolo, infatti, i fisici erano generalmente convinti di essere arrivati alla fine del loro percorso, riuscendo a descrivere qualunque fenomeno fisico con la meccanica Newtoniana e con l’elettromagnetismo di Maxwell, e ritenendo di dover apportare solo minime correzioni a queste due grandi teorie.
Scarica la tesina di maturità scientifica 2010
Massimiliano Leoni, La teoria della Relatività e lo studio dei buchi neri.