Autore: Antonio Bernardo
Compito in classe I liceo scientifico: prodotti notevoli, primo criterio di congruenza
Presentazione di Octave
OCTAVE è un programma di calcolo numerico.
“Octave” è il nome del docente di uno dei corsi presso i quali John W. Eaton, il principale autore del programma, ne iniziò lo sviluppo.
Inizialmente utilizzato come programma per l’Ingegneria chimica, il suo utilizzo fu esteso ad ambiti matematici più generali.
E’ un programma open source mantenuto e sviluppato dal progetto GNU liberamente scaricabile dal sito www.octave.org.
Nella sezione download, occorre scegliere la versione adatta al sistema operativo utilizzato (nel nostro caso windows) e cliccare su Octave forge-windows installer per installare il programma (la versione da noi utilizzata è octave 2.1.73).
In seguito all’installazione verrà creato un collegamento sul desktop, basterà cliccarci su due volte per lanciare il programma
Il prompt sancisce l’inizio della fase interattiva.
–
Alcuni esempi
Creare una Matrice
Il comando per creare una matrice e per salvarla è:
>> A = [1,2,12; 4,5,6; 7,8,9]
Le virgole separano gli elementi sulla stessa riga (colonne), mentre il “;”indica il passaggio alla riga successiva.
Octave risponderà visualizzando la matrice nella forma tradizionale (righe x colonne)
A =
1 2 12
4 5 6
7 8 9
Calcolo Matriciale
Octave permette di effettuare operazioni su matrici. I simboli da usare sono i seguenti.
Matrice per uno scalare >>2*A
Moltiplicare 2 matrici A e B >>A*B
Matrice trasposta >>A’
Matrice inversa di A >>inv(A)
Determinante >>det(A)
Risolvere un’equazione lineare
Un sistema lineare in n incognite è così fatto
a11 x1 + a12 x2 + … + a1n xn = b1 a21 x1 + a22 x2 + … + a2n xn = b2 … an1 x1 + an2 x2 + … + ann xn = bn
E può essere scritto come Ax=B
Così che x=A-1*B
Risolvere il suddetto sistema in Octave è semplicissimo basta utilizzare l’operatore ‘\’.
>> A=[2,3,4;1,7,9;3,2,1]
A =
2 3 4
1 7 9
3 2 1
>> B=[1;7;3]
B =
1
7
3
>> A\B
ans =
-1.05000
4.30000
-2.45000
.
Help
La documentazione di supporto è disponibile sul prompt di Octave, fornisce informazioni sul comando che si vuole utilizzare semplicemente scrivendo il nome del comando dopo la parola “help”.
Esempio:

Se richiamato senza alcuna voce l’help stampa una lista di tutti gli operatori e funzioni disponibili.
Per esempio il comando “help help” descrive il comando help.
Il Circolo Matematico Cesenate
 Il Circolo Matematico Cesenate si propone lo scopo di divulgare nel territorio Cesenate, tramite corsi, conferenze, eventi, la Matematica e la Fisica che, in un mirabile unicum inscindibile, costituiscono il nucleo fondamentale del pensiero scientifico. Visita il sito del Circolo Matematico >>>
Il Circolo Matematico Cesenate si propone lo scopo di divulgare nel territorio Cesenate, tramite corsi, conferenze, eventi, la Matematica e la Fisica che, in un mirabile unicum inscindibile, costituiscono il nucleo fondamentale del pensiero scientifico. Visita il sito del Circolo Matematico >>>
Numeri, matrici, stringhe, operatori logici e commenti
Dati numerici
All’interno del linguaggio Octave un numero decimale può essere espresso attraverso diverse notazioni.
Esempi:
>>105
>>1.05 e+2
>>1050 e-1
Per i numeri complessi l’espressione è:
>>3+4i
>>3.0+4.0e-1i
L’unità immaginaria i va scritta senza lasciare spazi fra il numero e la i.
La funzione >>double(x) converte x in un tipo a doppia precisione
La funzione >>single(val) converte il valore numerico val in un tipo a singola precisione
La funzione >>complex(val) e >>complex(re,im) trasformano un valore reale in numero complesso.
–
Matrici
Nel linguaggio Octave la dimensione della matrice è determinata automaticamente quindi non è necessario esplicitarla. Inserendo per esempio una matrice:
a=[12
34]
L’espressione
>>[a,a]
Produce la matrice:
ans
>>[1212
3434]
Bisogna stare attenti al modo in cui vengono inseriti i dati nelle matrici in quanto, per esempio, l’espressione:
[1-1]
Viene vista come differenza dando come risultato 0, mentre:
[1 -1]
Viene interpretata come un vettore [1,-1].
Se i valori della matrice sono molto grandi o molto piccoli attraverso la funzione
>>fixed_point_format
Possono essere visualizzati in un formato fisso. Questa funzione, però, non è raccomandabile in quanto può produrre un risultato che potrebbe essere mal interpretato.
Matrici vuote
Una matrice potrebbe avere una o entrambe le dimensioni (righe e colonne) pari a 0; in questo caso nel programma Octave sarà visualizzato:
[ ]
La funzione
>>val=print_empty_dimensions()
Controlla appunto tale comportamento.
Per esempio l’espressione
Zeros (3,0)
Stamperà
>>ans=[ ] (3*0)
La matrice vuota potrebbe essere anche un modo conveniente per cancellare righe o colonne di matrici.
Range
L’espressione Range è definita dal valore del primo elemento nel range, dal valore dell’incremento tra gli elementi (se omesso è assunto pari a 1) e il massimo valore che gli elementi del range non eccederanno. Questi tre valori sono separati da colonne (il carattere “:”).
Esempio:
>>1:5 (incremento omesso)
>>ans [1,2,3,4,5,]
Esempio:
>>1:3:5
>>ans [1,4]
–
Valori logici
Il linguaggio di programmazione Octave permette di utilizzare valori logici come true o false il cui risultato sarà un valore logico che dipenderà dalla comparazione.
Altri operatori logici sono:
&= congiunzione logica
|= or
!= negazione logica
La funzione
>>logical (arg)
converte l’argomento in un valore logico.
–
Stringhe
Una stringa è una sequenza di caratteri compresi tra le doppie virgolette “ “ o le singole virgolette ‘ ‘ e può essere di qualsiasi lunghezza. Poiché le virgolette singole possono essere utilizzate per altri scopi in Octave, per denotare le stringhe è meglio utilizzare le doppie virgolette.
Le stringhe potrebbero essere concatenate utilizzando la notazione per definire le matrici.
Esempio:
>>[“foo”,”bar”,”baz”]
>>ans “foobarbaz”
E’ possibile creare una stringa anche senza inserire il testo, infatti la funzione
>> Blanks (n)
Crea una stringa di lunghezza n fatta solo di caratteri vuoti.
Mentre la funzione
>> Deblanks(s)
Rimuove gli spazi nulli dal vettore s.
–
Inserire i commenti
Il commento è un testo che compare nel programma per spiegare cosa fa e come lavora per una maggiore comprensione del lettore.
Nel linguaggio Octave il commento è preceduto dal carattere “#” o dal simbolo “%” e continua fino alla fine della linea.
Esempio:
# descrizione variabile utilizzata
–
Traduzione, sintesi e adattamento di http://www.gnu.org/software/octave/doc/interpreter/ (consultato il 06.03.2008)
121. Rompere bene le figure
 Personalmente sono affascinato dai problemi che si enunciano in maniera semplice, ma che per la loro soluzione hanno bisogno di non semplici dimostrazioni. La ricerca di queste dimostrazioni spesso ha impegnato matematici per molto tempo: infatti c’era bisogno di idee nuove! Quei problemi sono stati perciò catalizzatori positivi di studi e di approfondimenti tra branche diverse della Geometria, facendone scoprire insospettati legami.
Personalmente sono affascinato dai problemi che si enunciano in maniera semplice, ma che per la loro soluzione hanno bisogno di non semplici dimostrazioni. La ricerca di queste dimostrazioni spesso ha impegnato matematici per molto tempo: infatti c’era bisogno di idee nuove! Quei problemi sono stati perciò catalizzatori positivi di studi e di approfondimenti tra branche diverse della Geometria, facendone scoprire insospettati legami.
Attenzione ai segnali deboli e alla gestione dei rischi [G. Leopardi]
 I dialoghi di Leopardi hanno molto spesso una valenza filosofica oltre che letteraria e artistica. Il Dialogo di Cristoforo Colombo e Pietro Gutierrez, in particolare, può essere considerato un vero e proprio trattato delle situazioni problematiche soggette a rischio.
I dialoghi di Leopardi hanno molto spesso una valenza filosofica oltre che letteraria e artistica. Il Dialogo di Cristoforo Colombo e Pietro Gutierrez, in particolare, può essere considerato un vero e proprio trattato delle situazioni problematiche soggette a rischio.
Gut. …. Così per via di discorso, vorrei che tu mi dichiarassi precisamente, con tutta sincerità, se ancora hai così per sicuro come a principio, di avere a trovar paese in questa parte del mondo; o se, dopo tanto tempo e tanta esperienza in contrario, cominci niente a dubitare.
Col. Parlando schiettamente, e come si può con persona amica e segreta, confesso che sono entrato un poco in forse: tanto più che nel viaggio parecchi segni che mi avevano dato speranza grande, mi sono riusciti vani;…. Ma voglio solamente inferire, rispondendo alla tua richiesta, che quantunque la mia congettura sia fondata in argomenti probabilissimi, non solo a giudizio mio, ma di molti geografi, astronomi e navigatori eccellenti, coi quali ne ho conferito, come sai, nella Spagna, nell’Italia e nel Portogallo; nondimeno potrebbe succedere che fallasse: perché torno a dire, veggiamo che molte conclusioni cavate da ottimi discorsi, non reggono all’esperienza; e questo interviene più che mai, quando elle appartengono a cose intorno alle quali si ha pochissimo lume.
Gut. Di modo che tu, in sostanza, hai posto la tua vita, e quella dei tuoi compagni, in sul fondamento di una semplice opinione speculativa.
Col. Così è: non posso negare. Ma lasciando da parte che gli uomini tutto giorno si mettono a pericolo della vita con fondamenti più deboli di gran lunga, e per cose di piccolissimo conto, o anche senza pensarlo; considera un poco. Se al presente tu, ed io, e tutti i nostri compagni, non fossimo in su queste navi, in mezzo di questo mare, in questa solitudine incognita, in istato incerto e rischioso quanto si voglia; in quale altra condizione di vita ci troveremo a essere?….. Chi pose mai nel numero dei beni umani l’avere un poco di terra che ti sostenga? Niuno, eccetto i navigatori, e massimamente noi, che per la molta incertezza del successo di questo viaggio, non abbiamo maggior desiderio che della vista di un cantuccio di terra; questo è il primo che ci si fa innanzi allo svegliarci, con questo ci addormentiamo…. e presa terra, solamente a pensare di ritrovarci in sullo stabile, e di potere andare qua e la camminando a nostro talento, ci parrà per più giorni essere beati.
Gut. Tutto cotesto è verissimo: tanto che se quella tua congettura speculativa riuscirà così vera come è la giustificazione dell’averla seguita, non potremo mancar di godere questa beatitudine un giorno o l’altro.
Col. Io per me se bene non mi ardisco più di prometterlo sicuramente, contuttociò spererei che fossimo per goderla presto. Da certi giorni in qua, lo scandaglio come sai, tocca il fondo; e la quantità di quella materia che gli vien dietro, mi pare indizio buono. Verso sera, le nuvole intorno al sole, mi si dimostrano d’altra forma e di altro colore da quelle dei giorni innanzi. L’aria, come puoi sentire, è fatta un poco più dolce e più tepida di prima. Il vento non corre più, come l’addietro, così pieno, ne così dritto, ne costante; ma piuttosto incerto, e vario, e come fosse interrotto da qualche intoppo. Aggiungi quella canna che andava in sul mare a galla, e mostra essere tagliata da poco; e quel ramicello di albero con quelle coccole rosse e fresche. Anche gli stormi degli uccelli, benché mi hanno ingannato l’altra volta, nondimeno ora sono tanti che passano, e così grandi; e moltiplicano talmente di giorno in giorno; che penso vi si possa fare qualche fondamento; massime che vi si veggono intramischiati alcuni uccelli che, alla forma, non mi paiono dei marittimi. In somma tutti questi segni raccolti insieme, per molto che io voglia essere diffidente, mi tengono pure in aspettativa grande e buona.
Gut. Voglia Dio questa volta, ch’ella si verifichi.”
(Giacomo Leopardi, 1798-1837, Operette Morali, Dialogo di C. Colombo e P. Gutierrez ).
I dialoghi di Leopardi hanno molto spesso una valenza filosofica oltre che letteraria e artistica. Questo dialogo, in particolare, può essere considerato un vero e proprio trattato delle situazioni problematiche soggette a rischio. Nel seguito solo qualche considerazione e spunto di riflessione:
- Il grado di certezza e quindi l’entità dei rischi variano con il passare del tempo e con lo svolgersi degli eventi: la situazione deve essere continuamente monitorata.
- L’attenzione a tutti i segnali, anche quelli più deboli, è fondamentale per gestire al meglio i rischi di una iniziativa/progetto.
- Le opinioni delle persone più competenti ed esperte devono essere tenute in grande considerazione quando si esaminano le situazioni problematiche.
- La noia spinge spesso ad assumere rischi eccessivi per obiettivi futili; mentre invece un progetto interessante, impegnativo ma rischioso, può far apprezzare piccoli aspetti della vita.
- Anche l’esperienza pratica deve essere valutata attentamente sopratutto nelle situazioni in cui la dottrina consolidata e la ragione sono di poco aiuto.
- Assumere dei rischi può dare energia, motivazione e …. soddisfazione, in particolare se i risultati positivi si concretizzano.
- Osservare gli eventi, valutarne le probabilità ed anticipare possibili esiti positivi può creare sinergie utili per ottenere il successo.
Chi volesse riflettere sui problemi relativi alla follia umana e alle politiche sostenibili (per l’umanità? Per la biodiversità? Per il pianeta terra? Per l’universo?) può leggere il Dialogo di un Folletto e di uno Gnomo anch’esso tratto dalle Operette Morali.
Gno. Ma come sono andati a mancare quei monelli? (gli uomini e le donne)
Fol. Parte guerreggiando tra loro, parte navigando, parte mangiandosi l’un l’altro, parte ammazzandosi non pochi di propria mano, parte infracidando nell’ozio, parte stillandosi il cervello sui libri, parte gozzovigliando, e disordinando in mille cose; in fine studiando tutte le vie di far contro la propria natura e di capitar male…
Variabili
Le variabili permettono di dare un nome ai valori e richiamarli dopo. Il nome di una variabile può essere una sequenza di lettere, di numeri o barre. Octave non dà un limite alla lunghezza dei nomi delle variabili, ma di solito non è utile avere variabili con nomi lunghi più di 30 caratteri.
Esempi di nomi di variabili validi sono: x, x15, _foo_bar_baz,….
Tuttavia nomi come foobarbaz che cominciano e terminano con l’undersore (_) possono essere intesi come riservati all’uso interno di Octave.
NB: in Octave i simboli a e A sono variabili distinte.
Il nome di una variabile è un’espressione valida da sé e rappresenta il valore corrente della variabile.
Ci sono poi variabili che hanno un significato a sé nel programma.
Per esempio:
ans tiene la directory di lavoro corrente pi indica il raggio di un cerchio Alcuni di questi simboli inseriti in Octave sono costanti e non possono essere modificati. Gli altri possono essere usati e assegnati come tutte le altre variabili ma i loro valori sono anche usati e modificati automaticamente da Octave.
Le variabili di octave non sono fisse, quindi è possibile prima memorizzare un valore numerico in una variabile e dopo usare lo stesso nome per mettere il valore nella stringa nello stesso programma. Le variabili non possono essere usate prima che gli sia stato assegnato un valore se no dà errore.
Esempio di variabile reimpostata:
>>isvarname(nome) #dà vero se nome è un nome di variabile valido
–
Variabili globali
Una variabile dichiarata globale può essere utilizzata all’interno del corpo di una funzione senza doverla dichiarare come un parametro formale. Una variabile può essere dichiarata globale usando l’appellativo global.
Esempio:
>>global a
>>global ab
>>global c=2
Una variabile globale può essere introdotta una sola volta in una frase globale.
Per esempio, dopo aver inserito il seguente codice:
>>global gvar=1
>>global gvar=2
Il valore della variabile globale gvar è 1 non 2.
Il comando clear gvar non cancella questo comportamento, mentre clear all lo fa. E’necessario dichiarare una variabile come globale dentro il corpo di una funzione per utilizzarla.
Per esempio:
>>global x
>>function f()
>> x=1
>>endfunction
>> f() Non pone il valore della variabile globale x uguale a 1.
Per cambiare il valore della variabile globale x bisogna dichiarare che è globale anche nel corpo della funzione:
>>function f()
>>global x
>> x=1
>>endfunction
Passando una variabile globale in una lista di parametri di una funzione, Octave metterà una copia locale della variabile e non modificherà il valore globale.
Per esempio:
>>function f(x)
>> x=0
>>endfunction
E la definizione di x come variabile globale dall’inizio:
>>global x=13
L’espressione
>>f(x) porrà il valore di x dentro la funzione uguale a 0, ma il valore di x all’inizio rimane invariato perchè la funzione lavora con una copia del suo argomento.
– Funzione preimpostata: isglobal(name) Questa funzione dà 1 se name globalmente visibile se no dà 0.
Per esempio:
>>global x
>>isglobal(“x”)
>> >=1
Variabili persistenti
La differenza tra variabili persistenti e variabili globali è chele variabili persistenti sono locali, finalizzate ad una particolare funzione e non sono visibili al di fuori di essa. Una variabile può essere dichiarata persistente usando persistent.
Esempio:
>>persistent a
>>persistent ab
>>persistent c=2 Il comando static usato in C è equivalente a persistent. Al contrario delle variabili globali ad ogni inizio di frase sarà reimpostata la variabile.
Per esempio dopo aver eseguito il seguente codice:
>>persistent pvar=1
>>persistent pvar=2
Il valore della variabile persistente pvar sarà 2.
Mastermind numerico
 Devi indovinare il numero scelto dal computer. Se indovini una cifra nella posizione giusta ottieni un pallino verde, se indovini la cifra ma non la posizione ottieni una croce rossa. Devi indovinare tutte le cifre nella posizione giusta nel minor numero di tentativi. Per giocare trascina i numeri nel riquadro in basso a sinistra e premi "Verifica". Metti alla prova la tua intelligenza e scavalca la classifica. Vai al gioco >>>.
Devi indovinare il numero scelto dal computer. Se indovini una cifra nella posizione giusta ottieni un pallino verde, se indovini la cifra ma non la posizione ottieni una croce rossa. Devi indovinare tutte le cifre nella posizione giusta nel minor numero di tentativi. Per giocare trascina i numeri nel riquadro in basso a sinistra e premi "Verifica". Metti alla prova la tua intelligenza e scavalca la classifica. Vai al gioco >>>.
Se ti è piaciuto questo gioco acquista il Cd con tutti i giochi di Matematicamente.it, un cd didattico per imparare la matematica giocando, per bambini dai 5 in poi.
Derive: esempi pratici
 Il corso, senza scendere in particolari e formalismi matematici, vuole presentare delle esercitazioni per conoscere ed utilizzare lo strumento Derive XM: soluzione di equazioni con il metodo algebrico, il metodo grafico; soluzione di un sistema lineare con metodo algebrico e grafic; definizione e utilizzo di una funzione creata dall’utente; traslazione di una funzione, fascio di rette, fascio di circonferenze, disequazione di 2° grado, dominio di una funzione, derivata, matrici e sistemi, ricerca di radici…
Il corso, senza scendere in particolari e formalismi matematici, vuole presentare delle esercitazioni per conoscere ed utilizzare lo strumento Derive XM: soluzione di equazioni con il metodo algebrico, il metodo grafico; soluzione di un sistema lineare con metodo algebrico e grafic; definizione e utilizzo di una funzione creata dall’utente; traslazione di una funzione, fascio di rette, fascio di circonferenze, disequazione di 2° grado, dominio di una funzione, derivata, matrici e sistemi, ricerca di radici…
Operatori aritmetici, logici
Operatori aritmetici
X+Y addizione (se x e y sono matrici devono avere lo stesso numero di righe e di colonne)
X.+Y addizione elemento per elemento
X-Y sottrazione (se x e y sono matrici devono averelo stesso numerodirighee di colonne)
X.-Y sottrazione elemento per elemento
X*Y moltiplicazione (se x ey sono matricidevono avere lo stesso numero dirighe e di colonne)
X.*Y moltiplicazione elemento per elemento
X/Y divisione (concettualmente uguale a (inverse(Y’)*X’))
X./Y divisione elemento per elemento
X\Y divisione sinistra (concettualmente uguale a(inverse(X)*Y))
X.\Y divisione elemento per elemento
X^Y potenza tra matrici o scalari
X**Y
X.^Y potenza elemento per elemento
X.**Y
-X negazione
X’ trasposta
Operatori di comparazione
Gli operatori di comparazione danno come risultato 1 se la comparazione è vera, 0 se è falsa. Per le matrici gli operatori lavorano elemento per elemento.
Per esempio:
>> [1,2;3,4]= =[1,3;2,4]
>> ans 1 0
0 1
X<Y vero se x è minore di y
X<=Y vero se x è minore o uguale a y
X= = Y vero se x è uguale a y
X>=Y vero se x è maggiore o uguale a y
X>Y vero se x è maggiore di y
X !=Y vero se x è diverso da y
X<>Y vero se x è diverso da y
La funzione isequal (x1, x2, …) dà vero se tutti x1, x2, … sono uguali.
Operatori booleani elemento per elemento
Sono espressioni di comparazione che usano gli operatori booleani or, and (&), not(!). Un valore è falso se è 0, vero altrimenti (se è1).
Operatori di assegnazione
Un’assegnazione è un’espressione che memorizza un nuovo valore in una variabile.
Per esempio:
>> z=1
Assegna il valore 1 alla variabile z.
“=” è chiamato operatore di assegnazione. L’assegnazione può assegnare anche stringhe.
Esempio:
>> thing=”food”
>> predicate=”good”
>> message=[“this”,thing,”is”,predicate]
Assegna il valore “this food is good” alla variabile message (qui è illustrate anche la concatenazione di stringhe). La parte sinistra di un’assegnazione non può essere una variabile. Può anche essere un elemento di una matrice o una lista di valori di output. Questi sono tutti chiamati IVALUES e significa che possono apparire sulla parte sinistra dell’operatore di assegnazione. Se viene assegnato uno scalare ad un amatrice indicizzata questo pone tutti gli elementi chiamati dall’indice uguali al valore dello scalare.
Per esempio, se a è una matrice con almeno 2 colonne:
>> a(:,2)=5
Pone tutti gli elementi nella seconda colonna di a uguali a 5. Assegnare una matrice vuota “[ ]” permette di cancellare righe o colonne della matrice o del vettore.
Per esempio, data una matrice A 4*5, l’assegnazione:
>> A(3,:)=[ ]
Cancella la terza riga di a e l’assegnazione:
>> A(:,1:2:5)=[]
Cancella la prima, terza e quinta colonna.
Un’assegnazione è un’espressione quindi ha un valore. Infatti ponendo
>> z=1
È un’espressione che ha valore 1. Una conseguenza di ciò è che è possibile fare assegnazioni multiple contemporaneamente.
Esempio:
>> x=y=z=0
Assegna il valore
Si può anche assegnare una lista di valori:
>> [a,b,c]=[u,s,v]=svd (a)
Che è equivalente a:
>> [u,s,v]=svd (a)
>> a=u
>> b=s
>> c=v
Il numero di valori sul lato sinistro dell’espressione non può eccedere il numero di valori sul lato destro. Per esempio la seguente espressine produce errore:
>> [a,b,c,d]=[u,s,v]=svd (a)
>> error: element number 4 undefined in return list
>> error: evaluating assignment expression near line 8, coloumn 15
Un’assegnazione comune è quella di incrementare una variabile esistente con un valore dato, come:
>> a=a+2
Che può essere scritto in modo più compatto con l’operatore +=
>> a+=2
Operatori simili esistono anche per sottrazione, moltiplicazioni e divisioni.
Un’espressione della forma
>> expr1 op= expr2
È valutata come:
>> expr1=(expr1) op (expr2)
Dove op può essere un altro operatore come +, -, *, /.
Operatori di incremento
Incrementano o decrementano il valore di una variabile di 1. L’operatore di incremento è scritto “++”. Può incrementare la variabile prima o dopo che gli sia stato assegnato il valore. Per esempio, per preincrementare la variabile si scrive:
>> ++x
Aggiunge1 a x e dà il nuovo valore di x come risultato dell’espressione. E’ uguale all’espressione
>> x0x+1
Per postincrementare una variabile si scrive:
>> x++
Aggiunge 1 alla variabile x, ma da il valore che x aveva prima dell’incremento.
Per esempio, se x=2, il risultato dell’espressione x++ è 2 e il nuovo valore di x è 3.
Per gli elementi della matrice e del vettore, gli operatori di incremento e decremento lavorano su ogni elemento dell’operando. Espressioni di incremento e decremento:
++x incrementa la variabile x. Il valore dell’espressione è il nuovo valore di x. E’equivalente a x=x+1
–x decrementa la variabile x. E’ equivalente a x=x-1
X++ porta la x a essere incrementata. Il valore dell’ espressione è il vecchio valore di x
x– porta la x a essere decrementata. Il valore dell’espressione è il vecchio valore di x.
Operatori di precedenza
Determinano come gli operatori sono raggruppati, quando operatori diversi compaiono nella stessa espressione. Per esempio, * ha precedenza rispetto a 2+. Quindi l’espressione
>> a+b*c
Significa moltiplicare b*c e aggiungere a al prodotto (a+(b*c)).
E’ comunque opportuno utilizzare le parentesi quando c’è una combinazione inusuale di operatori, in quanto chi legge il programma potrebbe non ricordare qual è la precedenza.
I finalisti del Trofeo di scacchi Matematicamente.it 2009
 Il trofeo di scacchi è giunto alla fase finale, i 12 finalisti sono: 1. Firkle, 2. Amandy ,3. Cpeg52, 4. Bomber92, 5. Luky, 6. Nato_pigro, 7. Pumba91, 8. Battista_l, 9. Luca_92, 10. Pipppogol, 11. Andreatreno, 12. Lorenzo93. Tutti i finalisti dovranno confermare la propria adesione alla fase finale con un messaggio nell’apposito forum dedicato agli scacchi forum scacchi. I premi in palio sono: 1° classificato: coppa e PlayStation 3, 2° classificato: coppa e PlayStation Portable, 3° classificato: coppa e libro Gli scacchi di Luca Pacioli. Tutti i 12 partecipanti alla fase finale vinceranno la maglietta di Matematicamente.it Winner (se ancora non l’hanno vinta) e a scelta uno tra i seguenti premi: 1 pen drive a 4GB, 1 libro a scelta del costo max di 20,00€. Premio speciale per il migliore commentatore delle partite in finale: targa e pen dirve da 8GB o libro a scelta costo max di 30,00€. In bocca al lupo ai finalisti.
Il trofeo di scacchi è giunto alla fase finale, i 12 finalisti sono: 1. Firkle, 2. Amandy ,3. Cpeg52, 4. Bomber92, 5. Luky, 6. Nato_pigro, 7. Pumba91, 8. Battista_l, 9. Luca_92, 10. Pipppogol, 11. Andreatreno, 12. Lorenzo93. Tutti i finalisti dovranno confermare la propria adesione alla fase finale con un messaggio nell’apposito forum dedicato agli scacchi forum scacchi. I premi in palio sono: 1° classificato: coppa e PlayStation 3, 2° classificato: coppa e PlayStation Portable, 3° classificato: coppa e libro Gli scacchi di Luca Pacioli. Tutti i 12 partecipanti alla fase finale vinceranno la maglietta di Matematicamente.it Winner (se ancora non l’hanno vinta) e a scelta uno tra i seguenti premi: 1 pen drive a 4GB, 1 libro a scelta del costo max di 20,00€. Premio speciale per il migliore commentatore delle partite in finale: targa e pen dirve da 8GB o libro a scelta costo max di 30,00€. In bocca al lupo ai finalisti.
Regolamento della finale del torneo di scacchi
- I primi 12 del prima fase, cioè i primi 12 classificati al 30.11.2009 partecipano alla fase finale. La seconda fase del torneo si disputerà in modalità sincrona e si svolgeranno sul sito www.scacchisti.it, tutte le partite avranno durata massima di 10 minuti per giocatore.
- Dal primo dicembre i primi 12 classificati dovranno confermare la loro partecipazione alla finale con un messaggio su questo forum entro il 4 dicembre. Se uno o più giocatori che si sono classificati per la seconda fase non si iscrivono saranno sostituiti con i giocatori che si sono classificati dal 13-esimo posto in poi.
- I 12 finalisti saranno divisi in 4 gironi: A, B, C, D
Girone A: 1° classificato 8° classificato 12° classificato
Girone B: 2° classificato 7° classificato 11° classificato
Girone C: 3° classificato 6° classificato 10° classificato
Girone D: 4° classificato 5° classificato 9° classificato - In ogni girone di faranno 2 incontri di 2 partite ciascuno. Per esempio nel girone A si faranno le seguenti partite: 1°-8° 8°-1° 1°-12° 12°-1° 8°-12° 12°-8°
- Le partite si possono svolgere in qualsiasi ordine e in tempi da concordare tra i giocatori, purché si concludano entro il 10 dicembre.
- Per ogni partita il vincitore si farà carico di trascrivere la partita sul forum, indicandone anche l’esito della partita. Sarà compito della giuria aggiornare i punteggi. Il giocatore perdente è tenuto a verificare che il proprio avversario abbia riportato correttamente la partita e l’esito. In caso di parità sarà compito del nero riportare la partita e il suo esito.
- Chiunque può commentare le partite concluse, in questo modo partecipa al premio speciale per il miglior commentatore.
- Il primo di ogni girone passa alla finale della gara, in caso di parità supera il girone chi ha vinto più partite, in caso di ulteriore parità supera il girone chi ha perso meno partite, in caso di ulteriore parità i giocatori arrivati a pari merito disputeranno una finale.
- Nella fase finale giocheranno il vincitore del girone A contro il vincitore del girone D; il vincitore del girone B contro il vincitore del girone C. Passa il turno chi vince al meglio di 4 partite, se si finisce in parità, le sfide continuano finché non c’è uno scarto di due partite tra i due giocatori.
- I due vincitori disputeranno la finale per 1° e 2° posto, che sarà giocata al meglio di 6 partite o finché tra i due giocatori non ci sarà uno scarto di 2 partite. I perdenti disputeranno con modalità analoghe la finale per il 3° posto.
- Tutte le partite della finale si dovranno disputare entro il 18 dicembre, in modo che per il 20 dicembre potremo proclamare i vincitori.
Tutte le altre partite possono essere continuate regolarmente fino all’inzio del trofeo 2010.
If, switch, while, do-until, for, break, continue
Dichiarazioni
Possono essere una semplice espressione costante o una lista complicata di cicli e condizioni. Gli statements di controllo come IF, WHILE controllano il flusso di esecuzione dei programmi in Octave. Tutti gli statements di controllo iniziano con speciali parole chiave come IF e WHILE per distinguerli dalle espressioni semplici. Molti statements di controllo contengono altri statements; per esempio lo statement if contiene un altro statement che può o non può essere eseguito. Ogni statement di controllo ha un corrispondente end che segue la fine del controllo. Per esempio endif segue la fine dello statement if e endwhile segue la fine dello statement while. La lista degli statements presente fra if o while e il loro corrispondente end è chiamato il corpo dello statement di controllo.
Statement if
Prende le decisioni in octave. Ci sono 3 forme base di if.
Forma più semplice:
>> if (condizione)
>> Body
>> endif
Condizione è un’espressione che controlla cosa fare nel resto dello statement. Il body è eseguito solo se la condizione è vera. La condizione in uno statement if è considerata vera se il suo valore è diverso da zero e falsa se il suo valore è zero. Se la condizione è un vettore o matrice è considerata vera solo se non è vuoto/a e tutti gli elementi sono diversi da zero.
Seconda forma:
>> if (condizione)
>> body
>> else
>> else-body
>> endif
Se Condizione è vera, body viene eseguito altrimenti è eseguito elsebody.
Esempio:
>> if (rem(x,2)= =0)
>> printf (“x is even\n”)
>> else
>> printf (“x is odd\n”)
>> endif
In questo esempio se l’espressione rem (x,2)=0 è vera (quindi x è divisibile per 2), viene eseguito il primo printf altrimenti viene eseguito il secondo printf.
La terza forma di if permette di combinare decisioni multiple in un singolo statement.
Esempio:
>> if (condizione)
>> body
>> elseif (condizione)
>> else-body
>> endif
Si possono inserire un qualsiasi numero di elseif. Ogni condizione è testata a turno e di quella considerata vera viene eseguito il body. Se nessuna condizione è vera e c’è l’else viene eseguito il suo body. Ci può essere solo un else e deve trovarsi nell’ultima parte dello statement. Tra else e if non ci devono essere spazi se no Octave lo tratta come un nuovo if.
Statement switch
Valuta differenti azioni che dipendono dal valore di una variabile. E’ possibile utilizzando l’affermazione if nel seguente modo:
>> if (x= =1)
>> fai_ualcosa( );
>> elseif (x= =2)
>> fai_qualcos’_altro;
>> else
>> fai_qualcosa_diversa;
>> endif
Questo codice può essere molto ingombrante sia da scrivere che da mantenere. Per superare questo problema Octave prevede lo statement switch .
L’esempio sopra diventa:
>> switch (x)
>> case1
>> fai_qualcosa;
>> case 2
>> fai_qualcos’_altro;
>> otherwise
>> fai_qualcosa_diversa;
>> endswitch
Con questo codice la struttura ripetitiva del problema è più esplicita e il codice è più facile da leggere e da mantenere. Anche se x dovesse cambiare nome dovrebbe essere cambiata solo una linea.
La forma generale di switch è:
>> switch espressione
>> case label
>> lista_comandi
>> case label
>> lista_comandi
>>….
>> otherwise
>> lista_comandi
>> endswitch
Dove label può essere qualsiasi espressione.Uno dei vantaggi nell’usare switch invece di If è che le labels possono essere stringhe. Con if nn si può scrivere:
>> if (x= = “stringa”) # non è valido
Con switch invece si può scrivere:
>> switch (x)
>> case “stringa”
>> fai_qualcosa;
>>…..
>> endswitch
Statement while
Nella programmazione un ciclo è una parte di programma che è (o può essere eseguita) 2 o più volte in successione. While è lo statement di ciclo più semplice in Octave. Come con l’if , con while il ciclo viene eseguito fin quando la condizione è vera (valore diverso da zero).
La sua forma è:
>> while (condizione)
>> body
>> endwhile
La prima cosa che fa while è testare la condizione. Se è vera esegue il body. Dopo che l’ha eseguito, la condizione è testata di nuovo e se è ancora vera il body è eseguito di nuovo. Questo processo è eseguito finché la condizione è vera. Se inizialmente la condizione è falsa il body non è mai eseguito.
L’esempio sotto crea una variabile fib che contiene i primi 10 elementi della sequenza di Fibonacci:
>> fib=ones (1,10);
>> i=3;
>> while (i<=10)
>> fib(i)=fib (i-1)+fib(i-2);
>> i++;
>> endwhile
Qui il corpo del ciclo contiene 2 statement. Il ciclo lavora così: prima i è posto uguale a 3. Poi while testa se è minore o uguale a
Statement do-until
E’ simile alchile solo che questo esegue rapidamente lo statement fino a che la condizione non è vera e il test della condizione è alla fine del ciclo, così il corpo del ciclo è sempre eseguito almeno una volta. Come con if la condizione è vera se diversa da zero e falsa se è uguale a zero.
L’espressione di do-until è :
>> do
>> body
>> until (condizione)
Qui il body è uno statement o una lista di statements che sono chiamati corpo del ciclo e la condizione è l’espressione che controlla quante volte il ciclo sarà eseguito.
Questo esempio crea una variabile fib che contiene i primi 10 elementi della sequenza di Fibonacci:
>> fib =ones (1,10);
>> i=2;
>> do
>> i++;
>> fib(i)=fib(i-1)+fib(i-2);
>> until (i= =10)
Statement for
Il for è più utile in quanto può contenere iterazioni di cicli.
La forma generale è:
>> for var=espressione
>> body
>> endfor
Dove body può essere uno statement o una lista di statements, espressione è qualsiasi espressione valida e var può avere diverse forme. Di solito è un nome di variabile semplice o una variabile indicizzata. Se espressione è una struttura, var può anche essere un vettore con 2 elementi. L’assegnazione nel for lavora un po’ diversamente dalle normali assegnazioni in Octave. Invece di assegnare il risultato completo dell’espressione, assegna ogni colonna dell’espressione al var a turno. Se espressione è un range o un vettore riga o uno scalare, il valore di var sarà uno scalare ogni volta che il corpo del ciclo sarà eseguito. Se var è un vettore colonna o una matrice, var sarà un vettore colonna ogni volta che il corpo del ciclo è eseguito.
Il seguente esempio mostra un altro modo per creare un vettore che contenga i primi 10 elementi della sequenza di Fibonacci:
>> fib=ones (1,10);
>> for i=3:10
>> fib(i)=fib(i-1)+fib(i-2);
>> endfor
Questo codice analizza prima l’espressione 3:10, poi produce un range di valori da
Statement break
Si trova dentro i cicli for o while e può essere usato solo nel corpo del ciclo. Il seguente esempio mostra il divisore più piccolo di un numero intero dato e identifica anche i numeri primi:
>> num=103;
>> div=2;
>> while (div*div<=num)
>> if (rem(num,div)= =0)
>> Break;
>> endif
>> div++;
>> if (rem(num,div)= =0)
>> printf(“il più piccolo divisore di %d è %d/n”,num,div)
>> else
>> printf(“%d è prime\n”,num);
>> endif
Quando il resto è zero nel primo while Octave break (interrompe) il ciclo e procede allo statement seguente e il processo continua. Questo è diverso da exit che ferma l’intero programma.
Statement continue
Come break è usato solo nei cicli for e while. Questo statement salta il resto del corpo del ciclo passando all’altro ciclo che inizia subito (invece break salta tutto il ciclo).
Esempio:
>> # stampa gli elementi di un vettore casuale formato da numeri interi
>> # crea un vettore di 10 numeri interi casuali con valori da
>> vec=round(rand(1,10)*100);
>> # stampa ciò che noi vogliamo
>> for x=vec
>> if (rem(x,2) !=0)
>> continue;
>> endif
>> printf(“%d\n”,x);
>> endfor
Se uno degli elementi di vec è un numero dispari questo esempio salta la stampa dell’elemento e ritorna al primo statement nel ciclo.
Statement unwind_protect
Questo statement gestisce le eccezioni.
Forma generale:
>> unwind_protect
>> body
>> unwind_protect_cleanup
>> cleanup
>> end_unwind_protect
Dove nody e cleanup sono entrambi opzionali e possono contenere qualsiasi espressione o commando di Octave. Gli statements in cleanup sono sicuramente eseguiti indipendentemente dall’esito del controllo di body. Questo è utile per proteggere cambiamenti temporanei della variabile globale da possibili errori. Per esempio, il seguente codice mostra la rassegnazione del valore originario alla variabile globale frobnositcate anche se si verifica un errore mentre si esegue l’operazione indicizzata.
>> save_frobnositcate=frobnositcate;
>> unwind_protect
>> frobnositcate=true;
>>….
>> unwind-protect_clenup
>> frobnositcate=save_frobnositcate;
>> end_unwind_protect
Senza unwind_protect il valore di frobnositcate non sarebbe riassegnato se si verificasse un errore mentre si esegue l’operazione indicizzata perchè l’analisi si fermerebbe al punto dell’errore e lo statement riassegnerebbe il valore non eseguito.
Statement try
Questo statement gestisce le eccezioni.
Forma generale:
>> try
>> body
>> catch
>> cleanup
>> end_try_catch
Dove body e cleanup sono entrambi opzionali e possono contenere espressioni e comandi di Octave. Lo statement in cleanup sarà eseguito solo se si verifica un errore in body. Non sarà stampato nessun avviso o messaggio di errore mentre il body eseguito. Se riverifica un errore durante l’esecuzione del corpo, cleanup può usare la funzione lasterr per accedere al testo del messaggio che è stato stampato.
Linee di continuazione
Nel linguaggio Octave molti statments finiscono con un carattere di nuova linea e bisogna dire ad Octave di ignorarle per continuare lo statement da quella linea al testo. Le linee che finiscono con i caratteri “…” o “\” sono unite con la linea seguente prima che siano divise dal decodificatore di Octave.
Per esempio, le linee:
>> x=long_variable_nome
>> +longer_variable_nome\
>> -42
Forma uno statement singolo. Il carattere backslash (\)sulla seconda linea è interpretato come un carattere di continuazione non come un operatore di divisione.
Calcolo di Pi greco con Geogebra
 Questo programma realizzato con Geogebra dà un visualizzazione grafica e numerica del calcolo di Pi greco. Il valore di Pigreco viene calcolato come valore medio tra un poligono regolare circoscritto e uno inscritto a una stessa circonferenza di raggio unitario. Spostando un cursore viene progressivamente aumentato il numero dei lati del poligono migliorando l’accuratezza del calcolo di Pi greco.
Questo programma realizzato con Geogebra dà un visualizzazione grafica e numerica del calcolo di Pi greco. Il valore di Pigreco viene calcolato come valore medio tra un poligono regolare circoscritto e uno inscritto a una stessa circonferenza di raggio unitario. Spostando un cursore viene progressivamente aumentato il numero dei lati del poligono migliorando l’accuratezza del calcolo di Pi greco.
Obbligazioni per ricchi
 Uno dei luoghi comuni della finanza è che bisogna essere ricchi per avere accesso agli investimenti migliori. Lo ripetono quanti corteggiano la gente più danarosa con dovizia di espressioni inglesi (family office, high net worth individual ecc.), mentre poi spesso piazzano gli stessi fondi, gestioni e polizze di qualunque venditore porta a porta. In realtà può capitare addirittura il contrario. www.beppescienza.it
Uno dei luoghi comuni della finanza è che bisogna essere ricchi per avere accesso agli investimenti migliori. Lo ripetono quanti corteggiano la gente più danarosa con dovizia di espressioni inglesi (family office, high net worth individual ecc.), mentre poi spesso piazzano gli stessi fondi, gestioni e polizze di qualunque venditore porta a porta. In realtà può capitare addirittura il contrario. www.beppescienza.it
Infatti la crisi finanziaria del 2008 ha provocato le perdite maggiori proprio ad alcuni detentori di grossi patrimoni, mentre ha sfiorato i piccolissimi investitori. Costoro avevano i loro pochi risparmi sul conto in banca, in Bot o buoni postali e non ci hanno rimesso un euro. Viceversa hanno perso anche l’80% i possessori di alcuni fondi hedge, che poveracci proprio non sono, essendo previsti per essi versamenti minimi di 500 mila euro o dollari a testa.
Bocconi grossi. C’è però una fattispecie, forse l’unica, dove effettivamente un piccolo risparmiatore è svantaggiato. Si sta infatti diffondendo la moda di emettere obbligazioni acquistabili solo a partire da 50 mila euro o dollari e magari anche più.
Esempio eclatante è quello della Fiat. Ha due obbligazioni che scadono nel 2011, ma quella accessibile anche con qualche migliaia di euro rende solo il 3,6% lordo, mentre chi ne può investire cinquantamila ottiene il 4,8%. Analogo discorso vale per le Mediobanca o le Monte dei Paschi di Siena con scadenza 2015-2016, come mostra la tabella:
Codice ISIN – nome del titolo – taglio minimo
XS0253995368 FIAT FINANCE AND TRADE 5,625% 15/11/2011 € 50.000
XS0442431564 FIAT FINANCE AND TRADE 9% 30/07/2012 € 50.000
XS0129648621 FIAT FINANCE AND TRADE 6,75% 25/05/2011 € 1.000
XS0416215910 ASSICURAZIONI GENERALI 4,875% 11/11/2014 € 50.000
XS0218569962 GENERALI FINANCE BV 3,875% 06/05/2015 € 10.000
XS0242820586 MEDIOBANCA 3,75% 02/02/2016 € 50.000
XS0003877278 MEDIOBANCA 2,5% step coupon 29/07/2015 € 1.000
XS0210918123 MONTE DEI PASCHI SIENA 3,875% 02/02/2015 € 1.000
XS0255820804 MONTE DEI PASCHI SIENA 4,875% 31/05/2016 € 50.000
XS0376189857 STEEL CAP (SEVERSTAL) 9,75% 29/07/2013 $100.000
XS0190490606 STEEL CAP (SEVERSTAL) 9,25% 19/04/2014 $2.000
XS0203714802 TERNA 4,25% 28/10/2014 € 50.000
XS0193945655 ATLANTIA 5,875% 9/6/2024 € 100.000
XS0254095663 LOTTOMATICA 8,25%31/3/2066 CALL 2016 € 50.000
scarica la tabella completa
A scanso di equivoci ricordiamo che per il reddito fisso ci si esprime sempre in termini di valore nominale, per cui la somma effettivamente investita è più o meno maggiore con quotazioni sopra a 100 e inferiore nel caso contrario.
Di alcune società poi esistono solo titoli con pezzature grosse. È il caso di Terna, la proprietaria della rete elettrica italiana, e ciò vale pure per il suo prestito reale, uno dei pochissimi indicizzati a lungo termine all’inflazione nostrana e non europea.
Addirittura sconcertante è il caso della società autostradale Atlantia, che lo stesso giorno che emetteva un titolo da 100 mila euro (e ne ha emessi solo così) usciva con un’obbligazione in sterline con taglio da mille. Come dire? Porte aperte per i piccoli risparmiatori britannici e un limite elevato invece per quelli nostrani.
Il senso di tali comportamenti, per fortuna per ora solo di una minoranza di emittenti, è poco chiaro. La cosa potrebbe aver senso tutt’al più all’emissione per ragioni di praticità, ma allora basterebbe imitare la compagnia di viaggi tedesca Tui, che nel 2004 offrì un’obbligazione settennale a partire da 50 mila euro, prevedendone però la successiva libera trattazione a tagli da mille.
Sono perplessità condivise anche da un accorto gestore obbligazionario, qual è Marco Vinciguerra, che appunto osserva che “normalmente un investitore istituzionale fa acquisti nell’ordine dei milioni di euro o dollari e quindi non gli importa nulla di quale sia il lotto minimo di un titolo”.
Ma la cosa che più sconcerta è per molte di queste obbligazioni vale un regola davvero strana: il quantitativo trattato è infatti 50 mila ma sono possibili incrementi di mille (euro o dollari). Così addirittura, per esempio con le Italease 23-11-2010 a tasso variabile, uno potrebbe comprarne 56 mila, rivenderne poi 50 mila e trovarsi così ad averne seimila, per altro invendibili. Sembra quasi un giochetto.
Titoli di stato. Abbiamo visto i comportamenti di alcune società per azioni. Cosa fanno invece gli stati? Di regola emettono titoli con tagli accessibili praticamente a qualsiasi risparmiatore. Così per le Oat francesi, comprese quelle agganciate all’inflazione, il taglio minimo è addirittura un euro. È solo la Borsa Italiana che l’ha portato a 5 mila euro.
I titoli medio-lunghi dello Stato italiano (Btp, Cct ecc.) si possono comprare a multipli di mille euro e i buoni fruttiferi postali sono emessi addirittura a partire da 50 euro.
Diverso invece il caso dell’Iraq. Chi vuole puntare sulla ripresa o almeno la sopravvivenza del martoriato paese del Vicino Oriente ha a disposizione solo un titolo da 250 mila dollari, che per la cronaca valeva 66 dollari nel 2007 e ne vale ora 75, con una redditività a scadenza (2028) dell’8,5% lordo.
Articolo pubblicato su: La Repubblica, 23-11-2009, Affari & Finanza, p. 23
La più grande soddisfazione non è la conoscenza, ma il processo dell’apprendimento [Gauss]
 "La più grande soddisfazione non è la conoscenza, ma il processo dell’apprendimento, non il possesso del sapere ma il processo per raggiungerlo". Carl Gauss (1777, 1855)
"La più grande soddisfazione non è la conoscenza, ma il processo dell’apprendimento, non il possesso del sapere ma il processo per raggiungerlo". Carl Gauss (1777, 1855)
Il maestro aveva dato ai ragazzi (di circa 9 anni) un problema: sommare tutti i numeri da 1 a 60 invitandoli a portargli la soluzione non appena avessero la avessero calcolata. Pochi minuti dopo il piccolo Carl salta su, corre al tavolo e consegna la soluzione: 1+2+…+59 + 60 = 1830.
Come mai? Come ha fatto il monello? Sapeva già a memoria la soluzione?
Quando, dopo molto tempo, tutti avevano consegnato il compito, Carl, interrogato dal maestro su come avesse fatto, disse con semplicità di aver scritto mentalmente uno sotto l’altro il numero più alto e il numero più basso, poi il successivo più alto e il successivo più basso, e così via sino al termine, calcolando infine i totali di tutte le coppie che valevano sempre 61:
basso: 1 2 3 … 29 30
alto: 60 59 58 … 32 31
Totale: 61 61 61 …61 61
moltiplicare a mente 30×61 era poi stato facile poiché: 3×6 = 18 quindi 61×3 = 183 e 183×10 = 1830.
In generale la formula per sommare i primi n numeri naturali (caso particolare di progressione aritmetica) è: $n/2 * (n+1)$.
Il Princeps Mathematicorum, come poi venne chiamato, divenne anche un campione oltre che della matematica pura anche di quella applicata ed in special modo della geodesia, della fisica e dell’astronomia.
Gauss, le cui capacità di calcolo ricordano nel passato quelle di Archimede e nel futuro quelle di Von Neumann, non aveva alcun bisogno di aiuti esterni per calcolare le cose più difficoltose e complicate: i sistemi di equazioni lineari, le equazioni di grado n-esimo (a lui è dovuto il teorema fondamentale dell’algebra), i numeri e le variabili complesse, gli spazi curvi, gli integrali, le congruenze, le distribuzioni di probabilità, ecc.
Scoprì prima di ogni altro le geometrie non euclidee, ma non pubblicò nulla nel timore, come lui stesso disse, di suscitare le strida dei beoti.
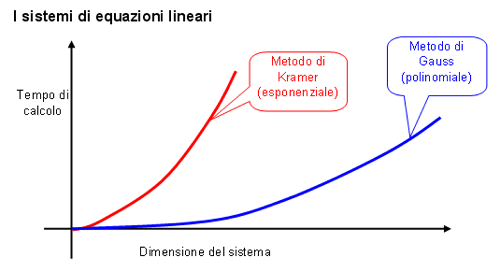
Disporre di algoritmi efficienti per risolvere i sistemi di equazioni lineari è fondamentale per affrontare problemi tecnici, economici, aziendali, di ricerca pura e di ricerca applicata. Ancora oggi nelle scuole molti insegnano il metodo di Cramer senza ricordare che la sua validità è puramente didattica e che l’applicabilità pratica è ridotta ai sistemi che abbiano meno di 10 equazioni in 10 incognite. Se programmassimo l’algoritmo di Cramer e quello di Gauss su un calcolatore in grado di eseguire un milione di operazioni significative (moltiplicazioni e divisioni) al secondo, il metodo di Cramer impiegherebbe più di un milione e mezzo di anni per risolvere un sistema di sole 20 equazioni in 20 incognite, mentre il metodo di Gauss impiegherebbe circa un centesimo di secondo. Se poi il sistema è costituito da 50 equazioni il tempo trascorso dall’origine dell’universo ad oggi non sarebbe sufficiente per calcolare la soluzione col metodo di Cramer (né in tempo utile concluderebbe l’operazione un computer capace di 1000 miliardi di operazioni al secondo), mentre il metodo di Gauss fornirebbe il risultato in meno di due decimi di secondo.
Gli errori di misura piccoli (sia positivi che negativi) sono più probabili degli errori di misura elevati; questa considerazione porta alla curva di distribuzione di Gauss (curva normale o curva a campana per la prima volta descritta da de Moivre nel 1733). La distribuzione di Gauss gode di una importante proprietà (teorema del limite centrale): se si ha un fenomeno casuale che dipende dalla somma di più variabili casuali (in genere ne bastano 10 o 12) allora il fenomeno totale ha una distribuzione di probabilità che tende alla curva di Gauss al crescere del numero delle variabili e indipendentemente dalla forma delle distribuzioni componenti.
In natura moltissime grandezze (dall’altezza delle persone, alla velocità delle molecole nei gas, al quoziente intellettivo, ecc.) seguono una curva di Gauss. Le curve a campana, che hanno degli asintoti che precipitano esponenzialmente verso lo zero, ci sono familiari e tendiamo ad usarle spesso, magari a sproposito come nella stima delle variazioni di prezzo dei titoli di borsa.
Negli ultimi anni B. Mandelbrot ed altri hanno mostrato che in finanza, come in altri sistemi complessi, gli eventi casuali non seguono le curve di Gauss, ma delle leggi di potenza che decrescono molto più lentamente dando luogo a degli eventi rari, i famosi cigni neri, molto più frequenti di quanto previsto con la curva normale di Gauss.
Se si hanno diverse osservazioni di uno stesso fenomeno, il valore x che minimizza i quadrati degli scarti delle varie osservazioni è dato dalla media aritmetica delle osservazioni stesse. Il metodo dei minimi quadrati consente di costruire rette e curve utili per interpolare ed extrapolare dai dati disponibili funzioni incognite.
La curva di Gauss ed il metodo dei minimi quadrati sono tra gli strumenti statistici e di calcolo delle probabilità più utilizzati per risolvere i problemi aziendali: dalla produzione al marketing, dalla qualità all’analisi del rischio, dall’analisi delle serie storiche alla pianificazione strategica.
"Come esprimerle la mia ammirazione e il mio stupore nel vedere il mio stimato corrispondente signor Le Blanc trasformarsi in un personaggio che dà un esempio così luminoso di ciò che io stenterei a credere. Il gusto per le scienze astratte, in generale, e per i misteri dei numeri, in particolare, e rarissimo: ma non è questo il motivo del mio stupore. Il fascino incantevole di questa scienza sublime si rivela solo a coloro che hanno il coraggio di immergersi nel suo studio. Ma quando una persona del sesso che, secondo i nostri costumi e pregiudizi, deve incontrare difficoltà infinitamente superiori a quelle degli uomini nel familiarizzare con queste scabrose ricerche, riesce nondimeno a sormontare gli ostacoli e a penetrare le parti più oscure della materia, allora senza dubbio ella deve possedere il coraggio più elevato, talenti straordinari e un genio superiore. Niente potrebbe in maniera altrettanto lusinghiera e inequivocabile fornirmi la prova che le attrattive di questa scienza, che ha arricchito la mia vita di gioie così numerose, non sono chimere quanto la predilezione di cui voi l’avete onorata." Lettera di Gauss alla matematica Sophie Germain.
Sophie Germain ebbe intense corrispondenze scientifiche con i maggiori matematici del suo tempo tra cui Lagrange, Legendre e Gauss, ma temendo di creare imbarazzo nei suoi corrispondenti, i quali avrebbero guardato con sospetto una "donna matematica", aveva creato il suo pseudonimo maschile: Monsieur Le Blanc. Le sue lettere ricche di problemi risolti ed idee feconde sulla teoria dei numeri, le avevano fatto subito guadagnare la stima del grande Gauss. Nel 1837, in occasione della celebrazione dei cento anni dell’università di Gottinga Gauss ricordava con rammarico Sophie Germain, ormai defunta, e dichiarava: "Ella ha dimostrato che anche una donna può realizzare qualcosa d’importante nella più rigorosa ed astratta delle scienze e per questa ragione avrebbe meritato una laurea ad honorem". L’aver riconosciuto le capacità di avere idee feconde e risolvere problemi da parte della metà della popolazione le cui capacità intellettuali erano all’epoca sistematicamente sottovalutate, fu certamente uno dei tanti meriti di Carl Friedrich Gauss.
Uno scudo a costo zero
 Il contribuente onesto ignora i problemi dell’evasore non consumista. Per il suo opposto, cioè l’evasore spendaccione, le cose sono molto più semplici. Deve solo riuscire a farsi pagare in contanti o ricorrere a teste di legno per incassare gli eventuali assegni. Ma poi sono infiniti i modi per spendere senza tante preoccupazioni i soldi incassati in nero: meretrici di lusso, gioielli, mobili antichi, viaggi in capo al mondo. www.beppescienza.it
Il contribuente onesto ignora i problemi dell’evasore non consumista. Per il suo opposto, cioè l’evasore spendaccione, le cose sono molto più semplici. Deve solo riuscire a farsi pagare in contanti o ricorrere a teste di legno per incassare gli eventuali assegni. Ma poi sono infiniti i modi per spendere senza tante preoccupazioni i soldi incassati in nero: meretrici di lusso, gioielli, mobili antichi, viaggi in capo al mondo. www.beppescienza.it
L’evasore parsimonioso ha invece una serie di difficoltà in più, soprattutto se vuole investire in ambito finanziario e non immobiliare, dove tanto quanto può sempre riuscire a pagare una parte in nero. Fino agli anni Ottanta, l’evasore risparmiatore poteva comprare obbligazioni e altri titoli in contanti. Ma con la dematerializzazione degli strumenti finanziari tutto è diventato maledettamente pericoloso. Se versa i soldi in una banca, a una s.i.m. o alla Posta, viene scoperto al primo accertamento fiscale un po’ serio.
Quindi la soluzione ideale è stata (ed è) esportare e investire clandestinamente quanto in paesi compiacenti: Svizzera, principati di Montecarlo e Lichtenstein o altri paradisi fiscali. Peccato che si tratti di località magari amene ma caratterizzate da commissioni esose, anche il quintuplo che in Italia, e gestori ancor più attivi nel saccheggiare i conti dei clienti.
Il ministro Giulio Tremonti, ma in realtà il governo tutto, si è preso a cuore questo problema offrendo il cosiddetto scudo fiscale, che permette il rimpatrio dei capitali a un prezzo modico. Ufficialmente si paga il 5%, che già di per sé sembra scandalosamente poco, visto che in alcuni casi è stato evaso oltre il 50% fra imposte e contributi vari. Eppure in realtà, approfittando delle pieghe della legge (e di qualche furbizia aggiuntiva) è possibile pagare molto meno.
Risparmiare sullo scudo. Prendiamo uno che abbia soldi nascosti all’estero, ragionando per semplicità su un milione di euro tondo. Un sempliciotto penserebbe che dovrà comunque scucire 50 mila euro per riportarli impunemente in Italia. Invece il suo costo finale può essere molto minore e, in alcuni casi limite, addirittura nullo. Vediamo come, rinviando per gli aspetti più tecnici e i dettagli numerici a un file scaricabile dalle mie pagine web all’Università di Torino (www.beppescienza.it).
Per cominciare è consentito prendere a riferimento quanto l’evasore aveva alla fine dell’anno scorso. La formula è un po’ complessa, ma nella sostanza l’aliquota passa ora dal 5% al 5,35% circa. Ciò può essere molto conveniente, perché a fine dicembre le quotazioni erano veramente basse. Quindi non è strano che lo stesso patrimonio valesse allora per esempio 580 mila euro e sia risalito solo nel 2009. Un tale recupero corrisponde esattamente a quello medio delle obbligazioni ad alto rendimento in euro, misurato dall’indice Merrill Lynch Global Bond Euro High Yield. Così l’importo da versare al fisco scende a 31 mila euro, che è poi solo il 3,1% di quanto viene rimpatriato.
Però non è finita. Il nostro contribuente può versare l’imposta dovuta con contanti provenienti da incassi in nero senza correre rischi. Infatti il conto scudato non compare sotto il suo nome nel caso di una normale verifica del fisco nelle banche. Quindi, in un certo senso, l’operazione gli costa la metà rispetto a quanto gli costerebbe se i suoi soldi arrivassero da guadagni dichiarati e tassati. E in questo modo siamo scesi all’1,6%, rispetto a quel già generoso 5% previsto da Tremonti.
Ma c’è anche altro. Con gli investimenti finanziari (azioni, obbligazioni e simili) i guadagni rispetto al prezzo di acquisto sono tassati al 12,5% e le perdite permettono un’ analoga minore imposta. Solo che con lo scudo fiscale siamo nel paese della Cuccagna, perché è lecito non pagare l’imposta sulle plusvalenze, ovvero sui cosiddetti “capital gain”, ma mantenere le minusvalenze per ridurre quanto dovuto in futuro. Per giunta i prezzi di acquisto basta autocertificarli, perché il fisco è galantuomo e si fida ciecamente dei contribuenti.
Così, grazie a tale meccanismo e ai diversi alti e bassi dei mercati negli anni scorsi, può finire che uno “rimpatria” una perdita media del 10-15%, corrispondente a un potenziale credito d’imposta nell’ordine dell’1,5% del patrimonio riportato in Italia. Insomma, basta una discreta ripresa delle quotazioni dei titoli e lo scudo diventa a costo zero.
[Valore dell’indice Merrill Lynch Global Bond Euro High Yield: 92,45 a fine 2008 e 158,35 a fine ottobre 2009; aliquote fiscali per l’esempio di evasione considerato: Irpef 43%, addizionali 2%, Irap 3,9% per complessivi 48,9%.]
Il nostro fortunato evasore – fortunato perché vive in Italia – potrà quindi riprendere a esportare capitali, nell’attesa di un scudo-quater nel 2010 dopo l’attuale, detto anche scudo-ter. Fantasie? Mica tanto, visto che al primo scudo fiscale (2002) ne seguì un altro già l’anno dopo.
La cosa non è stata però denunciata da nessun sindacato, partito o economista dell’opposizione, come pure da nessuna di quelle associazioni di consumatori che pure inveiscono sempre contro tutto e tutti. In compenso sullo scudo-ter si sono lette critiche infondate, come quella rivolta dagli economisti de Lavoce.info. In particolare, Silvia Giannini e Maria Cecilia Guerra hanno scritto (29-9-2009) che esso “non necessariamente servirà a fare tornare i capitali in Italia, perché il rimpatrio è obbligatorio solo se le somme sono presso paradisi fiscali […] In tutti gli altri casi i capitali possono rimanere dove sono. Il gettito raccolto con lo scudo è una tantum e non potrà dunque andare a finanziare interventi permanenti”.
Questo è sbagliato, perché all’Erario spettano le stesse imposte sui capitali “scudati”, sia che rientrino in patria sia che restino presso banche estere. Semmai è vero che il gettito a regime non sarà alto. Ammettendo con un certo ottimismo il rientro di 100 miliardi di euro e una redditività annua del 4%, il fisco italiano incasserà 0,5 miliardi di euro l’anno sui relativi interessi, dividendi e capital gain.
Articolo pubblicato su il Fatto Quotidiano, 4-11-2009 p. 18
Functions e script files
Funzioni e script files
I programmi più complicati di octave possono spesso essere semplificati definendo funzioni.
Le funzioni possono essere definite direttamente sul prompt di comando o in files esterni e possono essere richiamate solo come funzioni già impostate.
Definire funzioni
La forma più semplice è
Function name
Body
endfunction
Un nome di funzioni valido, come per la variabile, può essere una sequenza di lettere, numeri e underscores, ma non iniziare con un numero. Il body è la parte più importante perché dice cosa la funzione effettivamente fa. Normalmente ci stanno delle informazioni sulla funzione e la sintassi per passare i parametri alla funzione è:
function name(arg-list)
body
endfunction
dove arg-list è una lista di argomenti della funzione separati da virgola.
Lo scopo dell’inserimento della funzione è quello di ottenere informazioni di output della funzione definita. La sintassi, per esempio, di una funzione che ritorna un valore è:
function ret-var=nome(arg-list)
body
endfunction
ret-var è il nome della variabile che contiene il valore di output della funzione.
Le variabili usate nel corpo della funzione sono variabili locali.
Valori di output multipli
Al contrario di altri programmi Octave consente di definire funzioni che danno come output più valori. La sintassi è:
function[ret-list]=nome(arg-list)
body
endfunction
dove ret-list è una lista di nomi di variabili separate da una virgola che conterranno il valore di output della funzione. La lista dei valori di output (ret-list in tal caso) deve avere almeno un elemento.
Script files
E’ un file che contiene ogni sequenza dei comandi octave.
Al contrario di un file function non deve iniziare con la parola function. Un’altra differenza sta nel fatto che le variabili richiamate in uno script non sono locali.
E’ possibile definire più di una funzione in uno script files e caricarle (ma non eseguirle) tutte, una per volta.
Salvare file di fuzioni
I file vengono salvati con l’estensione .m, questo per mantenere una compatibilità con la nomenclatura usata da Matlab.
I file possono essere memorizzati in una qualsiasi directory che poi deve essere specificata all’interno di octave. Octave quando incontra una funzione cerca il suo nome in quelle predefinite, nel caso non vengano trovate va a cercarla in file esterni (.m) specificata nella lista di directory all’interno della variabile d’ambiente LOADPATH.
Ad esempio LOADPATH=”:/root/octave” specifica che i file .m si troveranno nella directory “/root/octave” . In caso di più directory queste vengono separate dai due punti (“:”).
Comandi
Sono speciali classi di funzioni.
Un comando può essere chiamato come una funzione ordinaria, ma può anche essere richiamato senza parentesi. Esempio
my_command hello world
equivale a
my_command(“hello”,”world”)
Una funzione può essere usata come comando se accetta stringhe come argomenti di input. Per far ciò, la funzione deve essere definita come un comando, che può essere fatto con il comando “mark_as_command”. Esempio
mark_as_command name
dove name è la funzione che deve essere chiamata come un comando.
Una difficoltà si ha quando le stringhe di argomenti di input sono memorizzate in una variabile.
Siccome octave non può dire la differenza tra il nome di una variabile e una stringa ordinaria, non è possibile passare una variabile come input al comando.
Una interpretazione geometrica della media aritmetica, geometrica, armonica, quadratica
 Una breve nota in cui si dà una interpretazione geometrica delle principali medie all’interno di un semicerchio: la media aritmetica è uguale al raggio della semicirconferenza, La media geometrica è uguale alla lunghezza del segmento CH, la media armonica è uguale alla lunghezza del segmento KC, la media quadratica è uguale alla lunghezza del segmento QH…
Una breve nota in cui si dà una interpretazione geometrica delle principali medie all’interno di un semicerchio: la media aritmetica è uguale al raggio della semicirconferenza, La media geometrica è uguale alla lunghezza del segmento CH, la media armonica è uguale alla lunghezza del segmento KC, la media quadratica è uguale alla lunghezza del segmento QH…
Una notte da Leonidi
 Questa sera (17 novembre 2009) abbiamo un importante appuntamento con lo sciame meteorico delle leonidi, con picco massimo previsto per le 22:50 (ora italiana). Preparate molti desideri da esprimere perché le "stelle cadenti" che vedremo saranno tante. Troverete gli orari dell’evento, ed altri utili consigli sul mio blog Siderus Nuncius. Buon divertimento!
Questa sera (17 novembre 2009) abbiamo un importante appuntamento con lo sciame meteorico delle leonidi, con picco massimo previsto per le 22:50 (ora italiana). Preparate molti desideri da esprimere perché le "stelle cadenti" che vedremo saranno tante. Troverete gli orari dell’evento, ed altri utili consigli sul mio blog Siderus Nuncius. Buon divertimento!
Grafici
Plotting bidimensionale
I comandi di base del plotting sono
>>axes()
>>axes(proprietà, valore, ..)
>>axes(h)
>>plot(args)
Questa funzione produce grafici bidimensionali. Sono possibili diverse combinazioni di argomenti.La più semplice è:
>>plot(y)
Dove l’argomento indica le coordinate x e y prese come indici degli elementi. Per salvare un grafico si usa il comando print. Se c’è più di un argomento è scritto:
>>plot(x,y,fmt,…)
Oppure
>>plot(x,y, proprietà, valore, ….)
Dove x, y, proprietà, valore sono opzionali e può esserci qualsiasi numero di argomenti.
I valori x e y sono interpretati come:
Ø Se c’è un solo argomento le coordinate x e y sono considerate indici di elementi che iniziano con 1;
Ø Se x è un vettore e y una matrice, le colonne (o righe) di y sono rappresentate rispetto a x;
Ø Se y è un vettore e x una matrice, y è rappresentato rispetto alle colonne (o righe) di x;
Ø Se entrambi gli argomenti sono vettori, gli elementi di y sono rappresentati rispetto a quelli di x;
Ø Se entrambi gli argomenti sono matrici le colonne di y sono rappresentate rispetto a quelle di x. In questo caso entrambe le matrici devono avere lo stesso numero di righe e colonne.
Ø Se entrambi gli argomenti sono scalari viene rappresentato un singolo punto.
Grafici tridimensionali
– functionfile: plot3(args)
questa funzione produce grafici tridimensionali. Sono possibili diverse combinazioni di argomenti. La forma più semplice è:
>>plot3(x,y,z)
Dove gli argomenti rappresentano i vertici dei punti disegnati in 3 dimensioni.
Se tutti gli argomenti sono vettori della stessa lunghezza viene rappresentata una singola linea continua. Se sono tutti matrici, ogni colonna della matrice è trattata come una linea separata. Possono essere dati solo due argomenti:
>>plot3(x,c)
Dove le parti reale e immaginaria del secondo argomento sono considerate rispettivamente come le coordinate y e z.
Se è dato un solo argomento:
>>plot3(c)
Dove le parti reali e immaginarie dell’argomento sono considerati rispettivamente come valori y e z.
Per salvare un grafico si usa il comando print.
Per fare il grafico di gruppi di due o un argomento, si separa ciascun gruppo con una stringa vuota:
>>plot3(x1,c1,’’,c2,’’,….)
Manipolare grafici esistenti
–functionfile: axis(limits)
L’argomento “limits”dovrebbe essere un vettore di due, quattro o sei elementi.
Il primo e il secondo elemento indicano i limti inferiore e superiore per l’asse x. Il terzo e il quarto elemento per l’assey. Il quinto e il sesto per l’asse z.
Senza gli argomenti axis assegna in automatico l’ampiezza. Con un argomento x=axis dà gli assi correnti. L’argomento limits è opzionale:possono essere usate stringhe nell’argomento per specificare le varie proprietà degli assi. Esempio:
>>axis([1,2,3,4],“square”);
Annotazioni sul grafico
– functiofile: title(titolo)
crea un titolo
– functionfile: legend(st1,st2)
mette una legenda sul grafico corrente usando le stringhe specificate come etichetta.
Si possono usare strighe indipendenti(st1,st2..), una matrice di stringhe(matstr) o un vettore di stringhe (cell) per specificare la legenda. Per dare il nome agli assi è usato il comando “labels”.
-functionfile: xlabel(string);
-functionfile: ylabel(string)
Stampare il grafico
– functiofile: print(filename,options)
stampa un grafico o lo stampa in un file.
Filename definisce il nome del file da stampare. Se non è specificato nessun file, l’output è stampato.
Relazione finale di tirocinio SSIS: Le equazioni si secondo grado
 All’inizio di ogni lezione ho riassunto gli argomenti della lezione precedente tramite un rapido scambio di battute con il gruppo classe e tramite l’utilizzo di schematizzazioni, così come al termine di ogni lezione ho tracciato un breve riassunto evidenziando le parti più significative degli argomenti trattati. Ho esplicitato le conoscenze e le competenze richieste per ogni porzione di contenuto. Al termine del percorso ho proposto una prova di verifica formativa/sommativa sul raggiungimento degli obiettivi dichiarati. L’argomento va inserito nel secondo quadrimestre di una II Istituto Professionale.
All’inizio di ogni lezione ho riassunto gli argomenti della lezione precedente tramite un rapido scambio di battute con il gruppo classe e tramite l’utilizzo di schematizzazioni, così come al termine di ogni lezione ho tracciato un breve riassunto evidenziando le parti più significative degli argomenti trattati. Ho esplicitato le conoscenze e le competenze richieste per ogni porzione di contenuto. Al termine del percorso ho proposto una prova di verifica formativa/sommativa sul raggiungimento degli obiettivi dichiarati. L’argomento va inserito nel secondo quadrimestre di una II Istituto Professionale.
Unità didattica di Matematica: Le Equazioni di secondo grado
SUDDIVISIONE MACROSCOPICA
SUDDIVISIONE DETTAGLIATA DEI CONTENUTI
CONTENUTO A: Introduzione alle Equazioni di secondo grado
INTRODUZIONE ALLE EQUAZIONI DI SECONDO GRADO
CONTENUTO B: La Risoluzione di un’equazione di secondo grado incompleta
RISOLUZIONE DI UN’EQUAZIONE DI SECONDO GRADO INCOMPLETA PURA
RISOLUZIONE DI UN’EQUAZIONE DI SECONDO GRADO INCOMPLETA SPURIA
RISOLUZIONE DI UN’EQUAZIONE DI SECONDO GRADO INCOMPLETA MONOMIA
CONTENUTO C: La Risoluzione di un’equazione di secondo grado completa
RISOLUZIONE DI UN’EQUAZIONE DI SECONDO GRADO COMPLETA
IL DISCRIMINANTE E LE SOLUZIONI
SCHEMATIZZAZIONE:
CONTENUTO D: Relazioni tra coefficienti e soluzioni e scomposizione di un trinomio di secondo grado
LA RELAZIONE FRA LE RADICI E I COEFFICIENTI DI UN’EQUAZIONE DI SECONDO GRADO
SCOMPOSIZIONE DI UN TRINOMIO DI SECONDO GRADO
LABORATORIO D’INFORMATICA: UTILIZZO DEL FOGLIO DI EXCEL
CONTENUTO E: Verifica
VERIFICA FORMATIVA/SOMMATIVA
ATTIVITÀ DI RECUPERO
RISULTATI DELLA PROVA DI VERIFICA
Bibliografia
Scarica la relazione finale SSIS
Scarica il foglio excel per la risoluzione dell’equazione di II grado
Mercato e liberismo [Adam Smith]
 Non ho mai visto che sia stato raggiunto molto da coloro… che pretendevano di trafficare per il bene pubblico.
Non ho mai visto che sia stato raggiunto molto da coloro… che pretendevano di trafficare per il bene pubblico.
"La causa principale del progresso nelle capacità produttive del lavoro, nonché della maggior parte dell’arte, destrezza e intelligenza con cui il lavoro viene svolto e diretto, sembra sia stata la divisione del lavoro. In genere essa è più spinta nei paesi più industriosi che godono di un più alto livello di civiltà. Questo grande aumento della quantità di lavoro che, a seguito della divisione del lavoro, lo stesso numero di persone riesce a svolgere, è dovuto a tre diverse circostanze:
primo, all’aumento di destrezza di ogni singolo operaio;
secondo, al risparmio del tempo che di solito si perde per passare da una specie di lavoro a un’altra,
e infine all’invenzione di un gran numero di macchine che facilitano e abbreviano il lavoro e permettono a un solo uomo di fare il lavoro di molti.
Gran parte delle macchine di cui si fa uso nelle manifatture in cui il lavoro è suddiviso, furono invenzioni di comuni operai.
Nelle prime macchine a vapore (James Watt era uno scozzese contemporaneo di Smith) un ragazzo era espressamente occupato ad aprire e chiudere alternativamente la comunicazione fra la caldaia e il cilindro, a seconda che il pistone salisse o scendesse. Uno di questi ragazzi, a cui piaceva giocare con i compagni, osservò che, legando un laccio ad un’altra parte della macchina la maniglia della valvola che apriva questa comunicazione, la valvola si sarebbe aperta e chiusa senza bisogno della sua assistenza, lasciandolo libero di divertirsi con i suoi compagni di gioco. Ecco così che uno dei più notevoli perfezionamenti che siano stati apportati a questa macchina fin da quando fu inventata fu la scoperta di un ragazzo che voleva risparmiarsi il lavoro.
Non tutti i perfezionamenti delle macchine, però, sono derivati dalle invenzioni di coloro che le usavano abitualmente. Molti perfezionamenti sono stati realizzati grazie all’ingegnosità dei costruttori di macchine, quando costruirle divenne il contenuto di una professione specifica, e altri dalla ingegnosità dei cosiddetti filosofi o speculativi".
"I monopolisti, mantenendo il mercato continuamente a corto, non soddisfacendo mai pienamente la domanda effettiva, vendono i loro prodotti molto al di sopra del prezzo naturale e fanno salire i propri emolumenti, sia che consistano in salari sia che consistano in profitti, molto al di sopra del loro livello naturale: Il prezzo del monopolio… è in ogni possibile occasione il più alto che si può spremere dal compratore…".
"Non appena i capitali si sono accumulati nelle mani di singole persone alcune di loro li impiegheranno naturalmente nel mettere al lavoro gente operosa, a cui forniranno materiali e mezzi di sussistenza, allo scopo di trarre profitto dalla vendita delle loro opere o da ciò che il loro lavoro aggiunge al valore dei materiali… Il valore che gli operai aggiungono ai materiali si divide dunque in questo caso in due parti, una delle quali paga il loro salario, mentre l’altra paga i profitti di chi li impiega, e ciò in rapporto all’entità del capitale che ha anticipato per i materiali e i salari".
"Non è dalla benevolenza del macellaio, del birraio o del fornaio che ci aspettiamo il nostro desinare, ma dalla considerazione del loro personale interesse. Non ci rivolgiamo alla loro umanità, ma al loro egoismo, e parliamo dei loro vantaggi e mai delle nostre necessità. Ciascun individuo, impiegando il proprio capitale in modo da dare il massimo valore al suo prodotto, mira soltanto al proprio guadagno ed è condotto da una mano invisibile a promuovere un fine che non entrava nelle sue intenzioni… Non ho mai visto che sia stato raggiunto molto da coloro che pretendono di trafficare per il bene pubblico".
"Ogni sistema che cerca… di attirare verso una particolare specie d’industria una parte del capitale della società maggiore di quella parte che vi sarebbe attirata naturalmente… ritarda, anziché accelerare, il progresso della società verso la reale ricchezza e grandezza".
"Quando la quantità di un bene che vien portato al mercato scende sotto il livello della domanda effettiva… il prezzo di mercato salirà… Quando la quantità portata al mercato eccede la richiesta effettiva di un dato bene… il prezzo di mercato scenderà".
"Per quanto egoista si possa ritenere l’uomo, sono nettamente presenti nella sua natura alcuni principi che lo rendono partecipe alle fortune altrui, e che rendono per lui necessaria l’altrui felicità, nonostante da essa egli non ottenga altro che il piacere di contemplarla".
(Adam Smith, Scozia, 1723 – 1790, Ricchezza delle nazioni, Teoria dei sentimenti morali)
l primo pensiero di Smith riporta due espressioni "paesi più industriosi" e "più alto livello di civiltà" che oggi sarebbero considerate da molti offesa al ‘politically correct’ e al ‘relativismo culturale’ imperanti; ma per un buon funzionamento delle organizzazioni, compresa la loro capacità di fronteggiare i problemi, è necessario avere degli obiettivi dichiarati, riconoscere i meriti di chi li ha conseguiti, capire l’importanza della modernità e delle macchine (oggi diremmo della ricerca e della tecnologia) per perseguire l’efficienza e l’efficacia dei processi che implicano una maggiore ricchezza (oggi diremmo valore) per tutti gli attori interessati o comunque coinvolti (stakeholders).
Un altro aspetto interessante di questo pensiero è che Smith individua tre livelli, tutti importanti, in grado di contribuire alla creatività e alla innovazione dei processi e della tecnologia:
1) chi usa e impiega operativamente le macchine
2) chi progetta e costruisce le macchine
3) i filosofi e gli speculativi che si occupano di ricerca operativa, qualità e teoria dei sistemi.
La ricchezza delle nazioni, secondo Smith, dipende da due elementi: il numero di lavoratori produttivi e la produttività di ciascun lavoratore. Nel tempo la produttività aumenta man mano che progredisce la divisione del lavoro (Smith fu il primo a porre in evidenza il fatto che la ricchezza di una nazione, o di una organizzazione aumenta quando individui diversi collaborano specializzandosi nelle diverse attività necessarie alle creazione del prodotto), che è favorita dall’espansione dei mercati, a sua volta legata allo sviluppo economico.
Francesco Daveri, sul Sole-24 Ore del 13 Giugno 2004 scrive: "Fino a diecimila anni fa (se si pensa alla storia del genere umano come ad una giornata di 24 ore, ciò vuol dire: fino a due minuti e mezzo fa !) gli uomini vivevano in piccoli gruppi che basavano il loro sostentamento sulla caccia, sulla pesca e sulla raccolta dei frutti della terra e degli alberi. In quel contesto, la divisione del lavoro necessaria a procurarsi i mezzi per la sussistenza era molto limitata". Sino d’allora sembra però che gli uomini fossero principalmente cacciatori e le donne principalmente raccoglitrici. "Poi è cominciato un grandioso esperimento sociale, in cui la divisione del lavoro è divenuta sempre più pronunciata. Oggi ogni nostro gesto si basa, trae beneficio e qualche volta subisce gli effetti di una divisione dei ruoli e del lavoro tra noi stessi e una miriade di persone che non conosciamo (e che probabilmente non conosceremo mai).
Il primo punto da chiarire è come sia stato possibile arrivare ad un simile stato di cose (di cui la recente ondata di globalizzazione è solo la punta dell’iceberg). Senza peccare eccessivamente di determinismo, ciò deve essere perchè la delega della produzione di beni e servizi a estranei è tipica della società moderna, è socialmente vantaggiosa.
La divisione del lavoro consente, infatti tra l’altro, una più efficace condivisione dei rischi cui le nostre esistenze individuali sono inevitabilmente soggette".
"Nello stesso tempo, come sottolineava Adamo Smith, la divisione del lavoro consente a ognuno di specializzarsi nei compiti che sa fare meglio. Tutto ciò è andato a beneficio dell’efficienza e ha quindi accresciuto la probabilità di sopravvivenza. Ma questo non basta. Per spiegare perchè la divisione del lavoro si è affermata bisogna ricordare che ad essa sono associati non solo vantaggi per la società nel suo complesso, ma anche vantaggi individuali… Per generare i benefici della divisione del lavoro occorre che gli individui si attengano, nei confronti dell’infinita complessità del mondo che li circonda… alla capacità di ognuno di svolgere il proprio compito specifico senza porsi troppe domande escatologiche, come suggerito dal teorema della mano invisibile di Smith".
Oggi molti economisti sono più attenti a come viene suddivisa la torta piuttosto che alla sua dimensione: anche se essa è molto piccola poco importa, l’essenziale è che le parti siano eguali. Per Smith al contrario, l’aspetto più importante è la ricchezza totale, la dimensione della torta, e solo in secondo luogo ci si pone il problema della sua ripartizione (se la dimensione della torta è irrilevante lo sarà pure la sua suddivisione).
Le parti del pensiero di Smith sopra riportati illustrano argomenti cruciali relativi al funzionamento delle organizzazioni: alcuni di questi sono stati mal compresi e fieramente avversati dagli economisti moderni, alcuni sono stati del tutto dimenticati, altri infine vengono ricordati senza che la paternità sia riconosciuta ad il loro autore.
La torre di Hanoi
 La Torre di Hanoi è un rompicapo matematico: inizia con tutti i dischi incolonnati su un paletto in ordine decrescente, dal più grande al più piccolo. Scopo del gioco è portare tutti dischi su un altro paletto, spostando un disco alla volta e senza mettere un disco più grande su un disco più piccolo. Vai al gioco della Torre di Hanoi >>>.
La Torre di Hanoi è un rompicapo matematico: inizia con tutti i dischi incolonnati su un paletto in ordine decrescente, dal più grande al più piccolo. Scopo del gioco è portare tutti dischi su un altro paletto, spostando un disco alla volta e senza mettere un disco più grande su un disco più piccolo. Vai al gioco della Torre di Hanoi >>>.
Se ti picciono questi giochi compra il CD con tutti i giochi logico-matematici >>>.
Quando vediamo un libro, chiediamoci se contiene qualche ragionamento astratto sui numeri [Hume]
 Se ci viene alle mani qualche volume, per esempio di teologia o di metafisica scolastica, domandiamoci: contiene qualche ragionamento astratto sulla quantità o sui numeri? No. Contiene qualche ragionamento sperimentale su questioni di fatto e di esistenza? No. E allora gettiamolo nel fuoco perchè non contiene che sofisticherie ed inganni. David Hume, 1711-1776.
Se ci viene alle mani qualche volume, per esempio di teologia o di metafisica scolastica, domandiamoci: contiene qualche ragionamento astratto sulla quantità o sui numeri? No. Contiene qualche ragionamento sperimentale su questioni di fatto e di esistenza? No. E allora gettiamolo nel fuoco perchè non contiene che sofisticherie ed inganni. David Hume, 1711-1776.
"Come le scienze dell’uomo costituiscono l’unico fondamento per le altre scienze, così la sola base solida per le scienze dell’uomo deve essere l’esperienza e l’osservazione. E non dobbiamo sorprenderci che l’applicazione della filosofia sperimentale alla ricerca morale abbia tardato più di un secolo rispetto alla sua applicazione alle scienze naturali; si tratta infatti dello stesso tratto di tempo che separa l’origine di queste scienze: da Talete a Socrate , infatti, la distanza temporale è quasi equivalente tra il mito Bacone e alcuni filosofi inglesi (Locke, Shaftesbury, Mandeville, Butler, etc.) che hanno iniziato a porre la scienza dell’uomo su di un nuovo livello… Questo dimostra che per quanto le altre nazioni possano rivaleggiare con noi in poesia, e superarci in alcune altre arti dilettevoli, i progressi della ragione e della filosofia non possono che essere raggiunti in una terra di tolleranza e di libertà".
"Io ho di me stesso l’immagine di un uomo, il quale dopo aver cozzato in molti scogli, ed evitato a malapena il naufragio passando in una secca, conservi ancora la temerarietà di mettersi per mare con lo stesso battello sconquassato, con l’intatta ambizione di tentare il giro del mondo nonostante queste disastrose circostanze".
"Mi si potrebbe chiedere se sono sicuramente convinto delle argomentazioni che vado propugnando con tanta fatica e se sono realmente uno di quelli scettici i quali sostengono che tutto è incerto e che in nessuna cosa possiamo giungere a un giudizio attendibile di verità o di falsità: risponderei che la domanda è del tutto superflua e che né io né nessun altro è mai stato sinceramente e a lungo di questa opinione. Per assoluta e inevitabile necessità la natura ci ha costretti a giudicare come a respirare e a sentire… Chiunque si sia preso la pena di confutare i cavilli dello scetticismo totale ha in realtà combattuto senza antagonista… la mia intenzione era soltanto quella di far constatare al lettore la verità della mia ipotesi: che tutti i nostri ragionamenti intorno alle cause e agli effetti derivino da nient’altro che dall’abitudine; e che il credere è più propriamente un atto della parte sensitiva che non della parte cogitativa della nostra natura".
"Da cose che appaiono simili ci aspettiamo effetti simili. Questa è la somma di tutte le nostre conclusioni sperimentali". (David Hume, 1711-1776. Ricerche sull’intelletto umano e sui principi della morale).
I libri non dovrebbero mai essere bruciati, ma Hume vuole mettere in guardia contro il pregiudizio metafisico e antiscientifico. E’ interessante confrontare il passo sopra citato con quello attribuito a Buddha (Non credete a una cosa perchè molti ne parlano…). Anche nelle organizzazioni capita che certe decisioni (investimenti, dismissioni, nuove strategie etc.) siano prese ignorando (o peggio manipolando) dati di fatto ed elaborazioni numeriche: in questo caso non si è fuorviati dalla metafisica, ma da altri interessi che non coincidono con quelli della sopravvivenza e della crescita dell’organizzazione.
Il secondo pensiero pone l’accento sull’insopprimibile ritardo delle scienze dell’uomo, e quindi anche dei problemi delle organizzazioni, rispetto alle scienze della natura: per Hume la ragione umana è schiava delle passioni, ma senza passioni la ragione non potrebbe esistere. La tolleranza e la libertà (filosofia anglosassone), rispetto ad altre arti dilettevoli (filosofia ed arte continentale), sono fucina di idee e stimolo alla realizzazione del cambiamento.
Nei testi sopra riportati, la mente impegnata nella soluzione di problemi, viene rappresentata con la metafora della navigazione; tale metafora, anche se con significati diversi, sarà ripresa nel 1900 dal positivista logico O. Neurath. Wittgenstein con la sua filosofia ha concluso che non esistono problemi filosofici (ma solo linguistici) e pertanto si è trovato nella situazione di colui che "salito a livelli superiori deve gettare la scala di cui si è servito" rimanendo così intrappolato; Hume al contrario ritiene che la sua posizione, agnostica più che scettica, benché indimostrabile come qualunque filosofia, sia l’unico strumento pratico che consente di affrontare con spirito critico e tollerante i problemi reali della vita.
Il quarto pensiero ricorda le difficoltà in cui ricorre lo scetticismo radicale nella soluzione pratica dei problemi. Lo scetticismo non può essere confutato mediante la ragione, e questo asserto comporterà il risveglio di Kant dal sonno dogmatico, ma esso non fornisce alcun appiglio per risolvere le situazioni problematiche (ne lo forniscono le filosofie dei nostri giorni da esso malamente derivate quali il relativismo, il post-modernismo, il pensiero debole ecc.).
David Hume è un lucidissimo critico del principio di causalità (vedi il quinto pensiero) e mette in guardia dal ritenere che successioni temporali di eventi siano necessariamente indizio di connessione causale.
Ad esempio – sostiene Hume – se, non conoscendo i meccanismi interni degli orologi, ascoltiamo un orologio A suonare sistematicamente 5 secondi prima di un orologio B potremmo sospettare che il suono di A sia "causa" dello "effetto" suono di B. In statistica questo effetto è stato chiamato, in tempi molto successivi a Hume, collinearità; è celebre l’esempio che mostrava matematicamente una forte correlazione tra consumi di whisky e calo delle vocazioni religiose.
Nelle organizzazioni il principio di causa ed effetto è fondamentale sia per impostare piani strategici sia per controllare i processi realizzativi (vedi ad esempio i diagrammi causa-effetto o diagrammi a spina di pesce utilizzati nel controllo della qualità).
Come sostiene Hume chiunque ha combattuto contro lo scetticismo totale ha combattuto senza antagonista, quello contro cui il filosofo vuole mettere in guardia, ed il consiglio è prezioso per qualunque organizzazione, è l’uso affrettato e indiscriminato della induzione per inferire da fatti particolari regole generali.
Quasi tutti i filosofi dell’inizio del Settecento, e in particolare Hobbes, Locke e Leibnitz ritenevano che le leggi matematiche, ed in particolare la geometria euclidea, fossero inerenti al progetto dell’universo. L’unica eccezione significativa fu Hume che nel suo Trattato (1739) negò l’esistenza di leggi o successioni necessarie di eventi nell’universo, sostenendo che da queste successioni gli esseri umani erano indotti a concludere che esse si sarebbero sempre ripetute nello stesso modo. La scienza è quindi puramente empirica: in particolare le leggi della geometria euclidea non sono verità fisiche necessarie.
L’influenza di Hume fu storicamente soppiantata dalla risposta data da Kant nella Critica della ragion pura, ma alcuni filosofi posteriori, tra cui Bertrand Russell, ritennero al contrario che il razionalismo di Kant e l’idealismo di Hegel potessero essere confutati con gli argomenti usati da Hume.
Assieme ad A. Smith (vedi), economista scozzese contemporaneo e amico, Hume può essere considerato un antesignano della filosofia culturale ed economica della ‘globalizzazione’; valga per tutti il seguente pensiero da lui scritto nel 1742: "Nulla è più favorevole alla nascita della civiltà e della cultura di un numero di stati indipendenti collegati dal commercio e dalla politica".
Il N.10 completo di Matematicamente.it Magazine
 Il N. 10 di Matematicamente.it Magazine: 115. La cosiddetta Geometria non euclidea di Felix Klein; 116. Curva segmentata; 117. Lo studio dei poliedri con il software libero Cartesio; 118. I teoremi di punto fisso e i film di azione; 119. Il metodo di Gauss per il calcolo della Pasqua; 120. Recensioni.
Il N. 10 di Matematicamente.it Magazine: 115. La cosiddetta Geometria non euclidea di Felix Klein; 116. Curva segmentata; 117. Lo studio dei poliedri con il software libero Cartesio; 118. I teoremi di punto fisso e i film di azione; 119. Il metodo di Gauss per il calcolo della Pasqua; 120. Recensioni.
![]() Scarica da qui la rivista di matematica Matematicamente.it Magazine N.10 Luglio 2009.
Scarica da qui la rivista di matematica Matematicamente.it Magazine N.10 Luglio 2009.
$(root(3)(x^2y)-root(3)(xy^2))^3+(root(3)(xy^2)+root(3)(x^2y))^3$

$root(3)((x^3+y^3)/(x^2+y^2)) : root(4)((x^2-xy+y^2)/(x^4-y^4))
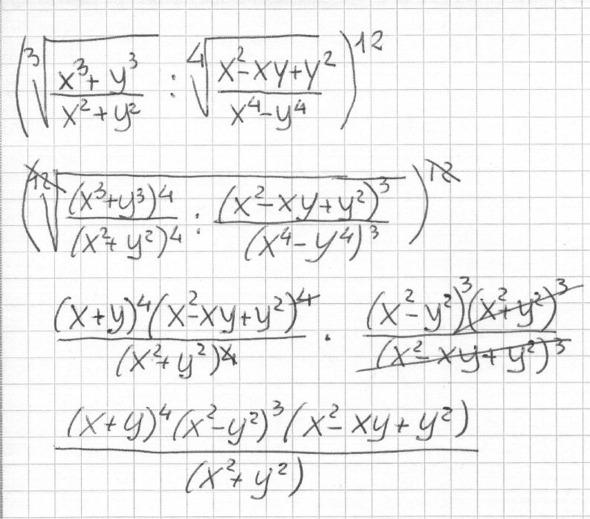
Dati gli insiemi A={x/xè divisore di 12}, B={x/xè divisore di 20}} calcola AUB…

Dati gli insiemi A={x in Z /-7 x 14} e B={…} calcola AUB…
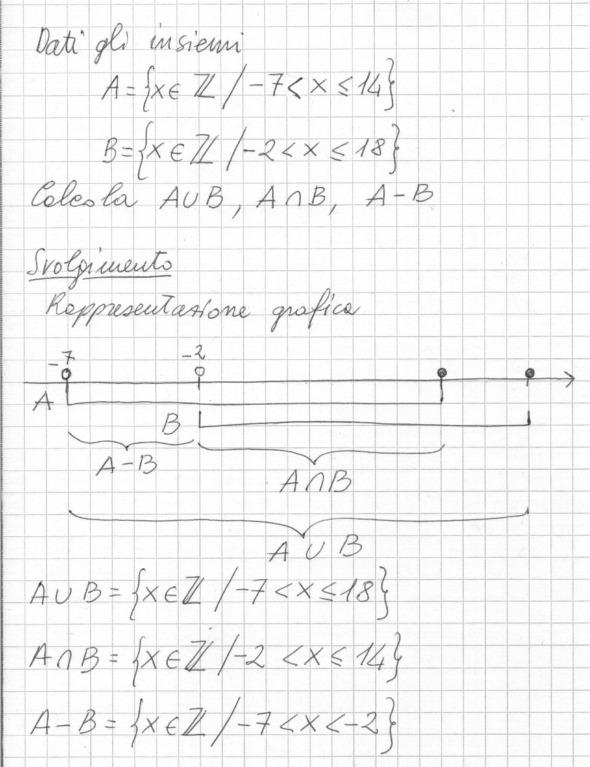
Un foglio Excel per risolvere i Sudoku
 Questo foglio Excel aiuta a risolvere i Sudoku; il file quando viene aperto si presenta con tutte le caselle vuote, man mano che trascrivete i numeri noti del gioco automaticamente nelle altre celle vengono eliminati i numeri che non possono essere inseriti. Quando avete inserito tutti i numeriti noti, le possibilità si ridurranno di molto e man mano compariranno i suggerimenti per risolvere completamente il gioco.
Questo foglio Excel aiuta a risolvere i Sudoku; il file quando viene aperto si presenta con tutte le caselle vuote, man mano che trascrivete i numeri noti del gioco automaticamente nelle altre celle vengono eliminati i numeri che non possono essere inseriti. Quando avete inserito tutti i numeriti noti, le possibilità si ridurranno di molto e man mano compariranno i suggerimenti per risolvere completamente il gioco.
Una ipotesi fittizia può spiegare molti fenomeni [Eulero]
 "E poiché la costruzione dell’universo è perfetta ed è opera di un Creatore di immensa saggezza, nulla in esso ha luogo in cui non compaia qualche legge di massimo o minimo". "Anche se non ci è permesso di penetrare negli intimi misteri della natura per apprendere le vere cause dei fenomeni, può nondimeno accadere che una certa ipotesi fittizia sia sufficiente a spiegare molti fenomeni", Leonhard Euler 1707-1783.
"E poiché la costruzione dell’universo è perfetta ed è opera di un Creatore di immensa saggezza, nulla in esso ha luogo in cui non compaia qualche legge di massimo o minimo". "Anche se non ci è permesso di penetrare negli intimi misteri della natura per apprendere le vere cause dei fenomeni, può nondimeno accadere che una certa ipotesi fittizia sia sufficiente a spiegare molti fenomeni", Leonhard Euler 1707-1783.
"Quando il mio cervello suscita nella mia coscienza la sensazione di un albero o di una casa, io dichiaro, senza esitazione, che un albero o una casa esistono realmente al di fuori di me, e di essi io conosco il luogo, la dimensione e le altre caratteristiche. Pertanto non si trovano né uomini né animali che mettano in dubbio tale verità. Se un contadino potesse concepire di avere tali dubbi e sostenesse, ad esempio, di non credere nell’esistenza del suo controllore e giudice nel momento in cui egli è davanti a lui, sarebbe giustamente preso per pazzo; ma quando un filosofo propone riflessioni di questa natura, egli si aspetta che noi ammiriamo la sua sapienza e la sua sagacia, poiché esse sono infinitamente superiori a quelle della gente comune". (Euler: Lettere a una principessa della Germania: confutazione degli idealisti)
Lo svizzero Leonardo Eulero contende ad Archimede, Newton e Gauss la fama del più grande matematico di tutti i tempi. Certamente i suoi interessi furono vastissimi e spaziano dalla matematica pura a quella applicata, dalla teoria dei numeri, all’analisi infinitesimale al problem solving. Eulero, diversamente da altre persone di genio, fu compreso dai propri contemporanei. Johann Bernoulli in una lettera a lui indirizzata scrisse: "Io presento l’analisi superiore come se essa fosse nella sua fanciullezza, ma voi la state portando alla maturità". Pierre Simon de Laplace ripeteva: "Leggete Euler, leggete Euler, egli è il maestro di noi tutti".
Come matematico si occupo di: serie infinite, geometria differenziale, funzioni complesse, frazioni continue, calcolo delle variazioni, equazioni differenziali, logica degli insiemi, ecc. Come fisico di: propagazione del suono, corde vibranti, natura del calore, canali e opere idrauliche, ingegneria navale, ecc.
Eulero scrisse più di 200 libri e fu certamente il matematico più prolifico in molti rami di questo sapere: ci sono le formule di Euler, i polinomi di Euler, le costanti di Euler, gli integrali euleriani, le rette di Euler, ecc.. Si potrebbe pensare che questo enorme volume di attività escludesse Eulero da qualunque altro interesse nella vita, ma non fu così. Euler si sposò, ebbe tredici figli e fu sempre attento alla sua famiglia e ai suoi bisogni. Educò personalmente figli e nipoti, costruì per loro giochi scientifici e passò molte serate a leggere o riassumere i racconti della Bibbia. Anche se non aveva mai studiato filosofia, e un giorno rimpianse di non averlo fatto, amava esprimere le sue opinioni (vedi ad esempio le Lettere a una principessa della Germania) attirandosi le critiche del terribile Voltaire, che per altro se la prese anche con Leibnitz identificato con il dott. Pangloss afflitto da inguaribile ottimismo.
Un grande contributo di Eulero alla matematica applicata e alla soluzione di problemi fu l’uso di un linguaggio e di una notazione che per molti aspetti corrispondono a quelli usati oggi: nessun matematico, da solo, contribuì in così larga misura come lui, con la felice invenzione di notazioni, a dare alla matematica la forma che essa presenta ancora oggi. Tra i risultati, che hanno anche forte valenza applicativa per le organizzazioni e per l’economia, è da ricordare il concetto e la notazione moderna di funzione [y = f(x1, x2,….)] ed il relativo calcolo dei massimi e minimi impostato in maniera generalizzata e non solo per problemi specifici come avevano fatto Keplero ed altri.
Eulero generalizzò anche il concetto di punti estremi e quello di funzioni estremizzanti dando la prima trattazione sistematica del calcolo delle variazioni. Tra le tecniche di risoluzione dei problemi messe a punto da Euler vi fu lo sviluppo del metodo algoritmico. Esso funzionava in modo tale da ottenere in prima istanza un risultato approssimativo che però poteva essere reinserito nell’algoritmo in modo che risultasse un poco più preciso. Questo secondo risultato poteva essere di nuovo sottoposto all’algoritmo per generare un altro risultato ancora più preciso e così via. Due secoli dopo, con l’avvento dei computer, questo modo di procedere divenne la base per risolvere una vasta classe di problemi di calcolo numerico. 
La teoria dei grafi si classifica come capitolo della topologia, in pratica si tratta (vedi figura) di strutture geometriche in cui un insieme di nodi è collegato da un insieme di archi. Il primo scritto su di essi comparve nel 1736 ad opera di Eulero. Oggi I grafi consentono di modellare e studiare una grande quantità di sistemi (trasporto, assegnazione, flusso, progettazione, produzione, ecc.) e di reti (elettriche, stradali, ferroviarie, aeroportuali, sociali, informatiche, ecc.). Essi costituiscono anche la base delle tecniche reticolari di programmazione dei progetti.
Uno numero primo
 Nella Teoria dei numeri si riscontrano diverse posizioni sulla primalità del numero 1, Guido Carolla presenta alcune delle problematiche che si riscontrano quando si considera 1 numero primo.
Nella Teoria dei numeri si riscontrano diverse posizioni sulla primalità del numero 1, Guido Carolla presenta alcune delle problematiche che si riscontrano quando si considera 1 numero primo.
$root(3)((x^3-2x^2y+xy^2)/(x^2y+2xy^2+y^3))*root(4)((y/x)^3)*sqrt((x^2+xy)/(xy-y^2))*root(12)(y…)

$root(4)((a/b-b/a)(a/b+b/a))*sqrt((ab)/(a^2-b^2))*root(4)(1/b^2-1/a^2)*root(4)((a^2+b^2)/(a^2b^2))$

I Sudoku di ottobre 2009
 24 Sudoku da stampare di diversi livelli, da facilissimi a difficili, in 6 comode pagine da stampare VAI>>>. – Sudoku on line molto facile – Sudoku on line facile – Sudoku on line difficoltà media – Sudoku on line difficile.
24 Sudoku da stampare di diversi livelli, da facilissimi a difficili, in 6 comode pagine da stampare VAI>>>. – Sudoku on line molto facile – Sudoku on line facile – Sudoku on line difficoltà media – Sudoku on line difficile.
I nobel per la fisica
 I premi Nobel per la fisica del 2009 sono stati assegnati a Charles K. Kao "per i fondamentali risultati sulla trasmissione della luce su fibra per la comunicazione ottica" e a Willard S. Boyle e George E. Smith "per l’invenzione del circuito a semiconduttore per i sensori CCD" (Charge-Coupled Device), la tecnologia che si usa per le fotocamere e le videocamere digitali e che trasforma impulsi luminosi in un segnali elettrici. I tre scienziati hanno contribuito a creare le fondamenta dell’attuale società ‘connessa’, hanno creato molte innovazioni pratiche per la vita di tutti i giorni e fornito nuovi strumenti per l’esplorazione scientifica.
I premi Nobel per la fisica del 2009 sono stati assegnati a Charles K. Kao "per i fondamentali risultati sulla trasmissione della luce su fibra per la comunicazione ottica" e a Willard S. Boyle e George E. Smith "per l’invenzione del circuito a semiconduttore per i sensori CCD" (Charge-Coupled Device), la tecnologia che si usa per le fotocamere e le videocamere digitali e che trasforma impulsi luminosi in un segnali elettrici. I tre scienziati hanno contribuito a creare le fondamenta dell’attuale società ‘connessa’, hanno creato molte innovazioni pratiche per la vita di tutti i giorni e fornito nuovi strumenti per l’esplorazione scientifica.
Charles Kuen Kao è nato a Shanghai nel 1933, si è specializzato preso l’Imperial College di Londra, è stato direttore degli Engineering at Standard Telecommunication Laboratories, ad Harlow, in Gran Bretagna e prorettore della Chinese University of Hong Kong. E’ stato il pioniere nell’uso delle fibre ottiche per le telecomunicazioni.
Willard Sterling Boyle è nato nel 1924 in Canadda a Amherst, ha studiato alla McGill University. Ha diretto la divisione di scienze della comunicazione dei Bell Laboratories fino al 1979.
George Elwood Smith è nato nel 1930 a White Plains, nello Stato di New York, ha studiato all’Università di Chicago, è stato direttore della divisione per i circuti integrati VLSI dei Bell Laboratories fino al 1986.
120. Recensioni
Arrigo Amadori, Luca Lussardi, Un’introduzione alla Teoria della Relatività, Aracne editrice, 2009.
Beppe Scienza, Il Risparmio Tradito, Come difendersi da bancari, assicuratori… e giornalisti, Prefazione di Beppe Grillo, Edizioni Libreria Cortina, Torino, 2009.
Calcolo e visualizzazione della traiettoria di un proiettile con il metodo di Schmidth
 Nella prima parte di questa ricerca si vuole trovare un modo per calcolare e visualizzare la traiettoria di un proiettile, con Matlab. Prima di affrontare la parte relativa all’algoritmo e al calcolo numerico, è opportuno richiamare alcuni concetti di balistica, e di fisica, sui quali sarà basata la soluzione del problema.
Nella prima parte di questa ricerca si vuole trovare un modo per calcolare e visualizzare la traiettoria di un proiettile, con Matlab. Prima di affrontare la parte relativa all’algoritmo e al calcolo numerico, è opportuno richiamare alcuni concetti di balistica, e di fisica, sui quali sarà basata la soluzione del problema.
Non ci sarebbe bisogno di discussioni tra due filosofi [Leibnitz]
 Non ci sarebbe bisogno di discussioni tra due filosofi… basterebbe che prendessero in mano le loro matite e si dicessero l’un l’altro: "calcoliamo !".
Non ci sarebbe bisogno di discussioni tra due filosofi… basterebbe che prendessero in mano le loro matite e si dicessero l’un l’altro: "calcoliamo !".
Secondo Leibniz il primo obiettivo della organizzazione delle scienze e delle arti dovrebbe essere di: «produrre abbastanza nutrimento per la nazione al fine […] di migliorare le industrie, di facilitare la sorte della mano d’opera manuale […] attraverso il progresso tecnologico, di rendere sempre ad un prezzo abbordabile le macchine termiche, motore di base dell’ azione meccanica, al fine che tutti possano costantemente sperimentare tutti i tipi di pensieri ed idee innovatrici, proprie a loro stessi e agli altri, senza perdere tempo prezioso.»
G.W. Leibnitz (1646, 1716), La Società e l’Economia
Il suo pensiero economico mosse una critica anticipata a Karl Marx. Secondo Leibniz infatti la ricchezza di una nazione non risiede tanto nelle ore di lavoro incorporate nei beni (e "nel sudore" necessario a produrli), ma piuttosto nella capacità di una nazione di produrre beni per le persone, poiché esse sono la principale ricchezza di una società che consiste nella disponibilità di un capitale umano, di conoscenze e di un’industria manifatturiera in grado di garantire un futuro alla crescita economica. Perciò ogni nazione, secondo Leibniz, dovrebbe investire nell’istruzione e mantenere una propria industria manifatturiera.
"Io penso che mai le controversie possano essere condotte a termine e che mai si può imporre silenzio alle sette se non siamo ricondotti dai ragionamenti complicati ai calcoli semplici, dai vocaboli di significato incerto e vago a caratteri determinati… si deve fare in modo che ogni paralogismo non sia null’altro che un errore di calcolo… Fatto ciò se dovessero sorgere delle controversie, non ci sarebbe bisogno di discussioni tra due filosofi più che tra due contabili. Infatti basterebbe che prendessero in mano le loro matite, sedessero ai loro tavoli e si dicessero l’un l’altro (magari con un amico per testimone, se piacerà loro): calcoliamo." G.W. Leibnitz , De Arte Combinatoria
La speranza di Leibnitz di poter risolvere molti problemi ricorrendo al calcolo e alla logica anticipa di circa tre secoli l’approccio della ricerca operativa (metodi quantitativi e ottimizzazione) alla soluzione dei problemi delle organizzazioni. Certamente Leibnitz non riuscì nel suo intento di fondare una logica nuova nè in quello di ridurre qualunque controversia ad un problema di calcolo tuttavia egli è riconosciuto precursore della logica moderna, fondatore (assieme ad I. Newton) dell’analisi infinitesimale e scopritore, della numerazione binaria (re-inventata due secoli dopo da G. Boole).
Per quanto riguarda la logica è importante l’introduzione del principio di ragion sufficiente per le verità di fatto accanto a quello aristotelico di non contraddizione per le verità di ragione. Nella formulazione più generale (Monadologia, 32) il principio suona così: niente può esistere o accadere, e nessuna proposizione esser vera, senza una ragione sufficiente perchè sia così anziché altrimenti. Leibnitz riconosceva Archimede di Siracusa (vedi) anticipatore del principio per la sua affermazione: "se sui piatti di una bilancia sono posti pesi uguali, non c’è ragione per cui uno si abbassi e l’altro si alzi".
L’analisi infinitesimale ed in particolare le derivate e gli integrali hanno molta più importanza nella soluzione di problemi scientifici e tecnici di quanta ne abbiano nella soluzione dei problemi delle organizzazioni, tuttavia essi sono strumenti di modellazione utili anche in questo campo. Si pensi ad esempio (aziende che lavorano su produzioni di serie) alla produzione di una linea di montaggio (derivata) e allo stoccaggio dei pezzi prodotti in magazzino (integrale), oppure (aziende che lavorano per progetti) allo istogramma di carico delle risorse (derivata) e alla curva ad S progressiva dell’avanzamento fisico (integrale).
Senza entrare nel merito della disputa Leibnitz-Newton sull’analisi infinitesimale è indubbio che, per quanto riguarda la chiarezza della esposizione e la notazione adottata, quella di Lebnitz è sicuramente vincente e tutt’ora adottata (ad esempio: dy/dx = derivata, S allungata = integrale – vedi, nella scheda relativa a Cartesio, un esempio grafico di curva integrale ad ad S).
Leibnitz era molto interessato alla lingua cinese, pensava che la scrittura fosse una lingua sapienziale capace, come i geroglifici egiziani di esprimere i concetti tramite disegni stilizzati. Un missionario della compagnia di Gesù, appena tornato dall’Oriente, gli fece conoscere l’ I Ching il libro dei mutamenti, antichissimo testo cinese, usato come strumento oracolare per la comprensione delle situazioni problematiche. Il filosofo fu affascinato dal sistema di 64 (= $2^6$) esagrammi, ognuno dei quali è composto da sei tratti ciascuno dei quali può rappresentare una linea spezzata o una intera. Attribuendo a questo simbolismo un senso matematico che in origine non aveva affatto, Leibnitz vi scorse un perfetto esempio di progressione di numeri binari (0=0, 1=1, 2=10, 3=11, 4=100, 5=101, 6=110, ecc.). Se si legge la linea spezzata come 0 e la linea intera come 1, gli esagrammi cinesi formano delle sequenze che possono essere lette come numeri.
Leibnitz, che tra l’atro progettò una calcolatrice più evoluta di quella di Pascal, aveva intuito il principio basilare su cui si è sviluppata la moderna rivoluzione informatica, scienza in qualche modo imparentata con quel calcolo del pensiero che sempre andò inseguendo con il nome di "Lingua Combinatoria Universale".
119. Il metodo di Gauss per il calcolo della Pasqua
 La Pasqua è la festività in cui i Cristiani celebrano la crocifissione e resurrezione di Gesù Cristo. Nel Concilio di Nicea, indetto da Costantino nel 325, si stabilì che la Pasqua avrebbe dovuto celebrarsi la prima domenica dopo la prima luna piena che segue l’equinozio di primavera. Da questa semplice regola si sono sviluppati i metodi per il calcolo della data della Domenica di Pasqua compreso quello di Gauss che illustreremo in questo articolo.
La Pasqua è la festività in cui i Cristiani celebrano la crocifissione e resurrezione di Gesù Cristo. Nel Concilio di Nicea, indetto da Costantino nel 325, si stabilì che la Pasqua avrebbe dovuto celebrarsi la prima domenica dopo la prima luna piena che segue l’equinozio di primavera. Da questa semplice regola si sono sviluppati i metodi per il calcolo della data della Domenica di Pasqua compreso quello di Gauss che illustreremo in questo articolo.
$(x-4)/(x+1)+1/(x-3)=2x+28/3$
Verifica scritta, classe I, gennaio 2009,
Calcola la misura dei lati di un rettangolo noto il loro rapporto e il perimetro
Calcola la misura dei lati di un rettangolo sapendo che il loro rapporto è 3/7 e che il perimetro è di 80cm.
Soluzione
Indichiamo con a e b le misure dei lati da trovare.
Dati noti
$a/b=3/7$
$2p=80cm$
Obiettivo
a e b
Svolgimento
$a:b=3:7$
Applicando la proprietà del comporre
$(a+b):a=(3+7):3$
Ricordiamo che a+b è la metà del perimetro, quindi
$a+b=40cm$
Pertanto $40:a=10:3$
$a=(40*3)/10=12$
Per calcolare b utilizziamo la formula
$a+b=40$
da cui
$b=40-a=40-12=28$
Potrebbero interessarti
Videolezione: Le proporzioni
Test su Rapporti e proporzioni
All’apertura del salvadanaio di Sonia si sono contate 700 monete da 1€ e da 2€. Sapendo che il lo…
All’apertura del salvadanaio di Sonia si sono contate 700 monete da 1€ e da 2€. Sapendo che il loro rapporto è di 3 a 2, calcola quante monete da 2€ Sonia deve aggiungere alle monete possedute per avere sei banconote da 200€.
Soluzione
X sia il numero di monete da 1€
Y sia il numero di monete da 2€.
Si sa che sussiste la seguente proporzione:
$X : Y = 3 : 2$
Applicando la proprietà del comporre si ha:
$(x+y):x = (3+2):3$
Poiché tutte le monete sono 700 si ha $x+y=700$
$700:x = 5:3$
$x= (700 * 3)/5 = 2100/5 = 420$
$y=700-420 = 280$
In tutto ha:
$420*1 +280*2 =420+560=980 $
Per orrenere 6 banconote da 200€ deve avere $6*200=1200$
Gli mancano quindi 1200€-980€=220€
In monete da 2€ sono 220:2=110 monete.
Deve quindi aggiungere 110 monete da 2 euro.
I vincitori del Premio Maturità 2009
 I vincitori del Premio Maturità 2009: vincono un Asus Eepc ciascuno:
I vincitori del Premio Maturità 2009: vincono un Asus Eepc ciascuno:
– Francesca Melendez del Liceo Classico di Palermo con la tesina "Il figlio del dolore".
– Daniele Moretto del Liceo Scientifico di Dolo con la tesina "Le galassie a spirale".
– Lorenzo Marelli del Tecnico Industriale di Cesano Maderno con la tesina dal titolo: "Impianto semaforico per utenti non vedenti".
Sono pervenute circa 350 tesine, molte delle quali di ottima fattura; la commissione, dovendo sceglierne solo tre da premiare ha scelto quelle sopra indicate ma ne sono arrivate tante altre degne di merito. Matematicamente.it e Studentville.it ringraziano tutti i partecipanti ed esprimono a tutti i neo-maturati i migliori auguri.
I vincitori del Premio Maturità 2009: vincono un Asus Eepc ciascuno:
– Francesca Melendez del Liceo Classico di Palermo con la tesina "Il figlio del dolore": il lavoro è un contributo originale su una tematica che ha particolare rilevanza nel contesto socio-culturale che in questo periodo storico ci troviamo a vivere e che ci induce a riflettere sulla nostra capacità e volontà di comprendere culture diverse dalla nostra attraverso la condizione dell’essere donna; il tema è affronatato in maniera articolata ed esauriente ed interseca differenti discipline, il punto di forza del lavoro è la capacità critica e l’originalità grafico-espressiva. 
– Daniele Moretto (nella foto a destra con il premio) del Liceo Scientifico di Dolo con la tesina "Le galassie a spirale": il lavoro nasce da uno stage presso l’osservatorio astronomico di Asiago, organizzato dal Dipartimento di Astronomia dell’Università di Padova, per il progetto “Il cielo come Laboratorio”; il progetto prevedeva per gli studenti che avrebbero avuto accesso allo stage, con il superamento di un esame, la realizzazione di una ricerca di astronomia che affrontasse uno specifico problema o argomento a livello quanto più vicino al professionale.
– Lorenzo Marelli del Tecnico Industriale di Cesano Maderno con la tesina dal titolo: "Impianto semaforico per utenti non vedenti": l’idea che è alla base del progetto indica non solo sensibilità alle applicazioni tecnologiche a scopo sociale ma anche capacità inventiva, coerenza e concretezza del progetto rispetto all’obiettivo.
In redazione sono pervenute circa 350 tesine, molte delle quali di ottima fattura; la commissione, dovendo sceglierne solo tre da premiare ha scelto quelle sopra indicate ma ne sono arrivate tante altre degne di merito; per scelta della commissione vengono nominate solo le tre vincitrici del premio. Matematicamente.it e Studentville.it ringraziano tutti i partecipanti ed esprimono a tutti i neo-maturati i migliori auguri.
Ottobre scienza a Torino
 Un viaggio nel mondo delle scienze, mostre, laboratori, conferenze e spettacoli dal 3 al 18 ottobre 2009 a Torino: è la 2° edizione di Ottobre Scienza (inaugurazione venerdì 2 ottobre alle ore 16 presso il Museo Regionale di Scienze Naturali).
Un viaggio nel mondo delle scienze, mostre, laboratori, conferenze e spettacoli dal 3 al 18 ottobre 2009 a Torino: è la 2° edizione di Ottobre Scienza (inaugurazione venerdì 2 ottobre alle ore 16 presso il Museo Regionale di Scienze Naturali).
Fisica, Geometria, ma anche Astronomia, Sport e Arte: dal 3 al 18 ottobre Torino apre le porte alla seconda edizione di «Ottobre Scienza», il grande evento che unisce esperti dell’ambito e appassionati, invitandoli ad intraprendere un affascinante viaggio alla scoperta delle discipline scientifiche. Decine di esperimenti dal vivo, mostre interattive, conferenze e laboratori animeranno le sale del Museo di Scienze Naturali e del Ce.Se.Di (Centro Servizi Didattici della Provincia), nonché del L.S. Copernico di Torino e dell’I.I.S Maxwell di Nichelino, mentre al Collegio San Giuseppe sarà in scena lo spettacolo teatrale Fermi tutti.
Nata nel 2007 grazie al lavoro congiunto di studenti e professori provenienti da trenta scuole della provincia del capoluogo piemontese, la manifestazione è il momento conclusivo dell’attività di raccolta e rielaborazione del ricco patrimonio di idee presente negli istituti. E proprio al loro interno, durante tutto l’anno scolastico, vengono concepite e realizzate mostre e laboratori che gli studenti stessi presentano al grande pubblico, insieme ad animatori specializzati.
Il progetto di coinvolgere insegnanti e giovani delle scuole superiori nel lavoro creativo di ideazione delle esibizioni nasce dalla convinzione che possano diventare protagonisti nel panorama della divulgazione scientifica. L’offerta di una formazione di alto livello è anche un’occasione per stimolare nei ragazzi un’ulteriore motivazione ad intraprendere studi in tale ambito e, più in generale, un interesse da parte di tutti coloro che sono incuriositi dal mondo delle scienze.
L’accesso a tutte le attività è gratuito e garantito previa prenotazione sul sito www.ottobrescienza.it , ad eccezione delle mostre e dei laboratori, per i quali occorre sostenere esclusivamente il costo della guida (3-5€ per i singoli; a partire da 30€ per i gruppi organizzati).
La precedente edizione di «Ottobre Scienza» ha visto la partecipazione di oltre 5000 studenti e il grande entusiasmo suscitato tra i visitatori ha fatto aumentare notevolmente le richieste di altri insegnanti ed istituti di partecipare in modo più attivo alla realizzazione di questi eventi.
I LABORATORI
Fisica del quotidiano: indagine nel caos elettromagnetico Lampadine che galleggiano nel vuoto, dischi levitanti e freni invisibili sono alcuni dei fenomeni elettromagnetici davanti ai quali si troveranno le classi e il pubblico che parteciperà a questo laboratorio. L’attività è strutturata come un’indagine scientifica in cui il pubblico, con l’aiuto dell’animatore, cercherà di mettere un pò d’ordine in una quantità di fenomeni elettromagnetici apparentemente slegati tra loro, come farebbe un investigatore della polizia, alla ricerca di un collegamento tra indizi apparentemente inutili o scorrelati.
.::Rivolto a: scuole elementari, medie inferiori e superiori.
.::A cura di: Corso di Studi in Fisica dell’Università di Torino, attraverso il progetto Lauree Scientifiche, in collaborazione con INFN Sezione di Torino e Associazione Officine Scienza
.::Dove: Museo Regionale di Scienze Naturali di Torino
Una famiglia interessante di luoghi geometrici Quanti luoghi geometrici possiamo realizzare avendo a disposizione due punti fissi e una costante? Dall’asse di un segmento, alla "Circonferenza di Apollonio", agli "Ovali di Cassini" questo laboratorio guida gli studenti alla costruzione di alcuni luoghi noti e altri meno noti, sia al computer sia utilizzando macchine matematiche progettate per l’occasione.
.::Rivolto a: scuole medie superiori
.::A cura di: liceo A. Moro di Rivarolo
.::Dove: CESEDI di Torino
LO SPETTACOLO
Fermi tutti a cura del liceo scientifico P. Gobetti di Torino Ispirandoci alla lettura del libro "Atomi in famiglia" di Laura Fermi e alla visione del film "I ragazzi di via Panisperna" di Gianni Amelio, abbiamo deciso di realizzare questo spettacolo il cui obiettivo è presentare la fisica in un modo piuttosto inusuale. Infatti non ci addentreremo in un insieme di regole e formule teoriche, ma, attraverso le parole di Laura Fermi, racconteremo anche la storia della prima metà del XX secolo, la vita familiare, le difficoltà, le soddisfazioni, il disagio di uomini che hanno posto le basi della fisica attuale. Ma FERMI TUTTI…proporremo anche alcune riflessioni sulle finalità della ricerca scientifica. Esiste un’etica alla quale è possibile riferirsi? Sarebbe, infatti, utile avere un’ "etica universale dell’uomo"… ma saremo mai in grado di elaborarla?
.:: Quando: 15 ottobre 2009 – ore 21.00. 16 ottobre 2009 – ore 11.00.
.:: Dove: Collegio San Giuseppe – Via San Francesco da Paola, 23 – Torino
LE MOSTRE
Lo sport nella scienza e nell’arte È possibile coniugare l’analisi di un gesto atletico con la comprensione di un fenomeno fisico o con le emozioni trasmesse da un’opera d’arte? Cercheremo di farlo con la mostra Lo sport nella scienza e nell’arte. Mostreremo da dove nasce il movimento, scopriremo le leggi che governano il moto dei corpi anche attraverso l’osservazione di tuffi, acrobazie sul ghiaccio o evoluzioni in aria di atleti di diverse discipline sportive. Ci concentreremo sul segreto dell’equilibrio: scopriremo come può un equilibrista camminare su un filo, giocheremo con il nostro stesso baricentro e con alcuni simpatici oggetti che sembrano non voler cadere mai. Partendo dall’analisi del corpo umano, rifletteremo sul rapporto tra cibo ed energia e sulle leggi che governano la circolazione dei fluidi. Scopriremo insieme gli innovativi materiali che stanno rivoluzionando lo sport e che ogni giorno permettono di battere record sempre più ambiziosi. Faremo la conoscenza di Isaac-2, un prototipo di robot alto come un ragazzo di 15-16 anni che sfiderà, nella categoria umanoidi, altri robot come lui nella coppa intercontinentale di calcio per robot che si terrà a Singapore nel 2010.
..::Rivolta a: Scuole elementari, medie inferiori e superiori
..::A cura di: L.C. Gioberti, L.S. Gobetti, L.S. Cattaneo, Collegio Sacra Famiglia, L.S. Faà di Bruno e ITIS Casale di Torino, L.S. Amaldi di Orbassano, Liceo Valdese di Torre Pellice e Liceo Monti di Chieri, Museo Regionale di Scienze Naturali, Accademia di Belle Arti di Torino, il gruppo Isaac-Team del Politecnico di Torino, il SUISM di Torino e la rete di scuole per la RoboCupJunior Italiana
..::Presso il Museo Regionale di Scienze Naturali di Torino
Misure terrestri e misure spaziali Nel 1971, durante la missione Apollo-15, un astronauta lasciò cadere contemporaneamente sul suolo lunare una piuma e un martello e il mondo poté osservare per la prima volta che, come Galileo aveva intuito circa 400 anni prima, questi due oggetti giungevano al suolo nello stesso istante. Ma com’è possibile che esperimenti effettuati sul nostro pianeta possano fornire previsioni attendibili sul comportamento di oggetti così lontani da noi? Lungo il percorso della mostra Misure terrestri e misure spaziali mostreremo come sia possibile ricavare numerose informazioni sui corpi che popolano l’universo (la loro temperatura, età, composizione chimica, …) partendo da misure effettuate sulla Terra o raccogliendo alcune informazioni che pianeti e astri ci inviano sotto forma di onde elettromagnetiche e raggi cosmici. Studieremo poi il fenomeno della gravitazione, dalle valutazioni di Galileo fino alla Relatività Generale di Einstein, per approdare ad una applicazione di tutti questi concetti alla nostra stella, il Sole.
..::Rivolta a: Scuole elementari, medie inferiori e superiori
..::A cura di: L.S. G. Bruno, L.S. Faà di Bruno, L.S. N. Copernico, ITIS Peano di Torino, L.S. M. Curie di Grugliasco, L.C. Porporato di Pinerolo e L.S. E. Fermi di Arona, Museo Regionale di Scienze Naturali, A.I.F., Corso di Studi in Fisica, Centro Astronomico Val Pellice, Osservatorio astronomico di Pino Torinese
..::Presso il Museo Regionale di Scienze Naturali di Torino
C’era una volta… l’equilibrio e il movimento La mostra permetterà di ammirare la bellezza di antiche apparecchiature scolastiche, ancora perfettamente funzionanti, usate dagli studenti di due Licei Classici di Torino tra la fine XIX e l’inizio del XX secolo. Gli strumenti esposti, eleganti nella costruzione e pregiati nei materiali, sono raggruppati in due sezioni: equilibrio, movimento e unità di misura. Scopriremo insieme con quali strumenti venivano spiegate le leggi della dinamica e della statica e come si facesse ad insegnare ai giovani studenti provenienti dalla campagna quanto fosse lungo un metro o quanto fosse voluminoso un litro: un tentativo di insegnare il Sistema Metrico Decimale ai giovani di inizio secolo.
..::Rivolta a: Scuole elementari, medie inferiori e superiori
..::A cura di: L.C. Gioberti di Torino, L.C. Monti di Chieri, Collegio San Giuseppe di Torino
..::Presso il Museo Regionale di Scienze Naturali di Torino
Facciamo le uova "Mi sento che non posso fare l’uovo!" Cosa significa? "Vuol dire che mi trovo in uno stato di tensione misto a scoramento, cerco un modo per superare l’inquietudine ma non riesco a trovare un qualcosa che possa giovare allo scopo." Tutto nasce da questa stravagante affermazione. Chi non ha mai sperimentato su sé stesso questi stati d’animo anche tra i banchi di scuola? E allora, perché non rendere più vivace e piacevole l’attività scolastica, utilizzando la ricerca attiva come metodo per soddisfare le curiosità? La mostra invita il visitatore a provare da sé a “fare le uova” e aprire una finestra su un mondo fatto di giochi, tradizioni, miti, arte e matematica che coinvolge grandi e piccini.
..::Rivolta a: Scuole elementari, medie inferiori e superiori
..::A cura del Liceo A. Moro di Rivarolo e con la collaborazione di alcuni studenti della scuola media Gozzano ed una classe quinta elementari
..::Presso il Museo Regionale di Scienze Naturali di Torino
Acqua, Aria, Æsperimenti e Analogie Cosa vuol dire spiegare un fenomeno? Significa tentare di ricondurre un fenomeno complesso a più fenomeni semplici già noti. Per spiegare i fenomeni fisici sono stati introdotti un numero di termini tecnici di gran lunga superiore al numero di vocaboli utilizzati in un corso di lingua straniera. Navigando tra correnti d’acqua, elettriche e di entropia esploreremo uno dei tentativi più radicali ed efficaci di innovazione didattica nell’insegnamento della fisica di base: il metodo dell’università di Karlsruhe. Parole, illustrazioni ed esperimenti interattivi mostranno la potenza esplicativa di questo linguaggio unificante.
..::Rivolta a: Scuole elementari, medie inferiori e superiori
..::A cura di: Corrado Agnes del Dipartimento di Fisica del Politecnico di Torino e di Angelo Merletti del L. S. Curie di Pinerolo con i suoi studenti del Club della Fisica
..::Presso il Museo Regionale di Scienze Naturali di Torino
I tre problemi classici dell’antichità Il visitatore con in mano una riga non graduata ed un compasso percorrerà un viaggio alla scoperta della geometria così come era studiata da Pitagora ed Euclide, costruendo alcune figure notevoli per poi scontrari con i tre dei problemi geometrici più affascinanti dell’antichità che per più di 1500 anni hanno appassionato i matematici di tutto il mondo: "La quadratura del cerchio", "La trisezione dell’angolo" e "la duplicazione del cubo".
..::Rivolta a: Scuole medie superiori
..::A cura del liceo A. Moro di Rivarolo
..::Presso il CESEDI di Torino
Miti e costellazioni: il planetario, un viaggio tra le stelle La mostra risulta suddivisa in due parti: una parte di argomento astronomico strumentale/letterario, che si articola nell’esposizione di antiche sfere armillari, accompagnate da cartelloni che illustrano la visione del cielo secondo Dante e una parte più spettacolare che si svolge all’interno del Planetario (di Experimenta). Lungo questo percorso verranno mostrati i moti delle Terra e dei pianeti del sistema solare insieme a una descrizione delle principali costellazioni visibili alle nostre latitudini e dei miti ad esse legati.
..::Rivolta a: Scuole elementari, medie inferiori e superiori
..::A cura di: L.S. Copernico, ITIS Peano di Torino, L.C. Porporato di Pinerolo
..::Presso il L.S. N. Copernico di Torino
Educazione al consumo consapevole di acqua ed energia nella giornata "tipo" dello studente La mostra prevede un percorso suddiviso in otto exhibit: i primi quattro consentiranno di sperimentare le differenze che comportamenti diversi determinano nel consumo dell’acqua e illustrano le tecniche di depurazione necessarie connesse con la sua redistribuzione. Gli altri quattro exhibit sono invece dedicati ai consumi energetici e consentono di confrontare il dispendio legato ai diversi comportamenti, attraverso misurazioni dirette.
..::Rivolta a: Scuole elementari, medie inferiori e superiori
..::L’intera iniziativa è nata nell’ambito del Progetto "Scuola del consumo consapevole", patrocinato dalla Regione Piemonte, a cura dell’IIS Maxwell di Nichelino
..:: A cura di: IIS J:C: Maxwell di Nichelino
..::Presso l’IIS Maxwell di Nichelino
LE CONFERENZE
Scienza che nasce dall’esperienza: quando il campo sportivo diventa un laboratorio di robotica
Relatore: ISAAC Team del Politecnico di Torino Lunedì 5 ottobre 2009 – ore 11.00 Museo Regionale di Scienze Naturali di Torino
L’astronomia nell’arte
Relatore: Prof. Piero Galeotti, Dipartimento di Fisica Generale dell’Università di Torino Lunedì 5 ottobre 2009 – ore 21.00 Museo Regionale di Scienze Naturali di Torino
Come funziona il GPS?
Relatore: Ing. Fabio Dovis, Politecnico di Torino Mercoledì 7 ottobre 2009 – ore 11.00. Museo Regionale di Scienze Naturali di Torino
La Bio-Meccanica: strumento al servizio degli Sportivi con Disabilità
Relatori: Sig.ra Tiziana Nasi, Ing. Paolo Marchetti, Interverranno atleti paralimpici Lunedì 12 ottobre 2009 – ore 11.00 Accademia delle Scienze di Torino
La matematica dell’uovo Relatori: Prof.ssa Gemma Gallino, Prof. Giorgio Pidello, Insegnanti Mercoledì 14 ottobre 2009 – ore 9.00 e ore 11.00. Museo Regionale di Scienze Naturali di Torino
Acqua, Aria, Æsperimenti e Analogie Imparare Fisica con le Correnti
Relatori: Prof. Corrado Agnes (Politecnico di Torino), Prof. Angelo Merletti (Insegnante) Giovedì 15 ottobre 2009 – ore 11.00 Museo Regionale di Scienze Naturali di Torino
Matematica e realtà: quinto convegno annuale
 Il Convegno apre il quinto anno del Progetto nazionale Matematica&Realtà. Nel 2008-09 hanno aderito 28 unità locali con 68 laboratori e circa 2000 studenti. L’obiettivo è di offrire l’opportunità di un dibattito costruttivo su proposte di innovazione didattica per sviluppare relazioni con il mondo “reale”. In linea con le tematiche dell’indagine OCSE-PISA, il Progetto si propone di stimolare i ragazzi ad utilizzare le conoscenze e le competenze matematiche acquisite a scuola, per orientarsi nella società e saper gestire le proprie scelte.
Il Convegno apre il quinto anno del Progetto nazionale Matematica&Realtà. Nel 2008-09 hanno aderito 28 unità locali con 68 laboratori e circa 2000 studenti. L’obiettivo è di offrire l’opportunità di un dibattito costruttivo su proposte di innovazione didattica per sviluppare relazioni con il mondo “reale”. In linea con le tematiche dell’indagine OCSE-PISA, il Progetto si propone di stimolare i ragazzi ad utilizzare le conoscenze e le competenze matematiche acquisite a scuola, per orientarsi nella società e saper gestire le proprie scelte.
L’esigenza di un rinnovamento nell’insegnamento-apprendimento della matematica è oggi ampiamente condivisa da tutte le componenti della scuola e dell’università. Alle tradizionali motivazioni interne alla dinamica didattica, principalmente legate alle difficoltà di apprendimento, si stanno aggiungendo e sovrapponendo nuove e pressanti esigenze provenienti dal mondo esterno.
L’attuale società della conoscenza richiede, ad ogni livello, un continuo aggiornamento delle conoscenze e delle competenze individuali. Per affrontare e superare problemi e compiti del quotidiano e svolgere un ruolo consapevole e attivo nella società, è indispensabile saper utilizzare le conoscenze ed abilità apprese a scuola.
La Matematica, in quanto strumento chiave per la descrizione e la comprensione del mondo reale, è una disciplina fortemente coinvolta in questo processo. In particolare, i modelli matematici – che sono la base del metodo scientifico – si stanno diffondendo in tutti gli ambiti, invadendo prepotentemente il nostro quotidiano. Da linguaggio elitario della scienza e della tecnologia, la modellizzazione si è trasformata in un efficace strumento di comunicazione di massa.
Matematica&Realtà (M&R) è un progetto nazionale promosso nel 2005 dal Progetto Innovamatica1, in collaborazione con il Centro PRISTEM2, allo scopo di stimolare una profonda innovazione didattica in Matematica. Rivolto principalmente ai ragazzi dai 13 ai 19 anni, nasce dall’esperienza pluriennale acquisita da Innovamatica in tema di ricerca e sperimentazione didattica3.
Lo spirito con cui M&R si rivolge a Docenti e Studenti è quello di un approccio sperimentale alla Matematica e propone una educazione alla modellizzazione per tutti gli studenti, indipendentemente dalla futura prosecuzione dei loro studi.
In linea con le tematiche dell’indagine OCSE-PISA, si propone di stimolare i ragazzi ad utilizzare le conoscenze e le competenze matematiche acquisite a scuola, per orientarsi nella moderna società della conoscenza e gestire le proprie scelte in modo consapevole e attivo.
![]() Scarica il programma del convegno
Scarica il programma del convegno
![]() Scarica il progetto Matematica e realtà
Scarica il progetto Matematica e realtà
In un triangolo rettangolo la somma e la differenza fra i cateti misurano rispettivamente 52cm e…
In un triangolo rettangolo la somma e la differenza fra i cateti misurano rispettivamente 52cm e 16cm. Calcola il perimetro di un triangolo simile sapendo che la sua ipotenusa misura 45cm.
Soluzione
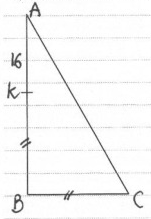 Come prima cosa calcoliamo le lunghezze dei cateti.
Come prima cosa calcoliamo le lunghezze dei cateti.
Sapendo che la loro differenza è di $ 16 cm $, allora togliendo da $ AB $ un segmento $ KB ~= BC $ rimane un segmento $ AK $ di $ 16 cm $.
$ AB + BC $ si compone quindi di un segmento di $ 16 cm $ e di due segmenti pari a $ BC $.
$ 52 cm = bar(AB) + bar(BC) = 16 cm + 2 bar(BC) $, da qui si ottiene:
$ bar(BC) = ( 52 cm – 16 cm) : 2 = 18 cm $
$ bar(AB) = 16 cm + bar(BC) = 16 cm + 18 cm = 34 cm $.
Per mezzo del teorema di Pitagora si ricava $ AC $:
$ bar(AC) = sqrt(bar(AB)^2 + bar(BC)^2) = sqrt(34^2 + 18^2) cm = sqrt(1156+324) cm ~~ 38.47 cm $
Il perimetro di $ ABC $ è $ 2p(ABC) = 34 cm * 18 cm + 38,47 cm = 90.47 cm$
Per calcolare il perimetro del triangolo simile si scrive la proporzione:
$ 2p(ABC) : AC = 2p(A’B’C’) : A’C’ $
$ 90.47 cm : 38.47 cm = 2p(A’B’C’) : 45 cm $
$ 2p(A’B’C’) = 90.47 / 38.47 cdot 45 cm = 105.83 cm$
La stazione spaziale passa sulle nostre teste
Quattro passaggi della Stazione Spaziale Internazionale sopra le nostre teste nei prossimi quattro giorni. Tutti e quattro i passaggi sono in senso longitudinale alla nostra Penisola, quindi le condizioni di visibilità saranno favorevoli per tutti gli italiani, tempo permettendo. Di seguito l’elenco dei passaggi.
, i cui dati (e immagini) provengono dal sito “www.heavens-above.com”:
24 Settembre 2009
Sorge sopra l’orizzonte alle 19:49 in direzione Nord-Ovest E’ 10° sopra l’orizzonte alle 19:51 in direzione Nord-Ovest Massima altezza (58°) alle 19:54 in direzione Nord-Nord-Est Entra nell’ombra alle 19:55 in direzione Est La luminosita sarà di magnitudine -3,2.
25 Settembre 2009
Sorge sopra l’orizzonte alle 20:13 in direzione Ovest-Nord-Ovest E’ 10° sopra l’orizzonte alle 20:15 in direzione Ovest-Nord-Ovest Massima altezza (35°) alle 20:18 in direzione Sud-Ovest Entra nell’ombra alle 20:19 in direzione Sud-Ovest La luminosita sarà di magnitudine -2,1.
26 Settembre 2009
Sorge sopra l’orizzonte alle 19:02 in direzione Nord-Ovest E’ 10° sopra l’orizzonte alle 19:04 in direzione Nord-Ovest Massima altezza (61°) alle 19:07 in direzione Nord-Est Entra nell’ombra alle 19:10 in direzione Est-Sud-Est La luminosita sarà di magnitudine -3,3.
27 Settembre 2009
Sorge sopra l’orizzonte alle 19:27 in direzione Ovest-Nord-Ovest E’ 10° sopra l’orizzonte alle 19:29 in direzione Ovest-Nord-Ovest Massima altezza (34°) alle 19:32 in direzione Sud-Ovest Entra nell’ombra alle 19:34 in direzione Sud-Sud-Est La luminosita sarà di magnitudine -1,9.
Tutti gli orari sono riportati nella nostra Ora Locale, ma sono riferiti al mio Parco di Salve (LE). Tuttavia, con buona approssimazione, sono validi per tutta la nostra Penisola.
Nelle mappe riportate sopra potete vedere le traiettorie della ISS, le parti tratteggiate si riferiscono al suo ingresso nell’ombra terrestre, quindi in quel tratto la stazione spaziale, pur essendo sopra di noi, non si potra vedere. Ci tengo a sottolineare la particolare luminosità di questi passaggi, soprattutto quelli del 24 e del 26 che con una magnitudine rispettivamente di -3,2 e -3,3 porterà la Stazione spaziale ad essere l’oggetto più luminoso del cielo, addirittura più luminoso di Giove (mag. -2,75) ben visibile in tutte queste sere.
Vi ricordo che, se volete, potrete cimentarvi in qualche semplice foto per riprendere la “strisciata” dei vari passaggi.
Se volete condividere le vostre foto inviatele a [email protected]
Buona visione !
