Luca Francesca ha intervistato Luca Lussardi sul nuovo libro scritto con Arrigo Amadori su un’introduzione alla teoria della relatività; un libro pensato per studenti universitari.
Luca Francesca ha intervistato Luca Lussardi sul nuovo libro scritto con Arrigo Amadori su un’introduzione alla teoria della relatività; un libro pensato per studenti universitari.
Domanda: Relatività, un tema molto interessante e molto attuale. Di solito spiegata alla spicciola e semplificata. Come è nata l’idea di un libro proprio su questo argomento? Qual è lo scopo?
Risposta: Indubbiamente la teoria della relatività è una teoria che viene spesso spiegata in modo troppo semplicistico e a volte fuorviante. Il nostro obiettivo, con questo libro, è proprio quello di presentare una possibile semplice introduzione alla teoria della relatività che non fosse troppo pesante dal punto di vista tecnico ma che allo stesso tempo fornisse un valido fondamento di pensiero a tutti coloro che vogliono conoscere le basi di questa importantissima parte della fisica moderna. L’idea di scrivere un testo di introduzione alla teoria della relatività è nata dagli interessi comuni tra Arrigo e me, lui per la teoria della relatività, io per la geometria differenziale, la quale fornisce il linguaggio geometrico naturale della fisica. Speriamo di dare un valido supporto a tutti coloro che si aspettano una lettura scorrevole, semplice ma ricca di spunti notevoli di approfondimento.
Domanda: Il lettore tipo a cui consigliereste il libro.
Risposta: Il nostro testo potrebbe essere utilizzato come supporto ad un corso universitario di relatività per studenti di matematica o fisica. Il lettore tipo è quindi uno studente universitario, ma non solo: chiunque abbia una buona conoscenza dell’analisi in dimensione finita può intraprendere la lettura del nostro lavoro.
Domanda: Tu sei un matematico e Arrigo Amadori un fisico. Quanto di matematico è suo e quanto di fisico tuo… insomma come vi siete spartiti i compiti?
Risposta: La matematica e la fisica sono intimamente collegate tra loro, nessuna delle due potrebbe esistere senza l’altra, almeno nella forma in cui le conosciamo oggi. Scrivere un libro di fisica vuol quindi dire anche scrivere un libro di matematica. La stesura del testo è stata interamente un lavoro di collaborazione; va da sé che il formalismo matematico è stato più curato da me mentre la parte fisico-concettuale è stata più curata da Arrigo, ma in generale si può parlare di contributo diviso esattamente in parti uguali in ogni parte del testo.
Domanda: I requisiti che ritieni fondamentali per la corretta comprensione del libro quali sono? E quali altri letture consiglieresti per completare?
Risposta: Una buona conoscenza dell’analisi matematica in dimensione finita e possibilmente una discreta conoscenza dei fondamenti della meccanica analitica. Per completare il lavoro uno può approfondire come vuole; potrebbe approfondire la parte di relatività continuando su testi moderni e molto più specialistici di fisica teorica, oppure potrebbe anche studiarsi la geometria differenziale nella veste in cui oggi viene classicamente presentata, ovvero con uno stile molto più moderno e astratto rispetto a quello utilizzato nel nostro testo.
Domandda: E ora una domanda tecnica. L’ introduzione dei tensori secondo la loro formulazione originale e non quella “moderna”. Quali sono le motivazioni dietro a una tale scelta?
Risposta: Questa domanda me l’aspettavo, e credo che sia uno dei “punti di forza” del nostro trattato. Il calcolo tensoriale è nato ai primi del Novecento, per opera di matematici italiani come Ricci Curbastro e Levi Civita, ed è nato in un contesto puramente geometrico-differenziale. E’ affascinate e stupefacente come poi tale teoria sia diventata il fondamento matematico su cui Einstein appoggiò poi la teoria della relatività generale. Il calcolo tensoriale si è poi evoluto durante gli anni e oggi viene presentato, in genere, sotto un aspetto molto più algebrico e astratto. Quello che secondo noi però viene a mancare oggi è il giusto raccordo tra l’astrazione matematica della geometria riemanniana e il vecchio calcolo tensoriale “alla Levi-Civita”, fatto sporcandosi le mani con le coordinate locali. Soprattutto in vista della teoria della relatività sarebbe necessario riprendere sempre in mano i conti “dei vecchi” (leggi dei saggi) i quali alla fin fine aiutano davvero a capire dove sta l’idea e il concetto fondamentale. Per tutto questo devo ringraziare Bruno Bigolin, professore ordinario di Geometria presso l’Università Cattolica di Brescia, mio maestro di Geometria.
Domanda: Da quali fonti avete attinto per la stesura?
Risposta: Per quanto riguarda la parte di relatività ristretta e generale la fonte principale è stata “Lev Davidovic Landau e Evgenij Mihajlovic Lifsic, Teoria dei campi, Editori riuniti, Roma 1999”, mentre per quanto riguarda la parte più teorico-matematica il riferimento essenziale è stato “Tullio Levi Civita, Lezioni di Calcolo Differenziale assoluto, trad. di E. Persico, Stock editore, Roma 1925”. Vari altri testi possono essere utlizzati allo scopo nostro, altri riferimenti si trovano nella Bibliografia.
Domanda: Che tipo di apprezzamento vi aspettate e quale invece è la critica più temuta?
Risposta: Partiamo dal fondo: la critica che temo di ppiù è quella di essere stato troppo carente, riduttivo e semplicistico nella parte del formalismo matematico, sia nella parte di calcolo tensoriale sia lungo la parte “fisica” del trattato. Forse questa critica mi potrebbe essere mossa da un matematico che si aspetta un testo di teoria della relatività che contenga il calcolo tensoriale come oggi viene presentato, e in questo punto la nostra scelta è stata invece di altro tipo. L’apprezzamento che più ci farebbe piacere avere sarebbe quello di persone che capiscono e diventano padroni dei fondamenti concettuali della teoria stessa: non ha importanza che uno con il nostro libro capisca alla perfezione la teoria della relatività, anche perché forniamo solo un’introduzione alla teoria stessa; quello che vorremmo è invece che le persone che leggono con cura il nostro testo possano comprendere la base concettuale su cui eventualmente poi sviluppare lo studio e l’approfondimento di parti e sottoparti della teoria stessa più moderne.
Domanda: I punti forti del vostro libro sono chiarezza di esposizione e semplicità. Non temete di semplificare troppo?
Risposta: E’ una paura fondata per quanto riguarda l’apparato matematico dato al testo, però in matematica si fa sempre a tempo a rendere rigorose le cose. La cosa importante è che uno capisca il concetto, l’idea che sta dietro ad una teoria, perché funziona un approccio invece di un altro. Questo aspetto della teoria della relatività noi lo abbiamo curato nel dettaglio. Se poi uno è desideroso di ampliare e approfondire astraendo anche la conoscenza matematica necessaria lo può fare avendo una solida base concettuale di partenza.
Domanda: Molto interessanti i codici Php in coda. Di chi è stata l’idea?
Risposta: L’idea qui è completamente unilaterale, ed è di Arrigo. Ho trovato anche io molto interessante la cosa, soprattutto perché molto spesso cimentarsi nei conti di calcolo tensoriale “a mano” può essere davvero noioso e potrebbe far perdere il filo del ragionamento.
Ancora un ringraziamento a Luca (e anche ad Arrigo) per il suo tempo e per l’interessantissimo libro che mi sento di consigliare e che ho inserito nella mia libreria personale.
 Dialogo tra due personaggi di un film americano (ma vanno bene anche certi cartoni animati giapponesi!) colonna sonora potrebbe essere Sonne, dei Rammstein. Ma non me non importa niente. Io me ne sto nascosto dietro un bidone di benzina, a temere per la mia vita. Trattengo il respiro e assaporo quelli che potrebbero essere i miei ultimi istanti. Loro sono in due. Lei: la pupa con il bazooka. Lui: tipo tranquillo vestito da impiegato che tanto tranquillo non è…
Dialogo tra due personaggi di un film americano (ma vanno bene anche certi cartoni animati giapponesi!) colonna sonora potrebbe essere Sonne, dei Rammstein. Ma non me non importa niente. Io me ne sto nascosto dietro un bidone di benzina, a temere per la mia vita. Trattengo il respiro e assaporo quelli che potrebbero essere i miei ultimi istanti. Loro sono in due. Lei: la pupa con il bazooka. Lui: tipo tranquillo vestito da impiegato che tanto tranquillo non è… 
 Cartesio è un software libero che permette la costruzione e la manipolazione di poliedri, favorisce l’esplorazione degli effetti prodotti dalle trasformazioni geometriche sulle figure solide. Il programma è essenzialmente rivolto agli studenti degli ultimi anni della scuola superiore e dei primi anni dell’università, ma può essere utilizzato anche nella scuola del primo ciclo e nel biennio della secondaria per attività didattiche coinvolgenti.
Cartesio è un software libero che permette la costruzione e la manipolazione di poliedri, favorisce l’esplorazione degli effetti prodotti dalle trasformazioni geometriche sulle figure solide. Il programma è essenzialmente rivolto agli studenti degli ultimi anni della scuola superiore e dei primi anni dell’università, ma può essere utilizzato anche nella scuola del primo ciclo e nel biennio della secondaria per attività didattiche coinvolgenti.  Il matematico e teologo inglese Thomas Bayes (1702-1761) introdusse l’uso induttivo della probabilità e gettò le basi dell’inferenza statistica nel saggio: Sulla soluzione di un problema relativo alla dottrina del caso, che fu pubblicato pubblicato postumo nel 1763.
Il matematico e teologo inglese Thomas Bayes (1702-1761) introdusse l’uso induttivo della probabilità e gettò le basi dell’inferenza statistica nel saggio: Sulla soluzione di un problema relativo alla dottrina del caso, che fu pubblicato pubblicato postumo nel 1763. 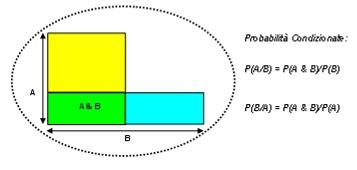 In figura le probabilità condizionate ed il teorema di Bayes sono illustrate con l’aiuto dei diagrammi di Eulero – Venn.
In figura le probabilità condizionate ed il teorema di Bayes sono illustrate con l’aiuto dei diagrammi di Eulero – Venn.  Bisogna scorgere la cosa con un solo sguardo, tutta in una volta, e non per processo di ragionamenti, almeno sino ad un certo limite. E’ così raro che i geometri siano spiriti fini e che gli spiriti fini siano geometri: infatti i geometri pretendono trattare geometricamente queste cose fini e si rendono ridicoli, volendo cominciare con le definizioni e farvi seguire i principi, che non è proprio la maniera di condursi in questo genere di ragionamenti". Blaise Pascal (1623-1662), Pensieri: Spirito di geometria e spirito di finezza.
Bisogna scorgere la cosa con un solo sguardo, tutta in una volta, e non per processo di ragionamenti, almeno sino ad un certo limite. E’ così raro che i geometri siano spiriti fini e che gli spiriti fini siano geometri: infatti i geometri pretendono trattare geometricamente queste cose fini e si rendono ridicoli, volendo cominciare con le definizioni e farvi seguire i principi, che non è proprio la maniera di condursi in questo genere di ragionamenti". Blaise Pascal (1623-1662), Pensieri: Spirito di geometria e spirito di finezza.  Luca Francesca ha intervistato Luca Lussardi sul nuovo libro scritto con Arrigo Amadori su un’introduzione alla teoria della relatività; un libro pensato per studenti universitari.
Luca Francesca ha intervistato Luca Lussardi sul nuovo libro scritto con Arrigo Amadori su un’introduzione alla teoria della relatività; un libro pensato per studenti universitari.  Da un mio lavoro di ricerca di nuove funzioni che ha per titolo "Alcune curve e superfici di famiglie di segmenti" ho scelto una curva denominata: "rete intrecciata a maglia rombica". Per la ricerca del suo diagramma e delle sue equazioni (funzione a cinque parametri e a due variabili) utilizzo le traslazioni di assi e le simmetrie. Per partire è necessario introdurre una funzione ausiliaria il cui studio darà origine alla curva, nella quale poi si praticheranno le suddette operazioni. Una volta determinate le equazioni della "rete intrecciata a maglia rombica", la loro rappresentazione nel piano cartesiano avviene per segmenti.
Da un mio lavoro di ricerca di nuove funzioni che ha per titolo "Alcune curve e superfici di famiglie di segmenti" ho scelto una curva denominata: "rete intrecciata a maglia rombica". Per la ricerca del suo diagramma e delle sue equazioni (funzione a cinque parametri e a due variabili) utilizzo le traslazioni di assi e le simmetrie. Per partire è necessario introdurre una funzione ausiliaria il cui studio darà origine alla curva, nella quale poi si praticheranno le suddette operazioni. Una volta determinate le equazioni della "rete intrecciata a maglia rombica", la loro rappresentazione nel piano cartesiano avviene per segmenti.  La traduzione italiana di Ueber die sogenannte Nicht-Euklidische Geometrie, memoria presentata alla Società Reale delle Scienze di Gottinga, pubblicata il 30 agosto 1871. Si tratta della prima memoria di F.Klein sulle geometrie non euclidee; l’autore conclude il proprio saggio con "Esistono solo tre casi in cui questi piani sono immaginari […]: 1. La superficie fondamentale è immaginaria. In questo caso la geometria è ellittica. 2. La superficie fondamentale è reale, non rigata e ci racchiude. È l’ipotesi della geometria iperbolica. 3. La superficie fondamentale è degenerata in una curva immaginaria. È l’ipotesi della usuale geometria parabolica."
La traduzione italiana di Ueber die sogenannte Nicht-Euklidische Geometrie, memoria presentata alla Società Reale delle Scienze di Gottinga, pubblicata il 30 agosto 1871. Si tratta della prima memoria di F.Klein sulle geometrie non euclidee; l’autore conclude il proprio saggio con "Esistono solo tre casi in cui questi piani sono immaginari […]: 1. La superficie fondamentale è immaginaria. In questo caso la geometria è ellittica. 2. La superficie fondamentale è reale, non rigata e ci racchiude. È l’ipotesi della geometria iperbolica. 3. La superficie fondamentale è degenerata in una curva immaginaria. È l’ipotesi della usuale geometria parabolica."  Luigino mette ordine tra i suoi animaletti di plastica. Hai tre minuti di tempo per cliccare di volta in volta sull’oggetto più pesante. Attenzione scegli l’oggetto più pesante solo in base alle indicazioni delle bilance, non ti fare confondere dalla grandezza dell’oggetto: una farfalla può essere più pesante di un elefantino.
Luigino mette ordine tra i suoi animaletti di plastica. Hai tre minuti di tempo per cliccare di volta in volta sull’oggetto più pesante. Attenzione scegli l’oggetto più pesante solo in base alle indicazioni delle bilance, non ti fare confondere dalla grandezza dell’oggetto: una farfalla può essere più pesante di un elefantino.  "Volendo risolvere qualche problema si deve fin da principio considerarlo come già risolto, e assegnare una lettera ad ogni linea che si ritiene necessaria per costruirlo, sia a quelle che non sono note, sia alle altre. Poi senza far nessuna differenza tra quelle note e le incognite, bisogna svolgere il problema seguendo quell’ordine che più naturalmente di ogni altro mostra in qual modo le rette dipendono mutuamente le une dalle altre, fino a che non si sia riusciti a trovare il procedimento per esprimere una stessa quantità in due modi, fino cioè a che non si sia pervenuti a ciò che si chiama Equazione". René Descartes (1596-1650). La Geométrie.
"Volendo risolvere qualche problema si deve fin da principio considerarlo come già risolto, e assegnare una lettera ad ogni linea che si ritiene necessaria per costruirlo, sia a quelle che non sono note, sia alle altre. Poi senza far nessuna differenza tra quelle note e le incognite, bisogna svolgere il problema seguendo quell’ordine che più naturalmente di ogni altro mostra in qual modo le rette dipendono mutuamente le une dalle altre, fino a che non si sia riusciti a trovare il procedimento per esprimere una stessa quantità in due modi, fino cioè a che non si sia pervenuti a ciò che si chiama Equazione". René Descartes (1596-1650). La Geométrie. 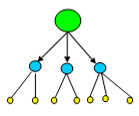 Dopo il dubbio sistematico la seconda regola è quella di scomporre ogni problema in sottoproblemi più semplici. Questo principio di modularità che procede per scomposizione gerarchica è fondamentale in ogni tipo di organizzazione basti citare: gli organigrammi societari, la distinta base nelle aziende di produzione di serie, i diagrammi causa effetto nel controllo della qualità, le strutture di disaggregazione dei costi, la work breakdown structure nelle aziende operanti per progetto, le strutture di descrizione dei rischi.
Dopo il dubbio sistematico la seconda regola è quella di scomporre ogni problema in sottoproblemi più semplici. Questo principio di modularità che procede per scomposizione gerarchica è fondamentale in ogni tipo di organizzazione basti citare: gli organigrammi societari, la distinta base nelle aziende di produzione di serie, i diagrammi causa effetto nel controllo della qualità, le strutture di disaggregazione dei costi, la work breakdown structure nelle aziende operanti per progetto, le strutture di descrizione dei rischi. 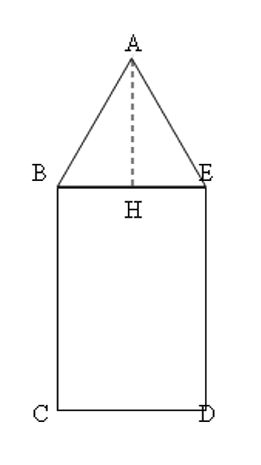 Dati noti
Dati noti  Il software open source eXeLearning è liberamente scaricabile dal sito
Il software open source eXeLearning è liberamente scaricabile dal sito 
 figura 2
figura 2  Figura 3
Figura 3 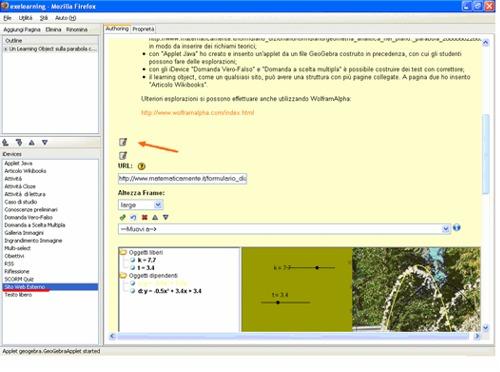 Figura4
Figura4 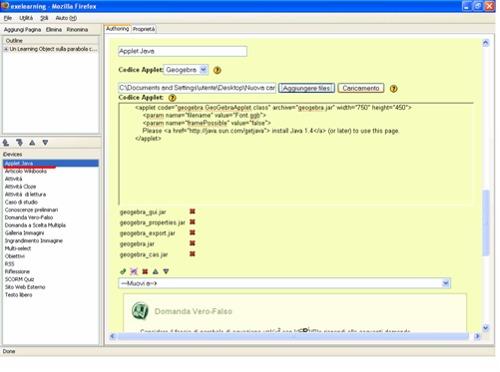 Figura 5
Figura 5 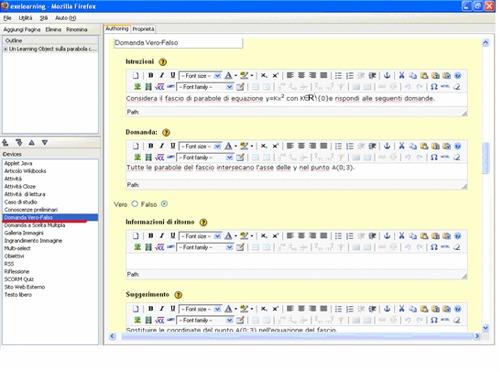 Figura 6
Figura 6 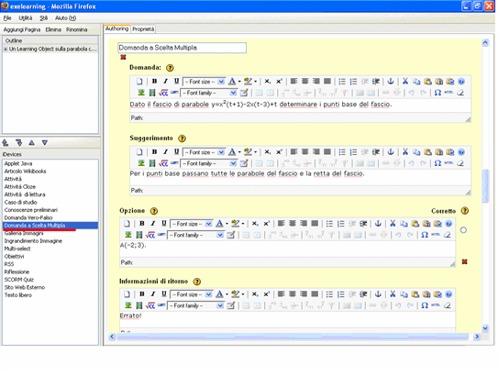 Figura 7
Figura 7 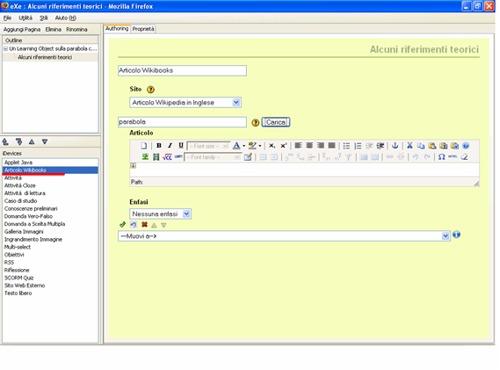 Figura 8
Figura 8 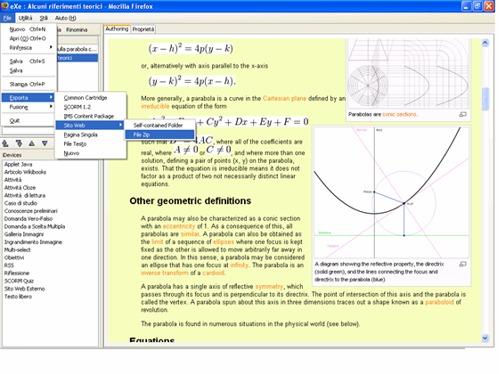 Figura 9
Figura 9  20 sudoku da stampare in pdf
20 sudoku da stampare in pdf Dati noti
Dati noti  Il numero aureo è uno dei personaggi affascinanti e stranamente onnipresenti della Matematica. Trovato direttamente come numero, o riconosciuto come rettangolo aureo o come regola estetica, è sicuramente una presenza tanto importante da non potersi trascurare in ogni discorso sulla efficacia della matematica nella descrizione del mondo . Nella presente di attività la sezione aurea viene usata come stimolatore di interesse verso la Geometria proponendo un’introduzione alla disciplina meno “scolastica” e più motivante.
Il numero aureo è uno dei personaggi affascinanti e stranamente onnipresenti della Matematica. Trovato direttamente come numero, o riconosciuto come rettangolo aureo o come regola estetica, è sicuramente una presenza tanto importante da non potersi trascurare in ogni discorso sulla efficacia della matematica nella descrizione del mondo . Nella presente di attività la sezione aurea viene usata come stimolatore di interesse verso la Geometria proponendo un’introduzione alla disciplina meno “scolastica” e più motivante.  Tesi di laurea triennale in matematica. Lo scopo che ci poniamo in questa tesi è quello di formulare un modello matematico, e una metodologia che permetta la descrizione dell’evoluzione di alcuni tra i più interessanti fenomeni che si presentano in natura. L’equazione che ci accompagna e detta di reazione-diffusione.
Tesi di laurea triennale in matematica. Lo scopo che ci poniamo in questa tesi è quello di formulare un modello matematico, e una metodologia che permetta la descrizione dell’evoluzione di alcuni tra i più interessanti fenomeni che si presentano in natura. L’equazione che ci accompagna e detta di reazione-diffusione.  Lo scopo di queste pagine è quello di dimostrare la formula di Binet per i numeri di Fibonacci facendo uso dell’algebra lineare.
Lo scopo di queste pagine è quello di dimostrare la formula di Binet per i numeri di Fibonacci facendo uso dell’algebra lineare. 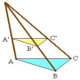 Devo confessare apertamente che non ho mai avuto gusto per lo studio e per la ricerca né in geometria né in fisica se non in quanto esse potevano servirmi come mezzi per arrivare a una qualche sorta di conoscenza delle cause prossime… per il bene e la comodità della vita, nel mantenere la salute, nella pratica di qualche arte… avendo osservato che buona parte delle arti si basa sulla geometria, come fra le altre il taglio delle pietre in architettura, l’arte delle meridiane e in particolare l’arte della prospettiva. (Girarard Desargues (1591-1661), ingegnere e architetto)
Devo confessare apertamente che non ho mai avuto gusto per lo studio e per la ricerca né in geometria né in fisica se non in quanto esse potevano servirmi come mezzi per arrivare a una qualche sorta di conoscenza delle cause prossime… per il bene e la comodità della vita, nel mantenere la salute, nella pratica di qualche arte… avendo osservato che buona parte delle arti si basa sulla geometria, come fra le altre il taglio delle pietre in architettura, l’arte delle meridiane e in particolare l’arte della prospettiva. (Girarard Desargues (1591-1661), ingegnere e architetto) 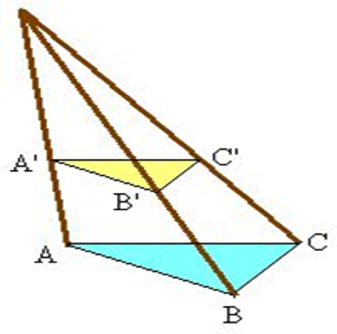 "Devo confessare apertamente che non ho mai avuto gusto per lo studio e per la ricerca né in geometria né in fisica se non in quanto esse potevano servirmi come mezzi per arrivare a una qualche sorta di conoscenza delle cause prossime… per il bene e la comodità della vita, nel mantenere la salute, nella pratica di qualche arte… avendo osservato che buona parte delle arti si basa sulla geometria, come fra le altre il taglio delle pietre in architettura, l’arte delle meridiane e in particolare l’arte della prospettiva.
"Devo confessare apertamente che non ho mai avuto gusto per lo studio e per la ricerca né in geometria né in fisica se non in quanto esse potevano servirmi come mezzi per arrivare a una qualche sorta di conoscenza delle cause prossime… per il bene e la comodità della vita, nel mantenere la salute, nella pratica di qualche arte… avendo osservato che buona parte delle arti si basa sulla geometria, come fra le altre il taglio delle pietre in architettura, l’arte delle meridiane e in particolare l’arte della prospettiva. Obiettivo della seguente raccolta di schede ed esercitazioni è sviluppare la consapevolezza di come sia possibile affrontare problematiche ordinarie attraverso tecniche di problem-solving informatico basate sul foglio elettronico. Destinatari Scuole medie superiori per tutti i corsi che prevedono applicazioni informatiche; Corsi di informatica a vario livello; Corsi universitari di informatica di base; Autodidatti. Le schede sono tratte dal libro di Denis Ruggeri, Foglio elettronico: strategie e pratica.
Obiettivo della seguente raccolta di schede ed esercitazioni è sviluppare la consapevolezza di come sia possibile affrontare problematiche ordinarie attraverso tecniche di problem-solving informatico basate sul foglio elettronico. Destinatari Scuole medie superiori per tutti i corsi che prevedono applicazioni informatiche; Corsi di informatica a vario livello; Corsi universitari di informatica di base; Autodidatti. Le schede sono tratte dal libro di Denis Ruggeri, Foglio elettronico: strategie e pratica.  Antonio Ambrosetti, già docente di Analisi matematica alla Scuola Normale di Pisa, attualmente insegna alla Scuola Internazionale Superiore di Studi Avanzati (SISSA) di Trieste, è socio nazionale dell’Accademia dei Lincei, autore di oltre 130 lavori scientifici: insomma un matematico a tutti gli effetti. Nell’argomentazione della sua tesi questa circostanza è significativa. Il prof. Ambrosetti sostiene di aver intrapreso la stesura di questo libro per contrastare una serie di libri, di tipo filosofico-divulgativo, che pretendono di dare una dimostrazione matematica alla non esistenza di Dio. L’autore si propone insomma di manifestare il suo dissenso contro la presenza dominante di una cultura pseudo-matematica per la quale l’ateismo è il risultato inevitabile e incontrovertibile della razionalità matematica.
Antonio Ambrosetti, già docente di Analisi matematica alla Scuola Normale di Pisa, attualmente insegna alla Scuola Internazionale Superiore di Studi Avanzati (SISSA) di Trieste, è socio nazionale dell’Accademia dei Lincei, autore di oltre 130 lavori scientifici: insomma un matematico a tutti gli effetti. Nell’argomentazione della sua tesi questa circostanza è significativa. Il prof. Ambrosetti sostiene di aver intrapreso la stesura di questo libro per contrastare una serie di libri, di tipo filosofico-divulgativo, che pretendono di dare una dimostrazione matematica alla non esistenza di Dio. L’autore si propone insomma di manifestare il suo dissenso contro la presenza dominante di una cultura pseudo-matematica per la quale l’ateismo è il risultato inevitabile e incontrovertibile della razionalità matematica.