$x^4-16y^4$
Scompongo mediante differenza di quadrati $A^2-B^2=(A+B)(A-B)$
$(x^2-4y^2)(x^2+4y^2)$
$(x-2y)(x+2y)(x^2+4y^2)$
$x^4-16y^4$
Scompongo mediante differenza di quadrati $A^2-B^2=(A+B)(A-B)$
$(x^2-4y^2)(x^2+4y^2)$
$(x-2y)(x+2y)(x^2+4y^2)$
$(2x-y)^2+y^2+2y(2x-y)$
E’ il quadrato di un binomio
$[(2x-y)+y]^2$
$(2x-y+y)^2$
$(2x)^2$
$4x^2$
$4a^2-4/3 ab+1/9 b^2$
E’ il quadrato di un binomio
$(2a-1/3 b)^2$
$7a^2+7ab-4a(a+b)^2-3a(a+b)$
Mediante scomposizione in fattori parziale
$7a(a+b)-4a(a+b)^2-3a(a+b)$
$a(a+b)[7-4(a+b)-3]$
$a(a+b)(4-4a-4b)$
$4a(a+b)(1-a-b)$
$6bx+y^2-3by-2xy+ay-3ab$
Faccio un raccoglimento a fattore comune parziale
Rimetto per comodità in ordine i termini
$6bx-3by-3ab+y^2-2xy+ay$
$-3b(-2x+y+a)+y(y-2x+a)$
$(-2x+y+a)(-3b+y)$
$(a-3b)-2(a-3b)^2-b(3b-a)$
$(a-3b)[1-2(a-3b)+b]$
$(a-3b)[1-2a+6b+b]$
$(a-3b)(1-2a+7b)]$
 Nel 1865, Julius Plücker, professore di matematica e fisica all’Università di Bonn, ha la ventura di trovare fra i propri studenti del primo corso un giovane dotato di eccezionale talento matematico, Felix Klein. Plücker lo fa nominare assistente, quando Klein ha solo diciassette anni.
Nel 1865, Julius Plücker, professore di matematica e fisica all’Università di Bonn, ha la ventura di trovare fra i propri studenti del primo corso un giovane dotato di eccezionale talento matematico, Felix Klein. Plücker lo fa nominare assistente, quando Klein ha solo diciassette anni.
 "I libri contabili dovrebbero venir chiusi ogni anno, specialmente in una società di persone poiché un controllo contabile frequente mantiene l’amicizia."
"I libri contabili dovrebbero venir chiusi ogni anno, specialmente in una società di persone poiché un controllo contabile frequente mantiene l’amicizia."
Luca Pacioli (1445-1517), Summa de Aritmetica et Geometrica, Proportioni et Proportionalita.
Ecco, in sintesi, cosa scrisse (1494) Pacioli nel “Riepilogo ovvero riassunto di tutto il presente Trattato affinché con poca fatica si possano ricordare le cose dette":
1) Tutti i creditori si devono mettere al Libro dalla tua mano destra e tutti i debitori dalla mano sinistra.
2) Tutte le partite che si mettono al Libro debbono essere doppie, cioè se tu fai uno creditore, devi farne uno debitore.
3) Ciascuna partita, a debito o a credito, deve comprendere tre cose: il giorno dell’operazione, la somma e la causa.
4) Il giorno in cui è scritto il debito deve essere il medesimo in cui è scritto il credito.
5) Occorre che il Libro sia sempre tenuto con una stessa moneta, ma dentro le partite, si possono indicare tutte le monete che si presentano: ducati, fiorini, scudi, ecc.
6) Con la moneta con cui hai cominciato il Libro, così bisogna terminarlo.
Queste sono le principale regole del “metodo” applicate e insegnate a Venezia nel secolo XV, probabilmente già dai primi anni del 1400; Pacioli le apprese nel suo primo viaggio a Venezia (1465). Infatti il primo Libro giornale conosciuto è del 1º Gennaio 1431 ed in esso i fatti di gestione sono regolarmente registrati in Partita Doppia.
I ragionieri medievali erano oppressi dalla facilità con cui commettevano errori di registrazione e dalla mancanza di ogni mezzo di controllo. L’idea geniale fu quella di usare questa doppia registrazione (addebiti, accrediti) e poi usare l’uguaglianza debiti = crediti come mezzo di verifica e di correzione degli errori.
Senza dubbio il metodo della Partita Doppia è nato come strumento per evitare il problema degli errori. Due ricordi personali sull’argomento.
Il primo riguarda gli anni di studio all’università (all’epoca la preparazione economica degli ingegneri era molto scarsa): mio padre mi dovette spiegare che Capitale e Utili stanno dalla parte delle passività poiché rappresentano un debito che l’azienda ha con i proprietari/azionisti.
Il secondo riguarda l’impressione che mi fece, iniziando a lavorare (per i ragionieri esistevano allora solo le calcolatrici da tavolo), il vedere che la maggior parte degli straordinari erano dovuti al lavoro degli addetti impegnati in quadrature contabili che richiedevano più tempo di qualunque altro lavoro dell’ufficio. Forse il più grande complimento del nostro secolo a Luca Pacioli, a San Sepolcro (sua città natale) e ai mercanti veneziani, viene da Tom Peters (ingegnere e consulente statunitense) che non ha esitato a definire la "partita doppia" come l’idea manageriale, tra quelle di tutti i tempi, che ha maggiormente contribuito al cambiamento e alla soluzione dei problemi delle organizzazioni.

 Il video corso completo di lezioni di matematica per la scuola secondaria di primo grado. 300micro lezioni di 5 minuti ciascuna su tutti gli argomenti della scuola media: aritmetica, geometria, algebra. Vai alle video lezioni di matematica >>
Il video corso completo di lezioni di matematica per la scuola secondaria di primo grado. 300micro lezioni di 5 minuti ciascuna su tutti gli argomenti della scuola media: aritmetica, geometria, algebra. Vai alle video lezioni di matematica >>
 La costruzione del portfolio non è cosa nuova. Essa risale, almeno come idea, all’antichità, quando gli artigiani che volevano procurarsi un lavoro, mostravano i loro artefatti nella convinzione che proprio attraverso l’esposizione dei prodotti, fosse possibile evidenziare le proprie abilità, il proprio talento, lo stile di lavoro.
La costruzione del portfolio non è cosa nuova. Essa risale, almeno come idea, all’antichità, quando gli artigiani che volevano procurarsi un lavoro, mostravano i loro artefatti nella convinzione che proprio attraverso l’esposizione dei prodotti, fosse possibile evidenziare le proprie abilità, il proprio talento, lo stile di lavoro.
Oggi, come allora, l’assunzione di un nuovo soggetto in un’azienda, sia pubblica che privata, prevede un esame degli artefatti, da parte di esperti, per valutare le competenze nell’ambito del lavoro che si accinge a svolgere. Tale esame può consistere in prove scritte quali test o domande aperte, ma può anche prevedere l’osservazione diretta del soggetto da parte di personale specializzato, attraverso colloqui e/o prove pratiche che può essere arricchita dall’analisi del curriculum esibito.
Nasce così l’esigenza di creare una cartella di presentazione che sia qualcosa di più di un elenco di certificazioni o di dichiarazioni di abilità acquisite. Serve che il soggetto possa disporre di una cartella multisfaccettata con cui egli possa presentarsi valorizzando tutti gli aspetti della sua personalità, senza tralasciare gli hobbies, i gusti, le ambizioni, i desideri. Non solo, ma da un po’ di tempo si sta cercando di inserire anche elementi che evidenzino le capacità trasversali dell’individuo, le cosiddette “soft skills”, che non sono abilità certificabili ma sono importantissime per ottenere risultati soddisfacenti in tutti i lavori. Allora si cerca di “raccontare” la propria predisposizione alla relazionalità, il senso dell’humor, lo charme, il carisma, la capacità di convincimento, la caparbietà, la forza, la resistenza, la dolcezza, la diplomazia…
Nella prima parte di questo elaborato viene effettuata una riflessione sulla validità dell’ePortfolio come strumento educativo e come cartella di presentazione da utilizzare in situazioni lavorative. Segue poi una ricognizione della diffusione dell’ePortfolio nel panorama europeo e mondiale, con particolare riferimento alla situazione italiana.
Nella seconda parte vengono invece esaminati i possibili strumenti per la creazione del portfolio digitale, individuando tra essi, quelli più adatti alla realizzazione di un progetto di ePortfolio nella scuola primaria. Nella terza ed ultima parte viene presentato, nel dettaglio, il progetto di ePortfolio attuato nella classe quarta della scuola a tempo pieno “C. Battisti” di Metato, Pisa. In questa sezione vengono evidenziati gli obiettivi fissati, le fasi di progettazione e attuazione, le scelte metodologiche effettuate.
A testimonianza di quanto realizzato, il lavoro svolto è ampiamente documentato con esempi di pagine prodotte dai bambini che hanno fruito della proposta educativa. Inoltre questa relazione è accompagnata da un cd-rom che contiene tutte le cartelle realizzate dagli alunni della classe quarta, che permette di apprezzare i particolari del lavoro svolto, navigando le pagine di ogni cartella.
Premessa 3
1. Aspetti teorici 4
1.1 Una definizione per il portfolio 4
1.2 Portfolio e educazione 5
1.3 Dal portfolio all’ePortfolio 8
1.4 Vantaggi e criticità dell’ePortfolio 11
1.5 Uno sguardo sul mondo 14
2. Strumenti per attuare l’ePortfolio 18
2.1 Quali strumenti 18
2.2 Vantaggi e svantaggi 19
2.3 Qualche osservazione. 22
3 Attuazione dell’ePortfolio nella scuola primaria: il caso della classe IV di Metato 23
3.1 Perché usare l’ePortfolio nella scuola primaria 23
3.2 Quali strumenti per un progetto di ePortfolio 25
3.3 Dall’idea alla realizzazione 28
3.4 Obiettivi, fasi di progettazione, attuazione, scelte metodologiche 29
3.4.1 Progettazione e obiettivi 29
3.4.2 Fasi di attuazione 30
3.4.3 Motivazioni e riflessioni sulle scelte metodologiche 39
Conclusioni 40
Webliografia
AA.VV. “Il punto su…lifelong learning”, Progetto CDS / Informazione e pubblicità per il FSE dell’ISFOL, Belliscioni, http://www.isfol.it/isfol/dnload/ips_il%20lifelong%20learning.pdf
Barrett H., Blog di discussione, http://electronicportfolios.org/blog/index.html
Commissione Europea, Bruxelles, 2002, “European report on Quality Indicators of lifelong learning. Fifteen Quality Indicators” , ec.europa.eu/education/policies/lll/life/report/quality/report_en.pdf
Commissione Europea, Bruxelles, dicembre 2003, “Implementazione delle strategie di lifelong learning in Europa”, http://ec.europa.eu/education/policies/2010/lll_report/lll_it_it.pdf
Commissione Europea, Bruxelles, maggio 2004, Progetto di ricerca di principi comuni europei per l’individuazione e la convalida dell’apprendimento non formale ed informale, http://ec.europa.eu/education/policies/2010/doc/validation2004_it.pdf
D’Andrea P., “Report sul curriculum vitae europeo” , abstract, http://www.asvi.it/web/Report conclusivo CV Europeo.doc
Flamini E., “Lo sviluppo delle competenze formali, non formali, informali attraverso la rete dei progetti Leonardo”, www.rete.toscana.it/sett/orient/fp/focus/docs/03_pl_miur_ab_i.doc
INDIRE, Seminario Internazionale sul “Lifelong Learning”, Benevento, 2003
Manganello F., ePortfolio Riflessioni e spunti operativi, http://www.slideshare.net/blueflavio/eportfolio-riflessioni-e-spunti-operativi/
“Progetto AlmaTwo”, Università di Bologna, http://almatwo.ei.unibo.it/wp-content/elab-D41_v1_1.pdf
Varanini F., Formato europeo per il Curriculum Vitae http://www.bloom.it/vara91.htm
Wikipedia, “Lifelong learning”, http://en.wikipedia.org/wiki/Lifelong_learning
Siti utili
http://www.aurbach.com/gp3/index.html (Grady Profile)
http://www.craie.it/percorsi/auto_presentazione.htm
http://electronicportfolios.org/ALI/research.html
http://electronicportfolios.org/reflect/index.html
http://www.pubblica.istruzione.it/risorse/pratiche/viguzzolo.pdf
http://www.nea.org/lessons/2004/tt040614.html
http://spazioscuola.altervista.org/index.htm
 Uno dei temi caratterizzanti (e più trascurati) del curricolo di matematica del liceo scientifico PNI riguarda le trasformazioni geometriche nel piano. Gli allievi dovrebbero apprenderne le definizioni in prima liceo, la classificazione in seconda, le equazioni in terza, la trattazione matriciale in quarta e infine, in quinta, dovrebbero saperle applicare ai grafici di funzione reale. Occorre pertanto un’idea per renderle più user friendly, magari usando il PC, visto che siamo al PNI. Il deus ex machina della situazione è il software open-source Geogebra, usando il quale ho personalmente constatato come la mia azione didattica potesse utilmente giovarsi di ciò che i ragazzi chiamano “vedere a cosa serve la Matematica”, un “toccare con mano” che li riempie di soddisfazione. Ho poi chiesto aiuto al gatto di Arnol’d, da sempre disponibile ed abituato ad essere deformato in ogni direzione.
Uno dei temi caratterizzanti (e più trascurati) del curricolo di matematica del liceo scientifico PNI riguarda le trasformazioni geometriche nel piano. Gli allievi dovrebbero apprenderne le definizioni in prima liceo, la classificazione in seconda, le equazioni in terza, la trattazione matriciale in quarta e infine, in quinta, dovrebbero saperle applicare ai grafici di funzione reale. Occorre pertanto un’idea per renderle più user friendly, magari usando il PC, visto che siamo al PNI. Il deus ex machina della situazione è il software open-source Geogebra, usando il quale ho personalmente constatato come la mia azione didattica potesse utilmente giovarsi di ciò che i ragazzi chiamano “vedere a cosa serve la Matematica”, un “toccare con mano” che li riempie di soddisfazione. Ho poi chiesto aiuto al gatto di Arnol’d, da sempre disponibile ed abituato ad essere deformato in ogni direzione.
I soldi in banca sono al sicuro? Ci si può fidare dei titoli di Stato? Le assicurazioni possono fallire? La crisi finanziaria ha accresciuto i dubbi e i timori dei risparmiatori. Per questo la Regione Piemonte, tramite la Scuola del Consumo Consapevole, ha organizzato una conferenza nel corso della quale, presentando la guida “Come salvare i propri soldi” contenuta nel mio ultimo libro, affronterò i temi suddetti e risponderò a domande del pubblico. Risparmiatori e operatori del settore sono quindi invitati venerdì 17 aprile 2009, alle ore 18, presso il Centro Congressi della Regione Piemonte, corso Stati Uniti n. 23, Torino. www.beppescienza.it

 "Vessare la proprietà privata significa uccidere negli uomini la volontà di guadagnare di più, riducendoli a temere che la spoliazione sia la conclusione dei loro sforzi. Una volta privati della speranza di guadagnare essi non si prodigheranno più. Gli attentati alla proprietà privata fanno crescere il loro avvilimento. Se essi sono universali e se investono tutti i mezzi di esistenza, allora la stagnazione degli affari è generale, a causa della scomparsa di ogni incentivo a lavorare.
"Vessare la proprietà privata significa uccidere negli uomini la volontà di guadagnare di più, riducendoli a temere che la spoliazione sia la conclusione dei loro sforzi. Una volta privati della speranza di guadagnare essi non si prodigheranno più. Gli attentati alla proprietà privata fanno crescere il loro avvilimento. Se essi sono universali e se investono tutti i mezzi di esistenza, allora la stagnazione degli affari è generale, a causa della scomparsa di ogni incentivo a lavorare.
Ibn Khaldun (Tunisi 1332-1406), Muqaddima.
Al contrario, a lievi attentati alla proprietà privata corrisponderà un lieve arresto del lavoro. Poiché la civiltà, il benessere e la prosperità pubblica dipendono dalla produttività e dagli sforzi che compiono gli uomini in tutte le direzioni, nel loro proprio interesse e per il loro profitto. Quando gli uomini non lavorano più per guadagnarsi la vita e cessa ogni attività lucrativa, la civiltà deperisce ed ogni cosa va di male in peggio. Gli uomini per trovare lavoro si disperdono all’estero. La popolazione si riduce. Il paese si svuota e le sue città cadono in rovina. La disintegrazione della civiltà coinvolge lo Stato come ogni alterazione della materia è seguita dall’alterazione della forma". Ibn Khaldun (Tunisi 1332-1406), Muqaddima.
Khaldun, storico, filosofo, ed economista è da molti considerato il fondatore della sociologia avendo a lungo studiato le dinamiche delle relazioni di gruppo. Da alcuni è visto come un anticipatore di Nicolò Machiavelli, ma il brano sopra riportato mostra anche come abbia anche anticipato alcune idee liberali di Adamo Smith. Da un punto di vista metodologico Kaldun fu innovativo nel senso che sottopose il giudizio storico al vaglio della ragione piuttosto che a quello della religione o dell’ideologia.
Secondo Kaldun allo stato competono alcune funzioni limitate: difendere la comunità contro l’aggressione ingiustificata, proteggere la proprietà privata, vigilare sulla correttezza degli scambi commerciali tra i cittadini, evitare la svalutazione ed esercitare una saggia guida politica. Denunciò l’alto prelievo fiscale e la competizione tra governo e privato, dal momento che la minore produttività rappresenta un disincentivo al lavoro ed alla fine distrugge lo stato.
A. Smith dirà che non è dalla benevolenza (cioè dell’altruismo) del macellaio o del birraio che possiamo attendere grandi risultati, ma dal fatto che essi, sapendo di operare per la loro sopravvivenza ed il loro interesse, ottengano risultati positivi e utili per l’intera organizzazione sociale. La proprietà privata è segno identitario del diritto dei singoli a possedere i frutti del proprio lavoro e dei rischi sostenuti. Se si nega il diritto alla proprietà e alla remunerazione le organizzazioni languono, si ha una stagnazione negli investimenti, nell’innovazione, nella ricerca e gli individui migliori si disperdono all’estero (come accade oggi e da anni in Italia).
 In questa unità didattica si delinea un percorso che consente allo studente di comprendere il concetto di Trasformazione Geometrica e classificarne le varie tipologie, sia dal punto di vista grafico sia da quello analitico. L’attività si è svolta principalmente in laboratorio d’informatica utilizzando anche il programma Cabri.
In questa unità didattica si delinea un percorso che consente allo studente di comprendere il concetto di Trasformazione Geometrica e classificarne le varie tipologie, sia dal punto di vista grafico sia da quello analitico. L’attività si è svolta principalmente in laboratorio d’informatica utilizzando anche il programma Cabri.
Unità didattica di Matematica: Le Trasformazioni Geometriche del Piano
INTRODUZIONE
Con la presente unità didattica si vuole delineare un percorso che consenta allo studente di comprendere il concetto di Trasformazione Geometrica e classificarne le varie tipologie sia dal punto di vista grafico che dal punto di vista analitico. L’attività si è svolta fondamentalmente in laboratorio d’Informatica tramite l’utilizzo di slide e del programma Cabri che sono stati presentati in parallelo per dare la possibilità allo studente di verificare immediatamente le proprietà che di volta in volta vengono enunciate e di costruire egli stesso alcune trasformazioni particolari che si possono ottenere dalla composizione di altre viste in precedenza.
All’inizio di ogni lezione ho riassunto gli argomenti della lezione precedente tramite un rapido scambio di battute con il gruppo classe e tramite l’utilizzo di mappe concettuali, così come al termine di ogni lezione sempre tramite l’utilizzo di mappe concettuali ho tracciato un breve riassunto evidenziando le parti più significative. Ho esplicitato le conoscenze e competenze richieste per ogni porzione di contenuto.
Al termine del percorso ho proposto un test finale da me redatto con scopo di verifica sommativa sul raggiungimento degli obiettivi dichiarati; ho comunicato anche la percentuale per cui ogni esercizio concorre alla valutazione totale. Il compito, corretto e valutato, è stato riconsegnato in classe con una correzione collettiva e un commento individualizzato per ogni alunno.
COLLOCAZIONE NEL CURRICOLO
L’argomento va inserito o nel secondo bimestre di una III liceo scientifico PNI o nell’ultimo modulo della programmazione curriculare di una III liceo scientifico tradizionale.
TEMPO RICHIESTO: 14 ORE
PREREQUISITI
– Conoscenza degli elementi fondamentali della geometria euclidea;
– Conoscenza degli elementi fondamentali del piano cartesiano;
– Eventuale conoscenza di elementi di Geometria dello spazio;
– Conoscenza degli elementi fondamentali dell’algebra delle matrici;
– Conoscenza degli elementi fondamentali delle funzioni trigonometriche e delle loro proprietà;
– Risoluzione di equazioni, sistemi e disequazioni.
– Concetto di congruenza
– Perpendicolarità e parallelismo fra rette
– Concetto di relazione e funzione
– Elementi di calcolo matriciale
– Concetto di vettore e le operazioni relative
OBIETTIVI COGNITIVI
– Conoscere le definizioni delle trasformazioni geometriche presentate e le relative equazioni
– Acquisire il concetto di trasformazione del piano
– Acquisire dimestichezza con i vari tipi di trasformazioni
– Saper enunciare i teoremi relativi
OBIETTIVI OPERATIVI
– Saper ricavare le equazioni di una trasformazione
– Saper ricavare l’espressione analitica dalla curva trasformata
– Riconoscere il tipo di trasformazione e classificarle
– Applicare i teoremi relativi
– Saperle applicare alla Fisica (moti relativi)
– Costruire la figura trasformata di una data
– Costruire ingrandimenti e riduzioni in scala di una figura piana
– Individuare gli invarianti di una trasformazione
– Riconoscere figure simmetriche
– Classificare i poligoni in base alle loro proprietà di simmetria
– Riconoscere figure omotetiche e disegnare la corrispondente in una omotetia di una figura
– Effettuare la traslazione di una figura
– Effettuare la rotazione di una figura
– Trovare il vettore che caratterizza una traslazione
– Eseguire una trasformazione con Cabri
OBIETTIVI FORMATIVI
– Uso di un linguaggio pertinente e appropriato
– Saper scegliere la migliore strategia tra quelle proposte (sintetica, analitica o grafica) per la risoluzione di problemi
– Sviluppare la capacità di rilevare la presenza di isometrie in natura e nelle opere artistiche
– Sviluppare capacità intuitive, logiche, analitiche e sintetiche
– Acquisire l’attitudine a riesaminare criticamente ed a sistemare logicamente quanto viene via via appreso
– Acquisire l’attitudine a studiare ogni questione attraverso l’analisi di tutti i suoi fattori.
MEZZI
– Libro di testo
– Lavagna e gesso
– Fotocopie
– Lucidi
– Presentazione con MS-Power Point
– Laboratorio d’Informatica
CONTENUTI
SUDDIVISIONE MACROSCOPICA:
– Contenuto A: 3 ore
– Introduzione all’argomento delle trasformazioni;
– Esempi di figure trasformate mediante trasformazioni geometriche di vario tipo (ombre, foglio di gomma, movimento della giostra, specchi, caleidoscopio);
– Definizione di affinità;
– Proprietà delle affinità;
– Equazioni delle affinità;
– Classificazione delle affinità
– Contenuto B: 3 ore
– Definizione di isometria
– Proprietà delle isometrie
– Classificazione delle isometrie
– Definizione di simmetrie
– Classificazione delle simmetrie:
– simmetrie assiali
– simmetrie centrali
– Proprietà delle simmetrie
– Equazioni delle simmetrie
– Figure dotate di un asse di simmetria
– Contenuto C: 3 ore
– Composizione di simmetrie:
– Traslazione
– Rotazione
– Simmetria centrale
– Contenuto D: 3 ore
– Definizione, Proprietà, Equazioni e Classificazione di omotetie con cenni di richiamo a uguaglianza e similitudine (k = 1, k diverso da 1)
– Nota storica: Le Trasformazioni e la Musica
– Un esempio applicativo: Il Biliardo
– Contenuto E: 1 ora
– Verifica formativa/sommativa
METODOLOGIE
– “Problem-solving”
– Intergruppo
– Lezione frontale
– Lezione in laboratorio d’Informatica: utilizzo di Cabri; volte alla scoperta di nessi, relazioni e leggi
– Esercitazioni guidate.
– Esercizi a casa
VERIFICA E VALUTAZIONE
Le verifiche saranno di due tipi in itinere e sommativa, la valutazione seguirà la griglia di valutazione del POF. Tipo di verifica: orale, scritta (tramite prova strutturata).
ATTIVITÀ DI RECUPERO
Ripetizione, tramite mappe concettuali e applicazione degli argomenti alla geometria descrittiva, dei contenuti fondamentali e delle proprietà fondamentali sia tramite lezione frontale sia tramite approfondimenti in laboratorio.
VERIFICA DI RECUPERO: Tramite prova orale e scritta.
Scarica la tesi di Spagnulo sulle trasformazioni geometriche
Scarica l’allegato con le costruzioni di Cabri
 Risolvi l’enigma del Il salto del cavallo e puoi ricevere gratuitamente la t-shirt "Matematicamente.it Winner". I primi 10 iscritti che andranno nella classifica del gioco con 63 mosse possono richiedere la maglietta a [email protected]. Occorre essere registrati alla community di matematicamente.it e inviare la mail dall’indirizzo email con cui si è registrati. VAI AL GIOCO >>
Risolvi l’enigma del Il salto del cavallo e puoi ricevere gratuitamente la t-shirt "Matematicamente.it Winner". I primi 10 iscritti che andranno nella classifica del gioco con 63 mosse possono richiedere la maglietta a [email protected]. Occorre essere registrati alla community di matematicamente.it e inviare la mail dall’indirizzo email con cui si è registrati. VAI AL GIOCO >>
Le magliette richieste:
1° blublu
2° ralf86
3° dadux_ita
4° michele.mazzucato
5° franced
6° sigurros
7° ldesieno
8° medicum82
9° cpeg52
10° piddu
11° Wolf80
12° Lurens
STOP, sono state vinte tutte le magliette, alla prossima gara con i giochi di Matematicamente.it
Milano, 28 Settembre 2009 Sede: FAST CENTRO CONGRESSI P.le R. Morandi, 2 Milano
Questo workshop è diretto sia a persone che si accostano per la prima volta al Project Management sia a quelle che ne hanno già una certa esperienza. L’obiettivo è illustrare i metodi e le tecniche disponibili (WBS, Gantt, PDM, Hystogram, S Curve, March Chart, Vendor Selection, Resource Control, Cost Control, Earned Value, Forecast, Risk Analysis, etc.) per una gestione efficace ed efficiente, prescindendo dagli specifici software e procedure presenti nelle singole aziende. Il workshop può essere frequentato sia come entry point di un percorso formativo sul PM, sia a valle di altri corsi già seguiti. A tutti i partecipanti sarà fornito un CD comprendente un work-book Excel composto da 21 fogli di lavoro ed un libro che ne descrive contenuti e metodologie impiegate.
In tal modo sarà possibile completare a casa o in ufficio la propria formazione secondo i rispettivi ritmi, interessi ed esigenze di lavoro. Grazie alla filosofia Open Source, i più esperti potranno poi utilizzare i 21 fogli come base di partenza per applicazioni personalizzate o come generatori di idee per realizzarne di nuove: per sé o per gli utenti finali della propria organizzazione. Il Seminario è svolto in maniera interattiva e prevede l’alternarsi dell’illustrazione dei fogli di lavoro da parte del docente con la ricerca delle soluzioni da parte dei partecipanti. I problemi saranno affrontati individualmente o in piccoli gruppi approntando manualmente grafici e tabelle ed effettuando i semplici calcoli necessari alla comprensione delle varie metodologie proposte. Il Corso è rivolto a coloro che lavorano/lavoreranno nei progetti (project manager, contract administrator, project engineer, procurement coordinator, construction manager, planning and control engineer, etc.), ma può essere utilmente seguito anche da posizioni di staff (proposal manager, risk manager, knowledge manager, Qa/Qc etc.) e, più in generale, da tutti coloro che vogliano accrescere le proprie capacità di problem solving e decision making. Gli argomenti e i metodi proposti riguardano persone che operano in qualunque tipo di organizzazione: impiantistica, costruzioni, energia, chimica, industria, componentistica e indotto, banche, information technology, ricerca e università, pubblica amministrazione, sanità e difesa, ecc..
 Lo scopo di questa tesi è analizzare i problemi connessi con l’introduzione dei concetti di frazioni/numeri razionali/numeri con la virgola nella scuola primaria e secondaria di primo grado. L’approccio sarà fatto da una punto di vista didattico e cercherò di valutare, per quanto possibile, i diversi aspetti e le problematiche legate alle varie possibilità di introduzione di tali concetti, il loro significato immediato relativo alle conoscenze pregresse degli alunni e alle loro convinzioni, coglierne i problemi a essi legati come gli ostacoli epistemologici ed errori frequenti di scrittura.
Lo scopo di questa tesi è analizzare i problemi connessi con l’introduzione dei concetti di frazioni/numeri razionali/numeri con la virgola nella scuola primaria e secondaria di primo grado. L’approccio sarà fatto da una punto di vista didattico e cercherò di valutare, per quanto possibile, i diversi aspetti e le problematiche legate alle varie possibilità di introduzione di tali concetti, il loro significato immediato relativo alle conoscenze pregresse degli alunni e alle loro convinzioni, coglierne i problemi a essi legati come gli ostacoli epistemologici ed errori frequenti di scrittura.
Questa tesi partecipa al concorso Condividi la tua tesi e vinci 3 iPhone 3G.
La grande quantità di letteratura presente su tali problemi didattici, e anche l’abitudine di molti autori di terminare le loro trattazioni con un’ipotesi di curricolo sull’insegnamento delle frazioni (dove molto spesso troviamo il suggerimento di introdurre le frazioni facendo riferimento alle “frazioni egizie”), mi consigliano l’introduzione di un preambolo storico.
Lo scopo è quello di far vedere che, così come è stato difficile nel corso dei millenni la nascita, l’evoluzione, la consapevolezza e l’assunzione di questi concetti a concetti matematici, tanto lo sarà nel processo di interiorizzazione nella mente di un allievo.
Indice
Prefazione
1. Prefazione storica
1.1. Storia delle frazioni
1.2. Gli Egiziani
1.3. La Mesopotamia
1.4. I Greci
1.5. I Cinesi
1.6. I Romani
1.7. Gli Indiani
1.8. Gli Arabi
1.9. Il Medioevo in Europa
Appendici :
1. L’occhio di Horus
2. La scomposizione delle frazioni egizie
3. L’epitaffio di Diofanto
4. Euclide di Alessandria
5. Mohammed ibn Musā detto al-Khowârizmî
6. Leredità dei 17 cammelli
2. Introduzione ai numeri razionali
2.1. La frazione come parte di un tutto a volte continuo a volte discreto
2.2. La frazione come quoziente
2.3. La frazione come rapporto (proporzioni)
2.4. La frazione come operatore
2.5. La frazione in probabilità
2.6. La frazione nei punteggi
2.7. La frazione come numero razionale
2.7.1. Numeri razionali e numeri decimali
a. Numeri decimali finiti
b. Numeri decimali periodici
2.8. La frazione come punto di una retta orientata
2.9. La frazione come misura
2.10. La frazione come indicazione di quantità di scelta in un tutto
2.11. La frazione e la percentuale
2.12. La frazione nel linguaggio quotidiano
2.13. Quanti sono i numeri razionali?
2.14. Gli errori frequenti
3. La didattica della matematica
3.1 Le misconcezioni
3.2 Noetica e semiotica delle frazioni
3.3 Conclusioni e consigli
Bibliografia
[1] Bachelard G.(1938) La formation de l’esprit scientifique.Paris,Vrin
[2] Bessot A., Panorama des cadres théoriques de la didactique des Maths en France, L’educazione Matematica, 1994, 1.
[3] Behr M.J., Lesh R., Post T.,Silver E.A. (1983).Rational-number concept.New York: Academic Press.
[4] Carl B. Boyer – Storia della matematica – Arnoldo Mondatori Editore – 1987
[5] Brousseau G., Thèorie des situations didactiques (didactique des mathèmatiques 1970-1990) ,1998, Grenoble ed. la Pensée Sauvage
[6] Brousseau G., Les obstacles epistemologiques et les problemes en Maths, RDM, 1983, Grenoble, ed. la Pensée Sauvage,Vol.4.2.
[7] Brousseau G., Fondements et méthodes de la didactique de mathématiques, RDM, 1986, Grenoble, ed. la Pensée Sauvage,Vol.7.2.
[8] Brousseau G., Theorisation des Phenomes d’Enseignement des Maths. These d’etat, Bordeaux,1986.
[9 ]Brousseau G., Le contrat didactique: Le milieu, RDM, 1988, Grenoble, ed. la Pensée Sauvage, Vol.9.3.
[10] Chevallard Y., La trasposition didactique du savoir savant au savoir enseigné,1991, Grenoble, ed. La Pensée Sauvage
[11] Chevalard Y. – Dimension instrumentale, dimension sémiotique de l’activitè matématique.Séminaire de didactique des Mathèmatiqes et de l’informatique de Grenoble.LSD2, IMAG,Università J.Fourier, Grenoble
[12] D’Amore B.- Le basi filosofiche, pedagogiche,epistemologiche e concettuali della didattica della matematica.-Pitagora Bologna (2003)
[13] B. D’Amore-Elementi di didattica della matematica-Pitagora Bologna 1999
[14] R. Duval –Registres de representations sémiotique et fonctionnement cognitif de la pensée. Annales de didactique et de sciences cognitives,ULP,IREM Strasbourg.
[15] Martha Isabel Fandiño Pinilla-Curricolo e valutazione in matematica
[16] Martha Isabel Fandiño Pinilla – Le frazioni aspetti concettuali e didattici – Pitagora editrice -2005
[17]E.Fischbein –Intuizione e dimostrazione in Matematica a scuola:teorie ed esperienza-Pitagora 1992 – 93 – [18] Freudehantal H., Ripensando l’educazione matematica (a cura di F.Manara), 1994, Brescia, ed. La Scuola. [19] L. Giovannoni – La matematica e la sua didattica -1996
[20] Godino J.D. & BataneroC. (1994) Significado istituzionale y personal de los objectos matematicos.recherches en didactique des matèmatiques
[21] Kline M.,. Storia del pensiero matematico, 1991, Torino Einaudi.
[22] G.Loria -Storia delle matematiche.- Hoepli Milano
[23] Marino T.- Spagnolo F., Gli ostacoli Epistemologici: Come si individuano e come si utilizzano nella ricerca in Didattica della Matematica, L’insegnamento della. matematica e delle scienze integrate, vol.19B, n.2, Aprile 1996.
[24] MarinoTeresa – Sugli ostacoli in didattica delle matematiche -Seminario GRIM 1997
[25] Rota G.C., Matematica e Filosofia: Storia di un malinteso,1990, BUMI, Serie VII, vol.IV-A,n.3, p.301.
[26] Guido Setter-Lo sviluppo mentale nella ricerca di Piaget-Giunti 1961
[27] Spagnolo F., Insegnare le matematiche nella scuola secondaria, 1998, Milano, ed.La Nuova Italia.
[28] Spagnolo F. – Valenti S., Errori matematici: un’occasione didattica, L’insegnamento della matematica, 1984, 7/1.
[29] Rosetta Zan- Dalla correzione degli errori all’intervento sulle difficoltà
[30] Rosetta Zan-Emozioni e difficoltà in matematica Siti consultati
[31] www.wikipedia.org
[32] http://web.unife.it/altro/tesi/A.Montanari/cina.htm
[33] http://web.math.unifi.it/archimede/archimede/note_storia/numeri/nume ri1/node13.html
[34] http://math.unipa.it/~grim/Tesi_Malisani_06_it.pdf
[35] http://math.unipa.it/~grim/
[36] http://www.ssis.unige.it/0607SostegnoLaviosa0607DDI_Lez2_lettura.pdf
[37] www.dm.unibo.it/rsddm/it/articoli/sbaragli/LDMS%203.pdf
[38] http://dipmat.math.unipa.it/~grim/conv_aicmgrim05_alongi.pdf
[39] http://didasp.tiedu.ch/~dm/ForBase/MIA1/Anno%2004%2005/MIA%2005%20D anilo/TDS.pdf
[40] http://math.unipa.it/~grim/Jdamoreital.Pdf
[41] http://www.dm.unito.it/mathesis/volumi/indice97.html
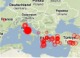 La mappa dei terremoti nel mondo istante per istante a cura del European-Mediterranean Seismological Centre http://www.emsc-csem.org/index.php?page=home&sub=gmap
La mappa dei terremoti nel mondo istante per istante a cura del European-Mediterranean Seismological Centre http://www.emsc-csem.org/index.php?page=home&sub=gmap
 Guglielmo di Occam, opponendosi alla complicazione di alcuni concetti teologici (creazione, attributi divini, immortalità dell’anima, ecc.) e all’esistenza degli universali, cioè delle proprietà indipendentemente dalle cose che le possiedono, arrivò a formulare il celebre principio denominato rasoio di Occam: "entia non sunt multiplicanda praeter necessitatem – gli enti non debbono essere moltiplicati oltre il necessario".
Guglielmo di Occam, opponendosi alla complicazione di alcuni concetti teologici (creazione, attributi divini, immortalità dell’anima, ecc.) e all’esistenza degli universali, cioè delle proprietà indipendentemente dalle cose che le possiedono, arrivò a formulare il celebre principio denominato rasoio di Occam: "entia non sunt multiplicanda praeter necessitatem – gli enti non debbono essere moltiplicati oltre il necessario".
Guglielmo di Occam, nato nel Surrey (G.B.) nel 1285 era un monaco francescano formatosi nell’ambito della filosofia scolastica e di poco posteriore a Ruggero Bacone, Tommaso d’Aquino e Duns Scoto. Scrisse su Aristotele ed in particolare cercò di liberare la filosofia di Aristotele da certe sovrastrutture imposte dai cristiani (Agostino) e dagli Arabi. 
Col ribadire la possibilità di studiare la logica e la conoscenza umana senza far riferimenti alla metafisica e alla teologia, l’opera di Occam incoraggiò la ricerca scientifica e per questo motivo egli può considerarsi, assieme a R. Bacone, un precursore degli empiristi britannici del XVII e del XVIII secolo. Opponendosi alla complicazione di alcuni concetti teologici (creazione, attributi divini, immortalità dell’anima, ecc.) e all’esistenza degli universali, cioè delle proprietà indipendentemente dalle cose che le possiedono, arrivò a formulare il celebre principio denominato rasoio di Occam: "entia non sunt multiplicanda praeter necessitatem – gli enti non debbono essere moltiplicati oltre il necessario".
Per Luciano De Crescenzo "era uno che andava subito al dunque e per riuscirci tagliava via tutto quello che a suo giudizio riteneva inutile o comunque superfluo".
Secondo il principio del rasoio non dovremmo includere nelle nostre teorie più di quanto sia strettamente necessario al loro sostegno.
L’idea si trova già presente in Aristotele, in Seneca (che nelle lettere a Lucilio scrisse: "non è mai poco quello che basta") e in molti predecessori medioevali di Occam.
Nell’affrontare i problemi il principio fornisce elementi essenziali per discriminare le possibili soluzioni e Bertrand Russell (La Saggezza dell’Occidente) lo interpreta come un principio che invita a servirsi delle soluzioni più semplici ed economiche: "è inutile fare con il più quello che può essere fatto con il meno".
Ad esempio nella riorganizzazione della pubblica amministrazione e degli enti locali in Italia si potrebbe pensare all’abolizione delle province e ad una ragionevole riduzione delle comunità montane. Nella politica, sanità, scuola, giustizia e previdenza si potrebbero ottenere risultati altrettanto buoni o forse migliori degli attuali eliminando gli sprechi (80 miliardi di Euro all’anno secondo Luca Ricolfi: "Ostaggi dello stato", Guerini 2008).
E’ comunque fuorviante e riduttivo pensare al rasoio di Occam come un banale e gretto invito al taglio dei costi di breve periodo per far cassa. Innanzi tutto si tenga presente che le spese oltre il necessario sono sempre risorse che vengono sottratte ad altre iniziative e, d’altro canto, le spese necessarie possono giustamente comprendere anche delle duplicazioni (ridondanze) come ad esempio i comandi in una navicella spaziale o i gruppi elettrogeni di un ospedale.
 Questa tesi è il risultato di un percorso didattico svolto in una terza media. Il percorso era dedicato all’evoluzione delle specie. I punti di forza sono: • Aver presentato separatamente i vari meccanismi che portano all’evoluzione delle specie (mutazioni e variabilità, selezione naturale, tempo), • Aver creato durante lo svolgimento del percorso il sito online delle lezioni [1] ad uso dei ragazzi, con i materiali prodotti ed usati a scuola, • Aver fatto svolgere ai ragazzi un’attività (una specie di "telefono senza fili basato sui disegni") che ha portato alla creazione di varie animazioni [2] e di un filmato che è stato poi reso pubblico su Internet per mezzo di YouTube [3]. • Aver usato diverse simulazioni al computer per vedere e giocare con gli effetti della selezione (si veda il sito delle lezioni).
Questa tesi è il risultato di un percorso didattico svolto in una terza media. Il percorso era dedicato all’evoluzione delle specie. I punti di forza sono: • Aver presentato separatamente i vari meccanismi che portano all’evoluzione delle specie (mutazioni e variabilità, selezione naturale, tempo), • Aver creato durante lo svolgimento del percorso il sito online delle lezioni [1] ad uso dei ragazzi, con i materiali prodotti ed usati a scuola, • Aver fatto svolgere ai ragazzi un’attività (una specie di "telefono senza fili basato sui disegni") che ha portato alla creazione di varie animazioni [2] e di un filmato che è stato poi reso pubblico su Internet per mezzo di YouTube [3]. • Aver usato diverse simulazioni al computer per vedere e giocare con gli effetti della selezione (si veda il sito delle lezioni).
[1] Sito delle lezioni: http://www.guzman.it/3EDinoCompagni2008/3EDinoCompagni2008.html
[2] Animazioni http://www.guzman.it/3EDinoCompagni2008/pesce/PesciMutantiColori.html
[3] Filmato con le animazione prodotte con i disegni dei ragazzi: http://www.youtube.com/watch?v=W0mgWEl2mjc
Indice
1. Introduzione. Riflessioni sui due anni di SSIS. 4
2. Riflessioni sull’esperienza del laboratorio di didattica 7
3. Tirocinio attivo: Percorso Didattico di Scienze.
I meccanismi dell’evoluzione. 9
Titolo del percorso didattico 10
Discipline interessate 10
Classe di riferimento e collocazione nel tempo scuola 10
Premessa e motivazioni della scelta 10
Collocazione del percorso didattico 11
Metodologie didattiche utilizzate 11
Obiettivo generale 13
Descrittori di competenze 13
Prerequisiti 13
Risorse 14
Fasi del percorso di scienze 16
Fase 1. Evoluzione: pensiamoci! (online ) 16
Fase 2. Era un pesce! (online ) 18
Fase 3. Ma chi lo dice che le specie evolvono? (online ) 22
Fase 4. La selezione? Proviamo! (online ) 24
Fase 5. Il rotolone del tempo !? (online ) 26
Fase 6. Cosa abbiamo imparato? 28
Fase 7. Vediamo se ho capito! (online ) 29
Verifica. (online ) 30
Come si sono svolte le lezioni di scienze 33
1 Discussione aperta ("brain storming") (online ) 34
2 I pesci mutanti. (online ) 41
3 Presentazione al computer (online ) 45
4 Simulazioni al computer (online ) 47
5-6 Il rotolone del tempo. (online ) 49
7 Verifica (online ) 50
Conclusioni 51
Il sito delle lezioni 52
Bibliografia e Siti Internet di riferimento 56
Siti con i materiali di questa tesi 57
Scarica la tesi Relazione finale di Tirocinio e Laboratorio di Didattica (Scienze Naturali per la Scuola Media) Animazioni, Simulazioni e l’Evoluzione delle Specie
 Cpeg52 (Antonio Motta, Usmate Velate -MI) è risultato il primo in classifica per il mese di maggio, vince la t-shirt di Matematicamente.it Winner e un libro omaggio.
Cpeg52 (Antonio Motta, Usmate Velate -MI) è risultato il primo in classifica per il mese di maggio, vince la t-shirt di Matematicamente.it Winner e un libro omaggio.
Il 2° trofeo di scacchi Matematicamente.it è aperto a tutti, con tanti ricchi premio in palio:
1° premio Play Station 3
2° premio Play Station Portable
3° premio il libro Gli scacchi di Luca Pacioli, offerto da Gorilla.it
Partecipa al trofeo di scacchi
La NASA offre la possibilità di inviare gratuitamente il proprio nome su Marte. La sonda “Mars Science Laboratory” partirà con qualche mese di ritardo a causa di intoppi tecnici, ma comunque entro la fine di ottobre 2009, altrimenti sarà troppo tardi.
Per qualche informazione sulla sonda seguite il blog di astronomia http://www.sidereus-nuncius.info/2008/10/12/ecco-il-nuovo-rover-che-sara-lanciato-su-marte/.
Il vostro nome verrà inserito in un microchip che sarà imbarcato a bordo della sonda che si recherà sul Pianeta Rosso. Vi verrà segnalato il numero del vostro certificato ed il link dove visualizzarlo. Ovviamente lo potrete anche stampare.
Per aderire all’iniziativa http://mars.jpl.nasa.gov/msl/participate/sendyourname/
 Come si leggono in inglese i termini matematici più comuni.
Come si leggono in inglese i termini matematici più comuni.
Calcolo numerico, calcolo letterale, prodotti notevoli, regola di Ruffini e teorema del resto.
 Il Web 2.0 è quindi un ambiente in cui si sono sviluppati e continuano a svilupparsi i siti e quelle applicazioni che mettono il controllo del contenuto (sia generato direttamente che non) nelle mani dell’utente. I punti cardine di questa evoluzione del Web risultano quindi essere la partecipazione degli utenti (e di conseguenza il formarsi di un’intelligenza collettiva), la trasformazione dei dati (remixability) e la loro creazione da parte degli utenti (User-generated content) ed infine il cambiamento di rotta del design centrato sulle esigenze dell’utente.
Il Web 2.0 è quindi un ambiente in cui si sono sviluppati e continuano a svilupparsi i siti e quelle applicazioni che mettono il controllo del contenuto (sia generato direttamente che non) nelle mani dell’utente. I punti cardine di questa evoluzione del Web risultano quindi essere la partecipazione degli utenti (e di conseguenza il formarsi di un’intelligenza collettiva), la trasformazione dei dati (remixability) e la loro creazione da parte degli utenti (User-generated content) ed infine il cambiamento di rotta del design centrato sulle esigenze dell’utente.
Questa tesi partecipa al concorso "Condividi la tua tesi e vinci tre Apple iPhone 3G". Se hai scritto una tesi, tesina SSIS o di master sui temi della didattica della matematica, della fisica, della didattica con le nuove tecnologie partecipa al concorso.
Il 2004 ha visto la diffusione di un nuovo termine associato ad Internet: il Web 2.0. Senza fare rumore questo nuovo termine sta in realtà entrando nelle vita di moltissimi italiani, segnandone le abitudini, così come il modo di cercare, consumare e specialmente condividere informazioni. Molte persone utilizzano YouTube per condividere e visionare video, Wikipedia per le ricerche scolastiche, pubblicano il proprio album fotografico utilizzando Flickr, gestiscono e leggono Blog di persone più o meno autorevoli e molto altro. Tutto questo senza aver mai sentito nominare il termine Web 2.0, a dimostrazione del fatto che il nome conta decisamente meno del livello di adozione di una tecnologia da parte degli utenti.
I punti cardine di questa evoluzione del Web risultano quindi essere la partecipazione degli utenti (e di conseguenza il formarsi di un’intelligenza collettiva), la trasformazione dei dati (remixability) e la loro creazione da parte degli utenti (User-generated content) ed infine il cambiamento di rotta del design centrato sulle esigenze dell’utente. Verranno approfonditi tutti questi elementi per capire quali sono i vantaggi e gli svantaggi nella logica dell’User-centered design. Ci saranno inoltre alcuni riferimenti a siti commerciali a dimostrazione del fatto che il Web 2.0 sta avendo un impatto imponente sui nuovi modelli di comunicazione e di business. Dare una definizione chiara e precisa di cosa sia il Web 2.0 è impossibile in quanto risulta essere ancora un’espressione giovane i cui contorni sono difficilmente definibili ma ciò che è certo è che il Web sta attraversando un periodo di innovazione che non si può ignorare.
Capitolo 1 – Il Web 2.0
In questo capitolo si accennerà la storia del Web soffermandosi sul Web 2.0 e mettendo in evidenza le principali differenze rispetto al Web 1.0. Si citeranno inoltre le varie definizioni di Web 2.0 circolanti in rete cercando di scoprire i punti comuni.
Capitolo 2 – I punti cardine del Web 2.0
In questo capitolo si studierà la mappa mentale inerente il Web 2.0 approfondendo i punti più importanti. La partecipazione degli utenti risulta essere il fulcro di questa innovazione del Web seguita poi dalla possibilità di poter manipolare e trasformare dati provenienti da altri siti (remixability). Ci si soffermerà inoltre sullo studio dell’usabilità delle nuove interfacce web e sull’utilizzo di nuove tecnologie come AJAX.
Capitolo 3 – Applicazioni Web
La nascita delle applicazioni Web ha reso possibile utilizzare Internet per compiti che prima erano esclusiva delle applicazioni Desktop. Sfruttare le potenzialità della rete significa poter condividere dati, collaborare con persone geograficamente lontane, avere programmi sempre aggiornati e molto altro. In questo capitolo si spiegheranno le potenzialità delle applicazioni Web e l’avvento dei primi sistemi operativi basati su Web.
Capitolo 4 – L’impronta grafica del Web 2.0
Il Web 2.0 ha portato un’innovazione anche allo stile grafico adottato dai siti e dalle varie applicazioni Web. Verrà stilata una lista atta a riassumere gli elementi grafici comuni a moltissimi siti Web 2.0 spaziando dallo studio dei font ai colori utilizzati.
Conclusione
È innegabile che il Web 2.0 stia dando nuova credibilità al web ma c’è già chi parla di Web 3.0. Tim Berners-Lee, il co-inventore del World Wide Web, crede molto in una terza fase di evoluzione del web caratterizzata da un approccio semantico dove le macchine non si limiteranno ad archiviare i contenuti ma anche a capirli. Il Web semantico porterà gli sviluppatori a dover creare software in grado di rispondere a richieste complesse in modo da estrarre maggior significato dall’attuale ragnatela di collegamenti. Il Web 3.0 sarà contraddistinto dall’emergere del “Data Web” ossia trasformare il Web in un database dove i dati verranno strutturati e pubblicati in modo da poter essere riutilizzati ed interrogati da remoto. Per rispondere a richieste complesse è necessario un percorso evolutivo verso l’Intelligenza Artificiale che porterà l’utente ad interagire con il Web in modo quasi umano. Come si può notare il Web è in continua evoluzione con lo scopo principale di trasformare Internet in uno strumento realmente a portata di uomo.
Università di Udine – Laurea Triennale in Tecnologie Web e Multimediale – Relatore: Prof. Elio Toppano – Autore: Daniele Simonin – 4 Ottobre 2007
 Considerate la vostra semenza:
Considerate la vostra semenza:
fatti non foste a viver come bruti,
ma per seguir virtute e canoscenza.
Li miei compagni fec’io sì aguti,
con questa orazion picciola, al cammino,
che a pena poscia li avrei ritenuti;
e volta nostra poppa nel mattino,
de’ remi facemmo ali al folle volo ………
Noi ci allegrammo, e tosto tornò in pianto,
ché de la nova terra un turbo nacque,
e percosse del legno il primo canto.
Tre volte il fé girar con tutte l’acque;
a la quarta levar la poppa in suso
e la prora ire in giù, com’altrui piacque,
infin che ‘l mar fu sovra noi richiuso».
Dante Alighieri (1265-1321), Divina Commedia, Inferno Canto XXVI
Per l’Ulisse di Dante, che metteva nell’inferno i personaggi che gli erano più simpatici, è il desiderio del sapere (fatti non foste a viver come bruti) che lo spinge al fare (de’ remi facemmo ali al folle volo). Interessante, per il problem solving, è anche il passo (li miei compagni fec’io si aguti….) in cui Ulisse mostra di saper motivare i suoi uomini.
Dante, oltre che poeta, fu un pensatore che sintetizzò mirabilmente il sapere medioevale infatti Bertrand Russell lo considerò, assieme a Machiavelli, Vico e Leopardi, uno dei pochi italiani degni di rientrare nel suo libro di filosofia: "La Saggezza dell’Occidente".
Forse l’aporia sapere/fare è fondante per molto pensiero filosofico, basti pensare al "Verum ipsum factum" di Vico o a Kant che sosteneva che: "L’esperienza senza la teoria è cieca, ma la teoria senza l’esperienza è un puro gioco intellettuale".
In tempi più recenti Mazzini fondò un movimento politico chiamato "Pensiero e azione" e di Marx è celebre la riflessione: "I filosofi hanno soltanto interpretato il mondo, ma ora si tratta di trasformarlo".
Ricordo un direttore della pianificazione e del sistema informativo che, riprendendo un celebre aforisma pedagogico, sosteneva esserci tre momenti, non sempre rigidamente sequenziali, nella carriera di una persona all’interno di una organizzazione:
Sapere; imparare il proprio mestiere, agire da spugne, conoscere l’azienda, le risorse, i clienti, i punti di forza e quelli di debolezza sia propri che dell’organizzazione.
Saper fare; agire con competenza nell’ambito della propria professionalità e funzione (sia essa ricerca, produzione, marketing, risorse umane, amministrazione, ecc.)
Saper far fare; coordinare delle risorse, porre degli obiettivi impegnativi ma realistici, gestire i conflitti, esercitare una leadership democratica, ma orientata ai risultati.
Discutendo gliene proposi un quarto (ripreso dal titolo di un libro di Aubrey e Tiliette):
Saper far sapere; puntare sulla ricerca, investire sul capitale intellettuale, incoraggiare i lavoratori della conoscenza, fare formazione, trasmettere a dipendenti e colleghi le proprie competenze.
 Lo sviluppo delle nuove tecnologie e la crescita inarrestabile di modelli di insegnamento–apprendimento a distanza, sempre più flessibili ed efficaci, basati sull’utilizzo delle tecnologie stesse, stanno determinando la nascita di una nuova società che possiamo definire “società cognitiva”.
Lo sviluppo delle nuove tecnologie e la crescita inarrestabile di modelli di insegnamento–apprendimento a distanza, sempre più flessibili ed efficaci, basati sull’utilizzo delle tecnologie stesse, stanno determinando la nascita di una nuova società che possiamo definire “società cognitiva”.
E’ una società che richiede un profondo rinnovamento delle istituzioni formative e dei modi di trasmettere ed acquisire il sapere; le scuole, ed in particolare le Università, devono essere in grado di formare i professionisti del futuro, capaci di acquisire sempre nuove conoscenze e competenze e di far fronte ad un mercato del lavoro sempre più aperto e flessibile.
Il ruolo dei docenti e dei discenti, all’interno del processo formativo, muta radicalmente poiché, i primi, si trovano ad acquisire nuove e complesse competenze relative all’insegnamento a distanza, oltre che il ruolo di guida del processo di apprendimento degli studenti; i secondi, invece, si rivestono di un ruolo attivo che permette loro di diventare veri e propri protagonisti nella creazione di un nuovo sapere e di una nuova conoscenza.
In questo contesto, assume un’importanza rilevante la figura del sistema di tutoring, il cui compito è quello di sostenere, stimolare, accompagnare i discenti nel loro percorso di formazione e aiutarli a sviluppare capacità cognitive superiori, grazie anche all’utilizzo di quegli strumenti che Donald A. Norman definisce “artefatti cognitivi”: ovvero le nuove tecnologie.
I sistemi tutoriali intelligenti (ITS: Intelligent Tutoring System) sono sistemi software progettati, principalmente, per supportare l’attività d’apprendimento di tipo specializzato e individualizzato.
Questi sistemi possono essere utilizzati nei normali processi educativi, nei corsi d’apprendimento a distanza, sotto forma di cd-rom oppure come applicazioni per la divulgazione delle conoscenze via internet.
I primi sviluppi dell’introduzione di programmi software, come mezzi ausiliari nell’apprendimento educativo, furono formalizzati nell’ambito del progetto CAI (Computer Aided Instruction). Questi programmi utilizzavano un albero di decisione per guidare lo studente da una sessione all’altra a seconda delle risposte formulate [Urban Lurain 1996]. Tuttavia, non prendevano in considerazione la diversità degli studenti e le loro specifiche necessità, background o storia.
I programmi CAI, quindi, non erano in grado di adattarsi al modo specifico di acquisire le conoscenze che lo studente aveva e non erano in grado di fornire un’attenzione individualizzata che invece il tutore umano assicurava [Bennett 1997].
I recenti sviluppi della ricerca nel campo dell’intelligenza artificiale hanno portato ad un nuovo campo d’applicazione, che prende il nome di Intelligent Tutoring System [Burns & Capps 1998]. La caratteristica di base di questi sistemi, è di considerare ogni studente come unico, creando un modello studente capace di registrarne le preferenze e i progressi nel corso del processo cognitivo [VanLehn 1998]. In più ciò che ne incrementa l’efficacia nell’insegnamento, è la propria capacità di adattarsi alle caratteristiche dello studente. Per far questo, il sistema deve cercare di avvicinarsi il più possibile al modo di ragionare dello studente. Deve, in altri termini, gestire i differenti aspetti della vaghezza, presenti nei dati espressi con parole reali.
L’intelligenza artificiale ha risolto questo problema utilizzando, tra l’altro, la logica fuzzy, nel tentativo di fornire una base robusta e sistematica tesa a gestire le imprecisioni linguistiche, che sono dovute all’assenza di confini ben definiti, entro i quali i costrutti linguistici possono trovarsi.
Inizieremo con il dare uno sguardo all’architettura di base di un sistema tutoriale intelligente e alla relativa logica fuzzy, per poi descrivere in dettaglio gli aspetti di alcuni authoring ITS che utilizzano modelli fuzzy. In particolare si inizierà con una trattazione dei Sistemi di Tutoring Intelligente su base web.
Alla fine, presenteremo nella parte B della bibliografia un elenco di authoring ITS, incontrati durante la stesura della tesi, che non usano modelli di tipo fuzzy.
Capitolo I Architettura di base di un ITS e logica Fuzzy …………………..5
1.0 Introduzione ……..…………………………………………………..5
2.0 La struttura modulare di un ITS …………………………………6
2.1 Il modello esperto ….…………………………………………….6
2.2 Il modello studente ……….………………………………………7
2.3 Il modello pedagogico …………………………………………..7
2.4 L’interfaccia utente ….……………………………………………8
3.0 Il modello studente, aspetti teorici e pratici …..………………..8
3.1 Classificazione dei modelli studente ….………………………8
3.2 La rappresentazione del modello studente ………………..10
4.0 La logica Fuzzy costruttrice del modello ……………………12
4.1 Concetti di base della logica Fuzzy …………………………13
4.2 Logica Fuzzy e linguaggio parlato ………………………….15
Riferimenti …..…………………………………………………………17
Capitolo II Il Sistema di tutoring I.T.W. ……………………………………..18
1.0 Introduzione …….…………………………………………………18
2.0 IWT: Intelligent Web Teacher ….………………………………19
3.0 Il modello della conoscenza ….…………………………………21
4.0 Il modello studente ……………………………………………….23
5.0 Il modello didattico ………………………………………………25
6.0 Conclusioni e sviluppi futuri …..………………………………..26
Riferimenti ………..……………………………………………………28
Capitolo III Un ITS fondato sul binomio Corba/WWW ………………….29
1.0 Introduzione ………………………………………………………29
2.0 Cosa è C.O.R.B.A.? ……………………………………………..30
2.1 Quali sono i componenti di C.O.R.B.A.? ….……………..31
3.0 L’architettura modulare del sistema ….….……………………33
4.0 Il modulo esperto ……….…………………………………………34
5.0 Il modulo studente ….….………………………………………….35
6.0 Conclusioni …………….………….……………………………….37
Riferimenti ….…………………..………………………………………39
Capitolo IV Il sistema adattivo ipermediale Alice ………….………………40
1.0 Introduzione ……….………………………………………………40
2.0 Descrizione del sistema Alice ….………………………………41
2.1 Il modello utente ……….……………………………………….42
3.0 Le tecnologie adattive ………………………………………….44
Riferimenti …….…..……………………………………………………45
Capitolo V La Piattaforma InterMediActor ………………………………..46
1.0 Introduzione ……………………….………………………………46
2.0 La piattaforma InterMediActor …….…………………………..48
3.0 Il modello studente ……….……………………………………….50
3.1 Il livello d’importanza ….…..…………………………………51
3.2 Il livello di difficoltà …..………………………………………51
3.3 I voti …..…………….……………………………………………53 II
3.4 I requisiti iniziali (pre-requisiti) della conoscenza ……….54
3.5 La defuzzificazione …….….…..……………………………….54
4.0 Conclusioni …………..…………………………………………….54
Riferimenti ……….…..…………………………………………………55
Capitolo VI Il Sistema INSPIRE ………….………………………………………56
1.0 Introduzione ………….……………………………………………56
2.0 L’architettura di INSPIRE ….…………………………………..57
3.0 Il problema del processo di diagnosi dello studente ….…….59
4.0 Il processo di diagnosi dello studente in INSPIRE ….………60
4.1 La creazione del modello della conoscenza esperta .…….62
4.2 Il processo di diagnosi …………………………………………65
5.0 Conclusioni ……….……………………………………………….67
Riferimenti …….…..……………………………………………………68
Capitolo VII I Sistemi Witness e Sherlock II …………………………………..69
1.0 Introduzione ………….……………………………………………69
2.0 Il sistema Witness ……….………………………………………..70
2.1 Le componenti del sistema ….……………………………….70
3.0 Le relazioni tra le diverse componenti del sistema ….………71
4.0 Il sistema Sherlock II ….………………………………………….74
Riferimenti …….……..…………………………………………………76
Bibliografia Generale ……………………………………………….77
Scarica la tesi: Analisi dei sistemi di tutoring intelligenti che utilizzano modelli Fuzzy
 "La maggior parte degli uomini ragiona in questo modo: si è sempre fatto così, si è sempre detto così, dunque deve essere così… ma chi vuole veramente conoscere la verità dei fenomeni naturali deve saper fare buon uso dell’esperienza." Ruggero Bacone (1214-1294), scienziato e filosofo.
"La maggior parte degli uomini ragiona in questo modo: si è sempre fatto così, si è sempre detto così, dunque deve essere così… ma chi vuole veramente conoscere la verità dei fenomeni naturali deve saper fare buon uso dell’esperienza." Ruggero Bacone (1214-1294), scienziato e filosofo.
"Se avessi il potere sopra le opere di Aristotele, le brucerei tutte perché lo studiarle è soltanto una perdita di tempo e una causa di errore, nonché una moltiplicazione di ignoranza al di là dell’immaginabile."
“Arriveremo a costruire macchine capaci di spingere grandi navi a velocità più forti che un’intera schiera di rematori e bisognose soltanto di un pilota che le diriga… e perfino congegni atti a percorrere i mari e i fiumi viaggiando nei profondi abissi… E macchine non molto grandi capaci di alzare e abbassare pesi di qualsiasi grandezza. Arriveremo a imprimere ai carri incredibili velocità senza l’aiuto di alcun animale. Arriveremo a costruire macchine alate, capaci di sollevarsi nell’aria come gli uccelli.” Ruggero Bacone (1214-1294), scienziato ed epistemologo.
Bacone attirò l’attenzione sull’importanza della matematica e dell’esperienza preconizzando i grandi progressi che avrebbero potuto essere realizzati mediante la scienza.
Le idee matematiche, egli afferma, sono innate in noi (più tardi Kant dirà che sono sintetiche a priori) e identiche alle cose che esistono in natura, perchè la natura è scritta nel linguaggio della geometria. La matematica rivela quindi la verità, essa è anteriore alle altre scienze perché tratta delle quantità (Aristotele insisteva molto sulla qualità delle sostanze).
Bacone mostra in un capitolo del suo Opus Maius che ogni scienza ha bisogno della matematica (la matematica è la porta e la chiave di tutte le scienze) e i suoi argomenti mostrano una profonda consapevolezza del ruolo della matematica nelle altre scienze; tuttavia apprezza pienamente l’importanza dell’esperienza come mezzo di scoperta e di verifica dei risultati ottenuti teoricamente o in qualunque altro modo: "Il ragionamento conclude una questione; ma esso non ci fa sentire certi e sicuri nella contemplazione della verità se non quando questa verità viene trovata anche con l’esperienza."
A Bacone furono attribuite, tra l’altro, le invenzioni degli occhiali e della polvere da sparo anche se non vi sono evidenze riguardo alla prima, e se la seconda è stata per certo usata dagli arabi in periodi precedenti.
Francescano di grande cultura (conosceva diverse lingue) oltre che insofferente delle regole dominanti, si interessò anche di magia, alchimia e astrologia, ma questo non deve stupire perché all’epoca, e sino ai tempi di Newton e oltre, esse facevano parte del normale bagaglio culturale di scienziati e filosofi. Se i tempi fossero stati maturi le idee di Ruggero Bacone sulla centralità della matematica e dell’esperienza avrebbero potuto anticipare di 400 anni la rivoluzione scientifica dell’occidente
 Il lavoro presentato è il frutto dell’attività di tirocinio svolta dall’autore (SILSIS-MI), presso un Liceo Scientifico di Milano. Si tratta di un’attività di insegnamento riguardante l’introduzione al Calcolo delle Probabilità per analizzare le situazioni di incertezza, in particolare i giochi cosiddetti d’azzardo.
Il lavoro presentato è il frutto dell’attività di tirocinio svolta dall’autore (SILSIS-MI), presso un Liceo Scientifico di Milano. Si tratta di un’attività di insegnamento riguardante l’introduzione al Calcolo delle Probabilità per analizzare le situazioni di incertezza, in particolare i giochi cosiddetti d’azzardo.
L’idea di proporre tale argomento è scaturita, dopo un’attenta attività di osservazione della classe, dalla programmazione curriculare, dal contesto scolastico ed anche da un giusto confronto con l’insegnante accogliente grazie alla splendida esperienza di grande collaborazione dovuta alla sua disponibilità e in particolare al suo metodo di insegnamento: dialogico comunicativo attraverso il quale discutere e proporre problemi da risolvere come casi di studio, metodologia che ho adottato durante il mio intervento attivo.
L’argomento è stato poi realmente preso in considerazione insieme all’insegnante accogliente a seguito dell’indagine sulla tendenza rispetto alla scelta universitaria: Economia e Commercio, Scienze della Comunicazione, e in generale facoltà che prevedono un corso introduttivo al Calcolo delle Probabilità già al I anno, al fine di fornire un’adeguata panoramica dell’argomento che spesso, per mancanza di tempo, viene un po’ trascurato nel programma curriculare, stimolando anche la curiosità degli allievi in proposito.
Lo sviluppo del progetto è stato articolato in 5 ore di incontri durante i quali sono stati affrontati anche degli esempi proposti come esercizi/problemi da risolvere inerenti agli argomenti trattati durante la lezione. Al termine della prima lezione ho fornito agli studenti gli appunti della stessa con i relativi esercizi e l’analogo per la lezione successiva.
Dalla seconda lezione in poi ho fornito alla fine di ogni intervento le dispense relative alla successiva lezione. Abbiamo adottato questa strategia per verificare il livello di attenzione alla prima lezione e per fornire, a più volenterosi, la possibilità di effettuare una lettura individuale prima della spiegazione in modo che gli studenti potessero testare la propria capacità di comprensione di un testo scritto.
Questa metodologia ha stimolato, in quasi tutti gli allievi, la curiosità di effettuare questa pre-lettura. Le lezioni sono, quindi, state sempre più partecipate e più scorrevoli. Alla fine, per verificare l’apprendimento dei concetti fondamentali (calcolo combinatorio, probabilità condizionata ed indipendenza e legge dei grandi numeri), è stata somministrata una prova sotto forma di test a risposta multipla (tempo concesso un’ora di lezione). La verifica ha dato risultati mediamente discreti.
SOMMARIO
Introduzione
Presentazione del contesto e analisi dell’esperienza di tirocinio
Prerequisiti
Contenuti: presentazione delle lezioni
Impariamo a contare
Probabilità di eventi
Calcolo combinatorio
Modelli probabilistici
Probabilità condizionata e indipendenza
Variabili aleatorie discrete e loro distribuzione
Valore atteso
Probabilità e giochi
Calcolo di probabilità nei giochi: lotto, superenalotto, dadi, roulette
Quote e guadagno probabile
Giochi equi/iniqui
Sistemi/strategia di gioco
Legge dei grandi numeri e giochi
Verifica dell’apprendimento
Conclusioni e analisi critica dell’esperienza
Appendici
Bibliografia
 Tantissimi esercizi svolti sulle equzioni di primo grado con verifica e sui problemi risolvibili con le equazioni di primo grado.
Tantissimi esercizi svolti sulle equzioni di primo grado con verifica e sui problemi risolvibili con le equazioni di primo grado.
 Tra i grandi scacchisti italiani del XVI secolo che si sfidavano presso le corti di re e mecenati è da annoverare il cutrese Giovanni Leonardo di Bona. Egli riuscì a sconfiggere, nel 1575, il campione di Spagna Ruy Lopez, vescovo di Segura presso la corte del re Filippo II di Spagna; per questa vittoria ottenne per Cutro il titolo di Città e per i suoi cittadini l’esenzione dalle tasse per vent’anni. Per ricordare questa impresa, a Cutro, “la città degli scacchi”, viene organizzato un torneo internazionale a cui partecipano campioni di tutto il mondo. Il torneo è ormai giunto alla XV edizione.
Tra i grandi scacchisti italiani del XVI secolo che si sfidavano presso le corti di re e mecenati è da annoverare il cutrese Giovanni Leonardo di Bona. Egli riuscì a sconfiggere, nel 1575, il campione di Spagna Ruy Lopez, vescovo di Segura presso la corte del re Filippo II di Spagna; per questa vittoria ottenne per Cutro il titolo di Città e per i suoi cittadini l’esenzione dalle tasse per vent’anni. Per ricordare questa impresa, a Cutro, “la città degli scacchi”, viene organizzato un torneo internazionale a cui partecipano campioni di tutto il mondo. Il torneo è ormai giunto alla XV edizione.

Percorrendo la strada statale SS106, a 15 Km. a Sud-Ovest da Crotone, in una zona collinare, all’ingresso della cittadina, ci si imbatte in un cartello: "Benvenuti a Cutro la città degli scacchi." Giunti al centro si scopre una piazza molto suggestiva, con una pavimentazione in marmo che rappresenta una grande scacchiera e, a margine, un obelisco sormontato da una statua intitolata a Giò Leonardo di Bona (1552-1597), detto il “Puttino” per la sua bassa statura, uno dei grandi campioni italiani del ‘500.
In un’epoca in cui il gioco degli scacchi era molto apprezzato presso le corti europee e si organizzavano sfarzosi tornei e contese con in palio ingenti premi, egli compì grandi imprese. Si narra che riuscì a liberare il fratello battendo a scacchi il capo dei pirati saraceno che lo aveva in ostaggio. Nel 1575, presso la corte del re di Spagna Filippo II, sconfisse il campione d’Europa del tempo, Ruy Lopez, vescovo di Segura, ottenendo il titolo di campione di scacchi “d’Europa e del Nuovo Mondo”. Per questa vittoria ottenne dal re la grazia che Cutro diventasse “Città” e i suoi cittadini fossero esentati dalle tasse per un ventennio.
 L’impresa è stata celebrata nell’opera di Luigi Mussini (1883) "Sfida scacchistica alla Corte di Spagna" (figura 1) che si trova presso il Monte dei Paschi di Siena.
L’impresa è stata celebrata nell’opera di Luigi Mussini (1883) "Sfida scacchistica alla Corte di Spagna" (figura 1) che si trova presso il Monte dei Paschi di Siena.
Dagli anni novanta la cultura scacchistica a Cutro ha avuto un notevole impulso, grazie all’impegno profuso dall’amministrazione comunale, dall’associazione e dal circolo scacchistici.
Fin dalle scuole elementari, i bambini imparano a giocare e si organizzano sfide a tutti i livelli. Ogni anno, il 12 agosto, sulla piazza-scacchiera, ha luogo la rappresentazione teatrale della vittoria del Puttino alla corte di Spagna, con figuranti in costume nel ruolo “scacchi viventi” che inscenano la partita (figura 2).
In primavera si organizza il torneo internazionale, cui partecipano campioni di fama mondiale.
 Quest’anno la manifestazione, che è giunta alla XV edizione, avrà luogo dal 18 al 26 Aprile. Essa comprende i seguenti tornei (si veda il regolamento alla pagina web http://www.altirchess.com/cutro/ ):
Quest’anno la manifestazione, che è giunta alla XV edizione, avrà luogo dal 18 al 26 Aprile. Essa comprende i seguenti tornei (si veda il regolamento alla pagina web http://www.altirchess.com/cutro/ ):
Magistrale – riservato ai giocatori con punteggio Elo F.I.D.E. o F.S.I. superiore a 1999;
Open – riservato ai giocatori con punteggio Elo F.I.D.E. o F.S.I. inferiore a 2000 (o privi di punteggio Elo);
Under 14 – riservato ai giocatori fino a 14 anni di età (nati dopo il 31.12.1994) – Torneo promozionale non valido per le variazioni Elo. Abbinamento: sistema svizzero.
Sitografia
Per ulteriori informazioni: http://www.comune.cutro.kr.it/?q=taxonomy/term/18
http://www.comune.cutro.kr.it/?q=node/485
http://www.cutroweb.it/content/view/13/30/1/1/
http://it.wikipedia.org/wiki/Cutro
http://scacchi.qnet.it/manuale/storia.htm
Ringraziamenti
Ringrazio il responsabile della manifestazione dr. Salvatore Perri per i documenti e le foto che mi ha prontamente fornito ([email protected]).

Figura 4 Torneo Internazionale 2008

Figura 5 Torneo Internazionale 2008

Figura 6 Torneo Internazionale 2008
 Come i cambiamenti sociali la speculazione filosofica le scoperte scientifiche e il progresso tecnologico hanno influito sulla concezione umana del Tempo
Come i cambiamenti sociali la speculazione filosofica le scoperte scientifiche e il progresso tecnologico hanno influito sulla concezione umana del Tempo
Scienze: Da Anassimandro a Newton: la storia delle scienze attraverso i modelli dell’universo
Fisica E Matematica: Da Newton a Maxwel: il campo gravitazionale e quello elettrico
Latino: Lucrezio: De rerum Natura, un poema nuovo Seneca: La riflessione morale sul tempo
Filosofia: S. Agostino e Bergson: il tempo soggettivo Marx: Il tempo dei lavoratori
Letteratura: Ungaretti: La parola per cogliere l’attimo
Storia dell’arte: Il Futurismo: il tempo della dinamicità La metafisica: Il tempo enigmatico
Storia: Il Boom Economico: dal tempo libero all’omologazione
Lingua inglese: Becket: Waiting for Godot: il tempo dell’uomo moderno
 Qui l’ispirazione è un classico: per appunto, la “dollar auction” di Martin Shubik. C’è bisogno di un po’ di gente, almeno una dozzina, direi. Più ce n’è, meglio è. Funziona, garantito!
Qui l’ispirazione è un classico: per appunto, la “dollar auction” di Martin Shubik. C’è bisogno di un po’ di gente, almeno una dozzina, direi. Più ce n’è, meglio è. Funziona, garantito!
 “Dov’è la matematica? Dove la si può concretamente incontrare? Nei libri, difficili, spesso incomprensibili ai più, che le sono dedicati? Nelle teste più brillanti che li hanno pensati? Nelle realizzazioni più strabilianti che ne sono derivate?[…] La sua presenza è in realtà percepibile dentro la nostra vita di tutti i giorni, dentro le nostre città e le nostre case.” BERTOLINI M. et al., Matemilano.
“Dov’è la matematica? Dove la si può concretamente incontrare? Nei libri, difficili, spesso incomprensibili ai più, che le sono dedicati? Nelle teste più brillanti che li hanno pensati? Nelle realizzazioni più strabilianti che ne sono derivate?[…] La sua presenza è in realtà percepibile dentro la nostra vita di tutti i giorni, dentro le nostre città e le nostre case.” BERTOLINI M. et al., Matemilano.
INTRODUZIONE
La geometria, come la matematica, non è una disciplina chiusa nelle regole di un libro, ma è percepibile nella realtà quotidiana; il punto di partenza del suo insegnamento diventa dunque l’esperienza concreta.
Occorre che conoscenze e abilità non risultino imposizioni formali ma, attraverso l’integrazione del sapere con il saper fare, rappresentino vere conquiste intellettuali. Invitare a scoprire la geometria nell’esperienza di tutti i giorni (nella natura, negli oggetti, nelle composizioni architettoniche, nell’arte) significa pensare a percorsi dai contenuti adeguati, realizzati in contesti efficaci, presentati con un linguaggio adatto, integrati con il contributo di altre discipline e, in particolare, sostenuti dall’idea che non si impara geometria se non si fa geometria.
La mia esperienza di tirocinio è stata guidata dal desiderio di presentare fatti e situazioni geometricamente ricche perché fossero i bambini stessi a costruire il concetto di simmetria su cui il percorso verteva. La realtà voleva essere punto di partenza e punto di arrivo, perché i bambini, dopo aver operato con oggetti concreti, immagini e figure geometriche, tornassero a riconoscere il concetto astratto nel loro mondo. Mentre i libri di testo il più delle volte affrontano la simmetria richiedendo all’alunno di completare figure su un piano quadrettato dove è tracciato unicamente l’asse verticale, il percorso voleva tentare di comunicare che la simmetria è intorno a noi: tutto dipende da come e cosa si vuole guardare!
La simmetria non è solo in un disegno di una farfalla stilizzata e un po’ squadrata sul libro, ma la si scopre in una collina che si rispecchia in un lago immobile, nella piuma colorata di un pavone, nel cerchione dell’auto del papà.
Il percorso voleva anche diventare occasione per rispondere ad alcune domande relative a come i bambini percepiscono la simmetria. Per questo si è pensato di sfruttare le potenzialità offerte dalla comunicazione per immagini derivanti dalla loro grande varietà e dal potere di coinvolgimento: esse spiazzano, richiamano il vissuto di ognuno di noi, alludono e rinviano ad altro, affascinano (non sono forse belle le immagini geometriche? E non c’è forse geometria nelle immagini belle?).
Alcune domande hanno guidato la scelta delle diverse immagini su cui i bambini avrebbero lavorato per estrapolare il concetto di simmetria le cui risposte, un domani, potrebbero essere utili per chi vorrà progettare un percorso didattico simile.
– E’ vero, come affermano alcune ricerche in campo psicologico, che i bambini percepiscono con più facilità la simmetria verticale?
– Nella ricerca della simmetria i bambini considerano il colore?
– E’ più facile riconoscere la simmetria in figure geometriche perfette o in immagini reali non precise?
– Nella scoperta della simmetria si osserva la figura nella sua globalità o vengono presi in considerazione i particolari?
– Uno sfondo non neutro confonde la ricerca della simmetria della figura in primo piano?
– Come si comporta un bambino di fronte ad immagini che possiedono innumerevoli simmetrie? E ad immagini che non hanno alcuna simmetria?
Dal punto di vista metodologico si voleva utilizzare una didattica di tipo attivo, che avrebbe previsto la partecipazione in prima persona di tutti gli alunni in quanto soggetti attivi e costruttori delle proprie conoscenze.
Chiedere ai bambini di mettersi in gioco concretamente con oggetti significativi dal punto di vista geometrico, di lavorare in gruppo e di partecipare ai momenti di discussione che avrebbero seguito le attività proposte, significava anche voler coinvolgere e motivare all’apprendimento.
Io e l’insegnante abbiamo ricoperto più ruoli:
quello di osservatore che annota le frasi più significative dei bambini, in modo da sviluppare successivamente la discussione in classe e intervenire, se necessario, con domande-stimolo per superare eventuali momenti di empasse; di mediatore che potenzia le conoscenze possedute dal bambino arricchendole di nuovi concetti;
di regolatore che guida la comunicazione e le relazioni;
di facilitatore che rende significativo l’apprendimento. L’obiettivo era trasformare la classe in un laboratorio dove alunni e docenti facessero esperienza concreta di geometria guidando i bambini senza fornire nozioni o soluzioni pronte e aiutandoli a porsi in un atteggiamento di ricerca per abituarsi a ragionare, a sperimentare e a costruire un sapere comune e condiviso.
INDICE
CAPITOLO 1. PERCEZIONE E SIMMETRIA
1.1 La percezione: teoria e modelli
1.2 Lo sviluppo percettivo
1.2.1 La percezione nell’infanzia
1.2.2 La percezione nella fanciullezza
1.2.3 Conclusioni
1.3 Il senso dell’ordine
1.3.1 La percezione della simmetria
1.3.2 Simmetria e asimmetria
1.4 La simmetria
1.4.1 Un modulo che si ripete
1.4.2 Diversi tipi di simmetria
1.4.3 Modelli concreti per parlare di simmetria
CAPITOLO 2. LA METODOLOGIA
2.1 L’alunno come soggetto attivo nell’apprendimento
2.1.1 Dewey e il discente attivo
2.1.2 Piaget e la costruzione attiva del sapere
2.2 Il ruolo dell’insegnante
2.2.1 Vygotskij e la Zona di Sviluppo Prossimale
2.2.2 Feuerstein e la mediazione dell’apprendimento
2.3 L’apprendimento cooperativo
2.3.1 Alcune basi teoriche
2.3.2 Il lavoro di gruppo: vantaggi e problemi
2.3.3 Organizzare il lavoro di gruppo
CAPITOLO 3. IL CONTESTO
3.1 La scuola
3.2 La classe
3.3 Progetto e obiettivi
CAPITOLO 4. IL PERCORSO
4.1 Per iniziare
4.2 Dalla realtà alle immagini del reale
4.2.1 1a attività – Una foglia e un’arancia
4.2.2 2a attività – Dall’oggetto alla sua impronta
4.2.3 3a attività – La linea magica
4.2.4 4a attività – Assi di simmetria visibili e invisibili
4.2.5 5a attività – La realizzazione di figure simmetriche
4.2.6 6a attività – Alla ricerca degli assi di simmetria
4.2.7 7a attività – Alla ricerca delle rotazioni
4.3 Dalle immagini del reale alle figure geometriche
4.3.1 8a attività – La verifica con i segnali stradali
4.3.2 9a attività – La simmetria delle figure geometriche
4.4 Dalle figure geometriche alla realtà
CONCLUSIONI
BIBLIOGRAFIA
Scarica la tesi Toccare per vedere, l’apprendimento della geometria con gli occhi e con le mani
I libri sono offerti gratuitamente da Gorilla.it, la grande libreria tecnica on line
9788861592278 Di duelli, scacchi e dilemmi Mondadori
9788842498865 pitagora si diverte vol. 2 Mondadori
9788842498469 Pitagora continua a divertirsi 70 giochi matematici Mondadori
9788842420040 Giochi matematici del medioevo Mondadori
9788842497097 Intorno Ai Numeri. Oggetti, Proprietà, Finzioni Utili Mondadori
9788842498452 Lobacevskij. L’invenzione Delle Geometrie Non Euclidee Mondadori
9788842491477 Da Pitagora a Borges. Discussioni in rete sull’infinito Mondadori Citrini Claudio
9788842495956 i matematici e le macchine intelligenti Mondadori
9788842496144 Matematica Mondadori Guerraggio Angelo
97888495918 Sulle orme del Caos. Comportamenti complessi Mondadori
048680630 Classic mechanics, 2nd edition Dover
0486636127 Tensor Calculus Dover
0486453138 Analythical geometry of three dimensions Dover
0486670473 Guide To Feynman Diagrams Dover
0486414531 combinatorial optimization Dover
048666620 Mathematics For The Physical Sciences Dover
0486656209 Number Theory And Its History Dover
0486466256 Partial Differential Equations Of Parabolic Type Dover
0486432610 Theoretical Mechanics Of Particles Dover
0486442780 Control systeme disign Dover
048665088x Digital Filters Dover
0486266206 greek astronomy Dover
0486240738 a history of greek mathematics I volume Dover
0486240746 a history of greek mathematics II volume Dover
0486428133 The Riemann Zeta Function Dover
0486246116 Short cut-Math Dover
0486659437 Games and decisions Dover
0486419746 Einstein’s legacy Dover
0486253465 Great experiments in Physic Dover
0486441628 Integral Equations Dover Dover
9780747591061 Harry Potter and the deathly allows Dover
 Intorno al 1200 alla corte di Federico II° a Palermo si tenne una gara o meglio una sfida non convenzionale: un illustre forestiero, Leonardo da Pisa detto Fibonacci, tentò la risoluzione di una equazione cubica $X^3 + 2X^2 + 10X = 20$. Leonardo, senza rivelare come era pervenuto al risultato, dette la seguente soluzione espressa in frazioni sessagesimali: $X = 1 +22/60 +7/(60^2) +42/(60^3) +33/(60^4) +4/(60^5) +40/(60^6) = 1.368808108$
Intorno al 1200 alla corte di Federico II° a Palermo si tenne una gara o meglio una sfida non convenzionale: un illustre forestiero, Leonardo da Pisa detto Fibonacci, tentò la risoluzione di una equazione cubica $X^3 + 2X^2 + 10X = 20$. Leonardo, senza rivelare come era pervenuto al risultato, dette la seguente soluzione espressa in frazioni sessagesimali: $X = 1 +22/60 +7/(60^2) +42/(60^3) +33/(60^4) +4/(60^5) +40/(60^6) = 1.368808108$
La soluzione trovata aveva un errore inferiore ad $1/31$ miliardi ed è molto migliore di quella che si può ottenere con l’opzione Strumenti-Ricerca obiettivo di Excel ($X = 1.368817555$).
Benché l’opera più importante di Leonardo si chiamasse Liber abaci nella disputa tra abachisti e algoritmisti egli si schierò tra i secondi. Per gli uni i conti si facevano meglio con l’abaco (una specie di pallottoliere) per gli altri con la penna seguendo passaggi e regole predefinite (uno dei primi algoritmi fu quello di Euclide per il calcolo del massimo comune divisore).
La vittoria fu all’epoca dalla parte degli algoritmisti e nel secolo scorso gli algoritmi (la parola viene dal nome del matematico arabo al-Khuwarizmi) furono la base per lo sviluppo dei software per computer dedicati al calcolo numerico e logico.
Fibonacci, studiando il problema della riproduzione dei conigli arrivò a definire una delle prime e più importanti serie matematiche: 1,2, 3, 5, 8, 13, 21, …. In questa serie ogni numero, a parte i primi due, è calcolato come la somma dei due precedenti.
La serie di Leonardo trovò inaspettate corrispondenze in natura (es. disposizione dei semi del girasole) ed in estetica (Il rapporto tra due valori successivi della serie tende all’infinito al rapporto aureo). L’efficiente metodo di Fibonacci per calcolare il minimo di una funzione monodimensionale o una radice di una equazione (sia essa algebrica o trascendente) è basato sull’uso della serie da lui individuata ed è più efficiente ed altrettanto robusto del metodo dicotomico inoltre, come quello, non richiede il calcolo delle derivate.
Nelle organizzazioni che debbono valutare grandi progetti d’investimento è importante il calcolo del tasso di rendimento interno (il massimo costo del denaro sopportabile dal progetto). Calcolare il tasso di rendimento interno di un progetto significa risolvere un’equazione polinomiale di grado $n$, dove $n$ rappresenta il numero degli anni di vita del progetto (per i progetti impiantistici anche 20 o più anni); se poi il cash-flow deve essere espresso su base mensile l’equazione da risolvere può essere di grado 200 o più.
Quando iniziai a lavorare negli anni 70 non esistevano le tabelle elettroniche (e neanche le funzioni finanziarie, tipo =TIR.COST() oggi disponibile in Excel, che comunque hanno parecchi limiti). Ricordo che usando il metodo dicotomico riuscimmo a ridurre il tempo di calcolo di un programma, che girava su microcomputer Olivetti P652, da una media di 20 minuti a meno di un minuto
 L’argomento prescelto per questo elaborato rispecchia in modo fedele la storia di vita e di ricerca del suo autore: nasce infatti dal desiderio di coniugare un decennale percorso di studi nell’ambito dei beni culturali e dell’archeologia con il più recente interesse per la pedagogia e per le discipline dell’ambito della formazione. Nasce, inoltre, dalla volontà di sostanziare in termini teorici il lavoro svolto in prima persona come operatore didattico nei musei e sul campo dei beni culturali del nostro territorio.
L’argomento prescelto per questo elaborato rispecchia in modo fedele la storia di vita e di ricerca del suo autore: nasce infatti dal desiderio di coniugare un decennale percorso di studi nell’ambito dei beni culturali e dell’archeologia con il più recente interesse per la pedagogia e per le discipline dell’ambito della formazione. Nasce, inoltre, dalla volontà di sostanziare in termini teorici il lavoro svolto in prima persona come operatore didattico nei musei e sul campo dei beni culturali del nostro territorio.
La tematica in esame corre il rischio, già nella definizione del titolo, di essere ambigua o nebulosa. I due ambiti d’indagine presi in esame, quello della didattica nel museo o nel territorio e quella delle nuove tecnologie, sono entrambi molto vasti ed in continua evoluzione; per questo motivo si è posta in più occasioni nel corso dell’elaborato la necessità di puntualizzare i confini della ricerca, di mettere a fuoco l’ambito d’indagine e, in alcuni casi, di operare precise scelte di campo. Perciò si è scelto di dare alla tesi una struttura rigorosa, che forse potrà apparire un po’ schematica, ma necessaria per poter sviscerare, si spera senza ambiguità, i nodi tematici fondamentali.
Nel primo capitolo si prende in esame la questione della didattica come “scienza –dice Franco Frabboni- della traslocazione della conoscenza” applicata al museo, ai beni culturali, al territorio, al patrimonio. Attraverso una breve storia delle definizioni sviluppate nel corso del Novecento nel dibattito italiano e in quello europeo, si arriva a definire quale campo d’indagine privilegiato quello della didattica dei beni culturali, terminologia fortemente inclusiva che permette di considerare in un’unica categoria “tutte le testimonianze aventi valore di civiltà”, fra cui, ovviamente, i musei e le mostre temporanee; ma anche gli scavi archeologici, gli antichi itinerari, il paesaggio con le sue specificità, gli archivi storici, i beni immateriali, le auto d’epoca…
Dopo avere definito la natura della conoscenza che si desidera “traslocare”, si individuano i tratti salienti della figura dell’operatore didattico, le specificità del suo agire e il (mancato) riconoscimento istituzionale della sua professionalità attraverso una breve analisi delle fonti legislative. Ne emerge il quadro un po’ sconfortante di una attività che, nell’ambito dell’organizzazione degli enti pubblici deputati alla tutela del patrimonio, è considerata uno dei “servizi aggiuntivi”, insieme ai servizi di pulizie e di ristorazione. Nell’ambito delle istituzioni formalmente deputate alla istruzione e formazione, la didattica dei beni culturali viene invece “relegata” negli spazi dedicati alle attività trasversali rispetto al curricolo, programmata attraverso percorsi interdisciplinari. Nonostante dunque sul piano teorico si ribadisca la necessità di valorizzarla e dare ad essa piena dignità, si tratta da ogni punto di vista di una attività didattica fortemente marginalizzata. Si vedrà infatti come, sul piano della riflessione pedagogica, la didattica dei beni culturali richiami l’importanza di costruire quello che Frabboni definisce un “sistema formativo integrato”, nel quale il territorio divenga il vero trait d’union dell’educazione permanente, uno strumento importante affinchè ogni individuo si costruisca una più forte identità sociale conquistando le chiavi della partecipazione attiva ad una società che diviene, contestualmente, più consapevole di sé e della propria storia. La didattica dei beni culturali si avvale di specifiche strategie che devono prevedere, rispetto al momento di fruizione diretta, un “prima” e un “dopo” altamente strutturati, la programmazione e la valutazione o, come efficacemente suggerisce Emma Nardi, pensare e valutare per ri-pensare. La didattica museale si confronta sistematicamente con un pubblico eterogeneo e sconosciuto, rispetto al quale diviene indispensabile prendere attentamente in esame le dinamiche che sorgono nel triangolo operatore- beni culturali- pubblico. Si giunge, così, a delineare una nuova e attuale prospettiva che mette a fuoco il museo (o il territorio), quale contesto privilegiato di sperimentazione per l’inclusione sociale e culturale delle diversità, a dispetto della sua storia di istituzione marcata da una valenza elitaria.
Nel secondo capitolo si proporrà una breve sintesi del dibattito relativo alle nuove tecnologie, anche in questo caso cercando di definire il campo delle “tecnologie dell’educazione”: il dibattito internazionale passa attraverso la valorizzazione del computer a cui si attribuisce un ruolo di “tutor” per potenziare l’individualizzazione in una prospettiva di insegnamento tradizionale, fino a promuovere l’uso delle tecnologie come supporto alla costruzione di modelli di insegnamento/apprendimento innovativi, su base partecipativa e costruttivista. Non sono le tecnologie, in sintesi, a modificare il mondo dell’educazione, ma queste divengono uno strumento potente nelle mani dell’insegnante, al quale spetta il compito di allestire adeguati ambienti formativi. Le nuove tecnologie, si vedrà, possono assumere un ruolo oltremodo significativo nella trasmissione di valori complessi nell’ambito dei beni culturali e delle arti visive. Trattandosi di strumenti efficaci su un piano “sinestetico” essi sono in grado di amplificare la percezione visiva e sensoriale dell’oggetto in esame, di trasmettere, ad esempio, gli esiti scientificamente complessi e problematici della ricerca storica attraverso quadri d’insieme ricostruttivi ed evocativi che sono in grado di raggiungere qualsiasi destinatario e di modulare perfettamente il contenuto da trasmettere. Verranno quindi esaminate le varie tipologie di strumenti utilizzati per potenziare la didattica museale e, in base all’analisi del loro funzionamento nel contesto della didattica dei beni culturali, si individuerà quale parametro saliente quello della loro “ubicazione”, dato dalla distinzione tra tecnologie “in presenza” e “ad accesso remoto”. Attraverso le nuove tecnologie in presenza si vedrà come divenga possibile implementare i confini della fruizione ed aumentarne la qualità; attraverso le nuove tecnologie a distanza, inoltre, è possibile agevolare la programmazione di quel “prima” e quel “dopo” che differenziano la didattica strutturata dalla divulgazione. Tutte queste diversificate applicazioni convergono a fornire alla didattica museale un contributo innovativo ed importante, che permette di trasformare il processo di apprendimento attivato dal museo; giungendo a concludere, sulla linea di Luciano Cecconi, che “quello multimediale è il mezzo per eccellenza della didattica museale”.
Infine, il terzo capitolo del lavoro verrà dedicato all’analisi di un caso: la vicenda di una mostra temporanea dedicata al mondo medievale supportata da numerose installazioni multimediali diversificate e complesse. Di questo evento verranno analizzate le fasi progettuali, le esperienze divulgative e didattiche e la fruizione da parte del pubblico; si considererà inoltre il risultato di un progetto strutturato di didattica dei beni culturali costruito intorno a questo evento, e svolto insieme a due classi di scuola primaria. Questa esperienza permetterà di concretizzare le varie parti della trattazione precedente: il problema dell’analisi delle differenti modalità di comunicazione col pubblico in museo, un esempio di progettazione trasversale al curricolo pensata intorno ai beni culturali, la funzione delle nuove tecnologie nelle loro diverse applicazioni nell’ottica degli allestitori e dei fruitori, le riflessioni dei bambini rispetto alla tecnologia, la possibilità di utilizzare la storia e i beni culturali come strumento di integrazione delle diversità.
Scarica le tesi LA PRATICA DIDATTICA FRA BENI CULTURALI E NUOVE TECNOLOGIE: L’ESPERIENZA DELLA MOSTRA “VIVERE IL MEDIOEVO”
 Io non so niente. Ignoro se chi m’ha creato m’ha destinato al Cielo o all’Inferno. Ma un liuto e una coppa e un bel volto sulla proda del campo son per me monete sonanti: a te la cambiale del Cielo. (Omar Khayyam: Robaiyyat)
Io non so niente. Ignoro se chi m’ha creato m’ha destinato al Cielo o all’Inferno. Ma un liuto e una coppa e un bel volto sulla proda del campo son per me monete sonanti: a te la cambiale del Cielo. (Omar Khayyam: Robaiyyat)
Omar Khayyam, nato in Persia intorno al 1050 d.C. scrisse un’ Algebra che andava oltre quella di al-Khuwarizmi fino ad includere equazioni di terzo grado.
Come i suoi predecessori arabi, Khayyam forniva per le equazioni di secondo grado tanto le soluzioni aritmetiche quanto quelle geometriche (sintetiche); per le equazioni di terzo grado generali, riteneva (erroneamente, come poi fu dimostrato durante il Rinascimento italiano da Del Ferro, Tartaglia, Cardano e Ferrari) che fossero impossibili soluzioni algebriche pertanto ne dava soluzioni geometriche avvertendo però che: " Questa – l’equazione cubica – non può essere risolta mediante la geometria piana (ossia facendo uso solo di riga e compasso) giacché contiene un cubo. Per la sua soluzione sono necessarie sezioni coniche".
Per equazioni superiori al terzo grado Khayyam non prevedeva la possibilità di usare metodi geometrici del genere perché lo spazio non contiene più di tre dimensioni: " Quello che viene chiamato dagli algebristi quadrato-quadrato è in termini di grandezza continua un fatto puramente teorico. Esso non esiste nella realtà in alcun modo".
Uno dei più fecondi contributi dell’eclettismo arabo fu la tendenza a colmare la frattura esistente tra l’algebra e la geometria. Il passo decisivo in questa direzione venne fatto molto più tardi da Cartesio, ma Khayyam si muoveva già in questa direzione quando scriveva: "Chiunque pensi che l’algebra sia uno stratagemma per conoscere ciò che non si sà, ha una idea sbagliata di essa. Non si dovrebbe fare alcuna attenzione al fatto che l’algebra e la geometria presentano un aspetto così diverso. L’algebra non è altro che la dimostrazione di fatti geometrici".
In tempi recenti lo Humanistic management ha fortemente criticato lo Scientific Management (in particolare A. Smith e F. Taylor) incoraggiando un approccio alla soluzione dei problemi delle organizzazioni basato prevalentemente sulla poesia, la filosofia, la musica, lo spettacolo, la comunicazione, ecc.. La critica si è concentrata sui metodi quantitativi, la statistica, l’ottimizzazione e l’approccio razionale ai problemi.
Il problem solving, come filosofia volta all’ottenimento di risultati, accetta contributi di qualunque tipo purché efficaci ed efficienti: in questa ottica il poeta e matematico Khayyam può essere il simbolo del superamento della contrapposizione tra la cultura umanistica e quella scientifica.
Il Fondo per Studenti Italiani offre un’ assistenza finanziaria, fino a 15.000 euro, sotto forma di prestito d’onore ai laureati italiani che vogliono iscriversi a un Master o Ph.D. presso università negli Stati Uniti.
La restituzione del capitale più un modesto contributo, che decorre dal momento dell’erogazione, avverrà in 24 rate trimestrali fisse (6 anni) da corrispondere solo dopo il 30mo mese successivo all’erogazione. *Dto il limitato ammontare del finanziamento, esso è particolarmente adatto come complemento ad altre borse.
Tutti i settori di studio saranno presi in considerazione, con priorità per Business Administration, Business Law e per specializzazioni in materie tecnico-scientifiche ed in tecnologie industriali avanzate.
Requisiti:
cittadinanza e residenza italiana;
diploma di laurea italiano, vecchio o nuovo ordinamento;
età massima 35 anni alla scadenza della domanda;
ottimo curriculum accademico e/o professionale;
ottima conoscenza della lingua inglese comprovata dal Toelf;
piano di studi o di ricerca per il corso prescelto;
ammissione all’università statunitense o situazione delle domande in corso.
Scadenza: 10 maggio 2009 per l’anno accademico 2009/2010.
 Il libro Gli scacchi di Luca Pacioli ha lo scopo di celebrare Fra’ Luca Pacioli, nato a Sansepolcro (Arezzo), nel 1445, conosciuto come eclettico matematico dell’epoca rinascimentale, codificatore, nei bilanci, dell’uso della partita doppia; Pacioli voleva insegnare e illustrare ai contemporanei il gioco degli scacchi, scrivendo un trattato di cui si era persa ogni traccia per cinquecento anni, il De ludo scachorum. Gorilla.it
Il libro Gli scacchi di Luca Pacioli ha lo scopo di celebrare Fra’ Luca Pacioli, nato a Sansepolcro (Arezzo), nel 1445, conosciuto come eclettico matematico dell’epoca rinascimentale, codificatore, nei bilanci, dell’uso della partita doppia; Pacioli voleva insegnare e illustrare ai contemporanei il gioco degli scacchi, scrivendo un trattato di cui si era persa ogni traccia per cinquecento anni, il De ludo scachorum. Gorilla.it
 Recentemente il trattato è stato riconosciuto a Gorizia, conservato presso l’Archivio di Stato: Aboca Museum Edizioni sta preparando un fedele e pregiato facsimile. Il libro Gli scacchi di Luca Pacioli è anche un commentario nel quale illustri esperti nel campo della paleografia, della linguistica e ovviamente degli scacchi, certificano non solo la paternità pacioliana del trattato, ma anche la vasta preparazione scacchistica e matematica dell’autore. Dei 114 partiti presentati dal Pacioli nel De ludo Scachorum alla fine del Quattrocento, 87 sono giocati alla vecchia maniera e 27 con le nuove regole "a la rabiosa", ancora oggi immutate. Questo testo, di estremo intersse per tutti gli appassionati di scacchi, di storia rinascimentale e di matematica, dimostra che questo gioco si presta a fondere la logica e l’istinto, rendendo relative perfino rigide regole numeriche e statistiche. Nel libro troviamo interessanti riferimenti alle conoscenze del frate di Sansepolcro, come il suo maestro Piero della Francesca, il suo compagno di viaggi e di corte Leonardo da Vinci, la splendida mecenate Isabella d’Este, alla quale il De ludo è dedicato. Sulla scacchiera, si può solo dire che rimane ancorata nella forma e forse nelle dimensioni a quelle dei proto-giochi delle civiltà egizio-indo-arabe, da cui possono essere derivati alcune misure “naturali” o pitagoriche. Ad esempio, ogni casella curiosamente ha il lato di 55 mm, numero che appartiene alla serie numerica di Fibonacci, così come il numero 8, che è alla base della struttura della stessa scacchiera. Inoltre, il totale delle caselle corrisponde al quadrato dell’8 (8*8 = 64), che dai pitagorici era considerato il numero della sapienza creativa del mondo. Senza considerare, poi, che l’8 include tutti i numeri simbolici inferiori. Ad un esperto di Fibonacci, di Euclide, di Archimede e dell’ordine naturale quale era il Pacioli, non potevano sfuggire i collegamenti simbolico-armonici con la scacchiera. Certo Pacioli non poteva prevedere che il suo interesse per un gioco, all’epoca interessante per trasmettere il sapere, fosse attuale ed oggetto di speculazioni scientifiche perfino nel terzo millennio. Con questa prestigiosa pubblicazione il Centro Studi Aboca Museum ha allargato i propri interessi, occupandosi dello studio di attività artistiche e scientifiche degli antichi concittadini di Borgo San Sepolcro e, in particolare, dei due vicini di casa Piero della Francesca e Luca Pacioli.
Recentemente il trattato è stato riconosciuto a Gorizia, conservato presso l’Archivio di Stato: Aboca Museum Edizioni sta preparando un fedele e pregiato facsimile. Il libro Gli scacchi di Luca Pacioli è anche un commentario nel quale illustri esperti nel campo della paleografia, della linguistica e ovviamente degli scacchi, certificano non solo la paternità pacioliana del trattato, ma anche la vasta preparazione scacchistica e matematica dell’autore. Dei 114 partiti presentati dal Pacioli nel De ludo Scachorum alla fine del Quattrocento, 87 sono giocati alla vecchia maniera e 27 con le nuove regole "a la rabiosa", ancora oggi immutate. Questo testo, di estremo intersse per tutti gli appassionati di scacchi, di storia rinascimentale e di matematica, dimostra che questo gioco si presta a fondere la logica e l’istinto, rendendo relative perfino rigide regole numeriche e statistiche. Nel libro troviamo interessanti riferimenti alle conoscenze del frate di Sansepolcro, come il suo maestro Piero della Francesca, il suo compagno di viaggi e di corte Leonardo da Vinci, la splendida mecenate Isabella d’Este, alla quale il De ludo è dedicato. Sulla scacchiera, si può solo dire che rimane ancorata nella forma e forse nelle dimensioni a quelle dei proto-giochi delle civiltà egizio-indo-arabe, da cui possono essere derivati alcune misure “naturali” o pitagoriche. Ad esempio, ogni casella curiosamente ha il lato di 55 mm, numero che appartiene alla serie numerica di Fibonacci, così come il numero 8, che è alla base della struttura della stessa scacchiera. Inoltre, il totale delle caselle corrisponde al quadrato dell’8 (8*8 = 64), che dai pitagorici era considerato il numero della sapienza creativa del mondo. Senza considerare, poi, che l’8 include tutti i numeri simbolici inferiori. Ad un esperto di Fibonacci, di Euclide, di Archimede e dell’ordine naturale quale era il Pacioli, non potevano sfuggire i collegamenti simbolico-armonici con la scacchiera. Certo Pacioli non poteva prevedere che il suo interesse per un gioco, all’epoca interessante per trasmettere il sapere, fosse attuale ed oggetto di speculazioni scientifiche perfino nel terzo millennio. Con questa prestigiosa pubblicazione il Centro Studi Aboca Museum ha allargato i propri interessi, occupandosi dello studio di attività artistiche e scientifiche degli antichi concittadini di Borgo San Sepolcro e, in particolare, dei due vicini di casa Piero della Francesca e Luca Pacioli.
Gorilla.it
 In questo lavoro descrivo un’attività svolta in classe: la costruzione e somministrazione di un questionario intitolato: “Io e il cellulare”, la tabulazione dei dati in un foglio elettronico Microsoft Excel, la creazione delle tabelle e dei grafici pivot per l’interrogazione del database.
In questo lavoro descrivo un’attività svolta in classe: la costruzione e somministrazione di un questionario intitolato: “Io e il cellulare”, la tabulazione dei dati in un foglio elettronico Microsoft Excel, la creazione delle tabelle e dei grafici pivot per l’interrogazione del database.
 Il Liceo Scientifico “L. Siciliani” di Catanzaro, in collaborazione con la Biblioteca Comunale “F. De Nobili”, intende celebrare il 14 marzo, una giornata importante sia per la Matematica (il 3.14, all’anglosassone) che per la Fisica (Einstein nacque il 14.3.1879). Il “p Day 2009” cittadino vuol essere l’occasione per riflettere su una ben più triste ricorrenza: i 70 anni dalla promulgazione delle leggi razziali,
Il Liceo Scientifico “L. Siciliani” di Catanzaro, in collaborazione con la Biblioteca Comunale “F. De Nobili”, intende celebrare il 14 marzo, una giornata importante sia per la Matematica (il 3.14, all’anglosassone) che per la Fisica (Einstein nacque il 14.3.1879). Il “p Day 2009” cittadino vuol essere l’occasione per riflettere su una ben più triste ricorrenza: i 70 anni dalla promulgazione delle leggi razziali,
dal loro fondamento col “Manifesto degli scienziati razzisti” (pubblicato la prima volta il 15.7.1938) fino al R.D.L. “Disciplina per l’esercizio delle professioni da parte dei cittadini di razza ebraica” del 29.6.1939.
Il prof. Angelo Guerraggio, coordinatore del Centro PRISTEM – ELEUSI dell’Università Bocconi di Milano, sab 14 marzo alle ore 9.00 presso l’Auditorium “A. Casalinuovo” di Catanzaro, discuterà con gli alunni il libro “Matematica in camicia nera – Il regime e gli scienziati” (Paravia Bruno Mondadori Editori, 2005).
In occasione del “p Day 2009” sarà istituito il Premio Ugo Libri, destinato ai primi classificati nelle quattro categorie (C1, C2, L1 ed L2) della fase provinciale dei Giochi Internazionali di Matematica, che si terranno sab 21 marzo 2009 nel nostro Liceo.
In una sessione d’esame di statistica, costituita da 3 appelli sono promossi un certo numero di studenti indicati in tabella con , riportando un voto medio e scarto quadratico medio s.q.m. Il voto medio dell’intera sessione è 26,4, mentre lo s.q.m. dell’intera sessione è 3,8. Calcola i dati mancanti voto medio al 3° appello e s.q.m. al 2° appello
 Ci si trova in una classe seconda dell’istituto professionale per i servizi alberghieri con quattro ore settimanali di matematica. La programmazione prevede una ricapitolazione dei contenuti dell’anno precedente, l’introduzione alla geometria analitica e lo studio dei sistemi di equazioni; all’inizio dell’anno è stato risolto qualche problema avente per modello un’equazione lineare, focalizzando l’attenzione sull’aspetto linguistico.
Ci si trova in una classe seconda dell’istituto professionale per i servizi alberghieri con quattro ore settimanali di matematica. La programmazione prevede una ricapitolazione dei contenuti dell’anno precedente, l’introduzione alla geometria analitica e lo studio dei sistemi di equazioni; all’inizio dell’anno è stato risolto qualche problema avente per modello un’equazione lineare, focalizzando l’attenzione sull’aspetto linguistico.
![]() Scarica il diario di bordo di Eredità e bagagli
Scarica il diario di bordo di Eredità e bagagli
Da diversi decenni il silicio è il materiale più usato in elettronica ed in generale nella realizzazione di microsistemi, per le sue notevoli proprietà elettriche e meccaniche. Tuttavia, il suo utilizzo in dispositivi che operino in ambienti “ostili” come quelli costituiti da alti flussi di radiazione, alte temperature o agenti chimici, presenta molte limitazioni e per questo motivo si stanno ricercando nuovi materiali.
Tra i vari materiali proposti in alternativa per la realizzazione di dispositivi adatti alle condizioni più severe, il diamante sintetico ed in particolare quello monocristallino SCD (Single Crystal Diamond), cresciuto per epitassia con tecnica CVD (Chemical Vapour Deposition) è senz’altro uno dei più promettenti. Infatti grazie alle sue notevoli proprietà, come l’alto punto di fusione, la bassa reattività chimica e l’estrema robustezza, sembra essere il candidato ideale per essere utilizzato senza danneggiamenti negli ambienti più ostili; per l’ampia gap tra banda di valenza e di conduzione è particolarmente adatto ad operare anche ad alta temperatura e in presenza di intensa luce visibile. Per la realizzazione di rivelatori a stato solido per radiazione e particelle ionizzanti, il diamante presenta quindi caratteristiche ottimali soprattutto per la sua resistenza al danno da radiazione. Possiede inoltre una elevata risoluzione dosimetrica, fondamentale in presenza di fasci incidenti di piccole dimensioni come, ad esempio, quelli della radioterapia ad intensità modulata (IMRT); i rivelatori attualmente disponibili, generalmente al silicio, sono spesso inadatti a rivelare campi di radiazione caratterizzati da elevati gradienti.
Da qualche anno sono in commercio rivelatori a diamante monocristallino naturale con ottime caratteristiche: piccole dimensioni, elevata sensibilità, alta resistenza al danno da radiazione, risposta equivalente a quella del tessuto umano, indipendenza dall’energia dei fotoni o delle particelle incidenti e linearità rispetto all’intensità della radiazione incidente. I rivelatori a diamante monocristallino naturale tuttavia, oltre ad essere molto costosi, necessitano di un trattamento di priming prima dell’uso e mostrano una non trascurabile dipendenza dal tasso di fotogenerazione. È poi usuale riscontrare un diverso comportamento tra vari rivelatori. Per superare questi limiti è in corso in vari istituti di ricerca il tentativo di sviluppare rivelatori per alte energie basati su diamante sintetico.
Il lavoro riportato nella tesi segue questa linea di attività. Esso riguarda sostanzialmente la caratterizzazione fotoelettrica di film di diamante CVD. Nella prima parte sono state studiate le caratteristiche di materiali policristallini. I campioni di diamante policristallino hanno però mostrato limiti di riproducibilità ed evidenti effetti memoria, apparentemente ineliminabili. Per questi motivi l’attenzione è stata successivamente rivolta al diamante sintetico monocristallo. La scelta di cambiare il materiale d’indagine è stata giustificata sulla base delle seguenti considerazioni. In questi ultimi anni sono stati sviluppati, presso l’università di Tor Vergata, dispositivi basati su film monocristallini SCD per la rivelazione di particelle pesanti e neutroni, sia termici che veloci; questi dispositivi hanno ottime prestazioni in termini di linearità, stabilità, affidabilità e mancanza di effetti di memoria. D’altra parte, già dagli anni novanta veniva dimostrata per il diamante la sostanziale indipendenza del meccanismo di trasporto di carica dal tipo di radiazioni e/o particelle incidenti e dal loro intervallo energetico. C’erano quindi buone possibilità che dispositivi simili a quelli per la rivelazione di particelle pesanti e neutroni potessero funzionare bene anche per elettroni e fotoni alle energie radioterapiche.
La seconda parte del lavoro è stata quindi svolta utilizzando otto prototipi di rivelatori in diamante sintetico monocristallino SCD. I dispositivi, realizzati presso i Laboratori del Dipartimento di Ingegneria Meccanica dell’Università di Roma Tor Vergata, sono costituiti da una innovativa struttura a film sottile: diamante drogato p/ diamante intrinseco/ metallo. La caratterizzazione dosimetrica è stata eseguita presso le strutture radioterapiche dell’ospedale San Filippo Neri di Roma. I dispositivi in SCD hanno mostrato prestazioni confrontabili e addirittura superiori a quelle di dosimetri commerciali in diamante naturale in termini di ripetibilità, stabilità, affidabilità e linearità della fotorisposta. I campioni di monocristallo, inoltre, non hanno evidenziato i fastidiosissimi effetti di memoria riscontrati nei materiali policristallini e sono risultati indipendenti dall’energia e dal tasso di fotogenerazione.
La tesi si articola in cinque capitoli.
Nel primo sono descritti i modelli teorici di generazione e trasporto di carica elettrica che sono alla base del meccanismo di rivelazione dei rivelatori in studio.
Nel secondo capitolo sono analizzate le proprietà del diamante, con particolare riferimento a quelle caratteristiche che ne fanno un candidato naturale per la realizzazione di rivelatori per radiazioni e particelle ionizzanti. Sempre nel secondo capitolo sono poi descritti i principali metodi di crescita del diamante sintetico, con particolare riguardo alla tecnica CVD (Chemical Vapour Deposition), che è la tecnica che viene utilizzata presso i Laboratori di “Tor Vergata” per la crescita di diamante monocristallino di ottima qualità per la realizzazione di dispositivi optoelettronici.
Nel terzo capitolo viene descritto il lavoro di caratterizzazione su rivelatori in diamante policristallino con misure di fotoconducibilità in funzione dell’intensità di radiazione incidente, effettuate con una sorgente laser Argon-Fluoro ad eccimeri nell’ultravioletto profondo, a 193nm e confrontate con misure analoghe con una sorgente di raggi X molli a 8 KeV, per cercare di mettere in correlazione i difetti presenti nel materiale con le proprietà fotoconduttive. I modelli teorici utilizzati per l’interpretazione delle misure sono quelli già descritti nel primo capitolo, in particolare i modelli di generazione–ricombinazione di Shockley – Read – Hall, sviluppati tra gli anni cinquanta e sessanta. Le misure effettuate possono essere interpretate con questi modelli, ma è evidente la difficoltà di costruire rivelatori affidabili in diamante sintetico policristallino.
I capitoli quattro e cinque descrivono il lavoro di realizzazione e di caratterizzazione di nuovi rivelatori in diamante sintetico monocristallino per radioterapia effettuato tra Tor Vergata e il S. Filippo. In particolare nel quarto capitolo viene delineato il percorso sperimentale che ha portato ai risultati principali del presente lavoro di dottorato; viene poi descritta la sorgente di particelle e radiazioni ionizzanti costituita dall’acceleratore per radioterapia del San Filippo e i dosimetri a stato solido per alte energie di uso clinico, sottolineando le problematiche che spingono allo sviluppo di nuovi dispositivi. Nel quinto capitolo vengono riportate e discusse le misure di caratterizzazione dei nuovi dosimetri in diamante sintetico monocristallino per elettroni e fotoni alle energie radioterapiche (6-18 MeV). Vengono infine riassunte le conclusioni del presente lavoro con lo sguardo rivolto alle prospettive di sviluppo nell’ambito del progetto DIARAD della matrice di dosimetri in diamante sintetico monocristallino per imaging dosimetrico di fondamentale utilità ad esempio nelle tecniche di radioterapia ad intensità modulata IMRT.
Scarica la tesi Rivelatori in diamante sintetico poli emonocristallino per radiazioni e particelle ionizzanti
 Come il sole eclissa le stelle con la sua lucentezza, cosi l’uomo di cultura eclisserà la fama degli altri nelle assemblee del popolo se proporrà problemi algebrici e ancor più se li risolverà. Un numero positivo diviso per un numero positivo o un numero negativo diviso per un numero negativo, dà un numero positivo. Zero diviso per zero non dà nulla. Un numero positivo diviso per un numero negativo dà un numero negativo. Un numero negativo diviso per un numero positivo dà un numero negativo. Un numero positivo o negativo diviso per zero è una frazione avente per denominatore zero. (Brahmagupta, circa 620 d.C.)
Come il sole eclissa le stelle con la sua lucentezza, cosi l’uomo di cultura eclisserà la fama degli altri nelle assemblee del popolo se proporrà problemi algebrici e ancor più se li risolverà. Un numero positivo diviso per un numero positivo o un numero negativo diviso per un numero negativo, dà un numero positivo. Zero diviso per zero non dà nulla. Un numero positivo diviso per un numero negativo dà un numero negativo. Un numero negativo diviso per un numero positivo dà un numero negativo. Un numero positivo o negativo diviso per zero è una frazione avente per denominatore zero. (Brahmagupta, circa 620 d.C.)
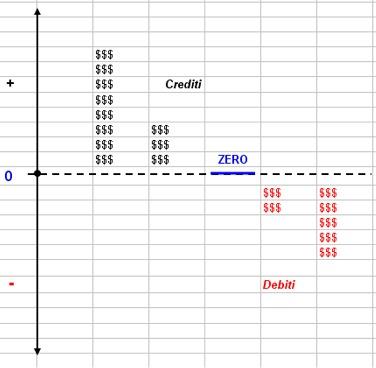 Le invenzioni dello zero, dei numeri negativi, e della notazione posizionale in base 10 sono tra le più importanti per la soluzione di problemi applicativi. Gli Hindu ebbero anche il merito di trattare i numeri irrazionali come qualunque altro numero (senza crearsi tutte le remore di cui avevano sofferto i greci) facendo nel calcolo tutte le approssimazioni ritenute necessarie.
Le invenzioni dello zero, dei numeri negativi, e della notazione posizionale in base 10 sono tra le più importanti per la soluzione di problemi applicativi. Gli Hindu ebbero anche il merito di trattare i numeri irrazionali come qualunque altro numero (senza crearsi tutte le remore di cui avevano sofferto i greci) facendo nel calcolo tutte le approssimazioni ritenute necessarie.
Per certo in America anche i Maya (e forse da qualche secolo prima degli Hindu) avevano il concetto di zero che veniva rappresentato con una specie di conchiglia chiusa.
La storia del numero zero è emblematica dello stupore che molti provano costatando che civiltà diverse, senza alcun contatto tra loro, siano arrivate ad esprimere gli stessi concetti matematici (cosa che non è accaduta con i diversi linguaggi).
La cultura applicativa e contabile degli Hindu portò con naturalezza ad assimilare i crediti con numeri positivi, i debiti con numeri negativi e lo zero con la perfetta compensazione tra debiti e crediti. Nel conto economico di una azienda i ricavi sono numeri positivi (neri) ed i costi negativi(rossi); l’ultima riga del conto (negli USA la bottom line) rappresenta la differenza tra ricavi e costi totali (profitti o perdite); da qui le espressioni: "azienda profondamente in rosso (deep in red)", "riportare una azienda in nero", "l’unica cosa che conta è la bottom line".
Oggi gli indiani conservano grandi competenze nella contabilità e nei servizi e, grazie alle reti informatiche e al diverso fuso orario, molte aziende americane inviano la sera i loro dati in India dove vengono elaborati e restituiti tempestivamente ed efficientemente il mattino successivo. Molte aziende internazionali che lavorano per progetto impiegano personale indiano per i ruoli di cost controller, planning and control engineer, contract manager, ecc.
 L’appuntamento con il Pi Day 2009, La Giornata della Matematica, è per il 3.14, sabato 14 marzo. Aula Magna del Politecnico di Torino, Corso Duca degli Abruzzi, 24, dalle 9 alle 12,30, ingresso libero. Per le classi che intendono partecipare è obbligatoria la prenotazione, con l’indicazione di un docente responsabile della classe. La prenotazione si effettua via e mail all’indirizzo:
L’appuntamento con il Pi Day 2009, La Giornata della Matematica, è per il 3.14, sabato 14 marzo. Aula Magna del Politecnico di Torino, Corso Duca degli Abruzzi, 24, dalle 9 alle 12,30, ingresso libero. Per le classi che intendono partecipare è obbligatoria la prenotazione, con l’indicazione di un docente responsabile della classe. La prenotazione si effettua via e mail all’indirizzo:
Programma
9 I saluti ai partecipanti
9,15 La bellezza dei numeri e il numero della bellezza, Alessandra Del Piccolo, Istituto Magistrale “Domenico Berti”, Torino
10 Pi greco nel cuore, Andrea Centomo, Liceo Statale “F. Corradini” di Thiene (VI)
10,45 Intervallo
11 Colori, suoni e magie del Pi greco, Egidio Battistini, Politecnico di Milano.
11,45 Pi greco in gara: In premio per chi ricorda più cifre un Netbook, con WI-FI, modem, webcam.
Da una comunicazione di Federico Peiretti