Autore: Antonio Bernardo

Temporale estivo

Tre amici studenti, Franco, Roberto, Marco, decidono di fare una camminata in montagna. Giunti in auto alle pendici montuose, iniziano una salita lunga e ripida. Al termine si trovano su di un grande altipiano. Splendidi prati e rocce, un ruscello. Aria fresca e pulita, grande silenzio. Lunga e piacevole passeggiata. Sulla via del ritorno li coglie il temporale. Pioggia forte e calo immediato della temperatura. I tre malcapitati non sono attrezzati a difendersi dalla pioggia.

Non rimane loro che marciare lungo i prati ormai ridotti ad una melma scivolosa. Dopo più di un’ora, inzuppati sino alle ossa, giungono all’auto. Dove ci saranno abiti di ricambio, coperte, generi di conforto? Nulla di tutto questo. Non resta che salire in auto e tornare mestamente in città battendo i denti. Evidentemente i tre ignorano la legge di Murphy. Una giornata da dimenticare.

Dopo alcuni decenni i tre ancora ricordano quel dolente pomeriggio. Uno di loro, un po’ maniaco di matematica e fisica, ripensa alla pioggia presa e comincia a riflettere. Si poteva forse prenderne meno correndo più veloci?

In generale: una persona sotto la pioggia corre verso un riparo. La sua velocità influenza la quantità di pioggia che prenderà? Consultare il web è rapido. In breve si scopre che il problema è un classico, studiato ormai da cervelli fini (A. De Angelis, Eur. Phys., 1987, 8, 201–202). Un fisico americano ha perfino creato un’applet che calcola la quantità di pioggia presa in funzione della velocità (http://www.dctech.com/physics/notes/0006.php).

Rivediamo la soluzione, limitandoci a considerare il caso di assenza di vento, quindi di una pioggia che cade verticalmente. L’uomo viene schematizzato come un parallelepipedo. La faccia superiore, perpendicolare alla pioggia sia So (superficie orizzontale) e rappresenta testa e spalle, la faccia frontale sia Sv (superficie verticale). Per effetto del moto relativo l’uomo in corsa riceve la pioggia obliquamente.

 

Le grandezze da considerare sono la velocità di caduta della pioggia (w), la velocità dell’uomo che corre (u), l’intensità della pioggia (I), la distanza (L) dal riparo, il volume di pioggia assorbita dall’uomo (V).

L’intensità (media) della pioggia si misura in mm/h e dunque è il rapporto tra la colonna di acqua che cade su di una qualsiasi superficie durante la pioggia e la durata della pioggia. La velocità relativa della pioggia (vettore vp ) si ottiene sommando i vettori velocità con la regola del parallelogramma: vp = w – u

Le fonti citate forniscono la soluzione:

$V = IL(S_o/u + S_v/w)$           (a)

Consideriamo u come unica variabile indipendente, mentre le altre sono assunte come parametri. Si vede immediatamente che V ha andamento iperbolico in funzione di u. La funzione V è sempre decrescente (derivata prima negativa). Quando u tende all’infinito V tende all’asintoto: $V = IL(S_v/w)$.

 

Conclusione: quanto più grande è u, ossia quanto più si corre, tanto minore è la quantità di pioggia assorbita. Ed anche: se due runner decidono di sfidarsi in una gara su un percorso assegnato, in caso di pioggia il più veloce dei due si bagna di meno.

Bene, ora vogliamo riproporre il problema in termini un pò diversi.

Piero e Giorgio, durante una passeggiata in pianura vengono colti dalla pioggia, che cade verticalmente. Piero, molto istintivo, propone di correre alla ricerca di un riparo. Giorgio, super-razionale, consiglia invece di restare immobili fin tanto che spiove; egli pensa che si tratti di una breve pioggia estiva che si risolverà in una decina di minuti. Correndo, egli immagina, si prenderà molta più pioggia, per effetto della velocità relativa. I due amici, inoltre, non sono a conoscenza di eventuali ripari dalla pioggia. Potrebbe non essercene per molti chilometri. I diversi punti di vista dei due amici non trovano un compromesso. Essi concordano allora che Piero correrà lungo il sentiero alla ricerca di un riparo, se esiste, dove fermarsi. In assenza di riparo, al termine della pioggia comunque si fermerà ad attendere l’amico. Giorgio, invece, resterà immobile sino a che spiove, poi riprenderà a camminare per raggiungere Piero.

Domanda 1 Chi dei due si bagna di più? Considerare i diversi possibili casi. Scrivere le equazioni che identificano il volume di pioggia assorbito da entrambi gli amici. Trarre le considerazioni opportune.

Domanda 2 Assumiamo che Piero non trovi riparo e che sia: So = 0,1 m2 , Sv = 0,6 m2 , t = 0,5 h la durata delle pioggia, u = 5 m/s, w = 2,5 m/s, I = 2 mm/h. Calcolare, con le formule di cui a Risposta 1, i volumi di pioggia assorbiti dai due amici e la durata della corsa di Piero.

Domanda 3 Assumiano che Piero trovi riparo dopo un tempo tr = 0,5 h e che sia: So = 0,1 m2 , Sv = 0,6 m2, t = 2h, u = 2 m/s, w = 4 m/s, I = 7 mm/h. Calcolare i volumi assorbiti dai due amici e la durata della corsa di Piero.

Domanda 4 Assumiano che Piero trovi riparo dopo un tempo tr = 0,5 h e che sia: So = 0,1 m2 , Sv = 0,6 m2, t = 2h, u = 1 m/s, w = 8 m/s, I = 8,5 mm/h. Calcolare i volumi assorbiti dai due amici e la durata della corsa di Piero.

La soluzione sarà pubblicata la prossima settimana

Intanto puoi inserire dei commenti per chiedere chiarimenti o dare la tua risposta.

Riferimenti
(1) A. De Angelis – Eur. Phys. 1987, 8, 201 – 202
(2) http://www.dctech.com/physics/notes/0006.php

Risposta 1

Cominciamo a renderci conto che esistono due possibilità: caso1: Piero non trova riparo, caso 2: Piero trova riparo.

Caso 1: non esiste riparo. Prendiamo in considerazione la formula (a). Essa si applica alla corsa di Piero, a patto introdurre una piccola modifica. La formula, nei termini scritti, contiene la distanza L dal riparo, ma Piero in questo caso non trova riparo. Per adattarla al caso occorre allora porre:

L = ut

dove t è la durata della pioggia, che coincide con la durata della corsa di Piero.

Quindi la (a) diventa:

V = Iu(So/u + Sv/w)t = I(So +u/w Sv )t (b)

La formula (b) definisce la quantità di pioggia che Piero prende correndo per un intervallo di tempo t alla velocità u.

Quanta pioggia prende Giorgio? Per rispondere basta notare che Giorgio, avendo deciso di rimanere immobile si comporta esattamente come un pluviometro(*). Il volume di acqua che prende è dato da:

V’ = I So t (c)

Infatti V’ rappresenta il volume di acqua che si accumula in un pluviometro di sezione So nel tempo t. Notiamo che la (c) non è altro che la (b) quando u = 0 Se dividiamo la (b) per la (c) otteniamo:

V/V’ = 1+ u/w* Sv/ So (d)

Il secondo membro è chiaramente > 1, dunque risulta V > V’

Concludiamo che, in questo Caso 1, Piero (l’uomo che corre) si bagna di più di Giorgio (l’uomo che resta immobile), per qualsiasi valore del rapporto u/w.

Caso 2: Piero trova riparo

Qui la situazione è diversa in quanto esistono due diverse durate di tempo: t la durata della pioggia tr la durata di tempo necessaria a Piero per raggiungere il riparo. E chiaramente: tr < t altrimenti si ricadrebbe nel Caso 1.

Dunque Piero raggiunge il riparo prima che termini di piovere. Possiamo allora riscrivere le equazioni (b) e (c), ma questa volta con durate di tempo diverse.

V = I(So +u/w Sv ) tr (e)

V’ = I So t (f)

Ed ancora, dividendo la prima per la seconda:

V/V’ = (1+ u/w* Sv/ So) tr /t

Qui abbiamo, a secondo membro:

(1+ u/w* Sv/ So) >1 tr /t < 1

In conclusione il rapporto V/V’ , dato dal prodotto dei due termini, può essere maggiore o minore di 1. Di conseguenza è possibile che si bagni di più l’uomo che corre oppure quello che sta immobile, secondo i valori dei parametri u/w e tr/t.

Vediamo una rappresentazione geometrica del Caso 2.

Possiamo riscrivere la formula in questo modo: V/ V’ = (a + b u/w) dove: 0 < a = t/ tr < 1 e 0 < b = Sv/ So* tr /t

Che nel piano di coordinate (u/w, V/V’) rappresenta un fascio di rette uscenti dal punto (0, a), tutte con coefficiente angolare positivo. Tale fascio incontra la retta orizzontale V/ V’=1 nel punto:

(u/w)* = (1 – a)/b = So/Sv( tr/t – 1)

E dunque, una volta assegnato il rapporto t/tr, che individua la retta del fascio corrispondente, quando u/w < (u/w)* risulta V < V’ dunque chi corre si bagna meno di chi sta fermo, mentre quando u/w > (u/w)* si verifica esattamente l’opposto.

Teniamo presente che le velocità u e w hanno dei limiti fisici: 0 < u < 10 m/s (da uomo immobile a recordman dei cento metri) 2 < w < 9 m/s (da misure) e quindi si ottiene: 0 < u/w < 5

Anche l’intensità della pioggia ha dei limiti fisici: 1 < I < 10 mm/h (da pioggerella a nubifragio).

Finora abbiamo assunto l’ipotesi implicita che il parametro Sv/So abbia lo stesso valore per Piero e Giorgio. Tuttavia nel caso che l’uno fosse smilzo, l’altro obeso, il rapporto sarebbe un po’ diverso e le formule (c)+(d) ed anche (d)+(e) dovrebbero riportare due valori diversi per il rapporto delle superfici.

Le risposte alle domande 2, 3, 4 sono riportate nel file EXCEL allegato>>>.

Hume

Il linguaggio della matematica

Forse non tutti sanno che la matematica non ha sempre avuto il linguaggio complesso per il quale è nota e, pensando ai matematici che ci hanno preceduti, siamo convinti che usassero il nostro stesso simbolismo. Scorrendo i testi degli antichi, invece, non troviamo nemmeno il simbolo di “=”, che ha fatto la sua comparsa solo nel 1575, in The Whetstone of Witte, scritto dal matematico e fisico gallese Robert Recorde, illustre sconosciuto per la maggior parte di noi.

Per “evitare la noiosa ripetizione”, Recorde ha pensato a questi due segmenti, scritti in forma più allungata, perché secondo lui non ci possono essere due cose più uguali di due segmenti.

Gli antichi Egizi usarono i geroglifici per indicare l’addizione e la sottrazione, con un paio di gambette che corrono verso o si allontanano da una quantità, ma solo con il sedicesimo secolo comincia il crescendo che ci porterà a scrivere la matematica come la conosciamo oggi.

Per renderci conto di come sia stato tortuoso il percorso, pensiamo alle cifre indo-arabiche, introdotte in Europa all’inizio del 1200 da Leonardo Fibonacci: hanno faticato a imporsi, in un’epoca in cui le cifre romane sembravano essere abbastanza per la matematica di allora, eppure la loro introduzione ha aiutato la matematica a progredire più speditamente, basti pensare alla difficoltà di eseguire le moltiplicazioni con i numeri romani.

Lo stesso percorso è avvenuto nell’ambito delle operazioni e dell’algebra più in generale. Si distingue tra algebra retorica, sincopata e simbolica che danno l’idea di questo crescendo: Diofanto ha introdotto l’algebra sincopata già nel III sec. a.C., con le abbreviazioni che compaiono nella sua Aritmetica, ma il suo simbolismo non è sopravvissuto.

All’epoca di Tartaglia, si è ritornati all’algebra retorica, come dimostrato dalla formula risolutiva delle equazioni di terzo grado: “Quando che ‘l cubo con le cose appresso se agguaglia a qualche numero discreto…” scritto in termini poetici, per memorizzare meglio la formula.

Nel primo testo matematico a stampa, Larte de labbacho, pubblicata nel 1478, le quattro operazioni sono indicate con “et” per l’addizione, “de” per la sottrazione, “fia” per la moltiplicazione e “in” per la divisione; gli scrittori di testi matematici prima del sedicesimo secolo si erano avventurati in espressioni simboliche e ci sono degli esempi di come abbiano sperimentato per velocizzare la scrittura.

Tra i nomi importanti, si possono evidenziare quelli di Nepero e di Leibniz, ma, dal punto di vista delle notazioni, il contributo più importante è stato quello offerto da Eulero, noto per i suoi grandi risultati in termini di formule, teoremi, equazioni e per aver ideato buona parte dei simboli matematici in uso ancora oggi, come f(x) per indicare la funzione, “e” per la base del logaritmo naturale, pigreco “π” per il rapporto tra la circonferenza e il suo diametro…

Nell’articolo pubblicato il 21 maggio di quest’anno su “The Guardian”, il noto quotidiano britannico, Joseph Mazur, autore di “Enlightening Symbols: A Short History of Mathematical Notation and its Hidden Powers”, confronta l’arte dello scrittore con quella del matematico. Ritiene che gli scrittori abbiano più libertà rispetto ai matematici: possono usare simboli per rappresentare le emozioni, come Emily Dickinson che non usa la parola “serpente” nelle sue poesie per non richiamare la connessione con il diavolo e il male, mentre, al contrario, Joseph Conrad descrive il fiume Congo proprio come un serpente, per richiamare le caratteristiche del diavolo. I simboli matematici, invece, servono per comprimere alcune informazioni complesse e per portare a una migliore comprensione, per quanto la maggior parte di coloro che odiano la matematica direbbe l’esatto contrario.

Non è rimasta grande traccia dei simboli “cattivi” che, con il tempo, sono stati superati da quelli più convenienti e, quindi, dimenticati, ma ci sono alcune cose simpatiche, come l’usanza di indicare i numeri negativi come preceduti da una mezzaluna crescente, mentre i numeri positivi erano indicati con la mezzaluna calante.

L’autore conclude l’articolo con il riferimento alle equazioni di Maxwell, le quattro equazioni che collegano tra loro i campi elettrico e magnetico: ne parla come di un poema matematico. Le equazioni sono la chiave per descrivere molte delle cose che usiamo attualmente, come il cellulare, ma, per quanto si presentino complesse come linguaggio, non sarebbe certo più facile scriverle e comprenderle nel linguaggio comune. È questa la forza della matematica, la chiave della sua universalità.

Daniela Molinari

Mario Livio, La sezione aurea

La sezione aurea, protagonista indiscussa di questo testo, ci accompagna nel mondo dell’arte, della musica, della poesia, della natura e della fisica, passando attraverso la storia della matematica. Dopo il primo capitolo, nel quale l’autore ci presenta il percorso che verrà affrontato nell’opera, nella prima metà Livio ripercorre la storia della matematica, fin dalla nascita dei sistemi di numerazione.

Pare che gli irrazionali siano dovuti alla scuola pitagorica e che l’incommensurabilità sia nata dal confronto tra la diagonale e il lato del quadrato. Per quanto alcuni studiosi suppongano che anche la piramide di Cheope porti in sé il rapporto aureo, non ci sono prove che gli Egizi lo conoscessero. Solo con Platone e i poliedri regolari, per la costruzione dei quali il rapporto aureo è indispensabile, si può dire che faccia la sua comparsa il più irrazionale degli irrazionali.

Con gli Elementi di Euclide, tale valore viene non solo nominato, ma anche discusso, perché permette di costruire il pentagono.

La matematica araba non offre grandi risultati dal punto di vista della geometria, puntando molto di più sull’algebra, perciò con il quinto capitolo – intitolato “Figlio di una buona disposizione” – approdiamo al 1200, con Fibonacci: nell’opera principale del matematico pisano, il Liber abbaci, la sezione aurea è usata consciamente per la soluzione di alcuni problemi, ma ne vengono aumentate anche le applicazioni. Inaspettatamente, grazie alla successione di Fibonacci, nella quale si intrecciano matematica e natura, ritroviamo la sezione aurea, anche se bisogna aspettare Keplero, che nota come il quoziente tra un numero della serie e il suo precedente tenda al rapporto aureo. D’altra parte, il fisico, divenuto famoso per le sue tre leggi dell’astronomia, ha individuato nei solidi platonici un ottimo modello per rappresentare le orbite dei pianeti.

Precedentemente, la collaborazione tra Luca Pacioli e Leonardo da Vinci ha portato alla pubblicazione, nel 1509, del Compendio de divina proportione, che ha permesso di aumentare l’interesse per la sezione aurea, dopo che il mondo dell’arte, con Piero della Francesca e Albrecht Dürer, si è avvicinato alla matematica, nella quale ha trovato la propria dimensione per affrontare lo studio della prospettiva. Per quanto, comunque, alcuni studiosi siano convinti di aver trovato la sezione aurea in molte opere pittoriche o architettoniche, solo conoscendo la struttura che ha dato origine all’opera possiamo in qualche modo essere certi della sua presenza. Ecco quindi che nelle opere di Paul Sérusier troviamo il rapporto aureo per “disciplinare” le sue invenzioni, mentre Le Corbusier, dopo un’iniziale diffidenza, ritiene, con il suo “Modulor”, di poter conferire dimensioni armoniose agli oggetti utilizzati da ognuno di noi nella quotidianità. L’autore presenta con precisione le varie ipotesi e, al termine della carrellata, interviene con il proprio punto di vista: la sezione aurea è meno diffusa, soprattutto tra le opere d’arte del passato, di quanto si pensi.

La ricerca della sezione aurea nell’arte, nella musica e nella poesia va a scontrarsi, direttamente, con il concetto di bellezza: se la bellezza matematica, per quanto difficile da capire per i profani, può in qualche modo essere spiegata, ciò che rende bella un’opera d’arte, un brano musicale o una poesia non è così chiaro, visto che va a toccare le corde della nostra emotività.

L’esplorazione di Livio si conclude con la scoperta, negli anni Ottanta del secolo scorso, dell’ingegnere israeliano Dany Schectman che ha trovato una lega metallica la cui struttura non assomiglia ai cristalli fino ad allora noti. La cosa sorprendente è che, fino a quel momento, si era rimasti convinti che, come nella tassellazione del piano non è possibile usare i pentagoni, così nell’ambito tridimensionale non possono esserci simmetrie quintuple.

Nel 1974, lo studio svolto da Roger Penrose, fisico di Oxford, impegnato nella tassellazione del piano con figure non regolari, ma che in qualche modo possono essere ricondotte a decagoni sovrapposti, è diventato fondamentale per capire le scoperte di Schectman. In altre parole, questa matematica, apparentemente slegata dalla realtà, ha spiegato la realtà. Un po’ come è successo con i frattali di Mandelbrot.

L’ultimo capitolo dell’opera indaga la concezione della matematica: scoperta? Invenzione? La posizione dell’autore è proprio a metà tra le due interpretazioni, un po’ come succede alla natura della luce, che è sia ondulatoria che corpuscolare. Quest’ultimo esempio, come altri nel corso della narrazione, ci rimanda alle origini dell’autore, che non è un matematico ma un astrofisico, ricercatore allo Space Telescope Science Institute.

Daniela Molinari

Elementi di Orientamento di Michele T. Mazzucato

Dopo lavori dedicati al binocolo, alla bussola e al globo terrestre, grazie ai suoi interessi che spaziano dalla topografia all’astronomia, Michele Mazzucato ha deciso di dedicare questa sua opera all’Orientamento.

Come ci dice nella presentazione il prof. Enrico Maddalena, che si occupa di orientamento da oltre quarant’anni, ciò che traspare dalle opere di Mazzucato è il suo entusiasmo per i fenomeni naturali, che indaga con spirito scientifico: “concretizza il suo stupore per la natura, affrontando gli argomenti che via via lo appassionano, con una indagine a tutto tondo, avvicinandosi a essi da ogni angolo.”

Il libro è un “prontuario che raccoglie utili informazioni, metodi semplici e pratici, numerosi dati e procedimenti passo-passo”. Il testo si divide in quattro parti, precedute da un indice dettagliato, che permette di trovare agevolmente ciò che è di proprio interesse.

Nella prima parte, dedicata alla bussola, lo strumento principe dell’orientamento, l’autore procede con la classificazione dello strumento a cui fa seguito una sua breve storia. Scopriamo così che i primi in Europa a usare la bussola furono gli amalfitani, che contribuirono a perfezionarla: importata dagli arabi, è in realtà stata inventata dai cinesi. D’altra parte, il magnetismo ha fatto la sua comparsa in Europa solo in un’epoca relativamente recente, mentre in Cina era utilizzato da secoli. Il capitolo procede poi con alcune indicazioni per l’uso pratico della bussola.

La seconda parte è dedicata all’orientamento: interessante la spiegazione su come individuare il Nord grazie a un orologio e al Sole, soprattutto se confrontata con quella di come si può raggiungere lo stesso obiettivo durante la notte, usando la Luna. In tal caso, il procedimento è più complesso, visto che bisogna usare un metodo diverso a seconda delle varie fasi lunari. Inoltre, l’autore ci fornisce le istruzioni per costruire un notturlabio, che ci aiuta a conoscere l’ora notturna con maggior precisione, grazie alla costellazione dell’Orsa Maggiore e alla Stella Polare.

La terza parte è dedicata alla cartometria e, in questo caso, ci sono indicazioni dettagliate su come misurare le distanze, le aree, le pendenze, utilizzando semplicemente una carta geografia. Non mancano, nelle determinazioni pratiche, interessanti applicazioni dei teoremi studiati al liceo, come il teorema di Talete che ci permette di determinare l’altezza di un oggetto, utilizzandone l’ombra o i triangoli, oppure l’applicazione della cinematica unidimensionale, per determinare – ad esempio – la profondità di un pozzo, con il metodo acustico.

L’ultima parte è dedicata alle appendici: dai rapporti di scala, che ci vengono descritti non solo con una tavola dettagliata, ma anche con un simpatico metodo pratico, agli elementi di trigonometria con le soluzioni dei triangoli, dalla direzione e nomenclatura dei venti alla posizione angolare del sole all’alba o al tramonto, fino ad arrivare ai fusi orari, le ventisette tavole ci permettono di ottenere tutte le informazioni necessarie per il nostro orientamento.

In conclusione, troviamo un glossario, dal quale possiamo ricavare anche le istruzioni per realizzare una bussola, e una bibliografia particolarmente ricca, a dimostrazione del grande lavoro di approfondimento svolto dall’autore. Interessanti e simpatiche le citazioni che accompagnano l’opera, come quella di apertura, da “Alice nel paese delle meraviglie” di Lewiss Carroll: “Inizia dall’inizio e vai avanti finché non arrivi alla fine: poi, fermati.”

Daniela Molinari

Considera la retta passante per A(0; 5) e B(-2; -3). Determina su tale retta un punto C la cui ascissa è tripla dell’ordinata. Considera la retta parallela all’asse x passante per A e la retta parallela all’asse y passante per B. Determina il punto

Considera la retta passante per A(0; 5) e B(-2; -3). Determina su tale retta un punto C la cui ascissa è tripla dell’ordinata. Considera la retta parallela all’asse x passante per A e la retta parallela all’asse y passante per B. Determina il punto D di intersezione di queste due rette e calcola l’area del triangolo DAC.

download pdf

Esercizio sulla circonferenza

SCARICA IL FILE PDF

Dal 2015 lezioni ed esami in inglese: nelle scuole italiane arriva il metodo Clil

Discutere un teorema di matematica in Inglese, commentare un brano di Leopardi con un impeccabile accento da lord, o magari spiegare le cause della Rivoluzione Francese usando la lingua della Regina Elisabetta. Tutto questo potrebbe diventare realtà, a partire da settembre, per molti studenti italiani.

L’anno scolastico 2014-2015, infatti, segnerà l’introduzione dell’insegnamento in lingua straniera di una materia non linguistica nell’ultimo anno di scuola superiore, come previsto dalla riforma Gelmini, che verrà attuata a partire dall’autunno in ogni singola parte.

Le materie che potranno essere insegnate in inglese saranno quelle di base nei licei (anche se la novità verrà estesa a tutte le scuole): italiano, matematica, storia, filosofia, geografia e storia dell’arte. Il metodo d’insegnamento che verrà usato si chiama Clil, content and language integrated learning, un sistema che dalla metà degli anni sessanta è stato sperimentato in Canada e poi è stato usato in altri Paesi.

Secondo le indicazioni del MIUR, in base agli insegnanti disponibili, ogni singola scuola potrà scegliere quale materia insegnare anche in inglese, attenendosi alla regola generale secondo la quale almeno il 50% delle ore di quella materia dovrà essere svolta in inglese.

I maturandi del 2015, quindi, potrebbero doversi confrontare con l’inglese, tanto agli scritti, quanto agli orali degli esami del prossimo giugno. Ogni consiglio di classe potrà stabilire se inserire domande in lingua tra i quesiti della terza prova scritta e durante il colloquio potrebbe esserci un docente a fare una domanda in inglese ai candidati, per comprendere il livello di competenza acquisito durante l’anno.

Se questa novità sembra entusiasmare tutti coloro che sperano da sempre nell’internazionalizzazione della scuola italiana, il tasto dolente è rappresentato proprio dalla carenza di insegnanti abilitati per l’insegnamento in lingua secondo il metodo Clil. Nonostante negli ultimi anni siano stati organizzati dal Miur numerosi corsi per formare gli insegnanti, e nonostante l’insegnamento in inglese sia stato avviato in alcune scuole in via sperimentale, il livello d’inglese richiesto dalla metodologia Clil non incontra le competenze di tutti gli insegnanti italiani. Il Miur, dal canto suo, non potendo garantire i fondi necessari per finanziare consulenti esterni per tutte le scuole, invita utopisticamente gli istituti ad avvalersi dei fondi di istituto – spesso ridotti all’osso – per aiutare l’insegnante e attuare le disposizioni imposte dal testo Gelmini.

L’introduzione in sordina dell’insegnamento in doppia lingua potrebbe servire come fase di rodaggio per un progetto che potrebbe davvero rappresentare un mattoncino per la rinascita della scuola italiana.

Compito in classe III liceo scientifico compito sulla circonferenza

Compito in classe del 29/01/2013 “LA CIRCONFERENZA” per il Liceo Scientifico 1. Determina e rappresenta graficamente l’equazione della circonferenza di diametro AB, con A(-3; 4) e B(1;1). 2. Scrivi l’equazione della circonferenza di centro C(1;4), passante per A(2; -1) e disegnala. Determina poi l’equazione della retta tangente alla circonferenza in A. 3. Determina l’equazione della circonferenza passante per i punti A(4; 1) e B(2;2) e avente il centro sulla retta r di equazione x -2y = 0. 4. Determina l’asse radicale e i punti di intersezione delle due circonferenze … 5. Determina l’equazione della circonferenza passante per i punti P(0;4) e Q(-2;2) e tangente alla retta r di equazione y – x + 4 = 0. 6. Considera la retta passante per A(0; 5) e B(-2; -3). Determina su tale retta un punto C la cui ascissa è tripla dell’ordinata. Considera la retta parallela all’asse x passante per A e la retta parallela all’asse y passante per B. Determina il punto D di intersezione di queste due rette e calcola l’area del triangolo DAC. 7. Dato il triangolo di vertici A(-4;3), B(-6; -3) e C(0; -5) determina l’equazione della circonferenza circoscritta.

download pdf

Compito sulla Circonferenza

SCARICA IL FILE PDF

Siope e gli Enti di Ricerca: considerazioni su 5 voci di spesa

Nella Comunicazione della Commissione europea 2006/C 323/01, a titolo “Disciplina comunitaria in materia di aiuti di Stato a favore di ricerca, sviluppo e innovazione”, viene riportata la seguente definizione di “Organismo di Ricerca”: «soggetto senza scopo di lucro, quale un’università o un istituto di ricerca, indipendentemente dal suo status giuridico (costituito secondo il diritto privato o pubblico) o fonte di finanziamento, la cui finalità principale consiste nello svolgere attività di ricerca di base, di ricerca industriale o di sviluppo sperimentale e nel diffonderne i risultati, mediante l’insegnamento, la pubblicazione o il trasferimento di tecnologie; tutti gli utili sono interamente reinvestiti nelle attività di ricerca, nella diffusione dei loro risultati o nell’insegnamento; le imprese in grado di esercitare un’influenza su simile ente, ad esempio in qualità di azionisti o membri, non godono di alcun accesso preferenziale alle capacità di ricerca dell’ente medesimo né ai risultati prodotti.”

 

La definizione è interessante e conforme al sentire comune, che vede in tali organismi la massima espressione di soggetti che, senza scopo di lucro, svolgono attività con finalità principali di ricerca (di base e/o industriale), sviluppo sperimentale e diffusione dei risultati, mediante insegnamento, pubblicazione o il trasferimento di tecnologie.

Pur non essendo strettamente contemplato dalla definizione, riterrei che un suo conseguente corollario è che tali organismi abbiano anche la benemerita fondamentale finalità di adoperarsi alla ‘formazione’ di coloro che ‘ricercano’ e/o che hanno l’attitudine a divenire ‘ricercatori’.

Ora quali potrebbero essere i parametri rispetto ai quali poter discettare in merito a qualcuna delle finalità primarie degli organismi di ricerca italiani, ed ove reperire i dati?

Ci viene in aiuto la recente apertura e libera messa a disposizione di dati del Siope, ovvero dei dati del Sistema Informativo delle Operazioni degli Enti Pubblici (www.siope.it – Copyright 2014 Siope – Banca D’Italia). Il Siope riporta, tra l’altro, proprio dati di sufficiente dettaglio in merito agli ‘Enti di Ricerca’ italiani, permettendo una libera consultazione ed estrazione di dati relativi a tali Enti, sotto forma di file excel e/o pdf (licenza IODL 2.0 – www.dati.gov.it/content/open-data-siope-continua-il-percorso-di-apertura-dei-dati-relativi-alla-finanza-pubblica – www.rgs.mef.gov.it/VERSIONE-I/e-GOVERNME1/SIOPE/ ).

In particolare selezionando sulla maschera principale del Siope come parametri e relativi valori: Comparto: Enti Ricerca; Sottocomparto: Enti di Ricerca – Amministrazione Centrale; Prospetto: Periodicità annuale – anno 2014; Tipo prospetto: Pagamenti per Cod. Gestionali; si perviene (alla data del 28 luglio 2014) ad un elenco di 39 Enti, dei quali 25 propongono, alla data citata, dati (file Excel) scaricabili e tutti contenenti all’interno la dicitura ‘Data ultimo aggiornamento 24-lug-2014’. Una rapida indagine dei dati presenti nei file Excel, ha permesso di osservare che solo in 22 dei 25 file scaricati è sempre presente una o più delle seguenti voci si spesa: 1426 – Spese correnti per brevetti 2101 – Dottorato di ricerca 2102 – Assegni di ricerca 2103 – Borse di studio 2104 – Studi, consulenze e indagini per attività di ricerca.

Nel seguito si valuteranno tali voci di spesa, con la precisazione che la scelta di appuntare l’attenzione solo su tali cinque voci segue la logica di voler tendere a verificare la oggettiva presenza di risultati innovativi ottenuti (ciò che è testimoniato dalla presenza di spese per brevetti) e di volere operare valutazioni in merito alle spese relative alle attività volte alla formazione dei ricercatori, ciò che, filosofeggiando, è tendenzialmente uno dei presupposti per una futura capacità di progresso della nazione Italia, sia nell’ambito più prettamente tecnologico/scientifico che culturale tout-court.

Continua… scarica il file completo

download SIOPE e gli enti di ricerca
Scarica il file PDF completo

Mettiti in gioco con l’Othello

36° ed. Campionati Assoluti di OTHELLO per Maestri e Candidati Maestri. 27° ed. Campionati “Categoria ” per A, B/I ed E. 1° Campionato Italiano Juniores (U12). Roma 6-7 settembre 2014. La Federazione Nazionale Gioco Othello dà appuntamento a Roma al The Dark Side via S.Maria Ausiliatrice 82 – 00181. Metro A – Furio Camillo, Colli Albani. Sabato 06 ore 11.00 – Sette turni. Domenica 07 – Fase Finale. Iscrizione gratuita per esordienti.

Cédric Villani, Il teorema vivente

Per rispondere alle domande che spesso gli vengono rivolte su come sia la vita di un matematico, Cédric Villani ha concepito questo splendido racconto, un romanzo che descrive “la genesi di un lavoro matematico, dal momento in cui si decide di lanciarsi nell’avventura, fino a quello in cui finalmente l’articolo che annuncia il nuovo risultato – il nuovo teorema – viene accettato per essere pubblicato su una rivista internazionale”.

Tutto ha inizio nel marzo del 2008: Cédric Villani vorrebbe dimostrare l’equazione di Boltzmann non omogenea. A partire dal confronto con matematici di sua conoscenza, l’idea diventa sempre più realtà: Clément Mouhot, che ha seguito nella sua tesi di dottorato anni prima, gli propone di usare lo smorzamento di Landau, mentre Étienne Ghys, suo collega a Lione, suggerisce il collegamento con la teoria Kolmogorov-Arnold-Moser.

Sono proprio i continui contatti con gli altri matematici a costruire la trama del nuovo teorema: una volta giunto ormai a compimento, saranno proprio le critiche, a volte anche molto pungenti, che aiuteranno il matematico a rimettere in discussione i suoi risultati e a giungere a un traguardo migliore.

In mezzo a questi incontri, la vita di Villani continua comunque indisturbata, mentre la sua mente continua a fare matematica, anche quando sembra che stia facendo altro. Eppure, come un padre qualsiasi – anche se molto eccentrico – Villani va a prendere i figli a scuola, leggendo un manga in metropolitana per ingannare il tempo, inventa favole per loro e partecipa alla loro vita in maniera attiva, tanto che i figli lo accompagnano nelle lunghe trasferte all’estero, anche quando ottiene di passare sei mesi a Princeton, all’inizio del 2009.

Per lui è un’ottima occasione: continuerà a collaborare con Mouhot a distanza – si scrivono tantissime mail, alcune delle quali sono riportate nel testo – ma potrà dedicarsi esclusivamente alla matematica, dimenticando gli incarichi amministrativi e i corsi universitari.

La consapevolezza di avere parecchio tempo a disposizione lo spinge a sottovalutare l’impegno richiesto dalla dimostrazione del teorema, tanto che è convinto di poter giungere a buon punto già dopo un paio di settimane e di poter presentare i propri risultati al seminario di fisica statistica organizzato dall’Università di Rutgers. Nemmeno il posticipo del seminario è sufficiente e Villani si ritrova a presentare una dimostrazione incompleta: non insiste sui dettagli, durante l’esposizione, ma sottolinea il significato del problema e la sua interpretazione fisica.

Pare che questo fosse il modo di procedere di Nash, l’eroe matematico di Villani: era solito annunciare dei risultati che non aveva ancora dimostrato, per poter procedere meglio con la dimostrazione, sotto pressione.

L’ambizione porta Villani a lavorare intensamente, senza risparmiarsi: l’obiettivo – che può ammettere solo a posteriori – è la vittoria della medaglia Fields, che infatti gli viene conferita nell’agosto del 2010.

Durante il suo cammino, Villani incontra numerosi ostacoli, come il rifiuto da parte della rivista “Acta Mathematica”: tutto sembra in ordine, ma l’editore della rivista considerata la più prestigiosa di tutte, ritiene che i risultati riportati nel lungo articolo non siano definitivi. Villani è disgustato e nemmeno la notizia di aver vinto il premio Fermat lo consola: il successo in un ambito non può compensarlo della frustrazione del rifiuto, “per consolarmi avrei almeno bisogno di coccole”, dichiara!

Insomma, un matematico estremamente umano, con le sue ambizioni, le sue paure di non farcela, il suo senso dell’umorismo… leggere questo romanzo è un’esperienza: Villani ci fa incontrare una matematica viva e al tempo stesso antica.

Al termine di alcuni dei capitoli, ci sono delle parti in corsivo nelle quali Villani ci racconta la storia della matematica, facendoci incontrare i grandi matematici ai quali si ispira, i suoi eroi, coloro che hanno reso questa disciplina inimitabile. Ci parla così della nascita della rivista “Acta Mathematica” e del terribile errore di Poincaré che si trasforma in una grande vittoria, ci racconta la fondazione dell’Institute for Advanced Study di Princeton, ci parla dei problemi ancora aperti e dei grandi problemi risolti e ci racconta di come sia stata istituita la medaglia Fields e a chi debba il suo nome.

Non mancano poi i riferimenti, anche nel momento della vittoria, agli amici che l’hanno accompagnato durante il cammino e che sono morti recentemente. Villani ci presenta la sua vita a 360°: la famiglia, le passioni, le sofferenze, i lutti, le vittorie, i risultati, la carriera… e nonostante i grandi risultati, resta una persona semplice, in difficoltà nel presentarsi a John Nash.

A coronamento dell’impresa, nel febbraio del 2010, giunge la telefonata di László Lovász, il presidente dell’Unione Matematica Internazionale: il comitato per la medaglia Fields ha deciso di conferirgli l’importante onorificenza.

Nel romanzo, si accelerano i tempi: il diario non è più così meticoloso, non ci sono più risultati da evidenziare e l’epilogo è datato 24 febbraio 2011: il giorno precedente l’articolo è stato finalmente accettato da “Acta Mathematica”.

Daniela Molinari

Diventare assi in matematica con l’allenamento quotidiano, il metodo Kumon

È un fatto che gli studenti che preferiscono la matematica ad un’attività sportiva non siano un gruppo così numeroso. Ma se provassimo a concepire la matematica come uno sport per cui allenarsi ogni giorno e ottenere sempre risultati migliori, potrebbe verificarsi un’inversione di rotta? Sembra proprio di sì! A confermarlo è il successo che il metodo Kumon ha in tutto il mondo.

Vediamo insieme di cosa si tratta. Il metodo Kemon si basa sull’idea che per diventare bravi in matematica e acquisire velocità nel calcolo, basta un impegno quotidiano e individuale di 10 minuti.

Ogni giorno gli studenti che vogliono migliorare il loro rendimento in matematica dovrebbero quindi dedicare questo breve lasso di tempo ad esercizi specifici per le loro abilità e il loro livello di competenza, la cui difficoltà andrà a crescere parallelamente alla bravura del ragazzo.

Nato negli anni Cinquanta in Giappone, dove è diffuso e utilizzato per la formazione numerica dei bambini dai 4 anni in su, nel resto del mondo, in particolare nei paesi anglofoni, sembra aver coinvolto già 4 milioni di adepti entusiasti.

In Italia il metodo Kumon approderà per la prima volta a settembre 2015, a Milano, grazie all’educatrice specializzata, Luisa Baggi, formatasi a Londra.

Se state pensando a una classe di doposcuola multilivello, siete sulla strada sbagliata. Nessuna lezione collettiva, nessun gruppo determinato dall’età o dalla classe a cui appartengono gli studenti che parteciperanno. Il Kumon è un metodo di apprendimento di successo, proprio perché si basa su un percorso di formazione estremamente individuale, concepito a misura di ogni singolo studente. Ciò implica una forte crescita personale degli studenti, che non si sentiranno in competizione con altri coetanei, e che vedranno premiati i loro progressi, e non saranno “puniti” per demerito o per qualche intoppo nell’apprendimento.

I ragazzi, quindi, saranno impegnati 10 minuti al giorno nello svolgimento dei loro esercizi. Ai genitori spetterà il compito quotidiano di correggerli. Ogni mese, poi, l’educatrice valuterà il percorso fatto dagli studenti, decidendo se assegnarli un nuovo livello, o se approfondire meglio quello in cui già si trovano. Il Kumon è infatti organizzato su 23 livelli, dalle addizioni al calcolo fattoriale e statistico, durante il primo incontro con l’educatrice ad ogni bambino viene assegnato il livello di partenza.

I risultati ottenuti dal Kumon sembrano essere straordinari. Alla fine dei 23 livelli gli studenti sembrano aver acquisito maggior confidenza con i numeri, ottime doti di calcolo e problem solving e maggiore sicurezza individuale. Non saranno solo i buoni voti in matematica a far amare il metodo Kumon dalle famiglie!

 

Serena De Domenico

Keith Devlin, I numeri magici di Fibonacci

La nostra vita è piena di numeri, sono addirittura indispensabili, con buona pace di chi continua a ripetere di odiare la matematica o di essere sempre stato un incapace in questa materia. Tra tutti i libri che hanno influito sullo sviluppo del sistema di numerazione, quello più importante è il Liber abbaci di Leonardo Fibonacci: quest’opera è stata un “ponte” che ha permesso all’aritmetica moderna di attraversare il Mediterraneo e giungere in Europa.

Proprio per la sua grande importanza, ma anche per il fatto che è spesso stata sottovalutata, Devlin – esperto divulgatore scientifico e matematico britannico – ha deciso di descriverci il lavoro di Fibonacci in un libro di dieci capitoli, numerati – in onore delle dieci cifre portate in Europa dal Liber abbaci – dallo 0 al 9.

Il titolo italiano porta con sé una certa ambiguità (quello inglese è “The man of numbers”): i “numeri magici” richiamano la sequenza di Fibonacci, nota anche a coloro che poco conoscono la matematica e legati al più celebre problema dei conigli, ma in realtà, il titolo fa riferimento alle cifre dallo 0 al 9, ovvero quei “numeri magici” che hanno portato alla matematica moderna introdotta in Occidente.

Liber abbaci, il titolo del libro di Fibonacci – che corrisponde alle prime parole dell’opera –, è traducibile come “Libro del calcolo”, anche se, paradossalmente, viene spesso nominato come “Libro dell’abaco”, quando l’obiettivo principale di quest’opera era proprio di fare matematica senza ricorrere a strumenti di calcolo come l’abaco dei numeri romani.

Percorrendo la storia dei numeri, dalle origini fino alla nascita del sistema di numerazione posizionale indo-arabico, Devlin sottolinea quanto il nuovo sistema di numerazione abbia semplificato la matematica, rendendo l’aritmetica “una faccenda del tutto banale: una volta che abbiamo disposto i due numeri nella posizione corretta, […] il resto del calcolo è pura procedura meccanica, una semplice routine”.

Il ruolo di Fibonacci nella diffusione di questo sistema di numerazione fu fondamentale. Leonardo Fibonacci ebbe la fortuna di nascere a Pisa, fulcro del commercio e della cultura, e di essere istruito alla “scuola di calcolo” di Bugia, piccola colonia romana e uno dei più importanti porti islamici sulla costa nord-africana, dove il padre assunse la sua carica diplomatica tra il 1180 e il 1185. Gli arabi avevano una visione molto pratica della matematica, la consideravano uno strumento indispensabile per i commercianti e gli ingegneri, e forse per questo motivo il Liber abbaci non si occupa solo di algebra, ma anche di matematica applicata.

Devlin descrive sia le fonti dell’opera, sia le nuove prospettive che l’opera stessa apre, insieme alle conseguenze che porta con sé: “La grandezza del Liber abbaci sta nella sua qualità, nella sua completezza e nella sua tempestività: era un buon libro, insegnava a mercanti, banchieri, uomini d’affari e studiosi tutto quello che dovevano sapere sui nuovi metodi aritmetici ed era il primo a farlo.”

Il nuovo sistema di numerazione fece fatica ad imporsi, vista la diffidenza dei contabili che consideravano i nuovi numeri facilmente alterabili, ma dopo le resistenze iniziali, ebbe risultati inaspettati. Fibonacci divenne una celebrità, tanto che ottenne un’udienza dall’imperatore Federico II e il suo libro divenne non solo fonte di ispirazione per i manuali successivi, a dimostrazione del particolare interesse per la matematica da parte del mondo commerciale, ma accompagnò anche la diffusione delle “scuole d’abbaco”, dove i ragazzi imparavano a usare il nuovo sistema numerico, e venivano istruiti per diventare i futuri uomini d’affari.

Interessante la conclusione dell’opera di Devlin, che chiude considerando l’influenza del Liber abbaci nei manoscritti successivi: questi non contengono materiali tratti direttamente dal testo di Fibonacci, altrimenti sarebbe stato chiaro fin da subito qual era la linea di discendenza, eppure in qualche modo lo ricordano.

Il ritrovamento, da parte della studiosa italiana Raffaella Franci, di un manoscritto anonimo nella Biblioteca Riccardiana di Firenze nel 2003 ha permesso di riconoscervi il Libro di merchaanti detto di minor guisa di Leonardo, “la fonte originale delle centinaia di libri d’abbaco pubblicati nei secoli successivi.”

Ecco quindi confermata l’ipotesi di Devlin, secondo la quale Fibonacci sia il padre della rivoluzione aritmetica avvenuta nel XIII secolo e conclusasi con la completa diffusione delle cifre indo-arabiche, alla fine del Quattrocento.

Daniela Molinari

Corsi di recupero: il modello delle scuole bellunesi tra sponsorizzazione e peer education

Tempi duri per la Scuola italiana, costretta a fronteggiare con risorse sempre più limitate bisogni che richiedono fondi e investimenti specifici, di cui non vede l’ombra. Da alcuni anni molte scuole hanno dovuto rinunciare o diminuire i corsi di recupero per gli studenti per carenza di soldi.

Il Mof, cioè i fondi a disposizione per migliorare l’offerta formativa delle scuole, è sempre più scarno e le famiglie non sempre possono permettersi di versare il contributo volontario richiesto dai singoli istituti.

Questo quadro mette alle luce la necessità delle scuole di reperire fondi anche fuori dal contesto pubblico tradizionale e sperimentare nuove soluzioni per permettere agli studenti di recuperare le insufficienze maturate durante l’anno scolastico. Così dalle scuole del bellunese arrivano due strategie innovative in grado di fornire nuova linfa alle scuole del territorio, ovvero la ricerca di sponsor privati (sul modello americano) e la diffusione della peer education.

Patron del progetto è Luxottica, gigante dell’industria mondiale, che dallo scorso anno porta avanti una collaborazione con la provincia di Belluno, dove l’azienda ha i suoi stabilimenti e dove risiedono i suoi lavoratori. Grazie ai fondi messi a disposizione da Luxottica, in oltre 10 istituti sono stati attivati corsi di recupero, i cui risultati positivi sono già stati riscontrati, attivati alla fine di ogni trimestre o quadrimestre, in modo da garantire un intervento formativo immediato.

Sempre in una scuola bellunese, il liceo Giustina Renier, sta dando i suoi frutti un altro intervento volto a colmare le lacune dei ragazzi meno preparati in matematica: la peer education. Si tratta di un metodo che vede gli studenti più bravi impegnati ad aiutare i compagni in difficoltà. L’efficacia del metodo si basa sul rapporto paritario tra compagni, sia sul piano della relazione che del lessico, e sul fatto che anche il compagno-docente ha la possibilità di fare proprie le nozioni che ha acquisito da poco, insegnandole all’altro.

Il progetto pilota, che ha visto coinvolti quasi 50 coppie di ragazzi, prevedeva incontri in orari extrascolastici, monitorati da docenti nelle vesti di tutor. Al momento l’esperimento sembra promettere bene. Sicuramente un ottimo modello a cui ispirarsi!

Numero 22 completo di Matematicamente.it

Su alcune dimostrazioni del I e del II teorema di Euclide di Nicola Carichino e Cosimo De Mitri. Giochi di abilità in 3D: Mastermind e Othello di Rosa Marincola. Curiose tipologie di numeri primi di Stefano Borgogni. Matematica e ideologia: la politica degli infinitesimali di Joseph W. Dauben. Costruire la sezione aurea di un segmento con la calcolatrice grafica di Maria Maddalena Bovetti. Declinazione e inclinazione gnomonica di un piano verticale di Michele T. Mazzucato. Se Giovenale… l’Analisi matematica scoperta da un antico illuminato di Enrico Colognesi. Lo scaffale dei libri.

download  N. 22 completo di Matematicamente.it Magazine 
Scarica il numero completo del Magazine

Due borse di studio da 1000 euro per studenti di Economia e Turismo

Venere.com, il sito di prenotazioni alberghiere online del gruppo Expedia, ha messo in palio due borse di studio per studenti meritevoli attraverso il suo programma “Borse di Studio Venere”. Si tratta della possibilità di ricevere un contributo di 1000 euro per tutti gli studenti iscritti presso un’università italiana alla facoltà di Economia o Scienze del Turismo.

Requisito fondamentale per la partecipazione al bando è riuscire a dimostrare interesse e competenza nel settore del turismo durante il percorso accademico. Inoltre saranno necessarie: una lettera di presentazione scritta da un tutor o un professore universitario, un attestato di iscrizione all’università con il piano di studi, una lettera motivazionale su come si intende usufruire della borsa di studio. Il contributo infatti coprirà le spese di libri di testo, materiali per il corso, tasse universitarie, viaggi di istruzione o spese quotidiane per il mantenimento.

“Noi crediamo molto nel valore delle risorse umane e nell’investimento sulla scoperta di nuovi talenti che possano contribuire alla crescita delle professionalità e delle competenze nel settore travel” – commenta lo staff di Venere – “per questo è nato il programma Borse di Studio Venere, per la valorizzazione e la crescita delle persone nell’ambito professionale del turismo”.

Tutti gli studenti interessati possono inviare via mail la candidatura entro e non oltre il 31 dicembre 2014 a [email protected] con oggetto “Candidatura per Borsa di Studio”, allegando tutta la documentazione richiesta nel bando integrale visibile al seguente link http://www.venere.com/blog/scholarship/it/2014/

Ricercatori italiani nel mondo

L’Istituto Thomson Reuters, principale fonte mondiale di informazioni, ha redatto l’Highly Cited Researchers 2014, ovvero un elenco delle maggiori menti scientifiche del mondo. L’elenco è stato stilato in base a due parametri: il numero di pubblicazioni scientifiche e il numero di citazioni, in modo da valutare l’importanza per le ricerche del settore.

Le citazioni considerate sono quelle degli ultimi 11 anni, ma effettuando una differenziazione all’interno degli stessi in modo da non penalizzare i ricercatori più giovani e riconoscendo inoltre i lavori che hanno avuto maggiore impatto.

Per compilare la lista, è stato utilizzato InCites, uno strumento di ricerca online, sviluppato per individuare il numero di citazioni del lavoro di un ricercatore, oltre al numero di articoli pubblicati. I ricercatori elencati sono 3215, suddivisi in ventuno ambiti di ricerca: si va dalla medicina alla farmacia, dall’informatica alla matematica, dalle scienze agrarie alla chimica… La classifica non comprende, però, la fisica delle particelle, dato che l’Istituto ha deciso di escludere pubblicazioni frutto di collaborazioni che contano più di cinquecento ricercatori e, in questo ambito, tali collaborazioni sono piuttosto comuni.

Tra i ricercatori citati circa il 2% sono italiani, ma non sono i 55 citati da molti siti: gli italiani sono alcuni di più, visto che se nell’elenco (http://highlycited.com/) cerchiamo “Italy” troveremo sì 55 nominativi, ma corrisponderanno solo a coloro che hanno la propria titolarità nelle università italiane.

In ogni caso, è importante sottolineare che la percentuale del 2% è raddoppiata in ambiti come la farmacologia, l’astrofisica, la matematica, le scienze agrarie e la medicina, a dimostrazione del nostro peso mondiale in alcuni ambiti più di altri.

Sono solo cinque le italiane citate: rispetto ai premiati, sono una percentuale inferiore al 10%, corrispondente alla media della presenza femminile nei ruoli di responsabilità in Italia.

Per i ricercatori premiati è stato preparato una sorta di “bollino”, ovvero una coccarda con la scritta “Highly cited” che i premiati possono pubblicare sulla propria pagina web.

Nel campo della medicina ricordiamo Michele Baccarani, nominato a marzo nel terzo Comitato che deve pronunciarsi sull’eventualità della sperimentazione del metodo Stamina. Insegnamento, ricerca scientifica e sperimentazione per la cura delle malattie più gravi sono il suo ambito di ricerca, in quanto coordinatore del centro per lo studio delle cellule staminali del Policlinico S. Orsola-Malpighi.

Per l’ambito matematico, cominciamo con Nicola Bellomo, del Politecnico di Torino e presidente della Simai, (Società Italiana Matematica Applicata e Industriale), proseguiamo con Giuseppe Marino dell’Università della Calabria, fino a Giuseppe Mingione dell’Università di Parma, giovanissimo professore ordinario, visto che ha ricevuto l’incarico nel 2005, a soli 33 anni. Vincitore di numerosi premi, si occupa della regolarità nell’ambito delle equazioni alle derivate parziali.

Nel campo dell’astrofisica, il riconoscimento è andato a Patrizia Caraveo, dirigente di ricerca e attualmente Direttore dell’Istituto di Astrofisica Spaziale e Fisica Cosmica di Milano, che ha collaborato a diverse missioni spaziali internazionali. C’è poi Andrea Cimatti, professore ordinario all’Università di Bologna, Paolo Giommi, direttore dell’ASI Science Data Center e Alvio Renzini, dell’Osservatorio Astronomico di Padova.

Una piccola curiosità: Bellomo, in un’intervista pubblicata online nel marzo del 2011, alla domanda “Quale calcolo la annoia maggiormente?” ha risposto: “Tutti!”, a dimostrazione del fatto che la bravura del matematico va oltre l’abilità nei calcoli!

Daniela Molinari

Olimpiadi internazionali di Matematica 2014: ottimi risultati per gli italiani

Si è concluso solo pochi giorni fa il consueto appuntamento estivo con le Olimpiadi Internazionali di Matematica. Si tratta della competizione di matematica più importante a livello mondiale per gli studenti under 20, ospitata ogni anno da una nazione diversa: quest’anno si è svolta a Città del Capo (Sudafrica) e ha raggiunto la 55esima edizione.

I vincitori della competizione sono stati l’australiano Alexander Grunning, il cinese Jiyang Gao e Po-Sheng Wu da Taiwan. Tutti e tre gli studenti hanno ottenuto il punteggio di 42, che equivale al massimo dei punti ottenibile alla fine della gara.

Ricco il bottino portato a casa dalla squadra italiana, composta da Dario Ascari (18 anni, Reggio Emilia), Francesco Ballini (18 anni, Castegnato – BS), Giovanni Italiano (18 anni, Roma), Matteo Migliorini (18 anni, Tollegno – BI), Dario Rancati (17 anni, Brescia) e Francesco Sala (18 anni, Ponte dell’Olio – PC). I nostri studenti hanno conquistato una medaglia d’oro, due d’argento, una di bronzo, e una menzione d’onore.

Il posto più alto in classifica, per le perfomance individuali, è stato Dario Ascari, giunto 15esimo. Davvero un ottimo piazzamento, se consideriamo la portata dell’evento, che ha visto partecipare 567 studenti, provenienti da oltre 101 Paesi. Non a caso, oltre che alla competizione individuale, viene stilata una classica che tiene conto dei risultati complessivi delle singole squadre-nazioni.

A conquistare il podio, in particolare, troviamo: Cina, USA, Russia, Taiwan e Giappone.

Le Olimpiadi di Matematica 2015 si svolgeranno proprio in casa di una delle nazioni vincitrici, in Cina, a partire dal 3 luglio. Le singole nazioni potranno iscriversi a partire da gennaio del prossimo anno. Gli studenti che comporranno le squadre verranno scelti in base ai risultati ottenuti durante le competizioni a livello locale e nazionale.

 

Il calcio e la scienza

Pare che anche il calcio si stia rassegnando a seguire le indicazioni della matematica, o perlomeno questo è quanto si evince dagli ultimi articoli pubblicati in occasione dei mondiali appena conclusi. Il primo input proviene dal grande Stephen Hawking che ha dato indicazioni abbastanza dettagliate alla nazionale inglese per affrontare al meglio la prova.

Probabilmente le sue indicazioni non sono state seguite adeguatamente, vista la prova deludente della sua nazionale, in ogni caso, il merito dello studio è quello di aver fatto intravvedere nuovi orizzonti, visto che ha fornito una serie di parametri da rispettare, dal clima all’altitudine, dal modulo di gioco alla nazionalità degli arbitri fino ad arrivare alle divise (anche se forse in tal caso era più una questione di scaramanzia).

D’altra parte, il matrimonio tra la matematica e lo sport è già avvenuto con successo in passato, basti pensare alle vittorie del team svizzero di Alinghi in coppa America, grazie alle simulazioni fluidodinamiche e alla modellistica matematica di Alfio Quarteroni.

È del 2012, invece, la formula del gol perfetto, ideata da quattro laureandi inglesi del Dipartimento di Fisica e Astronomia dell’Università di Leicester. L’equazione descrive il calcio perfetto, quello che può generare una traiettoria ad effetto e tra le grandezze fisiche coinvolte troviamo la densità dell’aria, il raggio e la massa del pallone, la sua velocità, la distanza da percorrere e la velocità angolare del pallone, supponendo che giri attorno al proprio asse.

Javier López Peña dell’University College di Londra e Hugo Touchette dell’Università Queen Mary sono andati oltre e, grazie alla teoria dei grafi, hanno analizzato il gioco e le strategie delle squadre in campo, dopodiché hanno previsto la nazione vincitrice… la Spagna! Per ogni squadra hanno costruito un grafo, in cui i giocatori sono stati rappresentati dai nodi e i passaggi effettuati dagli archi: la rete ha il vantaggio di offrire un’immagine della strategia di una squadra e permette di correggere i punti deboli grazie all’analisi delle performance dei singoli giocatori. La rete della Spagna mostrava una squadra ben collegata, con calciatori che giocavano con una buona sinergia.

Se invece di prevedere ci limitiamo a osservare ciò che è avvenuto, possiamo evidenziare il fatto che nelle fasi eliminatorie il 25% delle partite si è concluso ai rigori.

È quindi estremamente all’avanguardia l’articolo comparso sull’International Review of Sport and Exercise Psychology: spesso si considera la conclusione ai rigori come una lotteria, mentre lo studio evidenzia che il risultato potrebbe essere il frutto di una strategia e di una tecnica applicata da allenatori e giocatori. L’interazione tra portiere e calciatore è fondamentale e anche l’esultanza una volta realizzato il gol (o effettuata la parata) diventa un’arma per generare ansia negli avversari. Elemento centrale dei vari consigli è proprio il gioco di sguardi, la capacità di innervosire l’avversario, di mettergli ansia, di giocare con la paura di sbagliare che ogni giocatore, in una situazione del genere, si porta dentro, considerata la posta in gioco. E poi, la scelta dei tiratori deve essere effettuata dagli allenatori non solo sulla base delle abilità, ma anche valutando la psicologia del giocatore, che deve essere in grado di realizzare il tiro non mirando a dimostrare la propria bravura, ma responsabilmente, come si svolgerebbe un compito da non sbagliare.

Concludo la carrellata con la vera matematica presente al mondiale, in tutte le partite, anche nelle azioni più insignificanti: il pallone! Matematica insospettabile, come spesso succede nella quotidianità: forse non tutti sanno che il pallone da calcio non è perfettamente sferico, visto che è realizzato con un certo numero di pezzi piatti, che vengono cuciti o incollati e poi, gonfiando la camera d’aria all’interno, la pressione conferisce al solido una certa rotondità. Perché sia maggiormente simile a una sfera, deve avere un elevato numero di facce, di estensione minima. Inizialmente, si è scelto un solido platonico, l’icosaedro, opportunamente troncato, in modo da ottenere 20 facce esagonali e 12 facce pentagonali al posto dei 20 triangoli equilateri. Il brazuca, invece, ovvero il pallone dei mondiali 2014, è costituito da sei pezzi piani, che vengono piegati al momento dell’assemblaggio: potremmo perciò dire che si è trattato di un… cubo! Il video con le fasi di assemblaggio del brazuca: https://www.youtube.com/watch?v=ZDd-IX2-yA0

Morten Brask, La vita perfetta di William Sidis

Quello di Morten Brask è il “tentativo letterario di mettere in luce in qualche modo il destino di un uomo”, un uomo apparentemente molto fortunato. Il romanzo ci mostra fin dal principio le contraddizioni di questo personaggio geniale: da un lato, un ragazzino di nemmeno dodici anni che parla a dei professori di Harvard ininterrottamente per due ore della quarta dimensione, dall’altro un ultraquarantenne che vive nascondendosi, senza riuscire ad affrontare con serenità la propria genialità, cercando in continuazione la solitudine.

Il testo non segue uno sviluppo lineare, cronologico, ma offre al lettore continui salti temporali, costruendoci l’immagine di William Sidis, con le sue contraddizioni e le sue paure, come in un puzzle. Conosciamo così l’infanzia difficile della madre, cresciuta in Ucraina e gli ideali del padre, russo, che ha rischiato di passare la sua vita in galera per offrire ai contadini una possibilità di riscatto.

La sua infanzia è sorprendente: i genitori, in particolare il padre, sono convinti che lui possa imparare semplicemente per imitazione e gli lasciano quindi la libertà di esplorare, limitandosi a offrirgli degli stimoli e così a tre anni ha già imparato il latino autonomamente e a sei diventa oggetto della curiosità dei giornalisti.

Il suo percorso scolastico è rapido e lo porta a concludere il liceo a soli otto anni. Ha la possibilità di iscriversi a Harvard e comincia il suo percorso nell’ottobre del 1909, ma per sopravvivere ai compagni di scuola e ai loro scherzi non gli resta che una cosa da fare: isolarsi!

Di Harvard gli resta solo Sharfman, che sarà vicino a lui anche poco prima della sua morte. Il suo percorso di laurea lascia la madre molto delusa, visto che non si è laureato con il massimo possibile, mentre il padre guarda oltre, invitandolo a valutare con attenzione le offerte di lavoro: comincia ad insegnare ad Harvard, ma il rapporto con gli studenti non è certo facile.

Poco più che ventenne, proprio grazie ai suoi ideali socialisti, incontra Martha Foley e scopre l’amore: insieme partecipano alla manifestazione del primo maggio, che si conclude in mezzo ai disordini, con il ferimento e l’arresto di molti manifestanti, tra cui William.

Quando comincia il processo che lo vede imputato, i genitori, per salvarlo dal carcere, lo fanno dichiarare mentalmente instabile e lo rinchiudono nel sanatorio che gestiscono. Quando riesce di nuovo a contattare Martha, questa si è ormai costruita una vita, senza di lui.

Dopo un’infanzia piena di promesse e una giovinezza durante la quale si respira solo tristezza, la vita adulta sembra non avere alcuno sbocco: passa da un lavoro a un altro, perché non vuole che si accorgano delle sue doti e, quando gli propongono delle mansioni più adeguate alle sue capacità, si licenzia e cerca altro.

Persino all’ufficio collocamento è costretto a mentire: la sua abilità nel risolvere il test di Stanford-Binet gli guadagna il rimprovero dell’addetto che pensa che abbia copiato, visto che non è possibile che l’abbia fatto tutto giusto.

Sharfman cerca di offrigli un po’ di normalità e lo porta in un bordello, per offrirgli una serata da uomo, ma William cerca quello che gli è stato portato via a vent’anni, cerca l’amore di Martha. Poco dopo, William si sente male per strada e viene ricoverato, per un’emorragia cerebrale: solo Sharfman entra a salutarlo, mentre la madre, fuori con i giornalisti, non osa entrare, dopo che si sono evitati per anni.

William muore solo, a quarantasei anni.

Brask ci guida nell’incontro con William, un incontro che disorienta e lascia molte domande dietro di sé: è davvero impossibile conciliare la genialità con la socialità? Forse non sbagliano gli amici dei genitori quando li invitano a farlo giocare con gli altri bambini, ma come è possibile per William avere un rapporto normale con gli altri bambini quando non ha strumenti per comunicare con loro, visto che non parla la loro lingua? Lui conosce argomenti che a loro non dicono assolutamente nulla e lui non conosce niente della vita di un bambino della sua età.

I suoi genitori sono convinti di avergli offerto il meglio: “Gli ho insegnato a osservare le cose con attenzione, ad analizzare, combinare e trarre conclusioni logiche. […] È questo che ho dato a nostro figlio: un’educazione volta a stimolare le comuni e naturali attitudini all’attività intellettuale che tutti i bambini hanno. Tutti i bambini. Mio figlio non è un genio.” Per quanto William Sidis ci colpisca per la sua genialità, al lettore resta l’impressione che la sua genialità sia stata coltivata più degli affetti: William è cresciuto sproporzionato, con un grande cervello ma un cuore impreparato ad affrontare la vita.

Brask ricostruisce per noi i dialoghi che danno ritmo alla narrazione, traendo ispirazione e attingendo materiale dagli scritti del protagonista, dai giornali dell’epoca, da tutto ciò che è stato scritto su di lui, ma ci ricorda che i ritratti che vengono tratteggiati sono frutto della sua immaginazione.

Daniela Molinari

Scelta tra investimenti industriali

Il Board di una grande multinazionale ritiene che sia giunto il momento di espandere l’attività produttiva per prepararsi a meglio difendere e consolidare la posizione nel mercato sempre più complesso e competitivo. Il CFO (Chief Financial Officer) assicura la possibilità di disporre di capitali da due fonti. Sharehorders (azionisti) e banche di sistema. Complessivamente egli ritiene di poter assemblare un capitale di investimento compreso tra 200 e 300 milioni di dollari.

Il planning department ha individuato tre possibili (diversi) business meritevoli di analisi/investimento. Sulla base di dati del mercato attuale e di ragionevoli proiezioni future, il vice-presidente delle vendite ha stilato, insieme alla pianificazione, e con la collaborazione dei competenti uffici tecnici, un profilo dei flussi di cassa netti (entrate-uscite) anno per anno per i tre business (dati in milioni di dollari per anno):

ANNO 0 1 2 3 4 5 6 7 8 9 10 11
F1 -120 -50 -70 -20 -15 30 50 65 70 80 120 100
F2 -200 -40 -20 30 50 70 130 130 65 30 3,5 2
F3 -60 -20 -20 10 60 110 -180 90 90 80    

 

I valori negativi (in questo problema) rappresentano esclusivamente costi di investimento, mentre quelli positivi rappresentano i flussi di cassa netti (ricavi delle vendite -costi).

Domanda 1

Assumendo che il tasso di sconto dei flussi (WACC) sia pari al 5%, determinare per i tre businesses il flusso di cassa attualizzato (profilo A) e la curva dei valori cumulati del profilo A (Somme). Tracciare sul medesimo diagramma i tre profili (Somme). Confrontare i tre businesses F1, F2, F3 in base ai seguenti indici finanziari:
1) NPV (Net Present Value). Esso è il valore finale del profilo (Somme)
2) DPB (Payback). E’ il periodo di tempo necessario perché il profilo Somme raggiunga il valore zero, al termine della risalita dai valori negativi (si ottiene, in modo approssimato, del grafico suddetto).
3) IRR (Tasso interno di Redditività (determinabile con opportuna funzione EXCEL). Se come tasso di sconto si assume il Tir il Cash Flow cumulato (Somme) a fine vita termina a zero.
4) PI (Ritorno a valori attuali/investimento attualizzato).
5) PMT (Annual Payment). E’ il pagamento (valori correnti) annuo equivalente allo NPV. Assimilabile allo EVA (Economic Value Added). Comparando i cinque indici proporre la graduatoria (dal più al meno interessante) per i businesses. Spiegare perché il confronto è stato fatto sulla base di flussi finanziari attualizzati e non a valori correnti (quelli dei flussi F1, F2, F3).

Valutare le tre proposte alternative d’investimento considerando oltre alla entità degli investimenti necessari e alla durata dei progetti:
0) Il grafico dei tre flussi di cassa scontati e cumulati (Somme) dei tre progetti.
1) Il valore economico totale attualizzato generato.
2) La velocità di rientro dei capitali e la liquidità dell’iniziativa.
3) Il massimo costo del denaro sopportabile dal progetto.
4) Il valore economico generato per dollaro investito.
5) Il valore economico medio generato per ogni anno.

Domanda 2

Rifare lo stesso confronto nell’ipotesi che siano cambiate le condizioni finanziarie. Considerare i due casi: WACC = 7.5%, WACC = 10%

Domanda 3

Come sempre avviene, anche per questo problema il management deve prendere una decisione di investimento in condizioni di incertezza. E’ questo il rischio di impresa. Supponiamo che nel nostro caso il rischio stia nella previsione del tasso di interesse (WACC). Sulla base di diversi scenari macroeconomici il WACC potrebbe variare dal 5% al 10%. Decidere, comparando le tre valutazioni gia fatte, quale dei tre business il management dovrebbe raccomandare al board.

download SOLUZIONE
Il file XLS della soluzione del problema di scelta tra investimenti industriali

209. Se Giovenale…

“Crescit amor nummi quantum ipsa pecunia crescit”: così Giovenale, poeta latino, in un celebre verso delle Satire (XIV, 139), definisce l’ingordigia di chi è ricco e vorrebbe esserlo sempre di più. Non è di Giovenale, tuttavia, né delle sue pur belle opere che desidero parlare: l’autore latino è qui solo uno strumento per un irreale ma affascinante volo della fantasia, un somnium, in cui si immagina il nostro poeta penetrare nel mondo dell’analisi matematica e in essa manifestare un genio insospettato.

download pdf

Se Giovenale…

SCARICA IL FILE PDF

Miur: stanziati 4 milioni di euro per la promozione della cultura scientifica

Da qualche giorno sul sito del Miur è possibile prendere visione del bando per ottenere i finanziamenti stanziati per le “Iniziative per la diffusione della cultura scientifica”. Si tratta di un progetto storico del Ministero dell’Istruzione, che da oltre 20 anni finanzia numerose attività rivolte alla promozione delle scienze in Italia, settore su cui si investe troppo poco, ma in cui vantiamo numerose eccellenze.

Possono concorrere alla gara sia soggetti privati che pubblici. Il bando è infatti aperto a musei, centri delle scienze e delle tecniche, scuole, ed enti culturali, che si pongono come obbiettivo la realizzazione di mostre, convegni, prodotti editoriali e multimediali ideati per avvicinare i profani al mondo variegato delle scienze, e per mettere alla luce i progressi raggiunti sui vari fronti della scienza. Grazie al denaro stanziato, quindi, sarà possibile fornire benzina a quelle attività scolastiche, e non, spesso messe da parte per mancanza di fondi.

Quest’anno, però, c’è una novità, riguardante il settore dell’istruzione. Proprio alla scuola, infatti, il Miur ha riservato un’ampia fetta del finanziamento, oltre il 30%, che corrisponde a 1.300.000 euro. Questi fondi andranno agli istituti che investiranno il denaro ricevuto in progetti utili per avvicinare gli studenti alla Ricerca e agli studi scientifici e per creare un ponte tra Università e formazione superiore, e in attività volte a far comprendere l’importanza delle scienze della vita quotidiana. Tali finanziamenti, inoltre, potranno essere sfruttati per potenziare e aumentare le attività di laboratorio e per e lo sviluppo di ricerche e sperimentazioni delle metodologie migliori per rendere più efficace la didattica della scienza, con particolare attenzione all’utilizzo delle nuove tecnologie.

Il bando prevede lo stanziamento di quasi 4 milioni di euro, e oltre i fondi destinati esclusivamente alle scuole, sono stati disposti altri due tipi di finanziamento dedicati ai soggetti pubblici e privati di valore diverso. È possibile presentare le domande online a partire dal 14 luglio e fino alle ore 16.00 del 10 settembre attraverso il portale Sirio (http://roma.cilea.it/Sirio ). Potete visionare il bando completo qui:

http://attiministeriali.miur.it/anno-2014/luglio/dd-01072014.aspx

Economia USA: quando fuori dalla crisi?

Il 18 dicembre dello scorso anno 2013 la Banca Centrale Americana, la Fed, annunciava la fine del suo terzo Qe (Quantitative easing) e l’inizio del relativo tapering che normalmente segue il Qe.

1. Quantitative easing e Tapering

Il 18 dicembre dello scorso anno 2013 la Banca Centrale Americana, la Fed, annunciava la fine del suo terzo Qe (Quantitative easing) e l’inizio del relativo tapering che normalmente segue il Qe.

Per Quantitative easing deve intendersi la politica monetaria messa in atto dalla Fed più volte a partire dal gennaio 2009; tale politica, mirando ad abbattere la bassa inflazione o la deflazione (inflazione negativa) ossia a creare reflazione (creare cioè un’inflazione moderata), consiste nell’immettere nel sistema nuova moneta, ossia liquidità, per destinarla all’economia reale e prevede l’acquisto di titoli di Stato USA e di bond legati ai mutui; acquisto che consente di:
a) mantenere al rialzo i prezzi e quindi al ribasso i rendimenti di tali titoli;
b) incentivare gli operatori di mercato, che vendono tali titoli alla Fed, a spostare la liquidità incassata verso investimenti su titoli più rischiosi e quindi più remunerativi come azioni o obbligazioni societarie con l’effetto di farne salire i loro prezzi.

Dall’ottobre 2012, ossia da quando ha iniziato il suo terzo Qe, la Fed ha iniettato nel sistema 85 miliardi di dollari al mese fino a dicembre 2013.

Per tapering invece deve intendersi la progressiva riduzione da parte della Fed degli stimoli monetari previsti dal Qe precedente.

Attualmente la Fed, durante questo terzo tapering, ha ridotto gli stimoli, limitandosi a iniettare nel sistema 35 miliardi di dollari al mese.

Come si è detto la Fed ha messo in atto tre Qe a partire dal gennaio 2009 e la loro durata è la seguente:

Qe1 da genn 2009 ( Ib= 2,23%; Dol/Eur= 0,72) a febb 2010 ( Ib= 3,60%; Dol/Eur= 0,73)

Qe2 da nov 2010 ( Ib= 2,62%; Dol/Eur= 0,72) a magg 2011 ( Ib= 3,28%; Dol/Eur= 0,70)

Qe3 da 0tt 2012 ( Ib= 1,62%; Dol/Eur= 0,78) a dic 2013 ( Ib= 3,04%; Dol/Eur= 0,73)

Ovviamente il tapering, che segue il proprio Qe, si pone tra la fine del proprio Qe e l’inizio del Qe successivo. Si osservi che tra parentesi è stato indicato con Ib il rendimento del bond decennale USA in percentuale e con Dol/Eur il cambio contro euro del dollaro, ossia espresso in termini di euro necessari per acquistare un dollaro, rilevati entrambi all’inizio del mese di partenza e alla fine del mese di chiusura del Qe.

Un attento lettore, proprio sulla base di quanto qui prima affermato, potrebbe rimanere sorpreso nell’osservare che, durante ogni Qe, Ib si trovi a salire anziché a scendere e la cosa in senso assoluto potrebbe sembrare inaspettata; ma non lo è nel momento in cui si venga a sapere che ogni Qe, di fatto, col suo periodo si trovi pressoché inserito nel percorso di andata della parabola del ciclo economico in cui, come mi è capitato di affermare in altre occasioni, Ib tende ovviamente a salire con le forze del mercato, sicché il Qe in tale circostanza ha svolto solo il ruolo di freno a mano contro la risalita dei tassi ossia di Ib.

Di contro Ib è fortemente sceso nei tapering successivi ai Qe, (ogni tapering si è pressoché svolto sul secondo ramo della parabola del ciclo) e oggi, dopo aver raggiunto il valore 3,04 % alla fine del dicembre 2013, alla fine del terzo Qe, staziona intorno al 2,5%; fatto questo che ci fa pensare che l’andamento di Ib sia del tutto concorde col suo andamento passato o storico, concordia che ci spingerebbe a giudicare quasi ininfluente ogni Qe messo in atto dalla Fed almeno in relazione all’obiettivo di portare al ribasso Ib ossia i tassi di rendimento a lunga.

Allora lo strumento Qe serve a quasi poco o niente, dato anche che per alcuni economisti esso non salva l’economia ma serve solo a far salire i mercati azionari?

Riteniamo che con ragionevolezza si possa contrastare il giudizio di tali economisti, qualora, anziché focalizzarci sull’effetto relativo al ribasso dei rendimenti, si sposti invece la nostra attenzione sull’effetto reflazionistico del Qe verso l’economia.

Il confronto con la crisi del ‘29-’30, quando la allora molto giovane Fed (cominciò ad operare nel 1914) non adottò simili politiche monetarie, potrebbe apparire inadeguato ma non del tutto visto che l’economia del 2008 precipitava ad una velocità molto più alta di quella del ‘29-’30 e che gli utili del DJIA nel 2008 sono stati negativi, cosa mai avvenuta nella sua storia neppure nel ‘29-’30.

Analizziamo allora tale confronto servendoci del grafico di fig.1 qui sotto riportato; in esso è stata riportata anche l’inflazione media annua del 2014 ovviamente calcolata fino al mese di maggio e risultata pari a 1,7 %.

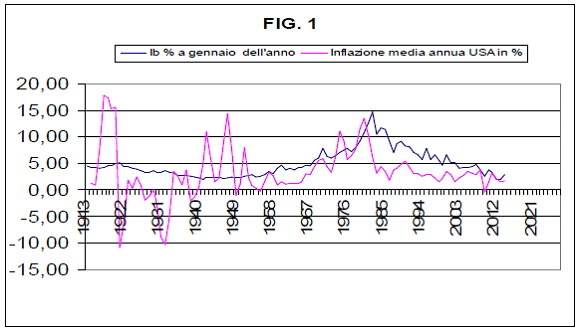
In tale grafico si può osservare che dal valore 0,00 % del 1929 l’inflazione media annua si è portata al valore di -10,30 % (negativo) del 1932 fino a raggiungere il primo valore positivo 3,50 % solo nel 1934; nel ’33 era ancora a -5,2% (negativo). Nella crisi attuale invece l’inflazione media annua, dopo aver raggiunto il valore negativo pari a -0,40% il 2009, si è portata subito verso l’alto facendo rilevare nei seguenti anni fino ad oggi i seguenti valori tutti positivi: 1,60%; 3,10%; 2,10%; 1,50%; 1,70%.

Ovvio quindi concludere che mentre nella crisi del ’29 la deflazione c’è stata e si è manifestata forte per un periodo persistentemente lungo, nella crisi del 2008 la deflazione è stata subito abbattuta sul nascere visto che aveva fatto appena capolino nel 2009, manifestandosi in particolar modo nel mese di luglio di quello stesso anno (-2,1%, inflazione annua in dato mensile) e poi anche continuativamente da marzo a ottobre sempre dello stesso anno.

Ma il 2009 è lo stesso anno in cui la Fed a gennaio ha lanciato il suo primo Qe e tale tempistica, anche nel ricordo di quanto accaduto nella crisi del ’29 in assenza di interventi di politica monetaria, mi induce a credere che i Qe della Fed abbiano prodotto o quantomeno contribuito a produrre l’effetto reflazionistico di cui si parlava in precedenza, effetto che ha mitigato la crisi e ridotto il rischio di una ricaduta in recessione o addirittura in deflazione dell’economia USA.

Certo la reflazione danneggia i bassi redditi, abbattendone il loro potere d’acquisto, ma sicuramente evita i danni ben peggiori che la deflazione certamente arreca all’economia e anche a chi un reddito non lo ha o è indebitato (Stati compresi).

Quando la domanda di beni e servizi scarseggia, un po’ di reflazione mitiga la crisi e consente di prendere tempo per aspettare tempi migliori senza sprofondare nel pantano della deflazione. Può addirittura anche accadere, come nel caso dell’economia USA a partire dal 2009, quindi in presenza degli stimoli monetari di cui si è detto, che essa si riprenda manifestando buoni dati macroeconomici.

L’ottimismo di alcuni operatori interpreta tali dati come segnali di uscita dalla crisi salvo poi ricredersi quando tali dati sono negativi: vedi il -2,9 % del Pil statunitense registrato nel primo trimestre 2014 e diffuso il 25 giugno scorso.

Per evitare di cadere in facili ottimismi, riteniamo opportuno evidenziare che la crisi è ancora in corso e continuerà ad esserlo finché la Fed manterrà in atto politiche di stimolo monetario o la forward guidance di tassi pari a zero.

Né c’è da entusiasmarsi per il fatto che la data del 18 dicembre 2013, indicata all’inizio di questo primo paragrafo, forse potrà passare alla storia come quella di uscita dell’economia statunitense dalla crisi; potrebbe essere vero ma meglio non fidarsi visto che è ancora in corso il tapering relativo al terzo Qe e che la Fed , anche se è poco probabile, potrebbe adottare una nuova fase di Qe.

Allora come rispondiamo alla domanda posta a titolo del presente articolo?

Procediamo per gradi.

2. L’andamento di Ib e dell’inflazione come indicatori di cambiamento per una possibile uscita dalla crisi e quindi dal rischio incombente e opprimente della deflazione.

Quando l’economia USA potrà considerarsi fuori dalla crisi?

Sulla base di quanto precedentemente esposto la risposta più ovvia alla precedente domanda sarebbe: “Quando le politiche economiche di stampo keynesiano (comprendenti anche i Qe di cui si è detto) messe in atto dalla Fed e dal governo degli Stati Uniti indurranno la Fed stessa ad aumentare per la prima volta il tasso di riferimento dei fed funds”, il cui ultimo aumento risale al giugno 2006. Ma una tale risposta, pur essendo ovvia, ragionevole e immediata, è tuttavia insoddisfacente per chi sa già che, al momento del primo rialzo del tasso dei fed funds, Ib sarà già salito e pertanto desideri rilevare la ripresa dell’economia USA prima del rialzo del tasso della Fed, magari cogliendolo nell’andamento al rialzo di Ib che generalmente precede il rialzo della Fed.

Insomma tale risposta è insoddisfacente per chi volesse cogliere l’inizio dell’estuario della crisi più che la fine dello stesso.

Un’altra risposta, alternativa alla precedente, potrebbe essere: “Quando la Fed avrà annunciato la fine del tapering in corso e successivamente si sarà sottratta alla forward guidance di tassi d’interesse a breve pari a zero”.

Anche questa risposta tuttavia non è soddisfacente in quanto ci porrebbe di fronte al rischio elevato di un significativo prolungamento della forward guidance di tassi pari a zero che non ci consentirebbe di cogliere tempestivamente l’inizio della ripresa USA.

Infatti Paul Krugman, risaputamene di scuola Keynesiana, in un suo articolo pubblicato su il Sole 24 Ore del 15 sett.2013 e in un altro precedente del 29 giugno 2013 ha fortemente sostenuto che per modificare le aspettative di finanzieri e imprenditori è necessario che la Fed prometta in modo credibile che sarà irresponsabile e cioè che dall’inizio della eventuale ripresa aspetterà che l’inflazione cresca e inoltre lascerà passare molto tempo (molto più tempo che la gente si aspetta) prima di alzare il tasso di riferimento. E poiché la Fed sta già avendo un comportamento simile a quello suggerito dal Nobel Krugman, c’è da star sicuri che il tasso di riferimento dei fed funds sarà aumentato solo a ripresa inoltrata, ossia con ritardo rispetto all’avvio della ripresa stessa. Le due risposte in realtà sono quasi simili differiscono solo per l’insoddisfazione che insitamente creano.

L’insoddisfazione insita nella prima risposta invita a seguire l’andamento di Ib.

L’insoddisfazione insita nella seconda risposta invita a seguire l’andamento dell’inflazione, unica variabile, il cui aumento potrà indicare l’inizio della ripresa USA visto che, in un significativo prolungamento della forward guidance di tassi pari a zero con la Fed che tiene bassi i tassi alla breve, è molto probabile che restino bassi anche i tassi alla lunga ossia i valori di Ib , potendo succedere quindi che Ib si muova al rialzo in ritardo rispetto all’inflazione, fatto questo ampiamente sperato dalla Fed che potrebbe così stabilire tassi reali negativi (ossia un tasso di inflazione maggiore di Ib) anche nella parte lunga dei tassi, ossia dei tassi dei titoli decennali e trentennali, creando repressione finanziaria.

La repressione finanziaria infatti migliora i debiti degli stati e sfavorisce il rentier che successivamente, a fronte di un reddito negativo, dovuto ai tassi reali negativi, ricavato da titoli finanziari, potrebbe venderli per investire nell’economia reale, facendo sì salire i tassi a lunga, ossia Ib, ma comunque con ritardo rispetto alla salita dell’inflazione.

Da quanto sopra è evidente che per cogliere l’inizio dell’estuario della crisi, sarà necessario monitorare gli andamenti di Ib, dell’inflazione annua USA e del tasso reale dato dalla differenza tra Ib e il tasso di inflazione.

Osserviamo quindi l’andamento di Ib a partire dal 2012 così come riportato in fig. 2.

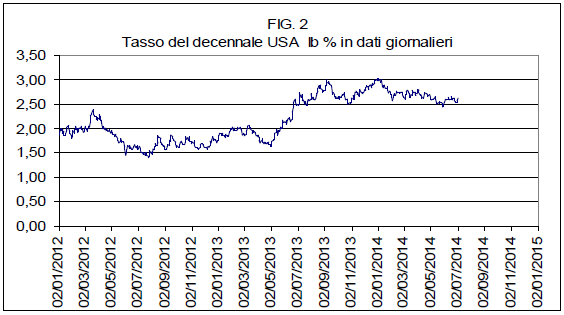
Si è deciso di partire dal 2012 perché in tale anno si sono registrati i seguenti eventi per noi significativi:
1) l’inizio del ciclo economico corrente, quello ancora in corso, che il nostro modello economico pone al lunedì 4 giugno 2012 con valore di Ib pari a 1,53 %; ciclo per il quale il nostro modello ipotizza il punto di inversione dello stesso, ipotesi questa solo momentanea, al 22 novembre 2013 (Ib pari a 2,753 %);

2) il minimo storico assoluto di Ib, pari a 1,40, valore conseguito il 24 luglio 2012, seguito due giorni dopo, il 26 luglio, dallo storico discorso a Londra di Mario Draghi “E credetemi, sarà abbastanza” col quale ha fermato la caduta dei mercati e in particolare quella dell’Euro e del tasso del Bund tedesco che pure aveva già raggiunto il suo minimo storico pari a 1,16 % il 23 luglio 2012;

3) l’inizio del terzo Qe della Fed, annunciato nel settembre 2012, avvenuto, come già detto nell’ottobre 2012 (Ib= 1,62%) e poi conclusosi a dicembre 2013 (Ib= 3,04%), seguito dal tapering in corso che al momento vede Ib oscillare tra il 2,75 e il 2,50 %.

Se la nostra ipotesi d’inversione di ciclo, posta al 22 novembre 2013, dovesse rivelarsi esatta, allora Ib dovrebbe continuare a scendere, come sta facendo da inizio gennaio 2014 e come sempre è successo durante ogni tapering della Fed e dopo ogni inversione di ciclo. È ovvio che finché il trend di Ib a partire dal suo picco di gennaio 2014 sarà fortemente discendente, ogni speranza di inizio ripresa dovrà riporsi nel cassetto, tanto più se il valore di Ib dovesse andare a rivedere il suo minimo storico, come sta invece già ora succedendo al tasso del Bund decennale tedesco che il 26 giugno 2014 ha raggiunto il valore di 1,24%, indicando quanto sia lontana anni luce ogni ipotesi di ripresa in Europa e paventando anzi il rischio che l’Europa possa trascinare in recessione anche gli Stati Uniti.

Ma, pur essendo consapevoli delle indicazioni di breve periodo che il nostro modello attualmente ci fornisce (la data, 22 novembre 2013, per l’ipotetica inversione di ciclo che si coordina con la configurazione di overshoot su Ib, materializzatasi a partire dal 31 ottobre 2013, haimè proprio dalla data della morte di mia madre, configurazione che, pur assopitasi un po’, è ancora in atto), volendo avventurarci in previsioni di medio lungo periodo, solo nei limiti di quanto il nostro modello potrebbe consentirci e solo al fine di cogliere l’inizio dell’estuario della crisi, allora diciamo di essere propensi a credere che la nostra ipotesi di inversione di ciclo sia effettivamente solo momentanea e che, o vera o sbagliata che sia (nel senso che l’evoluzione del ciclo corrente potrebbe indicare un’inversione spostata più in là nel tempo), molto probabilmente Ib nella sua discesa nel ciclo corrente non rivedrà i minimi del 2012.

In tal senso riteniamo quindi che il ciclo corrente verrà a porsi come il primo ciclo economico che dal novembre 1981 terminerà con un valore di Ib più alto di quello registrato al suo inizio (1,53%) e poniamo alla base di questa nostra opinione le seguenti tre considerazioni sugli eventi probabili che ciascuna di esse descrive:

a) Il ciclo corrente, stando al nostro modello è inserito in una località instabile di lungo periodo LILP, così come da noi definita nell’articolo “Ontologia applicata al DJIA:conseguenze”; in tale località di lungo periodo, iniziata nel luglio 2010, il nostro ciclo corrente è il terzo dopo i primi due che si sono chiusi, anch’essi, come tutti i cicli della LSLP (località stabile di lungo periodo) che ha preceduto la LILP corrente, con i due rispettivi punti, PEI, di avvicinamento all’equilibrio nei quali Ib ha manifestato sempre un valore decrescente fino a raggiungere nel PEI del secondo ciclo il valore prossimo al minimo storico pari a 1,46%, il venerdì primo giugno 2012. C’è ragione di credere che questa volta il nostro ciclo corrente possa comportarsi in modo diverso rispetto a tutti quelli (otto) che l’hanno preceduto fin dal novembre 1981? È solo questione di probabilità e, in una LILP avanzata, la probabilità che il suo ciclo corrente si chiuda con un valore di Ib più alto di quello registrato nel PEI precedente, da cui lo stesso ciclo ha avuto origine, è alta.

b) Si è venuto a creare da luglio 2012 a giugno 2014 un forte scostamento tra Ib e il tasso del Bund decennale tedesco; infatti se lo spread Ib- Bund si aggirava intorno a 0,25% nel luglio 2012 oggi tale valore si aggira intorno a 1,3% con un valore di Ib che oscilla tra 2,75 e 2,60%; spread che ovviamente indica come la marcia dell’economia USA verso l’uscita della crisi abbia acquistato sempre più velocità rispetto a quella dell’economia tedesca ed europea e che probabilmente sarà l’economia USA a trascinare fuori dalla crisi quella europea magari con Ib che durante il tapering corrente si mantenga a lungo sui livelli attuali o giù di lì senza mai scendere però sotto il valore di 2,00- 2,30% (al di sotto del quale la nostra ipotesi di inversione di ciclo riprenderebbe forza, allontanando momentaneamente l’ipotesi di ripresa) per poi, verso la fine del tapering stesso, riprendere a salire.

c) Negli Stati uniti l’inflazione è tornata ad aumentare e sta riducendo il tasso reale relativo a Ib con una tendenza che probabilmente renderà tale tasso negativo, come la Fed spera e come si può osservare dal grafico di fig.3 che qui segue:

 

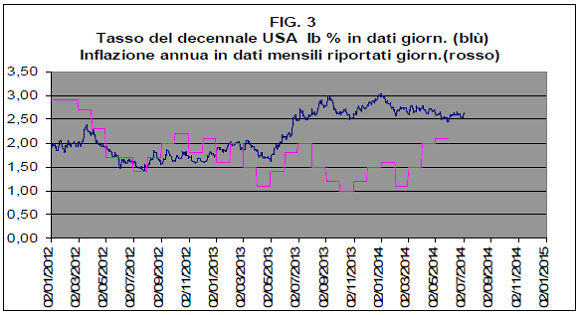
3. Le condizioni di uscita dalla crisi e il rischio di overshoot su Ib

Il materializzarsi degli eventi probabili descritti nelle nostre tre considerazioni precedenti creerà le condizioni minime concomitanti indicanti l’inizio dell’estuario della crisi, condizioni che possiamo così sintetizzare:

1) Ib persistentemente maggiore del 2,30% con manifesta tendenza al rialzo nella fase finale del tapering corrente.

2) Tasso annuo di inflazione persistentemente maggiore del 2% con tendenza al rialzo.

3) Tasso reale relativo a Ib persistentemente basso o negativo.

Ma per poter raggiungere la fine dell’estuario della crisi, al pieno realizzarsi delle condizioni suddette se ne dovranno aggiungere delle altre, quali:

4) Tasso di disoccupazione persistentemente sotto il 6% e tendente a diminuire per convergere verso il tasso di inflazione.

5) Annuncio di fine tapering della Fed e subentro della BCE alla Fed nel ruolo di garante della liquidità globale nel quadro di una exit strategy condivisa tra Fed e BCE al fine di evitare bolle e ricadute dell’economia; exit strategy condivisa le cui tracce noi già riscontriamo, a parti invertite tra le due banche centrali, nella tempistica dei punti 2) e 3) riportati precedentemente nel paragrafo 2.

6) Fine della forward guidance di tassi d’interesse a breve pari a zero e uscita dalla exit strategy con il primo rialzo del tasso di riferimento dei fed funds.

Da quanto sopra si può dedurre quanto lungo e difficile possa essere il percorso di uscita dalla crisi; basti pensare al -2,9% del Pil statunitense registrato nel primo trimestre di quest’anno e diffuso il 25 giugno scorso per rendersi conto della natura degli ostacoli che possono intralciare il percorso dell’economia USA.

Ma l’ostacolo più grande secondo noi è la configurazione di overshoot su Ib, configurazione che, pur in fase di assopimento, il nostro modello attualmente segnala ancora; l’overshoot su Ib preoccupa la Fed ed era una preoccupazione anche per Keynes che nella sua Teoria generale osservava come il valore effettivo del tasso è governato dall’opinione prevalente su quello che sarà il suo valore futuro e che il tasso può fluttuare a lungo intorno al valore normale atteso, valore che può assestarsi su livelli troppo elevati per garantire la piena occupazione e il consumo.

Per la Fed il percorso di uscita dalla crisi dovrebbe finire tra circa un anno; noi abbiamo cercato di delinearne le tappe, non ci resta che sperare in una sua felice conclusione: speriamo bene. Contando di tornare sull’argomento, intanto prepariamoci a interpretare i profitti del secondo trimestre delle società americane che certamente forniranno informazioni utili sull’attuale andamento dell’economia USA.

Giacomo De Laurentis (ing.)

Polignano a Mare (BA)

5 luglio 2014

Matematica test 2

Test di Matematica per la terza prova, un semplice ripasso dei principali argomenti di matematica per la maturità

MATEMATICA TEST1

Matematica test 1

Test di Matematica per la terza prova, un semplice ripasso dei principali argomenti di matematica per la maturità

MATEMATICA TEST1