 Un modo innovativo di insegnare l’analisi matematica nei licei. Primi passi nel calcolo infinitesimale, primi passi tra le derivate, trovare la tangente a una curva, problemi di massimo e minimo, calcolo di aree, l’integrale definito, calcolo approssimato di integrali, NSA infinitesimi e numeri iperreali, le derivate, integrali, infinito, limiti, asintoti, approssimazione polinomiale, studio di funzione, confronto tra NSA e Anqalisi Classica, applicazioni alla fisica. Il libro è gratuito nel formato pdf, nel formato cartaceo costa 16.50 euro senza spese di spedizione. Scarica gratuitamente il libro dallo shop di Matematicamente.it >>>
Un modo innovativo di insegnare l’analisi matematica nei licei. Primi passi nel calcolo infinitesimale, primi passi tra le derivate, trovare la tangente a una curva, problemi di massimo e minimo, calcolo di aree, l’integrale definito, calcolo approssimato di integrali, NSA infinitesimi e numeri iperreali, le derivate, integrali, infinito, limiti, asintoti, approssimazione polinomiale, studio di funzione, confronto tra NSA e Anqalisi Classica, applicazioni alla fisica. Il libro è gratuito nel formato pdf, nel formato cartaceo costa 16.50 euro senza spese di spedizione. Scarica gratuitamente il libro dallo shop di Matematicamente.it >>>
Prefazione
L’analisi nei licei Analisi nei licei sì o no? E se sì in che modo e in che misura? Una domanda che si ripropone ad ogni riforma o riordino delle scuole superiori. Nei licei italiani l’analisi fu inserita a inizio Novecento in occasione della riforma Credaro; a stilarne i programmi fu chiamato Guido Castelnuovo che così giustificò questa scelta:
«Ma se si vuole che l’allievo delle scuole medie senta di questa matematica moderna il soffio ispiratore ed intravveda la grandezza dell’edifizio, occorre parlargli del concetto di funzione ed indicargli sia pure sommariamente, le due operazioni che costituiscono il fondamento del Calcolo infinitesimale.»
Allora l’analisi fu inserita solo nel liceo moderno, che fu poi soppresso dalla riforma Gentile del 1923 e in qualche misura sostituito dal liceo scientifico che ereditò l’analisi come materia conclusiva del corso di matematica. Nei licei classici dove il peso della matematica fu ridimensionato l’analisi continuò a restare fuori, come del resto la geometria analitica.
Di fatto la geometria analitica fu inserita dopo la guerra nei libri di testo del liceo classico e collocata tra la prima e seconda liceo (terzo e quarto anno); l’analisi continuò a restarne fuori con l’eccezione della sperimentazione PNI diffusisi tra gli anni Ottanta e Novanta.
Negli istituti tecnici l’analisi c’è sempre stata e viene in genere trattata già nel quarto anno di corso, a volte anticipando anche al terzo. Ma come viene affrontata l’analisi nei licei?
Caratteristiche di fondo sono:
1. L’analisi è in genere posta al termine del corso di studi.
2. Si segue la sequenza limiti, derivate, integrali come all’Università, con inevitabili alleggerimenti ma sempre secondo l’impostazione Cauchy-Weierstrass.
3. Nessun cenno viene fatto alla storia del calcolo infinitesimale.
4. Obiettivo principale se non unico sembra essere quello di addestrare gli studenti in vista delle facoltà scientifiche.
Un simile approccio presenta più di un difetto:
1. La collocazione al termine del corso comporta molto spesso il taglio degli ultimi argomenti, e si tratta quasi sempre degli integrali, cassando così proprio una della due operazioni fondamentali di cui parlava Castelnuovo, in una certa misura la più importante di tutte. È quasi la norma che lo studente debba studiare in gran dettaglio i limiti e i teoremi sui limiti e solo in modo frettoloso gli integrali.
2. Questa collocazione rende di fatto impossibili ogni collegamento con il programma di Fisica.
3. Si comincia dai limiti, scontrandosi con le ben note difficoltà della definizione epsilon-delta di Weierstrass e con la notevole complicazione di quasi tutte le dimostrazioni.
4. Non viene fatto alcun cenno alla storia dell’analisi che viene presentata come una dottrina caduta dal cielo così com’è; non sembra questa la scelta didatticamente migliore in un liceo.
L’approccio NSA presentato in questo libro cerca di superare questi difetti, anche se verosimilmente si tratta solo di un primo tentativo che può essere migliorato.
Il libro si basa sull’esperienza personale dell’autore, esperienza che può certamente essere migliorata, ma che mi pare sufficiente a convincere dei vantaggi che questo approccio darebbe all’insegnamento dell’analisi.
INTRODUZIONE STORICA
Il ritorno dell’infinitesimo È un ramo della matematica dai molti nomi, all’inizio si chiamò calcolo infinitesimale, o anche calcolo differenziale, poi fu detto calcolo sublime, sin dall’inizio ebbe anche il nome di analisi a volte come analisi matematica, altre come analisi infinitesimale.
Chi oggi studia analisi nelle scuole secondarie o all’Università faticherà a capire il motivo di quell’aggettivo infinitesimale che ogni tanto riappare.
Perché oltre ad aver cambiato più volte di nome, l’analisi ha anche cambiato le sue stesse fondamenta.
All’inizio con Leibniz, insieme a Newton padre fondatore di questa disciplina, a fondamento di tutto era l’infinitesimo, numero infinitamente piccolo eppure diverso da zero, derivate e integrali si definivano semplicemente come rapporti o somme di infinitesimi. La prima contestazione arrivò nel Settecento ad opera di George Berkeley filosofo empirista e vescovo anglicano che mise in luce gli aspetti contraddittori degli infinitesimi definendoli spettri di quantità estinte (ghosts of departed quantities).
Nonostante queste critiche il calcolo divenne rapidamente uno strumento irrinunciabile per i matematici ma soprattutto per fisici e ingegneri e le critiche di Berkeley restarono sullo sfondo di fatto irrisolte.
Solo nell’Ottocento il problema delle basi dell’analisi fu preso di petto e risolto in modo radicale principalmente ad opera di Augustin Cauchy che ridefinì derivate e integrali in termini di limiti invece che di infinitesimi e poi di Karl Weierstrass che diede una definizione rigorosa di limite, quella nota come epsilon-delta.
Gli infinitesimi divenuti superflui furono cacciati dall’universo matematico; di fatto continuarono a essere usati con il nuovo nome di differenziali.
Il rigore di Cauchy e Weierstrass comportava però un prezzo elevato: una considerevole complicazione di buona parte delle definizioni e delle dimostrazioni dell’analisi. La definizione epsilon-delta è astrusa e di non immediata comprensione per gli studenti, le dimostrazioni vengono ad essere più complicate e oscure, per esempio le regole di derivazione della funzione composta o della funzione inversa, di dimostrazione quasi immediata usando gli infinitesimi, richiedono dimostrazioni lunghe e contorte usando l’approccio di Cauchy e Weierstrass.
Certamente di questa idea era Abraham Robinson, nostalgico degli infinitesimi di Leibniz, che tra il 1960 e il 1966 riuscì a dare un fondamento logico rigoroso a questi numeri che Berkeley aveva considerato spettrali.
Nel suo libro Non-standard Analysis Robinson scriveva:
However in spite of this shattering rebuttal, the idea of infinitely small or infinitesimal quantities seems to appeal naturally to our intuition
Robinson in realtà non era un analista ma un logico-matematico e fu proprio un teorema della logica, quello di compattezza che gli fornì lo strumento per reintrodurre con tutti gli onori gli infinitesimi (numeri non standard) nella matematica, dopo un secolo di esilio.
L’analisi rifondata da Robinson si basa nuovamente sugli infinitesimi, e prende il nome di Analisi Non Standard, in inglese Non Standard Analisis (NSA).
Kurt Gıdel uno dei più grandi matematici del Novecento, che di Robinson era amico, nel marzo 1973 disse in un discorso a favore della NSA4:
[…]This state of affairs should prevent a rather common misinterpretation of Non-standard Analysis, namely the idea that it is some kind of extravagance or fad of mathematical logicians. Nothing could be farther from the truth. Rather there are good reasons to believe that Non-standard Analysis in some version or other, will be the analysis of the future.
e subito dopo specificò così le ragioni che dovrebbero fare della NSA l’analisi del futuro.
One reason is the just mentioned simplification of proofs, since simplification facilitates discovery. Another, even more convincing reason, is the following: Arithmetic starts with the integers and proceeds by successively enlarging the number system by rational and negative numbers, irrational numbers etc. But the next quite natural step after the reals, namely the introduction of infinitesimals, has simply been omitted […].
Sono passati quasi quarant’anni da questa profezia di Gıdel e la NSA sembra ancora confinata in un Limbo, in particolar modo in Italia dove finora ha incontrato più diffidenza che altro. Al di là delle ragioni enunciate da Gıdel la NSA presenta un altro aspetto interessante e cioé che sembra particolarmente adatta ad un primo approccio all’analisi, in particolare nelle scuole secondarie; l’ambizione di questo libro è proprio quella di mostrare come questo sia possibile.
Ma è proprio necessaria l’analisi nei licei?
Nel corso degli anni si sono spesso alzate voci contro lo studio dell’analisi nei licei. Ne riporto solo due:
a) Nell’era dei computer e del calcolo numerico, è opportuno dare più peso alla matematica del discreto e meno a quella del continuo; e l’analisi è per eccellenza la matematica del continuo.
b) È inutile insegnare analisi nei licei perché in poco tempo non è possibile per lo studente comprendere a fondo concetti così difficili; gli studenti arrivano all’Università illudendosi di conoscere l’analisi quando in realtà ne hanno capito ben poco.
Il punto a) è, a mio avviso, il più valido; in effetti sarebbe necessario dare più spazio alla matematica discreta o a quella dell’incerto (probabilità e statistica); a questo punto di tempo per fare anche analisi rischia di restarne ben poco. A mio modo di vedere il punto a) impone semmai di ridimensionare lo studio dell’analisi non di cassarlo del tutto. Una persona di cultura dovrebbe pur avere una qualche idea su derivate e integrali. In effetti l’insegnamento dell’analisi nei licei ha finito per andare ben al di là di quell’indicare sommariamente di cui parlava Castelnuovo. Forse sarebbe opportuno tornare a quell’obiettivo minimale. Riguardo il punto b) si tratta di un vecchio argomento che può essere usato, ed è stato usato, per molti argomenti considerati difficili. Nella sua prefazione al volumetto "Il calcolo infinitesimale" W. W. Sawyer scrive:
Se mi si chiedesse di scrivere su un foglio di carta tutte le proposizioni di cui sono veramente certo, quelle proposizioni che dovrebbero essere valide in ogni tempo e in ogni luogo, ebbene io restituirei quel foglio in bianco.
Concetti molto simili erano già stati espressi dal già citato Guido Castelnuovo agli inizi del Novecento come risulta da questa antologia di citazioni:
Ciò che si sa dal professore o dall’allievo – mi fu detto – sia pur limitato, ma deve sapersi perfettamente. Orbene, io sono uno spirito mite e tollerante; ma tutte le volte che questa frase mi fu obiettata, un maligno pensiero mi ha attraversato come un lampo la mente. Oh, se potessi prendere in parola il mio interlocutore, e con magico potere riuscissi a spegnere per un istante nel suo cervello tutte le cognizioni vaghe per lasciar sussistere soltanto ciò che egli sa perfettamente! Voi non immaginate mai quale miserando spettacolo potrei presentarvi! Ammesso pure che dopo una cosi crudele mutilazione qualche barlume rimanesse ancor nel suo intelletto, e di ciò fortemente dubito, somiglierebbe questo ad un gioco di fuochi folletti sperduti in tenebre profonde e sconfinate. La verità è che noi nulla sappiamo perfettamente …
E’ questo il torto precipuo dello spirito dottrinario che invade la nostra scuola. Noi vi insegniamo a diffidare dell’approssimazione, che è realtà, per adorare l’idolo di una perfezione che è illusoria…
il ragionamento formalmente perfetto non è né l’unico, né, molte volte, il miglior modo per giungere alla verità. È ben spesso preferibile ricorrere ad un ragionamento approssimato, i cui passi successivi vengano sottoposti al riscontro dei fatti, per sceverare via, via il vero dal falso, piuttosto che affidarsi ad una logica impeccabile, chiudendo gli occhi al mondo esterno. Ora la matematica (come oggi si insegna nelle scuole di cultura generale) disprezza a torto quel primo tipo di procedimento logico, e condanna in tal modo l’unica forma di ragionamento che sia concessa alla maggioranza degli uomini!
Questo libro
Questo libro raccoglie, riorganizza e amplia materiale da me utilizzato per l’insegnamento dell’analisi nelle ultime due classi del liceo classico utilizzando un approccio che chiamerò NSAlight nel senso che ricalca l’analisi NSA ma con molti alleggerimenti.
Nel corso degli anni ho cambiato molte volte l’ordine e la collocazione dei vari argomenti dell’analisi, qui ne propongo uno, che non è necessariamente l’unico possibile.
La prima parte intitolata “Primi passi nel calcolo infinitesimale” ricalca in realtà più l’analisi di Leibniz che quella NSA, cerca di partire dagli esempi per arrivare a definizioni abbastanza rigorose, ma senza insistere troppo sul formalismo e sul rigore. Vengono introdotte sia le derivate sia gli integrali, ma solo per polinomi. Qui l’importante è abituarsi ai concetti di derivata ed integrale più che insistere su definizioni rigorose e complicazioni di calcolo. In questo modo è già possibile qualche non spregevole interazione con la Fisica. Questa è la parte svolta nel penultimo anno di corso.
La seconda parte utilizza più decisamente l’approccio NSA ed estende l’analisi anche a funzioni irrazionali, esponenziali, logaritmiche e goniometriche; alla fine vi è anche una trattazione dei limiti e di alcuni problemi correlati (asintoti). Nel testo sono intercalati anche alcuni capitoli di analisi numerica, in particolare sul calcolo approssimato delle aree e degli integrali e sull’approssimazione polinomiale (polinomi di Taylor e Maclaurin).
Paolo Bonavoglia Venezia, maggio 2011

 Tutta la fisica di base per i licei e il biennio universitario, parte prima. Il libro è gratuito nella versione pdf. La copia a stampa costa 16.00 euro, spedizione gratuita per l’Italia. Calcolo vettoriale, Cinematica del punto materiale, Dinamica del punto materiale, Lavoro e potenza, L’energia, Dinamica dei sistemi di particelle, Urti, Sistemi ruotanti, Equilibrio dei corpi rigidi, Moto armonico, Gravitazione, Fluidi. Il libro è rilasciato con la licenza Creative Commons. Per scaricare il libro di fisica gratuitamente
Tutta la fisica di base per i licei e il biennio universitario, parte prima. Il libro è gratuito nella versione pdf. La copia a stampa costa 16.00 euro, spedizione gratuita per l’Italia. Calcolo vettoriale, Cinematica del punto materiale, Dinamica del punto materiale, Lavoro e potenza, L’energia, Dinamica dei sistemi di particelle, Urti, Sistemi ruotanti, Equilibrio dei corpi rigidi, Moto armonico, Gravitazione, Fluidi. Il libro è rilasciato con la licenza Creative Commons. Per scaricare il libro di fisica gratuitamente 
 Il moto armonico può essere considerato come la proiezione di un moto circolare uniforme su una retta r. Mentre il punto si muove con moto circolare uniforme, la sua proiezione si muove con moto armonico lungo un segmento. Intuitivamente, si capisce che la sua velocità non è costante: ha valore massimo nella regione centrale del segmento, e decresce man mano che ci si avvicina ad uno degli estremi.
Il moto armonico può essere considerato come la proiezione di un moto circolare uniforme su una retta r. Mentre il punto si muove con moto circolare uniforme, la sua proiezione si muove con moto armonico lungo un segmento. Intuitivamente, si capisce che la sua velocità non è costante: ha valore massimo nella regione centrale del segmento, e decresce man mano che ci si avvicina ad uno degli estremi.  Talvolta … un problema che dovrebbe essere risolvibile per mezzo di regole e procedimenti noti, resiste al reiterato assalto dei più abili membri del gruppo entro la cui competenza viene a cadere. In altre circostanze, uno strumento dell’apparato di ricerca, progettato e costruito per gli scopi della ricerca normale, non riesce a funzionare nella maniera aspettata, rivelando una anomalia che, nonostante i ripetuti sforzi, non può venir ridotta a conformarsi all’aspettativa professionale…
Talvolta … un problema che dovrebbe essere risolvibile per mezzo di regole e procedimenti noti, resiste al reiterato assalto dei più abili membri del gruppo entro la cui competenza viene a cadere. In altre circostanze, uno strumento dell’apparato di ricerca, progettato e costruito per gli scopi della ricerca normale, non riesce a funzionare nella maniera aspettata, rivelando una anomalia che, nonostante i ripetuti sforzi, non può venir ridotta a conformarsi all’aspettativa professionale… 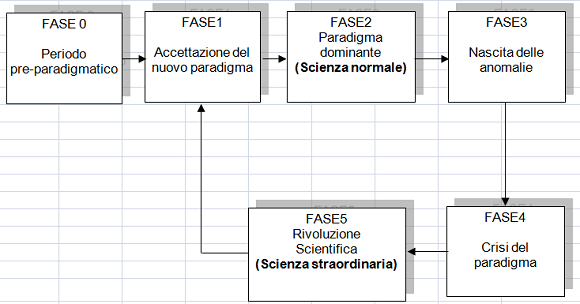
 La prova nazionale invalsi di italiano per la secondaria di primo grado
La prova nazionale invalsi di italiano per la secondaria di primo grado  La prova invalsi di matematica per la scuola secondaria di primo grado (terza media)
La prova invalsi di matematica per la scuola secondaria di primo grado (terza media)  C’è una divergenza molto vasta fra quelli che si potrebbero considerare oggi i teorici dei sistemi ‘animati’ e i teorici di sistemi ‘inanimati’ e non è affatto certo che si tratti di una divergenza destinata a ridursi e ancor meno a scomparire, nel prossimo futuro. Ci sono alcuni che ritengono che questa divergenza rifletta la strutturale inadeguatezza della matematica tradizionale – la matematica di punti, funzioni, insiemi, misure di probabilità etc. ben definiti – a far fronte all’analisi dei sistemi biologici;
C’è una divergenza molto vasta fra quelli che si potrebbero considerare oggi i teorici dei sistemi ‘animati’ e i teorici di sistemi ‘inanimati’ e non è affatto certo che si tratti di una divergenza destinata a ridursi e ancor meno a scomparire, nel prossimo futuro. Ci sono alcuni che ritengono che questa divergenza rifletta la strutturale inadeguatezza della matematica tradizionale – la matematica di punti, funzioni, insiemi, misure di probabilità etc. ben definiti – a far fronte all’analisi dei sistemi biologici; 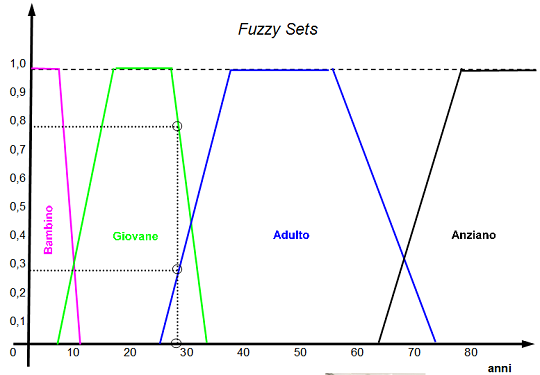
 Obiettivo del presente articolo è quello di trovare l’equazione del reticolo della dama ovvero l’equazione del contorno dei 64 quadrati che compongono la dama. Sarà grazie all’aiuto della rete intrecciata a maglia rombica che si potrà ottenere tale risultato.
Obiettivo del presente articolo è quello di trovare l’equazione del reticolo della dama ovvero l’equazione del contorno dei 64 quadrati che compongono la dama. Sarà grazie all’aiuto della rete intrecciata a maglia rombica che si potrà ottenere tale risultato.  Quello dell’insegnamento/apprendimento della matematica è un problema che negli ultimi anni è andato crescendo sempre più. Tra gli argomenti più ostici per i nostri studenti di ogni ordine e grado ci sono le frazioni, le quali – nonostante la semplicità con cui possono essere introdotte (si pensi alle classiche porzioni di torte) – ben presto diventano incomprensibili, soprattutto per quel che riguarda le operazioni di cui vengono dotate. Questo ci ha indotti a occuparci di frazioni nell’ambito della scuola dell’obbligo, con l’intento di smussarne alcune asperità; anche perché l’argomento è fondamentale per il successivo passaggio ai numeri reali.
Quello dell’insegnamento/apprendimento della matematica è un problema che negli ultimi anni è andato crescendo sempre più. Tra gli argomenti più ostici per i nostri studenti di ogni ordine e grado ci sono le frazioni, le quali – nonostante la semplicità con cui possono essere introdotte (si pensi alle classiche porzioni di torte) – ben presto diventano incomprensibili, soprattutto per quel che riguarda le operazioni di cui vengono dotate. Questo ci ha indotti a occuparci di frazioni nell’ambito della scuola dell’obbligo, con l’intento di smussarne alcune asperità; anche perché l’argomento è fondamentale per il successivo passaggio ai numeri reali.  Vari metodi per moltiplicare due numeri: moltiplicazione egizia o metodo dei raddoppi, moltiplicazione russa o metodo dei raddoppi e dimezzamenti, moltiplicazione indiana e araba, moltiplicazione arba per gelosia, moltiplicazione cinese o grafica, moltiplicazione per scapezzo, moltiplicazione per crocetta, moltiplicazione. per castelluccio,
Vari metodi per moltiplicare due numeri: moltiplicazione egizia o metodo dei raddoppi, moltiplicazione russa o metodo dei raddoppi e dimezzamenti, moltiplicazione indiana e araba, moltiplicazione arba per gelosia, moltiplicazione cinese o grafica, moltiplicazione per scapezzo, moltiplicazione per crocetta, moltiplicazione. per castelluccio,  Per secoli il fascino dei numeri primi ha catturato l’interesse dei più grandi matematici. Le proprietà di questi eleganti oggetti sono state a lungo esplorate e in questi ultimi decenni, con l’evoluzione delle tecnologie informatiche, hanno trovato estese applicazioni nell’ambito della cosiddetta Crittografia a chiave pubblica. Nelle pagine che seguono cercheremo di capire quali profonde problematiche si celano dietro la bellezza dei numeri primi e comprenderemo come essi vengono applicati nelle moderne tecniche crittografiche.
Per secoli il fascino dei numeri primi ha catturato l’interesse dei più grandi matematici. Le proprietà di questi eleganti oggetti sono state a lungo esplorate e in questi ultimi decenni, con l’evoluzione delle tecnologie informatiche, hanno trovato estese applicazioni nell’ambito della cosiddetta Crittografia a chiave pubblica. Nelle pagine che seguono cercheremo di capire quali profonde problematiche si celano dietro la bellezza dei numeri primi e comprenderemo come essi vengono applicati nelle moderne tecniche crittografiche.  Una eclisse totale di Luna si verificherà la sera del 15 giugno in un orario molto comodo per noi italiani. L’intero fenomeno infatti sarà visibile già dalla prima serata e si concluderà a mezzanotte. In questa occasione la Luna si immergerà completamente nel cono d’ombra terrestre assumendo la caratteristica colorazione rossastra: la famosa LUNA ROSSA, che avrà una durata di ben 100 minuti. Tutto il tempo quindi per goderci con calma il fenomeno e fotografarlo.
Una eclisse totale di Luna si verificherà la sera del 15 giugno in un orario molto comodo per noi italiani. L’intero fenomeno infatti sarà visibile già dalla prima serata e si concluderà a mezzanotte. In questa occasione la Luna si immergerà completamente nel cono d’ombra terrestre assumendo la caratteristica colorazione rossastra: la famosa LUNA ROSSA, che avrà una durata di ben 100 minuti. Tutto il tempo quindi per goderci con calma il fenomeno e fotografarlo.  Dobbiamo scoprire che pensare la realtà è, tra tutte, l’avventura più difficile. Significa navigare tra mutilazione e confusione, tra sclerosi e deriva, tra razionalizzazione e irrazionalità, assieme e contro ragione e follia… Il Problema – il gioco del pensiero- è di lasciarci intrattenere abbastanza dalle nostre pulsioni nella misura in cui esse ci regalano immaginazione e invenzione, ma senza cessare di controllarle, senza cessare di mettere alla prova quello che costituisce la sola e la più potente resistenza alle nostre razionalizzazioni: la complessità del reale. E’ in quel momento che la complessità del reale può stimolare la complessità del pensiero. Edgar Morin (1921) Introduzione al pensiero complesso.
Dobbiamo scoprire che pensare la realtà è, tra tutte, l’avventura più difficile. Significa navigare tra mutilazione e confusione, tra sclerosi e deriva, tra razionalizzazione e irrazionalità, assieme e contro ragione e follia… Il Problema – il gioco del pensiero- è di lasciarci intrattenere abbastanza dalle nostre pulsioni nella misura in cui esse ci regalano immaginazione e invenzione, ma senza cessare di controllarle, senza cessare di mettere alla prova quello che costituisce la sola e la più potente resistenza alle nostre razionalizzazioni: la complessità del reale. E’ in quel momento che la complessità del reale può stimolare la complessità del pensiero. Edgar Morin (1921) Introduzione al pensiero complesso.  I comandi principali di MS-DOS, sistema operativo a riga di comando, monoutente e monotask: come si accede al prompt del DOS, percorso di file e cartelle, uscita dalla linea di comando, autorun, autocomplete, cambiare directory…
I comandi principali di MS-DOS, sistema operativo a riga di comando, monoutente e monotask: come si accede al prompt del DOS, percorso di file e cartelle, uscita dalla linea di comando, autorun, autocomplete, cambiare directory…  In questo articolo vengono esaminate tre congetture di P. Erdös riguardanti insiemi composti da un numero finito di punti nel piano. Nella prima dati n punti si considerano le distanze determinate dalle coppie di punti della configurazione e si cerca di disporli in modo che il numero delle distanze sia minimo. Nella seconda…
In questo articolo vengono esaminate tre congetture di P. Erdös riguardanti insiemi composti da un numero finito di punti nel piano. Nella prima dati n punti si considerano le distanze determinate dalle coppie di punti della configurazione e si cerca di disporli in modo che il numero delle distanze sia minimo. Nella seconda…  Un sistema può essere composto tanto da persone quanto da oggetti fisici: il magazziniere e gli impiegati d’ufficio sono parte del sistema "magazzino"; gli organi di direzione di un impresa sono un sistema per la ripartizione delle risorse e la regolazione delle attività dell’impresa stessa; una famiglia è un sistema per vivere e per allevare figli. In una società primitiva, i sistemi esistenti erano quelli che si manifestavano in natura e le loro caratteristiche erano accettate come fenomeni di origine divina, sottratti alla comprensione o al controllo umano.
Un sistema può essere composto tanto da persone quanto da oggetti fisici: il magazziniere e gli impiegati d’ufficio sono parte del sistema "magazzino"; gli organi di direzione di un impresa sono un sistema per la ripartizione delle risorse e la regolazione delle attività dell’impresa stessa; una famiglia è un sistema per vivere e per allevare figli. In una società primitiva, i sistemi esistenti erano quelli che si manifestavano in natura e le loro caratteristiche erano accettate come fenomeni di origine divina, sottratti alla comprensione o al controllo umano. 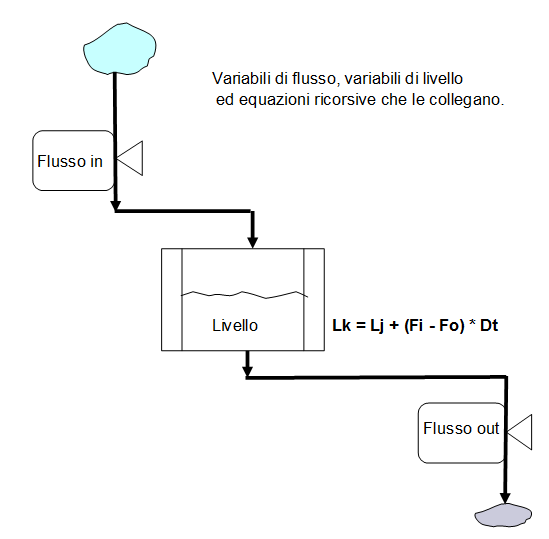
 I tassi d’interesse sono grandezze finanziarie non direttamente quotate sui mercati finanziari, infatti sono ricavati da altri strumenti finanziari il cui prezzo, invece, viene registrato sui mercati. Le informazioni implicite nei tassi di mercato di diverse attività finanziarie forniscono indicazioni prospettiche sulle aspettative del mercato riguardo a numerosi fattori fondamentali, come l’evoluzione futura delle attività economiche e l’inflazione, nonché l’andamento del costo del denaro. L’analisi di tali aspettative è importante per l’attuazione di politiche di gestione del rischio di tasso d’interesse.
I tassi d’interesse sono grandezze finanziarie non direttamente quotate sui mercati finanziari, infatti sono ricavati da altri strumenti finanziari il cui prezzo, invece, viene registrato sui mercati. Le informazioni implicite nei tassi di mercato di diverse attività finanziarie forniscono indicazioni prospettiche sulle aspettative del mercato riguardo a numerosi fattori fondamentali, come l’evoluzione futura delle attività economiche e l’inflazione, nonché l’andamento del costo del denaro. L’analisi di tali aspettative è importante per l’attuazione di politiche di gestione del rischio di tasso d’interesse.  "Non ci può più essere alcun dubbio che i presupposti dell’economia delle organizzazioni, cioè le assunzioni di una razionalità perfetta, sono contrarie ai fatti. Non è un problema di maggiore o minore approssimazione; questi presupposti non descrivono neanche lontanamente i processi che gli esseri umani adottano per prendere delle decisioni in situazioni complesse". Herbert Simon (1916, 2001), Rational Decision Making in business organizations.
"Non ci può più essere alcun dubbio che i presupposti dell’economia delle organizzazioni, cioè le assunzioni di una razionalità perfetta, sono contrarie ai fatti. Non è un problema di maggiore o minore approssimazione; questi presupposti non descrivono neanche lontanamente i processi che gli esseri umani adottano per prendere delle decisioni in situazioni complesse". Herbert Simon (1916, 2001), Rational Decision Making in business organizations. 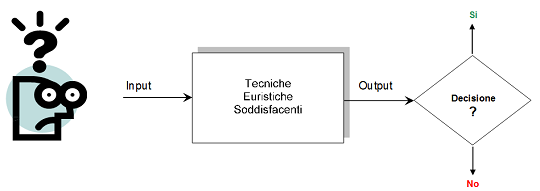

 Non fu un’uscita felice quella di Nikita Krusciov, che definì «dipinti dalla coda di un asino» i quadri di Jackson Pollock. Era una stupidaggine che scaturiva dagli astrusi e oscuri meandri dell’ortodossia sovietica, secondo la quale l’arte astratta era un bidone, un trastullo capitalistico. Tant’è vero che il moscovita Wassily Kandinsky, che l’aveva inaugurata negli anni ’10 del Novecento, dovette scappare a Parigi, dove morì da cittadino francese.
Non fu un’uscita felice quella di Nikita Krusciov, che definì «dipinti dalla coda di un asino» i quadri di Jackson Pollock. Era una stupidaggine che scaturiva dagli astrusi e oscuri meandri dell’ortodossia sovietica, secondo la quale l’arte astratta era un bidone, un trastullo capitalistico. Tant’è vero che il moscovita Wassily Kandinsky, che l’aveva inaugurata negli anni ’10 del Novecento, dovette scappare a Parigi, dove morì da cittadino francese.  "La filosofia penso debba essere fatta da spiriti scientifici, e in servigio della scienza" «La filosofia della natura è caduta nel nulla. I nuovi idealisti credono di sbarazzarsi del suo peso morto ritenendo ogni forma di studio della natura come una maniera di attività pratica, indifferente al pensiero. In tal guisa, non solo impoveriscono l’idealismo ma, ciò che è più grave per dei pensatori storicisti, commettono un errore antistorico. Perché tutta la storia della filosofia, almeno della filosofia occidentale, prende norma e ispirazione dal pensiero naturalistico». Federigo Enriques (1871 – 1946)
"La filosofia penso debba essere fatta da spiriti scientifici, e in servigio della scienza" «La filosofia della natura è caduta nel nulla. I nuovi idealisti credono di sbarazzarsi del suo peso morto ritenendo ogni forma di studio della natura come una maniera di attività pratica, indifferente al pensiero. In tal guisa, non solo impoveriscono l’idealismo ma, ciò che è più grave per dei pensatori storicisti, commettono un errore antistorico. Perché tutta la storia della filosofia, almeno della filosofia occidentale, prende norma e ispirazione dal pensiero naturalistico». Federigo Enriques (1871 – 1946) 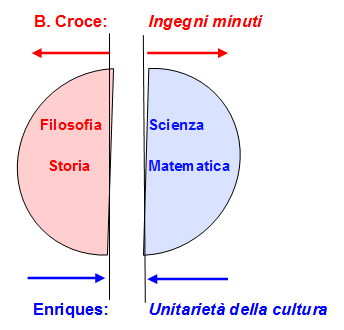
 Il primo contatto con la matematica è mediato dalla scuola, dove tradizionalmente questa scienza ci viene introdotta con un approccio formale e con scarsa attenzione per gli aspetti storici, linguistici e culturali. Fermamente convinto della natura culturale ed umanistica della matematica e dell’informatica, sono invece favorevole ad un approccio storico, che evidenzi le forti correlazioni e gli stretti intrecci con le altre scienze e soprattutto con la filosofia. Immaginiamo dunque che, in un Liceo, in seguito ad una pianificazione interdisciplinare, alcune lezioni di lingue classiche vengano riservate per raccontare che …
Il primo contatto con la matematica è mediato dalla scuola, dove tradizionalmente questa scienza ci viene introdotta con un approccio formale e con scarsa attenzione per gli aspetti storici, linguistici e culturali. Fermamente convinto della natura culturale ed umanistica della matematica e dell’informatica, sono invece favorevole ad un approccio storico, che evidenzi le forti correlazioni e gli stretti intrecci con le altre scienze e soprattutto con la filosofia. Immaginiamo dunque che, in un Liceo, in seguito ad una pianificazione interdisciplinare, alcune lezioni di lingue classiche vengano riservate per raccontare che …  La programmazione lineare divenne di uso diffuso a partire dal 1947 in corrispondenza con la pianificazione delle attività militari. … E’ interessante notare che prima del 1947, nonostante la sua ampia applicabilità, la programmazione lineare era sconosciuta …
La programmazione lineare divenne di uso diffuso a partire dal 1947 in corrispondenza con la pianificazione delle attività militari. … E’ interessante notare che prima del 1947, nonostante la sua ampia applicabilità, la programmazione lineare era sconosciuta … 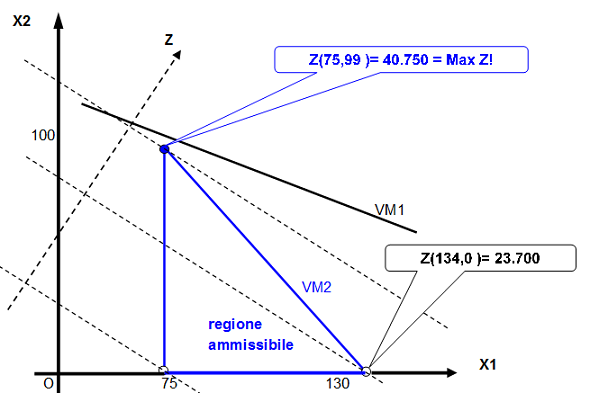
 Schede sintetiche per conoscere le varie porte del computer
Schede sintetiche per conoscere le varie porte del computer Animazione interattiva in Flash per ripassare le operazioni con i numeri relativi. Inserendo semplici espressioni è possibile vedere lo svolgimento passo passo delle operazioni. Per i ragazzi della secondaria di primo grado.
Animazione interattiva in Flash per ripassare le operazioni con i numeri relativi. Inserendo semplici espressioni è possibile vedere lo svolgimento passo passo delle operazioni. Per i ragazzi della secondaria di primo grado.  Animazione interattiva in Flash per studiare le proprietà del quadrato.
Animazione interattiva in Flash per studiare le proprietà del quadrato.  Animazione interattiva in Flash che ti permette di esercitarti con il calcolo della radice quadrata.
Animazione interattiva in Flash che ti permette di esercitarti con il calcolo della radice quadrata.  Animazione interattiva in Flash per ripassare proprietà e regola del parallelogramma, per studenti della secondaria di primo grado.
Animazione interattiva in Flash per ripassare proprietà e regola del parallelogramma, per studenti della secondaria di primo grado.  Animazione interattiva in Flash per ripassare il teorema di Pitagora, per studenti della secondaria di primo grado.
Animazione interattiva in Flash per ripassare il teorema di Pitagora, per studenti della secondaria di primo grado.  Animazione interattiva in Flash per capire un metodo empirico per calcolare il volume di un solido, per studenti della secondaria di primo grado.
Animazione interattiva in Flash per capire un metodo empirico per calcolare il volume di un solido, per studenti della secondaria di primo grado.  Animazione interattiva in per esercitarsi sulle operazioni con i monomi, per studenti della secondaria di primo grado.
Animazione interattiva in per esercitarsi sulle operazioni con i monomi, per studenti della secondaria di primo grado.  Animazione interattiva per esercitarsi sui prodotti notevoli, per studenti della secondaria di primo grado.
Animazione interattiva per esercitarsi sui prodotti notevoli, per studenti della secondaria di primo grado.  In questo numero, Cosimo De Mitri e Domenico Lenzi tornano a discutere dei postulati euclidei, in particolare del postulato sull’uguaglianza degli angoli retti. Carlo Sintini ci propone una coinvolgente esperienza didattica: come calcolare la massa di Giove a partire da una serie di otto foto di Giove e dei suoi quattro satelliti medicei. Stefano Borgogni presenta i “Puzzle”, ideati dal padre dell’autore molto prima che Martin Gardner pubblicasse i suoi articoli sui polimini. Gabriele Taddei affronta un problema classico sul profilo che deve avere un corpo per rendere minima la resistenza quando si muove in un fluido. Il lavoro di Pietro Romano consiste in una serie di attività didattiche da fare con il software di geometria dinamica Geogebra, software gratuito che si presta non solo per l’insegnamento della geometria ma anche della fisica e in particolare dell’ottica. In questo lavoro si fa largo uso degli slider che solitamente sono poco utilizzati e poco conosciuti. Roberto Chiappi presenta una sintesi dei suoi lunghi studi sul problem solving, finalizzati al miglioramento dei processi di project management e decision making. Per la sezione Lo scaffale dei libri Riccardo Travaglini ci presenta il libro “La Singolarità e vicina” di Ray Kurzweil e Marco Ruffinoni il libro “Nuova fisica per tutti” di Carlos Fiolhais.
In questo numero, Cosimo De Mitri e Domenico Lenzi tornano a discutere dei postulati euclidei, in particolare del postulato sull’uguaglianza degli angoli retti. Carlo Sintini ci propone una coinvolgente esperienza didattica: come calcolare la massa di Giove a partire da una serie di otto foto di Giove e dei suoi quattro satelliti medicei. Stefano Borgogni presenta i “Puzzle”, ideati dal padre dell’autore molto prima che Martin Gardner pubblicasse i suoi articoli sui polimini. Gabriele Taddei affronta un problema classico sul profilo che deve avere un corpo per rendere minima la resistenza quando si muove in un fluido. Il lavoro di Pietro Romano consiste in una serie di attività didattiche da fare con il software di geometria dinamica Geogebra, software gratuito che si presta non solo per l’insegnamento della geometria ma anche della fisica e in particolare dell’ottica. In questo lavoro si fa largo uso degli slider che solitamente sono poco utilizzati e poco conosciuti. Roberto Chiappi presenta una sintesi dei suoi lunghi studi sul problem solving, finalizzati al miglioramento dei processi di project management e decision making. Per la sezione Lo scaffale dei libri Riccardo Travaglini ci presenta il libro “La Singolarità e vicina” di Ray Kurzweil e Marco Ruffinoni il libro “Nuova fisica per tutti” di Carlos Fiolhais.