 L’attività di laboratorio, sia come spazio attrezzato tipico per l’insegnamento delle discipline scientifiche, sia come attività cooperativa e condivisa tra studenti e insegnanti, caratterizzata da un forte approccio operativo, riveste attualmente un ruolo di primo piano non solo nella sperimentazione ma anche nella didattica usuale. Obiettivo della ricerca di dottorato è stato quello di progettare sistemi usabili ed efficaci, nello stile del Web 2.0 per portare l’apprendimento delle discipline scientifiche e in particolare delle attività di laboratorio in senso lato nel paradigma di base dell’e-learning: anytime and anywere.
L’attività di laboratorio, sia come spazio attrezzato tipico per l’insegnamento delle discipline scientifiche, sia come attività cooperativa e condivisa tra studenti e insegnanti, caratterizzata da un forte approccio operativo, riveste attualmente un ruolo di primo piano non solo nella sperimentazione ma anche nella didattica usuale. Obiettivo della ricerca di dottorato è stato quello di progettare sistemi usabili ed efficaci, nello stile del Web 2.0 per portare l’apprendimento delle discipline scientifiche e in particolare delle attività di laboratorio in senso lato nel paradigma di base dell’e-learning: anytime and anywere.
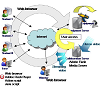
Le due principali tematiche di ricerca esposte in questa tesi sono: il laboratorio scientifico mediato dal Web, in particolare la progettazione e realizzazione di un software che consente di far controllare via Web a una classe virtuale strumenti di laboratorio reali: il telescopio del Dipartimento di Fisica e il microscopio del Dipartimento di Ingegneria dell’Innovazione dell’Università del Salento.
La seconda tematica ha riguardato la progettazione e realizzazione di strumenti di gestione e controllo di una comunità di studio on line (Online Learning Community OLC), con particolare riferimento alle attività didattiche laboratoriali (in senso lato) collaborative sincrone. In particolare, sono stati studiati strumenti di gestione e controllo per la community Matematicamente.it, la gara online MatematiCup condotta come laboratorio didattico di matematica, la gara online EcologicaCup come laboratorio di ecologia, l’Agenzia Simulata delle Entrate all’interno della rete italiana delle Imprese Formative Simulate come laboratorio di simulazione d’impresa.
La tesi si compone di tre capitoli. Nel primo si descrive l’evoluzione dell’elearning con particolare riferimento agli sviluppi del cosiddetto elearning 2.0 per fornire il contesto tecnologico e pedagogico della ricerca. Il secondo è dedicato ai laboratori remoti collaborativi. Nel terzo capitolo si descrive lo sviluppo della community Matematicamente.it e le altre attività di laboratorio ‘virtuale’ svolte con il DIDA-lab (dir. resp. Prof. M. A. Bochicchio), laboratorio di innovazione didattica con le tecnologie informatiche, presso il Dipartimento di Ingegneria dell’Innovazione, Università del Salento.
Scarica la tesi
INDICE
Abstract
Capitolo 1: Le ICT nella formazione
1.1 I modelli dell’elearning
1.2 Gli stili di apprendimento
1.3 Il quadro istituzionale
1.4 Questioni aperte e “research question”
Capitolo 2: I laboratori remoti
2.1 Il laboratorio nella didattica
2.2 Il laboratorio remoto
2.3 Il laboratorio remoto collaborativo
2.4 AstroNet
2.5 MicroNet
Capitolo 3: On line learning communities
3.1 Dal Web 2.0 all’elearning 2.0
3.2 Matematicamente.it
3.3 Laboratorio di matematica: Matematicup
3.4 Laboratorio di ecologia: EcologicaCup
3.5 Laboratorio d’impresa: Agenzia Simulata delle Entrate
Conclusioni
Bibliografia
Bibliografia e sitografia
[ADL 2004] Advanced Distribuited Learning, SCORM 2.0, 2004, http://www.adlnet.gov/scorm/downloads/index.aspx (21.02.2009)
[Agarwal 1998] Agarwal D. A., Sachs S. R., Johanston, W. E., The reality of collaboratories, in “Comput. Physt. Commun.” (110), 1998, pp.134-141.
[Aktan 1996] Aktan B., Bohus C. A., Crowl L. A., Shor M. H., Distance learning applied to control engineering laboratories, in “IEEE Transactions on Education” (39, 3), 1996, pp. 320–326.
[Anderson P. 2007] Anderson P., What is Web 2.0? Ideas, technologies and implications for education, JISC reports, 2007. http://www.jisc.ac.uk/media/documents/techwatch/tsw0701b.pdf (07.03.2009)
[Anderson T. 2005] Anderson T., Distance Learning – Social Software’s killer ap?, ODLAA 2005 Conference http://www.unisa.edu.au/odlaaconference/PPDF2s/13%20odlaa%20-%20Anderson.pdf (07.03.2009)
[Anderson T. 2006] Anderson T., PLEs versus LMS: Are PLEs ready for Prime time?, in “Virtual Canuck – Teaching and Learning in a Net-Centric World”, 2006,
http://terrya.edublogs.org/2006/01/09/ples-versus-lms-are-ples-ready-for-prime-time/ (08.03.2009)
[Asensio 2001] Jones, C., M. Asensio, et al., 2001, Effective networked learning in higher education: notes and guidelines, presentato in “Networked Learning in Higher Education Project (JISC/CALT)”, Lancaster University, 31.01.2001.
[Bartolomé 2008] Bartolomé A., Web 2.0 and New Learning Paradigms, in “eLearning Papers” (8) 2008, http://www.elearningpapers.eu/index.php?page=doc&doc_id=11654&doclng=9 (07.03.2009)
[Bateson 1972] Bateson G., Verso un’ecologia della mente, Adelphi, Milano, 1972.
[Bianchi 1] M. Bianchi, La Simulazione d’Impresa ed il Long Distance Support Center della Facoltà di Economia Della Università di Bologna Sede di Forlì, http://ei.unibo.it/materie/pdf/simurel1.pdf
[Bianchi 2] M. Bianchi, La Simulazione d’Impresa negli interventi di sviluppo dei paesi in transizione. http://ei.unibo.it/simulimpresa/worklast3.pdf
[Biolghini 2000] Biolghini D., Cengarle M. (a cura di), Net learning. Imparare insieme attraverso la rete, Milano, ETAS, 2000
[Biolghini 2000] Biolghini D., Cengarle M., Net learning. Imparare insieme attraverso la rete, Etas, Milano, 2000.
[Biolghini 2001] Biolghini D. (a cura di), Comunità in rete e Net learning, Milano, ETAS, 2001
[Bochicchio 2004] M. A. Bochicchio, A. Longo, UWA+: bridging Web systems design and Business process modelling, in “International Workshop on Web Engineering”, August 10, 2004, in conjunction with ACM Hypertext 2004, Santa Cruz, August 9-13, 2004.
[Bonaiuti 2006] Bonaiuti G., E-learning 2.0, Erikson, 2006.
[Boscarino 2004] Boscarino G. S., La didattica laboratoriale, Inserito n.9 gennaio 2004 di Scuola e Didattica, Editrice La Scuola, 2004, http://www.lascuola.it/webapp/Download/SD/PR005.pdf (24.02.2009)
[Calvani 1999] Calvani A., Rotta M., Comunicazione e apprendimento in Internet. Didattica costruttivistica in rete, Centro Studi Erickson, Trento, 1999.
[Calvani 2005] Calvani A., Comunità di pratica e di apprendimento, http://www.costruttivismoedidattica.it/articoli/Calvani%20-%20ComunitaApprendimento.pdf (09.03.2009)
[Calvani 2005b] Calvani A., Rete comunità e Conoscenza. Costruire e gestire dinamiche collaborative, Erickson, 2005
[Calvani 2006] Calvani A., Fini A., Pettenati M.C., Sarti L., Masseti M., Design of Collaborative Learning Environments: bridging the gap between CSCL theories and Open Source Platforms, in “Journal of e-Learning and Knowledge Society, (4) 2006
[Camizzi 2002] L. Camizzi, E. Mosa, F. Rossi, Un’esperienza di "collaborative learning" in matematica, Contenuti innovativi + apprendimento collaborativo + ambienti on line = la formula ideale per l’apprendimento e l’insegnamento della matematica!, INDIRE, http://www.bdp.it/content/index.php?action=read&id=1439 .
[Canfora 2004] Canfora G., Daponte P., and Rapuano S., Remotely accessible laboratory for electronic measurement teaching. Comput. Standards and Interfaces (26, 6), 2004, pp. 489-499.
[CEDFOP 2004] Tissot p., Terminology of vocational training policy, A multilingual glossary for an enlarged Europe, CEDFOP, 2004 http://www.cedefop.europa.eu/etv/Upload/Information_resources/Bookshop/369/4030_6k.pdf (22.02.2009)
[Cerini 1996] Cerini A., La simulazione nei processi formativi, F. Angeli, Milano, 1996.
[Clancey 1995] W. J. Clancey, “A tutorial on situated learning”, in Proceedings of the International Conference on Computers and Education (Taiwan) Self, J. (Ed.) Charlottesville, VA: AACE. 49-70, 1995; http://cogprints.org/323/0/139.htm
[Clough 2002] Clough M. P., Using the laboratory to enhance student learning, in “Learning Science and the Science of Learning”, R. W. Bybee, Ed. National Science Teachers Association, Washington, DC, 2002, 85–97.
[Cmuk 2006] Cmuk D., Mutapcic T., Zoino F., Remote versus classical laboratory in electronic measurements teaching – effectiveness testing, XVIII Imeko World Congress, Metrology for a Sustainable Development, Rio de Janeiro, Brazil, September 17 – 22, 2006.
[Conner 2004] Conner M. L., Informal learning, http://agelesslearner.com/intros/informal.html (22.02.2009)
[Criton 2005] Criton M., “Le origini: I giochi matematici fino al Medioevo”, in Lettera Matematica Pristem, n.54, 2005, p.54.
[Daponte 2007] Daponte P., Rapano S., Riccio M., Zoino F., Remote didactic laboratory in electronic measurements: quality of system testing, in “Instrumentation and Measurement Technology Conference”, 1-3 May 2007, Warsaw, Poland.
[Daponte 2007b] Andria G., Baccigalupi A., Borsic M., Carbone M., Da ponte P., De Capua C., Ferrero A., Grimaldi D., Liccardo A., Locci N. , Lanzolla A.M.L., Macii D., Muscas C., Peretto L., Petri D., Rapano S., Riccio M., Salicone S., Stefani F., Remote Didactic Laboratory “G. Savastano The Italian Experience for E-Learning at the Technical Universities in the Field of Electrical and Electronic Measurements: Overview on Didactic Experiments, in “IEEE transactions on instrumentation and measurement” (v. 56, n. 4), august 2007.
[Davidson 1990] Davidson, N.E. Cooperative learning in mathematics: a handbook for teachers, Addison-Wesley, 1990.
[Donzelli 2007] Donzelli P., Melina M.L., Progetto Digi Scuola (Ex Cipe Scuola), Didamatica 2007
[dos Santos 2006] J. A. dos Santos, 2006, Practice Firms and Networked Learning: Unaccomplished Potentialities, in “Proceedings of the Fifth International Conference on Networked Learning 2006”, Lancaster: Lancaster University, 10-12 April 2006.
[Downes 2005] Downes S., E-learning 2.0., eLearn Magazine, 2005,
http://www.elearnmag.org/subpage.cfm?section=articles&article=29-1 (07.03.2009)
[EU 2006] European social fund support to education and training – 2007-2013 http://ec.europa.eu/employment_social/esf/docs/educationandtraining_en.pdf (28.02.2009)
[Euler 2001] Euler M., Physics and physics education beyond 2000: views, issues and visions, in “Physics Teacher Education Beyond 2000”, Pintò R, Surinac S. eds, Elsevier, Paris, p. 3.
[Euler 2004] Euler M., Quality development: challenges on physics education, GIREP seminarproceedings, M. Michelini ed., Forum 2004, pp. 17-30. http://www.lernort-labor.de/download/Euler_Udine_03.pdf (24.02.2009)
[Falco 2002] Falco A., La simulazione d’impresa come laboratorio virtuale, Form@re, Eriksson, (14) 2002. http://formare.erickson.it/archivio/ottobre_02/falco.html (10.03.2009)
[Faucher 1985] Faucher G., The role of laboratories in engineering education, in “Int. J. Mechanical Eng. Education” (13), 1985, pp. 195–198.
[Fisica nella Scuola 1994] Aa. Vv., Strategie di insegnamento della fisica: il ruolo del problema e il ruolo del laboratorio, Speciale de La Fisica nella Scuola, XXVII, 4, 1994
[Franci 2005] Alcuino di York, Giochi matematici alla corte di Carlomagno, Problemi per rendere acuta la mente dei giovani, a cura di R. Franci, Edizioni ETS, 2005. ITC nella didattica delle discipline scientifiche, il laboratorio Antonio Bernardo Bibliografia e sitografia 86
[Galgano 2006] Galgano N., CMS Open Source Joomla!, http://www.joomladay.it/content/view/11/10/lang,it/ (10.03.2009)
[Gravier 2006] Gravier C., Fayolle J., Lelev N. G., A., Benmohamed H., Closing the gap between remote labs and learning management systems, in “The 1st International Conference on E-Learning in Industrial Electronics” Hammamet, Tunisia, 2006, pp. 130-134.
[Gravier 2006b] Gravier C., Fayolle J., Noyel G., A distributed online laboratory system for distant learning, in “The International Conference on Signal-Image Technology and Internet-Based Systems”, Hammamet, Tunisia, 2006pp. 345-354.
[Gravier 2007] Gravier C., Fayolle J., Bayard B., Ates M., Lardon J., Remote laboratories: Proposed guidelines, in “2nd International Conference on Digital Information Management”, Lyon, France, 28-31 Oct. 2007, pp 786-792.
[Gravier 2008] Gravier C., Fayolle J., Bayard B., Ates M., Lardon J., State of the Art About Remote Laboratories Paradigms – Foundations of Ongoing Mutations, iJOE – Volume 4, Issue 1, February 2008, pp. 19-25.
[Grimaldi 2002] Grimaldi R., Il portale FAR e i laboratori virtuali, Form@re, Eriksson, (14) 2002. http://formare.erickson.it/archivio/ottobre_02/grimaldi.html (10.03.2009)
[Harward 2004] Harward J., del Alamo J. A., Choudary V. S., DeLong K., Hardison J. L., Lerman S. R., Northridge J., Varadharajan C., Wang S., Yehia K., Zych D., BiLabs: A scalable architecture for sharing online laboratories, in “Int. Conf. Eng. Educ.” Gainesville, FL, Oct. 16–21, 2004.
[Harward 2008] Harward V.J., del Alamo J.A., Lerman S.R., Bailey P.H., Carpenter J., DeLong K., Felknor C., Hardison J., Harrison B., Jabbour I., Long P.D., Mao T., Naamani L., Northridge J., Schulz M., Talavera D., Varadharajan C., Wang S., Yehia K., Zbib R., Zych D., The iLab Shared Architecture: AWeb Services Infrastructure to Build Communities of Internet Accessible Laboratories, Proceedings of the IEEE (v. 96, N. 6), June 2008, pp. 931-950.
[IMS 2004] Instructional Management Systems Global Learning Consortium, Content Packaging Specification 1.1.4, 2004. http://www.imsglobal.org/content/packaging/#version1.1.4 (27.02.2009)
[Jones 1978] Jones J G, Lewis J L ed., The role of the Laboratory in Physics Education, Girep-Icpe Conference, Oxford 1978
[Ke 2006] Fengfeng Ke, Classroom goal structures for educational math game application, “Proceedings of the 7th international conference on Learning sciences”, June 2006, International Society of the Learning Sciences.
[Kolb 1984] Kolb D. A., Experiential Learning, Englewood Cliffs, NJ.: Prentice Hall, 1984. http://www.businessballs.com/freepdfmaterials/kolb_learning_styles_diagram_colour.pdf (22.02.2009)
[Lasala 2002] Lasala T., Lo spazio dei laboratori virtuali, Form@re, Eriksson, (14) 2002. http://formare.erickson.it/archivio/ottobre_02/lasala.html (10.03.2009)
[Lindsay 2007] Lindsay E., Long P., Imbrie P.K., Workshop – Remote Laboratories: Approaches for the Future, 37th ASEE/IEEE Frontiers in Education Conference, Milwaukee, WI, October 10 – 13, 2007.
[Lischka 2002] Lischka H., Bajnai J., Karagiannis D., Chalaris G., The Virtual Global University: The Realization of a fully Virtual University – Concept and Experiences, in “Proceedings of the workshop ICL”, 2002 http://www.eurodl.org/materials/contrib/2002/11html/icl_paper_final.htm (08.03.2009)
[Locatelo 2003] S. Locatello, G. Meloni, Apprendimento collaborativo in matematica, Pitagora Editrice, 2003. [Lombard 1997] Lombard M., Ditton, T., At the heart of it all: The concept of presence, in “J. Comput. Mediated Commun.” (3, 2), 1997
[Ma 2006] Ma J., Nickerson J. V., Hands-on, simulated, and remote laboratories: A comparative literature review, ACM Computing Surveys (CSUR), 38(3):1–24, 2006.
[Manca 2002] Manca S., Sarti L., Comunità virtuali per l’apprendimento e nuove tecnologie., Tecnologie Didattiche, (1) 2002, pp. 11-19
[Michelini 1999] Michelini M., Quale laboratorio per la formazione degli insegnanti: un contributo sul problema del laboratorio nella didattica della fisica, in “Uso del Laboratorio e Insegnamento della Fisica – Contributi teorici – Parte II”, MPIDir. Classica e AIF, Garamond, Roma
[Michelini 2002] Michelini M., Santi L., Un ambiente telematico per costruire un ponte tra il concreto e i modelli fisici, Form@re (16), dicembre 2002. http://formare.erickson.it/archivio/dicembre_02/michelini.html (24.02.2009)
[Michelini 2005] Bochicchio M., Longo A., Michelini M., Stefanel A., Blended activity using learning object in web openenvironments for primary school teachers formation in physics education, in M Michelini, S Pugliese Jona eds, Physics Teaching and Learning, Girep Book of sel. pap., GiperpForum, Udine 2005, pp. 103-112
[Nedic 2007] Nedic Z., Machotka J., Nafalski A., Remote laboratory netlab for effective interaction with real equipment over the internet, in “Conference on Human System Interactions”, Krakow, 25-27 May 2008.
[O’Reilly 2005] O’Reilly T., What is Web 2.0. Design Patterns and Business Models for the Next Generation of Software, http://oreillynet.com/pub/a/oreilly/tim/news/2005/09/30/what-is-web-20.html http://www.awaredesign.eu/articles/14-Cos-Web-2-0 (v. ita.) (06.03.2009)
[Paolini 2001] Baresi L., Garzotto F., Paolini P., Extendind UML for Modeling Web Applications, in "34th Hawaii International Conference on System Sciences, Hawaii, USA, 2001 ITC nella didattica delle discipline scientifiche, il laboratorio Antonio Bernardo Bibliografia e sitografia 88
[Paolini 2006] Paolini P., Mainetti L., Bolchini D., “Progettare siti Web e applicazioni mobili”, McGraw Hill, Milano.
[Parush 2002] Parush A., Hamm H., Shtub A., Learning histories in simulation-based teaching: The effects on self-learning and transfer, in “Computer and Education” (39), 2002, pp. 319-332.
[Perlmuter 2008] Perlmuter C., Didattica laboratoriale, http://www.mindmeister.com/maps/show_public/3545952 (24.02.2009)
[Piaget 1937] Piaget J., La construction du réel chez l’enfant, Paris, Delachaux et Niestlé, 1937.
[PISA 2006] AA. VV., Valutare le competenze in scienze, lettura e matematica, Quadro di riferimento di PISA 2006, Armando Editore, 2007, p. 17. http://www.invalsi.it/ricint/Pisa2006/sito/docs/Quadro_riferimento_PISA2006.pdf (08.03.2009)
[Preece 2003] Preece J., Maloney-Krichmar D., Online Communities: Focusing on sociability and usability, http://www.ifsm.umbc.edu/~preece/paper/7%20Handbook%20v1.7Final.pdf (09.03.2009)
[Protti 2002] Protti C., Laboratori virtuali e didattica della musica: i Music Games, Form@re, Eriksson, (14) 2002. http://formare.erickson.it/archivio/ottobre_02/protti.html (10.03.2009)
[Randel 1992] Randel, J., Morris, B., Wetzel, C. D., & Whitehall, B. (1992). The effectiveness of games for educational purposes: A review of recent research. Simulation & Gaming, 23(3), 261-276. [Reil 1993] Riel M., I circoli di Apprendimento, in “Tecnologie Didattiche”, (2) 1993 http://www.itd.cnr.it/TDMagazine/PDF02/circoli.pdf (09.03.2009)
[Richardson 1998] Richardson T., Stafford-Fraser Q., Wood K.R., Hopper A., Virtual Network Computing, in “IEEE Internet Computing” 2 (1), 1998, pp. 33–38. http://www.cl.cam.ac.uk/Research/DTG/attarchive/pub/docs/att/tr.98.1.pdf (3.3.2009)
[Sassi 2007] Lombardi, Monroy, Sassi, Testa, Ciclo di apprendimento Previsione – Esperimento – Confronto, http://143.225.163.184/_docenti/sassielena/ doc/sassi_lez_1_nota_3.pdf (3.3.2009)
[Schaffert 2008] Schafert S., Hilzensauer W., On the way towards Personal Learning Environments: seven crucial aspects, in “eLearning Papers”, 2008 http://www.elearningeuropa.info/files/media/media15971.pdf (08.03.2009)
[Sheridan 1992] Sheridan T. B., Musings on telepresence and virtual presence, in “ Presence: Teleoperators and Virtual Environments”, v.1 n.1, 1992, pp.120-126 ITC nella didattica delle discipline scientifiche, il laboratorio Antonio Bernardo Bibliografia e sitografia 89
[Tosh 2004] Tosh D., Werdmuller B., ePortfolios and weblogs: one vision for ePortfolio development, 2004 http://eduspaces.net/bwerdmuller/files/61/178/ePortfolio_Weblog.pdf (08.03.2009)
[Tosh 2005] Tosh D., A concept diagram for the Personal Learning Landscape, 2005 http://tesl-ej.org/ej34/m1.html (08.03.2009)
[Towes 2004a] Towes K., Encoding Best Practices for Live Video, 2004, www.adobe.com/devnet/flash/articles/flv_encoding_print.html (06.03.2009).
[Towes 2004b] Towes K., Encoding Best Practices for Prerecorded Flash Video, 2004, www.adobe.com/devnet/flash/articles/flv_live.html (06.03.2009).
[Trentin 1998] Trentin G., Insegnare e apprendere in rete. Prospettive didattiche, Zanichelli, Bologna, 1998.
[Trinchero 2002] Trinchero R., Apprendere in rete: laboratori virtuali e condivisione dell’esperienza, Form@re, Eriksson, (14) 2002 http://formare.erickson.it/archivio/ottobre_02/trinchero.html (09.03.2009)
[Tuttas 2001] J. Tuttas and B. Wagner, Distributed online laboratories.. International Conference on Engineering Education, Oslo, Norway, 2-10 Agosto 2001. pp. 7-11.
[Vygotskij 1934] Lev Vygotskij, Il processo cognitivo, Bollati Boringhieri, 1987. http://www.kolar.org/vygotsky/ (09.03.2009)
[Wenger 1999] Wenger E., Communities of Practice: Learning, Meaning, and Identity, Cambridge University Press, Cambridge,1999
[Wenger 2002] Wenger E., McDermott R., Synder W., Cultivating Communities of Practice, in “Journal of Knowledge Management Practice”, October 2002, 2002 http://www.tlainc.com/articl45.htm (09.03.2008)
[WG 12 2002] Learning Technology Standards Committee, Learning Object Metadata, IEEE publication, 2002. http://ltsc.ieee.org/wg12/ (27.02.2009)
 Mario Tozzi èil Presidente della Giuria scientifica dell’edizione 2011. Il 21 gennaio selezione della cinquina finalista in seduta pubblica; il 5 maggio proclamazione del vincitore.
Mario Tozzi èil Presidente della Giuria scientifica dell’edizione 2011. Il 21 gennaio selezione della cinquina finalista in seduta pubblica; il 5 maggio proclamazione del vincitore. 
 "…le scienze non cercano di spiegare, a mala pena tentano di interpretare, ma soprattutto fanno dei modelli. Per modello si intende un costrutto matematico che, con l’aggiunta di certe interpretazioni verbali, descrive dei fenomeni osservati. La giustificazione di un costrutto matematico del genere è soltanto e precisamente che ci si aspetta che funzioni – cioè descriva correttamente i fenomeni di un’area ragionevolmente ampia. Inoltre esso deve soddisfare certi criteri pratici ed estetici – cioè in relazione con la quantità di descrizione che fornisce, deve essere piuttosto semplice". John Von Neumann (1903 -1957)
"…le scienze non cercano di spiegare, a mala pena tentano di interpretare, ma soprattutto fanno dei modelli. Per modello si intende un costrutto matematico che, con l’aggiunta di certe interpretazioni verbali, descrive dei fenomeni osservati. La giustificazione di un costrutto matematico del genere è soltanto e precisamente che ci si aspetta che funzioni – cioè descriva correttamente i fenomeni di un’area ragionevolmente ampia. Inoltre esso deve soddisfare certi criteri pratici ed estetici – cioè in relazione con la quantità di descrizione che fornisce, deve essere piuttosto semplice". John Von Neumann (1903 -1957) 
 Il libro completo degli Elementi di Euclide (XV libri) tradotti da Federico Commandino da Urbino, dal libro orginale del 1575. Fotografie dal libro originale a cura di Carlo Sintini
Il libro completo degli Elementi di Euclide (XV libri) tradotti da Federico Commandino da Urbino, dal libro orginale del 1575. Fotografie dal libro originale a cura di Carlo Sintini  Io ammetterò certamente come empirico, o scientifico, soltanto un sistema che possa essere controllato dall’esperienza. Queste considerazioni suggeriscono che come criterio di demarcazione (tra scienza e non-scienza) non si deve prendere la ‘verificabilità’ ma la ‘falsificabilità’ di un sistema.
Io ammetterò certamente come empirico, o scientifico, soltanto un sistema che possa essere controllato dall’esperienza. Queste considerazioni suggeriscono che come criterio di demarcazione (tra scienza e non-scienza) non si deve prendere la ‘verificabilità’ ma la ‘falsificabilità’ di un sistema.  Biografia. Nato ad Atene intorno al 427 a.C. da una nobile famiglia, intraprese l’attività politica fin da giovane, ma in seguito all’arresto e alla condanna a morte del suo maestro Socrate, si ritirò dal mondo della politica per dedicarsi alla filosofia. Probabilmente su questa decisione incise anche la parentela con Crizia, il più autorevole dei Trenta Tiranni.
Biografia. Nato ad Atene intorno al 427 a.C. da una nobile famiglia, intraprese l’attività politica fin da giovane, ma in seguito all’arresto e alla condanna a morte del suo maestro Socrate, si ritirò dal mondo della politica per dedicarsi alla filosofia. Probabilmente su questa decisione incise anche la parentela con Crizia, il più autorevole dei Trenta Tiranni.  Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.
Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.  È con vero piacere che ho letto "Il pallino della matematica. Scoprire il genio dei numeri che è in noi" di Stanislas Dehaene. Inizialmente qualcuno può pensare che si tratti di un libro che, come tanti altri, espone in maniera semplice ed accattivamente alcuni concetti della matematica, la sua presenza o utilità nella realtà quotidiana, la sua bellezza, il piacere intelletuale che può dare o alcuni aneddoti relativi alla storia di questa disciplina da tante persone odiata e ritenuta ostica. In realtà, leggendolo si scopre tutt’altro: vengono indagati i motivi della diversa predisposizione verso la matematica da parte delle persone. L’autore, che insegna psicologia cognitiva sperimentale al Collège de France, espone qui i risultati delle sue ricerche sull’argomento in questione. Il libro collega così la matematica e la psicologia, molto distanti tra loro nell’immaginario comune (ma non mancano neanche riferimenti ad altre discipline, come la linguistica).
È con vero piacere che ho letto "Il pallino della matematica. Scoprire il genio dei numeri che è in noi" di Stanislas Dehaene. Inizialmente qualcuno può pensare che si tratti di un libro che, come tanti altri, espone in maniera semplice ed accattivamente alcuni concetti della matematica, la sua presenza o utilità nella realtà quotidiana, la sua bellezza, il piacere intelletuale che può dare o alcuni aneddoti relativi alla storia di questa disciplina da tante persone odiata e ritenuta ostica. In realtà, leggendolo si scopre tutt’altro: vengono indagati i motivi della diversa predisposizione verso la matematica da parte delle persone. L’autore, che insegna psicologia cognitiva sperimentale al Collège de France, espone qui i risultati delle sue ricerche sull’argomento in questione. Il libro collega così la matematica e la psicologia, molto distanti tra loro nell’immaginario comune (ma non mancano neanche riferimenti ad altre discipline, come la linguistica).  Una raccolta di suduku di tutti i livelli, crucipuzzle, crucinumero, cruciverba crittograto e altri enigmi .
Una raccolta di suduku di tutti i livelli, crucipuzzle, crucinumero, cruciverba crittograto e altri enigmi .  Ci sono soltanto due possibili conclusioni: Se il risultato conferma le ipotesi, allora hai appena fatto una misura. Se il risultato è contrario alle ipotesi, allora hai fatto una scoperta
Ci sono soltanto due possibili conclusioni: Se il risultato conferma le ipotesi, allora hai appena fatto una misura. Se il risultato è contrario alle ipotesi, allora hai fatto una scoperta  L’appendice conclusiva del libro di Amadori e Lussardi sulla Relatività: A.1 Tensore energia, impulso nella materia; listati dei principali blocchi dei programmi in PHP di calcolo numerico utilizzati per la RG.
L’appendice conclusiva del libro di Amadori e Lussardi sulla Relatività: A.1 Tensore energia, impulso nella materia; listati dei principali blocchi dei programmi in PHP di calcolo numerico utilizzati per la RG.  Era a piedi; andava solo, col suo passo randagio; gli occhi perduti nei suoi sogni perenni, che li velavano di nebbie azzurre. Era vestito come tutti gli altri, ma sembrava nella folla, un mendicante; e, sembrava, nel tempo stesso, anche un re. Un re in esilio
Era a piedi; andava solo, col suo passo randagio; gli occhi perduti nei suoi sogni perenni, che li velavano di nebbie azzurre. Era vestito come tutti gli altri, ma sembrava nella folla, un mendicante; e, sembrava, nel tempo stesso, anche un re. Un re in esilio  Le nuove emissioni sono indicizzate all’euribor e non più ai Bot semestrali. La loro introduzione ha fatto crollare i prezzi dei certificati in circolazione. Ma in caso di rischio-paese l’aggancio ai titoli nazionali fornisce una protezione del tasso interbancario.
Le nuove emissioni sono indicizzate all’euribor e non più ai Bot semestrali. La loro introduzione ha fatto crollare i prezzi dei certificati in circolazione. Ma in caso di rischio-paese l’aggancio ai titoli nazionali fornisce una protezione del tasso interbancario. 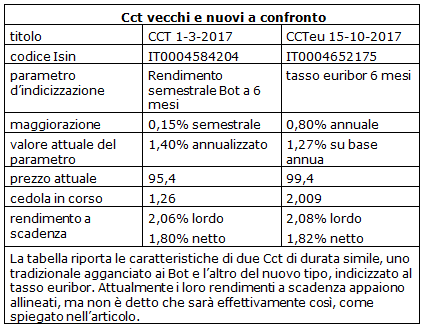
 Come scoprire con la matematica tutti i segreti del paranormale. Mariano Tomatis presenta in una conferenza spettacolo il libro "La magia dei numeri". 17 dicembre 2010 presso il liceo Gramsci di Ivrea.
Come scoprire con la matematica tutti i segreti del paranormale. Mariano Tomatis presenta in una conferenza spettacolo il libro "La magia dei numeri". 17 dicembre 2010 presso il liceo Gramsci di Ivrea.  Le macchine possono trascendere alcune delle limitazioni dei loro progettisti… gli strumenti per pilotare (dal greco ‘pilota’, al latino ‘gubernator’ all’italiano ‘cibernetica’) una nave sono veramente una delle prime e meglio sviluppate forme di meccanismo con controreazione.
Le macchine possono trascendere alcune delle limitazioni dei loro progettisti… gli strumenti per pilotare (dal greco ‘pilota’, al latino ‘gubernator’ all’italiano ‘cibernetica’) una nave sono veramente una delle prime e meglio sviluppate forme di meccanismo con controreazione. 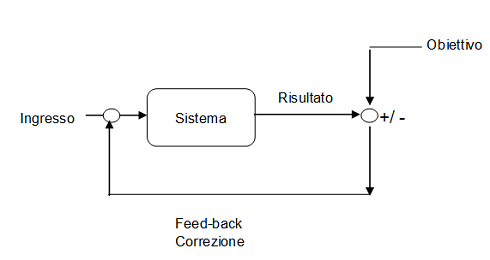
 La logica studia il corretto ragionare, e quindi è trasversale a tutti gli altri argomenti studiati. La logica o i concetti ad essa collegati è stata inserita in quasi tutti i moduli in cui si articola la programmazione annuale della classe, oltre a dedicarle un modulo in cui viene trattata più specificamente, insieme alla geometria. Non sono richiesti, pertanto, particolari prerequisiti per la sua trattazione, mentre qualunque conoscenza pregressa può fornire materiali da analizzare con gli strumenti della logica, attraverso i quali è possibile raggiungere un maggior grado di chiarezza e comprensione dei concetti.
La logica studia il corretto ragionare, e quindi è trasversale a tutti gli altri argomenti studiati. La logica o i concetti ad essa collegati è stata inserita in quasi tutti i moduli in cui si articola la programmazione annuale della classe, oltre a dedicarle un modulo in cui viene trattata più specificamente, insieme alla geometria. Non sono richiesti, pertanto, particolari prerequisiti per la sua trattazione, mentre qualunque conoscenza pregressa può fornire materiali da analizzare con gli strumenti della logica, attraverso i quali è possibile raggiungere un maggior grado di chiarezza e comprensione dei concetti.  L’articolo prende spunto dal labirintico universo nel quale è ambientato uno dei più affascinanti racconti di Borges. Nella prima sezione viene presentato un approccio originale e intuitivo, volto alla stima di un grande fattoriale; successivamente si sposta il focus sul calcolo “a mani nude” di 25656000. Questo risultato viene sfruttato nell’ultima parte per giungere ad una conclusione per certi versi paradossale, circa uno dei temi centrali della storia: l’impossibilità di reperire il libro della Verità. Il tutto è corredato da un’appendice che chiarisce alcuni curiosi retroscena.
L’articolo prende spunto dal labirintico universo nel quale è ambientato uno dei più affascinanti racconti di Borges. Nella prima sezione viene presentato un approccio originale e intuitivo, volto alla stima di un grande fattoriale; successivamente si sposta il focus sul calcolo “a mani nude” di 25656000. Questo risultato viene sfruttato nell’ultima parte per giungere ad una conclusione per certi versi paradossale, circa uno dei temi centrali della storia: l’impossibilità di reperire il libro della Verità. Il tutto è corredato da un’appendice che chiarisce alcuni curiosi retroscena.  Risolvere i problemi è una questione di abilità vera e propria come, permettetemi il paragone, il nuotare. Qualunque abilità pratica può essere acquisita con l’imitazione e l’esercizio. Sforzandosi di imparare a nuotare si imitano i gesti e gli sgambettii di coloro che riescono a stare a galla nell’acqua e, a poco a poco, si impara a nuotare… nuotando. Per imparare a risolvere i problemi, è necessario osservare ed imitare come vi riescono altre persone ed infine si riesce a risolvere i problemi… risolvendoli. George Polya, Come risolvere i problemi di matematica, logica ed euristica nel metodo matematico.
Risolvere i problemi è una questione di abilità vera e propria come, permettetemi il paragone, il nuotare. Qualunque abilità pratica può essere acquisita con l’imitazione e l’esercizio. Sforzandosi di imparare a nuotare si imitano i gesti e gli sgambettii di coloro che riescono a stare a galla nell’acqua e, a poco a poco, si impara a nuotare… nuotando. Per imparare a risolvere i problemi, è necessario osservare ed imitare come vi riescono altre persone ed infine si riesce a risolvere i problemi… risolvendoli. George Polya, Come risolvere i problemi di matematica, logica ed euristica nel metodo matematico.  E’ giunto al quinto anno, il ciclo di conferenze “Matematica e…”, negli anni precedenti era denominato “Matematica & Realtà”. Si tratta di in una serie di incontri pomeridiani rivolti agli studenti degli ultimi anni delle scuole superiori che hanno per obiettivo quello di dare spunti di riflessione sui collegamenti tra la matematica e le altre discipline, anche in vista della realizzazione della tesina per l’esame di stato. Gli incontri si terrano a Urbino presso il palazzo Battiferri (sede della facoltà di Economia) .
E’ giunto al quinto anno, il ciclo di conferenze “Matematica e…”, negli anni precedenti era denominato “Matematica & Realtà”. Si tratta di in una serie di incontri pomeridiani rivolti agli studenti degli ultimi anni delle scuole superiori che hanno per obiettivo quello di dare spunti di riflessione sui collegamenti tra la matematica e le altre discipline, anche in vista della realizzazione della tesina per l’esame di stato. Gli incontri si terrano a Urbino presso il palazzo Battiferri (sede della facoltà di Economia) .  Un sistema di numerazione è un sistema utilizzato per rappresentare i numeri e le operazioni che si possono effettuare su di essi. Presso tutte le culture con qualche forma di organizzazione sono state sviluppate notazioni numerali, talora assai rudimentali, fino ad arrivare al sistema oggi più diffuso, quello posizionale decimale.
Un sistema di numerazione è un sistema utilizzato per rappresentare i numeri e le operazioni che si possono effettuare su di essi. Presso tutte le culture con qualche forma di organizzazione sono state sviluppate notazioni numerali, talora assai rudimentali, fino ad arrivare al sistema oggi più diffuso, quello posizionale decimale.  Anna Cerasoli è tra le più attive divulgatrici della matematica per bambini e ragazzi. In questo libro si cimenta con una fiaba. Chi è asino resta asino per sempre? Chi ha un cervello di gallina non può imparare la matematica? Anna Cerasoli è convintissima che non è vero: con un po’ di determinazione e tanta buona volontà “tutto cambia”, come diceva il filosofo.
Anna Cerasoli è tra le più attive divulgatrici della matematica per bambini e ragazzi. In questo libro si cimenta con una fiaba. Chi è asino resta asino per sempre? Chi ha un cervello di gallina non può imparare la matematica? Anna Cerasoli è convintissima che non è vero: con un po’ di determinazione e tanta buona volontà “tutto cambia”, come diceva il filosofo.  Mentre lavoravo con stafilococchi di diversi ceppi, alcune piastre di coltura furono collocate da una parte sul banco del laboratorio e di tanto in tanto venivano esaminate. Nel corso di tali esami queste piastre si trovavano necessariamente esposte all’aria e vennero contaminate da vari microrganismi. Si è rilevato che, intorno a una grande colonia di muffa contaminatrice, le colonie di stafilococchi diventavano trasparenti ed erano evidentemente soggette a lisi (dissoluzione). Fleming, A., British Journal of Experimental Pathology, 1929.
Mentre lavoravo con stafilococchi di diversi ceppi, alcune piastre di coltura furono collocate da una parte sul banco del laboratorio e di tanto in tanto venivano esaminate. Nel corso di tali esami queste piastre si trovavano necessariamente esposte all’aria e vennero contaminate da vari microrganismi. Si è rilevato che, intorno a una grande colonia di muffa contaminatrice, le colonie di stafilococchi diventavano trasparenti ed erano evidentemente soggette a lisi (dissoluzione). Fleming, A., British Journal of Experimental Pathology, 1929.  In queste pagine vengono trattate le unità di misura delle grandezze elettromagnetiche, al fine di migliorare la comprensione delle relazioni tra i vari sistemi di unità di misura che, tra la fine del XIX secolo e gli inizi del XX, si sono succeduti e che, spesso, sono anche stati utilizzati in forma ibrida. Inizialmente, tutte le relazioni importanti dell’elettromagnetismo vengono introdotte senza fare riferimento ad alcuno dei sistemi di unità di misura. Così facendo, ci si ritroverà in presenza di tre costanti arbitrarie (una elettrica, una magnetica, ed una elettromagnetica), che risulteranno collegate dalla relazione che esprime la velocità della luce.
In queste pagine vengono trattate le unità di misura delle grandezze elettromagnetiche, al fine di migliorare la comprensione delle relazioni tra i vari sistemi di unità di misura che, tra la fine del XIX secolo e gli inizi del XX, si sono succeduti e che, spesso, sono anche stati utilizzati in forma ibrida. Inizialmente, tutte le relazioni importanti dell’elettromagnetismo vengono introdotte senza fare riferimento ad alcuno dei sistemi di unità di misura. Così facendo, ci si ritroverà in presenza di tre costanti arbitrarie (una elettrica, una magnetica, ed una elettromagnetica), che risulteranno collegate dalla relazione che esprime la velocità della luce.  Si tratta di accoppiare tutte le nazioni del mondo con le loro capitali inserendo una "x" nella griglia proposta. Alla fine, ovvero dopo aver inserito la 194-esima capitale, compare il risultato in percentuale degli accoppiamenti corretti. Durante la compilazione una riga e una colonna di color rosso, poste a fianco delle nazioni e delle capitali, aiutano a capire quali e quanti accoppiamenti mancano alla conclusione. Un semplice giochino, lungo e noiso forse, che mostra le potenzialità didattiche di strumenti come Excel.
Si tratta di accoppiare tutte le nazioni del mondo con le loro capitali inserendo una "x" nella griglia proposta. Alla fine, ovvero dopo aver inserito la 194-esima capitale, compare il risultato in percentuale degli accoppiamenti corretti. Durante la compilazione una riga e una colonna di color rosso, poste a fianco delle nazioni e delle capitali, aiutano a capire quali e quanti accoppiamenti mancano alla conclusione. Un semplice giochino, lungo e noiso forse, che mostra le potenzialità didattiche di strumenti come Excel.  L’attività di laboratorio, sia come spazio attrezzato tipico per l’insegnamento delle discipline scientifiche, sia come attività cooperativa e condivisa tra studenti e insegnanti, caratterizzata da un forte approccio operativo, riveste attualmente un ruolo di primo piano non solo nella sperimentazione ma anche nella didattica usuale. Obiettivo della ricerca di dottorato è stato quello di progettare sistemi usabili ed efficaci, nello stile del Web 2.0 per portare l’apprendimento delle discipline scientifiche e in particolare delle attività di laboratorio in senso lato nel paradigma di base dell’e-learning: anytime and anywere.
L’attività di laboratorio, sia come spazio attrezzato tipico per l’insegnamento delle discipline scientifiche, sia come attività cooperativa e condivisa tra studenti e insegnanti, caratterizzata da un forte approccio operativo, riveste attualmente un ruolo di primo piano non solo nella sperimentazione ma anche nella didattica usuale. Obiettivo della ricerca di dottorato è stato quello di progettare sistemi usabili ed efficaci, nello stile del Web 2.0 per portare l’apprendimento delle discipline scientifiche e in particolare delle attività di laboratorio in senso lato nel paradigma di base dell’e-learning: anytime and anywere.