Michela Bertolani
PROFESSIONE MATEMATICO
Interviste scelte a 12 matematici italiani,
288 pp., SciBooks Edizioni, Pisa, 2005

Professione matematico è una raccolta di 12 interviste ad altrettanti matematici, molti dei quali noti al grande pubblico: dall’immancabile Piergiorgio Odifreddi all’eclettico Michele Emmer , da Edoardo Vesentini a Corrado De Concini , da Enrico Giusti a Giorgio Israel , da Mario Primicerio ad Alfio Quarteroni , cui si aggiungono alcuni nomi noti più agli "addetti ai lavori" come Giuseppe Da Prato , Franco Fagnola , Giuseppe Tomassini e Carlo Traverso .

Il libro copre, in altre parole, un po’ tutti i principali settori della matematica: dall’analisi alla geometria, dall’algebra alla fisica matematica, dall’informatica alla statistica, dalla teoria dei numeri alla logica. Diciamo subito che si tratta di un volume molto agile e piacevole da leggere e ricco di spunti stuzzicanti per i cultori della matematica e non solo, e, dobbiamo ammetterlo, decisamente nuovo nel panorama editoriale italiano. Ma vediamo quali sono alcuni dei temi trattati.

Le interviste, come si può intuire dalle seguenti e dalle moltissime altre domande a cui il libro fornisce interessanti e originali risposte, sono focalizzate, più che sulla matematica, sul mestiere del matematico da una parte (è un po’ una raccolta di 12 biografie), e su come si diventi un matematico dall’altra (con tutti i consigli che uno studente o un ricercatore desidererebbe ricevere):

Cosa fa un matematico? Quali doti occorrono per fare questo mestiere, così antico eppure così poco conosciuto? E quanto si guadagna? Come si riesce, in Italia, a fare carriera? Chi è favorito nei concorsi? Quali sono gli aspetti positivi e quelli negativi della vita di un ricercatore? Come si raggiungono livelli di eccellenza? Perché i nostri cervelli migliori fuggono all’estero? Quali sono le prospettive di lavoro per i giovani che si laureano in matematica? E le sedi migliori per studiare?

Introducendosi, domanda dopo domanda, negli aspetti più intimi dei personaggi intervistati, si scopre che molti di essi non immaginavano di diventare matematici, come ad esempio il fisico-matematico ed ex sindaco di Firenze Mario Primicerio ("Mi iscrissi a ingegneria, ma dopo un anno cambiai e mi iscrissi a fisica …"), mentre altri avevano le idee chiare sin da piccoli, come Giuseppe Tomassini, della Normale di Pisa ("Ho sempre pensato di fare il matematico, sin dalle scuole medie …").

Dalle lettura del libro emerge come tutti i matematici abbiano storie molto diverse fra loro, cosa che del resto sottolinea anche Edoardo Vesentini ("Il matematico è difficilmente inquadrabile, e gli stereotipi non sono attendibili in tal senso …"). Le loro storie si intrecciano spesso con quelle di grandi matematici del recente passato, come il geniale ma distrattissimo Ennio De Giorgi ("Una lettera che non aprì conteneva proprio la comunicazione della vincita del premio ‘Caccioppoli’: dunque poi lo dovettero andare a cercare perché, appunto, non ne sapeva nulla! ") o ancora attivi, come il "nostro" più grande di tutti, Enrico Bombieri, descritto dal suo ex collaboratore dei "tempi d’oro" Enrico Giusti ("Devo dire che ne ho visti davvero pochi così, con un quantità di conoscenze gigantesca! ").

Innumerevoli sono i consigli ai giovani matematici. Occorre evitare, ad esempio come osserva Giusti, di occuparsi di questioni troppo facili o, al contrario, troppo difficili ("Altrimenti, passano poi quindici anni e Tizio, non riuscendo a ‘cavare un ragno dal buco’, sprofonda nella depressione più totale, oppure smette di dedicarsi alla matematica e si mette a fare il ciabattino! "). Inoltre è importante avere sempre il coraggio di rimettersi in gioco, come sottolinea Alfio Quarteroni, a cui la barca Alinghi deve il successo nell’America’s Cup ("Non dobbiamo pensare che ‘l’ottimo locale’, ‘il massimo locale’, sia la ‘soluzione giusta’ della nostra vita. […] Quindi occorre compiere le scelte giuste – contattare i maestri giusti, recarsi nei posti giusti – ma anche osare, avere il coraggio di muoversi …").

Preziosissimi, poi, sono i suggerimenti pratici diretti a chi inizia la carriera universitaria. Il concorso di dottorato, come osserva Carlo Traverso, è il primo ostacolo da affrontare ("Per gli studenti che hanno un curriculum più applicato, talvolta risulta molto difficile farsi valere, soprattutto nel caso in cui la commissione sia composta da matematici puri …"). Attenzione, poi, a dove e con chi si pubblicano gli articoli di ricerca che vengono valutati nei concorsi accademici ("Se esiste una collaborazione fissa tra due persone, per cui la loro firma è comune nei vari articoli pubblicati dal candidato, la commissione si pone il problema di stabilire chi dei due meriti il posto …"). 

Non mancano, infine, una quantità di gustosissimi aneddoti. A cominciare dagli scherzi compiuti nel "tempio" della matematica italiana, la Scuola Normale di Pisa, raccontati per filo e per segno da Franco Fagnola ("Certe volte, infine, se il ragazzo era chiuso nella propria camera, gliela allagavamo da sotto l’uscio servendoci di un secchio d’acqua… "). Per non parlare, naturalmente, degli aneddoti riguardanti situazioni di competizione per premi prestigiosi o sui classici matematici "con la testa fra le nuvole" ("Un mio amico, al secondo anno della Normale, si dimenticò completamente di chiedere il rinvio del servizio di leva, ragion per cui l’anno seguente dovette partire per il militare …").

Professionalmente curata da Michela Bertolani, una giovane divulgatrice scientifica freelance al suo primo libro, Professione matematico è dunque un’opera interessante e ben riuscita, diretta a un pubblico molto vasto e trasversale, e che presenta il pregio di essere onesta in senso intellettuale e culturale, come non poteva essere altrimenti, dato il calibro e la scelta dei personaggi intervistati. Di questi tempi, non è poco!

Un brevissimo estratto e una scheda del libro sono disponibili nel sito dell’editore:

http://www.scibooks.it/professione_matematico.htm

V. Villani, Cominciamo da Zero, Domande, risposte e commenti per saperne di più sui perché della Matematica (Aritmetica e Algebra), Pitagora Editrice, Bologna, 2003

Cominciamo da Zero è un invito a riflettere su alcuni punti cruciali della matematica che si insegna nella scuola superiore di 1° e 2° grado. La prima domanda posta dall’autore è proprio: zero è un numero? Più precisamente, la domanda è: zero appartiene all’insieme dei numeri naturali? Come è noto, solo in tempi recenti (XVI secolo circa) i matematici hanno riconosciuto allo zero un diritto di cittadinanza tra i numeri . Tuttavia, sono rimasti incerti se collocare lo zero tra i numeri naturali. Si tratta di una pura questione convenzionale ma il comportamento dello zero è atipico rispetto a quello degli altri numeri: rispetto all’addizione svolge il ruolo di elemento neutro, rispetto alla moltiplicazione permette la validità della legge di annullamento del prodotto, nella definizione di numero fattoriale, invece, si comporta come un intruso : n!=1x2x3x…(n-1)xn, se si iniziasse da 0 la definizione non avrebbe senso. Queste anomalie fanno dello zero un numero particolare che solitamente non viene inserito tra i numeri naturali, anche se, secondo l’autore, la tendenza recente è di considerarlo un numero naturale.

Un’altra questione sulla quale permangono incertezze è: il numero 1 è un numero primo? I matematici escludono 0 e 1 dalla lista dei numeri primi, per conservare il teorema fondamentale dell’aritmetica: ogni numero naturale diverso da 0 e da 1 o è primo, o è il prodotto di fattori primi. Tale decomposizione in fattori primi è unica a meno dell’ordine dei fattori. E’ evidente allora che se si includesse 0 o 1 tra i numeri primi, verrebbe meno l’unicità della scomposizione in fattori. Per esempio, si avrebbe 6=1x2x3=1x1x2x3=1x1x1x2x3=…; analogamente 0=0x1=0x2=0x3=0x1x2x3=…

Perché meno per meno fa più? Non sempre insegnanti e libri di testo danno una motivazione convincente di questa scelta convenzionale. Il motivo è che la regola dei segni scelta dai matematici è l’unica per la quale l’addizione e la moltiplicazione nell’insieme dei numeri relativi continuano a godere delle stesse proprietà formali di cui godono le omonime operazioni nell’insieme dei numeri naturali. Per esempio, quanto deve valere il prodotto (-14)X(-6)?

Per la proprietà di annullamento del prodotto: ((-14)+(+14))X(-6)=0X(+6)=0;

per la proprietà distributiva: ((-14)+(+14))X(-6)=((-14)x(-6))+((+14)X(-6))=(-14)X(-6)+(-84).

Dalle due proprietà segue che (-14)X(-6) deve essere l’opposto di -84.

Quando si amplia l’insieme dei numeri naturali qual è il passaggio corretto,  da N a Z e poi da Z a Q, oppure da N a Q⁺ e poi da Q⁺ a Z? I due percorsi di ampliamento da N a Q sono equivalenti. Storicamente si è passati dai numeri interi alle frazioni e dopo alcuni millenni si è giunti ai numeri negativi. Nell’approccio moderno si preferisce passare da N a Z in modo da mettere in evidenza la struttura algebrica dei numeri interi relativi, che nell’approccio storico viene saltata.

Perché nelle espressioni aritmetiche le parentesi sono a volte necessarie e a volte superflue? La risposta è dovuta al fatto che in alcuni casi eliminando le parentesi il risultato delle operazioni non è univocamente determinato. Tuttavia, perché nell’espressione 5+(3×7) le parentesi possono essere eliminate mentre nell’espressione (5+3)x7 devono essere mantenute? Si tratta di una scelta convenzionale che trova una sua giustificazione nel fatto che la proprietà distributiva della moltiplicazione rispetto all’addizione è asimmetrica: l’espressione (5+3)x7 è equivalente a (5×7)+(3×7), il 7 compare due volte. Si coglie meglio l’efficacia di questa convenzione nel calcolo letterale, nel quale si usa scrivere a+2ab intendendo (a)+(2xaxb) e non (a+2)xaxb. La convenzione scelta permette di raggruppare ed evidenziare i monomi, nonché di scrivere nel modo più semplice la forma normale di un polinomio.

A quale numero corrispondono i numeri decimali periodici di periodo 9? Contrariamente a ciò che si pensa abitualmente non c’è una perfetta corrispondenza biunivoca tra l’insieme delle frazioni e l’insieme dei numeri decimali. Fanno eccezione i numeri decimali che hanno come periodo 9. Passando dalle frazioni ai numeri decimali non si trova mai un caso di questo tipo, in altre parole, non c’è nessuna frazione che origina un numero decimale con periodo 9. Viceversa, la regola di trasformazione dai numeri decimali alle frazioni vale anche in questo caso. Per esempio, 14,7(9) – il 9 è periodico – genera la frazione 1332/90 che a sua volta genera il numero decimale 14,78. Ciò fa pensare che 17,7(9) e 17,8 siano lo stesso numero; effettivamente, si dimostra che è così.

Perché le operazioni con i numeri decimali sono difficili? Ci sono diversi casi in cui si fa fatica a operare con i numeri decimali. Per esempio alla domanda: Due spaghi sono lunghi il primo 1,27 m e il secondo 1,8 m. Qual è lo spago più lungo? Sul piano linguistico uno e ventisette è più lungo di uno e otto, perciò a volte si è portati a dire che 1,27 è maggiore di 1,8. D’altra parte, quando si esprime il tempo "il treno delle otto e cinque parte prima di quello delle otto e ventitre". Un altro esempio difficile è il seguente: Qual è il doppio di 1,7 m?  Spesso si ha come risposta 2,14. Dal punto di vista matematico, questi fraintendimenti nascono dal considerare i numeri decimali come coppie di numeri, perciò (1;27) sembra maggiore di (1;8); analogamente, il doppio di (1;7) sembra essere (2;14). Per evitare questi fraintendimenti nell’uso comune delle frazioni, le regole di scrittura delle somme in euro devono essere obbligatoriamente fatte con due cifre decimali. Pertanto si scriverà 1,27 e 1,80, da cui risulta evidente che la seconda somma è maggiore della prima; si scriverà anche 1,70 (invece di 1,7) per cui sarà più semplice calcolare il doppio.

Come si approssima un numero reale? Le espressioni linguistiche che si usano per indicare l’approssimazione di numeri sono diverse. Una scrittura del tipo r=6,4537… significa che del numero r sono note la parte intera e le prime quattro cifre decimali; i puntini di sospensione indicano che il numero prosegue con cifre decimali che non sono esplicitate. In altre parole, il numero r è compreso tra 6,4537 e 6,4538. In questo caso si dice che sono note quattro cifre esatte del numero r . Se di un numero reale r si conosce un valore approssimato a e si sa che il valore vero di r è compreso tra 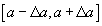si dice che il numero r è conosciuto con un errore assoluto delta a (si usa anche dire che il numero è noto con una precisione delta a). Se di un numero sono note una quantità eccessiva di cifre decimali esatte rispetto all’uso che se ne intende fare (per esempio, del numero pi greco sono note miliardi di cifre ma molto spesso nei calcoli è sufficiente considerarne due o tre). I metodi per ridurre il numero di cifre decimali sono essenzialmente due. Il troncamento consiste nell’eliminare le cifre che non interessano. L’arrotondamento consiste invece nello scegliere, tra i numeri che hanno la quantità voluta di cifre decimali, quello che meglio approssima il numero: si deve controllare la prima cifra decimale da omettere, se essa è 0 o 1 o 2 o 3 o 4 il valore arrotondato coincide con il valore troncato; se essa è 5 o 6 o 7 o 8 o 9 il valore arrotondato si ottiene dal valore troncato aumentando di un’unità la sua ultima cifra decimale.

Cosa afferma il teorema di identità dei polinomi? Una formulazione abbastanza comune del teorema di identità dei polinomi afferma: due polinomi sono formalmente uguali se e solo se sono funzionalmente uguali . A una lettura superficiale, questo teorema può sembrare una banalità. Invece non lo è: il teorema di identità dei polinomi mette in evidenza un legame estremamente importante e per nulla banale tra Algebra e Analisi. Dal punto di vista algebrico, due polinomi A(x) e B(x) si dicono formalmente uguali se e solo se hanno lo stesso grado e, scritti in forma normale, i coefficienti dello stesso grado sono tutti uguali. Dal punto di vista analitico, i due polinomi si dicono funzionalmente uguali se e solo se individuano la stessa funzione, ossia A(k)=B(k) per ogni valore di k appartenente al dominio delle funzioni polinomiali. Il teorema afferma, allora, che se due polinomi sono uguali dal punto di vista algebrico lo sono anche da quello analitico. Si comprende meglio il teorema se si fanno alcuni esempi in cui esso non è valido.  Per esempio, sin² x e 1-cos² x sono formalmente diversi ma funzionalmente uguali.

Ogni teoria matematica consta essenzialmente di postulati e di teoremi, perché sono usati tanti termini come postulato, assioma, principio, teorema, lemma, corollario, proposizione, legge, regola, proprietà, criterio? Le ragioni sono di due ordini: da una parte l’evoluzione storica del linguaggio matematico dall’altra considerazioni di opportunità didattica (non sempre condivisibili). Postulato e assioma sono oggi dei sinonimi. Euclide aveva usato il termine assioma per indicare nozioni comuni non collegate strettamente con la matematica (il tutto è maggiore della parte) e aveva usato postulato per indicare proprietà matematiche da assumere come vere. Gli studi sui fondamenti della matematica, già nell’Ottocento avevano messo in evidenza l’inconsistenza teorica di questa distinzione. Nel seguito i matematici hanno adottato indifferentemente l’uno o l’altro termine. Per esempio, Peano usa il termine postulati mentre Hilbert il termine assiomi. Teorema, lemma, corollario, proposizione, legge, regola, proprietà e criterio sono invece tutti sinonimi. Si riserva il termine teorema agli enunciati più importanti; a un numero ristretto di teoremi di una teoria si usa dare la qualifica di teorema fondamentale (teorema fondamentale dell’aritmetica, teorema fondamentale dell’algebra, teorema fondamentale del calcolo integrale, …) Lemma indica un teorema poco significativo di per se stesso ma utile per dedurre un teorema importante. Corollario indica un teorema facilmente ottenibile come conseguenza di un altro teorema. Proposizione è del tutto simile a teorema e si usa per indicare una qualsiasi affermazione dimostrabile della matematica, nella logica indica una frase della quale sia possibile stabilire se è vera o falsa. Legge , regola e proprietà indicano teoremi di natura algoritmica-calcolativa (regola di Ruffini, regola di Cartesio, legge di annullamento del prodotto, proprietà del permutare, …) Questi ultimi termini sono usati anche con significati diversi da quello di teorema. Per esempio, la legge empirica del caso indica fatti osservabili sperimentalmente. La regola dei segni è invece una definizione; anche le proprietà associativa, commutativa e distributiva sono definizioni. Il termine criterio indica solitamente una condizione necessaria e sufficiente (criterio di uguaglianza dei triangoli) anche se il criterio del rapporto per la convergenza di una serie è una condizione solo sufficiente. Il termine principio è usato a volte come sinonimo di assioma (principio del terzo escluso), a volte come sinonimo di teorema (principio di identità dei polinomi). Il principio di induzione ha invece una posizione dubbia, alcuni lo identificano con uno dei postulati di Peano, altri invece come teorema che discende da quel postulato.

Questi sono soltanto alcuni degli argomenti trattati nel libro di Villani, che è, a mio avviso, un punto di riferimento importante su tante questioni sulle quali non solo gli studenti ma qualche volta anche gli insegnanti hanno dei dubbi. Nelle argomentazioni esposte nel libro, gli studenti troveranno modo di approfondire e trovare una risposta a tanti interrogativi, gli insegnanti troveranno le argomentazioni che sono alla base di tante scelte che matematici e autori di manuali di matematica hanno fatto.

Antonio Bernardo

"Vedi quanto si estende l’Umbria da est a ovest, da nord a sud. Poi prendi il punto di mezzo."

"E bravi polli!"

Il dispositivo flip-flop è nel telecomando della TV. 

Un gruppetto di ragazzi trascorre una vacanza estiva in Umbria. Sarebbe stata una vacanza come tutte le altre tra passeggiate, buone cenette, cattivi pranzi in casa, afa e tanto caldo se …

U n omicidio, una rapina, una sparizione, un disastro? Daniele Funaro, ordinario di Analisi Numerica alla Facoltà di Scienze dell’Università di Modena e Reggio Emilia, dà prova che questi ingredienti non sono necessari per scrivere una storia che tenga con il fiato sospeso.

… una frase banale letta su un giornale forse altrettanto banale "Perugia è il centro dell’Umbria" trascina la comitiva in appassionate discussioni dall’esito non sempre scontato. Gradualmente, partendo da questa frase, Clara e i suoi amici trascorrono gli assolati dopopranzo in piacevoli e animate discussioni nel mondo della matematica e della fisica. Il centro dell’Umbria sarà, infatti, un luogo da scoprire ragionando da matematici esploratori, partendo dalla prima cosa che viene in mente (il centro del quadrato in cui è inscritta l’Umbria, fig. 1), cercando un punto che sia invariante rispetto alla disposizione della cartina dell’Umbria e quindi il baricentro .

Durante questo percorso, Clara e i suoi si imbattono in temi teorico-filosofici (astrazione matematica, problemi di esistenza e unicità, uso del calcolatore), nozioni matematiche (invariante, baricentro, numeri irrazionali, numeri immaginari, figure convesse, limite, continuità, serie), problemi pratici (problemi di equilibrio, dispositivo flip-flop, distribuzione delle scorte).

"Di quella vacanza, a parte qualche gita fuori porta, rimasero tra i ricordi proprio i lunghi approfondimenti epistemologici, condotti intorno al tavolaccio di marmo."

Il libro non contiene formule ma numerosi disegni che fanno capire al volo l’idea matematica che c’è sotto le problematiche esposte. Per questo motivo, può essere una piacevole lettura per gli studenti delle scuole superiori, per i loro insegnanti e per chiunque voglia imparare un po’ di matematica divertendosi.

A. Bernardo