" Bisognerebbe cominciare intanto a sfatare alcuni miti: nelle colture biologiche non si usano agrofarmaci. Sarebbe bello, ma gli insetti purtroppo non sanno leggere, non dicono: questo campo è biologico, attacchiamo quello convenzionale. Si usano allora altri agrofarmaci, detti tradizionali. Sono migliori di quelli moderni? Meno invasivi? Purtroppo no. E’ il caso del rame, metallo pesante che può, in dosi elevate, danneggiare la microfauna o anche, il rotenone. Provate a cercarlo sui portali di lavori scientifici: gli studi sugli effetti di questo principio chimico sono inquietanti". (Antonio Pascale da: "La sinistra bio-illogica", La Lettura – Corsera,11 marzo 2012
Bisognerebbe cominciare intanto a sfatare alcuni miti: nelle colture biologiche non si usano agrofarmaci. Sarebbe bello, ma gli insetti purtroppo non sanno leggere, non dicono: questo campo è biologico, attacchiamo quello convenzionale. Si usano allora altri agrofarmaci, detti tradizionali. Sono migliori di quelli moderni? Meno invasivi? Purtroppo no. E’ il caso del rame, metallo pesante che può, in dosi elevate, danneggiare la microfauna o anche, il rotenone. Provate a cercarlo sui portali di lavori scientifici: gli studi sugli effetti di questo principio chimico sono inquietanti". (Antonio Pascale da: "La sinistra bio-illogica", La Lettura – Corsera,11 marzo 2012
Antonio Pascale è uno scrittore e giornalista, ma anche un agronomo, nato Napoli nel 1966. Più che riprendere le tematiche sulle due culture di C.P. Snow, i suoi incisivi saggi e articoli sembrano volti a descrivere i problemi generati, nella società italiana, da intellettuali, politici e opinion leader, a causa della loro ideologica e preconcetta avversione alle conquiste della modernità e delle nuove tecnologie. Ecco come il genetista Guido Barbujani recensisce, su L’Indice, il saggio di Pascale "Scienza e sentimento":
"Tempo fa un prestigioso intellettuale italiano ha messo l’insegnamento della scienza al tredicesimo, cioè penultimo, posto fra le priorità per la riforma della scuola (e quello della filosofia al primo). Dissentendo dalle colonne dello stesso quotidiano, un altro famoso intellettuale ha confuso i virus con i batteri. Sono cose, direbbe Antonio Pascale, che ti rovinano la giornata. Nel suo Scienza e sentimento (Einaudi 2008) se ne elencano parecchie, di cose che ti rovinano la giornata: le inserzioni pubblicitarie di salumi che dicono "Purezza sì chimica no"; gli elzeviri sui bei tempi andati; i "letterati puri" che commemorano il mondo succosamente naturale di ieri, al contrario di quello tristemente artificiale di oggi.
Non se ne può più: e non perché non ci sia da interrogarsi su come la chimica e la genetica abbiano trasformato il nostro modo di vivere e di alimentarci, ma per la povertà degli argomenti messi in campo. Siamo il paese europeo che investe di meno nella ricerca e nella formazione universitaria, l’ignoranza scientifica dilaga e c’è chi se ne vanta; eppure siamo sempre lì a paventare lo strapotere della techne a scapito della psiche. Quello che manca in molte riflessioni del genere, anche in quelle abbastanza sensate, è la comprensione di cosa siano davvero scienza e tecnologia: dei loro limiti e delle loro potenzialità; gli psicologi parlerebbero di mancanza di un principio di realtà. A ricostruire, con molto buon senso, alcuni elementi di realtà si dedica appunto Pascale, che fa lo scrittore ma ha una laurea in agraria, e si sente. Il suo libro è una puntigliosa rivendicazione dei meriti della scienza: documentatissima, pacata, ma anche molto agguerrita. È anche una singolare autobiografia intellettuale, la storia di come (muovendo, direbbe Darwin, "dalla convinzione opposta") Pascale si sia lasciato alle spalle l’irrazionalismo della prima giovinezza, e si sia armato di scrupolo e pazienza per attraversare la linea d’ombra della maturità. Maturità che in questo caso significa soprattutto saper leggere nei fenomeni naturali per quello che sono, senza filtri sentimentali e senza ricorrere a brutali semplificazioni.
L’hanno scritto in molti, e benissimo Michele Serra: più il mondo intorno a noi si fa complicato e più affiora un desiderio (reazionario, in senso letterale) di semplificazione. Titoli di giornali, comizi, trasmissioni radio e tv: dappertutto sembra che il sapere umano debba, e possa, essere tradotto in pillole di elementare semplicità (vedi De Bono). Invece il mondo è complesso (vedi Morin), ed è impossibile comprenderlo se non siamo disposti a fare gli sforzi necessari: ci sono risposte semplici per tutte le domande complicate, solo che, accidenti, sono sempre sbagliate. Particolarmente sbagliate sono quelle che giocano sulla contrapposizione fra naturale e perciò amico dell’essere umano, e artificiale, cioè gravido di rischi. In pagine di grande chiarezza, Pascale illustra quanta chimica e quanta biotecnologia ci siano nell’agricoltura, anche in quella biologica. Da quando i nostri antenati neolitici hanno cominciato a produrre il cibo, tutta la frutta che mangiamo è geneticamente modificata. Si possono commettere errori; a Pascale, però, sembra assurdo sostenere che si stava meglio quando si stava peggio, cioè quando si manipolavano (come oggi) i geni delle piante ma (al contrario di oggi) a casaccio, senza sapere cosa si stava combinando. Sembra anche a me.
Insomma, è insulso rimpiangere i pomodori rossi e sugosi, che peraltro non sono mai scomparsi. Ha senso invece ragionare su se e quanto i rischi della manipolazione, chimica e genetica, prevalgano sui rischi della non-manipolazione, che non sono zero come molti credono. "I chimici di fesserie ne hanno fatte", scrive Pascale, ma se vogliamo davvero combatterne i guasti, l’unica è imparare meglio la chimica, non buttarla a mare. La difesa dell’ambiente, o anche solo della tavola su cui mangiamo, è una cosa serissima e ora anche una prospettiva di profonda trasformazione del mondo produttivo. Ma si tratta di sviluppare tecnologie controllate e sostenibili, non di tornare ai radicchi raccolti a mano, anche solo perché quei radicchi non basterebbero per sfamarci tutti quanti. Proprio perché la posta in gioco è altissima, la partita va giocata con serietà. Il catastrofismo di certo ambientalismo radicale è forse l’immagine speculare del radicale disinteresse per l’ambiente che ostenta l’attuale governo del paese. Il punto giusto dove collocarci, dice Pascale, è invece in mezzo: nel punto da cui si può entrare nel dettaglio e affrontare i problemi per quello che sono.
Alla fine della lettura, resta soprattutto impresso il tono di una voce che narra, interroga e si interroga, con profonda onestà. Se qualcuno potrà dissentire da alcune delle tesi di questo libro, non si può non essere grati all’autore per il coraggio di porsi e porci interrogativi che tanti evitano, per pigrizia intellettuale o soltanto perché la moda è un’altra".
Ma ecco come in un articolo pubblicato sull’inserto La lettura del Corsera del 27-Nov-2011 lo stesso Pascale parla delle numerose Bufale Scientifiche italiane:
"La democrazia dovrebbe seguire uno schema elementare. Le opinioni vanno lette dai politici e poi tradotte in leggi. A opinioni approfondite corrisponderanno leggi serie; di contro, opinioni superficiali produrranno leggi modeste. La domanda è: in Italia, come sono raccontati dagli opinion leader alcuni fattori scientifici quali innovazione in agricoltura, piano energetico, ricerca sulle staminali? La risposta è spiacevole: molti degli opinion leader italiani non sono pratici di metodologia scientifica, per cui non sanno fornire un orientamento. Gli errori sono frequenti, le correzioni assenti. Per esempio, in campo energetico, spesso, si confonde la potenza installata con l’energia erogata: è successo quando si è parlato della Puglia come della prima regione in Italia per produzione di energia eolica e solare. Mettendo, però, sul piatto delle esportazioni energetiche pulite, anche l’energia prodotta dal carbone. In altri campi, come quello degli Ogm, dall’inesattezza si passa alla bufala. Mario Capanna (ex sessantottino / parlamentare), una volta, durante una puntata di «Uno Mattina», sostenne di aver visto un Ogm particolare: la fragola pesce, ormai nota leggenda metropolitana. Purtroppo queste dichiarazioni costruiscono un immaginario che premia la semplificazione culturale. È anche vero che i suddetti opinion leader hanno occupato un posto che gli scienziati non sembrano più reclamare. Perché l’impressione è che, a parte alcuni nomi noti, come Umberto Veronesi (oncologo) o Silvio Garattini (medico e farmacologo), la maggioranza degli scienziati abbia rinunciato a una sana, autorevole e costante divulgazione. Come mai? Gilberto Corbellini (storico della medicina) e Elena Cattaneo (farmacologa: ricerca sulle cellule staminali) avanzano un’ipotesi (sul sito «Scienza in rete»): «Va considerato il cronico asservimento di molte istituzioni scientifiche al mondo della politica, la quale spesso sceglie direttamente, e senza procedure di peer review, i responsabili degli enti scientifici e a chi dare i soldi per le ricerche".
Dunque, niente polemiche pubbliche, altrimenti mettiamo a rischio i finanziamenti. Oppure, altra ipotesi: si dicono tante di quelle sciocchezze, soprattutto sul web, che è impossibile stare dietro a tutto. Però questa latitanza è antimoderna, e sta diventando pericolosa. Si rischia di consegnare la discussione pubblica a comici e letterati apocalittici. Quando Carlo Petrini (gastronomo, slow food) giustificando sull’«Espresso» il suo no agli Ogm sostenne una tesi antiscientifica – e cioè che le piante mal sopportano le modifiche genetiche – non si trovò un biologo, un genetista che intervenisse per redarguire Petrini e ristabilire la verità scientifica: le piante si evolvono grazie alle continue modifiche genetiche. Come fare? Forse basterebbe organizzarsi. Costruire un autorevole sito, stile Royal Society, oppure un altro che semplicemente aggreghi vari blog scientifici: www.newclear.it , http://biotecnologiebastabugie.blogspot.com , www.galileo2001.it , www.scienzainrete.it , e ancora www.salmone.org e www.darwinweb.it . Questi siti spesso riportano documenti analitici e seri, passati in peer review – cioè rivisti pubblicamente e dunque autorevoli strumenti di discussione. Solo rivitalizzando il metodo scientifico si potrà tornare a essere un popolo di santi, poeti, navigatori. E, non ultimo, di scienziati".
Su La Lettura del Corsera del 19-Feb-2011 Pascale affronta il tema della "decrescita gentile" o "dell’abbondanza frugale" (Serge Latouche) oggi tanto caro a molti sociologi, ambientalisti, climatologi, nutrizionisti, conduttori televisivi, scrittori, intellettuali, politici, ecc.:
… nella trasmissione Che tempo che fa del 29 gennaio 2012, Daniel Pennac tenta un raccordo tra l’amletica frase di Bartleby lo scrivano (Herman Melville) — «Preferirei di no» — e l’attuale crisi finanziaria: «La crisi viene da un eccesso di desiderio ». Di fronte a questo accumulo di inutili desideri, meglio una posizione di radicale ma gentile disappunto: «Preferirei di no». Una decrescita gentile…
… sono un consumatore, se compro qualcosa non faccio sottili differenze tra merci e beni, e anzi tento di accrescere il mio personale Pil. Non è che questa parola sta diventando una classica parola ameba? Di quelle che significano tutto e niente. In realtà decrescere è facilissimo: basta autoridursi lo stipendio. Produzione e reddito sono infatti la stessa cosa. Meno reddito, minor produzione, consumi più bassi. Ci toccherà fare un gesto coraggioso: andare dal nostro editore e chiedere di meno. Purtroppo siamo soggetti a un’equazione matematica. L’ha scritta J. M. Keynes: Y (Pil) = C (consumi) + I (investimenti) + G (spesa pubblica) + X (differenza tra esportazioni e importazioni). Se vogliamo divertirci e scrivere un po’ di formule inverse, e se assumiamo che G e X rimangano costanti, il Pil finisce per essere determinato solo da consumi e investimenti: Y = C + I. Perciò, se si riducono i consumi, il reddito si ridurrà, a meno che non aumentino gli investimenti. Ma siccome gli investimenti attuali sono guidati dalle aspettative delle imprese sui futuri profitti, e quindi su quelli che saranno i consumi futuri, una riduzione generalizzata dei consumi finirà col produrre un ristagno degli investimenti. Risultato? Crisi economica e riduzione del reddito. La questione allora andrebbe formulata con un po’ di rigore matematico: quanto siamo disposti a perdere in termini di reddito per salvare il pianeta dall’eccesso di desiderio? C’è poi un’altra questione: consumare meno significa consumare meglio? Qualità e quantità vanno di solito di pari passo, perché la qualità costa e i poveri, sempre e dovunque, consumano non solo meno, ma anche peggio dei ricchi.
Ancora un dubbio: ma chi sono quelle persone che stabiliscono cosa possiamo e cosa non possiamo consumare? Cos’è il lusso? Ci sarà un comitato? Insomma oltre al quanto vogliamo decrescere, con quali strumenti intendiamo farlo? Se diamo uno sguardo globale (www.gapeminder.org), notiamo che benessere e reddito sono in crescita, aumenta la vita media e decresce la mortalità infantile. A questi cittadini del mondo, chi gli dice: dovete fermarvi? Oppure: «Preferirei di no»? Purtroppo, è vero, le risorse disponibili sono in diminuzione, è necessario produrre con meno input energetici: il segreto si chiama innovazione. Si può fare. L’abbiamo già fatto. Nel 1880 i nostri avi dovevano lavorare sei ore per avere un’ora di luce. Ora basta mezzo secondo. Non siamo i primi a vedere nero. Il reverendo Thomas Malthus, aveva previsto una pessima fine per il nostro pianeta: meno risorse, più popolazione, più lotta per dividersi la torta; all’epoca non eravamo nemmeno un miliardo. Negli Anni 60 il club di Roma (vedi Forrester) segnalò un problema analogo.
Per mantenere un buon livello di reddito, è necessario gestire i rifiuti e le scorie. Per farlo abbiamo solo una strada: ricerca e innovazione tecnologica. In fondo, e per esempio, una bottiglia di plastica meno spessa e più degradabile si può produrre se e solo se cresceranno (e non decresceranno) i contribuiti e la cultura dei chimici, dei fisici, dei matematici, dei microbiologici. Se crescerà la cultura e la competenza di contro decresceranno le dichiarazioni facili e le parole amebe.
Su La Lettura del Corsera del 20-Mag-2012 Pascale scrive l’articolo "Movimenti, è l’età dei Lulu". I comitati che si battono contro Tav, inceneritori, e campi ogm non sono più Nimby, perché l’interesse egoistico è mascherato dalla difesa della qualità della vita:
"… il concetto del Nimby (Not in May Back Yard, non nel mio giardino) è stato superato. Meglio parlare di Lulu (Locally Unwanted Land Use, uso localmente indesiderato del territorio). Una consistente letteratura sull’argomento evidenzia che solo una piccola parte degli oppositori a opere sgradite dichiarano che la contestazione è avanzata tenendo presente i vantaggi e gli svantaggi per il proprio giardino. Magari si vergognano a risultare egoisti, ma molti di loro fanno riferimento a interessi generali, per esempio: le grandi multinazionali e non le persone comuni avrebbero tratto beneficio dalla costruzione di un opera. Quindi: dal mio giardino a oltre il mio giardino. Cambia cioè il focus delle rivendicazioni, non solo la difesa del proprio territorio, ma tutela della qualità della vita… Si ha poca voglia di analizzare i fatti laicamente. Diventiamo pigri, e così rischiamo di rimanere seduti , comodamente nel nostro orticello, vero o virtuale o intellettuale che sia".
Nel libro "Pane e Pace. Il cibo, il progresso, il sapere nostalgico" Chiarelettere, Milano 2012, Antonio Pascale scrive:
"… in questi anni alcuni inquinamenti culturali, sapere nostalgico (eh! I vecchi tempi!!), cattiva informazione, visioni bucoliche e mistiche della terra, semplificazioni coatte, incompetenza diffusa hanno creato opinioni malsane nei cittadini. Si sa le opinioni vengono lette dai politici e tradotte in leggi. Buone opinioni, buone leggi e viceversa. Se si liberalizzasse il mercato, se si eliminassero la miriade di controlli inutili si darebbe la possibilità alla ricerca pubblica italiana di occuparsi (a basso costo) delle colture adatte ai nostri territori. Chi non innova muore e vale soprattutto per le colture agricole".
 Prova INVALSI per la classe quarta della scuola primaria anno scolastico 2004-2005, prova di matematica, semplici problemi con le operazioni, riconoscimento di figure piane e di solidi, piano cartesiano, calcolo mentale, operazioni inverse, statistica e rappresentazione tabulare di dati…
Prova INVALSI per la classe quarta della scuola primaria anno scolastico 2004-2005, prova di matematica, semplici problemi con le operazioni, riconoscimento di figure piane e di solidi, piano cartesiano, calcolo mentale, operazioni inverse, statistica e rappresentazione tabulare di dati… ![]() Scarica il test originale nel formato PDF
Scarica il test originale nel formato PDF 

 Salve colleghi, quando la didattica è impostata nel modo giusto può succedere che anche noi posiamo imparare dai ragazzi. Vi racconto in queste righe un episodio molto interessante. Qualche anno fa in una classe prima ho fatto fare una divisione tra polinomi del tipo (3x5 − 12x4 + 31x3 − 47x2 + 38x − 12) : (3x2 − 6x + 4) I ragazzi svolsero la divisione nel seguente modo…
Salve colleghi, quando la didattica è impostata nel modo giusto può succedere che anche noi posiamo imparare dai ragazzi. Vi racconto in queste righe un episodio molto interessante. Qualche anno fa in una classe prima ho fatto fare una divisione tra polinomi del tipo (3x5 − 12x4 + 31x3 − 47x2 + 38x − 12) : (3x2 − 6x + 4) I ragazzi svolsero la divisione nel seguente modo…  La storia narrata in questo romanzo è appassionante, ma anche sconcertante: i due protagonisti, Mattia e Alice – ragazzi decisamente problematici – vengono descritti con il loro disagio psichico, del quale non viene tralasciato alcun particolare. Le due vicende si dipanano in un intreccio continuo, dalla fanciullezza all’età adulta, fino a quando entrambi trovano la propria strada. La lettura è semplice: considerato che Mattia studia matematica all’università, alcune volte ci sono dei riferimenti a questa materia, ma la priorità è data alle difficoltà della crescita dei due protagonisti.
La storia narrata in questo romanzo è appassionante, ma anche sconcertante: i due protagonisti, Mattia e Alice – ragazzi decisamente problematici – vengono descritti con il loro disagio psichico, del quale non viene tralasciato alcun particolare. Le due vicende si dipanano in un intreccio continuo, dalla fanciullezza all’età adulta, fino a quando entrambi trovano la propria strada. La lettura è semplice: considerato che Mattia studia matematica all’università, alcune volte ci sono dei riferimenti a questa materia, ma la priorità è data alle difficoltà della crescita dei due protagonisti.  Problema 1.4. Un gruppo di esperti ha valutato i programmi economici di cinque formazioni politiche (Rossi, Azzurri, Bianchi, Neri e Arancioni). Tutti i programmi sono stati considerati da quattro prospettive diverse: Fisco, Crescita, Lavoro, Conti pubblici. Per ogni prospettiva è stata considerata l’efficacia e la realizzabilità del programma. Sia l’efficacia (capacità di ottenere risultati positivi) che la realizzabilità (effettiva possibilità di attuazione) sono state valutate qualitativamente con un giudizio ternario: alta, media, bassa. La tabella sottostante riporta per ogni formazione politica, e per ogni criterio considerato, la valutazione del programma, effettuata dagli esperti, in termini di efficacia e realizzabilità.
Problema 1.4. Un gruppo di esperti ha valutato i programmi economici di cinque formazioni politiche (Rossi, Azzurri, Bianchi, Neri e Arancioni). Tutti i programmi sono stati considerati da quattro prospettive diverse: Fisco, Crescita, Lavoro, Conti pubblici. Per ogni prospettiva è stata considerata l’efficacia e la realizzabilità del programma. Sia l’efficacia (capacità di ottenere risultati positivi) che la realizzabilità (effettiva possibilità di attuazione) sono state valutate qualitativamente con un giudizio ternario: alta, media, bassa. La tabella sottostante riporta per ogni formazione politica, e per ogni criterio considerato, la valutazione del programma, effettuata dagli esperti, in termini di efficacia e realizzabilità.  Scriptlandia è costituita da un piccolo arcipelago nel mondo virtuale 3D edMondo. È una realtà finalizzata a percorsi didattici sperimentali basati su applicazioni d’intelligenza artificiale che il MIUR e l’INDIRE conducono con docenti di alcune scuole. La classe III A Sistemi Informativi Aziendali sotto la mia guida di docente d’informatica ha avviato un percorso innovativo sull’uso delle tecnologie in classe. In questo spazio protetto, gli utenti autorizzati e registrati, accedono mediante avatar che possono camminare, volare e teletrasportarsi da una regione all’altra.
Scriptlandia è costituita da un piccolo arcipelago nel mondo virtuale 3D edMondo. È una realtà finalizzata a percorsi didattici sperimentali basati su applicazioni d’intelligenza artificiale che il MIUR e l’INDIRE conducono con docenti di alcune scuole. La classe III A Sistemi Informativi Aziendali sotto la mia guida di docente d’informatica ha avviato un percorso innovativo sull’uso delle tecnologie in classe. In questo spazio protetto, gli utenti autorizzati e registrati, accedono mediante avatar che possono camminare, volare e teletrasportarsi da una regione all’altra. Nel marzo del 1851 venne inaugurato un celebre esperimento pubblico che permise di dimostrare, prima volta nella storia, la rotazione della Terra attorno al proprio asse polare attraverso l’effetto della forza apparente di Coriolis senza ricorrere a osservazioni astronomiche. All’interno del Panthéon parigino venne sospeso alla cupola centrale un pendolo costituito da una sfera metallica dal peso di 28 chilogrammi mediante un cavo d’acciaio lungo 67 metri e 1,4 millimetri di diametro.
Nel marzo del 1851 venne inaugurato un celebre esperimento pubblico che permise di dimostrare, prima volta nella storia, la rotazione della Terra attorno al proprio asse polare attraverso l’effetto della forza apparente di Coriolis senza ricorrere a osservazioni astronomiche. All’interno del Panthéon parigino venne sospeso alla cupola centrale un pendolo costituito da una sfera metallica dal peso di 28 chilogrammi mediante un cavo d’acciaio lungo 67 metri e 1,4 millimetri di diametro. Nella straordinaria eredità scientifica lasciataci dagli antichi greci, ci sono tre celebri problemi “impossibili” da risolvere: La quadratura del cerchio, cioè la determinazione di un quadrato di area uguale a quella di un cerchio dato, la duplicazione del cubo, ovvero l’individuazione del lato del cubo di volume doppio rispetto a un cubo di lato assegnato, la trisezione dell’angolo, ossia la precisazione dell’angolo terza parte di un angolo fissato. La scoperta delle sezioni coniche, chiamate comunemente coniche, è un risultato “collaterale” della duplicazione del cubo…
Nella straordinaria eredità scientifica lasciataci dagli antichi greci, ci sono tre celebri problemi “impossibili” da risolvere: La quadratura del cerchio, cioè la determinazione di un quadrato di area uguale a quella di un cerchio dato, la duplicazione del cubo, ovvero l’individuazione del lato del cubo di volume doppio rispetto a un cubo di lato assegnato, la trisezione dell’angolo, ossia la precisazione dell’angolo terza parte di un angolo fissato. La scoperta delle sezioni coniche, chiamate comunemente coniche, è un risultato “collaterale” della duplicazione del cubo… Appuntamenti di filosofia e scienza presso l’Associazione Culturale ASIA di Bologna: 10 febbraio – 10 marzo – 14 aprile 2013. Con questi tre incontri prosegue la riflessione sul rapporto fra scienza e filosofia, già iniziata lo scorso anno con il corso “Dal tacchino di Russell ai conigli di Quine”. L’attenzione sarà posta su una delle più rivoluzionarie, e allo stesso tempo efficaci, teorie fisiche del XX secolo: la Meccanica quantistica.
Appuntamenti di filosofia e scienza presso l’Associazione Culturale ASIA di Bologna: 10 febbraio – 10 marzo – 14 aprile 2013. Con questi tre incontri prosegue la riflessione sul rapporto fra scienza e filosofia, già iniziata lo scorso anno con il corso “Dal tacchino di Russell ai conigli di Quine”. L’attenzione sarà posta su una delle più rivoluzionarie, e allo stesso tempo efficaci, teorie fisiche del XX secolo: la Meccanica quantistica.  Yet another excellent entrant in the Very Short Introductions series: Okasha, Lecturer in Philosophy at the University of York, gives a well-organized brief tour of the main topics in the Philosophy of Science. The key idea of the series of Very Short Introductions published by Oxford University Press since 1995 is to ask an expert to introduce readers to the essential notions of a subject, which is actually stimulating, since there is something very pleasant about holding in one’s hand a small book that can serve as a serious introduction to a very thoughtful topic.
Yet another excellent entrant in the Very Short Introductions series: Okasha, Lecturer in Philosophy at the University of York, gives a well-organized brief tour of the main topics in the Philosophy of Science. The key idea of the series of Very Short Introductions published by Oxford University Press since 1995 is to ask an expert to introduce readers to the essential notions of a subject, which is actually stimulating, since there is something very pleasant about holding in one’s hand a small book that can serve as a serious introduction to a very thoughtful topic. 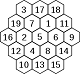 In un precedente articolo pubblicato su questa stessa rivista (N.13, agosto 2010) si era parlato dei quadrati magici. Questo articolo intende riprendere l’argomento, trattando questa volta figure diverse dal quadrato che presentano analoghe caratteristiche “magiche”, ossia disposizioni di numeri interi in forma geometrica tali che la somma rimanga sempre costante lungo tutti gli allineamenti possibili, che dipendono dalle caratteristiche delle figure stesse. In particolare, vengono esaminate diverse tipologie di esagoni magici e stelle magiche.
In un precedente articolo pubblicato su questa stessa rivista (N.13, agosto 2010) si era parlato dei quadrati magici. Questo articolo intende riprendere l’argomento, trattando questa volta figure diverse dal quadrato che presentano analoghe caratteristiche “magiche”, ossia disposizioni di numeri interi in forma geometrica tali che la somma rimanga sempre costante lungo tutti gli allineamenti possibili, che dipendono dalle caratteristiche delle figure stesse. In particolare, vengono esaminate diverse tipologie di esagoni magici e stelle magiche. In questa breve dispensa ho semplicemente trascritto in LATEX il contenuto di questa discussione:
In questa breve dispensa ho semplicemente trascritto in LATEX il contenuto di questa discussione:  Nell’approntare un budget di costo o nel programmare nel tempo il carico delle risorse, è necessario, a partire dai valori totali stimati, fare delle mensilizzazioni che tengano conto dei transitori iniziali e finali, dei periodi normali, delle percentuali di abbattimento di specifici periodi e della maggior produttività che può essere ottenuta in altri momenti.
Nell’approntare un budget di costo o nel programmare nel tempo il carico delle risorse, è necessario, a partire dai valori totali stimati, fare delle mensilizzazioni che tengano conto dei transitori iniziali e finali, dei periodi normali, delle percentuali di abbattimento di specifici periodi e della maggior produttività che può essere ottenuta in altri momenti. 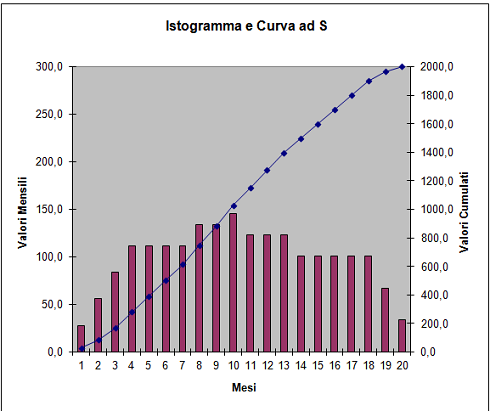
 E’ dato un quadrato ABCD, di lato AB=a. Il vertice A coincide con l’origine di un riferimento cartesiano Axy e i vertici B e D cadono rispettivamente sugli assi x e y del riferimento. Facciamo traslare in modo uniforme il segmento DC fino a farlo coincidere con il lato AB e nello stesso tempo facciamo ruotare di moto uniforme il lato AD sino a farlo coincidere con lo stesso lato AB. Trovare l’equazione del luogo geometrico dei punti di intersezione dei due segmenti durante il loro movimento. Esso è detto trisettrice di Ippia.
E’ dato un quadrato ABCD, di lato AB=a. Il vertice A coincide con l’origine di un riferimento cartesiano Axy e i vertici B e D cadono rispettivamente sugli assi x e y del riferimento. Facciamo traslare in modo uniforme il segmento DC fino a farlo coincidere con il lato AB e nello stesso tempo facciamo ruotare di moto uniforme il lato AD sino a farlo coincidere con lo stesso lato AB. Trovare l’equazione del luogo geometrico dei punti di intersezione dei due segmenti durante il loro movimento. Esso è detto trisettrice di Ippia.  Il nipote ritiene Petros Papachristos, fratello di suo padre, la pecora nera della famiglia: di lui non conosce altro che le critiche del padre, nonostante lo zio non dia l’impressione di meritarsele, visto che è cortese, rispettoso e gentile e, a Ekali, conduce una vita semplice, dedicandosi al giardinaggio e agli scacchi. A quattordici anni, il mistero che circonda lo zio diventa per il nipote una vera ossessione. La lettera della Società Matematica Ellenica offre al nipote una buona occasione per saperne di più: con la scusa della riunione settimanale dei boy-scout, raggiunge lo zio a Ekali, ma non ottiene nulla. Il padre è infuriato, ma poi decide di soddisfare la sua curiosità: questo stravagante personaggio ha mostrato fin dalla fanciullezza un’eccezionale predisposizione per la matematica.
Il nipote ritiene Petros Papachristos, fratello di suo padre, la pecora nera della famiglia: di lui non conosce altro che le critiche del padre, nonostante lo zio non dia l’impressione di meritarsele, visto che è cortese, rispettoso e gentile e, a Ekali, conduce una vita semplice, dedicandosi al giardinaggio e agli scacchi. A quattordici anni, il mistero che circonda lo zio diventa per il nipote una vera ossessione. La lettera della Società Matematica Ellenica offre al nipote una buona occasione per saperne di più: con la scusa della riunione settimanale dei boy-scout, raggiunge lo zio a Ekali, ma non ottiene nulla. Il padre è infuriato, ma poi decide di soddisfare la sua curiosità: questo stravagante personaggio ha mostrato fin dalla fanciullezza un’eccezionale predisposizione per la matematica.  Questo articolo è stato liberamente tratto, ed illustrato, da un vecchio intervento di Martin Gardner sulle pagine di Scientific American. Viene presa in esame la possibilità di saturare il piano, cioè ricoprirlo senza lasciare spazi vuoti o sovrapposizioni, usando dei poligoni. Ma si badi bene, poligoni tutti dello stesso tipo, altrimenti il problema offre infinite soluzioni, e diviene banale.
Questo articolo è stato liberamente tratto, ed illustrato, da un vecchio intervento di Martin Gardner sulle pagine di Scientific American. Viene presa in esame la possibilità di saturare il piano, cioè ricoprirlo senza lasciare spazi vuoti o sovrapposizioni, usando dei poligoni. Ma si badi bene, poligoni tutti dello stesso tipo, altrimenti il problema offre infinite soluzioni, e diviene banale. 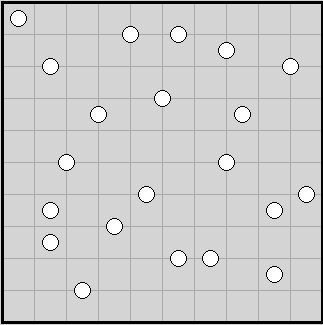
 Physion è un simulatore di fisica con il quale puoi costruire oggetti di ogni forma e dimensione, applicare forze, modificare la gravità, inventare scene e mondi senza limiti all’immaginazione, le uniche leggi a cui obbedisce sono quelle della fisica. In altre parole puoi “sperimentare” le leggi fisiche in un modo inventato da te. Un programma divertente, che stimola la fantasia e l’intelligenza di bambini e adulti, e abitua a pensare in termini di leggi fisiche. Questo manuale, scritto da Sergio Balsimelli, di cui Matematicamente.it ha già pubblicato il manuale di Geogebra, è strutturato in modo pratico, un breve cenno agli strumenti di base e 100 esercizi con illustrazione ed elementi di programmazione.
Physion è un simulatore di fisica con il quale puoi costruire oggetti di ogni forma e dimensione, applicare forze, modificare la gravità, inventare scene e mondi senza limiti all’immaginazione, le uniche leggi a cui obbedisce sono quelle della fisica. In altre parole puoi “sperimentare” le leggi fisiche in un modo inventato da te. Un programma divertente, che stimola la fantasia e l’intelligenza di bambini e adulti, e abitua a pensare in termini di leggi fisiche. Questo manuale, scritto da Sergio Balsimelli, di cui Matematicamente.it ha già pubblicato il manuale di Geogebra, è strutturato in modo pratico, un breve cenno agli strumenti di base e 100 esercizi con illustrazione ed elementi di programmazione.  Questo testo si rivolge sia agli studenti della scuola secondaria superiore che ai loro docenti. Gli studenti troveranno un’efficace presentazione dei diversi linguaggi dell’algebra e della geometria e delle corrispondenze che si stabiliscono fra di essi, in particolare nell’ambito dell’Algebra lineare. Per i docenti il testo rappresenta un utile supporto all’insegnamento di vecchie e nuove parti della geometria, che consente loro anche di affrontare alcune tematiche previste dalle recenti Indicazioni Nazionali.
Questo testo si rivolge sia agli studenti della scuola secondaria superiore che ai loro docenti. Gli studenti troveranno un’efficace presentazione dei diversi linguaggi dell’algebra e della geometria e delle corrispondenze che si stabiliscono fra di essi, in particolare nell’ambito dell’Algebra lineare. Per i docenti il testo rappresenta un utile supporto all’insegnamento di vecchie e nuove parti della geometria, che consente loro anche di affrontare alcune tematiche previste dalle recenti Indicazioni Nazionali.  I testi scolastici di fisica possono apparire ostili e minacciosi; l’autore si è proposto con questo libro di estrarre la bellezza dei principi della fisica per proporli in un modo nuovo e originale che si serve della suspense del giallo, raccontando sette storie intriganti di un commissario e un professore di fisica. La tensione investigativa, la quotidianità, le digressioni su piccoli e grandi temi del vivere, rendono i sette gialli un’occasione di piacevole apprendimento, libero da obblighi scolastici e da schemi rigidi di studio.
I testi scolastici di fisica possono apparire ostili e minacciosi; l’autore si è proposto con questo libro di estrarre la bellezza dei principi della fisica per proporli in un modo nuovo e originale che si serve della suspense del giallo, raccontando sette storie intriganti di un commissario e un professore di fisica. La tensione investigativa, la quotidianità, le digressioni su piccoli e grandi temi del vivere, rendono i sette gialli un’occasione di piacevole apprendimento, libero da obblighi scolastici e da schemi rigidi di studio.  In questo numero presentiamo due articoli di didattica relativi ai teoremi di Pitagora ed Euclide, gli autori mettono in evidenza alcuni aspetti a volta trascurati nell’insegnamento. Giovanni Lucca ci presenta uno studio su lunule e lenti all’interno di cerchi. Continua il lavoro di Bruno Sanchini sulla descrizione analitica di alcuni gruppi di segmenti. Alfino Grasso mostra come la simmetria ci aiuti nella risoluzione di problemi semplici e complessi. Infine, la secolare questione dell’attraversamento del fiume e un po’ di libri interessanti da leggere.
In questo numero presentiamo due articoli di didattica relativi ai teoremi di Pitagora ed Euclide, gli autori mettono in evidenza alcuni aspetti a volta trascurati nell’insegnamento. Giovanni Lucca ci presenta uno studio su lunule e lenti all’interno di cerchi. Continua il lavoro di Bruno Sanchini sulla descrizione analitica di alcuni gruppi di segmenti. Alfino Grasso mostra come la simmetria ci aiuti nella risoluzione di problemi semplici e complessi. Infine, la secolare questione dell’attraversamento del fiume e un po’ di libri interessanti da leggere.  Bisognerebbe cominciare intanto a sfatare alcuni miti: nelle colture biologiche non si usano agrofarmaci. Sarebbe bello, ma gli insetti purtroppo non sanno leggere, non dicono: questo campo è biologico, attacchiamo quello convenzionale. Si usano allora altri agrofarmaci, detti tradizionali. Sono migliori di quelli moderni? Meno invasivi? Purtroppo no. E’ il caso del rame, metallo pesante che può, in dosi elevate, danneggiare la microfauna o anche, il rotenone. Provate a cercarlo sui portali di lavori scientifici: gli studi sugli effetti di questo principio chimico sono inquietanti". (Antonio Pascale da: "La sinistra bio-illogica", La Lettura – Corsera,11 marzo 2012
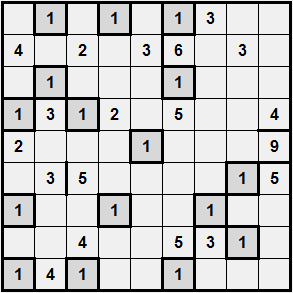
Bisognerebbe cominciare intanto a sfatare alcuni miti: nelle colture biologiche non si usano agrofarmaci. Sarebbe bello, ma gli insetti purtroppo non sanno leggere, non dicono: questo campo è biologico, attacchiamo quello convenzionale. Si usano allora altri agrofarmaci, detti tradizionali. Sono migliori di quelli moderni? Meno invasivi? Purtroppo no. E’ il caso del rame, metallo pesante che può, in dosi elevate, danneggiare la microfauna o anche, il rotenone. Provate a cercarlo sui portali di lavori scientifici: gli studi sugli effetti di questo principio chimico sono inquietanti". (Antonio Pascale da: "La sinistra bio-illogica", La Lettura – Corsera,11 marzo 2012  Regole del gioco. La griglia è divisa in caselle, alcune delle quali già numerate, ed altre vuote. 1) Bisogna riempire il resto della griglia, in modo che ogni casella contenga un numero; 2) più caselle adiacenti con lo stesso numero formano una "regione", e due "regioni" adiacenti non possono contenere lo stesso numero; 3) Le "regioni" devono avere un’area pari al numero che contiene ciascuna delle loro caselle.
Regole del gioco. La griglia è divisa in caselle, alcune delle quali già numerate, ed altre vuote. 1) Bisogna riempire il resto della griglia, in modo che ogni casella contenga un numero; 2) più caselle adiacenti con lo stesso numero formano una "regione", e due "regioni" adiacenti non possono contenere lo stesso numero; 3) Le "regioni" devono avere un’area pari al numero che contiene ciascuna delle loro caselle.